物理奥赛培训教程-相对论基础讲义

z v ux u x = 1 u v / c2 x u y u = y 2 (1 u xv / c ) uz u z = 2 (1 u xv / c )
洛伦兹速度变换满足光速不变性的假设。
推导过程：
4．由洛伦兹变换讨论相对论时空
h h t = = 1 (v / c ) 2 v v
到达地面的子数与产生的子数的百分比
地球
到达地面的子数与产生的子数的百分比
N t h 1 (v / c ) = et = exp[ ] N 0 v 0
2
N t h 1 (v / c ) 2 ] = et 0 = exp[ N 0 v 0
ct A vt A = l
A
c l0 2l 0 v v c l 2l c
c l0
B
S
v l B A
tA =
l cv
ctB vtB = l
l tB = cv
t A tB
结论：
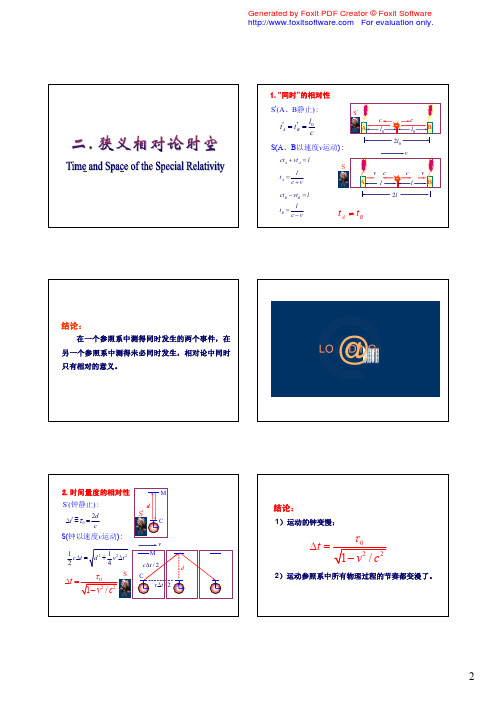
在一个参照系中测得同时发生的两个事件，在 另一个参照系中测得未必同时发生，相对论中同时 只有相对的意义。
2.时间量度的相对性
v
S 宇航员 l0
M
题2 尽快知道有无外星人的“好办法”： 某外星 M离地球 2万光年（即光从地球传播到该外 星需 2 万年时间），某宇航员以速度 v从地球出发 驶向该外星。假设宇航员估计自己还能活 100年， 问：该宇航员是否可能在有生之年抵达外星？若 可能，其速度v至少为多大？
t =
l0 2 ´104 c = v v
vr
t1
L/2
v
t1
L/2
张
李
王
( =
1 1 vr2 / c 2
t 2
L/2
=
1 2 ) 1 2
vr
李测得，张第 n次拍手的时间： tn L tn = = 2( n 1) 1 2 2v
v
t n
L/2
tn
L/2
李
v
张
王
张测得，张第二次拍手(王第 一次拍手)的时间：
4
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
（2） 王测得，张的速度大小 2v vr = 1 2 王第一次拍手的时间： t1 t1 = = t1 1 vr2 / c 2
M d
S(钟静止) :
2d t 0 = c
S
结论：
C
1）运动的钟变慢：
S(钟以速度v运动) :
v
1 1 ct = d 2 v 2t 2 2 4
M
c t / 2
t =
d
0
1 v2 / c 2
t =
0
1 v / c
2 2
S
C
2）运动参照系中所有物理过程的节奏都变漫了。
（1） 李测得：张第一次拍手的时间： L t1 = 2v
v
t1
L/2
t1
v
L/2
李 王
张
设张测得他第一次拍手的时间为 t1, 则 t1 v t1 = ( = ) c 1 2
t1 = t1 1 2 =
L 1 2 2v
李测得，张第一次拍手时，张的时钟的读数也为t1, 但此时李自己的时钟读数为 t1。
S : P( x , y , z , t ) S :P( x , y , z , t )
2.洛伦兹坐标变换
S: P( x , y , z , t ) S :P( x , y , z , t )
x = ( x vt ) y = y z = z t = (t vx / c 2 )
v
t1
张第 n次拍手时，张、王同学之间的距离：
= t1 = 2 t1 t2
张 以此类推，张测得，张第 n次 拍手的时间： L = 2( n 1) t1 = 2( n1) 1 2 tn 2v
L/2
李 王
dn = tn 2v = 2( n1) L = (
以宇航员为参照系 (S)。 外星 M与地球间的距离：
v S
地球
v
S 宇航员 l M
题 3 子在相对自身静止的惯性参考系中的平均寿命 宇宙射线与大气在离地面 h = 1.24 ´10 4 m 0 2.0 ´ 10 6 s 。 高空某处发生核反应产生一批子， 以 v = 0.99c 的速度向 下运动并衰变。根据放射性衰变定律，相对给定惯性参 考系，若 t = 0 时刻的粒子数为 N(0)，则 t 时刻剩余的粒 子数为 N t = N 0 e t ，式中 为相对该惯性系粒子的平 均寿命。试估算能到达地面的子数与产生的子数的百 分比。不考虑重力和地磁场对子运动的影响。
结论：
1）运动的尺变短：
S(尺以速度v运动) :
l ct1 vt1 = l t1 = c v l ct2 vt 2 = l t2 = cv S 2l l
l = l0 1 v 2 / c 2
2）运动参照系中所有物体沿运动方向的尺度缩短了。
t =
t =
c 1 v 2 / c2 t
)
S : (u x , u y , u z ) S : (u x , u y , uz )
z O O x v x
1 v2 / c2
——洛伦兹坐标变换
ux v = u x 1 ux v / c 2 uy u y = (1 u x v / c2 ) uz = u z (1 u x v / c2 )
v
c
1 2.5 ´ 105
0.99988c
解1：以地面为参照系 (S)
子到达地面的时间
子 S
解2：以子为参照系(S)
子产生处到地面的距离
子 S
v
h v 子平均寿命 t=
h
S 地球
h = h 1 (v / c) 2
子到达地面的时间
h
vS=源自01 (v / c ) 2
1 v / c
2 2
l

l = l0 1 v 2 / c 2
解： （1） 以儿子为参照系(S)：
v
S
S
2
t =
题 1 父与子：有一对父子，父亲 30 岁，儿子 10 岁那年， 父亲去作太空旅行，速度为 0.99c 。 （1）在地面上的儿子看来，他 50 岁时，其天上的父亲 为几岁（设为 x 岁）？ （2）在天上的父亲看来，他 x 岁时，其地面上的儿子为 几岁 ?
2
y S
) ( x1, t1)， ( x1, t 2
t1 t2
O
考虑到横向长度不变，得：
3．洛伦兹速度变换
y S
y S P
x = ( x vt ) y = y z = z 2 t = (t vx / c )
( 1
x = ( x vt ) y = y z = z 2 t = (t vx / c )
x = ( x vt ) y = y z = z 2 t = (t vx / c )
S : (u x , u y , u z ) S : (u x , u y , uz )
u x =
u y =
4.1 时间量度的相对性
vx1 /c ) t1 = (t1
O
O
v
x
x = vt x 1 v 2 / c 2
zz y S y S P
x = x 1 v 2 / c 2 vt
y S y S P
x vt x = 1 v2 / c2 2 t = t vx / c 2 1 v / c2
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
1.“同时”的相对性
S(A、B静止) :
S
l0 t A = tB = c
S(A、B以速度v运动) :
y S y S P
O z z
O
x v
x O z z
vt O x
x 1 v2 / c2
vt x x O z O
x 1 v / c v
2 2
x
x
x
v
z
5
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
l = l0 1 v 2 / c 2 = 2 ´104 c 1 v 2 / c 2
宇航员抵达外星所需时间：
t =
l c = 2 ´104 ´ 1 v 2 / c 2 v v
c 100 2 ´10 ´ 1 v 2 / c 2 v
4
为使宇航员在有生之年抵达外星，必须
0 t
= exp(
1.24 ´104 1 0.992 ) 5.0% 0.99 ´ 3.0 ´ 108 ´ 2.0 ´106
= exp(
1.24 ´ 104 1 0.992 ) 5.0% 0.99 ´ 3.0 ´ 108 ´ 2.0 ´ 106
解：
题 4 相对于站立在地面的李同学， 张同学以相对论速率 v 向 右运动，张同学以同样速率向左运动。当张、李、王相遇 时，三位同学各自把自己时钟的读数调整到零。在地面参 照系中观察，当张、王同学之间的距离为 L 时，张同学拍一 下手。 （1）求张同学拍手时其随身携带的时钟的读数。 （2）从王同学自身静止的参照系看，在张同学拍手这一事 件发生的深刻，王同学也拍一下手。从张同学自身静止的 参照系看，在王同学拍手这一事件发生的深刻，张同学第 二次拍一下手。照此持续下去。求在地面参照系中观察， 当张同学第 n 次拍手时，张、王同学之间的距离。