The probability for wave packet to remain in a disordered cavity
最近鲁棒优化进展Recent Advances in Robust Optimization and Robustness An Overview

Recent Advances in Robust Optimization and Robustness:An OverviewVirginie Gabrel∗and C´e cile Murat†and Aur´e lie Thiele‡July2012AbstractThis paper provides an overview of developments in robust optimization and robustness published in the aca-demic literature over the pastfive years.1IntroductionThis review focuses on papers identified by Web of Science as having been published since2007(included),be-longing to the area of Operations Research and Management Science,and having‘robust’and‘optimization’in their title.There were exactly100such papers as of June20,2012.We have completed this list by considering 726works indexed by Web of Science that had either robustness(for80of them)or robust(for646)in their title and belonged to the Operations Research and Management Science topic area.We also identified34PhD disserta-tions dated from the lastfive years with‘robust’in their title and belonging to the areas of operations research or management.Among those we have chosen to focus on the works with a primary focus on management science rather than system design or optimal control,which are broadfields that would deserve a review paper of their own, and papers that could be of interest to a large segment of the robust optimization research community.We feel it is important to include PhD dissertations to identify these recent graduates as the new generation trained in robust optimization and robustness analysis,whether they have remained in academia or joined industry.We have also added a few not-yet-published preprints to capture ongoing research efforts.While many additional works would have deserved inclusion,we feel that the works selected give an informative and comprehensive view of the state of robustness and robust optimization to date in the context of operations research and management science.∗Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France gabrel@lamsade.dauphine.fr Corresponding author†Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France mu-rat@lamsade.dauphine.fr‡Lehigh University,Industrial and Systems Engineering Department,200W Packer Ave Bethlehem PA18015,USA aure-lie.thiele@2Theory of Robust Optimization and Robustness2.1Definitions and BasicsThe term“robust optimization”has come to encompass several approaches to protecting the decision-maker against parameter ambiguity and stochastic uncertainty.At a high level,the manager must determine what it means for him to have a robust solution:is it a solution whose feasibility must be guaranteed for any realization of the uncertain parameters?or whose objective value must be guaranteed?or whose distance to optimality must be guaranteed? The main paradigm relies on worst-case analysis:a solution is evaluated using the realization of the uncertainty that is most unfavorable.The way to compute the worst case is also open to debate:should it use afinite number of scenarios,such as historical data,or continuous,convex uncertainty sets,such as polyhedra or ellipsoids?The answers to these questions will determine the formulation and the type of the robust counterpart.Issues of over-conservatism are paramount in robust optimization,where the uncertain parameter set over which the worst case is computed should be chosen to achieve a trade-off between system performance and protection against uncertainty,i.e.,neither too small nor too large.2.2Static Robust OptimizationIn this framework,the manager must take a decision in the presence of uncertainty and no recourse action will be possible once uncertainty has been realized.It is then necessary to distinguish between two types of uncertainty: uncertainty on the feasibility of the solution and uncertainty on its objective value.Indeed,the decision maker generally has different attitudes with respect to infeasibility and sub-optimality,which justifies analyzing these two settings separately.2.2.1Uncertainty on feasibilityWhen uncertainty affects the feasibility of a solution,robust optimization seeks to obtain a solution that will be feasible for any realization taken by the unknown coefficients;however,complete protection from adverse realiza-tions often comes at the expense of a severe deterioration in the objective.This extreme approach can be justified in some engineering applications of robustness,such as robust control theory,but is less advisable in operations research,where adverse events such as low customer demand do not produce the high-profile repercussions that engineering failures–such as a doomed satellite launch or a destroyed unmanned robot–can have.To make the robust methodology appealing to business practitioners,robust optimization thus focuses on obtaining a solution that will be feasible for any realization taken by the unknown coefficients within a smaller,“realistic”set,called the uncertainty set,which is centered around the nominal values of the uncertain parameters.The goal becomes to optimize the objective,over the set of solutions that are feasible for all coefficient values in the uncertainty set.The specific choice of the set plays an important role in ensuring computational tractability of the robust problem and limiting deterioration of the objective at optimality,and must be thought through carefully by the decision maker.A large branch of robust optimization focuses on worst-case optimization over a convex uncertainty set.The reader is referred to Bertsimas et al.(2011a)and Ben-Tal and Nemirovski(2008)for comprehensive surveys of robust optimization and to Ben-Tal et al.(2009)for a book treatment of the topic.2.2.2Uncertainty on objective valueWhen uncertainty affects the optimality of a solution,robust optimization seeks to obtain a solution that performs well for any realization taken by the unknown coefficients.While a common criterion is to optimize the worst-case objective,some studies have investigated other robustness measures.Roy(2010)proposes a new robustness criterion that holds great appeal for the manager due to its simplicity of use and practical relevance.This framework,called bw-robustness,allows the decision-maker to identify a solution which guarantees an objective value,in a maximization problem,of at least w in all scenarios,and maximizes the probability of reaching a target value of b(b>w).Gabrel et al.(2011)extend this criterion from afinite set of scenarios to the case of an uncertainty set modeled using intervals.Kalai et al.(2012)suggest another criterion called lexicographicα-robustness,also defined over afinite set of scenarios for the uncertain parameters,which mitigates the primary role of the worst-case scenario in defining the solution.Thiele(2010)discusses over-conservatism in robust linear optimization with cost uncertainty.Gancarova and Todd(2012)studies the loss in objective value when an inaccurate objective is optimized instead of the true one, and shows that on average this loss is very small,for an arbitrary compact feasible region.In combinatorial optimization,Morrison(2010)develops a framework of robustness based on persistence(of decisions)using the Dempster-Shafer theory as an evidence of robustness and applies it to portfolio tracking and sensor placement.2.2.3DualitySince duality has been shown to play a key role in the tractability of robust optimization(see for instance Bertsimas et al.(2011a)),it is natural to ask how duality and robust optimization are connected.Beck and Ben-Tal(2009) shows that primal worst is equal to dual best.The relationship between robustness and duality is also explored in Gabrel and Murat(2010)when the right-hand sides of the constraints are uncertain and the uncertainty sets are represented using intervals,with a focus on establishing the relationships between linear programs with uncertain right hand sides and linear programs with uncertain objective coefficients using duality theory.This avenue of research is further explored in Gabrel et al.(2010)and Remli(2011).2.3Multi-Stage Decision-MakingMost early work on robust optimization focused on static decision-making:the manager decided at once of the values taken by all decision variables and,if the problem allowed for multiple decision stages as uncertainty was realized,the stages were incorporated by re-solving the multi-stage problem as time went by and implementing only the decisions related to the current stage.As thefield of static robust optimization matured,incorporating–ina tractable manner–the information revealed over time directly into the modeling framework became a major area of research.2.3.1Optimal and Approximate PoliciesA work going in that direction is Bertsimas et al.(2010a),which establishes the optimality of policies affine in the uncertainty for one-dimensional robust optimization problems with convex state costs and linear control costs.Chen et al.(2007)also suggests a tractable approximation for a class of multistage chance-constrained linear program-ming problems,which converts the original formulation into a second-order cone programming problem.Chen and Zhang(2009)propose an extension of the Affinely Adjustable Robust Counterpart framework described in Ben-Tal et al.(2009)and argue that its potential is well beyond what has been in the literature so far.2.3.2Two stagesBecause of the difficulty in incorporating multiple stages in robust optimization,many theoretical works have focused on two stages.Regarding two-stage problems,Thiele et al.(2009)presents a cutting-plane method based on Kelley’s algorithm for solving convex adjustable robust optimization problems,while Terry(2009)provides in addition preliminary results on the conditioning of a robust linear program and of an equivalent second-order cone program.Assavapokee et al.(2008a)and Assavapokee et al.(2008b)develop tractable algorithms in the case of robust two-stage problems where the worst-case regret is minimized,in the case of interval-based uncertainty and scenario-based uncertainty,respectively,while Minoux(2011)provides complexity results for the two-stage robust linear problem with right-hand-side uncertainty.2.4Connection with Stochastic OptimizationAn early stream in robust optimization modeled stochastic variables as uncertain parameters belonging to a known uncertainty set,to which robust optimization techniques were then applied.An advantage of this method was to yield approaches to decision-making under uncertainty that were of a level of complexity similar to that of their deterministic counterparts,and did not suffer from the curse of dimensionality that afflicts stochastic and dynamic programming.Researchers are now making renewed efforts to connect the robust optimization and stochastic opti-mization paradigms,for instance quantifying the performance of the robust optimization solution in the stochastic world.The topic of robust optimization in the context of uncertain probability distributions,i.e.,in the stochastic framework itself,is also being revisited.2.4.1Bridging the Robust and Stochastic WorldsBertsimas and Goyal(2010)investigates the performance of static robust solutions in two-stage stochastic and adaptive optimization problems.The authors show that static robust solutions are good-quality solutions to the adaptive problem under a broad set of assumptions.They provide bounds on the ratio of the cost of the optimal static robust solution to the optimal expected cost in the stochastic problem,called the stochasticity gap,and onthe ratio of the cost of the optimal static robust solution to the optimal cost in the two-stage adaptable problem, called the adaptability gap.Chen et al.(2007),mentioned earlier,also provides a robust optimization perspective to stochastic programming.Bertsimas et al.(2011a)investigates the role of geometric properties of uncertainty sets, such as symmetry,in the power offinite adaptability in multistage stochastic and adaptive optimization.Duzgun(2012)bridges descriptions of uncertainty based on stochastic and robust optimization by considering multiple ranges for each uncertain parameter and setting the maximum number of parameters that can fall within each range.The corresponding optimization problem can be reformulated in a tractable manner using the total unimodularity of the feasible set and allows for afiner description of uncertainty while preserving tractability.It also studies the formulations that arise in robust binary optimization with uncertain objective coefficients using the Bernstein approximation to chance constraints described in Ben-Tal et al.(2009),and shows that the robust optimization problems are deterministic problems for modified values of the coefficients.While many results bridging the robust and stochastic worlds focus on giving probabilistic guarantees for the solutions generated by the robust optimization models,Manuja(2008)proposes a formulation for robust linear programming problems that allows the decision-maker to control both the probability and the expected value of constraint violation.Bandi and Bertsimas(2012)propose a new approach to analyze stochastic systems based on robust optimiza-tion.The key idea is to replace the Kolmogorov axioms and the concept of random variables as primitives of probability theory,with uncertainty sets that are derived from some of the asymptotic implications of probability theory like the central limit theorem.The authors show that the performance analysis questions become highly structured optimization problems for which there exist efficient algorithms that are capable of solving problems in high dimensions.They also demonstrate that the proposed approach achieves computationally tractable methods for(a)analyzing queueing networks,(b)designing multi-item,multi-bidder auctions with budget constraints,and (c)pricing multi-dimensional options.2.4.2Distributionally Robust OptimizationBen-Tal et al.(2010)considers the optimization of a worst-case expected-value criterion,where the worst case is computed over all probability distributions within a set.The contribution of the work is to define a notion of robustness that allows for different guarantees for different subsets of probability measures.The concept of distributional robustness is also explored in Goh and Sim(2010),with an emphasis on linear and piecewise-linear decision rules to reformulate the original problem in aflexible manner using expected-value terms.Xu et al.(2012) also investigates probabilistic interpretations of robust optimization.A related area of study is worst-case optimization with partial information on the moments of distributions.In particular,Popescu(2007)analyzes robust solutions to a certain class of stochastic optimization problems,using mean-covariance information about the distributions underlying the uncertain parameters.The author connects the problem for a broad class of objective functions to a univariate mean-variance robust objective and,subsequently, to a(deterministic)parametric quadratic programming problem.The reader is referred to Doan(2010)for a moment-based uncertainty model for stochastic optimization prob-lems,which addresses the ambiguity of probability distributions of random parameters with a minimax decision rule,and a comparison with data-driven approaches.Distributionally robust optimization in the context of data-driven problems is the focus of Delage(2009),which uses observed data to define a”well structured”set of dis-tributions that is guaranteed with high probability to contain the distribution from which the samples were drawn. Zymler et al.(2012a)develop tractable semidefinite programming(SDP)based approximations for distributionally robust individual and joint chance constraints,assuming that only thefirst-and second-order moments as well as the support of the uncertain parameters are given.Becker(2011)studies the distributionally robust optimization problem with known mean,covariance and support and develops a decomposition method for this family of prob-lems which recursively derives sub-policies along projected dimensions of uncertainty while providing a sequence of bounds on the value of the derived policy.Robust linear optimization using distributional information is further studied in Kang(2008).Further,Delage and Ye(2010)investigates distributional robustness with moment uncertainty.Specifically,uncertainty affects the problem both in terms of the distribution and of its moments.The authors show that the resulting problems can be solved efficiently and prove that the solutions exhibit,with high probability,best worst-case performance over a set of distributions.Bertsimas et al.(2010)proposes a semidefinite optimization model to address minimax two-stage stochastic linear problems with risk aversion,when the distribution of the second-stage random variables belongs to a set of multivariate distributions with knownfirst and second moments.The minimax solutions provide a natural distribu-tion to stress-test stochastic optimization problems under distributional ambiguity.Cromvik and Patriksson(2010a) show that,under certain assumptions,global optima and stationary solutions of stochastic mathematical programs with equilibrium constraints are robust with respect to changes in the underlying probability distribution.Works such as Zhu and Fukushima(2009)and Zymler(2010)also study distributional robustness in the context of specific applications,such as portfolio management.2.5Connection with Risk TheoryBertsimas and Brown(2009)describe how to connect uncertainty sets in robust linear optimization to coherent risk measures,an example of which is Conditional Value-at-Risk.In particular,the authors show the link between polyhedral uncertainty sets of a special structure and a subclass of coherent risk measures called distortion risk measures.Independently,Chen et al.(2007)present an approach for constructing uncertainty sets for robust opti-mization using new deviation measures that capture the asymmetry of the distributions.These deviation measures lead to improved approximations of chance constraints.Dentcheva and Ruszczynski(2010)proposes the concept of robust stochastic dominance and shows its applica-tion to risk-averse optimization.They consider stochastic optimization problems where risk-aversion is expressed by a robust stochastic dominance constraint and develop necessary and sufficient conditions of optimality for such optimization problems in the convex case.In the nonconvex case,they derive necessary conditions of optimality under additional smoothness assumptions of some mappings involved in the problem.2.6Nonlinear OptimizationRobust nonlinear optimization remains much less widely studied to date than its linear counterpart.Bertsimas et al.(2010c)presents a robust optimization approach for unconstrained non-convex problems and problems based on simulations.Such problems arise for instance in the partial differential equations literature and in engineering applications such as nanophotonic design.An appealing feature of the approach is that it does not assume any specific structure for the problem.The case of robust nonlinear optimization with constraints is investigated in Bertsimas et al.(2010b)with an application to radiation therapy for cancer treatment.Bertsimas and Nohadani (2010)further explore robust nonconvex optimization in contexts where solutions are not known explicitly,e.g., have to be found using simulation.They present a robust simulated annealing algorithm that improves performance and robustness of the solution.Further,Boni et al.(2008)analyzes problems with uncertain conic quadratic constraints,formulating an approx-imate robust counterpart,and Zhang(2007)provide formulations to nonlinear programming problems that are valid in the neighborhood of the nominal parameters and robust to thefirst order.Hsiung et al.(2008)present tractable approximations to robust geometric programming,by using piecewise-linear convex approximations of each non-linear constraint.Geometric programming is also investigated in Shen et al.(2008),where the robustness is injected at the level of the algorithm and seeks to avoid obtaining infeasible solutions because of the approximations used in the traditional approach.Interval uncertainty-based robust optimization for convex and non-convex quadratic programs are considered in Li et al.(2011).Takeda et al.(2010)studies robustness for uncertain convex quadratic programming problems with ellipsoidal uncertainties and proposes a relaxation technique based on random sampling for robust deviation optimization sserre(2011)considers minimax and robust models of polynomial optimization.A special case of nonlinear problems that are linear in the decision variables but convex in the uncertainty when the worst-case objective is to be maximized is investigated in Kawas and Thiele(2011a).In that setting,exact and tractable robust counterparts can be derived.A special class of nonconvex robust optimization is examined in Kawas and Thiele(2011b).Robust nonconvex optimization is examined in detail in Teo(2007),which presents a method that is applicable to arbitrary objective functions by iteratively moving along descent directions and terminates at a robust local minimum.3Applications of Robust OptimizationWe describe below examples to which robust optimization has been applied.While an appealing feature of robust optimization is that it leads to models that can be solved using off-the-shelf software,it is worth pointing the existence of algebraic modeling tools that facilitate the formulation and subsequent analysis of robust optimization problems on the computer(Goh and Sim,2011).3.1Production,Inventory and Logistics3.1.1Classical logistics problemsThe capacitated vehicle routing problem with demand uncertainty is studied in Sungur et al.(2008),with a more extensive treatment in Sungur(2007),and the robust traveling salesman problem with interval data in Montemanni et al.(2007).Remli and Rekik(2012)considers the problem of combinatorial auctions in transportation services when shipment volumes are uncertain and proposes a two-stage robust formulation solved using a constraint gener-ation algorithm.Zhang(2011)investigates two-stage minimax regret robust uncapacitated lot-sizing problems with demand uncertainty,in particular showing that it is polynomially solvable under the interval uncertain demand set.3.1.2SchedulingGoren and Sabuncuoglu(2008)analyzes robustness and stability measures for scheduling in a single-machine environment subject to machine breakdowns and embeds them in a tabu-search-based scheduling algorithm.Mittal (2011)investigates efficient algorithms that give optimal or near-optimal solutions for problems with non-linear objective functions,with a focus on robust scheduling and service operations.Examples considered include parallel machine scheduling problems with the makespan objective,appointment scheduling and assortment optimization problems with logit choice models.Hazir et al.(2010)considers robust scheduling and robustness measures for the discrete time/cost trade-off problem.3.1.3Facility locationAn important question in logistics is not only how to operate a system most efficiently but also how to design it. Baron et al.(2011)applies robust optimization to the problem of locating facilities in a network facing uncertain demand over multiple periods.They consider a multi-periodfixed-charge network location problem for which they find the number of facilities,their location and capacities,the production in each period,and allocation of demand to facilities.The authors show that different models of uncertainty lead to very different solution network topologies, with the model with box uncertainty set opening fewer,larger facilities.?investigate a robust version of the location transportation problem with an uncertain demand using a2-stage formulation.The resulting robust formulation is a convex(nonlinear)program,and the authors apply a cutting plane algorithm to solve the problem exactly.Atamt¨u rk and Zhang(2007)study the networkflow and design problem under uncertainty from a complexity standpoint,with applications to lot-sizing and location-transportation problems,while Bardossy(2011)presents a dual-based local search approach for deterministic,stochastic,and robust variants of the connected facility location problem.The robust capacity expansion problem of networkflows is investigated in Ordonez and Zhao(2007),which provides tractable reformulations under a broad set of assumptions.Mudchanatongsuk et al.(2008)analyze the network design problem under transportation cost and demand uncertainty.They present a tractable approximation when each commodity only has a single origin and destination,and an efficient column generation for networks with path constraints.Atamt¨u rk and Zhang(2007)provides complexity results for the two-stage networkflow anddesign plexity results for the robust networkflow and network design problem are also provided in Minoux(2009)and Minoux(2010).The problem of designing an uncapacitated network in the presence of link failures and a competing mode is investigated in Laporte et al.(2010)in a railway application using a game theoretic perspective.Torres Soto(2009)also takes a comprehensive view of the facility location problem by determining not only the optimal location but also the optimal time for establishing capacitated facilities when demand and cost parameters are time varying.The models are solved using Benders’decomposition or heuristics such as local search and simulated annealing.In addition,the robust networkflow problem is also analyzed in Boyko(2010),which proposes a stochastic formulation of minimum costflow problem aimed atfinding network design andflow assignments subject to uncertain factors,such as network component disruptions/failures when the risk measure is Conditional Value at Risk.Nagurney and Qiang(2009)suggests a relative total cost index for the evaluation of transportation network robustness in the presence of degradable links and alternative travel behavior.Further,the problem of locating a competitive facility in the plane is studied in Blanquero et al.(2011)with a robustness criterion.Supply chain design problems are also studied in Pan and Nagi(2010)and Poojari et al.(2008).3.1.4Inventory managementThe topic of robust multi-stage inventory management has been investigated in detail in Bienstock and Ozbay (2008)through the computation of robust basestock levels and Ben-Tal et al.(2009)through an extension of the Affinely Adjustable Robust Counterpart framework to control inventories under demand uncertainty.See and Sim (2010)studies a multi-period inventory control problem under ambiguous demand for which only mean,support and some measures of deviations are known,using a factor-based model.The parameters of the replenishment policies are obtained using a second-order conic programming problem.Song(2010)considers stochastic inventory control in robust supply chain systems.The work proposes an inte-grated approach that combines in a single step datafitting and inventory optimization–using histograms directly as the inputs for the optimization model–for the single-item multi-period periodic-review stochastic lot-sizing problem.Operation and planning issues for dynamic supply chain and transportation networks in uncertain envi-ronments are considered in Chung(2010),with examples drawn from emergency logistics planning,network design and congestion pricing problems.3.1.5Industry-specific applicationsAng et al.(2012)proposes a robust storage assignment approach in unit-load warehouses facing variable supply and uncertain demand in a multi-period setting.The authors assume a factor-based demand model and minimize the worst-case expected total travel in the warehouse with distributional ambiguity of demand.A related problem is considered in Werners and Wuelfing(2010),which optimizes internal transports at a parcel sorting center.Galli(2011)describes the models and algorithms that arise from implementing recoverable robust optimization to train platforming and rolling stock planning,where the concept of recoverable robustness has been defined in。
CABAC 上下文自适应算术编码

High Throughput CABAC EntropyCoding in HEVCVivienne Sze,Member,IEEE,and Madhukar Budagavi,Senior Member,IEEEAbstract—Context-adaptive binary arithmetic coding(CAB-AC)is a method of entropy codingfirst introduced in H.264/A VC and now used in the newest standard High Efficiency Video Coding(HEVC).While it provides high coding efficiency,the data dependencies in H.264/A VC CABAC make it challenging to parallelize and thus,limit its throughput.Accordingly,during the standardization of entropy coding for HEVC,both coding efficiency and throughput were considered.This paper highlights the key techniques that were used to enable HEVC to potentially achieve higher throughput while delivering coding gains relative to H.264/A VC.These techniques include reducing context coded bins,grouping bypass bins,grouping bins with the same context, reducing context selection dependencies,reducing total bins, and reducing parsing dependencies.It also describes reductions to memory requirements that benefit both throughput and implementation costs.Proposed and adopted techniques up to draft international standard(test model HM-8.0)are discussed. In addition,analysis and simulation results are provided to quantify the throughput improvements and memory reduction compared with H.264/A VC.In HEVC,the maximum number of context-coded bins is reduced by8×,and the context memory and line buffer are reduced by3×and20×,respectively.This paper illustrates that accounting for implementation cost when designing video coding algorithms can result in a design that enables higher processing speed and lowers hardware costs,while still delivering high coding efficiency.Index Terms—Context-adaptive binary arithmetic coding (CABAC),entropy coding,high-efficiency video coding(HEVC), video coding.I.IntroductionH IGH EFFICIENCY Video Coding(HEVC)is currentlybeing developed by the Joint Collaborative Team for Video Coding(JCT-VC).It is expected to deliver up to a 50%higher coding efficiency compared to its predecessor H.264/A VC.HEVC uses several new tools for improving coding efficiency,including larger block and transform sizes, additional loopfilters,and highly adaptive entropy coding. While high coding efficiency is important for reducing the transmission and storage cost of video,processing speed and area cost also need to be considered in the development of next-generation video coding to handle the demand for higher resolution and frame rates.Manuscript received April16,2012;revised July7,2012;accepted August 21,2012.Date of publication October2,2012;date of current version January 8,2013.This paper was recommended by Associate Editor F.Wu.The authors are with Texas Instruments,Dallas,TX75243USA(e-mail: sze@;madhukar@).Color versions of one or more of thefigures in this paper are available online at .Digital Object Identifier10.1109/TCSVT.2012.2221526Context-adaptive binary arithmetic coding(CABAC)[1]is a form of entropy coding used in H.264/A VC[2]and also in HEVC[3].While CABAC provides high coding efficiency, its data dependencies cause it to be a throughput bottleneck for H.264/A VC video codecs[4].This makes it difficult to support the growing throughput requirements for next-generation video codecs.Furthermore,since high throughput can be traded off for power savings using voltage scaling [5],the serial nature of CABAC limits the battery life for video codecs that reside on mobile devices.This limitation is a critical concern,as a significant portion of the video codecs today are battery operated.Accordingly,both coding efficiency and throughput improvement tools,and the tradeoff between these requirements,were investigated in the standard-ization of entropy coding for HEVC.The tradeoff between coding efficiency and throughput exists,since dependencies are a result of removing redundancy,which improves coding efficiency;however,dependencies make parallel processing difficult,which degrades throughput.This paper describes how CABAC entropy coding has evolved from H.264/A VC to HEVC(Draft International Stan-dard,HM-8.0)[3],[6].While both coding efficiency and throughput improvement tools are discussed,the focus of this paper will be on tools that increase throughput while maintaining coding efficiency.Section II provides an overview of CABAC entropy coding.Section III explains the cause of the throughput bottleneck.Section IV describes several key techniques used to improve the throughput of the CABAC engine.Sections V and VI describe how these techniques are applied to prediction unit(PU)coding and transform unit(TU) coding,respectively.Section VII compares the overall CABAC throughput and memory requirements of H.264/A VC and HEVC for both common conditions and worst-case conditions.II.CABAC Entropy CodingEntropy coding is a form of lossless compression used at the last stage of video encoding(and thefirst stage of video decoding),after the video has been reduced to a series of syntax elements.Syntax elements describe how the video sequence can be reconstructed at the decoder.This includes the method of prediction(e.g.,spatial or temporal prediction,intra prediction mode,and motion vectors)and prediction error,also referred to as residual.Table I shows the syntax elements used in HEVC and H.264/A VC.These syntax elements describe properties of the coding unit(CU),1051-8215/$31.00c 2012IEEETABLE ICABAC Coded Syntex Elements in HEVC and H.264/AVCHEVC H.264/A VCsplit−cu−flag,pred−mode−flag,part−mode,pcm−flag,mb−type,sub−mb−type,Coding unit Block structure and cu−transquant−bypass−flag,skip−flag,cu−qp−delta−abs,mb−skip−flag,mb−qp−delta, (CU)quantization cu−qp−delta−sign,end−of−slice−flag end−of−slice−flag,mb−field−decoding−flagprev−intra4x4−pred−mode−flag,prev−intra−luma−pred−flag,mpm−idx,prev−intra8×8−pred−mode−flag, Intra mode coding rem−intra−luma−pred−mode,rem−intra4x4−pred−mode,intra−chroma−pred−mode rem−intra8x8−pred−mode,intra−chroma−pred−mode Prediction unit merge−flag,merge−idx,inter−pred−idc,(PU)ref−idx−l0,ref−idx−l1,Motion data abs−mvd−greater0−flag,abs−mvd−greater1−flag,ref−idx−l0,ref−idx−l1,mvd−l0,mvd−l1abs−mvd−minus2,mvd−sign−flag,mvp−l0−flag,mvp−l1−flagno−residual−syntax−flag,split−transform−flag,cbf−luma,coded−block−flag,cbf−cb,cbf−cr,transform−skip−flag,last−significant−coded−block−pattern,coeff−x−prefix,last−significant−coeff−y−prefix,last−significant−transform−size−8x8−flag,Transform Unit (TU)Transform coefficient coeff−x−suffix,last−significant−coeff−y−suffix,coded−sub−significant−coeff−flag, coding block−flag,significant−coeff−flag,coeff−abs−level−last−significant−coeff−flag, greater1−flag,coeff−abs−level−greater2−flag,coeff−abs−level−coeff−abs−level−minus1,remaining,coeff−sign−flag coeff−sign−flag Sample adaptive sao−merge−left−flag,sao−merge−up−flag,sao−type−idx−luma,Loopfilter(LF)offset(SAO)sao−type−idx−chroma,sao−offset−abs,sao−offset−sign,n/a parameters sao−band−position,sao−eo−class−luma,sao−eo−class−chromaprediction unit(PU),transform unit(TU),and loopfilter(LF) of a coded block of pixels.For a CU,the syntax elements describe the block structure and whether the CU is inter or intra predicted.For a PU,the syntax elements describe the intra prediction mode or a set of motion data.For a TU,the syntax elements describe the residual in terms of frequency position,sign,and magnitude of the quantized transform coefficients.The LF syntax elements are sent once per largest coding unit(LCU),and describe the type(edge or band)and offset for sample adaptive offset in-loopfiltering. Arithmetic coding is a type of entropy coding that can achieve compression close to the entropy of a sequence by effectively mapping the symbols(i.e.,syntax elements)to codewords with a noninteger number of bits.In H.264/A VC, CABAC provides a9%to14%improvement over the Huffman-based CA VLC[1].In an early test model for HEVC (HM-3.0),CABAC provides a5%–9%improvement over CA VLC[7].CABAC involves three main functions:binarization,con-text modeling,and arithmetic coding.Binarization maps the syntax elements to binary symbols(bins).Context modeling estimates the probability of the bins.Finally,arithmetic coding compresses the bins to bits based on the estimated probability.A.BinarizationSeveral different binarization processes are used in HEVC, including unary(U),truncated unary(TU),k th-order Exp-Golomb(EGk),andfixed length(FL).These forms of binarization were also used in H.264/A VC.These various methods of binarization can be explained in terms of how they would signal an unsigned value N.An example is also provided in Table II.1)Unary coding involves signaling a bin string of lengthN+1,where thefirst N bins are1and the last bin isTABLE IIExample of Different Binarizations Used in HEVC Unary(U)Truncated Exp-Golomb Fixed N unary(TU)(EGk)length(FL)cMax=7k=0cMax=7 000100011010010001211011001101031110111000100011411110111100010110051111101111100011010161111110111111000111110711111110111111100010001110.The decoder searches for a0to determine when thesyntax element is complete.2)Truncated unary coding has one less bin than unarycoding by setting a maximum on the largest possible value of the syntax element(cMax).When N+1<cMax, the signaling is the same as unary coding.However, when N+1=cMax,all bins are1.The decoder searches for a0up to cMax bins to determine when the syntax element is complete.3)k th order Exp-Golomb is a type of universal code.Thedistribution can be changed based on the k parameter.More details can be found in[1].4)Fixed length uses afixed number of bins,ceil(log2(cMax+1)),with most significant bits signaled before least significant bits.The binarization process is selected based on the type of syntax element.In some cases,binarization also de-pends on the value of a previously processed syntax ele-ments(e.g.,the binarization of coeff−abs−level−remaining depends on the previous coefficient levels)or slice pa-rameters that indicate if certain modes are enabled(e.g., the binarization of partition mode,part−mode,depends on whether asymmetric motion partition is enabled).The ma-jority of the syntax elements use the binarization pro-cesses listed in Table II,or some combination of them(e.g.,coeff−abs−level−remaining uses U(prefix)+FL(suffix)[8];cu−qp−delta−abs uses TU(prefix)+EG0(suffix)[9]). However,certain syntax elements(e.g.,part−mode and intra−chroma−pred−mode)use custom binarization processes.B.Context ModelingContext modeling provides an accurate probability estimate required to achieve high coding efficiency.Accordingly,it is highly adaptive and different context models can be used for different bins and the probability of that context model is updated based on the values of the previously coded bins. Bins with similar distributions often share the same context model.The context model for each bin can be selected based on the type of syntax element,bin position in syntax element(binIdx),luma/chroma,neighboring information,etc.A context switch can occur after each bin.The probability models are stored as7-b entries[6-b for the probability state and1-b for the most probable symbol(MPS)]in a context memory and addressed using the context index computed by the context selection logic.HEVC uses the same probability update method as H.264/A VC;however,the context selection logic has been modified to improve throughput.C.Arithmetic CodingArithmetic coding is based on recursive interval division.A range,with an initial value of0to1,is divided into two subintervals based on the probability of the bin.The encoded bits provide an offset that,when converted to a binary fraction, selects one of the two subintervals,which indicates the value of the decoded bin.After every decoded bin,the range is updated to equal the selected subinterval,and the interval division process repeats itself.The range and offset have limited bit precision,so renormalization is required whenever the range falls below a certain value to prevent underflow. Renormalization can occur after each bin is decoded. Arithmetic coding can be done using an estimated proba-bility(context coded),or assuming equal probability of0.5 (bypass coded).For bypass coded bins,the division of the range into subintervals can be done by a shift,whereas a look up table is required for the context coded bins.HEVC uses the same arithmetic coding as H.264/A VC.III.Throughput BottleneckCABAC is a well-known throughput bottleneck in the video codec implementations(particularly,at the decoder). The throughput of CABAC is determined based on the number of binary symbols(bins)that it can process per second.The throughput can be improved by increasing the number of bins that can be processed in a cycle.However,the data dependencies in CABAC make processing multiple bins in parallel difficult and costly toachieve.Fig.1.Three key operations in CABAC:binarization,context selection,and arithmetic coding.Feedback loops in the decoder are highlighted with dashed lines.Fig.1highlights the feedback loops in the CABAC decoder. Below is a list and description of these feedback loops.1)The updated range is fed back for recursive intervaldivision.2)The updated context is fed back for an accurate proba-bility estimate.3)The context selection depends on the type of syntaxelement.At the decoder,the decoded bin is fed back to determine whether to continue processing the same syntax element,or to switch to another syntax element.If a switch occurs,the bin may be used to determine which syntax element to decode next.4)The context selection also depends on the bin position inthe syntax element(binIdx).At the decoder,the decoded bin is fed back to determine whether to increment binIdx and continue to decode the current syntax element,or set binIdx equal to0and switch to another syntax element. Note that the context update and range update feedback loops are simpler than the context selection loops and thus do not affect throughput as severely.If the context of a bin depends on the value of another bin being decoded in parallel, then speculative computations are required,which increases area cost and critical path delay[10].The amount of specula-tion can grow exponentially with the number of parallel bins which limits the throughput that can be achieved[11].Fig.2 shows an example of the speculation tree for significance map in H.264/A VC.Thus,the throughput bottleneck is primarily due to the context selection dependencies.IV.Techniques to Improve Throughput Several techniques were used to improve the throughput of CABAC in HEVC.There was a lot of effort spent in determining how to use these techniques with minimal coding loss.They were applied to various parts of entropy coding in HEVC and will be referred to throughout the rest of this paper.1)Reduce Context Coded Bins:Throughput is limited for context coded bins due to the data dependencies described in Section III.However,it is easier to process bypass coded bins in parallel since they do not have the data dependencies related to context selection(i.e.,feedback loops2,3,and4in Fig.1). In addition,arithmetic coding for bypass bins is simpler as it only requires a right shift versus a table look up for context coded bins.Thus,the throughput can be improved by reducing the number of context coded bins and using bypass coded bins instead[12]–[14].Fig.2.Context speculation required to achieve 5×parallelism when processing the significance map in H.264/A VC.i =coefficient position,i 1=MaxNumCoeff(BlockType)−1,EOB =end of block,SIG =significant −coeff −flag,LAST =last −significant −coeff −flag.2)Group Bypass Coded Bins:Multiple bypass bins can be processed in the same cycle if they occur consecutively within the bitstream.Thus,bins should be reordered such that bypass coded bins are grouped together in order to increase the likelihood that multiple bins are processed per cycle [15]–[17].3)Group Bins With the Same Context:Processing multiple context coded bins in the same cycle often requires speculative calculations for context selection.The amount of speculative computations increases if bins using different contexts and context selection logic are interleaved,since various combina-tions and permutations must be accounted for.Thus,to reduce speculative computations,bins should be reordered such that bins with the same contexts and context selection logic are grouped together so that they are likely to be processed in the same cycle [18]–[20].This also reduces context switching resulting in fewer memory accesses,which also increases throughput and reduces power consumption.This technique was first introduced in [18]and referred to as parallel context processing (PCP)throughout the standardization process.4)Reduce Context Selection Dependencies:Speculative computations are required for multiple bins per cycle decoding due to the dependencies in the context selection.Reducing these dependencies simplifies the context selection logic and reduces the amount of speculative calculations required to process multiple bins in parallel [11],[21],[22].5)Reduce Total Number of Bins:In addition to increasing the throughput,it is desirable to reduce the workload itself by reducing the total number of bins that need to be processed.This can be achieved by changing binarization,inferring the value of some bins,and sending higher level flags to avoid signaling redundant bins [23],[24].6)Reduce Parsing Dependencies:As parsing with CABAC is already a tight bottleneck,it is important to minimize any dependency on other video coding modules,which could cause the CABAC to stall [25].Ideally,the parsing process should be decoupled from all other processing.7)Reduce Memory Requirements:Memory accesses often contribute to the critical path delay.Thus,reducing memory storage requirements is desirable as fewer memory accesses increases throughput as well as reduces implementation cost and power consumption [26],[27].V .Prediction Unit CodingThe PU syntax elements describe how the prediction is performed in order to reconstruct the pixels.For inter prediction,the motion data are described by merge flag(merge −flag),merge index (merge −idx),prediction direction (inter −pred −idc),reference index (ref −idx −l0,ref −idx −l1),motion vector predictor flag (mvp −l0−flag,mvp −l1−flag)and motion vector difference (abs −mvd −greater0−flag,abs −mvd −greater1−flag,abs −mvd −minus2,mvd −sign −flag).For intra prediction,the intra prediction mode is described by prediction flag (prev −intra −luma −pred −flag),most probable mode index (mpm −idx),remainder mode (rem −intra −luma −pred −mode)and intra prediction mode for chroma (intra −chroma −pred −mode).Coding efficiency improvements have been made in HEVC for both motion data coding and intra mode coding.While H.264/A VC uses a single motion vector predictor (unless direct mode is used)or most probable mode,HEVC uses multiple candidate predictors and an index or flag is signaled to select the predictor.This section will discuss how to avoid parsing dependencies for the various methods of prediction and other throughput improvements.A.Motion Data CodingIn HEVC,merge mode enables motion data (e.g.,predic-tion direction,reference index,and motion vectors)to be inherited from a spatial or temporal (co-located)neighbor.A list of merge candidates are generated from these neighbors.merge −flag is signaled to indicate whether merge is used in a given PU.If merge is used,then merge −idx is signaled to indi-cate from which candidate the motion data should be inherited.merge −idx is coded with truncated unary,which means that the bins are parsed until a nonzero is reached or when the number of bins is equal to the cMax,the max allowed number of bins.1)Removing Parsing Dependencies for Merge:Determin-ing how to set cMax involved evaluating the throughput and coding efficiency tradeoffs in a core experiment [28].For optimal coding efficiency,cMax should be set to equal the merge candidate list size of the PU.Furthermore,merge −flag should not be signaled if the list is empty.However,this makes parsing depend on list construction,which is needed to determine the list size.Constructing the list requires a large amount of computation since it involves reading from multiple locations (i.e.,fetching the co-located neighbor and spatial neighbors)and performing several comparisons to prune the list;thus,dependency on list construction would significantly degrade parsing throughput [25],[29].To decouple the list generation process from the parsing process such that they can operate in parallel in HEVC,cMax is signaled in the slice header and does not depend on list size.To compensate for the coding loss due to the fixed cMax,combined and zero merging candidates are added when the list size is less than cMax as described in[30].This ensures that the list is never empty and that merge−flag is always signaled [31].2)Removing Parsing Dependencies for Motion Vector Prediction:If merge mode is not used,then the motion vector is predicted from its neighboring blocks and the difference between motion vector prediction(mvp)and motion vector (mv),referred to as motion vector difference(mvd),is signaled asmvd=mv-mvp.In H.264/A VC,a single predictor is calculated for mvp from the median of the left,top,and top-right spatial4×4neighbors. In HEVC,advanced motion vector prediction(AMVP)is used,where several candidates for mvp are determined from spatial and temporal neighbors[32].A list of mvp candidates is generated from these neighbors,and the list is pruned to remove redundant candidates such that there is a maximum of2candidates.A syntax element called mvp−l0−flag(or mvp−l1−flag depending on the reference list)is used to indicate which candidate is used from the list as the mvp. To ensure that parsing is independent of list construction, mvp−l0−flag is signaled even if there is only one candidate in the list.The list is never empty as the zero vector is used as the default candidate.3)Reducing Context Coded Bins:In HEVC,improve-ments were also made on the coding process of mvd it-self.In H.264/A VC,thefirst9bins of mvd are context coded truncated unary bins,followed by bypass coded third-order Exp-Golomb bins.In HEVC,the number of context coded bins for mvd is significantly reduced[13].Only the first two bins are context coded(abs−mvd−greater0−flag, abs−mvd−greater1−flag),followed by bypass codedfirst-order Exp-Golomb bins(abs−mvd−minus2).4)Reducing Memory Requirements:In H.264/A VC,con-text selection for thefirst bin in mvd depends on whether the sum of the motion vectors of the top and left4×4 neighbors are greater than32(or less than3).This requires 5-b storage per neighboring motion vector,which accounts 24576of the30720-b CABAC line buffer needed to support a4k×2k sequence.[27]highlighted the need to reduce the line buffer size in HEVC by modifying the context selection logic.It proposed that the motion vector for each neighbor befirst compared to a threshold of16,and then use the sum of the comparison for context selection,which would reduce the storage to1-b per neighboring motion vector.This was further extended in[33]and[34],where all dependencies on the neighbors were removed and the context is selected based on the binIdx(i.e.,whether it is thefirst or second bin).5)Grouping Bypass Bins:To maximize the impact of fast bypass coding,the bypass coded bins for both the x and y components of mvd are grouped together in HEVC[16]. B.Intra Mode CodingSimilar to motion coding,a predictor mode(most probable mode)is calculated for intra mode coding.In H.264/A VC,the minimum mode of the top and left neighbors is used as theTABLE IIIDifferences Between PU Coding in HEVC and H.264/AVCProperties HEVC H.264/A VCIntra mode AMVP Merge Intra mode MVP Max number of32511 candidates in listSpatial neighbor Used Used Used Used Used Temporal co-located Not Used Used Not Not neighbor used used used Number of contexts2102620 Max context coded2122798 bins per PUmost probable mode.prev−intra4x4−pred−mode−flag (or prev−intra8x8−pred−mode−flag)is signaled to indicate whether the most probable mode is used.If the most probable mode is not used,the remainder mode rem−intra4x4−pred−mode−flag(or rem−intra8x8−pred−mode−flag)is signaled.In HEVC,additional most probable modes are used to improve coding efficiency.A candidate list of most probable modes with afixed length of three is constructed based on the left and top neighbors.The additional candidate modes (DC,planar,vertical,+1or−1angular mode)can be added if the left and top neighbors are the same or unavailable. prev−intra−pred−mode−flag is signaled to indicate whether one of the most probable modes is used.If a most probable mode is used,a most probable mode index(mpm−idx)is signaled to indicate which candidate to use.It should be noted that in HEVC,the order in which the coefficients of the residual are parsed(e.g.,diagonal,vertical,or horizontal) depends on the reconstructed intra mode(i.e.,the parsing of the TU data that follows depends on list construction and intra mode reconstruction).Thus,the candidate list size was limited to three for reduced computation to ensure that it would not affect entropy decoding throughput[35],[36].1)Reducing Context Coded Bins:The number of context coded bins was reduced for intra mode coding in HEVC.In H.264/A VC,the remainder mode is a7-bin value where the first bin is context coded,while in HEVC,the remainder mode is a5-bin value that is entirely bypass coded.The most proba-ble mode index(mpm−idx)is also entirely bypass coded.The number of contexts used to code intra−chroma−pred−mode is reduced from4to1.2)Grouping Bypass Bins:To maximize the impact of fast bypass coding,the bypass coded bins for intra mode within a CU are grouped together in HEVC[17].C.Summary of Differences Between HEVC and H.264/AVC The differences between H.264/A VC and HEVC are sum-marized in Table III.HEVC uses both spatial and temporal neighbors as predictors,while H.264/A VC only uses spatial neighbors(unless direct mode is enabled).In terms of the impact of the throughput improvement techniques,HEVC has8×fewer maximum context coded bins per PU than H.264/A VC.HEVC also requires1.8×fewer contexts for PU syntax elements than H.264/A VC.VI.Transform Unit CodingIn video coding,both intra and inter prediction are used to reduce the amount of data that needs to be transmitted. Rather than sending the pixels,the prediction error is trans-mitted.This prediction error is transformed from spatial to frequency domain to leverage energy compaction properties, and after quantization,it can be represented in terms of a few coefficients.The method of signaling the value and the frequency position of these coefficients is referred to as transform coefficient coding.For regions with many edges (e.g.,screen content coding),coding gains can be achieved by skipping the transform from spatial to frequency domain [37],[38];when transform is skipped,the prediction error is coded in the same manner as transform coefficient coding(i.e., the spatial error is coded as transform coefficients).Syntax elements of the transform unit account for a signif-icant portion of the bin workload as shown in Table IV.At the same time,the transform coefficients also account for a significant portion of the total bits of a compressed video,and as a result the compression of transform coefficients signifi-cantly impacts the overall coding efficiency.Thus,transform coefficient coding with CABAC must be carefully designed in order to balance coding efficiency and throughput demands. Accordingly,as part of the HEVC standardization process, a core experiment on coefficient scanning and coding was established to investigate tools related to transform coefficient coding[39].It is also important to note that HEVC supports more transform sizes than H.264/A VC;H.264/A VC uses4×4and 8×8transforms,where as HEVC uses4×4,8×8,16×16, and32×32transforms.While these larger transforms provide significant coding gains,they also have implications in terms of memory storage as this represents an increase of4×to 16×in the number of coefficients that need to be stored per transform unit(TU).In CABAC,the position of the coefficients is transmitted in the form of a significance map.Specifically,the significance map indicates the location of the nonzero coefficients.The coefficient level information is then only transmitted for the coefficients with values greater than one,while the coefficient sign is transmitted for all nonzero coefficients.This section describes how transform coefficient coding evolved from H.264/A VC to thefirst test model of HEVC (HM-1.0)to the Draft International Standard of HEVC(HM-8.0),and discusses the reasons behind design choices that were made.Many of the throughput improvement techniques were applied,and new tools for improved coding efficiency were simplified.As a reference for the beginning and end points of the development,Figs.3and4show examples of transform coefficient coding in H.264/A VC and HEVC(HM-8.0),respectively.A.Significance MapIn H.264/A VC,the significance map is signaled by transmit-ting a significant−coeff−flag(SCF)for each position to indi-cate whether the coefficient is nonzero.The positions are pro-cessed in an order based on a zig–zag scan.After eachnonzero Fig.3.Example of transform coefficient coding for a4×4TU in H.264/AVC.Fig.4.Example of transform coefficient coding for a4×4TU in HEVC (HM-8.0).SCF,an additionalflag called last−significant−coeff−flag (LSCF)is immediately sent to indicate whether it is the last nonzero SCF;this prevents unnecessary SCF from being signaled.Different contexts are used depending on the position within the4×4and8×8transform unit(TU),and whether the bin represents an SCF or LSCF.Since SCF and LSCF are interleaved,the context selection of the current bin depends on the immediate preceding bin.The dependency of LSCF on SCF results in a strong bin to bin dependency for context selection for significance map in the H.264/A VC as illustrated in Fig.2.1)significant−coeff−flag(SCF):In HM-1.0,additional dependencies were introduced in the context selection of SCF for16×16and32×32TU to improve coding efficiency.The context selection for SCF in these larger TU depended on the number of nonzero neighbors to give coding gains between 1.4%to2.8%[42].Specifically,the context of SCF depended on up to ten neighbors as shown in Fig.5(a)[42],[43].To reduce context selection dependencies,and storage costs,[21]proposed using fewer neighbors and showed that it could be done with minimal cost to coding efficiency.For。
硫酸镁治疗小儿喘息性疾病的临床效果及安全性观察

· 沦 著 ·
硫 酸 镁 治 疗 小 儿 喘 息 性 疾 病 的 临 床 效 果 及 安 全 性 观 察
MHD Turbulence Revisited

P. Goldreich 1 and S. Sridhar 2 1 California Institute of Technology Pasadena, CA 91125, USA Inter-University Centre for Astronomy and Astrophysics Ganeshkhind, Pune 411 007, INDIA ABSTRACT Kraichnan (1965) proposed that MHD turbulence occurs as a result of collisions between oppositely directed Alfv´ en wave packets. Recent work has generated some controversy over the nature of non linear couplings between colliding Alfv´ en waves. We find that the resolution to much of the confusion lies in the existence of a new type of turbulence, intermediate turbulence, in which the cascade of energy in the inertial range exhibits properties intermediate between those of weak and strong turbulent cascades. Some properties of intermediate MHD turbulence are: (i) in common with weak turbulent cascades, wave packets belonging to the inertial range are long lived; (ii) however, components of the strain tensor are so large that, similar to the situation in strong turbulence, perturbation theory is not applicable; (iii) the breakdown of perturbation theory results from the divergence of neighboring field lines due to wave packets whose perturbations in velocity and magnetic fields are localized, but whose perturbations in displacement are not; (iv) 3–wave interactions dominate individual collisions between wave packets, but interactions of all orders n ≥ 3 make comparable contributions to the intermediate turbulent energy cascade; (v) successive collisions are correlated since wave packets are distorted as they follow diverging field lines; (vi) in common with the weak MHD cascade, there is no parallel cascade of energy, and the cascade to small perpendicular scales strengthens as it reaches higher wave numbers; (vii) For an appropriate weak excitation, there is a natural progression from a weak, through an intermediate, to a strong cascade.
激光专业英语

2011年技术物理学院08级(激光方向)专业英语翻译重点!!!作者:邵晨宇Electromagnetic电磁的principle原则principal主要的macroscopic宏观的microscopic微观的differential微分vector矢量scalar标量permittivity介电常数photons光子oscillation振动density of states态密度dimensionality维数transverse wave横波dipole moment偶极矩diode 二极管mono-chromatic单色temporal时间的spatial空间的velocity速度wave packet波包be perpendicular to线垂直be nomal to线面垂直isotropic各向同性的anistropic各向异性的vacuum真空assumption假设semiconductor半导体nonmagnetic非磁性的considerable大量的ultraviolet紫外的diamagnetic抗磁的paramagnetic顺磁的antiparamagnetic反铁磁的ferro-magnetic铁磁的negligible可忽略的conductivity电导率intrinsic本征的inequality不等式infrared红外的weakly doped弱掺杂heavily doped重掺杂a second derivative in time对时间二阶导数vanish消失tensor张量refractive index折射率crucial主要的quantum mechanics 量子力学transition probability跃迁几率delve研究infinite无限的relevant相关的thermodynamic equilibrium热力学平衡(动态热平衡)fermions费米子bosons波色子potential barrier势垒standing wave驻波travelling wave行波degeneracy简并converge收敛diverge发散phonons声子singularity奇点(奇异值)vector potential向量式partical-wave dualism波粒二象性homogeneous均匀的elliptic椭圆的reasonable公平的合理的reflector反射器characteristic特性prerequisite必要条件quadratic二次的predominantly最重要的gaussian beams高斯光束azimuth方位角evolve推到spot size光斑尺寸radius of curvature曲率半径convention管理hyperbole双曲线hyperboloid双曲面radii半径asymptote渐近线apex顶点rigorous精确地manifestation体现表明wave diffraction波衍射aperture孔径complex beam radius复光束半径lenslike medium类透镜介质be adjacent to与之相邻confocal beam共焦光束a unity determinant单位行列式waveguide波导illustration说明induction归纳symmetric 对称的steady-state稳态be consistent with与之一致solid curves实线dashed curves虚线be identical to相同eigenvalue本征值noteworthy关注的counteract抵消reinforce加强the modal dispersion模式色散the group velocity dispersion群速度色散channel波段repetition rate重复率overlap重叠intuition直觉material dispersion材料色散information capacity信息量feed into 注入derive from由之产生semi-intuitive半直觉intermode mixing模式混合pulse duration脉宽mechanism原理dissipate损耗designate by命名为to a large extent在很大程度上etalon 标准具archetype圆形interferometer干涉计be attributed to归因于roundtrip一个往返infinite geometric progression无穷几何级数conservation of energy能量守恒free spectral range自由光谱区reflection coefficient(fraction of the intensity reflected)反射系数transmission coefficient(fraction of the intensity transmitted)透射系数optical resonator光学谐振腔unity 归一optical spectrum analyzer光谱分析grequency separations频率间隔scanning interferometer扫描干涉仪sweep移动replica复制品ambiguity不确定simultaneous同步的longitudinal laser mode纵模denominator分母finesse精细度the limiting resolution极限分辨率the width of a transmission bandpass透射带宽collimated beam线性光束noncollimated beam非线性光束transient condition瞬态情况spherical mirror 球面镜locus(loci)轨迹exponential factor指数因子radian弧度configuration不举intercept截断back and forth反复spatical mode空间模式algebra代数in practice在实际中symmetrical对称的a symmetrical conforal resonator对称共焦谐振腔criteria准则concentric同心的biperiodic lens sequence双周期透镜组序列stable solution稳态解equivalent lens等效透镜verge 边缘self-consistent自洽reference plane参考平面off-axis离轴shaded area阴影区clear area空白区perturbation扰动evolution渐变decay减弱unimodual matrix单位矩阵discrepancy相位差longitudinal mode index纵模指数resonance共振quantum electronics量子电子学phenomenon现象exploit利用spontaneous emission自发辐射initial初始的thermodynamic热力学inphase同相位的population inversion粒子数反转transparent透明的threshold阈值predominate over占主导地位的monochromaticity单色性spatical and temporal coherence时空相干性by virtue of利用directionality方向性superposition叠加pump rate泵浦速率shunt分流corona breakdown电晕击穿audacity畅通无阻versatile用途广泛的photoelectric effect光电效应quantum detector 量子探测器quantum efficiency量子效率vacuum photodiode真空光电二极管photoelectric work function光电功函数cathode阴极anode阳极formidable苛刻的恶光的irrespective无关的impinge撞击in turn依次capacitance电容photomultiplier光电信增管photoconductor光敏电阻junction photodiode结型光电二极管avalanche photodiode雪崩二极管shot noise 散粒噪声thermal noise热噪声1.In this chapter we consider Maxwell’s equations and what they reveal about the propagation of light in vacuum and in matter. We introduce the concept of photons and present their density of states.Since the density of states is a rather important property,not only for photons,we approach this quantity in a rather general way. We will use the density of states later also for other(quasi-) particles including systems of reduced dimensionality.In addition,we introduce the occupation probability of these states for various groups of particles.在本章中,我们讨论麦克斯韦方程和他们显示的有关光在真空中传播的问题。
小波去噪阈值的确定和分解层数的确定
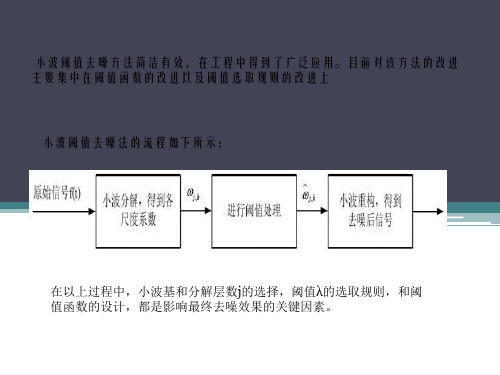
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.(根据计算后的小 波包系数重构原信号。)
1
0.5
0
-0.5
获得单个阈值,对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数) 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然 这一步是可选择的。) 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值 并应用于去噪) The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不 断测试来选择阈值优化去噪效果) a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
Posterior probability intervals for wavelet thresholding

Posterior probability intervals for wavelet thresholdingStuart Barber,Guy P.Nason,and Bernard W.SilvermanUniversity of Bristol,UK.AbstractWe use cumulants to derive Bayesian credible intervals for wavelet regression estimates.The first four cumulants of the posterior distribution of the estimates are expressed in terms of theobserved data and integer powers of the mother wavelet functions.These powers are closelyapproximated by linear combinations of wavelet scaling functions at an appropriatefiner scale.Hence,a suitable modification of the discrete wavelet transform allows the posterior cumulantsto be found efficiently for any given data set.Johnson transformations then yield the credibleintervals themselves.Simulations show that these intervals have good coverage rates,evenwhen the underlying function is inhomogeneous,where standard methods fail.In the casewhere the curve is smooth,the performance of our intervals remains competitive with establishednonparametric regression methods.Keywords:Bayes estimation;Cumulants;Curve estimation;Interval estimates;Johnson curves;Nonparametric regression;Powers of wavelets.1IntroductionConsider the estimation of a function from an observed data vector satisfyingwhere and the are independently distributed.There are many methods of estimating smooth functions,such as spline smoothing(Green and Silverman,1994),kernel estimation(Wand and Jones,1995),and local polynomial regression(Fan and Gijbels,1996).In most cases,such point estimates can be supplemented by interval estimates with some specified nominal coverage probability or significance level.A recent proposal for estimation of inhomogeneous is wavelet thresholding(Donoho and Johnstone1994,1995).The representation of in terms of a wavelet basis is typically sparse, concentrating most of the signal in the data into a few large coefficients,whilst the noise is spread “evenly”across the coefficients due to the orthonormality of the wavelet basis.The data is denoised by a thresholding rule of some sort to discard“small”coefficients and retain,possibly with some modification,those coefficients which are thought to contain the signal.Several authors have described Bayesian wavelet thresholding rules,placing prior distributions on the wavelet coefficients.We consider a means of approximating the posterior distribution of each ,using the same prior as the BayesThresh method of Abramovich,Sapatinas and Silverman (1998).Posterior probability intervals of any nominal coverage probability can then be calculated. Our approach can also be applied to other Bayesian wavelet thresholding rules,such as those surveyed by Chipman and Wolfson(1999),Abramovich and Sapatinas(1999),and Vidakovic(1998).We briefly review the wavelet thresholding approach to curve estimation in section2,including two Bayesian methods of wavelet thresholding.In section3,we derive our WaveBand method of estimating the posterior distribution of given the observed data.We present an example and simulation results in section4and make some concluding remarks in section5.2Wavelets and wavelet thresholding2.1WaveletsWavelets provide a variety of orthonormal bases of,the space of square integrable functions on;each basis is generated from a scaling function,denoted,and an associated wavelet,. The wavelet basis consists of dilations and translations of these functions.For,the wavelet at level and location is given by(1) with an analogous definition for.The scaling function is sometimes referred to as the father wavelet,but we avoid this terminology.A function can be represented as(2)with and.Daubechies(1992)derived two families of wavelet bases which give sparse representations of wide sets of functions.(Technically,by choosing a wavelet with suitable properties,we can generate an unconditional wavelet basis in a wide set of function spaces;for further details, see Abramovich et al.(1998).)Generally,smooth portions of are represented by a small number of coarse scale(low level)coefficients,while local inhomogeneous features such as high frequency events,cusps and discontinuities are represented by coefficients atfiner scales(higher levels).For our nonparametric regression problem,we have discrete data and hence consider the discrete wavelet transform(DWT).Given a vector,where,the DWT of is ,where is an orthonormal matrix and is a vector of the discrete scaling coefficient and discrete wavelet coefficients.These are analogous to the coefficients in(2),with.Our data are restricted to lie in,requiring boundary conditions;we assume that is periodic at the boundaries.Other boundary conditions include the assumption that is reflected at the boundaries,or the“wavelets on the interval”transform of Cohen,Daubechies and Vial(1993)can be used.The pyramid algorithm of Mallat(1989)computes in operations,provided. The algorithm iteratively computes the and from the.From the vector,the inverse DWT(IDWT)can be used to reconstruct the original data.The IDWT starts with the overall scaling and wavelet coefficients and and reconstructs the;it then proceeds iteratively tofiner levels,reconstructing the from the and.22.2Curve estimation by wavelet thresholdingSince the DWT is an orthonormal transformation,white noise in the data domain is transformed towhite noise in the wavelet domain.If is the DWT of,and thevector of empirical coefficients obtained by applying the DWT to the data,then,where is a vector of independent variates.Wavelet thresholding assumes implicitly that“large”and“small”represent signal and noise respectively.Various thresholding ruleshave been proposed to determine which coefficients are“large”and“small”;see Vidakovic(1999)or Abramovich,Bailey and Sapatinas(2000)for reviews.The true coefficients are estimated byapplying the thresholding rule to the empirical coefficients to obtain estimates,and the sampled function values are estimated by applying the IDWT to obtain where denotes the transpose of;symbolically,we can represent this IDWT as the sum(3)Confidence intervals for the resulting curve estimates have received some attention in the wavelet literature.Brillinger(1994)derived an estimate of var when the wavelet decomposition involved Haar wavelets,and Brillinger(1996)showed that is asymptotically normal under certain conditions. Bruce and Gao(1996)extended the estimation of var to the case of non-Haar wavelets,and gave approximate confidence intervals using the asymptotic normality of.Chipman, Kolaczyk and McCulloch(1997)presented approximate credible intervals for their adaptive Bayesian wavelet thresholding method,which we discuss in section2.3.2,while Picard and Tribouley(2000) derive bias corrected confidence intervals for wavelet thresholding estimators.2.3Bayesian wavelet regression2.3.1IntroductionSeveral authors have proposed Bayesian wavelet regression estimates,involving priors on the wavelet coefficients,which are updated by the observed coefficients to obtain posterior distributions .Point estimates can be computed from these posterior distributions and the IDWT employed to estimate in the usual fashion outlined above.Some proposals have included priors on ;we restrict ourselves to the situation where can be well estimated from the data.The majority of Bayesian wavelet shrinkage rules have employed mixture distributions as priors on the coefficients,to model the notion that a small proportion of coefficients contain substantial signal.Chipman et al.(1997)and Crouse,Nowak and Baraniuk(1998)considered mixtures of two normal distributions,while Abramovich et al.(1998),Clyde,Parmigiani and Vidakovic(1998)and Clyde and George(2000)used mixtures of a normal and a point mass.Other proposals include a mixture of a point mass and a-distribution used by Vidakovic(1998),and an infinite mixture of normals considered by Holmes and Denison(1999).More thorough reviews are given by Chipman and Wolfson(1999)and Abramovich and Sapatinas(1999).32.3.2Adaptive Bayesian wavelet shrinkageThe ABWS method of Chipman et al.(1997)places an independent prior on each:(4) where Bernoulli;hyperparameters,and are determined from the data by empirical Bayes methods.At level,the proportion of non-zero coefficients is represented by,while and represent the magnitude of negligible and non-negligible coefficients respectively.Given,the empirical coefficients are independently,so the posterior distribution is a mixture of two normal components independently for each. Chipman et al.(1997)use the mean of this mixture as their estimator,and similarly use the variance of to approximate the variance of their ABWS estimate of.Estimating each coefficient by the mean of its posterior distribution is the Bayes rule under the loss function.They plot uncertainty bands of sd.These bands are useful in representing the uncertainty in the estimate,but are based on an assumption of normality despite being a sum of random variables with mixture distributions.2.3.3BayesThreshThe BayesThresh method of Abramovich et al.(1998)also places independent priors on the coefficients:(5) where and is a probability mass at zero.This is a limiting case of the ABWS prior(4).The hyperparameters are assumed to be of the form and min for non-negative constants and chosen empirically from the data and and selected by the user. Abramovich et al.(1998)show that choices of and correspond to choosing priors within certain Besov spaces,incorporating prior knowledge about the smoothness of in the prior.Chipman and Wolfson(1999)also discuss the interpretation of and.In the absence of any such prior knowledge, Abramovich et al.(1998)show that the default choice,is robust to varying degrees of smoothness of.The prior specification is completed by placing a non-informative prior on the scaling coefficient,which thus has the posterior distribution,and is estimated by.The resulting posterior distribution of given the observed value of is again independent for each and is given by(6) where,withand.The BayesThresh approach minimises the loss in the wavelet domain by using the posterior median of as the point estimate;Abramovich et al.(1998)show4that this gives a level-dependent true thresholding rule.The BayesThresh method is implemented in the WaveThresh package for SPlus(Nason,1998).3WaveBand3.1Posterior cumulants of the regression curveWe now consider the posterior density of for each.From(3),we see that is the convolution of the posteriors of the wavelet coefficients and the scaling coefficient,(7)this is a complicated mixture,and is impractical to evaluate analytically.Direct simulation from the posterior is extremely time consuming.Instead we estimate thefirst four cumulants of(7)andfit a distribution which matches these values.Evaluating cumulants of requires the use of powers of wavelets for,and,which we discuss in section3.2.We thenfit a parametric distribution to in section3.3.If the moment generating function of a random variable is written,then the cumulant generating function is.We write for the th cumulant of,given by the th derivative of,evaluated at.Note that thefirst moments uniquely determine thefirst cumulants and vice-versa.Further details of cumulants and their properties and uses can be found in Barndorff-Nielsen and Cox(1989)or Stuart and Ord(1994,chapter3).Thefirst four cumulants each have a direct interpretation;and are the mean and variance of respectively,while is the skewness and is the kurtosis.If is normally distributed then both and are zero.We make use of two standard properties of cumulants.If and are independent random variables and and are real constants,then(8)and(9) Applying(8)and(9)to(7),we can see that the cumulants of are given by(10)Once the cumulants of the wavelet coefficients are known,this sum can be evaluated directly using the IDWT when,but for,and,the computation involves powers of wavelets.The posterior distributions(6)for the wavelet coefficients using BayesThresh are of the form ,where,,and is a point mass at zero.Then5so the moments of(6)are easily obtained.From these,we can derive the cumulants of:Since the scaling coefficient has a normal posterior distribution,thefirst two cumulants are and;all higher order cumulants are zero.3.2Powers of waveletsThe parallel between(10)and the sum(3)evaluated by the IDWT is clear,and we shall describe a means of taking advantage of the efficient IDWT algorithm to evaluate(10).For Haar wavelets, this is trivial;the Haar scaling function and mother wavelet are and,where is the indicator function,hence and.Moreover,,,and ,all terms which can be included in a modified version of the IDWT algorithm which incorporates scaling function coefficients.Since representing by scaling functions and wavelets works in the Haar case,we consider a similar approach for other wavelet bases.Following Herrick(2000,pp.69),we approximate a general wavelet,,by(11)for,where is a positive integer;the choice of is discussed below.We use scaling functions rather than wavelets as the span of the set of scaling functions at a given level is the same as that of the union of and wavelets at levels.Moreover,if scaling functionsare used to approximate some function,and both and have at least derivatives,then the mean squared error in the approximation is bounded by,where is some positive constant; see,for example,Vidakovic(1999,p.87).To approximate for somefixed,wefirst compute using the cascade algorithm (Daubechies,1992,pp.205),then take the DWT of and set the coefficients to be equal to the scaling function coefficients at level,where.Recall that the wavelets at level are simply shifts of each other;from(1),hence(12) As we are assuming periodic boundary conditions,the can be cycled periodically.6(a)0.00.20.40.60.8 1.0-0.100.00.1••••••••••(b)24680.00.20.40.60.8••••••••••(c)24680.00.20.40.60.81.0••••••••••(d)24680.00.20.40.60.8Approximation levelApproximation level Approximation levelM S E r a t i oM S E r a t i oM S E r a t i oFigure 1:Daubechies’extremal phase wavelet with two vanishing moments (panel a)and accuracy of estimating for by scaling functions at level .The mean square errors of the estimates,divided by the norm of ,are plotted against :panels (b),(c),and (d)show results for ,and respectively.The vertical lines are at level 3,the level at which exists.Owing to the localised nature of wavelets,the coefficientsused to approximatecan be found by inserting zeros into the vector of:Approximation (11)cannot be used for wavelets at the finest levels .Werepresent these wavelets by both scaling functions and wavelets at the finest level of detail,level,using the block-shifting technique outlined above to make the computations more efficient.In all the cases we have examined,has been sufficient for a highly accurate approximation;examples are shown in figures 1and 2.Consider approximating the powers of Daubechies’extremal phase wavelet with two vanishing moments;this wavelet is extremely non-smooth and so can be regarded as a near worst-case scenario for the approximation.Panel (a)of figure 1shows ,while panels (b)-(d)show the mean square error in our approximation divided by the norm of the function being approximated,for respectively.In each plot (b)-(d),the vertical line is at resolution level ,the level at which thewavelet whose power is being estimated exists.The approximation is excellent forin each case,with little improvement at level .70.00.20.40.60.8 1.00.00.040.080.00.20.40.60.8 1.00.00.040.080.120.00.20.40.60.8 1.00.00.040.080.00.20.40.60.8 1.0-0.03-0.02-0.010.00.010.00.20.40.60.8 1.0-0.03-0.02-0.010.00.010.00.20.40.60.8 1.0-0.03-0.02-0.010.00.010.00.20.40.60.8 1.00.0020.0060.0100.00.20.40.60.8 1.00.00.0040.0080.0120.00.20.40.60.8 1.00.0020.0060.010Figure 2:Approximations to powers of Daubechies’least asymmetric wavelet with eight vanishing moments;the powers are indicated at the top of each column.Solid lines are wavelet powers and dotted lines show approximations using scaling functions at level .From top to bottom,graphs show approximation at levels ,,and ;the original wavelet is at level .Figure 2shows approximations to powers of Daubechies’least asymmetric wavelet with eight vanishing moments as the approximation level increases.Again,the base wavelet is at level,and approximations are shown for (top row),,and(bottom row).In each case,the solid line is the wavelet power and the dotted line is the ing (12),we can now re-write (10)asfor suitable coefficients ,and use a modified version of the IDWT algorithm which incorporates scaling function coefficients to evaluate this sum.83.3Posterior distribution of the regression curveWe must now estimate from its cumulants.Edgeworth expansions give poor results in the tails of the distribution,where we require a good approximation.Saddlepoint expansions improve on this, but require the cumulant generating function,while we only have thefirst four cumulants. Therefore,we approximate by a suitable parametric distribution.A family of distributions is the set of transformations of the normal curve described by Johnson (1949).As well as the normal distribution,Johnson curves fall into three categories;(a)the lognormal,,with,(b)the unbounded,,and(c)the bounded,,with,to which Hill,Hill and Holder(1976)added a limiting case of curves whereand shown infigure3(solid line).Figure3also shows data formed by adding independent normally distributed noise to.The noise has mean zero and root signal to noise ratio(rsnr)3;the rsnr is defined to be the ratio of the standard deviation of the data points to the standard deviation of the noise,.Dotted lines infigure3mark upper and lower endpoints of99%credible intervals for for each calculated using our WaveBand method,using default parameters of,,and Daubechies’least asymmetric wavelet with eight vanishing moments.In this example,the credible intervals include the true value of in490of512cases,an empirical coverage rate of95.7%. The brief spikes which occur in the bands are typical of wavelet regression methods;they can be smoothed out by using different and,but this risks oversmoothing the data.9...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................0.00.20.40.60.8 1.00123Figure 3:Pointwise 99%WaveBand interval estimates (dotted line)for the piecewise polynomial signal (solid line).Dots indicate data on equally spaced points with the addition of independent normally distributed noise with mean zero and rsnr 3.Figure 4shows the mean,variance,skewness,and kurtosis of for each point .The mean is itself an estimate of and the variance is generally low except near the discontinuity at.We use the usual definitions of skewness and kurtosis,range from approximately -7.9to 7.5,and from approximately 1.7to almost 120,indicating that for some ,the posterior distribution has heavy tails.(For comparison the distribution has skewness 7.1and kurtosis 79.)The prior (5)has kurtosis ;note that in our example the largest values of kurtosis occur when the function is smooth;in these cases the majority of the wavelet coefficients are zero,and hence is small.4.2Simulation results4.2.1Inhomogeneous signalsWe investigated the performance of our WaveBand credible intervals by simulation on the piecewise polynomial example of Nason and Silverman (1994)(denoted “PPoly”)and the standard “Blocks”,“Bumps”,“Doppler”and “HeaviSine”test functions of Donoho and Johnstone (1994),shown in figure 5.For each test function,100simulated data sets of length were created with rsnr100.00.20.40.60.8 1.01230.00.20.40.60.8 1.00.00.040.080.120.00.20.40.60.8 1.0-550.00.20.40.60.8 1.0020*********M e a nV a r i a n c eS k e w n e s sK u r t o s i sFigure 4:Mean,variance,skewness and kurtosis for the piecewise polynomial data shown in figure 3.4and the WaveBand and ABWS credible intervals evaluated at each data point for nominal coverage probabilities 0.90,0.95,and 0.99.The default hyperparameters and were used for WaveBand and both methods used Daubechies’least asymmetric wavelet with eight vanishing moments.Table 1shows the coverage rates and interval widths averaged over all points and the 100replications,with standard error shown in brackets.The WaveBand intervals have higher empirical coverage rates in each case,although still below the nominal coverage probabilities.Average widths of the WaveBand credible intervals are always greater than those of the ABWS intervals;one reason is that the ABWS method typically has a lower estimated variance.Moreover,the WaveBand posterior of is typically heavier-tailed than the normal distribution,as we saw in the piecewise polynomial example.The performance of the WaveBand intervals improves as the nominal coverage rate increases.In part,this can be attributed to the kurtosis of the posterior distributions.As the nominal coverage rates increase,the limits of the credible intervals move out into the tails of the posterior distributions.With heavy-tailed distributions,a small increase in the nominal coverage rate can produce a substantially wider interval.Figure 6examines the empirical coverage rates of the nominal 99%credible intervals in more detail.Solid lines denote the empirical coverage rates of the WaveBand intervals for each ,and dotted lines give the equivalent results for the ABWS intervals.Coverage varies greatly across each signal;unsurprisingly,the coverage is much better where the signal is smoother and less variable.This can be seen most clearly in the results for the piecewise polynomial and HeaviSine test functions,110.00.20.40.60.8 1.001230.00.20.40.60.8 1.0-20240.00.20.40.60.8 1.00123450.00.20.40.60.8 1.0-0.40.00.40.00.20.40.60.8 1.0-6-4-2024P p o l yB l o c k sB u m p sH e a v i S i n eD o p p l e rFigure 5:The piecewise polynomial of Nason and Silverman (1994)and the test functions of Donoho and Johnstone (1994).12Simulation results comparing mean coverage rates(CR)and interval widths for ABWS and WaveBand(denoted WB)credible intervals on the piecewise polynomial,Blocks,Bumps,Doppler, and HeaviSine test functions.Each test function was evaluated on points,the rsnr was 4,and100replications were done in each case.Standard errors are given in brackets.All methods were employed with Daubechies’least asymmetric wavelet with8vanishing moments,and the default hyperparameters and were used for WaveBand.130.00.20.40.60.81.00.00.40.80.00.20.40.60.81.00.00.40.80.00.20.40.60.8 1.00.00.40.80.00.20.40.60.81.00.00.40.80.00.20.40.60.8 1.00.00.40.8C o v e r a g eC o v e r a g eC o v e r a g eC o v e r a g eC o v e r a g eFigure 6:Empirical coverage rates of nominal 99%interval estimates for the indicated test functions evalauted at equally spaced data points.In each case,100simulated data sets with a rsnr of 4were used.Solid and dotted lines indicate coverage rates for the WaveBand method and ABWS methods respectively.14with sharp drops in performance near the discontinuities,and in the excellent coverage in the lower-frequency portion of the Doppler signal and the long constant parts of the Bumps signal.4.2.2Smooth signalsThe major advantage of wavelet thresholding as a nonparametric regression technique is the ability to model inhomogeneous signals such as those considered in section4.2.1.However,wavelet thresholding can also be used successfully on smooth signals,and we now consider such an example, the function.Table2shows the performance of ABWS and WaveBand credible intervals and confidence intervals using smoothing splines for.The smoothing spline estimate of can be written spline,where is an matrix,so var spline.Hence we can construct an approximate confidence interval for as spline where,and consider the random variable,, where is a double exponential variate with density function.Given an observation of,the15RSNR =20.95CR Width CR Width 0.939(.008)0.300(.002)0.990(.003)0.471(.004)WB 00.600Nominal coverage probability0.900.99CR WidthWB0.850(.010)0.143(.002)0.981(.002)0.276(.002)Spline0.934(.008)0.159(.002)0.493(.016)0.078(.003)0.643(.017)0.122(.004)Table 2:Simulation results comparing the mean coverage rate (CR)and interval widths forWaveBand ,smoothing spline,and ABWS methods on the functionposterior probability that is,where is the density function of a standard normal random variable,not a scaling function,and denotes convolution.Write for the distribution function associated with,and let and;then isAcknowledgmentsThe authors are grateful for the support of the EPSRC(grant GR/M10229)and by Unilever Research; GPN was also supported by EPSRC Advanced Research Fellowship AF/001664.The authors wish to thank Eric Kolaczyk and Thomas Yee for programs that implement the ABWS and spline methods respectively.The authors are also grateful for the constructive comments of the Joint Editor and two referees.ReferencesAbramovich, F.,Bailey,T.C.and Sapatinas,T.(2000).Wavelet analysis and its statistical applications.The Statistician49,1–29.Abramovich,F.and Sapatinas,T.(1999).Bayesian approach to wavelet decomposition and shrinkage.In M¨u ller,P.and Vidakovic,B.,editors,Bayesian Inference in Wavelet Based Models,volume141 of Lecture Notes in Statistics,pages33–50.Springer-Verlag,New York.Abramovich,F.,Sapatinas,T.and Silverman,B.W.(1998).Wavelet thresholding via a Bayesian approach.J.R.Statist.Soc.B60,725–749.Barndorff-Nielsen,O.E.and Cox,D.R.(1989).Asymptotic Techniques for Use in Statistics.Chapman and Hall,London.Brillinger,D.R.(1994).Some river wavelets.Environmetrics5,211–220.Brillinger,D.R.(1996).Uses of cumulants in wavelet analysis.J.Nonparam.Statist.6,93–114. Bruce,A.G.and Gao,H.Y.(1996).Understanding WaveShrink:variance and bias estimation.Biometrika83,727–745.Chipman,H.,Kolaczyk,E.and McCulloch,R.(1997).Adaptive Bayesian wavelet shrinkage.J.Am.Statist.Ass.92,1413–1421.Chipman,H.A.and Wolfson,L.J.(1999).Prior elicitation in the wavelet domain.In M¨u ller,P.and Vidakovic,B.,editors,Bayesian Inference in Wavelet Based Models,volume141of Lecture Notes in Statistics.Springer-Verlag,New York.Clyde,M.and George,E.I.(2000).Flexible empirical Bayes estimation for wavelets.J.R.Statist.Soc.B62,681–698.Clyde,M.,Parmigiani,G.and Vidakovic,B.(1998).Multiple shrinkage and subset selection in wavelets.Biometrika85,391–402.Cohen,A.,Daubechies,I.and Vial,P.(1993).Wavelets on the interval and fast wavelet transforms.p.Harm.Analysis1,54–81.Crouse,M.,Nowak,R.and Baraniuk,R.(1998).Wavelet-based statistical signal processing using hidden Markov models.IEEE Trans.Signal Processing46,886–902.Daubechies,I.(1992).Ten Lectures on Wavelets.SIAM,Philadelphia.Donoho,D.L.and Johnstone,I.M.(1994).Ideal spatial adaptation by wavelet shrinkage.Biometrika 81,425–455.Donoho,D.L.and Johnstone,I.M.(1995).Adapting to unknown smoothness via wavelet shrinkage.J.Am.Statist.Ass.90,1200–1224.18。
物理学专业英语

华中师范大学物理学院物理学专业英语仅供内部学习参考!2014一、课程的任务和教学目的通过学习《物理学专业英语》,学生将掌握物理学领域使用频率较高的专业词汇和表达方法,进而具备基本的阅读理解物理学专业文献的能力。
通过分析《物理学专业英语》课程教材中的范文,学生还将从英语角度理解物理学中个学科的研究内容和主要思想,提高学生的专业英语能力和了解物理学研究前沿的能力。
培养专业英语阅读能力,了解科技英语的特点,提高专业外语的阅读质量和阅读速度;掌握一定量的本专业英文词汇,基本达到能够独立完成一般性本专业外文资料的阅读;达到一定的笔译水平。
要求译文通顺、准确和专业化。
要求译文通顺、准确和专业化。
二、课程内容课程内容包括以下章节:物理学、经典力学、热力学、电磁学、光学、原子物理、统计力学、量子力学和狭义相对论三、基本要求1.充分利用课内时间保证充足的阅读量(约1200~1500词/学时),要求正确理解原文。
2.泛读适量课外相关英文读物,要求基本理解原文主要内容。
3.掌握基本专业词汇(不少于200词)。
4.应具有流利阅读、翻译及赏析专业英语文献,并能简单地进行写作的能力。
四、参考书目录1 Physics 物理学 (1)Introduction to physics (1)Classical and modern physics (2)Research fields (4)V ocabulary (7)2 Classical mechanics 经典力学 (10)Introduction (10)Description of classical mechanics (10)Momentum and collisions (14)Angular momentum (15)V ocabulary (16)3 Thermodynamics 热力学 (18)Introduction (18)Laws of thermodynamics (21)System models (22)Thermodynamic processes (27)Scope of thermodynamics (29)V ocabulary (30)4 Electromagnetism 电磁学 (33)Introduction (33)Electrostatics (33)Magnetostatics (35)Electromagnetic induction (40)V ocabulary (43)5 Optics 光学 (45)Introduction (45)Geometrical optics (45)Physical optics (47)Polarization (50)V ocabulary (51)6 Atomic physics 原子物理 (52)Introduction (52)Electronic configuration (52)Excitation and ionization (56)V ocabulary (59)7 Statistical mechanics 统计力学 (60)Overview (60)Fundamentals (60)Statistical ensembles (63)V ocabulary (65)8 Quantum mechanics 量子力学 (67)Introduction (67)Mathematical formulations (68)Quantization (71)Wave-particle duality (72)Quantum entanglement (75)V ocabulary (77)9 Special relativity 狭义相对论 (79)Introduction (79)Relativity of simultaneity (80)Lorentz transformations (80)Time dilation and length contraction (81)Mass-energy equivalence (82)Relativistic energy-momentum relation (86)V ocabulary (89)正文标记说明:蓝色Arial字体(例如energy):已知的专业词汇蓝色Arial字体加下划线(例如electromagnetism):新学的专业词汇黑色Times New Roman字体加下划线(例如postulate):新学的普通词汇1 Physics 物理学1 Physics 物理学Introduction to physicsPhysics is a part of natural philosophy and a natural science that involves the study of matter and its motion through space and time, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic disciplines, perhaps the oldest through its inclusion of astronomy. Over the last two millennia, physics was a part of natural philosophy along with chemistry, certain branches of mathematics, and biology, but during the Scientific Revolution in the 17th century, the natural sciences emerged as unique research programs in their own right. Physics intersects with many interdisciplinary areas of research, such as biophysics and quantum chemistry,and the boundaries of physics are not rigidly defined. New ideas in physics often explain the fundamental mechanisms of other sciences, while opening new avenues of research in areas such as mathematics and philosophy.Physics also makes significant contributions through advances in new technologies that arise from theoretical breakthroughs. For example, advances in the understanding of electromagnetism or nuclear physics led directly to the development of new products which have dramatically transformed modern-day society, such as television, computers, domestic appliances, and nuclear weapons; advances in thermodynamics led to the development of industrialization; and advances in mechanics inspired the development of calculus.Core theoriesThough physics deals with a wide variety of systems, certain theories are used by all physicists. Each of these theories were experimentally tested numerous times and found correct as an approximation of nature (within a certain domain of validity).For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These theories continue to be areas of active research, and a remarkable aspect of classical mechanics known as chaos was discovered in the 20th century, three centuries after the original formulation of classical mechanics by Isaac Newton (1642–1727) 【艾萨克·牛顿】.University PhysicsThese central theories are important tools for research into more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them. These include classical mechanics, quantum mechanics, thermodynamics and statistical mechanics, electromagnetism, and special relativity.Classical and modern physicsClassical mechanicsClassical physics includes the traditional branches and topics that were recognized and well-developed before the beginning of the 20th century—classical mechanics, acoustics, optics, thermodynamics, and electromagnetism.Classical mechanics is concerned with bodies acted on by forces and bodies in motion and may be divided into statics (study of the forces on a body or bodies at rest), kinematics (study of motion without regard to its causes), and dynamics (study of motion and the forces that affect it); mechanics may also be divided into solid mechanics and fluid mechanics (known together as continuum mechanics), the latter including such branches as hydrostatics, hydrodynamics, aerodynamics, and pneumatics.Acoustics is the study of how sound is produced, controlled, transmitted and received. Important modern branches of acoustics include ultrasonics, the study of sound waves of very high frequency beyond the range of human hearing; bioacoustics the physics of animal calls and hearing, and electroacoustics, the manipulation of audible sound waves using electronics.Optics, the study of light, is concerned not only with visible light but also with infrared and ultraviolet radiation, which exhibit all of the phenomena of visible light except visibility, e.g., reflection, refraction, interference, diffraction, dispersion, and polarization of light.Heat is a form of energy, the internal energy possessed by the particles of which a substance is composed; thermodynamics deals with the relationships between heat and other forms of energy.Electricity and magnetism have been studied as a single branch of physics since the intimate connection between them was discovered in the early 19th century; an electric current gives rise to a magnetic field and a changing magnetic field induces an electric current. Electrostatics deals with electric charges at rest, electrodynamics with moving charges, and magnetostatics with magnetic poles at rest.Modern PhysicsClassical physics is generally concerned with matter and energy on the normal scale of1 Physics 物理学observation, while much of modern physics is concerned with the behavior of matter and energy under extreme conditions or on the very large or very small scale.For example, atomic and nuclear physics studies matter on the smallest scale at which chemical elements can be identified.The physics of elementary particles is on an even smaller scale, as it is concerned with the most basic units of matter; this branch of physics is also known as high-energy physics because of the extremely high energies necessary to produce many types of particles in large particle accelerators. On this scale, ordinary, commonsense notions of space, time, matter, and energy are no longer valid.The two chief theories of modern physics present a different picture of the concepts of space, time, and matter from that presented by classical physics.Quantum theory is concerned with the discrete, rather than continuous, nature of many phenomena at the atomic and subatomic level, and with the complementary aspects of particles and waves in the description of such phenomena.The theory of relativity is concerned with the description of phenomena that take place in a frame of reference that is in motion with respect to an observer; the special theory of relativity is concerned with relative uniform motion in a straight line and the general theory of relativity with accelerated motion and its connection with gravitation.Both quantum theory and the theory of relativity find applications in all areas of modern physics.Difference between classical and modern physicsWhile physics aims to discover universal laws, its theories lie in explicit domains of applicability. Loosely speaking, the laws of classical physics accurately describe systems whose important length scales are greater than the atomic scale and whose motions are much slower than the speed of light. Outside of this domain, observations do not match their predictions.Albert Einstein【阿尔伯特·爱因斯坦】contributed the framework of special relativity, which replaced notions of absolute time and space with space-time and allowed an accurate description of systems whose components have speeds approaching the speed of light.Max Planck【普朗克】, Erwin Schrödinger【薛定谔】, and others introduced quantum mechanics, a probabilistic notion of particles and interactions that allowed an accurate description of atomic and subatomic scales.Later, quantum field theory unified quantum mechanics and special relativity.General relativity allowed for a dynamical, curved space-time, with which highly massiveUniversity Physicssystems and the large-scale structure of the universe can be well-described. General relativity has not yet been unified with the other fundamental descriptions; several candidate theories of quantum gravity are being developed.Research fieldsContemporary research in physics can be broadly divided into condensed matter physics; atomic, molecular, and optical physics; particle physics; astrophysics; geophysics and biophysics. Some physics departments also support research in Physics education.Since the 20th century, the individual fields of physics have become increasingly specialized, and today most physicists work in a single field for their entire careers. "Universalists" such as Albert Einstein (1879–1955) and Lev Landau (1908–1968)【列夫·朗道】, who worked in multiple fields of physics, are now very rare.Condensed matter physicsCondensed matter physics is the field of physics that deals with the macroscopic physical properties of matter. In particular, it is concerned with the "condensed" phases that appear whenever the number of particles in a system is extremely large and the interactions between them are strong.The most familiar examples of condensed phases are solids and liquids, which arise from the bonding by way of the electromagnetic force between atoms. More exotic condensed phases include the super-fluid and the Bose–Einstein condensate found in certain atomic systems at very low temperature, the superconducting phase exhibited by conduction electrons in certain materials,and the ferromagnetic and antiferromagnetic phases of spins on atomic lattices.Condensed matter physics is by far the largest field of contemporary physics.Historically, condensed matter physics grew out of solid-state physics, which is now considered one of its main subfields. The term condensed matter physics was apparently coined by Philip Anderson when he renamed his research group—previously solid-state theory—in 1967. In 1978, the Division of Solid State Physics of the American Physical Society was renamed as the Division of Condensed Matter Physics.Condensed matter physics has a large overlap with chemistry, materials science, nanotechnology and engineering.Atomic, molecular and optical physicsAtomic, molecular, and optical physics (AMO) is the study of matter–matter and light–matter interactions on the scale of single atoms and molecules.1 Physics 物理学The three areas are grouped together because of their interrelationships, the similarity of methods used, and the commonality of the energy scales that are relevant. All three areas include both classical, semi-classical and quantum treatments; they can treat their subject from a microscopic view (in contrast to a macroscopic view).Atomic physics studies the electron shells of atoms. Current research focuses on activities in quantum control, cooling and trapping of atoms and ions, low-temperature collision dynamics and the effects of electron correlation on structure and dynamics. Atomic physics is influenced by the nucleus (see, e.g., hyperfine splitting), but intra-nuclear phenomena such as fission and fusion are considered part of high-energy physics.Molecular physics focuses on multi-atomic structures and their internal and external interactions with matter and light.Optical physics is distinct from optics in that it tends to focus not on the control of classical light fields by macroscopic objects, but on the fundamental properties of optical fields and their interactions with matter in the microscopic realm.High-energy physics (particle physics) and nuclear physicsParticle physics is the study of the elementary constituents of matter and energy, and the interactions between them.In addition, particle physicists design and develop the high energy accelerators,detectors, and computer programs necessary for this research. The field is also called "high-energy physics" because many elementary particles do not occur naturally, but are created only during high-energy collisions of other particles.Currently, the interactions of elementary particles and fields are described by the Standard Model.●The model accounts for the 12 known particles of matter (quarks and leptons) thatinteract via the strong, weak, and electromagnetic fundamental forces.●Dynamics are described in terms of matter particles exchanging gauge bosons (gluons,W and Z bosons, and photons, respectively).●The Standard Model also predicts a particle known as the Higgs boson. In July 2012CERN, the European laboratory for particle physics, announced the detection of a particle consistent with the Higgs boson.Nuclear Physics is the field of physics that studies the constituents and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those in nuclear medicine and magnetic resonance imaging, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology.University PhysicsAstrophysics and Physical CosmologyAstrophysics and astronomy are the application of the theories and methods of physics to the study of stellar structure, stellar evolution, the origin of the solar system, and related problems of cosmology. Because astrophysics is a broad subject, astrophysicists typically apply many disciplines of physics, including mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic and molecular physics.The discovery by Karl Jansky in 1931 that radio signals were emitted by celestial bodies initiated the science of radio astronomy. Most recently, the frontiers of astronomy have been expanded by space exploration. Perturbations and interference from the earth's atmosphere make space-based observations necessary for infrared, ultraviolet, gamma-ray, and X-ray astronomy.Physical cosmology is the study of the formation and evolution of the universe on its largest scales. Albert Einstein's theory of relativity plays a central role in all modern cosmological theories. In the early 20th century, Hubble's discovery that the universe was expanding, as shown by the Hubble diagram, prompted rival explanations known as the steady state universe and the Big Bang.The Big Bang was confirmed by the success of Big Bang nucleo-synthesis and the discovery of the cosmic microwave background in 1964. The Big Bang model rests on two theoretical pillars: Albert Einstein's general relativity and the cosmological principle (On a sufficiently large scale, the properties of the Universe are the same for all observers). Cosmologists have recently established the ΛCDM model (the standard model of Big Bang cosmology) of the evolution of the universe, which includes cosmic inflation, dark energy and dark matter.Current research frontiersIn condensed matter physics, an important unsolved theoretical problem is that of high-temperature superconductivity. Many condensed matter experiments are aiming to fabricate workable spintronics and quantum computers.In particle physics, the first pieces of experimental evidence for physics beyond the Standard Model have begun to appear. Foremost among these are indications that neutrinos have non-zero mass. These experimental results appear to have solved the long-standing solar neutrino problem, and the physics of massive neutrinos remains an area of active theoretical and experimental research. Particle accelerators have begun probing energy scales in the TeV range, in which experimentalists are hoping to find evidence for the super-symmetric particles, after discovery of the Higgs boson.Theoretical attempts to unify quantum mechanics and general relativity into a single theory1 Physics 物理学of quantum gravity, a program ongoing for over half a century, have not yet been decisively resolved. The current leading candidates are M-theory, superstring theory and loop quantum gravity.Many astronomical and cosmological phenomena have yet to be satisfactorily explained, including the existence of ultra-high energy cosmic rays, the baryon asymmetry, the acceleration of the universe and the anomalous rotation rates of galaxies.Although much progress has been made in high-energy, quantum, and astronomical physics, many everyday phenomena involving complexity, chaos, or turbulence are still poorly understood. Complex problems that seem like they could be solved by a clever application of dynamics and mechanics remain unsolved; examples include the formation of sand-piles, nodes in trickling water, the shape of water droplets, mechanisms of surface tension catastrophes, and self-sorting in shaken heterogeneous collections.These complex phenomena have received growing attention since the 1970s for several reasons, including the availability of modern mathematical methods and computers, which enabled complex systems to be modeled in new ways. Complex physics has become part of increasingly interdisciplinary research, as exemplified by the study of turbulence in aerodynamics and the observation of pattern formation in biological systems.Vocabulary★natural science 自然科学academic disciplines 学科astronomy 天文学in their own right 凭他们本身的实力intersects相交,交叉interdisciplinary交叉学科的,跨学科的★quantum 量子的theoretical breakthroughs 理论突破★electromagnetism 电磁学dramatically显著地★thermodynamics热力学★calculus微积分validity★classical mechanics 经典力学chaos 混沌literate 学者★quantum mechanics量子力学★thermodynamics and statistical mechanics热力学与统计物理★special relativity狭义相对论is concerned with 关注,讨论,考虑acoustics 声学★optics 光学statics静力学at rest 静息kinematics运动学★dynamics动力学ultrasonics超声学manipulation 操作,处理,使用University Physicsinfrared红外ultraviolet紫外radiation辐射reflection 反射refraction 折射★interference 干涉★diffraction 衍射dispersion散射★polarization 极化,偏振internal energy 内能Electricity电性Magnetism 磁性intimate 亲密的induces 诱导,感应scale尺度★elementary particles基本粒子★high-energy physics 高能物理particle accelerators 粒子加速器valid 有效的,正当的★discrete离散的continuous 连续的complementary 互补的★frame of reference 参照系★the special theory of relativity 狭义相对论★general theory of relativity 广义相对论gravitation 重力,万有引力explicit 详细的,清楚的★quantum field theory 量子场论★condensed matter physics凝聚态物理astrophysics天体物理geophysics地球物理Universalist博学多才者★Macroscopic宏观Exotic奇异的★Superconducting 超导Ferromagnetic铁磁质Antiferromagnetic 反铁磁质★Spin自旋Lattice 晶格,点阵,网格★Society社会,学会★microscopic微观的hyperfine splitting超精细分裂fission分裂,裂变fusion熔合,聚变constituents成分,组分accelerators加速器detectors 检测器★quarks夸克lepton 轻子gauge bosons规范玻色子gluons胶子★Higgs boson希格斯玻色子CERN欧洲核子研究中心★Magnetic Resonance Imaging磁共振成像,核磁共振ion implantation 离子注入radiocarbon dating放射性碳年代测定法geology地质学archaeology考古学stellar 恒星cosmology宇宙论celestial bodies 天体Hubble diagram 哈勃图Rival竞争的★Big Bang大爆炸nucleo-synthesis核聚合,核合成pillar支柱cosmological principle宇宙学原理ΛCDM modelΛ-冷暗物质模型cosmic inflation宇宙膨胀1 Physics 物理学fabricate制造,建造spintronics自旋电子元件,自旋电子学★neutrinos 中微子superstring 超弦baryon重子turbulence湍流,扰动,骚动catastrophes突变,灾变,灾难heterogeneous collections异质性集合pattern formation模式形成University Physics2 Classical mechanics 经典力学IntroductionIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science, engineering and technology.Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. Besides this, many specializations within the subject deal with gases, liquids, solids, and other specific sub-topics.Classical mechanics provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light. When the objects being dealt with become sufficiently small, it becomes necessary to introduce the other major sub-field of mechanics, quantum mechanics, which reconciles the macroscopic laws of physics with the atomic nature of matter and handles the wave–particle duality of atoms and molecules. In the case of high velocity objects approaching the speed of light, classical mechanics is enhanced by special relativity. General relativity unifies special relativity with Newton's law of universal gravitation, allowing physicists to handle gravitation at a deeper level.The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz【莱布尼兹】, and others.Later, more abstract and general methods were developed, leading to reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances were largely made in the 18th and 19th centuries, and they extend substantially beyond Newton's work, particularly through their use of analytical mechanics. Ultimately, the mathematics developed for these were central to the creation of quantum mechanics.Description of classical mechanicsThe following introduces the basic concepts of classical mechanics. For simplicity, it often2 Classical mechanics 经典力学models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it.In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.Classical mechanics uses common-sense notions of how matter and forces exist and interact. It assumes that matter and energy have definite, knowable attributes such as where an object is in space and its speed. It also assumes that objects may be directly influenced only by their immediate surroundings, known as the principle of locality.In quantum mechanics objects may have unknowable position or velocity, or instantaneously interact with other objects at a distance.Position and its derivativesThe position of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle.In general, the point particle need not be stationary relative to O, so r is a function of t, the time elapsed since an arbitrary initial time.In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry for the structure of space.Velocity and speedThe velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time. In classical mechanics, velocities are directly additive and subtractive as vector quantities; they must be dealt with using vector analysis.When both objects are moving in the same direction, the difference can be given in terms of speed only by ignoring direction.University PhysicsAccelerationThe acceleration , or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time).Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both . If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration , but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.Inertial frames of referenceWhile the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames .An inertial frame is such that when an object without any force interactions (an idealized situation) is viewed from it, it appears either to be at rest or in a state of uniform motion in a straight line. This is the fundamental definition of an inertial frame. They are characterized by the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth).A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame.A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are un-accelerated with respect to the distant stars are regarded as good approximations to inertial frames.Forces; Newton's second lawNewton was the first to mathematically express the relationship between force and momentum . Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":a m t v m t p F ===d )(d d dThe quantity m v is called the (canonical ) momentum . The net force on a particle is thus equal to rate of change of momentum of the particle with time.So long as the force acting on a particle is known, Newton's second law is sufficient to。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :c o n d -m a t /9801245v 2 [c o n d -m a t .m e s -h a l l ] 2 M a r 1998The probability for a wave packet to remain in a disordered cavity .Daniel lerDept.of Physics of Complex Systems,The Weizmann Institute of science,Rehovot,76100Israele-mail fndaniil@wicc.weizmann.ac.il(February 1,2008)We show that the probability that a wave packet will remain in a disordered cavity until the time t decreases exponentially for times shorter than the Heisenberg time and log-normally for times much longer than the Heisenberg time.Our result is equivalent to the known result for time-dependent conductance;in particular,it is independent of the dimensionality of the cavity.We perform non-perturbative ensemble averaging over disorder by making use of field theory.We make use of a one-mode approximation which also gives an interpolation formula (arccosh-normal distribution)for the probability to remain.We have checked that the optimal fluctuation method gives the same result for the particular geometry which we have chosen.We also show that the probability to re-main does not relate simply to the form-factor of the delay time.Finally,we give an interpretation of the result in terms of path integrals.PACS numbers:73.23.-b,03.65.NkThe interest of experimentalists in open quantum dots 1motivates the computation of the probability to remain in a weakly disordered cavity.This problem is similar to the computation of the time dependent conductance of weakly disordered samples 2–4.However the geometry of our problem allows a simple computation scheme,which is similar to the zero-dimensional non-linear σ-model.Let us assume that we have a weakly disordered open cavity and the whole system is filled by non-interacting fermions at zero temperature.At time t =0the Fermi level outside of the cavity decreases and particles begin to escape from the cavity.The probability for the par-ticles to remain in the cavity of volume S till time t is given by the ratiop (t )=S̺( r ,t )d r∂t−D ∇2̺(r ,t )=0(2)with the boundary conditions n ∇̺=0at the walls of the cavity ( n is normal to the boundary)and ̺+0.71ℓ n ∇̺=0at the open edge of the cavity.5Here ℓis the mean free path and the scattering is uniform.In further cal-culations we will use the open edge boundary condition ̺=0,assuming that ℓis much smaller than all the char-acteristic lengths of the system.The solution of the diffusion equation can be repre-sented as a sum over diffusion modes,each of them de-caying exponentially at its own rate.The “lowest”diffu-sion mode is computed in Appendix A for two examplesof circular and spherical cavities with the contact in the middle,see Fig.1.Therefore the probability to remain in the cavity behaves like p (t )=e −γt ,where γis the decay rate of the “lowest”diffusion mode.This escape rate is proportional to the size of the contact and may vary from zero to the inverse diffusion time through the system E c /¯h .In the rest of the paper we will use units where ¯h =1,and then we have in general0≤γ≤E c .(3)̺=0∇r ̺=0In order to compute the probability to remain in the cav-ity we should prepare our system in the stateρ( r 2, r 3,0)=d pe i p ( r 2− r 3)̺(r 2+ r 32))(5)where H ( p , r )is the Hamiltonian of the system,and ̺( r ,0)is one inside the cavity and zero outside.The quantum-mechanical expression for the probability to re-main is thereforep (t )=Sρ( r , r ,t )d r 2πνSdω2( r 1, r 2)G A E F −ω2∆arccosh 2t ∆2πνS dω2)T (E F −ω2πνSdω2( r 1, r 1)G A E F −ω2π,1),(11)where the superscript “unit”means that the form-factorwas computed as if the system is notsymmetrical under the time reversal,and p (t )isgivenbyEq.(7).From the definition Eq.(9)one can see that the form factor of the delay time K γ(t )approaches the form factor of the density of states K 0(t )when γgoes to zero and this is consistent with Eqs.(7)and (10).The decay rate of the lowest diffusion mode,γ→0,when the opening of the cavity becomes smaller L 1→0,see Eqs.(A3)and (A7).In this case all particles remains in the cavity forever and our solution gives p (t )→1.Our results are inconsistent with the random ma-trix theory 12–15,which predicts a power law decay of both K γ(t )and p (t )if the number of open channels is much smaller than the dimensionality of the Hamilto-nian.However,on the short time scale,t ∆≪1,one has from Eq.(7)−log(p (t ))=γt1−t ∆νSδ[t −T j ( r 1, r 2,E F )],(14)where T j is the time which takes the particle with energyE F to go from the point r 1to the point r 2along the path j .Equation (14)is equivalent to Eq.(1)and there-fore p diag (t )=e −γt is the classical probability to remain.2Therefore,the log-normal tail of the quantum probabil-ity to remain represented in Eq.(7)is determined by the off-diagonal part of the sum over trajectories in Eqs.(6) and(13).It is known that the integrals over coordinates in Eq.(14)can be computed by using the skeleton of the periodic orbits19,20p diag(t)= j T j∞ r=1δ(t−rT j)2πp diag(t),(16)which is in agreement with our result Eq.(10)taken for short times.Let us assume that the leakage is so small,that all gradients are small on the scale of the mean free path. The averaging of the product of two Green functions from Eq.(6)is given by the functional integralG R G A =2(πν)2 Q2=1Q12αβ( r1)kββQ21βα( r2)e−F[Q]DQ(17)F[Q]=πν2 SD(∇θ)2+D(∇θ1)2+2(iω−0)(cosθ−coshθ1) d r,(20)whereˆθ=0at the contact and n ∇ˆθ=0at the walls.The same boundary conditions were applied to Eq.(2)and therefore we can use the diffusion modes for comput-ing the functional integral overˆθ(r).Due to the conditionEq.(8a)only the lowest diffusion mode contributes andthe functional integral becomes a conventional integralover the amplitude of this modeˆΘ.The lowest diffusionmode is almost uniform,see Appendix A,and therefore1S Sθ21d r=Θ21,1S S coshθd r=coshΘ,1Q1221Q2112=−8ηη∗κκ∗(sin2Θ+sinh2Θ1)(21) We computed this factor explicitly from the expressions for Q12and Q21.This expression was computed in Ap-pendix3of Ref.6but the numeric coefficients are differ-ent.The model reduces to the conventional integralp(t)=−2(πν)2 dω2πe−iωt × e−F coshΘ1+cosΘ∆ γΘ2+Θ212 1max(−1,1−t∆/π)dλt∆/π+2λ2∆(arccos2(λ)+arccosh2(t∆/π+λ)).(24) For both short times t≪π/∆and long times t≫π/∆we can putλ=1in the exponent on the right hand side of Eq.(24).Then the integral can be computed exactly and we arrive at our interpolation formula Eq.(7).The computation of the form-factor is similar,K unitγ(t)=12∆(arccos2(λ)+arccosh2(t∆/π+λ)).(25)and Eq.(10)matches both short and long time asymp-totes of Eq.(25).Both results Eqs.(24)and(25)where derived under the condition Eq.(19)which becomes Eq.(8c)in the one-mode approximation.The functional integral overˆθ( r)in the theory with action Eq.(20)can be computed by the optimalfluctu-ation method3,4,23.The calculations are straightforward and give the same results,see Appendix B,where we have checked the three dimensional case.In the same way one can also check the two dimensional result.In the present work we have assumed that the opening or contact is small.If it is not the case for some system the result for the probability to remain may be different. In such a system one should consider the optimalfluctu-ations of the random potential24.In our geometry this method can be used for very long times,which broke the condition Eq.(8c).In summary,we have obtained the arccosh-normal dis-tribution for the probability to remain in a disordered cavity.We made use of the one-mode approximation, which is similar to both the zero-dimensionalσ-model and the optimalfluctuation method.Our result is not consistent with the random matrix theory prediction.ACKNOWLEDGMENTSIt is my pleasure to thank prof.Uzy Smilansky for important remarks and discussions.This work was sup-ported by Israel Science Foundation and the Minerva Center for Nonlinear Physics of Complex systems.γγγγγL22log L2We see that the mode is non-uniform for roughly L1< r<L2/2.Therefore the presence of the contact strongly affects the diffusion mode in a quarter of the cavity area. In the case of the three dimensional sphere it might be difficult to maintain the contact in the middle,but it is still interesting to compute the lowest diffusion mode.In three dimensions the lowest mode is independent of polar and azimuthal angles and depends only on the distance r from the center.The lowest mode in three dimensions is̺(r)∝13L1(r−L1)2γγ(L2−L1)2r −L1L2 2(A6)γ=3L1D/L32(A7) and its shape is similar to that which is shown in Fig.2.APPENDIX B:THE OPTIMAL FLUCTUATION METHOD IN THREE DIMENSIONS.According to the optimalfluctuation method the prob-ability to remain is given by the following system of equations3p(t)∝e−πνr),(B4) A/e A=iωL32∆e A(B6)p(t)∝e−3πDL32=e−πγπ(B7)whereγis given by Eq.(A7).This result is preciselyequal to our one mode result Eq.(7)in the long timelimit.。
