徐汇区北片2008学年八年级第二学期期末数学考试试卷
2008学年度8年级下学期期末测试数学试题及其答案1.1(印刷版)

-1-2008学年第二学期八年级 数学科期末测试题(答案附后)一、选择题(本大题共10小题,每小题2分,满分20分.在每小题给出的四个选项中,只有一项是符合题目要求的,请选出来,填入下表中相对应的表格.) 1.如图1,在等腰梯形ABCD 中,AD BC ∥,70B ∠=, 则C =∠(※).(A )60 (B ) 68 (C )70 (D )1102. 某校8年级(2)班的10名同学某天的早餐费用分别为(单位:元):2 、5、3、3 、4、5 、3 、6 、5、3, 在这组数据的众数是(※).a (A )3 (B ) 3.5 (C )4 (D )6 3. 如图2是一个外轮廓为矩形的机器零件平面示意图, 根据图中的尺寸(单位:m m ),可以计算出两圆孔 中心A 和B 的距离为(※)m m .(A )120 (B ) 135 (C ) (D )150 4. 下列运算正确的是(※).(A )61233()b a b a -= (B )121231111R R R R ++==(C ) 51233()b a b a -= (D )1212112R R R R +=+5.如图3,已知□ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点,点A 的坐标为(-2,3),则点C 的坐标为(※).D(A )(-3,2) (B)(-2,-3) (C )(3,-2) (D )(2,-3)A D CB图1 图2图3-2-6. 下面命题中错误..的是(※). (A )梯形是轴对称图形(B )三角形的三条中线交于一点(C )菱形的四条边都相等 (D )有一个角是直角的菱形是正方形7.已知广州市的土地总面积约为7434 km 2,人均占有的土地面积S (单位:km 2/人)随全市人口n (单位:人)的变化而变化,则S 与n 的函数关系式为(※). B (A )7434S n = (B )7434S n=(C ) 7434n S = (D )7434nS =8.如图4,直线l 上有三个正方形A 、B 、C ,若A 、C 的面积分别为5和11,则正方形B 的面积为(※).C(A )4(B )6(C )16(D )559. 如图5,函数y x m =+与(0)my m x=≠在同一坐标 系内的图象可能是(※).b10. 矩形的面积为12cm 2,周长为14cm ,则它的对角线长为(※).(A )5cm (B )6cm (C(D)二、填空题(共6题,每题2分,共12分,直接把最简答案填写在题中的横线上)11.当_________x =时,分式11x x +-的值为0. 12.点(1,3)在反比例函数ky x=的图象上,则_________.k = 13.人体中成熟的红细胞的平均直径为0.00000077m ,用科学记数法表示0.00000077的结果为 .14.写出命题“直角三角形两直角边的平方和等于斜边的平方”的逆命题:. 15. 如图6,在菱形ABCD 中,对角线6AC cm =,5BC cm =,则菱形ABCD 的面积为 .xxxx 图5 (B )(A) (C) (D)图4-3-16. 如图7是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为:2S 甲 2S 乙.三、解答题(本大题共9小题,满分68分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分6分,每题3分)计算: (1)2324510m m n n ÷; (2)2235325953x x x x x ÷⨯--+.图71 2 3 4 5 6 7 8 9 10ODCBA 图6-4-如图8,是反比例函数5m y x-=(1) 图象的另一支位于哪个象限?常数m (2) 在这个函数图象的某一支上任取两点(,)A a b 若a c <,那么b 和d 有怎样的大小关系?19.(本小题满分7分)在“心系灾区”自愿捐款活动中,某班50名同学的捐款情况如下表: (1)问这个班级捐款总数是多少元? (2)求这50名同学捐款的平均数、中位数. (3)从表中你还能得到什么信息?(只写一条即可)图8-5-有一道试题:“先化简,再求值:22361()399x x x x x -+÷+--,其中“x =.小亮同学在做题时把“x =x =,但他的计算结果确也是正确,请你说明这是什么原因?21.(本小题满分8分)如图9,在梯形ABCD 中,AE BC ⊥于E ,DF BC ⊥于F ,且BE CF =. (1) 求证:梯形ABCD 为等腰梯形;(2) 若2AD AE ==,4BC =,求腰AB 的长.图9FEDCB A-6-22.(本小题满分8分)某中学八年级同学去距学校10千米远的工厂参加综合实践活动,一部分同学骑自行车先走,半小时后,其余同学再乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学的速度的2.5倍,求骑车同学和汽车的速度.23.(本小题满分8分)如图9,已知ABC ∆的两边AB 、AC 的中点分别为M 、N . (1) 线段MN 是ABC ∆的什么线? (2) 求证://MN BC ,且12MN BC =.图9B-7-如图10,已知(4,2)A -、(,4)B n -是一次函数y kx b =+的图象与反比例函数m y x=的图象的两个交点.(1) 求此反比例函数和一次函数的解析式; (2) 根据图象写出使一次函数的值小于反比 例函数的值的x 的取值范围.(3)过A 作AC y ⊥轴于点C ,过B 作BD y ⊥ 轴于点,D 连结AD 、BC ,试判断四边形ADBC 是否是平行四边形?并求出此四边形的面积。
上海徐汇区北片联考初二数学试卷

期终考试初中北片联考 初二数学 试题(考试时间 90 分钟,满分100分)一、填空题(本大题共14题,每题2分,共28分)1.若直线32+=x y 与直线1-=kx y 平行,则________=k .2.若点(3,a )在一次函数13+=x y 的图像上,则=a .3.一次函数14-=x y , y 的值随x 值的增大而________.(填“增大”、“减小”或“不变”)4.如图,一次函数y kx b =+的图象经过A ,B 两点,则0kx b +>的解集是 .5.方程x x -=的根是 .6.方程33)2(42322=++-++x x x x ,若用换元法设232++=x x y ,原方程可变形为 . 7.方程04324=--x x 的根是 . 8.方程组⎩⎨⎧-=-=-3122y x y x 的解是 . 9.一个骰子六个面上的数字分别为1、2、3、4、5、6,投掷一次,向上的一面是奇数的概率是 .10.菱形的两条对角线长分别是6和8,则菱形的边长为 .11.如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同 形状的四边形,请写出其中一种四边形的名称 .12.梯形的上底、下底的长分别是2cm 和4cm ,那么此梯形的中位线 长是______cm 。
13.如图,把一张矩形纸片ABCD 沿EF 折叠后,点C D ,分别落在C D '',的位置上,EC '交AD 于点G .已知58EFG ∠=°,那么BEG ∠= °.14.如图,梯形ABCD 中,AB ∥CD ,CD AB 2=,AD a = , AB b =,请用向量ba 、表示向量= .二、选择题(本大题共4题,每题2分,共8分)15.如图,梯形ABCD 中,AD ∥BC ,AD=AB ,BC=BD ,∠A =100°,则∠C = ………………………………………………… ( )A.80°B.70°C.75°D.60°16.下列命题中错误的是………………………………………………… ( )(A )矩形的两条对角线相等;(B )等腰梯形的两条对角线互相垂直;(C )平行四边形的两条对角线互相平分;(D )正方形的两条对角线互相垂直且相等.17.如图,在周长为20cm 的□ABCD 中,AB ≠AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则△ABE 的周长为……………( )(A)15cm (B)20cm(C)5cm (D)10cm18.从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y kx b =+的系数k ,b ,则一次函数y kx b =+的图象不经过第四象限的概率是……………………( ). (A)21 (B) 31 (C) 41 (D) 61三、简答题(本大题共5题,每题6分,共30分)19.解方程212=-+x x 20.解方程:23416222+=---+x x x x21.解方程组:⎩⎨⎧=+=--320222y x y xy x22.小东从A 地出发以某一速度向B 地走去,同时小明从B 地出发以另一速度向A 地而行,如图所示,图中的线段1l 、2l 分别表示小东、小明离B 地的距离(千米)与所用时间(小时)的关系。
2008 年八年级(下)数学期末试卷

2008 年八年级(下)数学期末试卷满分120分(人教版版用)一、选择题(每小题3分,共18分)下列各小题均有四个答案,其中只有一个是正确的,请将正确答案的代号字母填入题后括号内。
1.已知反比例函数1y x=-,则其图象在平面直角坐标系中可能是( )2. 以下列各组数据为边长,可以构成直角三角形的是(). A .3、5、6 B .2、3、4 C .6、7、9 D .1.5、2、2.53. 对角线互相垂直平分且相等的四边形一定是( ). A.正方形 B.菱形 C.矩形 D.等腰梯形4. 在某城市,80%的家庭年收入不少于2.5万元,下面一定不少于2.5万元的是( ) A .年收入的平均数 B .年收入的众数 C .年收入的中位数 D .年收入的平均数和众数5.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是A B C D6.长沙地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,37,36,37,37(单位℃).则这组数据的中位数和众数分别是( ) A.36,37 B.37,36 C.36.5,37 D.37,36.5二、填空题(每小题3分,共27分) 7.函数3y x=-的图象经过点(1)a -,,则a = .8. 如图,直角AOB ∠内的任意一点P 到这个角的两边的距离之和为6,则图中四边形的周中点 中点长为 .9.方程2101x x-=-的解是 .10.使分式13x x -+有意义的x 的取值范围是 .11.化简:333x x x+-- = .12.如图,在等腰梯形ABCD 中,AD BC ∥,AC 、BD 相交于点O ,有如下五个结论: ①AOD BOC △∽△; ②DAC DCA ∠=∠; ③梯形ABCD 是轴对称图形;④AOB AOD △≌△; ⑤AC BD =. 请把其中正确结论的序号填写在横线上 .13.如图,E 、F 是 ABCD 对角线BD 上的两点,请你添加一个适当的条件: ,使四边形AECF 是平行四边形.14.某学校举行理科(含数学、物理、化学、生物四科)综合能力比赛,四科的满分都为综合成绩按照数学、物理、化学、生物四科测试成绩的的比例计分,则综合成绩的第一名是 .D15. 如图,已知圆柱体底面圆的半径为2π,高为2,AB CD ,分别是两底面的直径,AD BC ,是母线.若一只小虫从A 点出发,从侧面爬行到C 点,则小虫爬行的最短路线的长度是 (结果保留根式).三、解答题(本题共8道小题,第16小题8分,第9 ~ 20小题各9分,第21、22小题各10分,第23题11分,共75分)16.(8分)已知:两个分式1111A x x =-+-,221B x =-,其中 1x ≠±.下面三个结论:①A B =,②A B ,互为倒数, ③A B ,互为相反数.请问这三个结论中哪一个结论正确?为什么? 17.(9分)在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成.(1)求乙工程队单独完成这项工程所需的天数; (2)求两队合做完成这项工程所需的天数.18.(9分)你吃过拉面吗?实际上做拉面的过程中就渗透着数学知识:一定..体积的面团做成拉面,面条总长度y (m )是面条的粗细(横截面积)s (mm 2)的反比例函数,其图象如图所示.(1)写出y 与s 的函数关系式;(2)求当面条粗1.6 mm 2时,面条的总长度...是多少米?2)19.(9分)如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC =60°, ∠DAE =45°,点D 到地面的垂直距离DE =32m ,求点B 到地面的垂直距离BC .20.(9分)如图,在ABC △中,AB BC =,D、E、F分别是BC 、AC 、AB 边上的中点.(1) 求证:四边形BDEF 是菱形;(2) 若12AB =cm ,求菱形BDEF 的周长.21.(10分)为了调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了8名学生,他们每天完成作业所需时间(单位:分)分别为60,55,75,55,55,43,65,40.(I )求这组数据的众数、中位数;(II )求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过60分钟,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?22.(10分)已知:如图,在梯形ABCD 中,AD BC ∥,90ABC ∠= ,45C ∠=,BE CD ⊥于点E ,1AD =,CD =求:BE 的长.23.(11分)一次期中考试中,A B C D E ,,,,五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)60 ︒ 45 ︒ AB C D EA B D C(1(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A 同学在本次考试中,数学与英语哪个学科考得更好?友情提示:一组数据的标准差计算公式是S =,其中x 为n 个数据12n x x x ,,…,的平均数.八年级(下)期末试卷数学参考答案和评分标准(人教版)一、1.A 2.D 3.A 4.C 5.B 6.A二、7.3 8.12 9.1x =- 10.3x ≠- 11.1 12.①③⑤13.BE DF =等(只要符合条件即可 14.甲 15. 三、16.解:A B ,是互为相反数.2111(1)211(1)(1)1x x A x x x x x --+=-==-+-+--A B ∴=-.即A B ,是互为相反数. 17.解:(1)设乙工程队单独完成这项工程需要x 天,根据题意得:101120140x x ⎛⎫++⨯= ⎪⎝⎭解之得:60x = 经检验:60x =是原方程的解. 答:乙工程队单独完成这项工程所需的天数为60天.(2)设两队合做完成这项工程所需的天数为y 天,根据题意得: 1114060y ⎛⎫+=⎪⎝⎭解之得:24y = 答:两队合做完成这项工程所需的天数为24天.18.解:(1)设y 与s 的函数关系式为ky s=. 由图象可知,当4s =时,32y =,所以432128k =⨯=. 所以y 与s 的函数关系式为128y s=. (2)当 1.6s =时,128801.6y ==,所以面条的总长度是80m .19.解:在Rt △DAE 中,45DAE ∠=,DE =,s i n 45DEAD=∴.6AD =∴m . 在Rt △ACB 中,60BAC ∠=,6AB AD ==m ,s i n 60BCAB=∴.BC =∴.∴点B 到地面的垂直距离BC 为.20.解:(1)∵D 、E 、F 分别是BC 、AC 、AB 边上的中点,DE AB ∴∥ E FB C ∥ ∴四边形BDEF 是平行四边形.又12DE AB =,12EF BC =,且AB BC = DE EF =∴∴四边形BDEF 是菱形.另解: ∵D 、E 、F 分别是BC 、AC 、AB 边上的中点,12DE AB =∴,12EF BC =又AB BC =∵1122BD BF AB BC ===∴∴DE EF BF BD === ∴四边形BDEF 是菱形.(2)12AB =∵cm ,F 为AB 的中点, 6BF =∴cm ,∴菱形BDEF 的周长为:4624⨯=cm .21.解:(I )在这8个数据中,55出现了3次,出现的次数最多,即这组数据的众数是55; 将这8个数据按从小到大的顺序排列,其中最中间的两个数据都是55,即这组数据的中位数是55.(II ) 这8个数据的平均数是1(6055755555436540)568x =+++++++=(分).∴这8名学生完成家庭作业所需的平均时间为56分钟. 因为5660<,由此估计该班学生每天完成家庭作业的平均时间符合学校的要求.22.解:解:如图,过点D 作DF AB ∥交BC 于点F . 因为AD BC ∥,所以四边形ABFD 是平行四边形.所以1BF AD ==. 由DF AB ∥, 得90DFC ABC ∠=∠=.在Rt DFC △中,45C ∠=,CD =由cos CFC CD=, 求得2CF =.所以3BC BF FC =+=.在BEC △中,90BEC ∠=, sin BEC BC=.求得BE =.23.解:(1)数学考试成绩的平均分x 数学1(7172696870)705=++++=, 英语考试成绩的标准差S英语6=. (2)设A 同学数学考试成绩标准分为P 数学,英语考试成绩标准分为P英语,则P数学(7170)2=-=,P 英语1(8885)62=-÷=.P 数学>P 英语,∴从标准分来看,A 同学数学比英语考得更好.。
2008-2009-2010三年上海八年级第二学期数学期末试卷及评分标准

2008学年度第二学期期末质量抽测 初二数学试卷(考试时间:90分钟;满分:100分)一、选择题:(本大题共6题,每题2分,满分12分)1.下列四个函数中,一次函数是……………………………………………………………( ) (A)x x y 22-=; (B)2-=x y ; (C)11+=xy ; (D)1+=x y .2.在平面直角坐标系中,直线1y x =-经过…………………………………………( ) (A )第一、二、三象限; (B )第一、二、四象限; (C )第一、三、四象限;(D )第二、三、四象限.3.下列四个命题中真命题是 ……………………………………………………………( ) (A)矩形的对角线平分对角; (B)菱形的对角线互相垂直平分;(C) 梯形的对角线互相垂直;(D)平行四边形的对角线相等.4.如果点C 是线段AB 的中点,那么下列结论中正确的是………………………………( ) (A )0=+(B )0=- (C )=+ (D )=-5.从2,3,4,5,6中任取一个数,是合数的概率是…………………………………( ) (A )51; (B )52; (C )53; (D )54. 6.下列事件是必然事件的是 ……………………………………………………………( ) (A)方程34-=+x 有实数根; (B)方程0222=-+-xxx 的解是2=x ; (C)方程410x -=有实数根; (D)方程23x x =只有一个实数根.二、填空题:(本大题共12题,每题3分,满分36分) 7.一次函数23+=x y 的截距是_______________. 8.已知函数()31f x x =-,则(2)f =__________.9.已知一次函数4)2(+-=x k y ,y 随x 的增大而减小,那么k 的取值范围是_________. 10.已知一次函数123y x =+,当2y >-时,自变量x 的取值范围是_________. 11.已知一次函数的图像与x 轴交于点(3,0),且平行于直线32--=x y ,则它的函数解(第17题图)析式为_______________________.12.方程04324=--x x 的根是 . 13.用换元法解分式方程23202x x x x ---=-时,如果设2x y x-=,则原方程可化为关于y 的整式方程是_________________________.14.十二边形内角和为 度.15.如果等腰梯形的一条底边长8cm ,中位线长10 cm ,那么它的另一条底边长是 cm .16.一个可以自由转动的转盘被等分成六个扇形区域,并涂上了相应的颜色,如图所示.随意转动转盘,转盘停止后,指针指向蓝色区域的概率是 .17.如图,在平行四边形ABCD 中,已知AB=5 cm , AC=12㎝,BD=6㎝,则△AOB 的周长为 ㎝.18.平行四边形ABCD 中,3,4==BC AB ,∠B =60°,AE 为BC 边上的高,将△ABE 沿AE 所在直线翻折后得△AFE ,那么△AFE 与四边形AECD 重叠部分的面积是 .三、解答题:(本大题共7题,满分52分)19.(本题满分6分) 20.(本题满分6分)解方程: 011=-+-x x 解方程组:⎩⎨⎧=+=--320222y x y xy x21.(本题满分6分)如图,已知在梯形ABCD 中,AD // BC ,点E 在边BC 上,联结DE ,AC .(第16题图)OFEDCBAOGE DCBA(1)填空:=+___________;=-____________; (2)在图中求作:++. (不要求写作法,但要写出结论)22.(本题满分7分)如图,已知矩形ABCD 中,AC 与BD 交于点O ,AC BE ⊥,BD CF ⊥,垂足分别是E 、F .求证:CF BE =.23.(本题满分7分)如图,点O 是⊿ABC 内任意一点, G 、D 、E 分别为AC 、OA 、OB 的中点,F 为BC 上一动点,问四边形GDEF 能否为平行四边形?若可以,指出F 点位置,并给予证明.24.(本题满分8分)小李家离某书店6千米,他从家中出发步行到该书店,由于返回时步行速度比去时步行速度每小时慢了1千米,结果返回时多用了半小时,求小李去书店时的步行速度.A CEBD(第21题图)(第22题图)(第23题图)25.(本题满分12分,其中第(1)小题5分,第(2)小题3分,第(3)小题4分)在梯形ABCD 中, AD ∥BC ,cm AD CD AB 5===,BC =11cm ,点P 从点D 开始沿DA 边以每秒1cm 的速度移动,点Q 从点B 开始沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y(cm 2).(1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值; (3)在移动的过程中,是否存在x 使得PQ=AB ,若存在求出所有x 的值,若不存在请说明理由.CBP(第25题图)初二数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题2分,满分12分) 1.B ; 2.B ; 3.B ; 4.C ; 5.B ; 6.C ;二、填空题:(本大题共12题,每题3分,满分36分)7.2; 8.5; 9.k ﹤2;; 10.12->x 11.62+-=x y ; 12.21=x ,22-=x ; 13.0322=--y y ; 14.1800; 15.12; 16.31; 17.14; 18.437.三、解答题:(本大题共7题,满分52分) 19.(本题满分6分) 解:11+=-x x ……………………………………………………………………………(1分)1122+=+-x x x …………………………………………………………………… (1分) 032=-x x ……………………………………………………………………………(1分)解得3,021==x x ………………………………………………………………………(2分) 经检验原方程的根是3=x ……………………………………………………………(1分)20.(本题满分6分)解:由①得02=-y x 或0=+y x ……………………………………(2分)原方程组可化为:⎩⎨⎧=+=-3202y x y x 和⎩⎨⎧=+=+320y x y x ………………………… (2分)解这两个方程组得原方程组的解为:⎪⎪⎩⎪⎪⎨⎧==53,5611y x ⎩⎨⎧-==3322y x .……………………(2分)21.(本题满分6分)(1)AC , ………………………………………………………………………(4分) (2)画图………………………………………………………………………………(1分)结论………………………………………………………………………………(1分)22.(本题满分7分)证法一: 四边形ABCD 是矩形∴CD AB =,CD AB //………………………………………………………………(2分)∴CDF BAE ∠=∠……………………………………………………………………(1分)AC BE ⊥,BD CF ⊥∴ 90=∠=∠CFD BEA ……………………………………………………………(1分) ∴△ABE ≌△DCF ……………………………………………………………………(2分) ∴CF BE =……………………………………………………………………………(1分) 证法二: 四边形ABCD 是矩形∴BD AC =,BD BO 21=,AC CO 21=…………………………………………(2分) ∴CO BO =……………………………………………………………………………(1分)AC BE ⊥,BD CF ⊥∴90=∠=∠CFO BEO ……………………………………………………………(1分) COF BOE ∠=∠…………………………………………………………………(1分) ∴△BOE ≌△COF ……………………………………………………………………(1分) ∴CF BE =……………………………………………………………………………(1分)23.(本题满分7分)答:当F 为BC 中点时,四边形GDEF 为平行四边形……………………………(2分) 证明:∵G 、F 分别是AC 、BC 中点,∴GF ∥AB ,且GF =21AB ……………………………………………………(2分) 同理可得,DE ∥AB ,且DE =21AB …………………………………………(1分)∴GF ∥DE ,且GF =DE∴四边形GDEF 是平行四边形………………………………………………(2分)24.(本题满分8分)解:设小李去书店时的速度为每小时x 千米,根据题意得…………………………(1分)21616=--x x ……………………………………………………………………………(2分) 整理得0122=+-x x ………………………………………………………………(1分) 解得41=x ,32-=x (不合题意舍去)……………………………………………(2分) 经检验4=x 是原方程的根且符合题意………………………………………………(1分) 答:小李去书店时的速度为4千米/小时.…………………………………………(1分)25.(本题满分12分,其中第(1)小题5分,第(2)小题3分,第(3)小题4分)解:(1)过A 作BC AE ⊥垂足为E ,过D 作BC DF ⊥垂足为F 易证DF AE // ∵EF AD //∴四边形AEFD 是平行四边形∴EF=AD=5,AE=DF …………………………………………………………………(1分) ∵AB=CD=5∴RT △ABE ≌RT △DCF ∴BE=CF∵6=-=+EF BC CF BE ∴BE=CF=3在RT △ABE 中,422=-=BE AB AE …………………………………………(1分)∵AE BQ AP S ABQP ⋅+=)(21,x BQ x AP x PD 2,5,=-==∴x x x y 2104)25(21+=⨯+-=…………………………………………………(2分) 定义域为50<<x ……………………………………………………………………(1分) (2)同(1)理x x x AE PD CQ S QCDP 2224)211(21)(21-=⨯-+=⋅+=∵Q CD P ABQ P S S =∴x x 222210-=+…………………………………………………………………(1分) 解得3=x …………………………………………………………………………(1分) ∴当四边形ABQP 与四边形QCDP 的面积相等时3=x …………………………(1分) (3)当四边形ABQP 是平行四边形时,PQ=AB ,此时AP=BQ ,可得x x 25=-,解得35=x ………………………………………(2分) 当四边形QCDP 是平行四边形时,可得PQ=CD ∵CD=AB ∴PQ=AB 此时CQ PD =,可得x x 211-= 解得311=x …………………………………(2分) 综上所述,在移动的过程中,当35=x 或311时,PQ=AB .2009学年度第二学期期末质量抽测 初二数学试卷(完卷时间:90分钟,满分:100分)1.一次函数24--=x y 的截距是( ).(A)4; (B)-4;(C)2; (D)-2. 2.下面的方程组,不是二元二次方程组的是( ).(A) ⎩⎨⎧==-;2,32y x x (B)()()⎩⎨⎧=+--=;11,1x y x x y (C) ⎩⎨⎧=+=+;2,1yz x y x (D)⎩⎨⎧==-.2,1xy y x 3.在□ABCD 中,∠A =30°,则∠D 的度数是( )(A)30°; (B) 60°; (C) 120°; (D) 150°. 4.如图,DE 是△ABC 的中位线,下面的结论中错误的是( ).(A )AB DE 21=; (B )AB ∥DE ;(C )DE BC 2=; (D )DE AB 2=.5.如图,在□ABCD 中,AD AB +等于( ). (A) ; (B) AC ;(C) ; (D) .6.将一个圆盘分为圆心角相等的8个扇形,各扇形涂有各种颜色,如图.任意转动转盘,停止后指针落在每个扇形内的可能性大小都一样(当指针落在扇形边界时,统计在逆时针方向相邻的扇形内).则指针落在红色区域的概率是( ).(A) 81; (B) 83 ; (C) 53; (D) 43.二、填空题(每小题3分,共36分)7.方程13=-x 的解是 .8.如果过多边形的一个顶点共有3条对角线,那么这个多边形的内角和是 .9.已知O 是□ABCD 的对角线AC 与BD 的交点,AC =6,BD =8,AD =6,则⊿OBC 的周长等于 .10.如图,已知菱形ABCD 中,∠ABC 是钝角,DE 垂直平分边AB ,若AE =2,第4题图E DCBA 第5题图DCBA 第10题图E D CBA 第6题图则DB = .11.如图,已知梯形ABCD 中,AB ∥CD ,DE ∥CB ,点E 在AB 上,且 EB=4,若梯形ABCD 的周长为24,则△AED 的周长为 .12.已知等腰梯形的一条对角线与一腰垂直,上底与腰长相等,且上底的长度为1,则下底的长为 .13.如果一个等腰梯形的中位线的长是3cm ,腰长是2cm ,那么它的周长是 cm .14.如图,点D 、E 、F 分别是△ABC 三边的中点,则向量的相等向量是 ,相反向量是 ,平行向量是 (各写一个).15.=-AC AB .16.“顺次联结四边形四条边中点的四边形是矩形”是 事件(填“必然”或“随机”).17.掷一枚质地均匀的骰子(各面的点数分别为1,2,3,4,5,6),对于下列事件:(1)朝上一面的点数是2的倍数;(2)朝上一面的点数是3的倍数;(3)朝上一面的点数大于2.如果用321P P P 、、分别表示事件(1)(2)(3)发生的可能性大小,那么把它们从大到小排列的顺序是 .18.从-1,1中任取一个数作为一次函数b kx y +=的系数k ,从-2,2中任取一个数作为一次函数b kx y +=的截距b ,则所得一次函数b kx y +=经过第一象限的概率是 . 三、解答题(19、20题,每题5分;21、22题,每题6分,共22分)19.已知一次函数b kx y +=的图像过点(1,2),且与直线321+-=x y 平行.求一次函数b kx y +=的解析式.20.解方程:1121=---x xx x .第11题图E D CBA 第14题图F E DCBA21.已知:如图,AE ∥BF ,AC 平分∠BAD ,交BF 于点C ,BD 平分∠ABC ,交AE 于点D ,联结CD .求证:四边形ABCD 是菱形.22.如图,在平面直角坐标系中,O 为原点,点A 、B 、C 的坐标分别为(2,0)、(-1,3)、(-2,-2).(1)在图中作向量OB OA +; (2)在图中作向量-; (3)填空:=++ .FO EDC BA第21题图第22题图四、解答题(23、24题,每题7分;25、26题,每题8分,共30分)23.解方程组:⎩⎨⎧=+-=+.023,622y xy x y x24.一个不透明的口袋里装有2个红球和1个白球,它们除颜色外其他都相同. (1)摸出一个球再放回袋中,搅匀后再摸出一个球.求前后都摸到红球的概率(请用列表法或画树状图法说明).(2)若在上述口袋中再放入若干个形状完全一样的黄球,使放入黄球后摸到红球(只摸1次)的概率为51,求放入黄球的个数.25.如图,ABCD 是正方形,点G 是线段BC 上任意一点(不与点B 、C 重合),DE 垂直于直线AG 于E ,BF ∥DE ,交AG 于F . (1)求证:EF BF AF =-;(2)当点G 在BC 延长线上时(备用图一),作出对应图形,问:线段AF 、BF 、EF 之间有什么关系(只写结论,不要求证明)? (3)当点G 在CB 延长线上时(备用图二),作出对应图形,问:线段AF 、BF 、EF 之间又有什么关系(只写结论,不要求证明)?备用图二备用图一GG F EDCBA第25题图26.如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;(2)动点P在从A到B的移动过程中,设⊿APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时点P的坐标.第26题图2009学年度第二学期期末质量抽测初二数学试卷参考答案1.D 2.C 3.D 4.C 5.B 6.B 7.x =4 8.720° 9.13 10.4 11.16 12.2 13.10 14. EA CE 或 AE EC 或 EA CE 或或等 15. 16.随机 17.213P P P >> 18.4319.解:因为直线b kx y +=与直线321+-=x y 平行,所以 21-=k .----------------------------2分 因为直线b kx y +=过点(1,2),又21-=k ,所以2121=+⨯-b解得 25=b .----------------------------2分所以,所求函数解析式为 2521+-=x y .----------------------------1分20.解:设y xx =-1,则原方程化为022=--y y -------------------------------2分 解得1,221-==y y -----------------------------------------------------------------------2分当21=y 时,得1-=x -------------------------------------------------------------------1分当11-=y 时,得21=x -------------------------------------------------------------------1分 经检验,11-=x ,212=x 是原方程的解。
上海初二第二学期数学期末复习试卷[1]
![上海初二第二学期数学期末复习试卷[1]](https://img.taocdn.com/s3/m/2f46a2b4b9f3f90f76c61ba2.png)
上海初二第二学期数学期末复习试卷TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】(第5题图)上海市初二第二学期数学期末复 一、选择题1. 下列四边形中,是轴对称图形但不是中心对称图形的是( ) (A )等腰梯形; (B )平行四边形; (C )菱形; (D )矩形.2. 已知一个多边形的内角和是900°,那么这个多边形的边数是( ) (A ) 5; (B )6; (C ) 7; (D ) 8 .3. 如果点1122(,),(,)A x y B x y 都在一次函数3y x =-+的图像上,并且12x x <,那么1y 与2y 的大小关系正确的是( ) (A )12y y >; (B )12y y <; (C )12y y =; (D )无法判断 .4. 下列命题中真命题是( )(A ) 对角线互相垂直的四边形是矩形; (B ) 对角线相等的四边形是矩形; (C ) 四条边都相等的四边形是矩形; (D ) 四个内角都相等的四边形是矩形 .5.某体育公园内有一个形状是平行四边形的花坛(如图),并且AB ∥EF ∥DC ,BC ∥GH ∥AD ,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )(A )球落在红花丛中和绿花丛中的概率相等; (B )球落在紫花丛中和橙花丛中的概率相等;(C )球落在红花丛中和蓝花丛中的概率相等; (D )球落在蓝花丛中和黄花丛中的概率相等.6.一条直线y kx b =+,其中5k b +=-,6kb =,那么该直线经过的象限是…( ) A .第一、二、三象限; B .第一、二、四象限; C .第一、三、四象限; D .第二、三、四象限.7.如图,在平行四边形ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,联结EF 、CF ,那么下列结论中一定成立的个数是( ①∠DCF=21∠BCD ; ②EF=CF ; ③S ΔBEC =2S ΔCEF ; ④ (A )4个(B )3个;(C )2个;(D )1个; 二、填空题:8. 已知直线y kx b =+与直线112y x =-平行,且经过点(0,3),那么该直线的表达式 是_______ .9. 已知()2f x =,那么(1)f -=________ .10. 如图,已知四边形ABCD 是菱形,点E 在边BC 的延长线上,且CE=BC , EDCB A(第10题图)BOA那么图中与AD 相等的向量有:__________________. 11.方程3320x x -=的实数解是_________________________.12.某件商品连续两次降价后,零售价为原来的64%,那么此商品平均每次降价的百分率为_____________.13. 如图图案是由8个全等的等腰梯形拼成的,那么图中的1∠的大小是____ ________.14.化简:OA BC OC +-=__________________.15.布袋内装有大小、形状相同的3个红球和1个白球,从布袋中一次摸出两个球, 那么两个都摸到红球的概率是__________________.16. 在梯形ABCD 中,AD 17. 已知,在梯形ABCD 中,AD 18. 在平面直角坐标系xOy 中,已知点(4,0)A 、(1,2)B -、(2,3)C ,如果四边形ABCD 是平行四边形,那么D 的坐标是___________ .19. 将矩形ABCD (如图)绕点A 旋转后, 点D 落在对角线AC 上的点D ’,点C 落到C ’,如果AB =3,BC=4,那么CC ’ 的长为 .20.直线)0(111>+=k b x k y 与)0(222<+=k b x k y 相交于点)0,2(-,且两直线与 y 轴围成的三角形面积为4,那么21b b -的值是 三、解答题(本大题共7题,满分52分)21.如图,已知AB ∥CD ,AD 和BC 相交于点O ,AO =DO ,m AO =,n BO =. (1)用含m 、n 的式子表示向量CD ;(2)求作:n m +.(在原图中作图,不写作法,保留作图痕迹,写出结果). 22.某城市地铁兰线的起点A 站与终点B 站间的行程为60千米,通过信号控制系统的升级与地铁列车动力系统的改进,该线路地铁列车的行驶速度提高了15千米/小时,这样在不改变途经地铁站停靠时间的情况下,从起点A 站到终点B 站的行驶时间缩短了12分钟.如果该线路途经10个停靠站,每站停靠时间为2分钟,那么现在该线路地铁从起点A 站出发到终点B 站需要花多少时间DCB A(第19题图)(第13题DCBA23. 已知:如图,在梯形ABCD 中,DC ∥AB ,AD =BC =2,BD 平分∠ABC ,∠A =60°. 求:梯形ABCD 的周长.24.温度通常有两种表示方法:华氏度(单位:F ︒)与摄氏度(单位:C ︒),已知华氏度数y 与摄氏度数x 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:(1)选用表格中给出的数据,求y 关于x 的函数解析式(不需要写出该函数的定义域);(2)已知某天的最低气温是-5C ︒,求与之对应的华氏度数 .25. (1)已知:如图,在△ABC 中,M 、N 分别是边AB 、AC 的中点,D 是边BC 延长线上的一点,且CD =12BC ,联结CM 、DN . 求证:四边形MCDN 是平行四边形;(2) 已知:如图,在△ABC 中,M 是边ABCD =12BC ,作DN求证:四边形MCDN 是平行四边形.26. 如图,在平面直角坐标系xOy 中,直线AB例函数8y x=在第一象限内的图像相交于点B (m (1)求直线AB 的表达式;(2)将直线AB 向上平移后与反比例函数图像 在第一象限内交于点C ,且△ABC 的面积 为18,求平移后的直线的表达式 .27.已知:在矩形ABCD 中,AB =8,BC =12在矩形ABCD 边AB 、BC 、DA 上,AE =2.D(图1) (图2)(1)如图1,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图2,当四边形EFGH 为菱形时,设BF = x ,△GFC 的面积为S ,求S 关于x 的函数关系式,并写出函数的定义域 .HGFEDCBAHGFEDCBA。
上海市徐汇区2008学年第二学期期末考试初中北片联考预初数学试题(附标准答案)
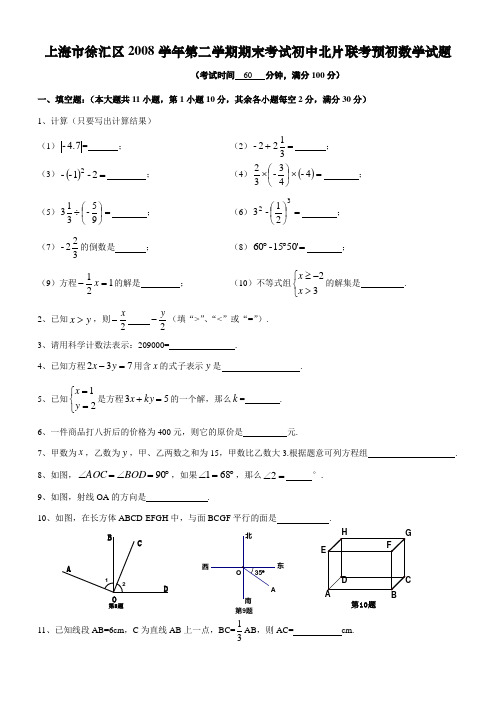
西东第9题第10题第8题上海市徐汇区2008学年第二学期期末考试初中北片联考预初数学试题(考试时间 60 分钟,满分100分)一、填空题:(本大题共11小题,第1小题10分,其余各小题每空2分,满分30分) 1、计算(只要写出计算结果)(1) 4.7-= ; (2)=+3122- ; (3)()=2-1--2;(4)()=⨯⎪⎭⎫⎝⎛⨯4-43-32 ;(5)=⎪⎭⎫⎝⎛÷95-313 ;(6)=⎪⎭⎫⎝⎛3221-3 ;(7)322-的倒数是 ;(8)=︒︒'5015-60 ;(9)方程121=-x 的解是 ;(10)不等式组⎩⎨⎧>-≥32x x 的解集是 .2、已知y x >,则2x-2y -(填“>”、“<”或“=”).3、请用科学计数法表示:209000= .4、已知方程732=-y x 用含x 的式子表示y 是 .5、已知⎩⎨⎧==21y x 是方程53=+ky x 的一个解,那么k = .6、一件商品打八折后的价格为400元,则它的原价是 元.7、甲数为x ,乙数为y ,甲、乙两数之和为15,甲数比乙数大3.根据题意可列方程组 . 8、如图,︒=∠=∠90BOD AOC ,如果︒=∠681,那么=∠2 °. 9、如图,射线OA 的方向是 .10、如图,在长方体ABCD-EFGH 中,与面BCGF 平行的面是 .11、已知线段AB=6cm ,C 为直线AB 上一点,BC=31AB ,则AC= cm.二、选择题:(本大题共5小题,每小题2分,满分10分)(每小题列出的四个答案中,有且只有一个是正确的,把正确答案的代号填入括号中) 12、下面四种说法中错误的是( )A 、零既不是正数也不是负数;B 、3-3-ππ=;C 、角的两条边越长,角越大;D 、长方体至少有两个面的面积相同.13、若方程534=-+y x ax 是关于y x 、的二元一次方程,则a 满足( )A 、4->a ;B 、4-<a ;C 、4-≠a ;D 、无法确定.14、已知b a >,则下列四个不等式不一定成立的是( )A 、22bc ac >;B 、1122+>+c b c a ;C 、b a -<-;D 、22+>+b a .15、下午三点三十分,钟面上时针与分针的夹角为( )A 、直角;B 、锐角;C 、钝角;D 、无法确定.16、如图,在长方体ABCD-EFGH 中,既与面ABCD 垂直又与面BCGF 平行的棱是( )A 、棱AE 与棱BF ;B 、棱AE 与棱DH ;C 、棱DH 与棱EH ;D 、棱DH 与棱GC.三、解答题:(本大题共有4题,每题7分,满分28分)17、计算:()24433831121-4132⨯⎪⎭⎫ ⎝⎛---⨯⎪⎭⎫ ⎝⎛÷⎪⎭⎫ ⎝⎛;18、解方程组:⎩⎨⎧=--=+1952134y x y x ;第16题19、解方程组:⎪⎩⎪⎨⎧=+-=+-=+19714z x z y y x ;20、不等式组:⎪⎪⎩⎪⎪⎨⎧-≤--<-x x x x 23312152157;(1)求这个不等式组的解集; (2)把不等式组的解集表示在数轴上; (3)写出这个不等式组的整数解.四、画图题:(不要求写作法)(本大题共有2题,21题6分,22题4分,满分10分) 21、如图,用直尺和圆规作图 (1)作BC 的中点D ,联结线段AD ; (2)作ACB ∠的角平分线,与AB 交于E ; (3)作AD 、CE 的交点F.31-1-2-322、在下面图形的基础上,补画长方体(虚线表示被遮住的线段)五、列方程或方程组解应用题(本大题共有3题,23题7分,24题7分,25题8分,满分22分)23、某商场购进一种电器,进货的成本为每件400元,按售价的8折出售时,每卖出一件商场可获10%的利润。
2023-2024学年上海市徐汇区八年级(下)期末数学试卷及答案解析

2023-2024学年上海市徐汇区八年级(下)期末数学试卷一.选择题(本大题共6题,每题2分,满分12分)【下列各题的四个选项中,有且只有一个选项是正确的】1.(2分)直线y=﹣2x+1在y轴上的截距是()A.﹣2B.﹣1C.1D.22.(2分)下列关于x的方程中,其中说法正确的是()A.方程x2+a3x﹣1=0是一元三次方程B.方程4x3+81=0是一元三次方程C.方程x=a2﹣2a﹣3是一元二次方程D.方程是分式方程3.(2分)用换元法解关于x的方程,如果设,那么原方程可化为()A.2t2﹣7t+6=0B.2t2+7t﹣6=0C.t2﹣7t+3=0D.t2+7t+3=04.(2分)已知关于x的一次函数y=(k2+1)x+b,那么它的图象一定经过()A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限5.(2分)下列命题中,真命题是()A.若,则B.若则C.若,则D.若,则6.(2分)已知四边形ABCD中,AC与BD交于点O,AB∥CD,那么下列命题中错误的是()A.如果AB=CD,AC⊥BD,那么四边形ABCD是菱形B.如果OB=OD,AC⊥BD,那么四边形ABCD是菱形C.如果AB=CD,OA=OD,那么四边形ABCD是矩形D.如果AD=BC,OA=OB,那么四边形ABCD是矩形二.填空题(本大题共10题,每题3分,满分30分)7.(3分)方程x3﹣8=0的根是.8.(3分)方程的解是.9.(3分)已知直线y=kx+b(k<0)经过点(﹣1,0),那么不等式kx+b>0的解集是.10.(3分)在分别标有1、2、3、4、6的五张卡片中随机抽取2张卡片,那么抽到的卡片上标的数恰好是一个素数和一个合数概率是.11.(3分)某企业的年产值三年内从1000万元增加到1331万元,如果这三年中每年的增长率相同,在求这三年中每年的增长率时,如果设这三年中每年的增长率为x,那么可以列出的方程是.12.(3分)已知:一个多边形的每一个内角都是160°,那么这个多边形的边数为.13.(3分)在直角坐标平面内,如果▱ABCD的两条对角线的交点正好与坐标原点重合,已知点A(3,2),那么点C的坐标是.14.(3分)在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=120°,,那么BD的长是.15.(3分)如图,在梯形ABCD中,AD∥BC,AC⊥BD,已知AC=m,BD=n,那么梯形ABCD的中位线长是(用含m、n的式子表示).16.(3分)如图,AC是矩形ABCD的对角线,已知AB=6,AC=10,点E在边BC上,将矩形ABCD沿直线AE翻折,如果点B恰好落在对角线AC上,那么CE的长是.三.(本大题共8题,第17-18题每题5分;第19-22题每题7分;第23题8分;第24题12分;满分58分)17.(5分)解方程:x+=3.18.(5分)解方程组:19.(7分)某街道因路面经常严重积水,需改建排水系统,市政公司准备安排甲乙两个工程队承接这项工程,据评估,如果甲乙两队合作施工,那么12天可完成;如果甲队先做10天后,剩下的工程由乙队单独承担,还需15天才能完工,甲乙两队单独完成此项工程各需多少天?20.(7分)如图,在梯形ABCD中,AB∥CD,AC与BD交于点O,且OD=OC.(1)求证:AD=BC;(2)设,,当CD=2AB时,试用向量、表示向量.21.(7分)某小区为美化小区环境,购买了两种规格的桂花树苗进行栽种,其中A种桂花树苗的价格为每株75元,B种桂花树苗的价格为每株100元,如果购买这两种桂花树苗共45株,其中A种桂花树苗的数量不超过B种桂花树苗数量的2倍.设购买A种桂花树苗x株,购买A、B两种桂花树苗的总费用是y元.(1)求y关于x的函数关系式;(2)根据(1)的结论,请你设计一种最省钱的购买方案,并求出此种方案的总费用.22.(7分)如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的中线,点E是AD的中点,过A作AF∥BC交BE的延长线于点F,联结CF.(1)求证:四边形ADCF是菱形;(2)如果AC=6,四边形ADCF的面积是30,求AB的长.23.(8分)在平面直角坐标系中,已知直线y=kx﹣k(k<0)经过定点P.(1)求点P的坐标;(2)一次函数的图象分别与x轴、y轴交于点B、C(如图),如果直线y=kx﹣k(k≠0)将△BOC的面积平分,求k的值;(3)在(2)的条件下,将直线y=kx﹣k(k≠0)向上平移2个单位后得到直线l,点A是直线l上的点,如果AO=AC,求点A的坐标.24.(12分)如图,点M是正方形ABCD的边AD上的一点,过点B作BN⊥BM交DC的延长线于点N,联结MN交BD于点E.(1)求∠BMN的大小;(2)如果∠ABM=2∠DNM,求证:EN=ME+BE;(3)如果AB=1,当∠DBN=∠DNB时,求DM的长.2023-2024学年上海市徐汇区八年级(下)期末数学试卷参考答案与试题解析一.选择题(本大题共6题,每题2分,满分12分)【下列各题的四个选项中,有且只有一个选项是正确的】1.【分析】根据截距就是“与坐标轴交点的纵坐标或横坐标”解答.【解答】解:根据题意,得b=1,所以直线y=2x+1在y轴上的截距是1.故选:C.【点评】本题考查了一次函数图象上的点的坐标特征.解答该题时,需熟练掌握截距的定义.2.【分析】根据一元二次方程、一元一次方程和分式方程的定义分别对每一项进行分析,即可得出答案.【解答】解:A、方程x2+a3x﹣1=0是一元二次方程,故本选项错误,不符合题意;B、方程4x3+81=0是一元三次方程,故本选项正确,符合题意;C、方程x=a2﹣2a﹣3是一元一次方程,故本选项错误,不符合题意;D、方程是一元一次方程,故本选项错误,不符合题意;故选:B.【点评】此题考查了方程的定义,熟练掌握一元二次方程、一元一次方程和分式方程的定义是解题的关键.3.【分析】根据题意将原方程换元后并整理即可.【解答】解:,设,则原方程化为+t=,整理得:2t2﹣7t+6=0,故选:A.【点评】本题考查换元法解分式方程,将原方程进行正确的换元是解题的关键.4.【分析】根据所给函数解析式,得出y随x的增大而增大,据此可解决问题.【解答】解:因为一次函数的解析式为y=(k2+1)x+b,所以k2+1>0,所以y随x的增大而增大,故不论b取何值,此函数图象一定经过第一、三象限.故选:B.【点评】本题主要考查了一次函数的性质,熟知一次函数的图象和性质是解题的关键.5.【分析】根据零向量、向量的模,逐项判断即可.【解答】解:A.若,则,故原说法是假命题,该选项不符合题意;B.若,则,故原说法是假命题,该选项不符合题意;C.若,则,故原说法是真命题,该选项符合题意;D.若,则,故原说法是假命题,该选项不符合题意;故选:C.【点评】本题主要考查了零向量、向量的模,解题的关键是掌握以上知识点.6.【分析】根据矩形和菱形的判定定理进行判断即可.【解答】解:A、如果AB∥CD,AB=DC,则四边形ABCD是平行四边形,又AC⊥BD,那么四边形ABCD是菱形;不符合题意;B、如果AB∥DC,OD=OB,则四边形ABCD是平行四边形,又AC⊥BD,那么四边形ABCD是菱形;不符合题意;C、如果AB∥DC,AB=CD,则四边形ABCD是平行四边形,又OA=OD,那么四边形ABCD是矩形;不符合题意;D、如果AD=CB,AC=BD,那么四边形ABCD是等腰梯形,不一定矩形,符合题意;故选:D.【点评】此题主要考查了矩形的判定和菱形的判定,关键是熟练掌握矩形和菱形的判定定理.二.填空题(本大题共10题,每题3分,满分30分)7.【分析】首先整理方程得出x3=8,进而利用立方根的性质求出x的值.【解答】解:x3﹣8=0,x3=8,解得:x=2.故答案为:x=2.【点评】此题主要考查了立方根的性质,正确由立方根定义求出是解题关键.8.【分析】先把分母中能够分解因式的分解因式,然后方程两边同时乘(x+1)(x﹣1),把分式方程化成整式方程,再利用分解因式法解一元二次方程,求出未知数的值,最后检验即可.【解答】解:,,x(x+1)=2,x2+x﹣2=0,(x+2)(x﹣1)=0,x+2=0或x﹣1=0,∴x1=﹣2,x2=1,检验:把x1=﹣2代入(x+1)(x﹣1)≠0,∴x=﹣2是原分式方程的解;把x2=1代入(x+1)(x﹣1)=0,∴x=1不是原分式方程的解,∴x=﹣2是原分式方程的解,故答案为:x=﹣2.【点评】本题主要考查了解分式方程,解题关键是熟练掌握解分式方程的一般步骤.9.【分析】将点(﹣1,0)代入直线的函数解析式,得出k=b,再根据k<0得出关于x的不等式即可解决问题.【解答】解:将点(﹣1,0)代入直线的函数解析式得,﹣k+b=0,则b=k.由kx+b>0得,kx+k>0,即k(x+1)>0.因为k<0,所以x+1<0,解得x<﹣1.故答案为:x<﹣1.【点评】本题主要考查了一次函数与一元一次不等式,熟知解一元一次不等式的步骤是解题的关键.10.【分析】先判断各个数据是素数还是合数,注意1既不是素数也不是合数,然后画出相应的树状图,再求出抽到的卡片上标的数恰好是一个素数和一个合数概率即可.【解答】解:1既不是素数也不是合数,2和3是素数,4和6是合数,树状图如下所示:由上可得,一共有20种等可能性,其中抽到的卡片上标的数恰好是一个素数和一个合数的可能性有8种,故抽到的卡片上标的数恰好是一个素数和一个合数概率为=,故答案为:.【点评】本题考查列表法与树状图法、素数、合数,解答本题的关键是明确题意,画出相应的树状图,求出相应的概率.11.【分析】由于某企业的年产值三年内从1000万元增加到1331万元,如果这三年中每年的增长率相同,在求这三年中每年的增长率时设这三年中每年的增长率为x,那么第二年变为1000(1+x),然后依此类推即可列出方程.【解答】解:∵企业的年产值三年内从1000万元增加到1331万元,这三年中每年的增长率相同,∴设这三年中每年的增长率为x,那么可以列出的方程是1000(1+x)3=1331.【点评】此题主要考查了高次方程在实际问题中的应用,解题的关键是正确理解题意,然后根据题目的数量关系列出方法解决问题.12.【分析】先求出这个多边形的每一个外角的度数,再用360°除即可得到边数.【解答】解:∵多边形的每一个内角都等于160°,∴多边形的每一个外角都等于180°﹣160°=20°,∴边数n=360°÷20°=18.故答案为:18.【点评】本题主要考查了多边形的内角与外角的关系,求出每一个外角的度数是关键.13.【分析】根据平行四边形的对称性和点A的坐标直接写出点C的坐标即可.【解答】解:∵平行四边形ABCD对角线的交点恰好与坐标原点重合,∴点A和点C关于原点中心对称,∵A(3,2),∴C(﹣3,﹣2),故答案为:(﹣3,﹣2).【点评】本题考查了平行四边形的性质的知识,解题的关键是了解平行四边形是中心对称图形,对称中心是对角线的交点,难度不大.14.【分析】根据矩形的性质得出OA=OC,OB=OD,AC=BD,于是推出OA=OC=OB=OD,再证∠AOD=60°,即可得出△AOD是等边三角形,即可求出OD的长,从而求出BD的长.【解答】解:如图,∵∠AOB=120°,∴∠AOD=180°﹣∠AOB=180°﹣120°=60°,∵四边形ABCD是矩形,∴OA=OC,OB=OD,AC=BD,∴OA=OC=OB=OD,∴△AOD是等边三角形,∴OD=AD=,∴OB=,∴BD=OD+OB=,故答案为:.【点评】本题考查了矩形的性质,等边三角形的判定与性质,熟练掌握矩形的性质是解题的关键.15.【分析】过点D作DE∥AC,交BC的延长线于点E,根据平行线的性质得到DE⊥BD,证明四边形ACED为平行四边形,根据平行四边形的性质得到CE=AD,DE=AC=m,根据勾股定理求出BE,再根据梯形中位线定理计算即可.【解答】解:如图,过点D作DE∥AC,交BC的延长线于点E,∵AC⊥BD,∴DE⊥BD,∵AD∥CE,DE∥AC,∴四边形ACED为平行四边形,∴CE=AD,DE=AC=m,∴AD+BC+BE,由勾股定理得:BE==,∴梯形ABCD的中位线长是,故答案为:.【点评】本题考查的是梯形的中位线、平行四边形的判定和性质、勾股定理,掌握平行四边形的判定定理是解题的关键.16.【分析】根据矩形的性质得到∠B=90°,根据勾股定理得到BC==8,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=90°,BE=B′E,根据勾股定理即可得到结论.【解答】解:∵四边形ABCD是矩形,∴∠B=90°,∵AB=6,AC=10,∴BC==8,∵将△ABE沿直线AE翻折,点B的对应点为点B′∴AB′=AB=6,∠AB′E=∠B=90°,BE=B′E,∴CB′=AC﹣AB′=4,∠CB′E=90°,∵CE2=CB′2+EB′2,∴CE2=42+(8﹣CE)2,∴CE=5,故答案为:5.【点评】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,熟练掌握折叠的性质是解题的关键.三.(本大题共8题,第17-18题每题5分;第19-22题每题7分;第23题8分;第24题12分;满分58分)17.【分析】移项后两边平方,即可得出一个一元二次方程,求出方程的解即可.【解答】解:x+=3,移项得:=3﹣x,两边平方得:2x﹣3=(3﹣x)2,整理得:x2﹣8x+12=0,解得:x1=2,x2=6,经检验:x=2是原方程的解,x=6不是原方程的增根,舍去,∴原方程的解是x=2.【点评】本题考查了解无理方程,能把无理方程转化成有理方程是解此题的关键.18.【分析】先把原方程组的每个方程化简,这样原方程组转化成四个方程组,求出每个方程组的解即可.【解答】解:由①得:(x+2y)2=9,x+2y=±3,由②得:x(x+y)=0,x=0,x+y=0,即原方程组化为:,,,,解得:,,,,所以原方程组的解为:,,,.【点评】本题考查了解二元一次方程组和解高次方程组,能把高次方程组转化成二元一次方程组是解此题的关键.19.【分析】根据“甲乙两个工程队合作施工12天可以完成”工程,可得等量关系:甲队12天的工作量+乙队12天的工作量=该项工程总量.根据“甲队先做10天后,剩下的工程由乙队单独承担,还需15天才能完工”,可得等量关系:甲队10天的工作量+乙队15天的工作量=该项工程总量.据此列式解答.【解答】解:设甲乙两队单独完成此项工程分别需要x天和y天.根据题意,可列出方程组:,解得:,经检验是原方程组的解,且符合题意,答:甲乙两队单独完成此项工程分别需要20天和30天.【点评】此题考查了分式方程的应用,正确理解题意找准等量关系列出方程是解答此题的关键.20.【分析】(1)根据全等三角形的判定证明△AOD≌△BOC,则可得AD=BC.(2)由题意得==,根据=+可得答案.【解答】(1)证明:∵OD=OC,∴∠ODC=∠OCD,∵AB∥CD,∴∠ODC=∠OBA,∠OCD=∠OAB,∴∠OBA=∠OAB,∴OA=OB,∵∠AOD=∠BOC,∴△AOD≌△BOC(SAS),∴AD=BC.(2)解:∵AB∥CD,CD=2AB,∴==.∴=+=+.【点评】本题考查平面向量、全等三角形的判定与性质,熟练掌握平面向量的运算法则、全等三角形的判定与性质是解答本题的关键.21.【分析】(1)根据“总费用=A、B两种树苗的费用和”列函数关系式;(2)根据一次函数的性质求解.【解答】解:(1)由题意得:y=75x+100(45﹣x)=﹣25x+4500;(2)由题意得:x≤2(45﹣x),解得:x≤30,又∵x≥0,∴0≤x≤30,∵﹣30<0,∴y随x的增大而减小,∴当x=30时,y有最小值,为﹣25×30+4500=3750(元),此时需要购买A种桂花树苗30棵,B种桂花树苗15棵,总费用3750元.【点评】本题考查了一次函数的应用,理解一次函数的性质是解题的关键.22.【分析】(1)由AF∥BC,得∠AFE=∠DBE,而∠AEF=∠DEB,AE=DE,即可证明△AFE≌△DBE,则AF=DB,因为AD是斜边BC上的中线,所以AD=DB=DC=BC,由AF∥DC,且AF=DC,证明四边形ADCF是平行四边形,而AD=DC,则四边形ADCF是菱形;=×6DF=30,求得DF=10,再证明四边形(2)联结DF,由菱形的性质得AC⊥DF,则S菱形ADCFABDF是平行四边形,则AB=DF=10.【解答】(1)证明:∵AF∥BC,∴∠AFE=∠DBE,∵点E是AD的中点,∴AE=DE,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS),∴AF=DB,∵AD是斜边BC上的中线,∴AD=DB=DC=BC,∴AF∥DC,且AF=DC,∴四边形ADCF是平行四边形,∵AD=DC,∴四边形ADCF是菱形.(2)解:联结DF,=30,∵四边形ADCF是菱形,且AC=6,S菱形ADCF∴AC⊥DF,∴×6DF=30,∴DF=10,∵AF∥DB,AF=DB,∴四边形ABDF是平行四边形,∴AB=DF=10,∴AB的长为10.【点评】此题重点考查平行线的性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质、菱形的面积公式等知识,证明△AFE≌△DBE是解题的关键.23.【分析】(1)由y=kx﹣k=k(x﹣1),即可求解;=S△BCO,即×3×4=2×y N,得到y N=3,即可求解;(2)由S△PBN(3)设点A(m,﹣12m+14),由AO=AC得:m2+(﹣12m+14)2=m2+(﹣12m+14﹣4)2,即可求解.【解答】解:(1)y=kx﹣k=k(x﹣1),当x=1时,y=0,即点P(1,0);(2)一次函数的图象分别与x轴、y轴交于点B、C,则点B(3,0)、C(0,4),设直线y=kx﹣k交BC于点N,交y轴于点M,=S△BCO,即×3×4=2×y N,则S△PBN则y N=3,即点N(,3),将点N的坐标代入y=kx﹣k得:3=k(﹣1),解得:k=﹣12;(3)平移后的一次函数表达式为:y=﹣12x+14,设点A(m,﹣12m+14),由AO=AC得:m2+(﹣12m+14)2=m2+(﹣12m+14﹣4)2,解得:m=1,即点A(1,2).【点评】本题考查的是一次函数综合运用,涉及到三角形的面积计算、等腰三角形的性质等,其中(2)确定点N的位置是解题的关键.24.【分析】(1)利用等角的余角相等求得∠ABM=∠CBN,证明△ABM≌△CBN(ASA),可证明BM=BN,可求得△BMN是等腰直角三角形,据此即可求解;(2)在EN上截取点F,使EF=EB,连接BF,证明△BEF是等边三角形,再证明△BEM≌△BFN(AAS),据此即可证明EN=ME+BE;(3)由已知结合△ABM≌△CBN,证明BM是∠ABD的角平分线,作MG⊥BD于点G,据此求解即可.【解答】(1)解:∵正方形ABCD,∴AB=BC,∠A=∠BCD=∠BCN=90°,∵BN⊥BM,∴∠MBN=90°,∴∠ABM=90°﹣∠MBC=∠CBN∴△ABM≌△CBN(ASA),∴BM=BN,∴△BMN是等腰直角三角形,∴∠BMN=45°;(2)证明:在EN上截取点F,使EF=EB,连接BF,如图1,由(1)知△ABM≌△CBN,∴∠AMB=∠CNB,∠BMN=∠BNM=∠BDM=45°,∴∠DBM=∠AMB﹣45°=∠CNB﹣45°=∠DNM,∵∠ABM=2∠DNM,∴∠ABM=2∠DBM,∵∠ABM+∠DBM=45°,∴∠DBM=∠DNM=15°,∴∠BEN=∠BDN+∠DNM=60°,∴△BEF是等边三角形,∴BE=BF,∠BEM=∠BFN=120°,∵∠BMN=∠BNM=45°,∴△BEM≌△BFN(AAS),∴ME=FN,∴EN=FN+EF=ME+BE;(3)解:由(1)知△ABM≌△CBN,∴∠ABM=∠CBN,∵四边形ABCD是正方形,∴∠ABD=∠CDB=∠CBD=45°,∵∠DBN=∠DNB,∴,∴∠ABM=∠CBN=67.5°﹣45°=22.5°,∴∠DBM=45°﹣22.5°=22.5°=∠ABM,即BM是∠ABD的角平分线,作MG⊥BD于点G,如图2,则AM=MG,∵BM=BM,∠BMA=∠BMG=90°,∴Rt△BMA≌Rt△BMG(HL),∴BG=AB=1,∵正方形ABCD,AB=1,∴,∠MDG=45°,∴,△GMD是等腰直角三角形,∴.【点评】本题考查了正方形的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理,正确引出辅助线解决问题是解题的关键。
八年级数学下册期末试卷(附含答案)精选全文完整版

可编辑修改精选全文完整版八年级数学下册期末试卷(附含答案)(满分:120分;考试时间:120分)一、选择题(共10小题,每小题3分,满分30分) 1、使1x -有意义的x 的取值范围是( )A x >1B x >-1C x ≥1D x ≥-1 2、在根式xy 、12、2ab 、x y -、2x y 中,最简二次根式有( )A 1个B 2个C 3个D 4个 3、下列计算正确的是( )A 20210=B 5630⨯=C 2236⨯=D 2(3)3-=- 4、一元二次方程x (x-2)=2-x 的根式( )A -1B 2C 1和2D -1和2 5、下列命题中,真命题的个数有( )①对角线互相平分的四边形是平行四边形; ②两组对角分别相等的四边形是平行四边形; ③一组对边平行,另一组对边相等的四边形是平行四边形;A 3个B 2个C 1个D 0个 6、在△ABC 中,三边长分别为a 、b 、c ,且a+c=2b ,c-a=12b ,则△ABC 是( )A 直角三角形B 等边三角形C 等腰三角形D 等腰直角三角形 7、某公司为了解职工参加体育锻炼情况,对职工某一周平均每天锻炼 (跑步或快走)的里程进行统计(保留整数),并将他们平均每天锻炼 的里程数据绘制成扇形统计图,关于他们平均每天锻炼里程数据 下列说法不正确的是( )A 平均每天锻炼里程数据的中位数是2B 平均每天锻炼里程数据的众数是2C 平均每天锻炼里程数据的平均数是2.34D 平均每天锻炼里程数不少于4km 的人数占调查职工的20% 8、疫情期间居民为了减少外出时间,更愿意使用APP 在线上购物,某购物APP 今年二月份用户比一月份增加了44%,三月份用户比二月份增加了21%,则二、三两个月用户的平均每月增长率是( )A 28%B 30%C 32%D 32.5% 9、有两个一元二次方程:M :ax 2+bx+c=0,N :cx 2+bx+a=0,以下四个结论中,错误的是( ) A 如果方程M 有两个不相等的实数根,那么方程N 也有两个不相等的实数根 B 如果方程M 有两根符号相同,那么方程N 也有两根符号相同 C 如果5是方程M 的一个根,那么15是方程N 的一个根D 如果方程M和方程N有一个相同的实数根,那么这个跟必是x=110、△ABC中,∠C=30°,AC=6,BD是△ABC的中线,∠ADB=45°,则AB=()二、填空题(共6小题,每小题3分,满分18分)11的结果是12、已知关于x的一元二次方程x2-bx+8=0,一个根为2,则另一个根是13、有一棵9米高的大树,如果大树距离地面4米处这段(没有断开),则小孩至少离开大树米之处才是安全的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008学年第二学期期终考试初中北片联考 初二数学 试题
14题,每题2分,共28分)
.若直线32+=x y 与直线1-=kx y 平行,则________=k . .若点(3,a )在一次函数13+=x y 的图像上,则=a
.
.一次函数14-=x y , y 的值随x 值的增大而________.(填“增大”、“减小”或“不)
.如图,一次函数y kx b =+的图象经过A ,B 两点,则0kx b +> 的解集是 . .方程
x x -=的根是 .
.方程33
)2(42322=++-++x x x x ,若用换元法设23
2++=x x y ,原方程可变形为 . .方程0432
4
=--x x 的根是 . .方程组⎩⎨
⎧-=-=-3
12
2
y x y x 的解是 .
.一个骰子六个面上的数字分别为1、2、3、4、5、6,投掷一次,向上的一面是奇数的概率是 .
.菱形的两条对角线长分别是6和8,则菱形的边长为 .
.如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同 形状的四边形,请写出其中一种四边形的名称
.
.梯形的上底、下底的长分别是2cm 和4cm ,那么此梯形的中位线
长是______cm 。
.如图,把一张矩形纸片ABCD 沿EF 折叠后,点C D ,分别落在C D '',的位置上,EC '交AD 于点G .已知58EFG ∠=°,那么BEG ∠= °.
第11题图
第13题图 第14题图 14.如图,梯形ABCD 中,AB ∥CD ,CD AB 2=,a
= , b =,请用向量b
a 、表示向量= .
二、选择题(本大题共4题,每题2分,共8分)
15.如图,梯形ABCD 中,AD ∥BC ,AD=AB ,BC=BD ,∠A =100°,则
∠C = ………………………………………………… ( ) A.80° B.70° C.75° D.60°
16.下列命题中错误的是………………………………………………… ( ) (A )矩形的两条对角线相等; (B )等腰梯形的两条对角线互相垂直; (C )平行四边形的两条对角线互相平分; (D )正方形的两条对角线互相垂直且相等.
17.如图,在周长为20cm 的□ABCD 中,AB ≠AD ,AC 、BD 相交于点O ,
OE ⊥BD 交AD 于E ,则△ABE 的周长为……………( ) (A)15cm (B)20cm
(C)5cm (D)10cm
18.从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y kx b =+的系数k ,b ,则一次函数y kx b =+的图象不经过第四象限的概率是……………………( ). (A) 21 (B) 31 (C) 41 (D) 6
1
A
B
E
C
D
F
G
C '
D '
A
B
C
D
O
E
D
C
B
A
三、简答题(本大题共5题,每题6分,共30分)
19.解方程212=-+x x
20.解方程: 2
3416222+=---+x x x x
21.解方程组:⎩
⎨⎧=+=--320
22
2y x y xy x
22.小东从A 地出发以某一速度向B 地走去,同时小明从B 地出发以另一速度向A 地而行,如图所示,图中的线段1l 、2l 分别表示小东、小明离B 地的距离(千米)与所用时间(小时)的关系。
⑴试用文字说明:交点P 所表示的实际意义。
⑵试求出A 、B 两地之间的距离。
23.如图,平行四边形ABCD 中,点E 、F 、G 、H 分别在AB 、BC 、CD 、AD 边上且AE =CG ,AH =CF . 求证:四边形EFGH 是平行四边形;
四、解答题(本大题共3题,每题8分,共24分)
24.某文具厂加工一种学习用具2500套,在加工了1000套后,采用了新技术,使每天比原
来多加工25套,结果提前了3天完成任务。
求该文具厂原来每天加工多少套这样的学习用具。
A
x(小时)
y(千米)
2.54
3
21
7.5
P
l 2
l 1
O
25.如图,在△ABC 中,AB =BC ,BD 是中线,过点D 作DE ∥BC ,过点A 作AE ∥BD ,AE
与DE 交于点E .
求证:四边形ADBE 是矩形.
26.如图,平行四边形ABCD 中,AB ⊥AC ,AB=1,BC =5.对角线AC 、BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交BC 、AD 于点E 、F .在旋转过程中,四边形BEDF 可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC 绕点O 顺时针旋转的最小度数.
E
A
D
B
C
(第25题图)
O F E
D C
B
A
27.(本题满分10分,第(1)小题3分,第(2)小题3分, 第(3)小题4分)
如图,在平面直角坐标中,四边形OABC 是等腰梯形,CB ∥OA ,OC=AB=4,BC=6,
∠COA=45°,动点P 从点O 出发,在梯形OABC 的边上运动,路径为O →A →B →C ,到达点C 时停止.作直线CP. (1)求梯形OABC 的面积;
(2)当直线CP 把梯形OABC 的面积分成相等的两部分时,求直线CP 的解析式; (3)当∆OCP 是等腰三角形时,请写出点P 的坐标(不要求过程,只需写出结果)
O A
B
C P
x
y。
