核递推最小二乘辨识算法仿真研究

合集下载

最小二乘参数辨识的matlab仿真程序注释与剖析

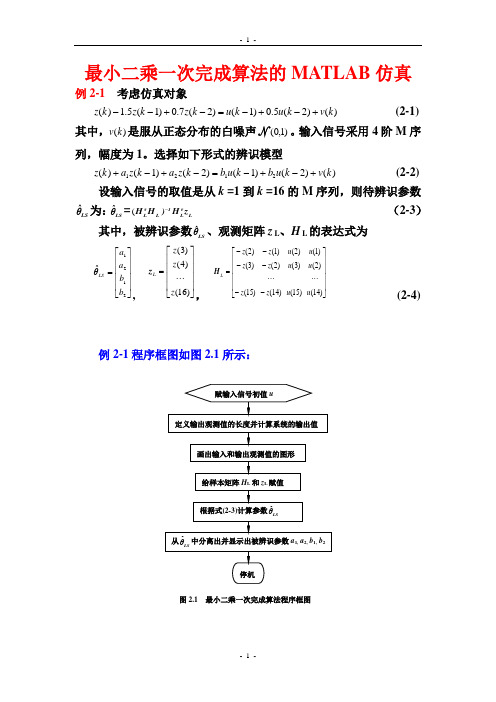
最小二乘一次完成算法的MATLAB 仿真例2-1 考虑仿真对象)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1)其中，)(k v 是服从正态分布的白噪声N )1,0(。

输入信号采用4阶M 序列，幅度为1。

选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (2-2)设输入信号的取值是从k =1到k =16的M 序列，则待辨识参数LS θˆ为：LSθˆ=L τL 1L τL z H )H H -( （2-3）其中，被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z ，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H(2-4)例2-1程序框图如图2.1所示：例2-1Matlab仿真程序如下：%二阶系统的最小二乘一次完成算法辨识程序，文件名：FLch3LSeg1.mu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16，步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on %画出输出观测值z的径线图形，并显示坐标网格u,z %显示输入信号和输出观测信号%L=14 %数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9)u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵H L赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示θˆLS%Display Parametersa1=c(1), a2=c(2), b1=c(3),b2=c(4) %从θˆ中分离出并显示a1、a2、b1、b2LS%End例2-1程序运行结果：u =[ -1，1，-1，1，1，1，1，-1，-1，-1，1，-1，-1，1，1]z =[ 0，0，0.5000，0.2500，0.5250，2.1125， 4.3012，6.4731，6.1988，3.2670，-0.9386， -3.1949，-4.6352，6.2165，-5.5800，-2.5185] HL =1.0000-1.0000-0.5000 0 -1.0000 1.0000 -0.2500 -0.5000 1.0000-1.0000-0.5250 -0.2500 1.0000 1.0000 -2.1125 -0.5250 1.0000 1.0000 -4.3012 -2.1125 1.0000 1.0000 -6.4731-4.3012 -1.0000 1.0000-6.1988-6.4731 -1.0000 -1.0000-3.2670-6.1988 -1.0000 -1.00000.9386-3.2670 1.0000 -1.00003.19490.9386 -1.0000 1.00004.63523.1949 -1.0000 -1.00006.21654.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000（14*4）ZL =[ 0.5000，0.2500，0.5250，2.1125，4.3012，6.4731，6.1988，3.2670，-0.9386，-3.1949， -4.6352，-6.2165，-5.5800，-2.5185]T （14*1）c =[ -1.5000，0.7000，1.0000，0.5000]Ta1 = -1.5000 a2 = 0.7000 b1 = 1.0000 b2 =0.5000-101-10010-10010对比：)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1) 可以看出,由于所用的输出观测值没有任何噪声成分，所以辨识结果无任何误差。

递推阻尼最小二乘法辨识算法公式的详细推导与说明

控制理论与控制工程学位课程《系统辨识》考试报告递推阻尼最小二乘法公式详细推导专业：控制理论与控制工程班级：2011双控（研）学生姓名：江南学号：20110201016任课教师：蔡启仲老师2012年06月29 日摘要在参数辨识中，递推最小二乘法是用得最多的一种算法。

但是，最小二乘法存在一些缺点，如随着协方差矩阵的减小，易产生参数爆发现象；参数向量和协方差矩阵的处置选择不当会使得辨识过程在参数收敛之前结束；在存在随机噪声的情况下，参数易产生漂移，出现不稳定等。

为了防止参数爆发现象，Levenberg 提出在参数优化算法中增加一个阻尼项，以增加算法的稳定性。

本文在一般的最小二乘法中增加了阻尼因子，构成了阻尼最小二乘法。

又根据实时控制的要求，详细推到了递推阻尼最小二乘公式，实现在线辨识。

关键字：系统辨识，最小二乘法，递推算法正文1.题目的基本要求已知单入单出系统的差分方程以及噪声，在应用最小二乘法进行辨识的时候，在性能指标中加入阻尼因子，详细推导阻尼最小二乘法的递推公式。

2.输入辨识信号和系统噪声的产生方法和理论依据 2.1系统辩识信号输入选择准则（1）输入信号的功率或副度不宜过大，以免使系统工作在非线性区，但也不应过小，以致信噪比太小，直接影响辩识精度；（2）输入信号对系统的“净扰动”要小，即应使正负向扰动机会几乎均等；（3）工程上要便于实现，成本低。

2.2白噪声及其产生方法（1）白噪声过程（2）白噪声是一种均值为0、谱密度为非0常数的平稳随机过程。

（3）白噪声过程定义：如果随机过程()t ω的均值为0，自相关函数为()()2R t t ωσδ= （2.2.1）式中()t δ 为狄拉克（Dirac) 分布函数，即(){(),00,01t t t dt δδ∞∞=≠∞==⎰-且t （2.2.2）则称该随机过程为白燥声过程。

2.3白噪声序列 (1) 定义如果随机序列{()}w t 均值为0，并且是两两不相关的，对应的自相关函数为()2,0,1,2w l R l l σδ==±± 式中{1,00,0l l l δ=≠=则称这种随机序列{()}w t 为白噪声序列。

递推最小二乘算法 simulink

递推最小二乘算法simulink 递推最小二乘算法是一种常用的数学算法，用于估计数据的最佳拟合曲线。

Simulink是一款强大的系统建模和仿真工具，它可以方便地进行算法的模拟和验证。

本文档将介绍如何在Simulink中使用递推最小二乘算法来实现数据的最佳拟合。

首先，我们需要明确递推最小二乘算法的基本原理。

递推最小二乘算法是一种迭代算法，根据已知的数据点，通过不断更新拟合曲线的参数，使得拟合曲线与实际数据的残差平方和最小化。

其核心思想是通过迭代计算，不断调整参数，逐步优化拟合效果。

在Simulink中，我们可以使用递归结构来实现递推最小二乘算法。

首先，我们需要建立一个递推模型框架，包括数据输入、参数更新、残差计算和拟合曲线输出等组件。

其次，我们需要确定递推算法的初始参数值，通常可以使用数据的平均值作为初始参数。

然后，我们可以通过迭代计算的方式，不断更新参数值，直到拟合曲线达到最佳效果。

在模型的具体实现中，我们可以使用Simulink中的线性系统模块、运算模块和数据存储模块等进行建模。

通过连接和配置不同的模块，我们可以构建一个完整的递推最小二乘算法模型。

在模型的验证过程中，我们可以使用Simulink提供的仿真功能，输入实际数据，并观察拟合曲线与实际数据的吻合程度。

需要注意的是，在使用递推最小二乘算法之前，我们需要确定一些参数，如迭代次数、收敛准则和阈值等。

这些参数的选择将直接影响到递推算法的收敛速度和拟合效果。

因此，我们需要根据具体的应用场景和数据特点进行合理选择和调整。

总结来说，递推最小二乘算法是一种有效的数据拟合算法，可以在Simulink中得到方便的实现和验证。

通过合理配置模型和参数，我们可以得到与实际数据最佳拟合的拟合曲线。

在实际应用中，递推最小二乘算法具有广泛的应用领域，如信号处理、系统辨识和机器学习等。

希望本文档能够帮助您更好地理解和应用递推最小二乘算法。

递推最小二乘估计及模型阶次辨识

实验二递推最小二乘估计(RLS)及模型阶次辨识(F-Test ）1 实验方案设计1.1 生成输入数据和噪声用M 序列作为辨识的输入信号，噪声采用标准正态分布的白噪声。

生成白噪声时，首先利用乘同余法生成U[0,1]均匀分布的随机数，再利用U[0,1]均匀分布的随机数生成标准正态分布的白噪声。

1.2 过程仿真辨识模型的形式取)()()()()(11k e k u z B k z z A +=--，为方便起见，取n n n b a == 即nn n n zb a b z b z B z a a a z a z A ------++++=++++=...1)(...1)(22112211用M 序列作为辨识的输入信号。

1.3 递推遗忘因子法数据长度L 取534，初值⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==1000010000100001)0(001.0)0(P θ 1.4 计算损失函数、噪声标准差损失函数⎥⎦⎤⎢⎣⎡+---+-=μθμττ)()1()()]1(ˆ)()([)1()(2k h k P k h k k h k z k J k J噪声标准差θλdim )(ˆ-=L L J1.6 F-Test 定阶法计算模型阶次统计量t)22,2(~222)1()1()()1,(----++-=+n L F n L n J n J n J n n t其中，)(∙J 为相应阶次下的损失函数值，L 为所用的数据长度，n 为模型的估计阶次。

若a t n n t >+)1,(，拒绝00:n n H >，若a t n n t <+)1,(，接受00:n n H >，其中αt 为风险水平α下的阀值。

这时模型的阶次估计值可取1+n 。

1.6 计算噪信比和性能指标噪信比22ye σση= 参数估计平方相对偏差i i i ni i i θθθθθδˆ~,~1221-=⎪⎪⎭⎫ ⎝⎛=∑= 参数估计平方根偏差ii i n i ini iθθθθθδˆ~,)()~(2122122-==∑∑== 2 编程说明M 序列中，M 序列循环周期取15124=-=p N ，时钟节拍t ∆=1Sec ，幅度1=a ，特征多项式为1)(56⊕⊕=s s s F 。

系统辨识实验二

《系统辨识》实验二要点实验二递推最小二乘估计(RLS)及模型阶次辨识(F-Test ）一、实验目的① 通过实验，掌握递推最小二乘参数辨识方法 ② 通过实验，掌握F-Test 模型阶次辨识方法二、实验内容1、仿真模型实验所用的仿真模型如下：框图表示模型表示)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z λ+-+-=-+-- 其中u (k )和z (k )分别为模型的输入和输出变量；v (k )为零均值、方差为1、服从正态分布的白噪声；λ为噪声的标准差（实验时，可取0.0、0.1、0.5、1.0）；输入变量u (k )采用M 序列，其特征多项式取1)(4⊕⊕=s s s F ,幅度取1.0。

2、辨识模型辨识模型的形式取)()()()()(11k e k u z B k z z A +=--为方便起见，取n n n b a ==，即nn nn zb z b z b z B z a z a z a z A ------+++=++++= 22112211)(1)(根据仿真模型生成的数据{}L k k u ,,1),( =和{}L k k z ,,1),( =，辨识模型的参数n n b b b a a a ,,,,,,2121 和；并确定模型阶次n ，同时估计出模型误差)(k e 的方差（应近似等于模型噪声)(k v 的方差，即为2λ）和模型的静态增益K 。

3、辨识算法① 采用递推遗忘因子法：[][][]⎪⎪⎩⎪⎪⎨⎧--=+--=--+-=-)1()()(1)()()1()()()1()()1()()()()1()(1k k k μk μk k k k k k k k k z k k k P h K I P h P h h P K h K τττθθθ 其中，遗忘因子10≤<μ(具体值根据情况自已确定)；数据长度L 可取100、300、500；初始值⎩⎨⎧==IP 2)0()0(a εθ。

递推最小二乘法原理

递推最小二乘法原理递推最小二乘法（Recursive Least Squares, 简称RLS）是一种经典的自适应滤波算法，它在信号处理、通信系统、控制系统等领域得到了广泛的应用。

本文将介绍递推最小二乘法的原理及其在实际应用中的一些特点。

首先，让我们来了解一下最小二乘法。

最小二乘法是一种数学优化方法，用于寻找一组参数，使得给定的模型与观测数据之间的误差平方和最小。

在线性回归问题中，最小二乘法可以用来拟合一个线性模型，以最小化观测数据与模型预测值之间的差异。

最小二乘法的基本思想是通过最小化误差的平方和来寻找最优的参数。

递推最小二乘法是最小二乘法的一种变种，它的特点在于可以实时地更新参数估计，适用于需要动态调整的系统。

在实际应用中，由于系统参数可能随时间变化，传统的最小二乘法在每次参数更新时都需要重新计算整个数据集，计算复杂度较高，不适合实时性要求高的场景。

而递推最小二乘法则可以通过递推的方式，实时地更新参数估计，适用于动态环境下的参数估计问题。

递推最小二乘法的原理可以用数学公式来描述。

假设我们有一个线性模型，\[y_k = \theta^T x_k + e_k\]其中\(y_k\)是观测数据，\(x_k\)是输入向量，\(\theta\)是待估计的参数，\(e_k\)是噪声。

我们的目标是通过观测数据\(y_k\)和输入向量\(x_k\)来估计参数\(\theta\)。

递推最小二乘法的核心思想是通过递推的方式，实时地更新参数\(\theta\)的估计值。

具体来说，我们可以通过以下递推公式来更新参数\(\theta\)的估计值，\[\theta_k =\theta_{k-1} + \frac{P_{k-1}x_k}{1 + x_k^T P_{k-1} x_k}(y_k x_k^T \theta_{k-1})\]其中\(\theta_k\)是第\(k\)次的参数估计值，\(\theta_{k-1}\)是第\(k-1\)次的参数估计值，\(P_{k-1}\)是第\(k-1\)次的参数估计误差的协方差矩阵。

递推最小二乘法原理

递推最小二乘法原理递推最小二乘法（Recursive Least Squares, RLS）是一种经典的自适应滤波算法，广泛应用于信号处理、通信系统、控制系统等领域。

它通过不断地更新参数估计，实现对信号的实时跟踪和预测。

本文将介绍递推最小二乘法的原理及其应用。

首先，我们来了解一下最小二乘法（Least Squares, LS）的基本原理。

最小二乘法是一种常见的参数估计方法，它通过最小化观测数据的残差平方和来确定参数的估计值。

对于线性模型，最小二乘法的估计值可以通过求解正规方程或者利用矩阵运算来得到。

然而，在实际应用中，数据通常是逐步到达的，因此需要一种能够实时更新参数估计的方法，这就是递推最小二乘法。

递推最小二乘法的核心思想是利用递推的方式不断更新参数估计，以适应数据的动态变化。

在每次新的数据到达时，根据当前的参数估计和新的数据，通过一定的计算方法得到更新后的参数估计。

这样，参数估计可以随着时间的推移而不断优化，从而更好地适应信号的变化。

在递推最小二乘法中，通常会引入一个遗忘因子（ForgettingFactor），用于衰减历史数据的影响，使算法更加关注最近的数据。

遗忘因子的选择对于算法的性能有着重要的影响，合理的遗忘因子可以平衡对历史数据和最新数据的重视程度，从而提高参数估计的准确性和稳定性。

除了参数估计，递推最小二乘法还可以用于信号预测和滤波。

通过不断更新参数估计，可以实现对信号的实时跟踪和预测，从而在控制系统和通信系统中发挥重要作用。

在实际应用中，递推最小二乘法通常与自适应滤波器相结合，构成自适应滤波系统，用于抑制噪声、提取信号等。

总之，递推最小二乘法是一种重要的自适应参数估计方法，具有实时性强、适应性好的特点，适用于动态环境下的信号处理和控制。

通过不断更新参数估计，可以实现对信号的准确跟踪和预测，为实际应用提供了有力的支持。

在未来的研究和工程实践中，递推最小二乘法仍将发挥重要作用，为各种领域的应用提供有效的解决方案。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ｑａＫＬ）ｅｎｅ…于２００４年提出能实现在线实时辨识，因而得到了广泛的应用。然ｓｕｒ，ＲＳ是由法国学者Ｅｇｌ
而，该方法仅是一种线性辨识方法，于非线性系统的，是将传统ＲＳ算法在特征空间中的直接应对它Ｌ
ＫＲＬＦ —ＫＲＳ，ｉｉｃｓｅ．ＴｅＫＲＬｌｏｔｍｎａｉｏａＳａｇｒｔｍｏａｅｒｎｎｉｅｒｙｔｍｄｎｆａｉｎａＳ，ＢＬｓｄｓｕｓｄｈＳａｇｒｈａｄｔｄｔｎｌｉｒｉＲＬｏｈｉｃｍｐｒｄｆｏｌａｓｌｉｓｏｎｓｅｉｅｔｃｔ．ｉｉｏｂｌｙｂｈｉｌｔｎｅａｌ．ＴｅｓｌｔｎｒｓｌｈｗａｅＫＲＬｅｔｃｔｎｍｅｈｄｉｂｉｕｌｕｅｏｏｔｅｔｄｔｎｉｔｙｔｅｓｍｕａｉｘｍｐｅｈｉａｉｅｕｔｓｏｔｔｔｉｏｍｕｏｓｈｈＳｉｎｉａｉｔｏｓｏｖｏｓｙｓｐｒｒｈｒｉｏ・ｄｉｆｏｉｔａｉｌＲＬｎｆａｉｔｏｈｔｅｎｔｄｎｆａｉｃｕａｙ，ｓｂｌｙｏｎｉｎｅｆｒｎｅａＳｉｅｉｃｔｎｍｅｈｄｗｅｈｒｉｅｉｅｉｃｔｎａｃｒｃｄｔｉｏｈｔｉｏｔｉｉｒａ —ｉｔｒｅｅｃ．ＨｏｖｒｉｅｔｒｅＫＲＬｅｔａｔｔｗｅｅｎｔｈｅｈＳｉｎｉｄ —
方法是一种非常经典的且应用最广泛的系统辨识方扰严重的情况下，识的稳定性也不令人满意。辨法。由于该方法不仅可减少计算量和存储量，且而核递推最小二乘法（ｅｅＲｃｒｖｅｓｋｒｌｅｕｓｅｌａｔ— ｎｉ
ｉｅｔｃｔｎｅｅｔｈｎｔｅＡＬ —ＫＳａｄＦｄｎｉａｉｆｃａｈＤｉｆｏｔＲＬＢ—ＫＲＬｔｏ．ｔｅＳ —ＫＲＬｄｎｆａｉｎｍｅｈｄｉａｔｕａｌｕｔｌｉｎＳｍｅｄｈＷｈＳｉｅｔｃｔｔｏｓｐｒｉｌｙｓｉｅｔｉｉｏｃｒｂａｍｅ
核递推最小二乘辨识算法仿真研究
李志农
（．州大学，南１郑河
赵匡何
南昌３０６）３０３
况
郑州４００；．昌航空大学，５０１２南江西
［关键词］核方法；非线性回归；递推最小二乘；稀化表示［摘要］论述了核递推最小二乘辨识思想和三种典型算法即ＡＤ—ＫＫ、Ｗ — ＲＳ和ＦＬＲＳＳＫＬ，Ｂ—ＫＬ，ＲＳ通过仿真研究，比较了
ＫＬＲＳ法比其他两种ＫＬＲＳ辨识算法获得了更好的辨识效果。Ｓ —ＫＫＷＲＳ法特别适用于时变非线性系统辨识。
［中图分类号］Ｔ７Ｔ１５３Ｔ９１Ｈ１；Ｈ６．；Ｎ１
［文献标志码】Ａ
［文章编号】１０ — ９６２１）２— ０１— ６０１４２（０１００００
Ｋｅｒｓｋｒｅｔｏｙｗｏｄ：ｅｎｌｍｅｈｄ；ｎｎｉｅｒｉｅｔｃｔｎ；ｒｃｒｉｅｌａｔｑａｅ；ｓａｓｅｒｓｎａｉｎｏｌａｄｎｆａｉｎｉｉｏｅｕｓｖｅｓ —ｓｕｒｐｅｒｐｅｅｔｔ．ｒｏ
２
２１年６０１月
第２５卷第２期
核递推最小二乘辨识算法仿真研究
用，过核函数将原始的非线性数据映射到高维特通
由上式可看出，在每次迭代中，了求估计权值为
征空间，其线性可分，使然后在特征空间中实施递推向量＆，要计算核矩阵Ｋ的逆，核矩阵的维数都且这样，矩阵的求逆涉及的最小二乘算法，巧妙的将非线性问题近似为线性问随着数据点的增加而增大，
ｍｎ（）ｌｌ＝∑ｌｌｉＷ＝Ｉ一ＴＪｅｄ
（）度过高，数据点将被丢掉；２则该如果６过一个给超
其中，是一个向量，含当前所有数据的期望输定的阀值，认为该数据点不能被已有的数据点ｄ包则出ｄ＝［ｄ】ｏ是更新向量权值。每次迭代线性表出，么已有数据集应该扩展，纳该数据ｄ，Ｔ，那接中通过新到来的数据点和期望输出来更新权值向量点。由此可见，技术相当于只使用了在给定精度该直到满足迭代终止条件，最终输出的即为所求下样本数据中线性无关的点，而最终选取的那些数
２１年６月０１第２５卷第２期
南昌航空大学学报（自然科学版）
ＪＵＲＯＮＡＬＯＦＮＡＨＡＮＨＡＮＮＣＧＧＫＯＩＲＳＴＮＡＵＲＣＥＥＮＧＵＮＶＥＩＹ（ＴＡＬＳＩＮＣＳ）
ｄｕ１１ｎ２０Ｖｏ．５．１２７修２０ — ６０
［基金项目］国家自然科学基金项目５０５２５７５０）湖南省机械设备健康维护重点实验室开（１３；７２８；７７０放基金项目２００）（９４０
［作者简介］李志农（９６１６一）男，，南昌航空大学无损检测技术教育部重点实验室教授，博士。主要研究方向：智能检测与信号处理。
ＳｍｕａｉｎＲｅｅｒｈｏｒｅｃｒｉｅＬｅｓｑａｅｉｌｔｓａｃｆＫｅｎｌＲｅｕｓｖａｔＳｕｒｏ
ＩｅｉｃｔｏｇｒｔｍｄｎｔｆａｉｎＡｌｏｉｈｉ
Ｌｉ—ｎｎＩＺｈｏｇ，ＺＨＡＯａｇＫｕｎＨＥａ２Ｋｕｎｇ
（．ｈｎｚｏｎｅｉ，ｈｎｚｏ，ｅａ５０１ｈｎ１ＺｅｇｈｕＵｉｎｔＺｅｇｈｕＨｎｎ４００，Ｃｉｖｙａ；２ＮｎｈｎａｇｏｇＵｉ￣ｔ，ａｃａｇＪｎｘ３０３Ｃｉ）．ａｃａｇＨｎｋｎｎｅｉＮｎｈｎ，ｉｇｉ０６，ｎｖｙａ３ｈａ
６＝ｍｎ【ａ（（）ｌｉｌｉｃ）一Ｉ
‘＝ｌ
（）５
其中，一个向量，（代表已有数据的任意ａ是０ｃ）
线性组合。如果６不能超过一个给定的阀值，则
认为该新到来的数据点与已有数据点的线性依赖程
—
ｖｒｉｇｎｎｉｅｒｓｓｅｉｅｔｃｔｎａｙｎｏｎａｙｔｍｄｎｉａｉ．ｌｉｆｏ
递推最ｄ－乘法（ｅｕｓｅｌａｔｑａｅＲＳｘＲｃｒｖｓ—ｓｕｒ，Ｌ）ｉｅ
的辨识，往往很难得到令人满意的结果，另外，干在
的权值向量，或称之为滤波器系数。
据点所组成的集合即是给定精度下样本数据的极大
核递推最小二乘（ＲＳ）法则是在特征空间线性无关组。这样一来，与计算的相当于只有极ＫＬ算参中实施标准最小二乘算法。在迭代次数为ｎ时，大线性无关组中的数据，么核矩阵的维数也就被那
ＡｂｔａｔＴｅｋｒｅｒｃｒｉｅｓｓｕｒＫＬ）ｉｅｔｃｔｎｔｅｒａｄｔｅｐｃｌａｇｒｍ，ｉｅＬ —ＫＬ，Ｗ — ｓｒｃ：ｈｅｎｌｅｕｓｅｌｔｑａｖａｅ（ＲＳｄｎｆａｏｈｏｎｈｅｔｉｌｉｉｉｉｙｒｙａｏｔｈ．．ＡＤＲＳＳ
１．ＡＬＤ —ＫＲＬＳ１
１核递推最小二乘辨识算法
给定系统的输入输出模型为ＹｎＨ（））＋（）（）＝ｎＲ（ｅｎ
近似线性依赖技术（ｐｒｉａｅｌｅｒｅｅｄＡｐｏｍｔｉａｐｎ— ｘｎｄ
ｅｃ，Ｌ技术由法国学者Ｅｇｌ２０ｎｙＡＤ）ｎｅ于０４年提出。其基本原理为当一个新数据点到来时，要考虑它需（）与现有数据集的线性依赖程度，过计算误差：１通
ｉｔｔｏｆａｉｎｍｅｈｄ，ｂｓｄｏｈＷ —ＫＲＳｍｅｈｄｈｓｔｅｕｉｕｌｉｇｗｉｄｗｐｒｒｎｅ，ｔｅＳ —ＫＲＬｔｏｂｍｎｅｔｒｃｏａｅｎｔｅＳＬｔｏａｈｎｑｅｓｉｎｎｏｅｏｍａｃｈＷｄｆＳｍｅｄｏｔｓｂｔｈｅ
传统递推最小二乘（Ｌ）ＲＳ辨识算法和核递推最小二乘（ＲＳ辨识算法对非线性系统的辨识能力。仿真研究表明，ＫＬ）不论是在辨识精度，稳定性还是抗干扰性方面，ＫＫＲＳ辨识算法明显优于传统ＲＳ辨识法。在这三种典型的ＫＬＫＲＳ辨识算法，Ｓ — Ｗ

核递推最小二乘辨识算法仿真研究

最小二乘参数辨识的matlab仿真程序注释与剖析

递推阻尼最小二乘法辨识算法公式的详细推导与说明

相关_最小二乘两步法在辨识中的应用与改进

递推最小二乘算法 simulink

递推最小二乘估计及模型阶次辨识

系统辨识实验二

递推最小二乘法原理

递推最小二乘法原理