2015届合肥二模数学(理)试题及答案
2015届高三合肥二模

(2)
①事物的联系是普遍的。中国经济受”三高“与三大
红利的影响,长期保持持续高速增长。 ②事物是变化发展的,事物的发展是前进行与曲折性 的统一,中国经济在过去30多年里保持高速增长 的同时也出现了波动性 ③矛盾具有特殊性,同一事物的矛盾在不同发展阶段 具有不同的特点。中国经济在经历30多年的快速 增长之后,已经逐步告别高速增长进步到”常态 增长“的新阶段使经济增长出现了新特征,要因 时制宜地转变经济增长模式。
合肥二模答案
1——5 BCBCD 6——10 CDBBB
11 A
38、(1) 改革开放30多年以来,我国经济始终保持高 速增长,但经济发展过程中也出现了波动性, 其中受到政策红利影响,改革开放、体制转 型及“入世“等政策的实施对经济推动作用 巨大(4分) 长期依赖高投资、高储蓄、高耗能的增长,积 累的矛盾和风险逐步凸显,2010年以来经 济增速出现持续下行现象。
39(3)
①文化与经济相互影响,相互交融。塑造国家形象需要全面 加强国家经济政治建设,提升国家综合国力 ②要继承和发扬中华优秀传统文化,推动文化创新。加强中 华文化的传播,提升中华文化的影响力 ③要弘扬和培育中华民族精神 ④要增强文化自觉和文化自信,建设社会主义文化强国
39(2) ① 实践具有能动性,转变观念,增强企业的投资吸引力说明 了这一点 ② 真理是具体的,针对经济运行中的问题,采取相应措施, 做到了主观与客观,理论与实践的具体的,历史的统一 ③认识具有反复性、无限性和上升性。经济发展中逐步认识 到无形资产的重要性,并重视策略调整与观念转变,体现 了追求真理是一个过程。
38(3)
① 提出上述要求是中国共产党的领导和执政地位决
定的 ②坚持与时俱进是党的性质宗旨的必然要求 ③提高驾驭经济的能力和水平是完善党的领导方式和 执政方式的需要 ④强化舆论引导是坚持党的指导思想,践行中国特色 社会主义理论体系的要求
2015安徽高考数学理科模拟试卷

2015安徽高考数学理科模拟试卷理科模拟试卷
满分:150分考试时间:120分钟
第?卷(选择题满分50分)
一、选择题:(本大题共10小题,每小题5分,共50分(在每小题给出的四个选
项中,只有一项是符合题目要求的)
i3
1(复数(i为虚数单位)的虚部是 2i?1
A(i ( ) 1
5 B(1 5 C( ?i 1
5 D(?1 5
2(集合M?{x|x2?2x?3?0},N?{x|x?a},若M?N,则实数a的取值范围是( ) A([3,??) B((3,??) C((??,?1] D((??,?1)
3(等比数列?an?中,a1?0,则“a1?a4”是“a3?a5” 的( )
A(充分而不必要条件 B(必要而不充分条件
C(充要条件 D(既不充分也不必要条件
4(一几何体的三视图如右图所示,则该几何体的体积为( )
A(200?9?
B(200?18?
C(140?9?
D(140?18?
第4题图 12
5(函数f(x)?ln
x?x
的图象大致是 (
)
A( B( C( D(
6(已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在
ABC 1。
2015年安徽中考模拟合肥庐阳区二模数学答案

2015年中考模拟试题数学参考答案1.C2.D3.C4.D5.C6.B7.A8.D9.D 10.B11.x ≤21且x ≠0 12.2)(3y x -13.32 14.①②④ 15.原式=2321133⨯-+-+=3.…………………………8分16.方程两边同乘)2)(1(+-x x ,得)2()2)(1(3+=+-+x x x x ,解得1=x . …………………………6分检验:当1=x 时,)2)(1(+-x x =0,因此1=x 不是原分式方程的解. 所以,原分式方程无解.…………………………8分17.(1)23 (9,7) ………………4分(2)2n(n+1) ………………6分理由:第2n 排的最后一个数是从2开始数的第(2+4+6+...+2n)个正偶数,故此数为2(2+4+6+...+2n)=2)22(2n n +⨯=2n(n+1).(合理即可) ………………8分18.(1)(2)(3)如图(1)………………2分 (2)………………4分 (3)………………8分19.(1)解:设甲、乙两家印刷社各印了a,b 张宣传单. ⎩⎨⎧=+=+6520.015.0400a b a b 解得⎩⎨⎧==100300a b 答:在甲印刷社印刷300张,在乙印刷社印刷100张.………………4分(2)甲印刷社:x y 15.0=………………6分 乙印刷社:⎩⎨⎧>+≤≤=)500(501.0)5000(20.0x x x x y………………8分当500x 0≤≤时,x 15.0<0.20x .选择甲印刷社;当x>500时,若0.15x<0.1x+50得x<1000,即500<x<1000.选择甲印刷社划算若0.15x=0.1x+50得x=1000,即x=1000.选择两家印刷社一样划算若0.15x>0.1x+50得x>1000,即x>1000.选择乙印刷社划算综上所述,0≤x<1000时选择甲印刷社划算,x=1000时选择两家印刷社一样划算, x>1000时选择乙印刷社划算 ……………10分20.过C 点作CD 垂直AB 于D 点,得∠CBD=60°,∴∠ACB=30°,∴AB=BC=4………………4分 在直角三角形BCD 中解得CD= 3.5;………………10分21.(1)树状图如下:由上图可知,某个同学抽签的所有等可能的情况有8种,具体如下:(1W ,1H ,1S )、(1W ,1H ,2S )、(1W ,2H ,1S )、(1W ,2H ,2S )、(1W ,3H ,1S )、(1W ,3H ,2S )、(1W ,4H ,1S )、(1W ,4H ,2S )、………………8分 (2)∵王强抽到化学、生物科都是准备较好的实验题目的有(1W ,2H ,1S )、(1W ,3H ,1S )共2种情况,∴他能同时抽到化学和生物都是准备较好的实验题的概率是4182=. ………………12分 22.证明:(1)∵AB=AC ,∴∠B=∠ACB ,又∵∠ACP=∠ACB ,∴∠B=∠ACP ,在△ABD 和△ACE 中,⎪⎩⎪⎨⎧=∠=∠=,,,CE BD ACE B AC AB ∴△ABD ≌△ACE ,∴AD=AE ;………………4分(2)∵∠B=∠ACB=∠ACP ,∠BCP=144°,∴∠B=∠ACB=∠ACP=72°,∴∠BAC=36°,由(1)知,△ABD ≌△ACE ,∴∠BAD=∠CAE ,∴∠BAD+∠DAC=∠CAE+∠DAC ,即∠DAE=∠BAC=36°. ………………8分(3)四边形CDFE 为菱形.理由如下:∵AB=AC ,AD ⊥BC ,∴BD=CD ,∠1=∠2,又∵BD=CE ,∴CE=CD ,由(1)知,△ABD ≌△ACE ,∴∠1=∠3,∴∠2=∠3,在△ADF 和△AEF 中,⎪⎩⎪⎨⎧=∠=∠=,,32,AF AF AE AD ∴△ADF ≌△AEF ,∴DF=EF ,∵EF ∥BC ,∴∠EFC=∠DCF ,∴∠EFC=∠ECF ,∴EC=EF ,∴CD=CE=EF=DF ,∴四边形CDFE 为菱形.(注:利用其他方法证明,只要正确即可)………………12分23.(1)如图建立平面直角坐标系,(以点O 为原点,OC 所在直线为y 轴,垂直于OC 的直线为x 轴) 设抛物线的函数解析式为2ax y =,由题意知点B '的坐标为(-3,3).∵点B '在旋转后的抛物线上,5分(2)①延长BD 到M 使BD MD =,连接AM 交OC 于点P ,则点P 即为所求.………………7分∴点M '的坐标为(3,3),设直线A M ''的函数解析式为b kx y +=, ∴用料最省时,点O 、P 之间的距离是5米. (注:利用相似形求出点O 、P 之间的距离也可)………………14分 P o。
2015年安徽省合肥市包河区中考数学二模试卷(解析版)

2015年安徽省合肥市包河区中考数学二模试卷一、选择题:每小题4分,共40分.1.(4分)比3大﹣1的数是()A.2B.4C.﹣3D.﹣22.(4分)下列运算正确的是()A.5ab﹣3ab=2B.(﹣a3)2=a6C.a2•a3=a6D.(a﹣b)2=a2﹣b23.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划的118.6%,有力地推动我省经济的快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103B.9.7982×108C.9.7982×1011D.9.7982×10124.(4分)如图所示的几何体是一个正三棱柱,以下不是其三视图的是()A.B.C.D.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为()A.60°B.70°C.90°D.110°6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是()A.B.C.D.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团的情况进行调查统计,制成了两幅不完整的统计图(如图).则以下结论正确的是()A.选科目E的有10人B.选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4°C.选科目A、B的人数占选体育社团人数的一半D.选科目A的占34%8.(4分)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD =6,则弦CD的长为()A.4B.2C.4D.89.(4分)如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y 与x的函数关系图象是()A.B.C.D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确的是()A.f(a)+f(﹣a)=0B.若f(a)=a,则a=0C.f(a)f()=1D.f(a)=f(1﹣a)二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1的解集是.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)的图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=.13.(5分)已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2,则弧AC的长为.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确的有(填上你认为所有正确结论的序号).三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3的值.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2+2)米.试求货车卸货时举升杠杆OB 的长.18.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称的△A′B′C′;(2)画出△ABC关于原点O成中心对称的△A1B1C1,并指出△A′B′C′与△A1B1C1的位置关系.五、每小题10分,共20分.19.(10分)如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐的由左到右填在所示表格里:(1)按照规律,表格中a=,b=,c=.(2)观察表中规律,第n个“正方形数”是;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.(1)判断四边形ADCE的形状,并证明.(2)若AC=BC=2,求BO的长.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别的概率;(2)若九年级的女同学是学校的“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”的概率.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.(1)求a的值及函数解析式;(2)据统计,个体司机的运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”的增加额b(元)之间的关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?2015年安徽省合肥市包河区中考数学二模试卷参考答案与试题解析一、选择题:每小题4分,共40分.1.(4分)比3大﹣1的数是()A.2B.4C.﹣3D.﹣2【解答】解:3+(﹣1)=2.故选:A.2.(4分)下列运算正确的是()A.5ab﹣3ab=2B.(﹣a3)2=a6C.a2•a3=a6D.(a﹣b)2=a2﹣b2【解答】解:A.5ab﹣3ab=(5﹣3)ab=2ab,故A错误;B.(﹣a3)2=a6,正确;C.a2•a3=a2+3=a5,故C错误;D.(a﹣b)2=a2﹣2ab+b2,故D错误.故选:B.3.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划的118.6%,有力地推动我省经济的快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103B.9.7982×108C.9.7982×1011D.9.7982×1012【解答】解:将9798.2亿用科学记数法表示为:9.7982×1011.故选:C.4.(4分)如图所示的几何体是一个正三棱柱,以下不是其三视图的是()A.B.C.D.【解答】解:A、是主视图,故此选项不合题意;B、不是其三视图,故此选项正确;C、是左视图,故此选项不合题意;D、是俯视图,故此选项不合题意;故选:B.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为()A.60°B.70°C.90°D.110°【解答】解:∵a∥b,∴∠3=∠5.∵∠3+∠4=110°,∴∠4+∠5=110°,∴∠6=∠4+∠5=110°,∴∠1+∠2=180°﹣110°=70°.故选:B.6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是()A.B.C.D.【解答】解:设男生有x人,女生有y人,由题意得,.故选:C.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团的情况进行调查统计,制成了两幅不完整的统计图(如图).则以下结论正确的是()A.选科目E的有10人B.选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4°C.选科目A、B的人数占选体育社团人数的一半D.选科目A的占34%【解答】解:该班的总人数是:12÷24%=50(人),则选科目E的人数是:50×10%=5(人),故选项A错误;选B科目的扇形的圆心角的度数是:360°×=50.4°,选D科目的扇形的圆心角的度数是:360°×=64.8°,则选科目B的扇形圆心角比选科目D的扇形圆心角的度数少14.4°,故选项B错误;A科目的人数是:50﹣9﹣16﹣11=14(人),则A和B科目的总人数是14+7=21,选科目A、B的人数占选体育社团人数不到一半,故选项C错误;选A科目的所占的百分比是:×100%=34%,故选项D正确.故选:D.8.(4分)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD =6,则弦CD的长为()A.4B.2C.4D.8【解答】解:连接OD,∵AB=9,∴OD=OA=4.5.设OE=x,则AE=4.5﹣x,∵弦CD⊥AB,∴CD=2DE,∠OED=∠AED=90°.∵AD=6,∴AD2﹣AE2=OD2﹣OE2,即62﹣(4.5﹣x)2=4.52﹣x2,解得x=,∴AE=4.5﹣x=4.5﹣=4,∴DE===2,∴CD=2DE=4.故选:A.9.(4分)如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y 与x的函数关系图象是()A.B.C.D.【解答】解:∵等边△ABC的边长是4,PB的长为x,PD⊥BC于D,DE⊥AC于E,EQ ⊥AB于Q,∴∠PDB=∠DEC=∠EQA=90°,∠PBD=∠CDE=∠AEQ=30°,∴BD=,CD=4﹣,CE=(4﹣)=2﹣,AE=4﹣(2﹣)=2+,AQ=(2+)=1+,∴当P在Q下方时,y=AB﹣PB﹣AQ=4﹣x﹣(1+)=﹣+3,当P在Q上方时,y=AQ﹣AP=(1+)﹣(4﹣x)=x﹣3,当y=0时,x=,当x=0时,y=3,当x=4时,y=,∴y=故选:D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确的是()A.f(a)+f(﹣a)=0B.若f(a)=a,则a=0C.f(a)f()=1D.f(a)=f(1﹣a)【解答】解:f(a)+f(﹣a)=a(a﹣1)﹣a(﹣a﹣1)=2a2,A不正确;f(a)=a,即a(a﹣1)=a,则a=0或2,B不正确;f(a)f()=a(a﹣1)×(﹣1)=2﹣a﹣,C不正确;f(a)=f(1﹣a),D正确,故选:D.二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1的解集是x<4.【解答】解:去分母得1+2x>3x﹣3,移项得2x﹣3x>﹣3﹣1,合并得﹣x>﹣4,系数化为1得x<4.故答案为x<4.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)的图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=﹣2.【解答】解:∵点A(2,2)是反比例函数y=(x>0)的图象上一点,∴m=2×2=4,∵点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,∴|n||m|=5,∴|n|=6,∵n<0,∴n=﹣6,∴m+n=﹣2,故答案为:﹣2.13.(5分)已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2,则弧AC的长为.【解答】解:连接OA,∵AD是⊙O的切线,∴∠OAD=90°,∴∠D+∠AOC=90°,∵AB=AD=2,∴∠B=∠D,∵OA=OB,∴∠B=∠OAB,∴∠AOC=2∠B=2∠D,∴∠AOC=60°,∴AO=AD=2,∴弧AC的长==,故答案为:.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确的有①③④(填上你认为所有正确结论的序号).【解答】解:∵BE⊥AC于G,CD⊥AB于F,∴∠AFC=∠AGB=90°,∴∠ABG+∠F AG=∠ACD+∠F AG=90°,∴∠ABG=∠ACD,∵BA=BE,CA=CD,∴∠D=∠DAC=,∠E=∠BAE=,∴∠D=∠E,故①正确;∵∠AFD=∠AGE=90°,∠D=∠E,∴△ADF∽△AEG,∴DF与GE不一定相等,故②错误;∵∠AFC=∠AGB,∠F AG=∠F AG,∴△AFC∽△ABG,∴=,故③正确;∵△ADF∽△AEG,∴,∴=,故④正确.故答案为:①③④.三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.【解答】解:原式=﹣==,当a=﹣3时,原式=﹣1.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3的值.【解答】解:原式=4x2﹣8x+4﹣2x2+4x+3=2x2﹣4x+7=2(x2﹣2x)+7,当x2﹣2x﹣8=0,即x2﹣2x=8时,原式=16+7=23.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2+2)米.试求货车卸货时举升杠杆OB的长.【解答】解:作OD⊥AB于D,设BD=x,∵∠BOC=75°,∠A=30°,∴∠ABO=45°,∴OD=BD=x,tan A=,∴AD==x,则x+x=2+2,解得x=2,∴OD=BD=2,由勾股定理,OB=2.18.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称的△A′B′C′;(2)画出△ABC关于原点O成中心对称的△A1B1C1,并指出△A′B′C′与△A1B1C1的位置关系.【解答】解:(1)如图所示,△A′B′C′即为所作;(2)如图所示,△A1B1C1即为所作,△A′B′C′与△A1B1C1关于直线y=﹣x成轴对称.五、每小题10分,共20分.19.(10分)如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐的由左到右填在所示表格里:(1)按照规律,表格中a=28,b=36,c=35.(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x﹣n.【解答】解:(1)∵前6个“三角形数”分别是:1=、3=、6=、10=、15=、21=,∴第n个“三角形数”是,∴a=.∵前5个“正方形数”分别是:1=12,4=22,9=32,16=42,25=52,∴第n个“正方形数”是n2,∴b=62=36.∵前4个“正方形数”分别是:1=,5=,12=,22=,∴第n个“五边形数”是,∴c==35.(2)第n个“正方形数”是n2;1+1﹣1=1,3+4﹣5=2,6+9﹣12=3,10+16﹣22=4,…,∴第n个“五边形数”是n2+x﹣n.故答案为:28、36、35;n2、n2+x﹣n.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.(1)判断四边形ADCE的形状,并证明.(2)若AC=BC=2,求BO的长.【解答】解:(1)菱形.证明如下:∵AE∥CD,CE∥AD,∴四边形ADCE是平行四边形,∵∠ACB=90°,AD=BD,∴CD=AD,∴四边形ADCE是菱形.(2)∵AC=BC=2,∴CD⊥AB,AB=2,∴EA⊥AB,AD=,∴AE=,在Rt△BAE中,BE==,∵AD=BD,AE∥DO,∴BO=BE=.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别的概率;(2)若九年级的女同学是学校的“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”的概率.【解答】解:(1)画树状图为:共有8种等可能的结果数,其中三位主持人恰好同性别的结果数为2,所以所选三位主持人恰好同性别的概率==;(2)画树状图为:共有20种等可能的结果数,其中两男的结果数为6,所以恰好为“两男一女”的概率==.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.(1)求a的值及函数解析式;(2)据统计,个体司机的运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”的增加额b(元)之间的关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?【解答】解:(1)由图象可得,t=时,y=0,设份子钱为m元,∴解得:m=200,∴a=﹣200,设函数解析式为:y=kt+b,把(0,﹣200),(,0)代入得:,解得:,∴y=30t﹣200.(2)设他需要运营x小时,根据题意可得:,解得:x=15,经检验,x=15是原方程的解,∴他需要运营15小时.(3)∵调整时必须保证个体司机在运营12小时时,收益率不低于,∴解得:b≤40,∴0≤b≤40,设公司效益为W元,则W==,∵0≤b≤40,∴当b=40时,W有最大值,最大为==33600,∴增加额b为40元时,公司效益最高.。
2015年高考数学(理)二轮专练:高档小题及答案解析(共2份试题)

B .t ≥D .t ≤的图象上的点(的图象大致为(
=⎩⎨⎧x 2
-4x +3, x ≤0
-x 2-2x +3,x >0,则不等式f (a 2-
10,…记为数列{a n},将可被5整除的三角形数按从小到大的顺序组成一个新数列{b},可以推测:
的图象,如图所示,则函数
-4<3a,整理得
已知不等式等价于不等式x+y+
∵双曲线C2:x2
3
-y2=1,
3
,又AC
BC
=3,∠ACB
1
)
PA⊥平面,所以BC⊥=PM2+MA2,
B.40 3
D.40
过抛物线y2=ax的焦点
的边长为2,D
为中心向下转动到稳定位置的过程中,
该空间几何体是一个四棱锥,其直观图如图所示.其体积为
k个1和它后面(2k
这个要求分组,每组数字的个数组成一个以2为首项、
=-
1
f(x)
得,f(x+
的周期函数,又因为函数
【解析】不等式组表示的平面区域如图中阴影部分所示,变换目标函数为
=x-z在y轴上的截距最大时.当
ADE转动的过程中,AD→)²(CA→+AE→)
21。
安徽省合肥市高考数学二模试卷(理科) Word版含解析
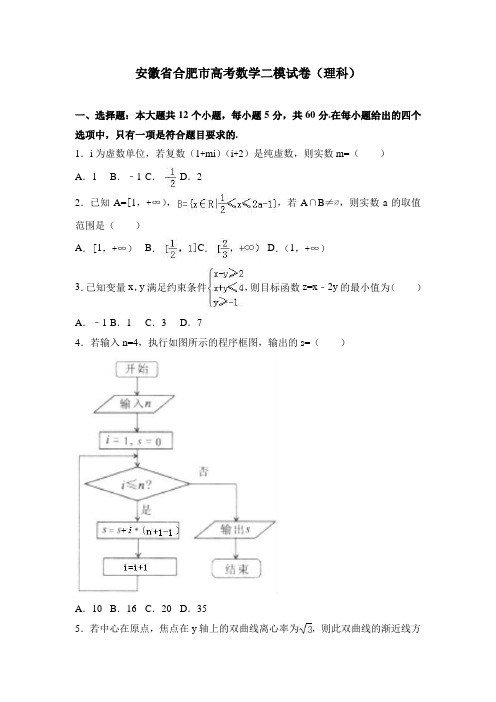
安徽省合肥市高考数学二模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i为虚数单位,若复数(1+mi)(i+2)是纯虚数,则实数m=()A.1 B.﹣1 C.D.22.已知A=[1,+∞),,若A∩B≠∅,则实数a的取值范围是()A.[1,+∞)B.C.D.(1,+∞)3.已知变量x,y满足约束条件,则目标函数z=x﹣2y的最小值为()A.﹣1 B.1 C.3 D.74.若输入n=4,执行如图所示的程序框图,输出的s=()A.10 B.16 C.20 D.355.若中心在原点,焦点在y轴上的双曲线离心率为,则此双曲线的渐近线方程为()A.y=±x B.C.D.6.等差数列{a n}的前n项和为S n,且S3=6,S6=3,则S10=()A.B.0 C.﹣10 D.﹣157.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为()A.B.C.28 D.8.对函数f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),则称(x0,f(x0))与(﹣x0,f(﹣x0))为函数图象的一组奇对称点.若f(x)=e x﹣a(e为自然数的底数)存在奇对称点,则实数a的取值范围是()A.(﹣∞,1) B.(1,+∞)C.(e,+∞)D.[1,+∞)9.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有()A.0条B.1条C.2条D.1条或2条10.已知5件产品中有2件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为ξ,则Eξ=()A.3 B.C.D.411.锐角△ABC中,内角A,B,C的对边分别为a,b,c,且满足(a﹣b)(sinA+sinB)=(c﹣b)sinC,若,则b2+c2的取值范围是()A.(5,6]B.(3,5)C.(3,6]D.[5,6]12.已知函数f(x)=xlnx﹣ae x(e为自然对数的底数)有两个极值点,则实数a 的取值范围是()A.B.(0,e) C.D.(﹣∞,e)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.等比数列{a n}满足a n>0,且a2a8=4,则log2a1+log2a2+log2a3+…+log2a9=.14.不共线向量,满足,且,则与的夹角为.15.在的展开式中,常数项为.16.已知关于x的方程(t+1)cosx﹣tsinx=t+2在(0,π)上有实根.则实数t 的最大值是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知,,函数f(x)=.(Ⅰ)求函数y=f(x)图象的对称轴方程;(Ⅱ)若方程f(x)=在(0,π)上的解为x1,x2,求cos(x1﹣x2)的值.18.某校计划面向高一年级1200名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了180名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有105人.在这180名学生中选择社会科学类的男生、女生均为45人.(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?选择自然科学类选择社会科学类合计男生女生合计附:,其中n=a+b+c+d.P(K20.500.400.250.150.100.050.0250.0100.0050.001≥k0)K00.4550.708 1.323 2.072 2.706 3.841 5.024 6.6357.87910.82819.如图1,矩形ABCD中,AB=1,AD=2,点E为AD中点,沿BE将△ABE 折起至△PBE,如图2所示,点P在面BCDE的射影O落在BE上.(Ⅰ)求证:BP⊥CE;(Ⅱ)求二面角B﹣PC﹣D的余弦值.20.如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.(Ⅰ)求p的值;(Ⅱ)求动点M的轨迹方程.21.已知f(x)=ln(x+m)﹣mx.(Ⅰ)求f(x)的单调区间;(Ⅱ)设m>1,x1,x2为函数f(x)的两个零点,求证:x1+x2<0.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ.(1)求出圆C的直角坐标方程;(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m ≠0)对称的直线为l'.若直线l'上存在点P使得∠APB=90°,求实数m的最大值.[选修4-5:不等式选讲]23.已知函数.(1)求函数f(x)的定义域;(2)若当x∈[0,1]时,不等式f(x)≥1恒成立,求实数a的取值范围.安徽省合肥市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i为虚数单位,若复数(1+mi)(i+2)是纯虚数,则实数m=()A.1 B.﹣1 C.D.2【考点】复数的基本概念.【分析】先求出(1+mi)(i+2)=2﹣m+(2m+1)i,再由复数(1+mi)(i+2)是纯虚数,能求出实数m.【解答】解:i为虚数单位,(1+mi)(i+2)=2﹣m+(2m+1)i,∵复数(1+mi)(i+2)是纯虚数,∴,∴实数m=2.故选:D.2.已知A=[1,+∞),,若A∩B≠∅,则实数a的取值范围是()A.[1,+∞)B.C.D.(1,+∞)【考点】交集及其运算.【分析】根据A与B的交集不为空集,求出a的范围即可.【解答】解:A=[1,+∞),,且A∩B≠∅,∴2a﹣1≥1,∴a≥1,故选:A.3.已知变量x,y满足约束条件,则目标函数z=x﹣2y的最小值为()A.﹣1 B.1 C.3 D.7【考点】简单线性规划.【分析】由约束条件画出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.【解答】解:画出不等式组件,表示的可行域,由图可知,当直线y=x﹣,过A点(3,1)时,直线在y轴上的截距最大,z有最小值为3﹣2×1=1.故选:B.4.若输入n=4,执行如图所示的程序框图,输出的s=()A.10 B.16 C.20 D.35【考点】程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的S,i的值,当i=5时不满足条件i≤n,退出循环,输出S的值.【解答】解:模拟执行程序框图,可得S=4,i=2,满足条件i=2≤4,S=10,i=3,满足条件i=3≤4,S=16,i=4,满足条件i=4≤4,S=20,i=5不满足条件i=5≤5,输出S=20,故选:C.5.若中心在原点,焦点在y轴上的双曲线离心率为,则此双曲线的渐近线方程为()A.y=±x B.C.D.【考点】双曲线的简单性质.【分析】根据题意,由双曲线的离心率可得c=a,进而结合双曲线的几何性质可得b=a,再结合焦点在y轴上的双曲线的渐近线方程可得答案.【解答】解:根据题意,该双曲线的离心率为,即e==,则有c=a,进而b==a,又由该双曲线的焦点在y轴上,则其渐近线方程为y=±x;故选:B.6.等差数列{a n}的前n项和为S n,且S3=6,S6=3,则S10=()A.B.0 C.﹣10 D.﹣15【考点】等差数列的前n项和.【分析】利用等差数列前n项和公式列出方程组,求出首项和公差,由此能求出S10的值.【解答】解:∵等差数列{a n}的前n项和为S n,且S3=6,S6=3,∴,解得a1=3,d=﹣1,∴S10=10×3+=﹣15.故选:D.7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为()A.B.C.28 D.【考点】由三视图求面积、体积.【分析】由题意,几何体为棱台,上底面为直角边长为2的等腰直角三角形,下底面为直角边长为4的等腰直角三角形,高为2,即可求出体积.【解答】解:由题意,几何体为棱台,上底面为直角边长为2的等腰直角三角形,下底面为直角边长为4的等腰直角三角形,高为2,体积为=,故选A.8.对函数f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),则称(x0,f(x0))与(﹣x0,f(﹣x0))为函数图象的一组奇对称点.若f(x)=e x﹣a(e为自然数的底数)存在奇对称点,则实数a的取值范围是()A.(﹣∞,1) B.(1,+∞)C.(e,+∞)D.[1,+∞)【考点】函数与方程的综合运用.【分析】由方程f(x)=﹣f(﹣x)有非零解可得e2x﹣2ae x+1=0有非零解,令e x=t,则关于t的方程t2﹣2at+1=0有不等于1的正数解,利用二次函数的性质列出不等式组解出a的范围.【解答】解:∵f(x)=e x﹣a存在奇对称点,∴f(x)=﹣f(﹣x)有非零解,即e x﹣a=a﹣e﹣x有非零解,∴e2x﹣2ae x+1=0有非零解.设e x=t,则关于t的方程t2﹣2at+1=0在(0,1)∪(1,+∞)上有解;∴,解得a≥1.若t=1为方程t2﹣2at+1=0的解,则2﹣2a=0,即a=1,此时方程只有一解t=1,不符合题意;∴a≠1.综上,a>1.故选B.9.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有()A.0条B.1条C.2条D.1条或2条【考点】直线与平面平行的判定.【分析】利用已知条件,通过直线与平面平行的性质、判定定理,证明CD∥平面EFGH,AB∥平面EFGH,得到结果.【解答】解:如图所示,四边形EFGH为平行四边形,则EF∥GF,∵EF⊄平面BCD,GH⊂平面BCD,∴EF∥平面BCD,∵EF⊂平面ACD,平面BCD∩平面ACD=CD,∴EF∥CD,∴CD∥平面EFGH,同理AB∥平面EFGH,故选C.10.已知5件产品中有2件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为ξ,则Eξ=()A.3 B.C.D.4【考点】离散型随机变量的期望与方差.【分析】由题意知ξ的可能取值为2,3,4,分别求出相应的概率,由此能求出Eξ.【解答】解:由题意知ξ的可能取值为2,3,4,P(ξ=2)==,P(ξ=3)=()×=,P(ξ=4)=1﹣P(ξ=2)﹣P(ξ=3)=1﹣=,∴Eξ==.故选:C.11.锐角△ABC中,内角A,B,C的对边分别为a,b,c,且满足(a﹣b)(sinA+sinB)=(c﹣b)sinC,若,则b2+c2的取值范围是()A.(5,6]B.(3,5)C.(3,6]D.[5,6]【考点】正弦定理;余弦定理.【分析】由已知利用正弦定理可得b2+c2﹣a2=bc.再利用余弦定理可得cosA,进而可求A,利用正弦定理,三角函数恒等变换的应用化简可得b2+c2=4+2sin(2B ﹣),利用B的范围,可求2B﹣的范围,利用正弦函数的图象和性质可求其范围.【解答】解:∵(a﹣b)(sinA+sinB)=(c﹣b)sinC,由正弦定理可得:(a﹣b)(a+b)=(c﹣b)c,化为b2+c2﹣a2=bc.由余弦定理可得:cosA===,∴A为锐角,可得A=,∵,∴由正弦定理可得:,∴可得:b2+c2=(2sinB)2+[2sin(﹣B)]2=3+2sin2B+sin2B=4+2sin(2B ﹣),∵B∈(,),可得:2B﹣∈(,),∴sin(2B﹣)∈(,1],可得:b2+c2=4+2sin(2B﹣)∈(5,6].故选:A.12.已知函数f(x)=xlnx﹣ae x(e为自然对数的底数)有两个极值点,则实数a 的取值范围是()A.B.(0,e) C.D.(﹣∞,e)【考点】利用导数研究函数的极值.【分析】求出函数的导数,问题转化为y=a和g(x)=在(0,+∞)2个交点,根据函数的单调性求出g(x)的范围,从而求出a的范围即可.【解答】解:f′(x)=lnx﹣ae x+1,若函数f(x)=xlnx﹣ae x有两个极值点,则y=a和g(x)=在(0,+∞)有2个交点,g′(x)=,(x>0),令h(x)=﹣lnx﹣1,则h′(x)=﹣﹣<0,h(x)在(0,+∞)递减,而h(1)=0,故x∈(0,1)时,h(x)>0,即g′(x)>0,g(x)递增,x∈(1,+∞)时,h(x)<0,即g′(x)<0,g(x)递减,故g(x)max=g(1)=,而x→0时,g(x)→﹣∞,x→+∞时,g(x)→0,若y=a和g(x)在(0,+∞)有2个交点,只需0<a<,故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.等比数列{a n}满足a n>0,且a2a8=4,则log2a1+log2a2+log2a3+…+log2a9=9.【考点】数列的求和.【分析】根据题意,由等比数列{a n}的性质可得a1•a9=a2•a8=a3•a7=a4•a6=a52=4,同时可得a5=2,再利用对数的运算法则有log2a1+log2a2+…+log2a9=log2(a1•a2•…•a9)=log2(29),计算即可得答案.【解答】解:根据题意,等比数列{a n}的各项都是正数,a1•a9=a2•a8=a3•a7=a4•a6=a52=4,则a5=2,则log2a1+log2a2+…+log2a9=log2(a1•a2•…•a9)=log2(29)=9,故答案为:9.14.不共线向量,满足,且,则与的夹角为.【考点】数量积表示两个向量的夹角.【分析】设与的夹角为θ,利用两个向量垂直的性质,两个向量数量积的定义,求得cosθ的值,可得θ的值.【解答】解:设与的夹角为θ,∵不共线向量,满足,且,则θ∈(0,π),∴(﹣2)=﹣2=﹣2||•||cosθ=﹣2cosθ=0,∴cosθ=,∴θ=,故答案为:.15.在的展开式中,常数项为﹣5.【考点】二项式定理的应用.=(﹣1)4﹣r(r=0,1,【分析】的展开式中的通项公式:T r+1==(﹣1)k x r﹣2k,令r﹣2k=0,2,3,4).的通项公式:T k+1即r=2k.进而得出.=(﹣1)4﹣r(r=0,【解答】解:的展开式中的通项公式:T r+11,2,3,4).==(﹣1)k x r﹣2k,∵的通项公式:T k+1令r﹣2k=0,即r=2k.r=0,k=0;r=2,k=1;r=4,k=2.∴常数项=1﹣×+×1=﹣5.故答案为:﹣5.16.已知关于x的方程(t+1)cosx﹣tsinx=t+2在(0,π)上有实根.则实数t 的最大值是﹣1.【考点】根的存在性及根的个数判断.【分析】分离参数可得t=,利用导数判断右侧函数的单调性求出最大值即可.【解答】解:∵(t+1)cosx﹣tsinx=t+2,∴t=,令f(x)=,则f′(x)==,令g(x)=sinx+2cosx﹣1,则g′(x)=cosx﹣2sinx,∴当x=arctan时,g′(x)=0,当0<x<arctan时,g′(x)>0,当arctan<x <π时,g′(x)<0,∴g(x)在(0,arctan)上单调递增,在(arctan,π)上单调递减,又g(0)=1,g(π)=﹣3,∴g(x)在(0,π)上只有一个零点,又g′()=0,∴当0<x<时,g(x)>0,当<x<π时,g(x)<0,∴当0<x<时,f′(x)>0,当<x<π时,f′(x)<0∴f(x)在(0,)上单调递增,在(,0)上单调递减,∴当x=时,f(x)取得最大值f()=﹣1.∴t的最大值为﹣1.故答案为﹣1.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知,,函数f(x)=.(Ⅰ)求函数y=f(x)图象的对称轴方程;(Ⅱ)若方程f(x)=在(0,π)上的解为x1,x2,求cos(x1﹣x2)的值.【考点】两角和与差的余弦函数;平面向量数量积的运算.【分析】(Ⅰ)由已知利用平面向量数量积的运算,三角函数恒等变换的应用化简可得函数解析式为f(x)=sin(2x﹣),利用正弦函数的对称性即可得解.(Ⅱ)由条件知,且,可求,利用诱导公式即可化简求值得解.【解答】解:(Ⅰ)=,令,得,即y=f(x)的对称轴方程为,(k∈Z).(Ⅱ)由条件知,且,易知(x1,f(x1))与(x2,f(x2))关于对称,则,∴.18.某校计划面向高一年级1200名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了180名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有105人.在这180名学生中选择社会科学类的男生、女生均为45人.(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?选择自然科学类选择社会科学类合计男生6045105女生304575合计9090180附:,其中n=a+b +c+d .P(K 20.500.400.250.150.100.050.0250.0100.0050.001≥k 0)K00.4550.708 1.323 2.072 2.706 3.841 5.024 6.6357.87910.828【考点】独立性检验.【分析】(Ⅰ)计算抽取的男生与女生人数,根据分层抽样原理求出对应男生、女生人数;(Ⅱ)根据统计数据,填写列联表,计算观测值,比较临界值得出结论.【解答】解:(Ⅰ)由条件知,抽取的男生为105人,女生为180﹣105=75人;男生选择社会科学类的频率为,女生选择社会科学类的频率为;由题意,男生总数为人,女生总数为人,所以,估计选择社会科学的人数为人;(Ⅱ)根据统计数据,可得列联表如下:选择自然科学类选择社会科学类合计男生6045105女生304575合计9090180计算观测值,所以,在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关.19.如图1,矩形ABCD中,AB=1,AD=2,点E为AD中点,沿BE将△ABE 折起至△PBE,如图2所示,点P在面BCDE的射影O落在BE上.(Ⅰ)求证:BP⊥CE;(Ⅱ)求二面角B﹣PC﹣D的余弦值.【考点】二面角的平面角及求法;直线与平面垂直的性质.【分析】(Ⅰ)点P在平面BCDE的射影O落在BE上,证明CE⊥平面PBE,推出PB⊥CE.(Ⅱ)以O为坐标原点,以过点O且平行于CD的直线为x轴,过点O且平行于BC的直线为y轴,直线PO为z轴,建立如图所示直角坐标系.求出平面PCD 的法向量,平面PBC的法向量利用空间向量的数量积求解二面角B﹣PC﹣D的余弦值即可.【解答】解:(Ⅰ)由条件,点P在平面BCDE的射影O落在BE上,∴平面PBE⊥平面BCDE,易知BE⊥CE,∴CE⊥平面PBE,而BP⊂平面PBE,∴PB⊥CE.(Ⅱ)以O为坐标原点,以过点O且平行于CD的直线为x轴,过点O且平行于BC的直线为y轴,直线PO为z轴,建立如图所示直角坐标系.则,,,设平面PCD的法向量为则,即,令,可得设平面PBC的法向量为则,即,令,可得∴考虑到二面角B﹣PC﹣D为钝二面角,则二面角B﹣PC﹣D的余弦值为.20.如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.(Ⅰ)求p的值;(Ⅱ)求动点M的轨迹方程.【考点】直线与圆锥曲线的综合问题;轨迹方程.【分析】(Ⅰ)由点A的横坐标为2,可得点A的坐标为(2,2),代入y2=2px,解p.(Ⅱ)设,,y1≠0,y2≠0.切线l1:,代入y2=2x,求出,得到l1方程为,同理l2方程为,联立直线方程组,求出M,利用CD方程为x0x+y0y=8,联立方程利用韦达定理,代入可知M(x,y)满足,求出动点M的轨迹方程.【解答】解:(Ⅰ)由点A的横坐标为2,可得点A的坐标为(2,2),代入y2=2px,解得p=1,(Ⅱ)设,,y1≠0,y2≠0.切线l1:,代入y2=2x得,由△=0解得,∴l1方程为,同理l2方程为,联立,解得,∵CD方程为x0x+y0y=8,其中x0,y0满足,,联立方程得,则,代入可知M(x,y)满足,代入得,考虑到,知.∴动点M的轨迹方程为,.21.已知f(x)=ln(x+m)﹣mx.(Ⅰ)求f(x)的单调区间;(Ⅱ)设m>1,x1,x2为函数f(x)的两个零点,求证:x1+x2<0.【考点】利用导数研究函数的单调性;函数零点的判定定理.【分析】(Ⅰ)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;(Ⅱ)构造函数g(x)=e mx﹣x,g(x)=e mx﹣x与y=m图象两交点的横坐标为x1,x2,问题转化为证明令,根据函数的单调性证明即可.【解答】解:(Ⅰ)∵f(x)=ln(x+m)﹣mx,∴,当m≤0时,∴,即f(x)的单调递增区间为(﹣m,+∞),无减区间;当m>0时,∴,由f'(x)=0,得,时,f'(x)>0,时,f'(x)<0,∴m>0时,易知f(x)的单调递增区间为,单调递减区间为,(Ⅱ)由(Ⅰ)知f(x)的单调递增区间为,单调递减区间为.不妨设﹣m<x1<x2,由条件知,即,构造函数g(x)=e mx﹣x,g(x)=e mx﹣x与y=m图象两交点的横坐标为x1,x2,由g'(x)=e mx﹣1=0可得,而m2>lnm(m>1),∴知g(x)=e mx﹣x在区间上单调递减,在区间上单调递增.可知欲证x1+x2<0,只需证,即证,考虑到g(x)在上递增,只需证由g(x2)=g(x1)知,只需证令,则,即h(x)单增,又,结合知h(x1)<0,即成立,即x1+x2<0成立.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ.(1)求出圆C的直角坐标方程;(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m≠0)对称的直线为l'.若直线l'上存在点P使得∠APB=90°,求实数m的最大值.【考点】简单曲线的极坐标方程.【分析】(1)由ρ=4cosθ得ρ2=4ρcosθ,即可求出圆C的直角坐标方程;(2)l:y=2x关于点M(0,m)的对称直线l'的方程为y=2x+2m,而AB为圆C 的直径,故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点,即可求实数m的最大值.【解答】解:(1)由ρ=4cosθ得ρ2=4ρcosθ,即x2+y2﹣4x=0,即圆C的标准方程为(x﹣2)2+y2=4.(2)l:y=2x关于点M(0,m)的对称直线l'的方程为y=2x+2m,而AB为圆C 的直径,故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点,故,于是,实数m的最大值为.[选修4-5:不等式选讲]23.已知函数.(1)求函数f(x)的定义域;(2)若当x∈[0,1]时,不等式f(x)≥1恒成立,求实数a的取值范围.【考点】函数恒成立问题;函数的定义域及其求法.【分析】(1)由根式内部的代数式大于等于0,求解绝对值的不等式,进一步分类求解含参数的不等式得答案;(2)把不等式f(x)≥1恒成立转化为|ax﹣2|≤3,记g(x)=|ax﹣2|,可得,求解不等式组得答案.【解答】解:(1)要使原函数有意义,则|ax﹣2|≤4,即﹣4≤ax﹣2≤4,得﹣2≤ax≤6,当a>0时,解得,函数f(x)的定义域为;当a<0时,解得,函数f(x)的定义域为.(2)f(x)≥1⇔|ax﹣2|≤3,记g(x)=|ax﹣2|,∵x∈[0,1],∴需且只需,即,解得﹣1≤a≤5,又a≠0,∴﹣1≤a≤5,且a≠0.4月11日。
合肥二模试题及答案

合肥二模试题及答案一、选择题(每题2分,共20分)1. 下列哪项不是合肥的著名景点?A. 逍遥津B. 包公祠C. 黄山D. 巢湖答案:C2. 合肥二模考试中,选择题的总分是多少?A. 10分B. 15分C. 20分D. 25分答案:C3. 合肥位于中国的哪个省份?A. 江苏省B. 浙江省C. 安徽省D. 湖北省答案:C4. 合肥二模考试的数学部分,填空题的总分是多少?A. 30分C. 40分D. 45分答案:B5. 合肥二模考试的英语部分,阅读理解题的总分是多少?A. 20分B. 25分C. 30分D. 35分答案:B6. 合肥二模考试的物理部分,实验题的总分是多少?A. 15分B. 20分C. 25分D. 30分答案:A7. 合肥二模考试的化学部分,计算题的总分是多少?A. 20分B. 25分C. 30分D. 35分答案:B8. 合肥二模考试的生物部分,选择题的总分是多少?B. 15分C. 20分D. 25分答案:C9. 合肥二模考试的地理部分,填空题的总分是多少?A. 15分B. 20分C. 25分D. 30分答案:B10. 合肥二模考试的语文部分,作文题的总分是多少?A. 40分B. 45分C. 50分D. 55分答案:C二、填空题(每题3分,共30分)11. 合肥的别称是______。
答案:庐州12. 合肥二模考试的数学部分,选择题的总分是______分。
答案:2013. 合肥二模考试的英语部分,完形填空题的总分是______分。
14. 合肥二模考试的物理部分,选择题的总分是______分。
答案:2015. 合肥二模考试的化学部分,选择题的总分是______分。
答案:2016. 合肥二模考试的生物部分,选择题的总分是______分。
答案:2017. 合肥二模考试的地理部分,选择题的总分是______分。
答案:2018. 合肥二模考试的语文部分,选择题的总分是______分。
答案:2019. 合肥二模考试的数学部分,填空题的总分是______分。
2015年中考数学二模试题附答案

2015年中考数学二模试题(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.下列运算中,正确的是 ……………………………………………………………………( )(A)1293=±3(C)030-=()(D)2139-=2.轨道交通给人们的出行提供了便捷的服务,据悉,上海轨道交通19号线即将开建,一期规划为自川桥路站至长兴岛,设6站,全长约为20600米.二期、远期将延伸到崇明岛、横沙岛,届时崇明县三岛将全通地铁.将20600用科学记数法表示应为 ………………………( )(A)52.0610⨯(B)320.610⨯(C)42.0610⨯(D)50.20610⨯3.从下列不等式中选择一个与12x +≥组成不等式组,如果要使该不等式组的解集为1x ≥,那么可以选择的不等式可以是 ………………………………………………………………( ) (A)1x >-(B)2x >(C)1x <-(D)2x <4.已知点11(,)A x y 和点22(,)B x y 是直线23y x =+上的两个点,如果12x x <,那么1y 与2y 的大小关系正确的是 …………………………………………………………………( )(A)12y y >(B)12y y <(C)12y y =(D)无法判断5.窗花是我国的传统艺术,下列四个窗花图案中,不是..轴对称图形的是…………………( )(A) (B) (C) (D) 6.已知在四边形ABCD 中,AC 与BD 相交于点O ,那么下列条件中能判定这个四边形是正方形的是 …………………………………………………………………( ) (A)AC BD =, AB CD ∥, AB CD = (B)AD BC ∥, A C ∠=∠(C)AO BO CO DO ===, AC BD ⊥(D)AO CO =, BO DO =, AB BC =二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】 7.因式分解:34x x -= ▲ . 8.2,那么x = ▲ .9.如果分式242x x -+的值为0,那么x 的值为 ▲ .10.已知关于x 的一元二次方程2610x x m -+-=有两个相等的实数根,那么m 的值为▲ . 11.已知在方程222232x x x x++=+中,如果设22y x x =+,那么原方程可化为关于y 的整式方程是 ▲ .12.布袋中有2个红球和3个黑球,它们除颜色外其他都相同,那么从布袋中取出1个球恰好是红球的概率为 ▲ .13.某学校在开展“节约每一滴水”的活动中,从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是 ▲ 吨.14.如图,在ABC ∆中,AD 是边BC 上的中线,设向量AB a =,AD b =,如果用向量,a b表示向量BC ,那么BC = ▲ .15.如图,已知ABC ∆和ADE∆均为等边三角形,点D 在BC 边上,DE 与AC 相交于点F ,如果9AB =,3BD =,那么CF 的长度为 ▲ .16. 如图,已知在O 中,弦CD 垂直于直径AB ,垂足为点E ,如果30BAD ∠=︒,2OE =,那么CD = ▲ .17.如果一个二次函数的二次项系数为1,那么这个函数可以表示为2y x px q =++,我们将(第14题图)ABCD(第15题图)A BCEFD(第16题图)B[],p q 称为这个函数的特征数.例如二次函数242y x x =-+的特征数是[]4,2-.请根据以上的信息探究下面的问题:如果一个二次函数的特征数是[]2,3,将这个函数的图像先向左平移2个单位,再向下平移3个单位,那么此时得到的图像所对应的函数的特征数为 ▲ .18.如图,在ABC ∆中,CA CB =,90C ∠=︒,点D 是BC的中点,将ABC ∆沿着直线EF 折叠,使点A 与点D 重合, 折痕交AB 于点E ,交AC 于点F ,那么sin BED ∠的值 为 ▲ .三、解答题(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6tan302x =︒-.20.(本题满分10分)解方程组:222230x y x xy y -=⎧⎨--=⎩21.(本题满分10分,第(1)小题5分、第(2)小题5分) 在Rt ABC ∆中,90BAC ∠=︒,点E 是BC 的中点, AD BC ⊥,垂足为点D .已知9AC =,3cos 5C =. (1)求线段AE 的长;(2)求sin DAE ∠的值.22.(本题满分10分,第(1)小题4分,第(2)小题6分)周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y (km)与小明离家时间x (h)的函数图像.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.(1)小明骑电动自行车的速度为 千米/小时,在甲地游玩的时间为 小时; (2)小明从家出发多少小时的时候被妈妈追上?A C FED(第18题图)(第21题图) CAB E D此时离家多远?23.(本题满分12分,每小题各6分)如图,ABC ∆中,2BC AB =,点D 、E 分别是BC 、AC 的中点,过点A 作AF BC ∥交线段DE 的延长线于点F ,取AF 的中点G ,联结DG ,GD 与AE 交于点H . (1)求证:四边形ABDF 是菱形; (2)求证:2DH HE HC =⋅.24.(本题满分12分,每小题各6分) 如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.(第24题图)A BDHG FEC(第23题图)25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分) 如图,在Rt ABC ∆中,90ACB ∠=︒,8AC =,4tan 3B =,点P 是线段AB 上的一个动点,以点P 为圆心,PA 为半径的P 与射线AC 的另一个交点为点D ,射线PD 交射线BC 于点E ,点Q 是线段BE 的中点.(1)当点E 在BC 的延长线上时,设PA x =,CE y =,求y 关于x 的函数关系式,并写出定义域;(2)以点Q 为圆心,QB 为半径的Q 和P 相切时,求P 的半径;(3)射线PQ 与P 相交于点M ,联结PC 、MC ,当PMC ∆是等腰三角形时,求AP 的长.(第25题图)(备用图1)BA CB九年级数学参考答案及评分说明一、选择题(本大题共6题,每题4分,满分24分) 1.D ; 2.C ;3.A ; 4.B ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.(2)(2)x x x +- 8.1 9.2 10. 10 11. 2320y y -+= 12.2513. 540 14.22b a - 15.216. 17.[]68, 18. 35三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6302x tan =-. 解:原式=21(1)212x x x x x --+-+……………………………………………………2分 122x x x x -=-++ ………………………………………………………2分 12x =+………………………………………………………………2分∵6302x tan =-6223=⨯-=………………………………………2分 ∴原式6=………………………………………………………………2分 20. (本题满分10分) 解方程组:222230x y x xy y -=⎧⎨--=⎩...............(1) (2)解:由(2)可得:(3)()0x y x y -+=∴30x y -=,0x y += ………………………………2分∴原方程组可化为:230x y x y -=⎧⎨-=⎩,2x y x y -=⎧⎨+=⎩ …………………………4分解得原方程组的解为1131x y =⎧⎨=⎩,2211x y =⎧⎨=-⎩ ………………………………4分21.(本题满分10分,第(1)小题5分、第(2)小题5分)(1)解:909oBAC AC ∠==∵, 93cos 5AC C AB BC ===∴ …………………………………………1分 15BC =∴ ………………………………………………………………2分 90oBAC ∠=∵,点E 是BC 的中点 11522AE BC ==∴ ……………………………………………………2分 (2)解:AD BC ⊥∵ 90oADC ADB ∠=∠=∴3cos 95CD CD C AC ===∴ 275CD =∴ …………………………………………………2分∵点E 是BC 的中点,BC=15 ∴CE=152 ∴DE=2110………………………………………1分 ∵90oADB ∠= ∴sin DAE ∠=2127101525DE AE =⨯= ……………………………2分 22. (本题满分10分,第(1)小题4分,第(2)小题6分)(1) 20;0.5 ……………………………………………………………各2分 (2)解:设小明出发x 小时的时候被妈妈追上.420(1)10203()3x x -+=⨯- ……………………………………3分解得:74x =……………………………………………………1分 ∴320(1)102010254x -+=⨯+= ……………………………1分答:当小明出发74小时的时候被妈妈追上,此时他们离家25千米.…1分23.(本题满分12分,每小题各6分)(1)证明:∵点D 、E 分别是BC 、AC 的中点∴DE//AB ,BC=2BD …………………………………………………1分 ∵AF//BC∴四边形ABDF 是平行四边形 ……………………………………………2分 ∵BC=2AB∴AB=BD …………………………………………………………………1分 ∴四边形ABDF 是菱形. …………………………………………………2分(2)证明:∵四边形ABDF 是菱形 ∴AF=DF∵点G 是AF 的中点 ∴FG=12AF ∵点E 是AC 的中点 ∴AE=CE ∵AF//BC ∴1EF AEDE CE== ∴EF=12DF , ∴FG=EF ……………………………………………………………1分 在△AFE 和△DFG 中AF DF F F EF GF =⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△DFG (S.A.S )∴∠FAE=∠FDG ………………………………………………………1分 ∵AF//BC ∴∠FA E=∠C∴∠FDG=∠C ………………………………………………………1分 又∵∠EHD=∠DHC (公共角)∴△HED ∽△HDC ……………………………………………………2分 ∴HE HDHD HC= ∴2DH HE HC = ………………………………………………………1分 24.(本题满分12分,每小题各6分)(1)解:∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩……………………………………………………1分解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩………………………………………………2分∴这个抛物线的解析式为:2142y x x =-- ………………………………1分 顶点为9(1,)2- ……………………………………………………………2分(2)如图:取OA 的中点,记为点N ∵OA=OC=4,∠AOC=90° ∴∠ACB=45°∵点N 是OA 的中点 ∴ON=2 又∵OB=2 ∴OB=ON 又∵∠BON=90° ∴∠ONB=45° ∴∠ACB=∠ONB ∵∠OMB+∠OAB=∠ACB ∠NBA+∠OAB=∠ONB∴∠OMB=∠NBA ………………………………………………………………2分 1° 当点M 在点N 的上方时,记为M 1 ∵∠BAN=∠M 1AB ,∠NBA=∠OM 1B , ∴△ABN ∽△AM 1B ∴1AN ABAB AM =又∵AN=2,∴110AM = 又∵A (0,—4)∴1(0,6)M ………………………………………………………………………2分 2° 当点M 在点N 的下方时,记为M 2点M 1与点M 2关于x 轴对称,∴2(0,6)M - ……………………………………2分 综上所述,点M 的坐标为(0,6)或(0,6)-25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分) (1)解:过点P 作PH ⊥AD ,垂足为点H∵∠ACB=90°,43tanB = ∴35sinA =∵PA x = ∴35PH x = ∵∠PHA=90° ∴222PH AH PA += ∴45AH x =……………………1分 ∵在⊙P 中,PH ⊥弦AD ∴45DH AH x ==, ∴85AD x = 又∵AC=8 ∴885CD x =- ………………………………………………1分∵∠PHA=∠BCA=90°,∴PH ∥BE ∴PH DHCE CD = ∴3455885x xy x=- ……………………………1分 ∴665y x =- (x 0<<5) (1)(2)∵PA=PD ,PH ⊥AD ∴∠1=∠2 ∵PH ∥BE∴∠1=∠B ,∠2=∠3 ∴PB=PE ∵Q 是BE 的中点∴PQ ⊥BE ………………………………………………………………………1分 ∴43PQ tanB =BQ = ∴35BQ cosB =BP = ∵PA x = ∴10PB x =- ∴365BQ x =-, 485PQ x =- 1°当⊙Q 和⊙P 外切时:PQ=AP+BQ∴438655x x x -=+- …………………………………………………………1分 53x = …………………………………………………………………1分2°当⊙Q 和⊙P 内切时,此时⊙P 的半径大于⊙Q 的半径,则PQ=A P —BQ ∴438(6)55x x x -=-- …………………………………………………………1分 321HQABP CED- 11 - 356x = ……………………………………………………………………1分 ∴当⊙Q 和⊙P 相切时,⊙P 的半径为53或356. (3)当△PMC 是等腰三角形,存在以下几种情况: 1°当MP=MC x =时 ,∵336(6)55QC x x =--= ∴45MQ x = 若M 在线段PQ 上时,PM+MQ=PQ ∴44855x x x +=- 4013x = ……………………………………………………………………1分 若M 在线段PQ 的延长线上时,PM —MQ=PQ ∴44855x x x -=- 8x = …………………………………………………………………………1分 2°当CP=CM 时∵CP=CM ,CQ ⊥PM∴PQ=QM=1122PM x = ∴41852x x -= 8013x = …………………………………………………………………………1分 3°当PM=PC x =时∵AP x = ∴PA=PC 又∵PH ⊥AC ∴AH=CH∵PH ∥BE ∴1AP AH BP CH== ∴110x x =- 5x = …………………………………………………………………………1分 综上所述:当△PMC 是等腰三角形时,AP 的长为4013或8013或5或8.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 合肥市2015年高三第二次教学质量检测 数学试题(理) 第Ⅰ卷(满分50分) 一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数iiz2143(其中i是虚数单位),则复数z的共轭复数z( ) A.i21 B. i21 C. i21 D. i21
解析:iiiiiiiiz215105)21)(21()21)(43(2143 ∴共轭复数iz21,选A 2.若集合}11|{xxM,则MCR( ) A. }1|{xx B. }10|{xx C. }10|{xx D. }1|{xx
解析:011xx或1x ∴}10|{xxMCR,选C
3.双曲线1222yx的离心率是( ) A. 23 B. 26 C. 3 D. 3
解析:由双曲线方程知22,1ba26c ∴26ace,选B 4.某空间几何体的三视图如图所示(其中俯视图中的弧线为四分之一圆),则该几何体的表面积为( ) A.45 B.48 C. 125 D. 128 - 2 -
解析:由三视图可知,该几何体是底面为41圆的柱体 1253)4(4222表S,选C
5.“1a”是“直线01:1yaxl与直线05)3(4:2ayaxl平行”的( ) A.充分且不必要条件 B.必要且不充分条件 C.充要条件 D.既不充分也不必要条件
解析:直线01:1yaxl与直线05)3(4:2ayaxl平行,则aaa51314 解得1a,∴是充要条件,选C
6.等差数列}{na的前n项和为nS,若5326243aaa,则7S( ) A.28 B.21 C.14 D.7
解析:411112435155)(3)3(2)2(6326adadadadaaaa ∴14a,∴7747aS,选D
7.已知函数xxxfcossin)(,若果存在实数1x,使得对任意的实数x,都有)2015()()(11xfxfxf成立,则的最小正值为( )
A.20151 B. 2015 C. 40301 D. 4030 - 3 -
解析:)4sin(2cossin)(xxxxf,∴2T 由题意,)(1xf为最小值,)2015(1xf为最大值 则ZkTk,)21(2015,解得)21(20152k 当0k时,2015,选B
8.如图所示,程序框图的输出结果是( ) A.7 B.8 C.9 D.10
解析:29log9log6log5log4log385438543aaaaT ∴当10log3T时,2T,此时10n,选D
9.某校开设5门不同的数学选修课,每位同学可以从中任选1门或2门课学习,甲、乙、丙三位同学选择的课没有一门是相同的,则不同的选法共有( ) A.330种 B.420种 C.510种 D.600种
解析:分三类:①甲、乙、丙三人每人都只选1门,有6035A种; ②三人中一人选2门,另两人选1门,有180232513ACA种; ③三人中一人选1门,另两人选2门,有90241513CCA种。 - 4 -
∴不同的选法共有330种,选A 10.已知ABC的三边长分别为cba,,,且满足acb3,则ac的取值范围为( ) A.),1( B.)2,0( C.)3,1( D.)3,0(
解析:由三角形边角关系,则abacacabacabbcacbaacba11313 ∴1131abacacab,两式相加得,420ac ∴ac的取值范围为)2,0(,选B 第Ⅱ卷(满分100分) 二、填空题(本大题共5小题,每小题5分,共25分。把答案填在答题卡的相应位置) 11.甲、乙两位同学5次考试的数学成绩(单位:分),统计结果如下: 学生 第一次 第二次 第三次 第四次 第五次 甲 77 81 83 80 79 乙 89 90 92 91 88 则成绩较为稳定的那位同学成绩的方差为
解析:80甲x,42甲s;90乙x,22乙s ∴成绩较为稳定的那位同学为乙,其方差为2
12.以平面直角坐标系的原点为极点,x轴非负半轴为极轴,建立极坐标系,两种坐标系取相同的长度单位。曲线1C的参数方程为atytx2(t为参数),曲线2C的极坐标方程为
cos4
,若1C与2C有两个不同的交点,则实数a的取值范围是
解析:曲线1C为02ayax;曲线2C为4)2(22yx, - 5 -
1C与2C有两个不同的交点,则333321|4|2aaa
13.已知点O是ABC内一点,且OCOBOA。若ABC与OBC的面积之比为3:1,则
解析:如图所示,因为ABC与OBC的面积之比为3:1,则1:3:OEAD ∴EOEDOA2 EBOEOB,ECOEOC ∴EDEOECEBOEOCOB2)( ∴2
14.已知,为钝角,若)sin(2)sin(,则)tan(的最小值是 解析:)sin(2)sin(,展开得 sincos2cossin2sincoscossin
∴tan3tancossinsincos3 ∴tan1tan32tan31tan2tantan1tantan)tan(2
∵,为钝角,则0tan,∴32tan1tan3 ∴0)tan(33,即最小值为33 - 6 -
15.定义:)()(1xfxf,当2n且Nn时,))(()(1xffxfnn。对于函数)(xf定义域内的0x,若存在正整数n是使得00)(xxfn成立的最小正整数,则称n是点0x的最小正周期,
0x称为)(xf的n周期点。已知定义在]1,0[上的函数)(xf的图象如图,对于函数)(xf,
下列说法正确的是 (写出所有正确命题的编号)。 ①0是)(xf的一个5周期点;
②3是点21的最小正周期; ③对于任意正整数n,都有32)32(nf; ④若0x是)(xf的一个2周期点,则]1,21(0x; ⑤若0x是)(xf的2周期点,则)(0xf一定是)(xf的2周期点。
解析:根据函数图象可得]1,21(,22]21,0[,21)(xxxxxf 21)0()0(0)1()0(1)21()0(21)0(21)0(4321ffffffff∴
1)21()0(5ff,①错误;21)))21((())21(()21(123ffffff,②正确;由函数解析式,
显然③正确;由002)(xxf,当]21,0[0x时,即002)21(2xx,解得310x,④错误;当]1,21(0x时,0000221)22()(xxxxf或002)22(2xx,解得
650x或320x,∴32)32(,31)65(,65)31(fff,⑤正确。
∴说法正确的是②③⑤。 - 7 -
三、解答题(本大题共6个小题,共75分。解答应写出文字说明、证明过程和演算步骤) 16.(本小题满分12分)
锐角ABC中,角CBA,,的对边分别为cba,,。已知Bctan是Abtan和Bbtan的等差中项。 (Ⅰ)求角A的大小; (Ⅱ)若)sin,(sinCBm,)cos,(cosCBn,求nm的取值范围。
解析:(Ⅰ)由题意知:BcBbAbtan2tantan ∴BBCBBBAABcossinsin2cossinsincossinsin, 即ACBABAcossin2sincoscossin ∴ACCcossin2sin,即21cosA
又A0,∴3A (Ⅱ)CBCCBBnm2sin212sin21cossincossin
)62sin(23)234sin(212sin21BBB
∵322020CBCB,∴26B ∴2343nm,即nm的取值范围是]23,43( 17.(本小题满分12分) 某商场为回馈大客户,开展摸球中奖活动,规则如下:从一个装有质地和大小完全相同的4个白球和1个红球的摸奖箱中随机摸出一球,若摸出红球,则摸球结束;若摸出白球(不放回),则向摸奖箱中放入一个红球后继续进行下一轮摸球,直到摸到红球结束。若大客户在第
n轮(Nn)摸到红球,则可获得1)21(10000n的奖金(单位:元)。
(Ⅰ)求某位大客户在一次摸球中奖活动中至少获得2500元奖金的概率; (Ⅱ)设随机变量为某位大客户所能获得的奖金,求随机变量的分布列与期望。
