沈阳工业大学实验报告非线性仿真
非线性仿真

2.5系统非线性环节的仿真在实际系统中,往往存在各种非线性特性,可将此当作非线性环节处理,这种环节的输入和输出之间关系是一种非线性函数关系,因此非线性环节的仿真就是用仿真语言来描述这些关系。
本节介绍几种典型的非线性环节的仿真算法。
2.5.1饱和环节饱和环节在控制系统中较普遍,例如饱和放大器、限幅装置、伺服阀饱和特性等。
饱和环节特性如图所示。
图2.5-1饱和特性该特性对应的数学表达式为:u u兰Cy = * c u >c (2.5-1)—c u < —c式中,c为饱和环节特征参数,斜率为1,该环节特性可用MATLAB编程仿真,利用上面算法的编写的MATLAB函数SATURATION,调用格式为:y = saturation (u,c)其中,u为输入;c为饱和环节特征参数,y为饱和环节输出Saturati on.m; amp209.m2.5.2死区环节在控制装置中,放大器的不灵敏区,伺服阀和比例阀阀芯正遮羞特性,传动元件静摩擦等造成的死区特性。
典型死区非线性环节特性如图2.5-2所示。
可用下面数学关系来描述:0 u兰cy = * u -c u >c (2.5-2)u + c u c —c式中,c为死区特征参数,斜率为1。
该环节可根据上述算法编写MATLAB函数deadzone供调用,格式如下:y 二deadzone(u, c)其中,u为环节输入;c为死区环节特征参数,y为死区环节输出。
Deadz on e.m; amp210m齿轮传动副和丝杆螺母传动副中存在传动间隙都属这一类非线性因素,它对系统精度带来影响。
齿隙非线性环节特性如图2.5-3所示。
图2.5-3齿隙特性当输入u增加时,输出沿a > b > d线段变化;当输入u减小时,输出沿d >e > a线段变化。
在线段bd上,输入增加时,当前输出值y(k)总是大于前一时刻的输出值y(k-1)。
而在ea上,输入减小时,当前输出y(k)总是小于前一时刻的输出值y(k-1)。
数值分析实验报告一

实验报告课程名称:实验项目:数值分析解方程/解方程组专业班级:机械工程姓名:李奇学号:201820065实验室号:实验组号:实验时间:批阅时间:沈阳工业大学实验报告(适用计算机程序设计类)专业班级:机械工程学号:201820065 姓名:李奇实验名称:解方程(适用计算机程序设计类)专业班级:机械工程学号:201820065姓名:李奇实验步骤或程序:1、编写牛顿法M文件器-C:1U er s\l I q i\ D e & kto p ^newto n. m newton.m ;;+1 - 5*115 f r:2 -f-dnput「请输入T (s) = ?);3 -df-dif f Cf >:4 -x0-input 请输入J8代初值W ):5 _e=input『请输入根的邊差限于”);€ -N= input「请输入送代炖册):f k=l;S -'while (k^N)S -x«xO:1€ -adpQ-eval (f^/evnl (df};L1 -辻abs (rl-jcO) <e12 -fprintf ( x-%. 6f VdS代次数为:・ sl# k)13 -treafc14 -else15 - xO=xl;16 -k=h+l:L:-end1S -end1© -if k>=N2C -fprintf ('矢飯S〉21 -end2、调用newton.m文件,输入求解皿酉tonfx附件A 沈阳工业大学实验报告3、运行结果如下®>> nekton请输入芳(x)=cos 'XJi青输Xiiffi初値期丸请输入很的误差®e-10"-6诸输入迭代戻数限皓8K-0.517757迭代次数为:64、编写割线法M文件(1)子程序厲- &U齟「班li qi\DeskiopXfun.m® >1 \珂+ 11 fixncticn y = fun(x)2 —y = cos (x)-x*e?;p :(2)主程序iN 斎器-C;\U s-e r5\ 11 q i\D e^kt o peseta nt, m A secant.m | +1function 咒 = seeant (xO, xl, t ol)2 -if narcin < 103 -toL m 1. Oe-S:end生-5 —x = M0 - fun (M0) * (xO - x 1) / (fuiiGiO) - fun (xl)):5 -n = 1:nvliile (aJbs (x0—xl)、tel)聪(n <—10005i =3 -xl = xC;0 -x0 - X ;10 -x = xO - funtxO) * (xO - xl> / (-fun<xO) - funtxl)):11 -n = n H- 1;12 -Mid13 --n5、调用secant.m文件,输入方程静令厅窗口>> secant* Q, 0^ 1 &运行结果如下命零行窗口>)secant(0T 0.2hle-6)n ■s axis =0,5178沈阳工业大学实验报告(适用计算机程序设计类)专业班级:机械工程 _______ 学号:201820065 姓名:李奇实验名称:解方程组沈阳工业大学实验报告附件B(适用计算机程序设计类)专业班级:机械工程________ 学号:201820065 姓名:李奇实验步骤或程序:1、编写高斯消元法M文件/ 涓辑器-C; ;U sfir5\ I i q i\D e skto p\G a u 5sxia oq u. mGaussxi doqu.m :v +1□ -function ERA. RB, n, Xl^auss^iaoqu (A f b) ■U为亲数拒蹲,h为右端顶2 -> A b]:惭向增广拒阵3 -nr length^);%右湍】页b的维敎4 -触寸沁(A):9 _J?E=rwk(B);%熠广矩阵日的秩6 =if RE-RAM7 ―disp(h提示:@^]RA'=KB,所以此方程期无18')8 =return9 -end10 —if RA—RB11 -if RA==n12 -disp C握示:因対RA>RE=m所以址方琨组有唯一的筒J13 一X=seros(n, 1);14 - f or p»1: n- 115 -□fox h=p十1: n16 —-E(k,p)/B(p,pk Bgp: n+1) -B (k n p: n4-l) -m*B tp, p:ffin+1):17 一卜end18 —L end19 -WCl-n,rr+L) ;A=Btl :n1I n) ;X(n)=b (n)/ACn>n);20 - □for q-n-1.-1:121 一X (q) = (b(q)-snni(A(q, f n) *X fq+1; n)))/A(q. q):22 -end23 -else24 -disp(提尔:凶为RA・RBC%肋以此万程组戸尢好第貼J25 -end26 - end2、调用Gaussxiaoqu.m文件,输入方程组Qa js n i -a DQU11. hi耒定史匿教书左宝'A 0泊5+3,-a. 6,-3.-3, 4; 5.-2.1* 3+ 2, 4,-<r2.7厂二H -无-臨«-3. -S, 2. 3, S;4. Z, ~3,认0.-2];冲b=riOT. 15 <5. 72;&3,fx >> b)3、运行结果如下帚令行哥口©>> t ausE5tiaoqii(.i T b J料提示;因X]RA-RB-n,所以就方程组有唯一的解-11. DOOO 3. 00004. 60003.2000 '7.500011-00003.0000ans =0 0-7. 5000 -11. 0000工 OCOO0 3,2000 -7. 5000 71. QOS3. OCOO4、编写高斯列主元法M文件N 编辑器-C:\U ser&\l i qi\D es ktci p\ G a u ss. m Gauss.rn 兰+I function [RATRB,n,XJ =Causs(A, b) B= U b];n^length ;RA=rank(A);RB=rank(Bk •:增广拒阵F的秩为系数拒阵,b拘右端1页为熠广葩辟州右端陨b的錐数%系数矩辟3痢秩10 -11 -12 -13- 14-15-16—17 -13 -19 -20 -21 -22 -23 -24 --26 -27 -23 -29刃31-32-33-cha=RB-R^;if cha>0disp (?提示::因対RA上眼所以此方程组无斛')returnendif RA=REif RA—ndispC H示£园为RA^RE^n,所以此方翟组有唯一的解*)X=zeros(n, 1) :C=3eros(l,n+l'i :El for p»1:n-1r 1Y> j' = »ax (abs (D (p: n a p))): 町拱出刮中绝对值最大的教C-E 血:):B'Cj+p-l. : )=C;for k=p+l: n 中涓元in=B 'kTpl/E (p, p) . E (k?p: n+L)=E 'k3p a+l)-tii*E (p?p: n+1).endb=B(L;n,nvi): 1=B(1 :n, 1 :n) ;X (n) =b (u)/ A(n Pn): 牛回代for Q-n-1: -1:1endelsedisp(:示:因为RA・EB<n,所以肚方種组有无穷參輪)end5、调用Gauss.m文件,输入方程组*4MU ©>> &SUSE UL b)丰走史回顫或妻里* *>> A-:4. 5. 3.-5. 6.-3.-3. 4 5. -2, 1.3,2. 4. -6 ?, -4.-'. 2. -5. -f. 4 5.-5. -S. f.3.3 4. 2.-3. ■). 0. -21:>> b=[lCCl. L6 -;□. ~2 ^S. :.5^. 1 ;3.72]庭冲為5&运行结果如下命令行窗口Vi X =-11, 00003. 0000X =-7. 5000-1L00Q03. 0000K =3. 2000-7. 5000-11. 00003. 00004. 60003. 2000-7- 5000-11. 00003. 00007、编写LU分解法M文件厨解辑:器* C:\Users\Jiqi\D&5.ktop\LLJ.m @ LU.m +1 H function LU (A, b3Z -五,rC*si=e U) : S租抽化矩阵扎b, L和U3 -tTFlengthCb):4 ->eye(n) : M为n断单位時5 —U=z^xos(ii) : SUJ^jn 阶零方薛8 —if n^=mT =dispC^i 于“无选烘行LU分解J3 -return;9 -end10 - Qfor 吐和断n-1阶顺序主子式是否为霍11 一12 -dispC提示;矩阵占存在対誓的顺序主子式』无法进行LU分解’)13 -return:14 -else1516 -end17 - -tnd13 - IZIfer j-1 n 初的舉行-去的弟行19 - U(l.20 --end21 - Sfor i-2;n 亂的第一列詁的第一列22 -L(i, 1)-A(i.l)/U(L1):23 --end24 -[fcr k=2: tt25 -Utk. k: nJ -AOc, k: n)-L (k, 1: k-1) «U(1: k-1. k: n):弔逐行算出U的第T行SB -L(k+1: n, H-CAOt+lm,k)-l (k+1 n, l :k-l) *11(1:k-1, k) )/U血k):弔遛列尊出L的第27 -_ end23 -L ®输出L储陡29 -U 霭输出u矩阵|30 -:v'serosfn., 1): 备开册解肯理姐Usc・y31 -y<l)=b<l);32 -Hfor k=2:n33 -ytk)=fc (k)-su»(L (k, l:fc-l j *y(l:Jc-O);34 - end35 -y36 - xW-yW/Ufn, n):37 -7 for k=nt-l: -1: 133 -X (k) - (y ^k) 'SUQ (U (kk+1: n) *y (k+l: n))) /U (k, k):t39 -end40 -X8、调用LU.m文件,输入方程组命务E 口®»LL(A F b)未走丸因数或变聿*A* 0» A-14, 5. 3,-5, 6, -3,-3^ l f 3,2, 4.-S;2, -4.-7, 2,-5P-2. 4; 5P2+3r3 A. 2,-3,O.e,-2];» b=[l(10r ]6:-75. 72:98. 2:57,1:3. 72];fx» LUd9、运行结果如下1. oooo 00001. 2500 1. aooo 0000. 5000 0. 7622 1. 0000 001. 2500 1.1032 1. 0064 1.oooo01.05CO0. ?8170. 339S-X 1915 1.0000u =4, 0000乩3000 —5. 6000-3, 0000-3.40000-8. 7250 10. 2000 7. 7500 -3.760000-12. 1742—9+ 4069 2.1682000 6.9677 9. 214800 00 6. 1907y =1QC. 1500-200. 9200201. 2567-4S.舲99IS. 6722□□2.0549206, 8016 24, 622C -31. &345 3. 0000。
自控仿真实验报告

一、实验目的1. 熟悉MATLAB/Simulink仿真软件的基本操作。
2. 学习控制系统模型的建立与仿真方法。
3. 通过仿真分析,验证理论知识,加深对自动控制原理的理解。
4. 掌握控制系统性能指标的计算方法。
二、实验内容本次实验主要分为两个部分:线性连续控制系统仿真和非线性环节控制系统仿真。
1. 线性连续控制系统仿真(1)系统模型建立根据题目要求,我们建立了两个线性连续控制系统的模型。
第一个系统为典型的二阶系统,其开环传递函数为:\[ G(s) = \frac{1}{(s+1)(s+2)} \]第二个系统为具有迟滞环节的系统,其开环传递函数为:\[ G(s) = \frac{1}{(s+1)(s+2)(s+3)} \](2)仿真与分析(a)阶跃响应仿真我们对两个系统分别进行了阶跃响应仿真,并记录了仿真结果。
(b)频率响应仿真我们对两个系统分别进行了频率响应仿真,并记录了仿真结果。
(3)性能指标计算根据仿真结果,我们计算了两个系统的性能指标,包括上升时间、超调量、调节时间等。
2. 非线性环节控制系统仿真(1)系统模型建立根据题目要求,我们建立了一个具有饱和死区特性的非线性环节控制系统模型。
其传递函数为:\[ W_k(s) = \begin{cases}1 & |s| < 1 \\0 & |s| \geq 1\end{cases} \](2)仿真与分析(a)阶跃响应仿真我们对非线性环节控制系统进行了阶跃响应仿真,并记录了仿真结果。
(b)相轨迹曲线绘制根据仿真结果,我们绘制了四条相轨迹曲线,以分析非线性环节对系统性能的影响。
三、实验结果与分析1. 线性连续控制系统仿真(a)阶跃响应仿真结果表明,两个系统的性能指标均满足设计要求。
(b)频率响应仿真结果表明,两个系统的幅频特性和相频特性均符合预期。
2. 非线性环节控制系统仿真(a)阶跃响应仿真结果表明,非线性环节对系统的性能产生了一定的影响,导致系统响应时间延长。
沈阳工业大学实验报告结构图仿真

实验报告
课程名称:计算机仿真
实验项目:面向结构图的线性系统仿真
专业班级:自动化1301班
姓名:杨某某学号:130000000 实验室号:电气楼207 实验组号: 5
实验时间:批阅时间:
指导教师:吴伟成绩:
沈阳工业大学实验报告
(适用计算机程序设计类)
专业班级:自动化1300班学号:130000000 姓名:杨某某实验名称:面向结构图的线性系统仿真
附件A 沈阳工业大学实验报告
(适用计算机程序设计类)
实验步骤或程序:
该系统由PI调节器和控制对象结构图构成,病引入负反馈。
则设置G1为控制部分传递函数,G2为被控对象传递函数
那么MATLAB命令为
G10=10;
G11=tf([1],[1 0]);
G1=G10+G11;
G2=tf([5],[0.18 0]);
Gop=G1+G2;
G=feedback(Gop,1)
仿真结果为:
观察下系统的阶跃响应:step(G);。
大学仿真实验实验报告

大学仿真实验实验报告大学仿真实验实验报告引言:大学仿真实验作为一种重要的实践教学方式,旨在通过模拟真实场景,培养学生的实践操作能力和解决问题的能力。
本文将对大学仿真实验进行详细的实验报告,以展示实验过程和结果。
实验目的:本次实验旨在通过使用仿真软件,模拟一个生产线的运行情况,以了解生产线的工作原理和优化方法。
实验过程:1. 确定生产线的基本参数:包括生产线的长度、每个工位的工作时间和工作效率等。
在仿真软件中,我们可以根据实际情况设置这些参数。
2. 模拟生产线的运行:在仿真软件中,我们可以设置生产线的初始状态,包括产品的种类和数量等。
通过模拟软件的运行,我们可以观察到生产线的整体运行情况。
3. 改变生产线的参数:在仿真软件中,我们可以随时改变生产线的参数,比如增加工位数量、调整工作时间等。
通过观察实验结果,我们可以比较不同参数下生产线的运行情况,并找到最优的参数设置。
实验结果:通过对生产线的仿真实验,我们得到了以下几个结果:1. 生产线的瓶颈工位:通过观察生产线的运行情况,我们发现某些工位的工作时间明显长于其他工位,这些工位往往是生产线的瓶颈。
通过对瓶颈工位的优化,我们可以提高整个生产线的效率。
2. 生产线的平衡:通过调整工位的工作时间和工作效率,我们可以使得生产线的工作更加平衡。
这样可以避免某些工位的负荷过大,提高整个生产线的效率。
3. 生产线的稳定性:通过观察生产线的运行情况,我们可以发现一些不稳定因素,比如工位之间的协调不足、工作时间的波动等。
通过优化这些因素,我们可以提高生产线的稳定性,减少生产线的故障和停机时间。
实验总结:通过本次实验,我们深入了解了生产线的工作原理和优化方法。
仿真实验为我们提供了一个模拟真实环境的机会,使我们能够更好地理解和掌握相关知识。
通过观察实验结果,我们可以得出一些结论,并提出一些建议,以改进生产线的工作效率和稳定性。
建议:基于本次实验的结果和观察,我们提出以下几点建议:1. 加强生产线的协调:在设计生产线时,应考虑各个工位之间的协调性,避免出现瓶颈工位。
软件实验四非线性电路仿真
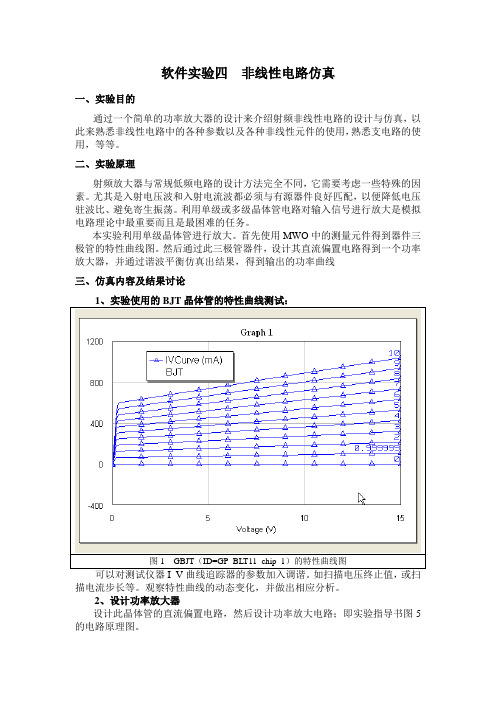
软件实验四非线性电路仿真一、实验目的通过一个简单的功率放大器的设计来介绍射频非线性电路的设计与仿真,以此来熟悉非线性电路中的各种参数以及各种非线性元件的使用,熟悉支电路的使用,等等。
二、实验原理射频放大器与常规低频电路的设计方法完全不同,它需要考虑一些特殊的因素。
尤其是入射电压波和入射电流波都必须与有源器件良好匹配,以便降低电压驻波比、避免寄生振荡。
利用单级或多级晶体管电路对输入信号进行放大是模拟电路理论中最重要而且是最困难的任务。
本实验利用单级晶体管进行放大。
首先使用MWO中的测量元件得到器件三极管的特性曲线图。
然后通过此三极管器件,设计其直流偏置电路得到一个功率放大器,并通过谐波平衡仿真出结果,得到输出的功率曲线三、仿真内容及结果讨论描电流步长等。
观察特性曲线的动态变化,并做出相应分析。
2、设计功率放大器设计此晶体管的直流偏置电路,然后设计功率放大电路;即实验指导书图5的电路原理图。
首先必须了解功率放大器的直流偏置。
测试不同频率下,I_METER与4的对3、分析1端口输入功率变化时2端口输出功率的变化情况将Port1的Pwr的值用变量p来代替,对p进行调谐,观察图4的变化情况,如下:(1)p=0~18时,Port1输入功率曲线与Port2输出功率曲线之间的关系与图4相同,两曲线之间的距离基本恒定。
可见,在该范围内,功率放大器在全频段起放大作用;但放大倍数随p的增大而减小。
(2)p=19~25时,两曲线之间的距离越来越小,直到p=25时,在频率点1.5GHz 处,两曲线重合。
(3)p大于25时,Port2输出功率曲线不会随着输入功率p的变化而变化。
4、分析1端口电压变化时2端口输出波形的变化情况在添加测量参数对话框,分别选择“NonlinearPower”、“Vtime”,测量时域电压波形。
图5图6测量的电压波形均为工作频率1.5GHz。
对比图5图6可见,输入功率越大,输入电压振幅越大,输出电压的时域波形越容易岐变。
非线性环节实验报告

非线性环节实验报告引言非线性系统在现实生活中的广泛应用引起了研究者们的极大关注。
非线性环节作为其中的重要组成部分,对系统的稳定性和性能起着至关重要的作用。
本实验通过建立一个非线性环节的模型,探究其对系统行为的影响,并分析非线性环节的性能和稳定性特性。
实验目的1. 建立一个非线性环节的数学模型;2. 分析非线性环节对系统行为的影响;3. 考察非线性环节的性能和稳定性特性。
实验原理非线性环节是指输入与输出之间不满足线性关系的部分。
在控制系统中,非线性环节可能会导致系统产生不确定性和非稳定的行为。
为了研究非线性环节的特性,本实验使用了一个常见的非线性函数作为实验模型,即sigmoid函数。
Sigmoid函数定义如下:f(x) = \frac{1}{{1+e^{-ax}}}其中,x代表输入,a代表一个可调节的参数,f(x)代表经过非线性环节后的输出。
实验步骤1. 首先,我们需要选择合适的参数a值来控制sigmoid函数的形状。
较小的a 值将导致sigmoid函数的输出变化更缓慢,而较大的a值则会使函数的曲线更陡峭。
本次实验选择a=2作为sigmoid函数的参数。
2. 在Matlab或Python等工具中编写代码,根据sigmoid函数的表达式计算输入x对应的输出f(x)。
3. 绘制x与f(x)之间的关系曲线,观察并分析非线性环节对系统行为的影响。
实验结果根据实验步骤所给出的sigmoid函数表达式和参数,我们得到了如下结果:import numpy as npdef sigmoid(x, a):return 1 / (1 + np.exp(-a * x))x = np.linspace(-10, 10, 100)a = 2y = sigmoid(x, a)import matplotlib.pyplot as pltplt.plot(x, y)plt.xlabel('Input (x)')plt.ylabel('Output (f(x))')plt.title('Nonlinear Link Function')plt.grid(True)plt.show()如上所示的代码及其运行结果,绘制了sigmoid函数的输入和输出之间的关系曲线。
非线性方程求解实验报告

数学实验报告非线性方程求解一、实验目的1.掌握用 MATLAB 软件求解非线性方程和方程组的基本用法,并对结果作初步分析;2.练习用非线性方程和方程组建立实际问题的模型并进行求解。
二、实验内容题目1【问题描述】(Q1)小张夫妇以按揭方式贷款买了1套价值20万元的房子,首付了5万元,每月还款1000元,15年还清。
问贷款利率是多少?(Q2)某人欲贷款50 万元购房,他咨询了两家银行,第一家银行开出的条件是每月还4500元,15 年还清;第二家银行开出的条件是每年还45000 元,20 年还清。
从利率方面看,哪家银行较优惠(简单假设:年利率=月利率×12)?【分析与解】假设初始贷款金额为x0,贷款利率为p,每月还款金额为x,第i个月还完当月贷款后所欠银行的金额为x i,(i=1,2,3,......,n)。
由题意可知:x1=x0(1+p)−xx2=x0(1+p)2−x(1+p)−xx3=x0(1+p)3−x(1+p)2−x(1+p)−x……x n=x0(1+p)n−x(1+p)n−1−⋯−x(1+p)−x=x0(1+p)n−x (1+p)n−1p=0因而有:x0(1+p)n=x (1+p)n−1p (1)则可以根据上述方程描述的函数关系求解相应的变量。
(Q1)根据公式(1),可以得到以下方程:150p(1+p)180−(1+p)180+1=0设 f(p)=150p(1+p)180−(1+p)180+1,通过计算机程序绘制f(p)的图像以判断解p的大致区间,在Matlab中编程如下:for i = 1:25t = 0.0001*i;p(i) = t;f(i) = 150*t*(1+t).^180-(1+t).^180+1;end;plot(p,f),hold on,grid on;运行以上代码得到如下图像:f(p)~p关系曲线图通过观察上图可知p∈[0.002,0.0022]。
Solution1:对于p∈[0.002,0.0022],采用二分法求解,在Matlab 中编程如下:clear;clc;x0=150000;n=180;x=1000;p0=0.002;p1=0.0022;while (abs(p1-p0)>1e-8)f0=x0*(1+p0).^n+x*(1-(1+p0).^n)/p0;f1=x0*(1+p1).^n+x*(1-(1+p1).^n)/p1;p2=(p0+p1)/2;f2=x0*(1+p2).^n+x*(1-(1+p2).^n)/p2;if (f0*f2>0 && f1*f2<0)p0=p2;elsep1=p2;end;end;p0结果得到p0=0.00208116455078125=0.2081%.所以贷款利率是0.2081%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
课程名称:计算机仿真
实验项目:非线性控制系统仿真
专业班级:自动化1301班
姓名:杨某某学号:130000000 实验室号:电气楼207 实验组号: 5
实验时间:批阅时间:
指导教师:吴伟成绩:
沈阳工业大学实验报告
(适用计算机程序设计类)
专业班级:自动化1300班学号:130000000 姓名:杨某某实验名称:非线性控制系统仿真
附件A 沈阳工业大学实验报告
(适用计算机程序设计类)
实验步骤或程序:
机器人动力系统简化结构图如下:
传递函数选择Simulink目录下的Continupus\Transfer Fcn
则仿真情况如下:
针对饱和非线性部分,新建satu.m文件:
function uc=satu(ur,s1)
if(abs(ur)>=s1)
if(ur>0)
uc=s1;
else uc=-s1;
end;
else uc=ur;
end;
针对死区非线性部分,新建dead.m文件:
function uc=dead(ur,s1)
if(abs(ur)>=s1)
if(ur>0)
uc=ur-s1;
else uc=ur+s1;
end;
else uc=0;
end;
end;
针对滞环非线性,新建backlash.m文件:
function [Uc,Ubb]=backlash(Urb,Ur,Ucb,S1)
if(Ur>Urb)
if((Ur-S1)>=Ucb)
Uc=Ur-S1;
else Uc=Ucb;
end;
else if(Ur<Urb)
if((Ur+S1)<=Ucb)
Uc=Ur+S1;
else Uc=Ucb;
end;
else Uc=Ucb;
end;
end;
Ubb=Ur;
主函数新建sp4.m文件:
P=[0.1 1 0.5 1;10 1 1 0;2 1 1 0;0 1 20 0];
WIJ=[1 0 1;2 1 1;3 2 1;4 3 1;1 4 -1];
n=4;
Y0=10;
Yt0=[0 0 0 0];
h=0.01;
T=0;
T0=0;
Tf=100;
Nout=4;
A=P(:,1);B=P(:,2);
C=P(:,3);D=P(:,4);
m=length(WIJ(:,1));
W0=zeros(n,1);W=zeros(n,n);
for k=1:m
if (WIJ(k,2)==0);W0(WIJ(k,1))=WIJ(k,3);
else W(WIJ(k,1),WIJ(k,2))=WIJ(k,3);
end;
end;
for i=1:n
if(A(i)==0);
FI(i)=1;
FIM(i)=h*C(i)/B(i);
FIJ(i)=h*h*C(i)/B(i)/2;
FIC(i)=1;FID(i)=0;
if(D(i)~=0);
FID(i)=D(i)/B(i);
else
end;
else
FI(i)=exp(-h*A(i)/B(i));
FIM(i)=(1-FI(i))*C(i)/A(i);
FIJ(i)=h*C(i)/A(i)-FIM(i)*B(i)/A(i);
FIC(i)=1;FID(i)=0;
if(D(i)~=0);
FIM(i)=(1-FI(i))*D(i)/A(i);
FIJ(i)=h*D(i)/A(i)-FIM(i)*B(i)/A(i); FIC(i)=C(i)/D(i)-A(i)/B(i);
FID(i)=D(i)/B(i);
else
end;
end;
end;
Y=zeros(n,1);X=Y;y=0;Uk=zeros(n,1);Ubb=Uk;
t=T0:h:Tf;N=length(t);
for k=1:N-1
Ub=Uk;
Uk=W*Y+W0*Y0;
for i=1:n
if(Z(i)~=0)
if(Z(i)==1)
Uk(i)=satu(Uk(i),S(i));
end;
if(Z(i)==2)
Uk(i)=dead(Uk(i),S(i));
end;
if(Z(i)==3)
[Uk(i),Ubb(i)]=backlash(Ubb(i),Uk(i),Ub(i),S(i));
end;
end;
end;
Udot=(Uk-Ub)/h;
Uf=2*Uk-Ub;
X=FI'.*X+FIM'.*Uk+FIJ'.*Udot;
Yb=Y;
Y=FIC'.*X+FID'.*Uf;
for i=1:n
if(Z(i)~=0)
if(Z(i)==4)
Y(i)=satu(Y(i),S(i));
end;
if(Z(i)==5)
Y(i)=dead(Y(i),S(i));
end;
if(Z(i)==6)
[Y(i),Ubb(i)]=backlash(Ubb(i),Y(i),Yb(i),S(i));
end;
end;
end;
y=[y,Y(Nout)];
end;
plot(t,y)
完成以上工作后,可在matlab Command Window输入命令: Z=[0 1 0 0];S=[0 5 0 0];
sp4
hold on
Z=[4 1 0 0];S=[1 5 0 0];
sp4
hold on
Z=[4 1 0 0];S=[2 5 0 0];
sp4
在不同非线性参数的情况下,输出-输入图像如下:。
