2010年国际小学数学竞赛队际赛个人赛
2010冬世界少年奥林匹克数学竞赛(中国区)河南选拔海选赛五年级A卷

世界少年奥林匹克数学竞赛(中国区)河南选拔海选赛五年级A 卷名____________辅导教师__________年级_______准考证号_________考场____考号------装-----------------------------订---------------------------线-------------------------------考生须知:1. 每位考生将获得考题一份。
考试期间,不得使用计算工具或手机。
2. 本卷共120分,第1至10题(每题6分),第11至16题(每题10分)3. 请将答案写在本卷上。
考试完毕时,所有考题及草稿纸会被收回。
4. 若计算结果是分数,请化至最简,并确保为真分数或带分数。
五年级试卷(本试卷满分120分 ,考试时间90分钟 )1. 找规律填数: 1, 3, 5, 7, 9, 11 。
2. 用1、2、3三个数字不重复排列可以组成 6 个不同的三位数。
3.定义新运算,a ※b=a ×b+b , 求2※3的值是 9 。
4. 进入百宝箱的密码是○□○□○,如果44÷4+○=18, □×(2+9)=66,那么进入百宝箱的密码是 76767 。
5. 有9个足球队,两两进行淘汰赛,最后产生一个冠军,共要赛 8 场.6. 下图中有 36 个长方形。
7. 切2刀,最多可以把一个饼分成 4 块。
8.一个数除以5,减去5,再乘以5,结果等于5,这个数是 30 。
9. 123×1+57×65-65×56= 188 。
10.鸡与兔共10只,脚共22只,问兔有 1 只。
世界少年奥林匹克数学竞赛(中国区)河南选拔海选赛五年级A 卷名____________辅导教师__________年级_______准考证号_________考场____考号------装-----------------------------订---------------------------线-------------------------------11.有一正方形操场,每边都栽种4棵树,四个角各种1棵。
小学数学速算竞赛方案

小学数学速算竞赛方案目录1. 竞赛概况 (2)1.1 竞赛目的 (2)1.2 竞赛对象 (3)2. 比赛规则 (3)2.1 比赛形式 (4)2.1.1 单项赛 (5)2.1.2 团体赛 (6)2.2 评分标准 (7)2.3 违纪行为及处罚 (8)2.4 比赛流程 (8)3. 参赛准备 (10)3.1 报名流程 (11)3.2 选手训练计划 (11)3.2.1 训练教材推荐 (12)3.2.2 训练方法指导 (13)3.3 比赛用具及所需材料 (14)4. 评审工作 (16)4.1 评审委员会组成 (17)4.2 计分方式 (18)4.3 结果公示 (18)5. 竞赛奖励 (19)5.1 奖项设置 (19)5.2 颁奖仪式 (21)6. 其他事项 (21)6.1 宣传推广 (22)6.2 安全的保障措施 (23)1. 竞赛概况小学数学速算竞赛旨在激发小学生对数学的兴趣,提高他们的计算能力和思维敏捷性,培养学生的数学素养和竞争意识。
竞赛内容涵盖四则运算、分数和小数的基本运算、简单的几何图形面积计算等,题目难度根据年级有所不同。
设有一等奖、二等奖、三等奖及优秀奖若干名,获奖者将获得证书及奖品。
由XX市教育局主办,XX小学承办,并邀请相关数学教育专家担任评委。
宣传工作将在竞赛前一个月启动,通过学校公告、家长群等方式进行广泛宣传。
报名工作将于竞赛前一周结束。
提供充足的饮水、饮食服务以及必要的文具用品,确保选手在比赛过程中的舒适与安全。
比赛结束后,组织委员会将对本次比赛进行全面总结,并向参赛学校和选手反馈情况,以便今后的改进和提高。
1.1 竞赛目的本小学数学速算竞赛旨在激发学生对数学的兴趣,提高学生的计算速度和准确性,培养学生的思维敏捷性和逻辑思维能力。
通过竞赛的形式,让学生在轻松愉快的氛围中学习数学知识,增强自信心,提高学习成绩。
本次竞赛也为学校选拔出优秀的数学人才,为今后的教育和学术发展提供有力支持。
1.2 竞赛对象本小学数学速算竞赛面向对象主要为在校的小学生,竞赛的具体年龄段通常为1年级至6年级。
数学建模竟赛的情况简介

第1教案数学建模及竞赛知识介绍目的要求:1. 了解数学建模的基础知识、相关的基本概念;2. 了解数学模型的特点和学习方法;3. 掌握数学建模的具体过程和步骤,教学重点及难点:重点:了解数学建模的一般步骤和方法,体会如何用数学的语言和方法表述和解决实际问题。
难点:体会如何用数学的语言和方法表述和解决实际问题。
教学方法手段:讲授法,案例教学法,多媒体创新点:应用和创新是数学建模的特点,也是素质教育的灵魂;不论用数学方法解决哪类实际问题,还是与其他学科想结合形成交叉学科,首先的和关键的一步是用数学的语言表述所研究的对象,即建立数学模型。
在高科技,特别是计算机技术迅速发展的今天,计算和建模正成为数学科学技术转化的主要途径。
教学过程:1.1 从现实对象到数学模型本节先讨论原型和模型,特别是数学模型的关系,再介绍数学模型的意义。
原型和模型原型(prototype)和模型(model)是一对对偶体。
原型指人们在现实世界里关心、研究或者从事生产、管理的实际对象。
在科技领域通常使用系统(system)、过程(process)等词汇,如机械系统、电力系统、生态系统、生命系统、社会经济系统,又如钢铁冶炼过程、导弹飞行过程、化学反应过程、污染扩散过程、生产销售过程、计划决策过程等。
本书所述的现实对象、研究对象、实际问题等均指原型。
模型则是指为某个特定目的将原型的某一部分信息减缩、提炼而构成的原型替代物。
特别强调构造模型的目的性。
模型不是原形原封不动的复制品,原型有各个方面和各种层次的特征,而模型只要求反映与某种目的有关的那些方面和层次。
一个原型,为了不同的目的可以有很多不同的模型,模型的基本特征是由构造模型的目的决定的。
例如:展厅里的飞机模型:外形上逼真,但是不一定会飞;航模竞赛的模型飞机:具有良好的飞行性能,在外观上不必苛求;飞机设计、试制过程中用大的数学模型和计算机模拟:要求在数量规律上真实反映飞机的飞行动态特征,毫不涉及飞机的实体。
2010年“陈省身杯”国际青少年数学邀请赛四年级试题

2010年“陈省身杯”国际青少年数学邀请赛四年级1. 计算17474719196634_____⨯+⨯+⨯+⨯=2. 十个连续自然数的和不大于100,这十个数的和最大是______。
3. “陈省身数学周”组委会为了奖励参加活动的学生,买来数学故事数和数学文化书共2010本,其中数学文化书是数学故事书的4倍,那么数学故事数有_____本。
4. 数学课上,李老师布置了两道题,结果有34人答对了第一题;有46人做对了第二题;没有人两道题全部做错。
如果这个班共有52人,那么两道题都做对的有_____人。
5. 为庆祝元旦,学校在大门口安装了50盏彩灯,彩灯按照“黄黄红绿绿红黄黄红绿绿红…”的顺序依次排列,则在这50盏彩灯中,共有黄色的彩灯_____盏。
6. 如图,观察这个数表并找出它的规律,这个数表第15行的第一个数是______。
(2523211917)16141210975421?身杯身省陈第6题图 第8题图 第9题图7. 2004年时,父亲的年龄是哥哥和弟弟年龄之和的4倍;而2010年时,父亲的年龄是哥哥和弟弟年龄之和的2倍,那么父亲出生在______年。
8. 在上面的方格表的每个小方格中填入一个字,使得方格表的每行、每列及每条对角线上的四个方格中的文字都是“陈”、“省”、“身”、“杯”,那么表中“?”所在的方格中应填的汉字是______。
9. 数一数,上图中共有_____个三角形。
10. 计算1(12)(123)(1234)(1298)(1299)_____-++++-++++-+++++++= 。
11. 将1、3、5、7、9、11、13、15、17这9个自然数填入到右图的圆圈中,使得每个正方形的四个角上的数字之和都相等,这个相等的和是_____。
12. A 、B 、C 、D 四名学生猜测自己的数学成绩。
A 说:“如果我得优,那么B 也得优。
”B 说:“如果我得优,那么C 也得优。
”C 说:“如果我得优,那么D 也得优。
2010年世界少年奥林匹克数学竞赛福建晋级赛答案

世界少年奥林匹克数学竞赛(中国区)选拔赛福建晋级赛三年级试题参考答案及评分标准一、填空题。
(每题6分,共计48分。
)1、324 7202、329763、6元4、155、226、3:157、1 5 8 8、莉莉二、计算题。
(每题8分,共计16分。
)9、1847-1928+628-136-64=1847-(1928-628)-(136+64)=1847-1300-200=34710、100-99+98-97+96-95+……+4-3+2-1=(100-99)+(98-97)+(96-95)+……+(4-3)+(2-1)=1+1+1+……+1=50三、解答题。
(共计56分)11、锯每根木料所用时间为:(10÷2-1)×3=12(分钟)………………………4分全部锯完需要的时间为:12×12=144(分钟)………………………………6分12、(1)正确划线(5分)(2)1+2+3+…+12=78 (1分) 78÷3=26 (1分)26=11+12+1+2 (1分)或26=5+6+7+8 (答对1个即可,答对2个加3分)13、第一个盘里打1个鸡蛋第二个盘里打2个鸡蛋第二个盘里打4个鸡蛋第二个盘里打8个鸡蛋…………………………………..4分因为1+2=3 2+3=5 2+4=6 1+2+4=7 1+8=9 2+8=10 1+2+8=11 4+8=12 1+4+8=132+4+8=14 1+2+4+8=15…………………………………..10分14、(12+13)×2+3×2×2=62(米) 12分15、根据题意,将5个小朋友所报的数求和:8+14+7+12+4=45由于丙报的数7的2倍是乙、丁两人心里想的两个数的和,丁报的数12的2倍是丙、戊两人心里想的两个数的和可见乙、丙、丁、戊四个小朋友心里想的数的和应是(7×2+12×2)=38………5分所以甲心里的数是:45-38=7………………………6分丙心里的数是:14×2-7=21…………………8分戊心里的数是:12×2-21=3…………………10分乙心里的数是:8×2-3=13……………………12分丁心里的数是:7×2-13=1……………………14分世界少年奥林匹克数学竞赛(中国区)选拔赛福建晋级赛四年级试题参考答案及评分标准一、填空题。
小学数学竞赛陈省身杯2009-2011年六年级真题
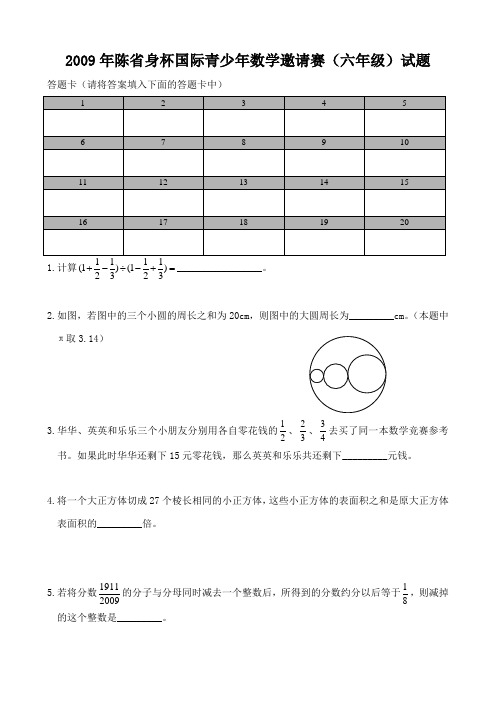
2009年陈省身杯国际青少年数学邀请赛(六年级)试题答题卡(请将答案填入下面的答题卡中)1.计算(1)(1)2323+-÷-+=_________________。
2.如图,若图中的三个小圆的周长之和为20cm,则图中的大圆周长为_________cm。
(本题中π取3.14)3.华华、英英和乐乐三个小朋友分别用各自零花钱的12、23、34去买了同一本数学竞赛参考书。
如果此时华华还剩下15元零花钱,那么英英和乐乐共还剩下_________元钱。
4.将一个大正方体切成27个棱长相同的小正方体,这些小正方体的表面积之和是原大正方体表面积的_________倍。
5.若将分数19112009的分子与分母同时减去一个整数后,所得到的分数约分以后等于18,则减掉的这个整数是_________。
6.如图中,一个小正六边形内接于一个圆,一个大正六边形外切于同一个圆。
若大正六边形的面积为10平方厘米,则其中小正六边形的面积为_________平方厘米。
7.1000以内的自然数,有些数不能被2整除,有些数不能被3整除,有些数不能被5整除,那么,这样的数共有_________个。
8.在下面的算式中,不同的汉子代表不同的数字,则其中四位数“我要加参”最小是_________。
比赛+ 陈省身我要参加.9.有三批货物共值152万元,第一、二、三批货物按重量比为2:4:3,按单价比为6:5:2,这三批货物分别值_________万元、_________万元和_________万元。
10.将2009除以一个两位数,所得的余数为7,则满足条件的两位数共有_________个。
11.计算1119111243234++++++=__________________。
12.A、B、C、D都是小于100的合数,并且A、B、C、D两两互质,则A+B+C+D的最大值为_________。
13.如图,两个正方形的中心相同,其对应边成45度角,若两个阴影三角形的面积分别为362cm和50362cm,则其中较大正方形的面积为_________2cm。
(共8套)世界少年奥林匹克数学竞赛真题附答案 六年级至四年级专版(全)

(共8套)世界少年奥林匹克数学竞赛真题 六年级至四年级专版(全)绝密★启用前世界少年奥林匹克数学竞赛(中国区)选拔赛地方海选赛(2016年10月)选手须知:1、本卷共三部分,第一部分:填空题,共计50分;第二部分:计算题,共计12分;第三部分:解答题,共计58分。
2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置。
3、比赛时不能使用计算工具。
4、比赛完毕时试卷和草稿纸将被收回。
六年级试题(A卷)(本试卷满分120分 ,考试时间90分钟 )一、填空题。
(每题5分,共计50分)1、有甲、乙两个两位数,甲数的27等于乙数的 23,这个两位数的差最多是 。
2、如果15111111111111111*=++++,242222222222*=+++,33*=3+33+333,那么7*4= 。
3、由数字0,2,8(既可全用也可不全用)组成的非零自然数,按照从小到大排列,2008排在第 个。
4、如图,正方形的边长是2(a+b ),已知图中阴影部分B 的面积是7平方厘米,则阴影部分A 和C 面积的和是 平方厘米。
5、一辆出租车与一辆货车同时从甲地出发,开往乙地出租车4小时到达,货车6小时到达,已知出租车 比货车每小时多行35千米。
甲乙两地相距 千米6、一个长方体铁块,被截成两个完全相同的正方体铁块,两个正方体铁块的棱长之和比原来长方体铁块的棱长之和增加了16厘米,则原来长方体铁块的长是 。
7、四袋水果共46个,如果第一袋增加1个,第二袋减少2个,第三袋增加1倍,第四袋减少一半,那么四袋水果的个数就相等了,则第四袋水果原先有 个。
8、有23个零件,其中有一个次品,不知它比正品轻还是重,用天平最少 次可以找出次品。
9、123A5能被55整除,则A= 。
10、在一次数学游戏中,每一次都可将黑板上所写的数加倍或者擦去它的末位数,假定一开始写的数是458,那么经过 次上述变化得到14.二、计算题。
(每题6分,共计12分)11、123200112320012002200220022002++++12、6328862363278624⨯-⨯省 市 学校 姓名 赛场 参赛证号∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕∕〇∕∕∕∕∕∕ 密 〇 封 〇 装 〇 订 〇 线 ∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕密 封 线 内 不 要 答 题a +六年级 第3页 六年级 第4页三、解答题。
2010小学数学奥林匹克试题预赛决赛

2010小学数学奥林匹克试题说明:此套试卷年份造假,因为我在百度文库看到的,核对了一下发现是2000年的考题,但是百度文库没有地方可以留言的,为了避免各位读者错误下载错误应用,只能再上传一份我下载的假题,以便各位在搜索的时候看到这份试卷,注意到我的说明,免得浪费大家的时间,哎我是被这个造假的人浪费了整整一天的时间,大家好自为之吧,也希望文库能留个对文章经行评论的地方!!!!!否则明知道是假的也没法提醒大家!!!!!!!!!!!!!!!!!!!!!!!!!!!(其实很简单看第五题就能发现不是2010年的题)预赛(A)卷1.计算: 12-22+32-42+52-62+…-1002+1012=________。
2.一个两位数等于其个位数字的平方与十位数字之和,这个两位数是________。
3.五个连续自然数,每个数都是合数,这五个连续自然数的和最小是________。
4.有红、白球若干个。
若每次拿出一个红球和一个白球,拿到没有红球时,还剩下50个白球;若每次拿走一个红球和3个白球,则拿到没有白球时,红球还剩下50个。
那么这堆红球、白球共有________个。
5.一个年轻人今年(2000年)的岁数正好等于出生年份数字之和,那么这位年轻人今年的岁数是________。
6.如下图, ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为_____平方厘米。
7.a是由2000个9组成的2000位整数,b是由2000个8组成的2000位整数,则a×b的各位数字之和为________。
8.四个连续自然数,它们从小到大顺次是3的倍数、5的倍数、7的倍数、9的倍数,这四个连续自然数的和最小是____。
9.某区对用电的收费标准规定如下:每月每户用电不超过10度的部分,按每度0.45元收费;超过10度而不超过20度的部分,按每度0.80元收费;超过20度的部分,按每度1.50元收费。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年国际小学数学竞赛
个人赛
1.一个电子广告牌正在显示三个“单词”:IMC 2010 INCHEON 。
由于系统出现故障导致每隔1分钟每个“单词”最前面的一个字符就被移动到该单词的末尾。
即,1分钟后,广告牌显示:MCI 0102 NCHEONI ;再过1分钟后,广告牌显示:CIM 1020 CHEONIN 。
请问几分钟后广告牌再度显示原来的三个“单词”? 答案:84。
提示:周期问题。
求3、4、7的最小公倍数。
2.请问102010-2010的各位数码之和是多少?
答案:18079。
提示:差是一个2010位数,最末四位是7990,万位以上都是9。
3.我们约定一种标记法:d n 表示各位数码都是d 的n 位数,例如53=555和
43958136=444999998333333.如果整数x 、y 、z 和w 满足2w 3x 5y +3y 5w 2x =53728z 5173,请问x+y+z+w 值是多少?
答案:15。
提示:首先观察到这一加法算式不可能出现进位,因此这三个数的位数应是相同的。
和中第一个数字5只能由2+3得到,第二个数字只能由2+5得到。
由此得y=3,w=5.而最后的三个7只能由5+2得到,7之前的数字5只能由3+2得到x=4,z=3.
4.丈夫的体重等于他的体重的41加上60千克,妻子的体重等于她的体重的51加上64千克。
请问丈夫与妻子的体重之差是多少千克?
答案:0千克。
提示:由“丈夫的体重等于他的体重的
4
1加上60千克”,可知60千克相当于丈夫体重的43,丈夫的体重=60÷43=80千克。
同理,妻子的体重=64÷(1-51)=80千克。
5.在四边形ABCD 中,AB=6厘米,AD=4厘米,BC=7厘米和CD=15厘米。
已知AC 的长度是整数(单位是厘米)。
请问AC 的长度是多少厘米?
答案:12厘米。
提示:由三角形两边之和大于第三边可知:
在△ABC中,AB+B C>AC,所以AC<=6+7=13;
在△ADC中,AD+AC>CD,所以AC>CD-AC=15-4=11
而AC的长度是一个整数,
综上所述,AC=12厘米。
6.一条河的水流速度是每小时1千米。
小明以固定的速度划一条小船。
他逆流划行了3小时,然后顺流划行返回原来的出发地点,用了2小时。
请问小明的出发地点与他开始返回的地点之间的距离有多少千米?
答案:12千米。
提示:差倍问题。
由“路程一定,速度跟时间成反比”知,顺流速度与逆流速度的比是3:2;
由“水流速度是1千米/小时”知,顺流速度比逆流速度每小时多2千米/小时;所以顺流速度=2×3=6千米/小时,单摆路程=6×2=12千米/小时。
7.在四边形ABCD中,AB//CD,且AD=BC。
如果用8个与ABCD相同的四边形能够拼成一个空心的正八边形(如图所示)。
请问∠BAD为多少度?
答案:112.50千米。
8.设abc、def为两个不同的三位数,满足abcdef-defabc能被2010整除,请问这两个三位数之和的最大值是多少?
答案1328。
提示:abcdef-defabc=abc×1000+def-(def×1000+abc)=999(abc-def),由“abcdef-defabc能被2010整除”,知999(abc-def)能被2010整除;
即333(abc-def)能被670整除。
因为333与670互质,所以(abc-def)必定能被670整除;
要想和最大,abc与def应尽可能大,最大可取999与329.
9.请问由4个4和5个5组成的所有不同的九位数的平均值是多少?
答案:506172839。
提示:由4个4和5个5组成的九位数有
!5!4!9
=126种。
这些九位数的各位数码只
能是4或者5.当某一个数位上的数码确定时,(1)当这个数码是4,则可能组成
的九位数有
!5!3!8
=56种;(2)当这个数码是4,则可能组成的九位数有
!4!4
!8
=70种。
故,所有这126个九位数的平均数=(555555555×70+444444444×56)÷126=506172839.
10.已知:如图,点E、F、G、H分别在长方形ABCD的AB、BC、CD、DA 边上,点P在长方形内部,且AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm²。
请问四边形PFCG的面积为多少cm²?
答案:9cm²。
提示:如图,△APH和△CPF的底AH=CF=2 cm,高的和等于4 cm,面积和是4 cm²;同理,△APE与△CPG的面积和是12 cm²;
所以四边形PFCG的面积是12+4-5=9cm²。
11.长度为8cm的素菜春卷的制作方法是:用一张大小为6c m×8cm的春卷皮把长
度为8cm的豆芽卷在里面。
有一天,菜商提供的豆芽的长度只有6cm.于是他们用另一种方式来卷春卷皮,得到长度为6cm的宽圆柱。
如果这两种大小的春卷在相接处都重叠了1cm的春卷皮,请问长度为8cm的春卷与长度为6cm的春卷的体积之比是什么?
答案:100:147。
提示:长春卷的周长是6-1=5 cm;短春卷的周长是8-1=7 cm;
圆柱的底面积的比等于周长的平方比,得长春卷与短春卷的底面积的比是25:49;同时乘各自的高,得长春卷与短春卷的体积比=(25×8):(49×6)=100:147.
12.给定23个连续奇数,其中最大的奇数是最小的奇数的5倍。
请问这23个奇数的平均值是多少?
答案:33。
提示:差倍问题。
23个连续奇数,最大数是最小数的5倍,相差22×2=44,用差倍问题的公式,可得最小数是11,最大数是55,平均数是33.
13.把数1,2,3,4,5,6,7,8和9不重复地填入小方格内,每个小方格内填一个数,使得有三个小方格的每行和每列的三个数之和都为13。
有两个数已经填入小方格内。
请问标有“※”处的小方格内所填的数是什么?
答案:4。
提示:如图,设转角的方格里填的三个数分别为m、n、p。
当所有行和列相加时,数字1,2,3,…,9均计算了1次,而m、n、p计算了2次。
因为四排的数的总和是13×4=52,数字1至9的和是45,所以m+n+p=7。
则m、n、p只能是1,2 ,4。
根据最大搭最小的原则,m=1。
最下面一行,和是13,说明另外两个数的和是8,而和等于8的两个数只有3种:(1,7)(2,6),(3,5),数字1和5已经出现,说明p只能是2。
所以n只能是4。
14.有5名学生参加四个科目的考试,每名学生每科的得分是w、x、y或z,如下表表示,每个学生四科的总分已经计算出来,除了生物这一科,其它科目的班级总分已经计算出来,请问生物这一科的班级总分是多少?
答案:424分。
提示:5名同学4科的总分等于4个班级的总分。
5名同学4科的总分=349+330+349+326+315=1669,生物总分=1669-416-428-401=424分。
15. 正整数n的各位数码都不为0,且它们的和为15,而2n的各位数码之和小于20.请问n的最大值为多少?
答案:5511111。
提示:题目中没有指出n中是否含数码2、3、4,为了使n的值尽可能大,可以把2、3、4分别分裂为11、111、1111.同理,题目中也没有指出n中是否含数码6、7、8、9,可以把6、7、8、9分别分裂为11111、111111、11111111、111111111或51、511、5111、51111。
因为n的各位数码和是15,则数码1的个数必须是15的倍数。
又2n的各位数码之和小于20,说明正整数n中数码1的个数必须小于10,这样数码1的个数只能是5。
符合条件的多位数只能是5511111。
