位错习题解答
(完整word版)第二章晶体结构缺陷习题答案

第二章晶体结构缺陷1.(错)位错属于线缺陷,因为它的晶格畸变区是一条几何线。
2.(错)螺型位错的柏氏失量与其位错线垂直,刃型位错的柏氏失量与其位错线是平行.3。
(错)肖特基缺陷是由于外来原子进入晶体而产生的缺陷。
4.(错)弗伦克尔缺陷是由于外来原子进入晶体而产生的缺陷。
二选择题1.非化学剂量化合物Zn1+x O中存在 A .A. 填隙阳离子B。
阳离子空位C. 填隙阴离子D. 阴离子空位2. 非化学计量化合物UO2+x中存在 C 。
A. 填隙阳离子B. 阳离子空位C。
填隙阴离子 D. 阴离子空位3.非化学剂量化合物TiO2-x中存在 D 。
A. 填隙阳离子B。
阳离子空位C。
填隙阴离子D。
阴离子空位4.螺型位错的位错线是 A 。
A。
曲线B。
直线C。
折线D。
环形线5.非化学剂量化合物ZnO1-x中存在 D 。
A。
填隙阳离子 B. 阳离子空位C. 填隙阴离子D。
阴离子空位6. 非化学计量化合物UO2+x中存在 C 。
A. 填隙阳离子B. 阳离子空位C. 填隙阴离子D. 阴离子空位三、名词解释1. 弗仑克尔缺陷原子离开其平衡位置二进入附近的间隙位置,在原来位置上留下空位所形成的缺陷,特点是填隙原子与空位总是成对出现。
2.固溶体:物种数:凡在固体条件下,一种组分(溶剂)内“溶解”了其它组分(溶质)而形成的单一、均匀的晶态固体称为固溶体。
四、解答题1.完成下列缺陷方程式,并且写出相应的化学式(1)NaCl 溶入CaCl 2中形成空位型固溶体;(2)CaCl 2溶人NaC1中形成空位型固溶体;解:(1)NaClNa Ca ’+ Cl Cl + V Cl ·Ca 1-x Na x Cl 2-x(2)CaCl 2Ca Na · + 2Cl Cl + V Na ' Na 1-2x Ca X Cl2完成下列缺陷方程式,并且写出相应的化学式(6分)(1)M gCl 2固溶在LiCl 晶体中形成填隙型Li 1-x Mg x Cl 1+x(2) SrO 固溶在Li 2O 晶体中形成空位型Li 2-2x Sr x O3.写出下列缺陷反应式①。
4.8习题

答:(1)单位位错b=a/2[110]
b=0.707a=2.828*10-10mm
位错受到的滑移力 f=τb=2.828*10-7M6*0.2828/(2000)=848.4 MPa τ ﹥ τG ﹥τw , 位错饶过粒子运动. (2) τw =Gb/ λ=6*106*0.2828/(200)=8484 MPa τw <τ ﹥ τG ,位错切过粒子运动
切过粒子所需的力
d1=10nm,F1= τG π(d1/2)2 = 2.5π*10-14MN d2=100nm,F2= τG π(d2/2)2= 2. 5π*10-12MN
位错线弯曲所需切应力为 τw =Gb/ λ=6*106*0.2828/(2000)
=8.484 *102MPa τ为1000MPa ,τ﹥τw ,为1000MPa
例题2
假定在某一面心立方点阵合金中弥散分布着与基体晶体点阵相同、晶体 取向一致且完全共格的球形有序结构的第二相粒子,粒子剪切强度τG 为1000MPa(1MPa=1MN/m2),G=6GPa,作用在滑移系统上的切 应力τ为1200MPa,基体的点阵常数a为0.4nm,(1)粒子间距λ为 2000nm,位错与粒子的交互作用方式,并说明原因(在基体滑移系 中与粒子交互作用的运动位错为单位位错); (2)粒子间距λ为 200nm,位错与粒子的交互作用方式?粒子的强化机制?
(1)上述滑移系统中当粒子直径分别为10nm和100nm时,位错与粒子的交 互作用方式,并说明原因(在基体滑移系中与粒子交互作用的运动位 错为单位位错);
(2)简述(1)中两种情况下粒子的强化机制。
答:(1)单位位错b=a/2[110] b=0.707a=2.828*10-10mm
位错受到的滑移力 f=τb=2.828*10-7MN/m
晶体缺陷习题讨论
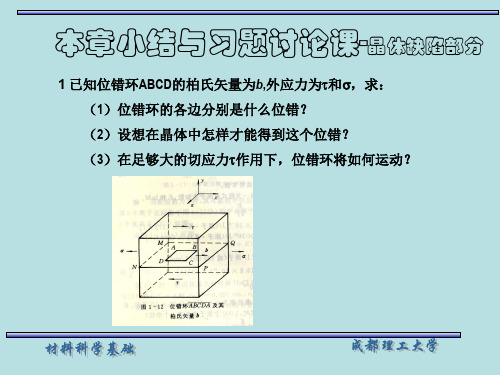
当位错移出晶体后,滑移面上部晶体相对于下部晶体在平行 于b的方向上滑移与b相同大小的距离;同时,晶体的左右两 侧面形成两个相反的台阶,台阶宽度与b的大小相同.
解:
(1)根据位错线与柏氏矢量关系判断:
⊥ 为刃型位错(BC, DA)
再根据右手定则确定正负:
A
(令顺时针方向为位错环线的正方向)
DA负刃型位错 BC正刃型位错
∥ 为螺型位错(AB, CD) 再根据规定确定左右: CD左螺型位错 D
AB 右螺型位错
B b
C
(2)设想在晶体中怎样才能得到这个位错?
a[001]
(2) a/2[110]
a/6[121] + a/6[211]
(3) a/2[110]
a/6[112] + a/3[111]
(4) a/2[101] + a/2[011]
a/2[110]
(5) a/3[112] + a/6[111]
a/2[111]
解:几何条件都满足,只判断能否满足能量条件. (1) (3/2)a2 > a2 (2) (1/2)a2 > (1/3)a2 (3) (1/2)a2 = (1/2)a2 (4) a2 > (1/2)a2 (5) (3/4)a2 =(3/4)a2
几何条件和能量条件全部满足,故所列位错 反应都能进行.
a/2[111] + a/2[111]
a[001]
(3) a/2[110]
a/6[112] + a/3[111]
位错理论与应用试题

位错理论与应用试题学院:材料科学与工程学院学生:老师:日期:2011年5月2日位错理论与应用试题:1、解释:层错、扩展位错、位错束集、汤姆森四面体(20分)(1)、层错是一种晶体缺陷。
如已知FCC结构的晶体,密排面{111}堆堆垛顺序为ABCABC……以“Δ”表示AB、BC、CA……次序,用“▽”表示相反次序,即BA、CB、AC……,则FCC的正常堆垛顺序为ΔΔΔ……,HCP 密排面{0001}按照…ABAB…顺序堆垛,则表示为:Δ▽Δ▽……若在FCC 中抽走一层C,则 A B C A B ↓ A B C A B C ΔΔΔΔ▽ΔΔΔΔΔ;插入一层A,则A B C A B ↓A↓C A B C ΔΔΔΔ▽▽△△△,即在“↓”处堆垛顺序发生局部错乱,出现堆垛层错,前者为抽出型层错,后者为插入型层错,可见FCC晶体中的层错可看成是嵌入了薄层密排六方结构。
(2)、一个全位错分解为两个或多个不全位错,其间以层错带相联,这个过程称为位错的扩展,形成的缺陷体系称为扩展位错。
(3)、扩展位错有时在某些地点由于某种原因会发生局部的收缩,合并为原来的非扩展状态,这种过程称为扩展位错的束集。
(4)、1953年汤普森(N. Thompson)引入参考四面体和一套标记来描述FCC 金属中位错反应,如下图。
将四面体以ΔABC为底展开,各个线段的点阵矢量,即为汤普森记号,它把FCC金属中重要滑移面、滑移方向、柏氏矢量简单而清晰地表示出来。
2、位错的起源、增值机制及位错的分类?(15分)(1)、位错的起源主要有两个:第一个是位错本来就存在于籽晶或者其它导致晶体生长的壁面中,这些位错有一部分在晶体赖以生长的表面露头,就扩展到成长着的新晶体中;另一个是新晶体成长时的偶然性所造成的位错生核,其中包括:杂质颗粒等引起的内应力所产生的不均匀生核,成长中的不同部分的表面(如枝晶表面)之间的碰撞产生新的位错,空位片崩塌所造成的位错环。
(2)、位错的增值机制是被广泛引用的弗兰克–里德(Frank-Read,简称为F-R)源机制,如下图:这种理论认为新位错的产生是原有位错增殖的结果。
材料物理习题答案2 缺陷和表面

7、位错反应的基本条件是什么?指出面心立方(fcc)和体心立方(bcc
)中的特征位错(以最短点阵矢量为柏矢量的位错),并判断以下位错反 应是否可以进行,为什么?
位错反应的条件:
(1)几何条件:柏氏矢量守恒性, 即:∑b前 = ∑b后 (2)能量条件:反应过程能量降低——反应驱动力,
即:∑︱b前︱²﹥∑︱ b后︱ ²
Hale Waihona Puke 贯穿全篇,却有两个句子别出深意,不单单是在写乐,而是另有所指,表达出另外一种情绪,请你找出这两个句子,说说这种情绪是什么。明确:醉翁之意不在酒,在乎山水之间也。醉能同其乐,醒能述以文者,太守也。这种情绪是作者遭贬谪后的抑郁,作者并未在文中袒露胸怀,只含蓄地说:“醉能同其乐,醒能述以文者,太守也。”此句与醉翁亭的名称、“醉翁之
关系,好泉酿好酒,好酒叫人醉。“醉翁亭”的名字便暗中透出,然后引出“醉翁亭”来。作者利用空间变幻的手法,移步换景,由远及近,为我们描绘了一幅幅山水特写。2.第二段主要写了什么?它和第一段有什么联系?明确:第二段利用时间推移,抓住朝暮及四季特点,描绘了对比鲜明的晦明变化图及四季风光图,写出了其中的“乐亦无穷”。第二段是第一段
江西)人,因吉州原属庐陵郡,因此他又以“庐陵欧阳修”自居。谥号文忠,世称欧阳文忠公。北宋政治家、文学家、史学家,与韩愈、柳宗元、王安石、苏洵、苏轼、苏辙、曾巩合称“唐宋八大家”。后人又将其与韩愈、柳宗元和苏轼合称“千古文章四大家”。
会员免费下载 关于“醉翁”与“六一居士”:初谪滁山,自号醉翁。既老而衰且病,将退休于颍水之上,则又更号六一居士。客有问曰:“六一何谓也?”居士曰:“吾家藏书一万卷,集录三代以来金石遗文一千卷,有琴一张,有棋一局,而常置酒一壶。”客曰:“是为五一尔,奈何?”居士曰:“以吾一翁,老于此五物之间,岂不为六一乎?”写作背景:宋仁宗庆历五年(1045年),
(完整word版)物理冶金学第四章习题及答案

(1)判断位错线上各段位错的类型。
(2)有一切应力施加于滑移面,且与柏氏矢量平行时两条位错线的滑移特征有何差异?
解:(1)在两根位错线上,除1~2、3~4段为刃型位错以外,其余各段均为螺型位错。
(3)在足够大的切应力 的作用下,位错环将如何运动?晶体将如何变形?
(4)在足够大的拉应力 的作用下,位错环将如何运动?它将变成什么形状?晶体将如何变形?
解:(1)AB是右螺型位错,CD是左螺型位错;根据右手法则,BC是正刃型位错,DA是负刃型位错。
(2)设想在完整晶体中有一个贯穿晶体的上、下表面的正四棱柱,它和滑移面MNPQ交于ABCDA。现让ABCDA上部的柱体相对于下部的柱体滑移 ,柱体外的各部分晶体均不滑移。这样,ABCDA就是在滑移面上已滑移区(环内)和未滑移区(环外)的边界,因而是一个位错环。
当两根异号刃型位错无限靠近时,相遇相消,其总能量为零。
7.在如图所示的立方体形晶体中,ABCD滑移面上有一个位错环,其柏氏矢量 平行于AC。
(1)指出位错环各部分的位错类型。
(2)指出使位错环向外运动所需施加的切应力的方向。
(3)位错环运动出晶体后晶体外形如何变化?
解:(1)1点为正刃型位错,2点为右螺型位错,3点为负刃型位错,4点为左螺型位错,其余均为混合位错。
3.证明位错线不能终止在晶体内部。
解:设有一位错C终止在晶体内部,如图所示,终点为A。绕位错C作一柏氏回路L1,得柏氏矢量b。现把回路移动到L2位置,按柏氏回路性质,柏氏回路在完整晶体中移动,它所得的柏氏矢量不会改变,仍为b。但从另一角度看,L2内是完整晶体,它对应的柏氏矢量应为0。这二者是矛盾的,所以这时不可能的。
材基第三章习题及答案

第三章 作业与习题的解答一、作业:2、纯铁的空位形成能为105 kJ/mol 。
将纯铁加热到850℃后激冷至室温(20℃),假设高温下的空位能全部保留,试求过饱和空位浓度与室温平衡空位浓度的比值。
(e 31.8=6.8X1013)6、如图2-56,某晶体的滑移面上有一柏氏矢量为b 的位错环,并受到一均匀切应力τ。
(1)分析该位错环各段位错的结构类型。
(2)求各段位错线所受的力的大小及方向。
(3)在τ的作用下,该位错环将如何运动?(4)在τ的作用下,若使此位错环在晶体中稳定不动,其最小半径应为多大?解:(2)位错线受力方向如图,位于位错线所在平面,且于位错垂直。
(3)右手法则(P95):(注意:大拇指向下,P90图3.8中位错环ABCD 的箭头应是向内,即是位错环压缩)向外扩展(环扩大)。
如果上下分切应力方向转动180度,则位错环压缩。
A B CDττ(4) P103-104: 2sin 2d ϑτdT s b =θRd s =d ; 2/sin 2θϑd d= ∴ τττkGb b kGb b T R ===2 注:k 取0.5时,为P104中式3.19得出的结果。
7、在面心立方晶体中,把两个平行且同号的单位螺型位错从相距100nm 推进到3nm 时需要用多少功(已知晶体点阵常数a=0.3nm,G=7﹡1010Pa )? (3100210032ln 22ππGb dr w r Gb ==⎰; 1.8X10-9J )8、在简单立方晶体的(100)面上有一个b=a[001]的螺位错。
如果它(a)被(001)面上b=a[010]的刃位错交割。
(b)被(001)面上b=a[100]的螺位错交割,试问在这两种情形下每个位错上会形成割阶还是弯折?((a ):见P98图3.21, NN ′在(100)面内,为扭折,刃型位错;(b)图3.22,NN ′垂直(100)面,为割阶,刃型位错)9、一个]101[2-=a b 的螺位错在(111)面上运动。
材料科学基础10.13习题课用

2019/9/16
(1)抽出一个(111)面的一个圆片,然后圆片
两侧再重新粘合
该位错环滑出表面 后是什么形状?
问题分析:相当于产生了一个位错环
相当于把(111)面割开相对向内位移一个(111)面 的面间距a[111]/3,然后去掉重合的部分, 所以其边缘形成的位错的柏氏矢量是a[111]/3
柏氏矢量:割面两侧相对位移a[0-11]/2, 所以位错b的是[0-11]a/2
割面边缘是[0-11]方向的位错,位错线与 柏氏矢量平行,它是螺型位错
割面边缘是[10-1]方向的位错,位错线与 柏氏矢量既不平行也不垂直,它是混合型 位错
2019/9/16
(3)插入(1-10)半原子面,此面终止在(111)面上
扭折
Y
B位错
小段位错是在原滑移面上
[0-10]方向的小段位错 [0-10]⋅[001]=0
B位错的滑移面是(001)
2019/9/16
柏氏矢量: a[1-10]/2 位错线方向(111) ×(1-10)=[11-2] 位错类型: [1-10] ·[11-2]=0 刃错 滑移面: [1-10] × [11-2]=(111)
2019/9/16
4.已知在某简单立方晶体的(100)面上有一刃型位错L,该 位错的柏氏矢量与(33-1)和(-1-11)面的晶带轴平行 (1)写出该位错的柏氏矢量和位错线的方向,并图示之;
2.一个位错环能否各部分都是螺位错?能否各部 分都是刃位错?为什么?请问位错环有几种类型?
位错环能否都是螺位错? 螺一位错个柏位错氏错环矢只量有不平一行个能于柏位氏各错矢部线量 分都是螺错
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1 练习题Ⅲ(金属所) 1. 简单立方晶体,一个Volltera过程如下:插入一个(110)半原子面,然后再位移2/]101[,其边缘形成的位错的位错线方向和柏氏矢量是什么? 2. 在简单立方晶体中有两个位错,它们的柏氏矢量b和位错的切向t分别是:位错(1)的
b(1)=a[010],t(1)=[010];位错(2)的b(2)=a[010],t(2)=[100]。指出两个位错的类型以及位错的滑移面。如果滑移面不是惟一的,说明滑移面所受的限制。 3. 以一个圆筒薄壁“半原子面”插入晶体,在圆筒薄壁下侧的圆线是不是位错? 4. 写出距位错中心为R1范围内的位错弹性应变能。如果弹性应变能为R1范围的一倍,则所涉及的距位错中心距离R2为多大?这个结果说明什么? 5. 面心立方晶体两个平行的反号刃型位错的滑移面相距50 nm,求它们之间在滑移方向以及攀移方向最大的作用力值以及相对位置。已知点阵常数a=0.3 nm,切变模量G=71010
Pa, =0.3。
6. 当存在过饱和空位浓度时,请说明任意取向的位错环都受一个力偶作用,这力偶使位错转动变成纯刃型位错。 7. 面心立方单晶体(点阵常数a=0.36 nm)受拉伸形变,拉伸轴是[001],拉伸应力为1MPa。
求b=a[101]/2及t平行于[121]的位错在滑移和攀移方向所受的力。 8. 若空位形成能为73kJ/mol,晶体从1000K淬火至室温(约300K),b约为0.3nm,问刃位错受的攀移力有多大?估计位错能否攀移? 9. 当位错的柏氏矢量平行x1轴,证明不论位错线是什么方向,外应力场的33分量都不会对位错产生作用力。 10. 证明在均匀应力场作用下,一个封闭的位错环所受的总力为0。 11. 两个平行自由表面的螺位错,柏氏矢量都是b,A位错距表面的距离为l1,B位错距表面的距离为l2,l2> l1,晶体的弹性模量为。求这两个位错所受的映像力。 12. 一个合金系,在某一温度下的fcc和hcp结构的成分自由能-成分曲线在同一成分有最小值。问这个成分合金在该温度下的扩散位错会不会出现铃木气团?为什么? 13. 设使位错滑移需要克服的阻力(切应力)对铜为9.8105 Pa,对3%Si-Fe合金为1.5108
Pa,铜、3%Si-Fe合金的切变模量分别是41010 Pa以及3.81011 Pa。问它们在表面的低位错密度层有多厚?已知点阵常数aCu=0.36 nm,aFe-Si=0.28 nm。 14. 简单立方晶体(100)面有一个b=[001]的螺型位错。(1)在(001)面有1个b=[010]的刃型位错和它相割,相割后在两个位错上产生弯结还是割阶?(2)在(001)面有一个b=[100]的螺型位错和它相割,相割后在两个位错上产生弯结还是割阶? 15. 立方单晶体如图所示,三个平行的滑移面上各有两个位错,位错的正向及柏氏矢量如图
中箭头所示:bⅠ、bⅢ、bⅤ和bⅥ平行[010]方向,bⅡ平行[100]方向,bⅣ平行于]101[方向,所有柏氏矢量的模相等;在作用下,假设位错都可以滑动。位错滑动后,问A相对 3-2
A'、B相对B'、C相对C’和D相对D’位移了多少? 16. 在面心立方晶体中,把2个平行的同号螺位错从100nm推近到8nm作功多少?已知a=0.3nm,=71010Pa。 17. 晶体中,在滑移面上有一对平行刃位错,它们的间距该多大才不致在它们的交互作用下发生移动?设位错的滑移阻力(切应力)为9.8105Pa,=0.3,=51010Pa。(答案以b表示) 18. 设沿位错每隔103b长度有一个割阶,外力场在滑移面滑移方向的分切应力为5105Pa,求位错在室温(约300K)下的滑移速度。b=0.3nm,自扩散系数Ds=0.009exp(1.9eV/kT)cm2s-1。
练习题Ⅲ解答(金属所) 1. 简单立方晶体,一个Volltera过程如下:插入一个(110)半原子面,然后再位移2/]101[,其边缘形成的位错的位错线方向和柏氏矢量是什么? 解:当简单立方晶体插入一个(110)半原子面,因为(110)面的面间距是[110]/2,相当Volltera过程的割面是(110),并相对位移了[110]/2,再填入半个(110)原子面;现在割面还要相对位
移2/]101[,即整个Volltera过程的位移为[110]/2+2/]101[=[010]。所以在边缘的位错的的柏氏矢量b=[010],(110)半原子面的边缘是位错,并考虑到刃型分量位错的版原子面的位置,位错线方向]011[。 2. 在简单立方晶体中有两个位错,它们的柏氏矢量b和位错的切向t分别是:位错(1)的b(1)=a[010],t(1)=[010];位错(2)的b(2)=a[010],t(2)=[100]。指出两个位错的类型以及位错的滑移面。如果滑移面不是惟一的,说明滑移面所受的限制。 解:位错(1)的b(1) t(1)=1]010[]010[,柏氏矢量与位错线平行但反向,所以是左螺位错。如果不考虑晶体学的限制,则以位错线为晶带轴的晶带的面都是滑移面。但是由于位错在密排面是容易滑动的,简单立方的密排面是{100},所以真正的滑移面是(100)和(010)。
位错(2)的b(2) t(2)= 0]100[]010[,柏氏矢量与位错线垂直,所以是刃型位错。刃型位错的 3-3
滑移面是惟一的,是位错线与柏氏矢量共面的面,其法线方向n是t(2)b(2)=[100],即滑移面是(100)面。 3. 以一个圆筒薄壁“半原子面”插入晶体,在圆筒薄壁下侧的圆线是不是位错? 解:不是,这个圆筒薄壁“半原子面”构成面缺陷。 如果在立方晶体插入(100)半原子面,如下图1所示。这时版原子面的边界ABCD是刃型位
错,若位错线方向如图所示,则柏氏矢量bⅠ=]001[。如果再插入(010)半原子面,半原子面
的边缘EFGH是刃位错,若位错线方向如图所示,则柏氏矢量bⅡ=]010[。现在(010)半原子面和原来插入的(100)半原子面相连,如图2所示,DC位错和EF位错连接在一起,这时C和F结合为一个位错结点,DC和EF结合为一个位错,其柏氏矢量bⅢ=bⅠ+bⅡ =]011[。按这样分析,如果插入一个四方薄壁半原子面,半原子面下方的四方形边缘是位错,但四个边位错的柏氏矢量各不相同,而四边形四个角各有一根位错伸向表面,这四个角都是位错结点,四根伸向表面的位错的柏氏矢量是结点两侧的位错的柏氏矢量之和。同理,如果插入形状是8面棱柱状的半原子面,在半原子面底部的8条边线是刃位错,他们的柏氏矢量各不相同,但8边形的8个顶角都是位错结点,由结点引向表面的线也是位错线,其柏氏矢量是8边形结点两边的位错的柏氏矢量之和。如此类推,插入多边形棱柱状的半原子面,在半原子面底部多边形线是刃位错,由结点引向表面的线也是位错线。但是,如果插入的是圆筒薄壁“半原子面”,这是上述多边形半原子面的极限情况,即多边形的边数趋向无限大,如果说有“位错”存在,则整个圆筒面都布满“位错”,实质上,圆筒面是“面缺陷”,其底部的圆线不是位错。
4. 写出距位错中心为R1范围内的位错弹性应变能。如果弹性应变能为R1范围的一倍,则所涉及的距位错中心距离R2为多大?这个结果说明什么?
解:距位错中心为R1范围内的位错弹性应变能为bRKbE12ln4。如果弹性应变能为R1范围的一倍,则所涉及的距位错中心距离R2为
bRKbbRKb2212ln4ln42
即 b
RR212
从上式看出,R2比R1大得多,即是说,应变能密度随距位错中心的距离是快速衰减的。
5. 面心立方晶体两个平行的反号刃型位错的滑移面相距50 nm,求它们之间在滑移方向以及攀移方向最大的作用力值以及相对位置。已知点阵常数a=0.3 nm,切变模量=71010 Pa, 3-4
=0.3。 解:A位错对B位错的作用力为Fi=ijk(jl)A(bl)B(k)B。位错A是正刃型位错,它处在x3轴,它的应力场有11、22、33和12项;位错B是负刃型位错,平行x3轴,所以上式中的k只能是3,柏氏矢量平行x1轴,所以式中的l只能是1。对于A位错对B位错的作用力的第一分量F1A→B,上式的i等于1,而k=3,那么j只能是2,但l=1,故:
22221
22212
BBA21123BA1)()()1π(2)(xxxxxbbF
面心立方晶体的柏氏矢量b=nm212.0nm)2/23.0(2/2a。在滑移面上单位长度B位错受的最大作用力的值为
N/m1058.3N/m1050)3.01π(2)10212.0(10725.0)1π(225.0)(39291022maxBA1xbF
受最大x1正向作用力的位置是=3/8,即x=50tan(3/8) nm=120.7 nm,y=50 nm,以及=7/8,即x1=50tan(7/8) nm=-20.7 nm,x2=50 nm;受最大x1负向作用力的位置是=/8,即x1=50tan(/8)nm=20.7 nm,x2=50 nm、以及=5/8,即x1=50tan(5/8) nm=-120.7 nm,x2=50 nm。 对于A位错对B位错在攀移方向的的作用力F2A→B,在作用力的式子中i=2,所以j只能为1。
22221
222122
BBA11213BA2)()3()1π(2)(xxxxxbbF
为了讨论方便,设n=x1/x2,上式变为故 22222222)1()13()1()13()1(2nnAnnxvb
FπBA
2
其中A是式中的常数项。为了求极值,上式对n取导,并令其等于零,得 0263nn
即 577.03/1 0nn; 时F2AB取得极值。F2AB随n的变化如下图所示。
