计量型控制图
计量型数据控制图要点

用I-MR图做改善前后的对比
文件: Before-after.mtw
用I-MR图做改善前后的对比
改善后均 值下降
改善后变 差减小
以上是图示化比较,最后还应通过统计检验进行比较。
控制图的判异规则
为了帮助鉴别出现在我们流程中的特殊原因事件,制定了 一套标准规则:
1、1点落在控制限之外 2、连续8点落在中心线同一侧 3、连续6点递增或递减 4、连续14点中相邻点升降交错 5、连续3点中有2点落在中心线同一侧的2-sigma限之外 6、连续5点中有4点落在中心线同一侧的1-sigma限之外 7、连续15点落在1-sigma限之内 8、连续8点落在中心线两侧,但无1点在1-sigma限之内
a.上一个月的数据是特殊 原因还是普通原因的结果 ?为什么? 普通原因。根据判异规则无 异常点。 b.人力资源经理是否采取 了适当的措施? 否 c.它应该预期的月培训成 本是多少?
$87154~$108246
解释单值图练习
案例#2—停工时间 一条包装线在3 月8 日到8 月23 日之间平均每周停工4.1 小时。由于很多问 题与电路开关有关,技术人员怀疑电涌保护装置发生故障。他们在8 月23 日这一周更换了它,并连续再收集了8 周的数据。
移动极差控制限
UCLR 3.267mR
单值控制限
LCLR 0
UCLXX2.66mR LCLXX2.66mR
单值移动极差图Minitab指令
文件: Individ.mtw
单值移动极差图Minitab输出
单值图可显现出 流程中心的稳定 性(中心位置)
移动极差图可显 现出短期变差的 稳定性
移动极差MR是相邻两个单值的差的绝对值; 看图顺序:先看极差图,再看均值图。
计量型控制图详细概述课件

02
计量型控制图的原理
中心线与控制限
中心线(CL)
控制图的中心线表示过程的期望值,通常为过程的平均值。 中心线是控制图的基础,所有数据点都围绕中心线上下波动 。
控制限(UCL、LCL)
控制限是用来判断过程是否处于受控状态的界限。上控制限 (UCL)和下控制限(LCL)分别表示数据点允许的最大和最 小波动范围。当数据点超出控制限时,表示过程可能失控。
程的稳定性和变异来源。
结合六西格玛管理和计量型控制图有助于改进过程性能,降低缺陷率, 提高客户满意度和竞争优势。
与自动化系统的结合
通过与自动化系统的结合,计量型控制图能够实现实 时数据采集、分析和可视化。自动化系统可以提供实 时的数据反馈,帮助企业快速响应异常情况,采取相 应措施进行调整。
单击此处添加正文,文字是您思想的提一一二三四五 六七八九一二三四五六七八九一二三四五六七八九文 ,单击此处添加正文,文字是您思想的提炼,为了最 终呈现发布的良好效果单击此4*25}
质量保证
控制图可以作为企业质量 保证体系的一部分,提供 数据支持,证明产品质量 的稳定性和可靠性。
实验研究中的应用
数据分析
计量型控制图在实验研究中用于 分析实验数据,评估实验结果的
一致性和可靠性。
实验优化
通过控制图分析,研究者可以找出 实验中的影响因素和最佳条件,优 化实验设计。
科学发现
在科学研究中,控制图可用于监测 实验过程中的关键参数,帮助研究 者发现新的科学规律和现象。
支持。
数据可视化与交互
通过数据可视化技术,将控制图 与大数据相结合,实现数据的直 观展示和交互操作,提高数据分
析的效率和效果。
数据预测与决策
基于大数据的预测模型,对生产 过程进行预测和预警,为生产决
@SPC基础知识之三-控制图

去除异常原因
Yes
绘制直方图 (辅助参考变异是否常态分布)
计算Pp/Ppk Yes
满足规格
No 检讨5M1E各方面
绘制控制用 控制图
提升过程能力 18
基本概念-控制图
控制图的阶段-分析~控制 ➢ 制作分析用控制图时,其中心线和上下控制界限,都是通过抽样方法,采集一定时期内、稳定生产状态下的数
据,计算得出。 ➢ 根据计算结果,制作分析用控制图,并确认保持在控制状态,而且过程能力符合要求,才能延长控制界限,应
9
基本概念-直方图
直方图-分布曲线-正态分布曲线 中心极限定理:基于概率论,稳定受控的过程中,大量随机变量会近似于服从正态分布。 正态分布中,无论均值μ和标准差σ是多少,质量特性值: ➢ 落在μ±3σ之间的概率为 99.73%; ➢ 两侧落在μ±3σ之外的概率为100% - 99.73%= 0.27%; ➢ 超过任意一侧,即大于μ-3σ或小于μ+3σ的概率为0.27%/2=0.135%≈1‰; ➢ 形成正态分布曲线图。控制图即基于这一理论而产生。
SPC基础知识 之三 控制图
制作日期:201808
目录
基本概念 直方图 控制图
常见问题 计量型控制图 计数型控制图
X--R图制作实例
2
基本概念
基本概念-直方图
直方图 将收集的数据,使用一定范围,在横轴上分成几个相等的区间; 将各区间内测量值出现的次数,累积起来的面积,使用柱状图表示。 直方图的目的 ➢ 可以直观反映数据分布的中心和宽度 ➢ 显示图形分布形状,观察过程波动状况 ➢ 比较测量值的分布与标准规格,观察差异 ➢ 决定是否需要进一步层别化 ➢ 分析改进方向和措施
控制上限
μ+σ μ+2σ μ+3σ
SPC控制图应用步骤简明教程

(二)可数型数据流程能力
数据不只是通过/不通过,还知道一件产品上与多少个缺点 DPU-Defects Per Unit 每件的平均缺点数 dpu=缺点总数量/总件数 FTY=e-dpu p(d)=1-FTY
drσ ≥50%
评价 接近稳定 不太稳定
不稳定 很不稳定
6西格玛相关
(一)连续型数据的流程能力
流程的西格玛水平:Z值 Z值可以描述流程的不合格率P(d)
ZUSL =
USL-X
ZLSL =
X-LSL
Z值与不合格率P(d)对应表
(二)可区分型数据流程能力
可区分型数据:通过/不通过 一次通过率First Time Yield FTY=合格数量/总数量
当过程受控时并经过过程能力评价满足要求时, 应可以延长控制限,以满足未来过程控制的需 要。如果过程中心线偏离目标值,可能需要针 对目标值进行调整。
返回
1.抽样计划的原则:合理的子组,即:组内出现特殊原因的机会最小,组间 出现特殊原因的机会最大。(子组内的变差代表的是零件间的变差, 而子组间的变差代表的是过程的变化)。 即:观测值的个数或样本量决定了控制图反映波动的能力。
式中
R
通常用 d 2
和
S C2
来估计。
2.过程性能:过程总变差的
6
范围,式中
通过用标准差S来估计。
3.如果过程处于统计受控状态,过程能力非常接近于过程性能。当过
程的能力和性能
6
之间存在较大差别时表示有特殊原因存在。
1. CP能力指数(过程位于中心): 2. CPK能力指数(过程不位于中心):
计量型统计过程控制

PPT文档演模板
2020/12/8
计量型统计过程控制
学习目的
完成对本模块的学习后,学员将能够:
建立下列控制图: 计量型 I-MR:Individuals and Moving Range(个体与移动极差图) Xbar&R:Xbr and Range(均值与极差图) Xbar&S:Xbar and Standard deviation(均值与标准差图)
够估计中心趋势和稳定性变化
•X,R
PPT文档演模板
X,R
06-9
计量型统计过程控制
X bar图
计量型控制图涉及连续性变量,其中所关 注的统计量是中心趋势和变异(散布)。
X bar图随时测量变量的中心趋势。它使用 来自大小为N的样本的平均值,或X-bar。
图的中心线由平均值的长期平均水平或Xdouble bar描绘出来。
如果找不到可归因原因,则该过程是处于 失控(统计上)状况
✓ 如果连续证据显示过程稳定的,则失控状况是一个假警报 ✓ 除非图形样式是由某一批产品所导致的,否则该过程是不稳定的,
并且必须采取措施来找出不稳定的根本原因
PPT文档演模板
06-12
计量型统计过程控制
•Xbar&R控制图界限
PPT文档演模板
UCL=12.95
(X图的系数通常为2.66)
对于MR图:
UCL=D4R n=2)
UCL=3.267*1.37)
UCL=4.48
LCL=X-E2R LCL=9.31-(2.66*1.37) LCL=5.67
LCL=D4R(D3.D4是基于 LCL=0*1.37) LCL=0
PPT文档演模板
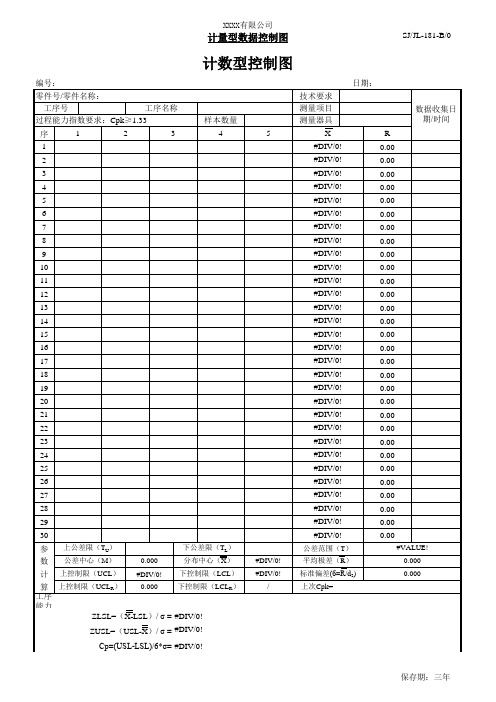
计量型控制图
计数型控制图Cpk=Z USL/3=#DIV/0!X 控制图R 控制图编制/日期: 审核/日期:批准/日期:X UCL CL+2σCL+1σCL CL-1σ CL-2σLCL #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!R UCL CL 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000。
控制图

与均值-极差控制图类似,这种控制图也是用于观察连续数据的均值和变异性(标准差) 的变化情况。如果点子在控制限内随机分布,且无异常点,说明过程处于控制状态;如果 点子超出控制限或出现异常点,说明过程可能失控。
3. 单值-移动极差控制图
这种控制图用于观察单个数据值和连续数据的变化情况。如果点子在控制限内随机分布, 且无异常点,说明过程处于控制状态;如果点子超出控制限或出现异常点,说明过程可能 失控。
4. 观察控制图
观察控制图上的点 子分布情况,判断 过程是否处于控制 状态。
5. 采取行动
如果发现异常点或 过程失控,采取适 当的措施解决问题 并防止问题再次发 生。
控制图的局限性
1. 数据必须是连续的
控制图只能用于观察连续的数据,对于离散的数据或非连续的数 据,需要采用其他方法进行分析。
2. 需要足够的样本数量
控制图原理
控制图基于中心极限定理和概率统计原理。中心极限定理表明,当样本量足够大时,任何随机变量的 取值都会围绕一个中心值波动,且这个波动是有限的。因此,我们可以通过控制图的上下限来判断过 程是否处于控制状态。
控制图的原理是通过对过程进行多次抽样,计算统计量(如均值、中位数、极差等),并将这些统计 量绘制在图上。通过观察图的走势,我们可以判断过程是否受控,并发现异常情况。如果过程受控, 则说明过程的质量稳定;如果过程失控,则说明过程的质量存在问题。
平均数与标准差控制图
总结词
平均数与标准差控制图是一种常用的统计 控制图,用于监控一组数据的平均值和标 准差。
VS
详细描述
平均数与标准差控制图由两个图表组成: 一个图表显示平均数,另一个图表显示标 准差。这种控制图适用于需要了解数据分 布情况的应用场景,如科学研究、质量控 制和金融分析等。
常规计量值控制图

1 均值-极差控制图
• 控制图对大波动灵敏,对小波动不灵敏
当n=4时
ARL=1 图对大波动监测效果显著,平均只需1个值就可以 发出失控信号。
而当θ=0.5σ时
ARL=44
对均值小漂移不敏感,平均需要44个值才能发 出失控信号。
1 均值-极差控制图
当过程稳态时,ARL值越大越好;说明控制图是稳 健的。 但过程已经发生异常波动,ARL值越小越好,说明 控制图是灵敏的
2 判稳判异准则
控制用控制图
控制用控制图由分析控制图转化而成,它用 于对生产过程进行连续监控。
按照确定的抽样间隔和样本大小抽取样本, 计算统计量数值并在控制图上描点,判断生产过 程是否异常。
控制用控制图在使用一般时间以后,应根据 实际情况对中心线和控制界限进行修改。
2 判稳判异准则
控制图判稳准则
4.1 均值-极差控制图
4.当R图受控时,认为过程的波动是稳定的,再分析 图,类似于对R图的分析,对任意失控情况及异常模式 分析原因。也可能要经过反复的“识别-纠正-重新计算 ”这一过程。
5.当两个图都显示稳定时,并且满足过程能力的要求, 可以用于实际的过程控制。一旦发现失控或出现异常模 式的信号时,应该及时分析原因,并采取行动。
9 80.69 80.49 82.16 84.29
10 81.72 81.12 80.77 80.60
11 80.98 81.33 81.60 80.70 12 80.42 82.20 80.13 80.24
13 81.11 81.13 82.22 81.17
14 82.40 81.41 82.93 83.13
21 81.06 82.06 82.76 82.46
22 82.55 83.53 82.94 81.89
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X 控制图
R 控制图
编制/日期: 审核/日期:批准/日期:
X UCL CL+2σCL+1σCL CL-1σ CL-2σLCL #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0! #DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!#DIV/0!
R UCL CL 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000 0.0000.0000.000。
