共轭分子与HMO法
合集下载
5.2 休克尔分子轨道法
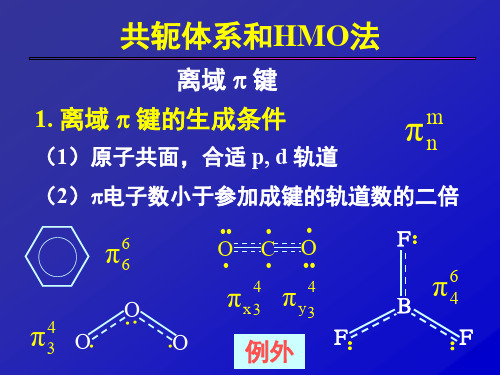
● Frost图与4m+2 Hukel规则（休克尔芳香性）
以2β为半径作圆，作一顶点正对最低点的内接正多边形，则各
顶点的位置为单环共轭多烯 分子轨道对应的能级。
E 2
E
E 2
图5-9 环烯烃 轨道能级图 由图看出：电子数为4m+2时，电子全部填充在成键的型分子轨道 上，且都以自旋反平行成对，体系较稳定，这就是休克尔规则的实质.
平面构型的多环芳烃的 HMO 法处理：
(1) 萘(C10H8)
0.555 0.518 1.000 1.000 1.000 0.404 0.104 0.452 0.725
各原子自由价：F1 F4 1.732 0.896 0.836 F2 F3 1.732 0.896 0.448 0.388
ψ2 = 0.602φ1 + 0.372φ2 - 0.372φ3 - 0.602φ4 ψ1 = 0.372φ1 + 0.602φ2 + 0.602φ3 + 0.372φ4
E E E … 0， 0， ， 0 c1 c2 cn
H1n ES1n c1 ... H 2 n ES2 n c2 0 ... ... ... ... H nn ESnn cn ...
E 的一元 n 次 代数方程,有n 个解。
久期方程有非零解，则其系数行列式应为零
x 1 0 0 同除以 并令x
E , 得久期行列式
1
x 1 0 x 1 x
0 1
0
0 0 1
求解久期行列式的方法很多，如对称性方法，群论方法，代 数余子式展开法等。代数余子式法是通用的方法。 代数余子式法展开
HMO理论的一些粗浅理解
HMO理论的一些粗浅理解休克尔分子轨道法（Hückel molecular orbital method）是用简化的近似分子轨道模型处理共轭分子中的π 电子的方法，1931年由E.休克尔（E. Hückel）提出，简称HMO。
这是一种最简单的分子轨道理论，在有机化学中应用得相当广泛，用以解决共轭分子的结构，探讨分子的性质和反应性能的半经验方法。
HMO法的基本内容：1、承认分子轨道理论的全部内容（1）将分子中每一个电子的运动，看作是在各原子核和其余电子的平均势场中运动（即单电子近似），其单电子的空间波函数为分子轨道；（2）分子轨道采用原子轨道的线性组合，用变分法得到分子轨道和能级；（3）分子轨道内电子排布符合能量最低原理、保里原理和洪特规则；组成分子轨道的原子轨道必须符合能量相近、最大重叠和对称性匹配这三个条件。
2、用HMO法处理共轭分子结构的假设（1）由于π电子在核和σ键所形成的整个分子骨架中运动，可将σ键和π键分开处理。
（2）共轭分子有相对不变的σ骨架，而π电子的状态决定分子的性质。
（3）各个碳原子上p轨道的库仑积分都相同，都等于α，相邻原子轨道间的交换积分都相等，用β表示,而非相邻原子轨道间的交换积分都等于零；不同原子轨道间的重叠积分为零；3、共轭烯烃久期行列式的规律全部由C组成的共轭烯烃，从分子骨架直接写久期行列式（1）画出σ骨架，将参与共轭的原子编号；（2）n个原子参加的共轭体系对应着n阶久期行列式；（3）n阶久期行列式主对角元Aij为x，x=(α-E)/β；（4）若ij两原子以π键键连，则Aij及Aji为1，其它元素均为0；（5）久期行列式沿主对角线对称；（6）对同一分子，若编号不一，其写出的久期行列式虽然不同，但求解的结果相同。
休克尔分子轨道的应用：休克尔分子轨道法是量子化学近似计算方法之一，它以简便迅速著称，适宜于计算平面共轭分子中的π电子结构。
在分析有机共轭分子的稳定性、化学反应活性和电子光谱，及研究有机化合物结构与性能的关系等方面有着广泛应用。
乙烯休克尔行列式
乙烯休克尔行列式
休克尔分子轨道法（Hückel molecular orbital method）是用简化的近似分子轨道模型处理共轭分子中的π电子的方法，1931年由E.休克尔（E. Hückel）提出，简称HMO。
这是一种最简单的分子轨道理论，在有机化学中应用得相当广泛，用以解决共轭分子的结构，探讨分子的性质和反应性能的半经验方法。
原理
在有机化合物中，包含着一大类共轭和芳香烃分子，它们的特点是参与共轭的原子都在一个分子平面上，每个原子都有一个垂直于分子平面的p原子轨道，在这个轨道上的电子称为π电子。
HMO法及共轭分子的结构
2 2 2 c12 + c 2 + c 3 + c 4 = 1
可得到与其能级相应的分子轨道波函数的系数。
c 例如， 1 = c 4 , c 2 = c 3 ，x = -1.62，得
1.62c1 + c 2 = 0
2c + 2c = 1
2 1 2 2
得：
c1 = c 4 = 0.372, c2 = c3 = 0.602
x 1 1 =0 x +1
x( x 1) 1 = 0
解得 x = -1.62 和 0.62。
当 c1 = c 4 , c 2 = c3 时，久期方程简化为
c1 + ( x 1)c2 = 0
xc1 + c2 = 0
即
x 1 =0 1 x 1
解得 x = 1.62 和 -0.62。 将解得的每个x值分别代回久期方程，并结合归一 化条件
2πk xn = 2 cos n 2πk Ek = α + 2 β cos , k = 0,1,2, , n 1 n 能级特点：
1. 当k =0 时，不论n为何值，都有 E0 =α+2β, E0对应最低 能级的分子轨道
2. 当k = n-k 时，
Enk
2π (n k ) = α + 2 β cos = Ek n
ψ 1 = 0.372φ1+ 0.602φ 2 + 0.602φ 3 + 0.372φ 4
ψ 2 = 0.602φ1+ 0.372φ 2 0.372φ 3 0.602φ 4 ψ 3 = 0.602φ1 0.372φ 2 0.372φ 3 + 0.602φ 4 ψ 4 = 0.372φ1 0.602φ 2 + 0.602φ 3 0.372φ 4
可得到与其能级相应的分子轨道波函数的系数。
c 例如， 1 = c 4 , c 2 = c 3 ，x = -1.62，得
1.62c1 + c 2 = 0
2c + 2c = 1
2 1 2 2
得：
c1 = c 4 = 0.372, c2 = c3 = 0.602
x 1 1 =0 x +1
x( x 1) 1 = 0
解得 x = -1.62 和 0.62。
当 c1 = c 4 , c 2 = c3 时，久期方程简化为
c1 + ( x 1)c2 = 0
xc1 + c2 = 0
即
x 1 =0 1 x 1
解得 x = 1.62 和 -0.62。 将解得的每个x值分别代回久期方程，并结合归一 化条件
2πk xn = 2 cos n 2πk Ek = α + 2 β cos , k = 0,1,2, , n 1 n 能级特点：
1. 当k =0 时，不论n为何值，都有 E0 =α+2β, E0对应最低 能级的分子轨道
2. 当k = n-k 时，
Enk
2π (n k ) = α + 2 β cos = Ek n
ψ 1 = 0.372φ1+ 0.602φ 2 + 0.602φ 3 + 0.372φ 4
ψ 2 = 0.602φ1+ 0.372φ 2 0.372φ 3 0.602φ 4 ψ 3 = 0.602φ1 0.372φ 2 0.372φ 3 + 0.602φ 4 ψ 4 = 0.372φ1 0.602φ 2 + 0.602φ 3 0.372φ 4
HMO法及共轭分子的结构
丁二烯的分子图
（1）离域可降低体系的能量。对比下面两式 H3C－CH2－CH=CH2 + H2 H2C=CH2－CH=CH2 + 2H2 H3C－CH2－CH2－CH3
H = 126.8 kJ -1 mol
H3C－CH2－CH2－CH3 mol H = 236.8 kJ -1 丁二烯加2H2转变成丁烷所放出的能量小于丁烯加H2 转变成丁烷的二倍：2×(-126.8)=-253.6 kJ -1）。这说 mol 明丁二烯形成离域键比看作两个小键能量低。差值-16.8 kJ -1相当于离域能0.48β 。 mol
(H 31 ES31 )c1 + ( H 32 ES32 )c2 + (H 33 ES33 )c3 + (H 43 ES43 )c4 =0
(H 41 ES41 )c1 + ( H 42 ES42 )c2 + (H 43 ES43 )c3 + ( H 44 ES44 )c4 =0
将Huckel近似代入，得
在基态的情况下，4个π电子的总能量为： EDπ= 2E1+2E2 = 4α+4.48β 如果把看成两个小π键，4个π电子的总能量为： ELπ= 4α+ 4β 离域能 DEπ= EDπ - ELπ = 0.48β
丁二烯的离域π键的特征量： 碳原子的π电荷密度 ρ1=ρ4= 2×0.3722+2×0.6022=1 ρ2=ρ3=2×0.6022+2×0.3722=1 碳原子间的π键键级 P12 = P34= 2×0.372×0.602+2×0.602×0.372=0.896 P23= 2×0.602×0.602+2×0.372×(-0.372)=0.448 原子的自由价 F1=F4=1.732-0.896=0.836 F2=F3=1.732-0.896-0.448=0.388
共轭体系和HMO法
xc1+c2=0 c1+(x+1)c2=0
x1 0
1 x 1
x2 + x - 1= 0
x= -1.62, 0.62
c1=-c4, c2=-c3
xc1+c2=0 c1+(x-1)c2=0
x1 0
1 x 1
x2 - x - 1= 0
x= 1.62, -0.62
x a E b
E=a - xb
E1=a + 1.62b E3=a - 0.62b
（4）化学反应性
H2C＝CH－CH＝CH2 1,4加成
H2C＝CH－Cl C－Cl键缩短，Cl 活泼性下降
p
4 3
C6H5 C
C6H5
C6H5
C C6H5
p 26 26
2Na
C6H5 ..
C6H5 C
.. C6H5 2-
C C6H5
p 28 26
3. 肽键
R1 O
R2 O
＝
－
＝
－
H2N－CH－C－OH + H－NH－CH－C－OH
r1 20.3722 + 2 0.6022 = 1.00 r2 2 0.6022 + 20.3722 = 1.00 r3 2 0.6022 + 2(0.372)2 = 1.00 r4 20.3722 + 2 (-0.602)2 = 1.00
1 0.3721+0.6022+0.6023+0.3724 2 0.6021+0.3722 - 0.3723 - 0.6024
a E
b
0
0
b a E
b
0
共轭体系的分子轨道理论
(H14 (H 24 (H 34 (H 44
− − − −
ES14 ES 24 ES34 ES 44
) ) ) )
= = = =
0 0 0 0
⎫ ⎪⎪ ⎬ ⎪ ⎪⎭
根据休克尔假设化简得：
c1(α − E)
c1β
两边同除β
+ +
c c
2 2
β
(α
−
E)
c2 β
x =α −E β
+ +
c3 c3
β
(α
c3β
=0
c3 + c4 x + c5
=0
c4 + c5 x + c6 = 0
⎪ ⎪⎪ ⎬ ⎪ ⎪
c1 +
c5 + c6 x = 0 ⎪⎭
σy
1
SxSy
c1 = c4 c2 = c3 = c5 = c6
2
6
3
5 σx
4
c1 x c1
+ 2c2 = 0 + c2 (x + 1) = 0
⎫ ⎬ ⎭
x 1
x
2 +1
• 一些无机分子及离子
缺电子大π键 m < n
H C
H
Cl CH
氯乙烯 π34
O 2C OO
CO3= π46
HH
C+ C
H
C
H
H 烯丙基阳离子π32
3. 离域效应：共轭体系的存在使体系能量降低,键 长平均化等等。
§4.2 休克尔分子轨道理论
4.2.1 HMO法的基本内容
1. 承认分子轨道理论的全部内容：
HMO方法 复旦解析
三、丁二烯的HMO处理
1．解休克尔行列式确定轨道及能量
1 2 3 4 H2C=CH–CH=CH2
x 1 0 0
1 x 1 0
0 1 x 1
0 0 0 1 x
C1 x C2 0 C1 C2 x C3 0 C2 C3 x C4 0 C3 C4 x 0
x 1 0 0
得到四个分子轨道及对应能量：
1 0.3717 1 0.6015 2 0.6015 3 0.3717 4 2 0.6015 1 0.3717 2 0.3717 3 0.6015 4 3 0.6015 1 0.3717 2 0.3717 3 0.6015 4 4 0.3717 1 0.6015 2 0.6015 3 0.3717 4
ˆ d H ii i H j
近似为第i个C原子2pz电子的平均能量，不考虑C原子位置 的差别,一律视为固定参数，是由实验推测的参数。 （2）交换积分β
0非键连 ˆ H ij i H j d 键连 β 决定了相邻的键的性质，称为成键参量，β 为负值， 为实验推测的参数。
0 0 0 0
.... .... .... 0 E
E 令 x
x 1 0 0 0 1 x 1 0 0 Dn ( x ) 0 1 x 1 0 0 0 0 1 x
C1 x C 2 0 C1 C 2 x C3 0 C 2 C3 x C 4 0 .......... .......... ...... C n 1 C n x 0
（3）重叠积分Sij
1(i j )归一化得到 S ij i j d 0(i j )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
σ键和π键总键级： 键和π键总键级： 键和
Prs = 1 + p rs
相邻原子间的键 级越大， 级越大，其键强度越 键长就越短。 大，键长就越短。
3. 自由价： 自由价：
原子参与形成化学键之后，还剩余的成键能力。 原子参与形成化学键之后，还剩余的成键能力。
原子成键度： 原子成键度：
原子r 原子r和周围其它原子间键级总和
得到四个π分子轨道及对应能量：
ψ 1 = 0.3717φ1 + 0.6015φ 2 + 0.6015φ3 + 0.3717φ 4 ψ 2 = 0.6015φ1 + 0.3717φ 2 0.3717φ3 0.6015φ 4 ψ 3 = 0.6015φ1 0.3717φ 2 0.3717φ 3 + 0.6015φ 4 ψ 4 = 0.3717φ1 0.6015φ 2 + 0.6015φ 3 0.3717φ 4
E1 = α + 1.618β E 2 = α + 0.618β E3 = α 0.618β E 4 = α 1.618β
2．结果讨论——能量及离域π轨道示意图 ．结果讨论 能量及离域π 能量及离域 （1）能级图
(2)离域能： 离域能： 丁二烯(基态)的π电子总能量： EDπ=2(α +1.618β )+2(α +0.618β )=4α +4.472β α β α β α β π 丁二烯(基态)的π电子定域能：ELπ=4(α +β ) α β π 丁二烯的π电子离域能 DEπ= EDπ - ELπ=0.472β β π π 定域能ELπ的规律：假设分子中有m个间隔的定域π键，则依 π 休克尔方法计算出有m个简并的α＋β最低能级，每个能级占据2个 电子，共2m个电子，则ELπ为 2m(α＋β) π 丁二烯有2个定域π键，m=2, ELπ = 4(α＋β) ； π 苯有3个定域π键, m=3, ELπ = 6(α＋β) 。 π 如果含有自由基（未成对电子），每一个自由基的能量为α。 离域能是对分子体系起稳定化作用的能量。共轭体系越大,则 离域能DEπ越负。
二、HMO理论的基本要点和休克尔行列式 理论的基本要点和休克尔行列式
1. σ-π分离近似和 电子近似 分离近似和π电子近似 分离近似和 有机共轭分子均为平面构型，如丁二烯，该平面为分子平面，所有C的 有机共轭分子均为平面构型，如丁二烯，该平面为分子平面，所有 的 AO和MO分成两类； 分成两类； 和 分成两类 轨道及其基函（ 在分子平面的反映下是对称的； ①σ轨道及其基函（sp2）在分子平面的反映下是对称的； 轨道及其基函 轨道及其基函（ 在分子平面的反映下，是反对称的， ②π轨道及其基函（C2pz）在分子平面的反映下，是反对称的，分子平 轨道及其基函 面为节面，由对称性相一致的原则， 轨道和 轨道不互相组合。 轨道和π轨道不互相组合 面为节面，由对称性相一致的原则，σ轨道和 轨道不互相组合。 在讨论共轭分子的结构时， 电子和π电子分开处理 在讨论共轭分子的结构时，把σ电子和 电子分开处理，在分子中把原 电子和 电子分开处理， 子核、内层电子、非键电子连同σ电子一起冻结为 分子实” 电子一起冻结为“ 子核、内层电子、非键电子连同 电子一起冻结为“分子实”，构成了由 σ键相连的分子骨架，π电子在分子骨架的势场中运动。 键相连的分子骨架， 电子在分子骨架的势场中运动 电子在分子骨架的势场中运动。 键相连的分子骨架 由于π电子在化学反应中比 电子易受到扰动 由于 电子在化学反应中比σ电子易受到扰动，在共轭分子的量子化学 电子在化学反应中比 电子易受到扰动， 处理中，只讨论π电子 电子， 电子近似. 处理中，只讨论 电子，即π电子近似 电子近似
N r = ∑ Prs
s
Nmax表示该原子最大成键度，定义某原子r的自由价为： Fr = N max N r = N max ∑ Prs
s
对于丁二烯, 对于丁二烯 F1 = F4 = 4.732-(1+1+1+0.894) = 0.838 F2 = F3 = 4.732-(1+1+1+0.894+0.447) = 0.391
四、苯分子的HMO处理 苯分子的 处理 要求会写苯分子的休克尔行列式 详细求解过程不要求。 结果讨论： 能级图 简并π轨道的讲解 离域能DEπ π分子轨道示意图（俯视图）
五、电荷密度、键级、自由价、分子图—HMO参量 电荷密度、键级、自由价、分子图 参量 1. 电荷密度：指每个原子π电子电荷的多少 电荷密度：指每个原子π
C 2 = 1.618C1 C = 1.618C1 得到： 3 C = C 1 4
∫ψ ∫ψ
i
* i dτ = 1,即： ψ * i dτ = ∫ (C1φ1 +C 2φ 2 + C 3φ 3 + C 4φ 4 ) 2 dτ = C1 2 +C 2 + C 3 + C 4 = 1 ψ
2 2 2 2
α近似为第i个C原子2pz电子的平均能量，不考虑C原子位置 的差别,一律视为固定参数α，是由实验推测的参数。 （2）交换积分β
0非键连 H ij = ∫ φi Hπφ j dτ = β键连 β决定了相邻的π键的性质，称为成键参量，β为负值， 为实验推测的参数。
（3）重叠积分Sij
1(i = j )归一化得到 S ij = ∫ φiφ j dτ = 0(i ≠ j )
4. 分子图
分 子 图
Fr prs
C
0.836 0.388 0.388 0.448 0.836 0.896 0.896
C
1.000
C
1.000
C1 x + C 2 = 0 C1 + C 2 x + C3 = 0 C 2 + C3 x + C 4 = 0 .......................... C n 1 + C n x = 0
久期方程得到简化
x
休克尔行列式
休克尔行列式构成法： ①行数和列数等于C原子个数； ②写出分子中C原子标号,列于行列式顶和侧； ③有C原子的地方为x，有π键的为1，其它为0。
1967年, C.Finder又提出 假想的 年 又提出: 又提出 炔丙双自由基中心C的 键级为 键级为2.828 ( 炔丙双自由基中心 的π键级为 若加上两个σ键为 这才是C原子 若加上两个 键为4.828), 这才是 原子 键为
假想的炔丙双自由基
的最大成键度. 不过, 为避免混乱, 的最大成键度 不过 为避免混乱 人们 通常还是采用Moffitt的定义 的定义. 通常还是采用 的定义
E=
Ψ * HπΨdτ ∫
∫Ψ Ψdτ
*
=
( ∑ C i φi )Hπ( ∑ Ci φi )dτ ∫ ( ∑ C i φi ) 2 dτ ∫
E E E = = =0 C1 C 2 C n
方程有非零解的条件是系数行列式（即久期行列式）为零。
4．休克尔近似 ． （1）库仑积分α
H ii = ∫ φ i Hπφ j dτ = α
处理过程： ①写出休克尔行列式，解出xi (i=1，2……n)，求出对应的Ei = α-βx； ②将xi 代回简化的久期方程，利用归一化条件确定系数，即得到π 轨道。
三、丁二烯的HMO处理 丁二烯的 处理 1．解休克尔行列式确定轨道及能量
1 2 3 4 H2C=CH–CH=CH2
x
1 0 0
C1 x + C2 = 0 C1 + C2 x + C3 = 0 C2 + C3 x + C4 = 0 C3 + C4 x = 0
2. 键 级
p rs = ∑ n j C jr C js
j
占据
为相邻原子） （rs为相邻原子） 为相邻原子
例如: 例如:p23=2×(0.6015×0.6015)+2×(0.3717)×(× × × × 0.3717)=0.448 ψ2 = 0.6015φ1 + 0.3717φ2 - 0.3717φ3 - 0.6015φ4 ψ1 = 0.3717φ1 + 0.6015φ2 + 0.6015φ3 + 0.3717φ4
即略去所有原子间pz的重叠。
在休克尔近似的基础上，链式共轭烯烃久期行列式化为：
α E β 0 β α E β β α E 0
.... 0 .... 0 .... 0
0 0
β
..... ..... .....
0 0 0
=0
.... .... .... 0 β α E
α E 令 x= β
x 1 0 0 1 x 1 0 Dn ( x ) = 0 1 x 1 0 0 1 0 0 0 =0
定义F 是因为W.E.Moffitt 定义 max= 4.732是因为 是因为 年提出假想的三亚甲基甲基（ 于1949年提出假想的三亚甲基甲基（后 年提出假想的三亚甲基甲基 来证实这一物种存在）中心 的 键级为 来证实这一物种存在）中心C的π键级为 1.732(若加上三个 键为 若加上三个σ键为 若加上三个 键为4.732)是C原子的 是 原子的 最大成键度. 最大成键度
1 x 1 0 =0 0 1 x 1 0 0 1 x
x 1 0 0
1 0 0 x 1 0 = 1 x 1 0 1 x
El<E2<E3<E4
如x1=-1.618代入简化后的久期方程，
C1 x + C 2 = 0 C + C x + C = 0 1 2 3 C 2 + C 3 x + C 4 = 0 C 3 + C 4 x = 0
单电子近似： ΗπΨ i = ΕiΨ i 2. 单电子近似
分子中每个π电子的运动状态均可用一个单电子波函数ψi来描 π 述，即π分子轨道， π 3. LCAO—MO近似 ： Ψ = ∑ C i φi 近似
Prs = 1 + p rs
相邻原子间的键 级越大， 级越大，其键强度越 键长就越短。 大，键长就越短。
3. 自由价： 自由价：
原子参与形成化学键之后，还剩余的成键能力。 原子参与形成化学键之后，还剩余的成键能力。
原子成键度： 原子成键度：
原子r 原子r和周围其它原子间键级总和
得到四个π分子轨道及对应能量：
ψ 1 = 0.3717φ1 + 0.6015φ 2 + 0.6015φ3 + 0.3717φ 4 ψ 2 = 0.6015φ1 + 0.3717φ 2 0.3717φ3 0.6015φ 4 ψ 3 = 0.6015φ1 0.3717φ 2 0.3717φ 3 + 0.6015φ 4 ψ 4 = 0.3717φ1 0.6015φ 2 + 0.6015φ 3 0.3717φ 4
E1 = α + 1.618β E 2 = α + 0.618β E3 = α 0.618β E 4 = α 1.618β
2．结果讨论——能量及离域π轨道示意图 ．结果讨论 能量及离域π 能量及离域 （1）能级图
(2)离域能： 离域能： 丁二烯(基态)的π电子总能量： EDπ=2(α +1.618β )+2(α +0.618β )=4α +4.472β α β α β α β π 丁二烯(基态)的π电子定域能：ELπ=4(α +β ) α β π 丁二烯的π电子离域能 DEπ= EDπ - ELπ=0.472β β π π 定域能ELπ的规律：假设分子中有m个间隔的定域π键，则依 π 休克尔方法计算出有m个简并的α＋β最低能级，每个能级占据2个 电子，共2m个电子，则ELπ为 2m(α＋β) π 丁二烯有2个定域π键，m=2, ELπ = 4(α＋β) ； π 苯有3个定域π键, m=3, ELπ = 6(α＋β) 。 π 如果含有自由基（未成对电子），每一个自由基的能量为α。 离域能是对分子体系起稳定化作用的能量。共轭体系越大,则 离域能DEπ越负。
二、HMO理论的基本要点和休克尔行列式 理论的基本要点和休克尔行列式
1. σ-π分离近似和 电子近似 分离近似和π电子近似 分离近似和 有机共轭分子均为平面构型，如丁二烯，该平面为分子平面，所有C的 有机共轭分子均为平面构型，如丁二烯，该平面为分子平面，所有 的 AO和MO分成两类； 分成两类； 和 分成两类 轨道及其基函（ 在分子平面的反映下是对称的； ①σ轨道及其基函（sp2）在分子平面的反映下是对称的； 轨道及其基函 轨道及其基函（ 在分子平面的反映下，是反对称的， ②π轨道及其基函（C2pz）在分子平面的反映下，是反对称的，分子平 轨道及其基函 面为节面，由对称性相一致的原则， 轨道和 轨道不互相组合。 轨道和π轨道不互相组合 面为节面，由对称性相一致的原则，σ轨道和 轨道不互相组合。 在讨论共轭分子的结构时， 电子和π电子分开处理 在讨论共轭分子的结构时，把σ电子和 电子分开处理，在分子中把原 电子和 电子分开处理， 子核、内层电子、非键电子连同σ电子一起冻结为 分子实” 电子一起冻结为“ 子核、内层电子、非键电子连同 电子一起冻结为“分子实”，构成了由 σ键相连的分子骨架，π电子在分子骨架的势场中运动。 键相连的分子骨架， 电子在分子骨架的势场中运动 电子在分子骨架的势场中运动。 键相连的分子骨架 由于π电子在化学反应中比 电子易受到扰动 由于 电子在化学反应中比σ电子易受到扰动，在共轭分子的量子化学 电子在化学反应中比 电子易受到扰动， 处理中，只讨论π电子 电子， 电子近似. 处理中，只讨论 电子，即π电子近似 电子近似
N r = ∑ Prs
s
Nmax表示该原子最大成键度，定义某原子r的自由价为： Fr = N max N r = N max ∑ Prs
s
对于丁二烯, 对于丁二烯 F1 = F4 = 4.732-(1+1+1+0.894) = 0.838 F2 = F3 = 4.732-(1+1+1+0.894+0.447) = 0.391
四、苯分子的HMO处理 苯分子的 处理 要求会写苯分子的休克尔行列式 详细求解过程不要求。 结果讨论： 能级图 简并π轨道的讲解 离域能DEπ π分子轨道示意图（俯视图）
五、电荷密度、键级、自由价、分子图—HMO参量 电荷密度、键级、自由价、分子图 参量 1. 电荷密度：指每个原子π电子电荷的多少 电荷密度：指每个原子π
C 2 = 1.618C1 C = 1.618C1 得到： 3 C = C 1 4
∫ψ ∫ψ
i
* i dτ = 1,即： ψ * i dτ = ∫ (C1φ1 +C 2φ 2 + C 3φ 3 + C 4φ 4 ) 2 dτ = C1 2 +C 2 + C 3 + C 4 = 1 ψ
2 2 2 2
α近似为第i个C原子2pz电子的平均能量，不考虑C原子位置 的差别,一律视为固定参数α，是由实验推测的参数。 （2）交换积分β
0非键连 H ij = ∫ φi Hπφ j dτ = β键连 β决定了相邻的π键的性质，称为成键参量，β为负值， 为实验推测的参数。
（3）重叠积分Sij
1(i = j )归一化得到 S ij = ∫ φiφ j dτ = 0(i ≠ j )
4. 分子图
分 子 图
Fr prs
C
0.836 0.388 0.388 0.448 0.836 0.896 0.896
C
1.000
C
1.000
C1 x + C 2 = 0 C1 + C 2 x + C3 = 0 C 2 + C3 x + C 4 = 0 .......................... C n 1 + C n x = 0
久期方程得到简化
x
休克尔行列式
休克尔行列式构成法： ①行数和列数等于C原子个数； ②写出分子中C原子标号,列于行列式顶和侧； ③有C原子的地方为x，有π键的为1，其它为0。
1967年, C.Finder又提出 假想的 年 又提出: 又提出 炔丙双自由基中心C的 键级为 键级为2.828 ( 炔丙双自由基中心 的π键级为 若加上两个σ键为 这才是C原子 若加上两个 键为4.828), 这才是 原子 键为
假想的炔丙双自由基
的最大成键度. 不过, 为避免混乱, 的最大成键度 不过 为避免混乱 人们 通常还是采用Moffitt的定义 的定义. 通常还是采用 的定义
E=
Ψ * HπΨdτ ∫
∫Ψ Ψdτ
*
=
( ∑ C i φi )Hπ( ∑ Ci φi )dτ ∫ ( ∑ C i φi ) 2 dτ ∫
E E E = = =0 C1 C 2 C n
方程有非零解的条件是系数行列式（即久期行列式）为零。
4．休克尔近似 ． （1）库仑积分α
H ii = ∫ φ i Hπφ j dτ = α
处理过程： ①写出休克尔行列式，解出xi (i=1，2……n)，求出对应的Ei = α-βx； ②将xi 代回简化的久期方程，利用归一化条件确定系数，即得到π 轨道。
三、丁二烯的HMO处理 丁二烯的 处理 1．解休克尔行列式确定轨道及能量
1 2 3 4 H2C=CH–CH=CH2
x
1 0 0
C1 x + C2 = 0 C1 + C2 x + C3 = 0 C2 + C3 x + C4 = 0 C3 + C4 x = 0
2. 键 级
p rs = ∑ n j C jr C js
j
占据
为相邻原子） （rs为相邻原子） 为相邻原子
例如: 例如:p23=2×(0.6015×0.6015)+2×(0.3717)×(× × × × 0.3717)=0.448 ψ2 = 0.6015φ1 + 0.3717φ2 - 0.3717φ3 - 0.6015φ4 ψ1 = 0.3717φ1 + 0.6015φ2 + 0.6015φ3 + 0.3717φ4
即略去所有原子间pz的重叠。
在休克尔近似的基础上，链式共轭烯烃久期行列式化为：
α E β 0 β α E β β α E 0
.... 0 .... 0 .... 0
0 0
β
..... ..... .....
0 0 0
=0
.... .... .... 0 β α E
α E 令 x= β
x 1 0 0 1 x 1 0 Dn ( x ) = 0 1 x 1 0 0 1 0 0 0 =0
定义F 是因为W.E.Moffitt 定义 max= 4.732是因为 是因为 年提出假想的三亚甲基甲基（ 于1949年提出假想的三亚甲基甲基（后 年提出假想的三亚甲基甲基 来证实这一物种存在）中心 的 键级为 来证实这一物种存在）中心C的π键级为 1.732(若加上三个 键为 若加上三个σ键为 若加上三个 键为4.732)是C原子的 是 原子的 最大成键度. 最大成键度
1 x 1 0 =0 0 1 x 1 0 0 1 x
x 1 0 0
1 0 0 x 1 0 = 1 x 1 0 1 x
El<E2<E3<E4
如x1=-1.618代入简化后的久期方程，
C1 x + C 2 = 0 C + C x + C = 0 1 2 3 C 2 + C 3 x + C 4 = 0 C 3 + C 4 x = 0
单电子近似： ΗπΨ i = ΕiΨ i 2. 单电子近似
分子中每个π电子的运动状态均可用一个单电子波函数ψi来描 π 述，即π分子轨道， π 3. LCAO—MO近似 ： Ψ = ∑ C i φi 近似