等腰三角形 典型题【重点】
专题03 等腰(直角)三角形中动点问题(老师版)

专题3等腰(直角)三角形中动点问题【典型例题】1.(2021·黑龙江集贤·八年级期末)如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为___.【答案】13.5【解析】【分析】连接MA、AD,易得MA=MC,则△CMD的周长为:MC+MD+CD=MA+MD+CD≥AD+CD,当M点在线段AD上时,△CMD的周长最小,再由面积可求得AD的长,从而可求得周长的最小值.【详解】如图,连接MA、AD∵EF垂直平分线段AC∴MA=MC∴△CMD的周长=MC+MD+CD=MA+MD+CD≥AD+CD∵点D为DC边的中点,BC=3∴1 1.52CD BC==∵AB=AC ∴AD⊥BC∴118 2BC AD⨯=即1318 2AD⨯=∴AD=12∴AD+CD=12+1.5=13.5即△MCD的周长的最小值为13.5故答案为:13.5【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质定理,三角形的面积,两点之间线段最短等知识,关键是利用线段的垂直平分线的性质定理作辅助线MA,把MC+MD的最小值问题转化为两点间线段最短来解决.【专题训练】一、填空题1.(2022·江苏昆山·八年级期末)如图,∠ABC=30°,AB=6,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,设点P的运动时间为t秒,当△ABP是以AB为底的等腰三角形时,t的值为______秒.【答案】【解析】【分析】过点P作PD⊥AB于点D,根据等腰三角形有性质得到BD=3,再根据30度角的直角三角形的性质结合勾股定理即可求解.【详解】解:过点P作PD⊥AB于点D,∵△ABP是以AB为底的等腰三角形,即BP=PA,∴BD=DA=12AB=3,∵∠ABC=30°,∴BP=2PD,即12BP=PD,∵BP2-PD2=BD2,∴BP2-14BP2=32,解得:BP=∵点P的运动速度是每秒1个单位长度,∴t的值为故答案为:【点睛】本题考查了等腰三角形的性质,含30度角的直角三角形的性质,勾股定理等知识点,解答本题的关键是明确题意,找出所求问题需要的条件.2.(2021·浙江·诸暨市暨阳初级中学八年级期中)如图∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=6,动点C从点A出发,以每秒1个单位沿射线AN运动,当运动时间t是_______秒时,△ABC是直角三角形.【答案】3或12【解析】【分析】分∠ACB=90°和∠ABC=90°两种情况,根据含30°角的直角三角形的性质求出AC,再求出答案即可.【详解】解:如图:当△ABC是以∠ACB=90°的直角三角形时,∵∠MAN=60°,∴∠ABC=30°,∴AC=13 2AB=,∴运动时间t=3311AC==秒,当△ABC是以∠ABC=90°的直角三角形时,∵∠MAN=60°,∴∠ACB=30°,∴AC=212AB=,∴运动时间t=121211AC==秒,当运动时间t是3或12秒时,△ABC是直角三角形.故答案为:3或12【点睛】本题考查了三角形的内角和定理和含30°角的直角三角形的性质,能熟记含30°角的直角三角形的性质是解此题的关键.3.(2022·新疆·乌鲁木齐市第四中学八年级期末)如图,在边长为6,面积为ABC中,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是_______【答案】【解析】【分析】由等边三角形的对称性得到MC=BM,再利用垂线段最段解题.【详解】解:过点C 作CN AB ⊥于点N ,BD Q 平分∠BAC ,△ABC 为等边三角形,BM MC∴=∴BM +MN MC MN =+,当CN AB ⊥时,=MC MN CN +最小等边△ABC 面积为6,CN ∴故答案为:【点睛】本题考查轴对称—最短路径问题、等边三角形的性质等知识,是重要考点,掌握相关知识是解题关键.4.(2021·福建省罗源第二中学八年级期中)如图,在等腰△ABC 中,AB =AC ,∠BAC =120°,BC =30cm ,一动点P 从B 向C 以每秒2cm 的速度移动,当P 点移动____________秒时,PA 与△ABC 的腰垂直.【答案】5或10【解析】【分析】根据等腰三角形性质求出∠B =∠C =30°,分PA ⊥AC 和PA ⊥AB 两种情况分类讨论,得到BP =10cm 或BP =20cm ,即可求出点P 移动的时间.【详解】解:∵AB =AC ,∠BAC =120°,∴∠B =∠C =30°.如图①,当PA ⊥AC 时,∵∠C =30°.∴PC =2AP ,∠APC =60°,∴∠B =∠BAP =30°,∴AP =BP ,∴PC =2BP ,∴BP =13BC =13×30=10cm ,∴P 点移动了10÷2=5(秒);如图②当PA⊥AB时,∵∠B=30°.∴PB=2BP,∠APB=60°,∴∠C=∠CAP=30°,∴AP=CP,∴BP=2CP,∴BP=23BC=23×30=20cm,∴P点移动了20÷2=10(秒).故答案为:5或10【点睛】本题考查了等腰三角形的性质与判定,直角三角形性质等知识,熟知相关定理,根据条件分类讨论是解题关键5.(2022·福建省泉州实验中学八年级期末)如图,在等腰△ABC中,∠BAC=30°,AB=AC,BC=4,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,△PQR周长的最小值是______.【答案】423【解析】【分析】过BC的中点P作AB,AC的对称点M,N,连接MN交AB与Q,交AC于R,则此时△PQR周长最小,求出MQ,RQ,RN即可解决问题.【详解】过点P作AB,AC的对称点M,N,连接MN交AB于Q,交AC于R,设AP交MN于点D,则PQ MQ =,PR RN =,∴PQR 周长为PQ QR PR MQ QR EN MN ++=++≥,当,,,M Q R N 四点共线时,即当点P 是BC 的中点时,PQR 的周长最小,如图∵30BAC ∠=︒,∴75B C ∠=∠=︒,150MPN ∠=︒,∴15M N ∠=∠=︒,∴75MQB PQB B ∠=∠=∠=︒,∴MN BC ∥,2PQ PB ==,同理2PR PC ==,∵⊥AP BC ,∴AP MN ⊥.DP MN∴⊥PQ PR =DQ DR∴=∵180757530PQR ∠=︒-︒-︒=︒,∴Rt PDQ 中,112QD PQ ==∴==2QR DQ =⨯=,∴PQR 周长的最小值是22PQ QR PR ++=+=4+.故答案为:4+【点睛】本题是三角形综合题,考查了轴对称的性质,等边三角形的性质,等腰三角形的性质,含30度角的直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.6.(2022·辽宁铁西·八年级期末)同学们,我们在今后的学习中会学到这个定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图,在Rt △ABC 中,∠ACB =90°,若∠ABC =30°,则12AC AB =.问题:在Rt △ABC ,∠ACB =90°,∠ABC =30°,AC D 是边BC 的中点,点E 是斜边AB 上的动点,连接DE ,把△BDE 沿直线DE 折叠,点B 的对应点为点F .当直线DF ⊥AB 时,AE 的长为_____.【答案】2或2【解析】【分析】如图1所示,设DF 与AB 交点为G ,先求出AB ==3BC ,由D 是BC 的中点,可以得到1322BD BC ==,由折叠的性质可知∠F =∠B =30°,BE =EF ,即可得到1324DG BD ==,1122EG EF BE ==,BG ==,由此即可求出AE 的长;如图2所示,同理可得1324DG BD ==,4BG ==,1122EG EF BE ==,则32BE BG GE BG =+==,AE AB BE =-=【详解】解:如图1所示,设DF 与AB 交点为G ,∵∠ABC =30°,∠ACB =90°,∴2AB AC ==∴BC =,∵D 是BC 的中点,∴1322BD BC ==,由折叠的性质可知∠F =∠B =30°,BE =EF ,∵DF ⊥AB ,∴∠DGB =∠FGB =90°,∴1324DG BD ==,1122EG EF BE ==,∴4BG ==,∴2332BE BG ==,∴AE AB BE =-=如图2所示,延长FD 与AB 交于点G ,同理可求出1324DG BD ==,4BG ==,1122EG EF BE ==,∴22BE BG GE BG =+==,∴2AE AB BE =-=,故答案为:2【点睛】本题主要考查了含30度角的直角三角形的性质,勾股定理,旋转的性质,熟练掌握含30度角的直角三角形的性质是解题的关键.7.(2021·全国·八年级专题练习)如图,60BOC ∠=︒,点A 是BO 延长线上的一点,10cm OA =,动点P 从点A 出发沿AB 以3cm/s 的速度移动,动点Q 从点O 出发沿OC 以1cm/s 的速度移动,如果点P Q ,同时出发,用(s)t 表示移动的时间,当t =_________s 时,POQ △是等腰三角形;当t =_________s 时,POQ △是直角三角形.【答案】52或54或10【解析】【分析】根据POQ ∆是等腰三角形,分两种情况进行讨论:点P 在AO 上,或点P 在BO 上;根据POQ ∆是直角三角形,分两种情况进行讨论:PQ AB ⊥,或PQ OC ⊥,据此进行计算即可.【详解】解:如图,当PO QO =时,POQ ∆是等腰三角形,103PO AO AP t =-=-,OQ t =,∴当PO QO =时,103t t -=,解得52t =;如图,当PO QO =时,POQ ∆是等腰三角形,310PO AP AO t =-=-,OQ t =,∴当PO QO =时,310t t -=,解得5t =;如图,当PQ AB ⊥时,POQ ∆是直角三角形,且2QO OP =,310PO AP AO t =-=-,OQ t =,∴当2QO OP =时,2(310)t t =⨯-,解得4t =;如图,当PQ OC ⊥时,POQ ∆是直角三角形,且2QO OP =,310PO AP AO t =-=-,OQ t =,∴当2QO OP =时,2310t t =-,解得:t =10.故答案为:52或5;4或10.【点睛】本题主要考查了等腰三角形的性质以及直角三角形的性质,解决问题的关键是进行分类讨论,分类时注意不能遗漏,也不能重复.二、解答题8.(2021·浙江余杭·八年级期中)如图,已知在ABC 中,90B ∠=︒,10AC =,6BC =,若动点P 从点B 开始,按B A C B →→→的路径运动,且速度为每秒2个单位长度,设出发的时间为t 秒.(1)出发2秒后,求CP 的长.(2)出发几秒钟后,CP 恰好平分ABC 的周长.(3)当t 为何值时,BCP 为等腰三角形?【答案】(1)PC 52(2)出发3秒钟后,CP 恰好平分△ABC 的周长(3)t =3或5.4或6或6.5时,△BCP 为等腰三角形【解析】【分析】(1)勾股定理求得AB 的长,进而根据速度求得出发2秒后BP 的长,Rt BCP △中勾股定理求解即可;(2)由于CP 恰好平分ABC 的周长,则P 点不可能位于线段BC 和AC 上,即对P 点在线段AB 上进行探究,根据题意列出一元一次方程,解方程求解即可;(3)①当P 在AB 上时,若BP =BC 时,②当P 在AC 上时,若BP =BC 时,③当P 在AC 上时,若CB =CP 时,④当P 在AB 上时,若PC =PB 时,根据题意列出一元一次方程解方程求解即可(1)由∠B =90°,AC =10,BC =6,∴AB =8,∵P 从点B 开始,按B →A →C →B ,且速度为2,∴出发2秒后,则BP =4,AP =6,∵∠B =90°,∴在Rt BCP △中,由勾股定理得PC 22226452BP BC +=+=;(2)P 点不可能位于线段BC 和AC 上,即对P 点在线段AB 上进行探究,根据题意可得,6+2t =10+8-2t ;解得t =3∴出发3秒钟后,CP 恰好平分△ABC 的周长(3)①当P 在AB 上时,若BP =BC 时,得到2t =6;则t =3,②当P 在AC 上时,若BP =BC 时,过点B 作BD AC ⊥,则68 4.810AB BC BD AB ⨯⨯===在Rt BDP △中,22226 4.8 3.6PD PD BD =-=-=在Rt ADB 中,22228 4.8 6.4AD AB BD =-=-=8 6.4 3.610.8BA AP BA AD PD ∴+=+-=+-=即210.8t =解得 5.4t =③当P 在AC 上时,若CB =CP 时,810612BA PA BA AC PC +=+-=+-=即212t =解得6t =④当P 在AC 上时,若PC =PB 时,15PA AB ==8513BA AP ∴+=+=得到2t=6;则t=6.5.综上可得t=3或5.4或6或6.5时,△BCP为等腰三角形.【点睛】本题考查了勾股定理,一元一次方程的应用,等腰三角形的性质与判定,分类讨论是解题的关键.9.(2022·吉林·八年级期末)如图,△ABC是等腰直角三角形,∠ACB=90°,AB=6.动点P从点A出发,以每秒2个单位长度的速度在射线AB上运动.点P出发后,连接CP,以CP为直角边向右作等腰直角三角形CDP,使∠DCP=90°,连接PD,BD.设点P的运动时间为t秒.(1)△ABC的AB边上高为;(2)求BP的长(用含t的式子表示);(3)就图中情形求证:△ACP≌△BCD;(4)当BP:BD=1:2时,直接写出t的值.【答案】(1)3(2)当0<t≤3时,PB=6-2t;当t>3时,PB=2t-6;(3)见解析(4)t的值为2或6.【解析】【分析】(1)根据等腰直角三角形的性质解答即可;(2)根据两种情况,利用线段之间关系得出代数式即可;(3)根据SAS证明△ACP与△CBD全等即可;(4)利用全等三角形的性质解得即可.(1)解:∵△ABC是等腰直角三角形,∠ACB=90°,AB=6,∴△ABC的AB边上高=12AB=3,故答案为:3;(2)解:∵AB=6,动点P从点A出发,以每秒2个单位长度的速度在射线AB上运动,∴点P在线段AB上运动的时间为62=3(秒),当0<t≤3时,PB=6-2t,当t>3时,PB=2t-6;(3)证明:∵△ABC是等腰直角三角形,∠ACB=90°,∴AC=BC,∵∠PCD=90°,CP=CD,∴∠ACP+∠PCB=90°,∠PCB+∠BCD=90°,∴∠ACP=∠BCD,在△ACP与△CBD中,AC BC ACP BCD CP CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACP ≌△CBD (SAS );(4)解:∵△ACP ≌△CBD ,∴AP =BD ,当BP :BD =1:2,即BD =2BP 时,当0<t ≤3时,2t =2(6-2t ),解得:t =2;当BP :BD =1:2,即BD =2BP 时,当t >3时,2t =2(2t -6),解得:t =6,综上所述,t 的值为2或6.【点睛】本题是三角形的综合题,关键是根据等腰直角三角形的性质和全等三角形的判定和性质解答.10.(2022·福建·厦门一中八年级期末)在锐角△ABC 中,∠B =45°,∠C =60°,AD ⊥BC 于点D.(1)如图1,过点B 作BG ⊥AC 于点G ,求证:AC =BF ;(2)动点P 从点D 出发,沿射线DB 运动,连接AP ,过点A 作AQ ⊥AP ,且满足AP AQ =.①如图2,当点P 在线线段BD 上时,连接PQ 分别交AD 、AC 于点M 、N .请问是否存在某一时刻使得△APM 和△AQN 成轴对称,若有,求此刻∠APD 的大小;若没有,请说明理由.②如图3,连接BQ ,交直线AD 与点F ,当点P 在线段BD 上时,试猜想BP 和DF 的数量关系并证明;当点P 在DB 的延长线上时,若27AD FD =,请直接写出PB BD 的值.【答案】(1)证明过程见解析.(2)①存在某一时刻使得△APM 和△AQN 成轴对称,∠APD =30°,理由见解析.②BP =2DF ,47PB BD =【解析】【分析】(1)根据已知条件,证明△BDF 和△ADC 全等,即可得出AC =BF .(2)①因为∠C =60°在Rt △ABC 中∠CAD =30°,∠PAQ =90°,由对称的性质可知∠PAD =∠QAC =30°,所以可以得出∠APD =60°;②过Q 作QE ⊥AD ,交AD 与点E ,可证△APD ≌△QAE ,得出AE =PD ,再证△APD ≌△QAE ,得出EF =DF ,再通过等量代换即可.(1)证明:∵AD ⊥BC∴∠ADB =∠ADC =90°又∵∠B =45°∴△ABD 是等腰直角三角形∴AD =BD∵BG ⊥AC∴∠BGC =90°又∵∠C =60°∴∠DAC =90°-∠C =90°-60°=30°∠FBD =90°-∠C =90°-60°=30°∴∠DAC =∠FBD在△BDF 和△ADC 中,FBD CDA BDF ADC BD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC ∴AC =BF(2)①存在某一时刻使得△APM 和△AQN 成轴对称∵AQ ⊥AP∴∠QAP =90°由(1)的证明知∠DAC =30°,根据对称的性质,得∠PAD =∠QAC =2QAP CAD ∠-∠=90︒︒-302=30°∵∠ADP =90°∴∠APD =90°-∠PAD =90°-30°=60°②BP =2DF理由如下:如图4所示,过Q 作QE ⊥AD ,交AD 与点E ,那么∠AEQ =∠FEQ =90°∴∠AQE +∠QAE =90°又∵∠PAD +∠QAE =90°∴∠AQE =∠PAD在△APD 和△QAE 中,AQE PAD AEQ PDA AQ AP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△APD ≌△QAE ∴AE =PD ;AD =QE∴DE =BP又∵AD =BD∴BD =QE在△QEF 和△BDF 中,QEF BDF EFQ DFB EQ DB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△QEF ≌△BDF∴EF =DF∴BP =2DF当点P 在DB 的延长线上时,如下图所示,由上述证明过程可知PB =2DF ,BD =AD又已知27AD FD∴DF =27AD∴PB =2×27BD =47BD ∴PB BD =47【点睛】本题考查了三角形全等的判定与性质,解题的关键是通过适当的作辅助线找等量关系从而得出三角形全等,再由全等的性质找出线段的关系,本题是一道压轴题,比较难.11.(2022·北京顺义·八年级期末)我们定义:在等腰三角形中,腰与底的比值叫做等腰三角形的正度.如图1,在△ABC 中,AB =AC ,AB BC的值为△ABC 的正度.已知:在△ABC 中,AB =AC ,若D 是△ABC 边上的动点(D 与A ,B ,C 不重合).(1)若∠A =90°,则△ABC 的正度为;(2)在图1,当点D 在腰AB 上(D 与A 、B 不重合)时,请用尺规作出等腰△ACD ,保留作图痕迹;若△ACD的正度是2,求∠A 的度数.(3)若∠A 是钝角,如图2,△ABC 的正度为35,△ABC 的周长为22,是否存在点D ,使△ACD 具有正度?若存在,求出△ACD 的正度;若不存在,说明理由.【答案】(1)22(2)图见解析,∠A =45°(335.【解析】【分析】(1)当∠A=90°,△ABC是等腰直角三角形,故可求解;(2)根据△ACD的正度是22,可得△ACD是以AC为底的等腰直角三角形,故可作图;(3)由△ABC的正度为35,周长为22,求出△ABC的三条边的长,然后分两种情况作图讨论即可求解.【详解】(1)∵∠A=90°,则△ABC是等腰直角三角形∴AB=AC∵AB2+AC2=BC2∴BC∴△ABC2故答案为:2 2;(2)∵△ACD1)可得△ACD是以AC为底的等腰直角三角形故作CD⊥AB于D点,如图,△ACD即为所求;∵△ACD是以AC为底的等腰直角三角形∴∠A=45°;(3)存在∵△ABC的正度为3 5,∴ABBC=35,设:AB=3x,BC=5x,则AC=3x,∵△ABC的周长为22,∴AB+BC+AC=22,即:3x+5x+3x=22,∴x=2,∴AB=3x=6,BC=5x=10,AC=3x=6,分两种情况:①当AC=CD=6时,如图过点A 作AE ⊥BC 于点E ,∵AB =AC ,∴BE =CE =12BC =5,∵CD =6,∴DE =CD −CE =1,在Rt △ACE 中,由勾股定理得:AE =在Rt △AED 中,由勾股定理得:AD =∴△ACD 的正度=AC AD =②当AD =CD 时,如图由①可知:BE =5,AE ,∵AD =CD ,∴DE =CE −CD =5−AD ,在Rt △ADE 中,由勾股定理得:AD 2−DE 2=AE 2,即:AD 2−(5−AD )2=11,解得:AD =185,∴△ACD 的正度=185365AD AC ==.综上所述存在两个点D ,使△ABD 具有正度.△ABD 35.【点睛】此题考查了等腰三角形的性质,解题的关键是理解正度的含义、熟知勾股定理与等腰三角形的性质.12.(2022·北京西城·八年级期末)在ABC 中,120BAC ∠=︒,AB AC =,AD 为ABC 的中线,点E 是射线AD 上一动点,连接CE ,作60CEM ∠=︒,射线EM 与射线BA 交于点F .(1)如图1,当点E 与点D 重合时,求证:2AB AF =;(2)如图2,当点E 在线段AD 上,且与点A ,D 不重合时,①依题意,补全图形;②用等式表示线段AB ,AF ,AE 之间的数量关系,并证明.(3)当点E 在线段AD 的延长线上,且ED AD ≠时,直接写出用等式表示的线段AB ,AF ,AE 之间的数量关系.【答案】(1)见解析;(2)AB AF AE =+,证明见解析;(3)当AD ED >时,AB AF AE =+,当AD ED <时,AB AE AF=-【解析】【分析】(1)根据等腰三角形三线合一的性质得60BAD CAD ∠=∠=︒,90ADC ∠=︒,从而可得在Rt ADB 中,30B ∠=︒,进而即可求解;(2)画出图形,在线段AB 上取点G ,使EG EA =,再证明()BGE FAE ASA ≅,进而即可得到结论;(3)分两种情况:当AD ED >时,当AD ED <时,分别画出图形,证明()BHE FAE ASA ≅或()NEF AEC ASA ≅,进而即可得到结论.【详解】(1)∵AB AC =,∴ABC 是等腰三角形,∵120BAC ∠=︒,∴30B C ∠=∠=︒,18012060FAC ∠=︒-︒=︒,∵AD 为ABC 的中线,∴60BAD CAD ∠=∠=︒,90ADC ∠=︒,∴6060120DAF CAD FAC ∠=∠+∠=︒+︒=︒,∵60CEM ∠=︒,∴906030ADF ∠=︒-︒=︒,∴180(12030)30AFD ∠=︒-︒+︒=︒,∴AD AF =,在Rt ADB 中,30B ∠=︒,∴22AB AD AF ==;(2)AB AF AE =+,证明如下:如图2,在线段AB 上取点G ,使EG EA =,∵60BAC ∠=︒,∴AEG △是等边三角形,∴60AEG ∠=︒,120BGE FAE ∠=∠=︒,∵ABC 是等腰三角形,AD 为ABC 的中线,∴EB EC =,BED CED ∠=∠,∴AEB AEC ∠=∠,即AEG GEB CEF AEF ∠+∠=∠+∠,∵60CEF AEG ∠=∠=︒,∴GEB AEF ∠=∠,在BGE △与FAE 中,GEB AEF EG EA BGE FAE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BGE FAE ASA ≅,∴GB AF =,∴AB GB AG AF AE =+=+;(3)当AD ED >时,如图3所示:与(2)同理:在线段AB 上取点H ,使EH EA =,∵60BAD ∠=︒,∴AEH △是等边三角形,∴120BHE FAE ∠=∠=︒,60AEH ∠=︒,∵ABC 是等腰三角形,AD 为ABC 的中线,∴BED CED ∠=∠,∵60CEF AEH ∠=∠=︒,∴HEB AEF ∠=∠,∴()BHE FAE ASA ≅,∴HB AF =,∴AB HB AH AF AE =+=+,当AD ED <时,如图4所示:在线段AB 的延长线上取点N ,使EN EA =,∵60BAD ∠=︒,∴AEN △是等边三角形,∴60AEN FNE ∠=∠=︒,∵60CEF AEN ∠=∠=︒∴NEF AEC ∠=∠,在NEF 与AEC △中,60FNE CAE EN EA NEF AEC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,∴()NEF AEC ASA ≅,∴NF AC AB ==,=,∴BN AF=-=-,∴AB AN BN AE AF∴AB AE AF=-.【点睛】本题考查全等三角形的判定与性质、等腰三角形的性质以及等边三角形的判定与性质,根据题意做出辅助线找全等三角形是解题的关键.。
专题19 等腰三角形(归纳与讲解)(解析版)

专题19 等腰三角形【专题目录】技巧1:等腰三角形中四种常用作辅助线的方法技巧2:巧用特殊角构造含30°角的直角三角形技巧3:分类讨论思想在等腰三角形中的应用【题型】一、等腰三角形的定义【题型】二、根据等边对等角求角度【题型】三、根据三线合一求解【题型】四、根据等角对等边证明等腰三角形【题型】五、根据等角对等边求边长【题型】六、等腰三角形性质与判定的综合【题型】七、等边三角形的性质【题型】八、含30°角的直角三角形【考纲要求】1.了解等腰三角形的有关概念,掌握其性质及判定.2.了解等边三角形的有关概念,掌握其性质及判定.3.掌握线段中垂线的性质及判定.【考点总结】一、等腰三角形【考点总结】二、等边三角形【考点总结】三、直角三角形【技巧归纳】技巧1:等腰三角形中四种常用作辅助线的方法【类型】一、作“三线”中的“一线”1.如图,在△ABC中,AB=AC,D是BC的中点,过点A作EF∥BC,且AE=AF.求证:DE=DF.【类型】二、作平行线法2.如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,PQ与直线BC相交于点D.(1)如图①,当点P为AB的中点时,求证:PD=QD.(2)如图②,过点P作直线BC的垂线,垂足为E,当P,Q在移动的过程中,线段BE,ED,CD中是否存在长度保持不变的线段?请说明理由.【类型】三、截长补短法3.如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.求证:BD+DC=AB.【类型】四、加倍折半法4.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,求∠C的度数.5.如图,CE,CB分别是△ABC,△ADC的中线,且AB=AC.求证:CD=2CE.参考答案1.证明:如图,连接AD.∵AB=AC,BD=CD,∴AD⊥BC.∵EF∥BC,∴AD⊥EF.∵AE=AF,∴AD垂直平分EF.∴DE=DF.2.(1)证明:如图①,过点P作PF∥AC交BC于F.①点P和点Q同时出发,且速度相同,①BP=CQ.①PF①AQ,①①PFB=①ACB,①DPF=①DQC.又①AB=AC,①①B=①ACB,①①B=①PFB,①BP=FP,①FP=CQ.在①PFD和①QCD中,①DPF=①DQC,①PDF=①QDC,FP=CQ,①①PFD①①QCD(AAS),①PD=QD.(2)解:线段ED的长度保持不变.理由如下:如图②,过点P作PF∥AC交BC于F.由(1)知PB=PF.∵PE⊥BF,∴BE=E F.由(1)知△PFD≌△QCD,∴FD=CD,∴ED=EF+FD=BE+CD=12BC,∴线段ED的长度保持不变.3.证明:如图,延长BD至E,使BE=AB,连接CE,AE.∵∠A BE=60°,BE=AB,∴△ABE为等边三角形.∴∠AEB=60°,AB=AE.又∵∠ACD=60°,∴∠ACD=∠AEB.∵AB=AC,AB=AE,∴AC=AE.∴∠ACE=∠AEC.∴∠DCE=∠DEC.∴DC=DE.∴AB=BE=BD+DE=BD+DC,即BD+DC=AB.4.解:在DC上截取DE=BD,连接AE,∵AD⊥BC,BD=DE,∴AD是线段BE的垂直平分线,∴AB=AE,∴∠B=∠AEB.∵AB+BD=DC,DE=BD,∴AB+DE=CD.而CD=DE+EC,∴AB=EC,∴AE=EC.∴∠EAC=∠C,可设∠EAC=∠C=x,∵∠AEB 为△AEC 的外角,∴∠AEB =∠EAC +∠C =2x ,∴∠B =2x ,∴∠BAE =180°-2x -2x =180°-4x.∵∠BAC =120°,∴∠BAE +∠EAC =120°,即180°-4x +x =120°,解得x =20°,则∠C =20°.5.证明:如图,延长CE 到点F ,使EF =CE ,连接FB ,则CF =2CE.∵CE 是△ABC 的中线,∴AE =BE.在△BEF 和△AEC 中,⎩⎨⎧BE =AE ,∠BEF =∠AEC ,EF =EC ,∴△BEF ≌△AEC(SAS). ∴∠EBF =∠A ,BF =AC.又∵AB =AC ,∴∠ABC =∠ACB.∴∠CBD =∠A +∠ACB =∠EBF +∠ABC =∠CBF.∵CB 是△ADC 的中线,∴AB =BD.又∵AB =AC ,AC =BF ,∴BF =BD.在△CBF 与△CBD 中,⎩⎨⎧CB =CB ,∠CBF =∠CBD ,BF =BD ,∴△CBF ≌△CBD(SAS).∴CF =CD.∴CD =2CE.技巧2:巧用特殊角构造含30°角的直角三角形【类型】一、直接运用含30°角的直角三角形的性质1.如图,在△ABC 中,∠C =90°,∠B =30°,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为E ,DE =1,则BC =( )A . 3B .2C .3D .3+22.如图,已知△ABC 中,AB =AC ,∠C =30°,AB ⊥AD ,AD =4 cm .求BC 的长.【类型】二、连线段构造含30°角的直角三角形3.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE =8,求CE的长.4.如图,已知在△ABC中,AB=AC,∠A=120°,DE垂直平分AB于点D,交BC 于点E.求证:CE=2BE.【类型】三、延长两边构造含30°角的直角三角形5.如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.【类型】四、作垂线构造含30°角的直角三角形6.如图,四边形ABCD中,∠B=90°,DC∥AB,AC平分∠DAB,∠DAB=30°.求证:AD=2BC.参考答案1.C2.解:∵AB=AC,∠C=30°,∴∠B=∠C=30°.又∵AB⊥AD,∴∠ADB=60°.又∵∠ADB=∠C+∠CAD,∴∠CAD=30°=∠C.∴CD=AD=4 cm.∵AB⊥AD,∠B=30°,∴BD=2AD=8 cm.∴BC=BD+CD=12 cm.3.解:连接AD,∵AB=AC,D为BC的中点,∴AD⊥BC,∠BAD=∠CAD=12∠BAC=12×120°=60°.在Rt△ADE中,∠EAD=60°,∴∠ADE=30°,∴AD=2AE=16.在△ABC中,AB =AC,∠BAC=120°.∴∠B=∠C=30°,∴AC=2AD=2×16=32.∴CE=AC-AE=32-8=24.4.证明:如图,连接AE.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∵DE垂直平分AB,∴BE=AE.∴∠BAE=∠B=30°.∴∠EAC=120°-30°=90°.又∵∠C=30°,∴CE=2AE.又∵BE=AE,∴CE=2BE.5.解:延长AD,BC交于点E.∵∠A=30°,∠B=90°,∴∠E=60°.又∵∠ADC=120°,∴∠EDC=180°-120°=60°.∴△DCE是等边三角形.设CD=CE=DE=a,则有2(1+a)=4+a,解得a=2.∴CD的长为2.6.证明:过点C作CE⊥AD交AD的延长线于E.∵DC∥AB,∠DAB=30°,∴∠CDE=30°.在Rt△CDE中,∠CDE=30°,∴CD=2CE.又∵AC平分∠DAB,∴∠DAC=∠BAC,又∵DC∥AB,∴∠BAC=∠DCA,∴∠DAC=∠DCA,∴AD=CD.又∵CE⊥AE,CB⊥AB,AC平分∠DAB,∴BC=CE,∴AD=2BC.7.证明:过点B作BE⊥AD交AD的延长线于点E,则∠DEB=90 °.∵∠BAD=30°,∴BE=12AB.∵AD⊥AC,∴∠DAC=90°,∴∠DEB=∠DAC.又∵BD=CD,∠BDE=∠CDA,∴△BED≌△CAD,∴BE=AC,∴AC=12AB.点拨:由结论AC=12AB和条件∠BAD=30°,就想到能否找到或构造直角三角形,而显然图中没有含30°角的直角三角形,所以过点B作BE⊥AD交AD的延长线于点E,这样就得到了直角三角形ABE,这是解决本题的关键.技巧3:分类讨论思想在等腰三角形中的应用【类型】一、当顶角或底角不确定时,分类讨论1.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角度数为()A.40°B.100°C.40°或70°D.40°或100°2.已知等腰三角形ABC中,AD⊥BC于D,且AD=12BC,则等腰三角形ABC的底角的度数为()A.45°B.75°C.45°或75°D.65°3.若等腰三角形的一个外角为64°,则底角的度数为________.【类型】二、当底和腰不确定时,分类讨论4.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为() A.8或10B.8C.10D.6或125.等腰三角形的两边长分别为7和9,则其周长为________.6.若实数x,y满足|x-4|+(y-8)2=0,则以x,y的值为边长的等腰三角形的周长为________.【类型】三、当高的位置关系不确定时,分类讨论7.等腰三角形一腰上的高与另一边的夹角为25°,求这个三角形的各个内角的度数.【类型】四、由腰的垂直平分线引起的分类讨论8.在三角形ABC中,AB=AC,AB边上的垂直平分线与AC所在的直线相交所得的锐角为40°,求底角∠B的度数.【类型】五、由腰上的中线引起的分类讨论9.等腰三角形ABC的底边BC长为5 cm,一腰上的中线BD把其分为周长差为3 cm的两部分.求腰长.【类型】六、点的位置不确定引起的分类讨论10.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有()A.7个B.6个C.5个D.4个11.如图,在△ABC中,BC>AB>AC,∠ACB=40°,如果D,E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数.参考答案1.D 2.C 3.32° 4.C 5.23或25 6.207.解:设AB=AC,BD⊥AC;(1)高与底边的夹角为25°时,高一定在△ABC的内部,如图①,∵∠DBC=25°,∴∠C=90°-∠DBC=90°-25°=65°,∴∠ABC=∠C=65°,∠A=180°-2×65°=50°.(2)当高与另一腰的夹角为25°时,如图②,高在△ABC的内部时,∵∠ABD=25°,∴∠A=90°-∠ABD=65°,∴∠C=∠ABC=(180°-∠A)÷2=57.5°;如图③,高在△ABC的外部时,∵∠ABD=25°,∴∠BAD=90°-∠ABD=90°-25°=65°,∴∠BAC=180°-65°=115°,∴∠ABC=∠C=(180°-115°)÷2=32.5°,故三角形各个内角的度数为:65°,65°,50°或65°,57.5°,57.5°或115°,32.5°,32.5°.点拨:由于题目中的“另一边”没有指明是“腰”还是“底边”,因此必须进行分类讨论,另外,还要结合图形,分高在三角形内还是在三角形外.8.解:此题分两种情况:(1)如图①,AB边的垂直平分线与AC边交于点D,∠ADE=40°,则∠A=50°,∵AB=AC,∴∠B=(180°-50°)÷2=65°.(2)如图②,AB边的垂直平分线与CA的延长线交于点D,∠ADE=40°,则∠DAE=50°,∴∠BAC =130°.∵AB=AC,∴∠B=(180°-130°)÷2=25°.故∠B的大小为65°或25°.9.分析:由于题目中没有指明是“(AB+AD)-(BC+CD)”为3 cm,还是“(BC+CD)-(AB+AD)”为3 cm,因此必须分两种情况讨论.解:∵BD为AC边上的中线,∴AD=CD,(1)当(AB+AD)-(BC+CD)=3 cm时,有AB-BC =3 cm,∵BC=5 cm,∴AB=5+3=8(cm);(2)当(BC+CD)-(AB+AD)=3 cm时,有BC-AB=3 cm,∵BC=5 cm,∴AB=5-3=2(cm),但是当AB=2 cm时,三边长分别为2 cm,2 cm,5 cm.而2+2<5,不能构成三角形,舍去.故腰长为8 cm.[来源:学*科*网Z*X*X*K]10.B11.解:(1)当点D、E在点A的同侧,且都在BA的延长线上时,如图①,∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,∵∠DCE=∠BEC-∠ADC,∴∠DCE=(180°-∠ABC)÷2-∠BAC÷2=(180°-∠ABC-∠BAC)÷2=∠ACB÷2=40°÷2=20°.(2)当点D、E在点A的同侧,且点D在D′的位置,E在E′的位置时,如图②,与(1)类似地也可以求得∠D′CE′=∠ACB÷2=20°.(3)当点D、E在点A的两侧,且E点在E′的位置时,如图③,∵BE′=BC,∴∠BE′C=(180°-∠CBE′)÷2=∠ABC÷2,∵AD=AC,∴∠ADC =(180°-∠DAC)÷2=∠BAC÷2, 又∵∠DCE′=180°-(∠BE′C +∠ADC),∴∠DCE′=180°-(∠ABC +∠BAC)÷2=180°-(180°-∠ACB)÷2=90°+∠ACB÷2=90°+40°÷2=110°.(4)当点D 、E 在点A 的两侧,且点D 在D′的位置时,如图④, ∵AD′=AC ,∴∠AD′C =(180°-∠BAC)÷2, ∵BE =BC ,∴∠BEC =(180°-∠ABC)÷2,∴∠D′CE =180°-(∠D′EC +∠ED′C)=180°-(∠BEC +∠AD′C) =180°-[(180°-∠ABC)÷2+(180°-∠BAC)÷2] =(∠BAC +∠ABC)÷2=(180°-∠ACB)÷2=(180°-40°)÷2=70°.综上所述,∠DCE 的度数为20°或110°或70°.【题型讲解】【题型】一、等腰三角形的定义例1、已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( ) A .9 B .17或22C .17D .22【答案】D【提示】分类讨论腰为4和腰为9,再应用三角形的三边关系进行取舍即可. 【详解】解:分两种情况:当腰为4时,449+<,所以不能构成三角形;当腰为9时,994,994+>-<,所以能构成三角形,周长是:99422++=. 故选:D .【题型】二、根据等边对等角求角度例2、如图,在①ABC 中,①A =40°,AB =AC ,点D 在AC 边上,以CB ,CD 为边作□BCDE ,则①E 的度数为( )A .40°B .50°C .60°D .70°【答案】D【提示】先根据等腰三角形的性质和三角形的内角和定理求出①C的度数,再根据平行四边形的性质解答即可.【详解】解:①①A=40°,AB=AC,①①ABC=①C=70°,①四边形ABCD是平行四边形,①①E=①C=70°.故选:D.【题型】三、根据三线合一求解例3、如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=()A.2B.3C.4D.5【答案】B【提示】根据尺规作图的方法步骤判断即可.【详解】由作图痕迹可知AD为①BAC的角平分线,而AB=AC,由等腰三角形的三线合一知D为BC重点,BD=3,故选B【题型】四、根据等角对等边证明等腰三角形例4、下列能断定①ABC为等腰三角形的是()A.①A=40°,①B=50°B.①A=2①B=70°C.①A=40°,①B=70°D.AB=3,BC=6,周长为14【答案】C【提示】根据三角形内角和计算角的度数,判断三角形中是否有相等的角;根据三角形的周长计算是否有相等的边即可判断.【详解】A.①C=180°−40°−50°=90°,没有相等的角,则不是等腰三角形,本选项错误;B、①①A=2①B=70°,①①B=35°,①①C=75°,没有相等的角,则不是等腰三角形,本选项错误;C 、①C=180°−40°−70°=70°,有相等的角,则是等腰三角形,本选项正确;D 、①AB=3,BC=6,周长为14,①AC=14−6−3=5,没有相等的边,则不是等腰三角形,本选项错误; 故选C .【题型】五、根据等角对等边求边长例5、如图,将矩形ABCD 折叠,使点C 和点A 重合,折痕为EF ,EF 与AC 交于点.O 若5AE =,3BF =,则AO 的长为( )A B C .D .【答案】C【提示】先证明,AE AF =再求解,,AB AC 利用轴对称可得答案. 【详解】解:由对折可得:,,AFO CFO AF CF ∠=∠= 矩形ABCD ,//,90,AD BC B ∴∠=︒ ,CFO AEO ∴∠=∠ ,AFO AEO ∴∠=∠ 5,AE AF CF ∴=== 3,BF =4,AB ∴==BC=8AC ∴===由对折得:12OA OC AC === 故选C .【题型】六、等腰三角形性质与判定的综合例6、如图,三条笔直公路两两相交,交点分别为A 、B 、C ,测得30CAB ∠=︒,45ABC ∠=︒,8AC =千米,求A 、B 两点间的距离. 1.4≈ 1.7≈,结果精确到1千米).【答案】A 、B 两点间的距离约为11千米. 【提示】如图(见解析),先根据直角三角形的性质、勾股定理可求出CD 、AD 的长,再根据等腰直角三角形的判定与性质可得BD 的长,然后根据线段的和差即可得. 【详解】如图,过点C 作CD AB ⊥于点D在Rt ACD △中,30CAD ∠=︒,8AC =千米118422CD AC ∴==⨯=(千米),AD == 在Rt BCD 中,45DBC ∠=︒Rt BCD ∴是等腰直角三角形4BD CD ∴==千米44 1.7410.811AB AD BD ∴=+=≈⨯+=≈(千米)答:A 、B 两点间的距离约为11千米.【题型】七、等边三角形的性质例7、如图,面积为1的等边三角形ABC 中,,,D E F 分别是AB ,BC ,CA 的中点,则DEF ∆的面积是( )A .1B .12C .13D .14【答案】D【提示】根据题意可以判断四个小三角形是全等三角形,即可判断一个的面积是14. 【详解】①,,D E F 分别是AB ,BC ,CA 的中点,且①ABC 是等边三角形, ①①ADF①①DBE①①FEC①①DFE, ①①DEF 的面积是14. 故选D .【题型】八、含30°角的直角三角形例8、如图,在Rt ABC 中, 90,30,1,C ABC AC cm ∠=︒∠=︒=将Rt ABC 绕点A 逆时针旋转得到Rt AB C ''△,使点C '落在AB 边上,连接BB ',则BB '的长度是( )A .1cmB .2cmCD .【答案】B【提示】由旋转的性质可知,'=60∠∠=CAB BAB ,进而得出'∆BAB 为等边三角形,进而求出'==2BB AB .【详解】解:① 90,30,1,C ABC AC cm ∠=︒∠=︒= 由直角三角形中,30°角所对的直角边等于斜边的一半可知, ①=2=2AB AC cm ,又①CAB =90°-①ABC =90°-30°=60°,由旋转的性质可知:'=60∠∠=CAB BAB ,且'=AB AB , ①'∆BAB 为等边三角形, ①'==2BB AB . 故选:B .等腰三角形(达标训练)一、单选题1.如图,在①ABC 中,AB 的垂直平分线分别交AB 、BC 于点D 、E ,连接AE ,若AE =4,EC =2,则BC 的长是( )A .2B .4C .6D .8【答案】C【分析】根据线段的垂直平分线的性质得到EB =EA =4,结合图形计算,得到答案. 【详解】解:①DE 是AB 的垂直平分线,AE =4, ①EB =EA =4,①BC =EB +EC =4+2=6, 故选:C .【点睛】本题考查的是线段的垂直平分线的性质,解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等.2.如图,在ABC 中,5AC =,7BC =,9AB =,用图示尺规作图的方法在边AB 上确定一点D .则ACD 的周长为( ).A .12B .14C .16D .21【答案】B【分析】根据题意得:尺规作图的方法所作的直线是BC 的垂直平分线,可得CD BD = ,从而得到ACD 的周长为AC CD AD ++ ,即可求解.【详解】解:根据题意得:尺规作图的方法所作的直线是BC 的垂直平分线, ①CD BD = , ①9AB =,①9CD AD AD BD AB +=+== , ①5AC =,①ACD 的周长为5914AC CD AD AC AB ++=+=+= . 故选:B .【点睛】本题主要考查了尺规作图——作已知线段的垂直平分线,线段垂直平分线的性质,熟练掌握线段垂直平分线上的点到线段两端的距离相等是解题的关键. 3.下列命题,错误的是( )A .有一个锐角和斜边对应相等的两个直角三角形全等B .如果①A 和①B 是对顶角,那么①A =①BC .等腰三角形两腰上的高相等D .三角形三边垂直平分线的交点到三角形三边的距离相等 【答案】D【分析】利用全等三角形的判定、对顶角的性质、等腰三角形的性质及垂直平分线的性质分别判断后即可确定正确的选项.【详解】解:A 、有一个锐角和斜边对应相等的两个直角三角形全等,正确,不符合题意; B 、如果①A 和①B 是对顶角,那么①A =①B ,正确,不符合题意; C 、等腰三角形两腰上的高相等,正确,不符合题意;D 、三角形三边垂直平分线的交点到三角形三顶点的距离相等,故原命题错误,符合题意. 故选:D .【点睛】考查了命题与定理的知识,解题的关键是了解全等三角形的判定、对顶角的性质、等腰三角形的性质及垂直平分线的性质,属于基础性知识,比较简单.4.如图,点F ,E 在AC 上,AD CB =,D B ∠=∠.添加一个条件,不一定能证明ADE CBF ≌的是( )A .AD BC ∥B .DE FB ∥C .DE BF =D .AE CF =【答案】D【分析】根据全等三角形的判定定理判断即可. 【详解】A :①AD BC ∥, ①A C ∠=∠,①在ADE 和CBF 中, A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩, ①()ADE CBF ASA ≌,正确,故本选项错误; B :①DE FB ∥, ①AED CFB ∠=∠, ①在ADE 和CBF 中,AED CFB D BAD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①()ADE CBF AAS ≌,正确,故本选项错误; C :①在ADE 和CBF 中, DE BF D B AD CB =⎧⎪∠=∠⎨⎪=⎩, ①()ADE CBF SAS ≌,正确,故本选项错误;D :根据AD CB =,D B ∠=∠,AE CF =不能推出ADE CBF ≌,错误,故本选项正确. 故选D .【点睛】本题考查全等三角形的判定的应用,平行线的性质.熟练掌握全等三角形的判定定理是解本题的关键.5.如图,矩形ABCD 的对角线AC 的垂直平分线分别交AD 、AC 、BC 于点E 、O 、F ,若1216AB BC ==,,则EF 的长为( )A .8B .15C .16D .24【答案】B【分析】根据矩形的性质得到AO =CO ,①AOE =①COF ,根据平行线的性质得出①EAO =①FCO ,根据ASA 推出①AEO ①①CFO ,由全等得到OE =OF ,推出四边形是平行四边形,再根据EF ①AC 即可推出四边形是菱形,根据垂直平分线的性质得出AF =CF ,根据勾股定理即可得出结论. 【详解】连接AF ,CE ,①EF 是AC 的垂直平分线, ①AO =CO ,①AOE =①COF =90°, ①四边形ABCD 是矩形, ①AD ①BC , ①①EAO =①FCO , 在①AEO 和①CFO 中,EAO FCO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=⎩, ①①AEO ①①CFO (ASA ), ①OE =OF , 又①OA =OC ,①四边形AECF 是平行四边形, ①EF ①AC ,①平行四边形AECF 是菱形, ①AE =CE , 设AE =CE =x ,①EF 是AC 的垂直平分线, ①AE =CE =x ,DE =16-x ,在Rt ①CDE 中,222CD DE AE +=,()2221216x x +-=,解得252x =, ①AE =252,①20AC =, ①12AO AC ==10,①152OE =, ①EF =2OE =15, 故选:B .【点睛】本题考查了矩形的性质,菱形的判定和性质,勾股定理,全等三角形的判定和性质,证得四边形AECF 是菱形是解题的关键.二、填空题6.如图,在ABC 中,90C ∠=︒,AD 平分CAB ∠,2BD CD =,点D 到AB 的距离为5.6,则BC =___cm .【答案】16.8【分析】过D 作DE ①AB 于E ,根据角平分线性质得出CD =DE ,再求出BD 长,即可得出BC 的长. 【详解】解:如图,过D 作DE ①AB 于E ,①①C =90°, ①CD ①AC , ①AD 平分①BAC , ①CD =DE ,①D 到AB 的距离等于5.6cm , ①CD =DE =5.6cm , 又①BD =2CD , ①BD =11.2cm ,①BC =5.6+11.2=16.8cm , 故答案为:16.8.【点睛】本题主要考查了角平分线性质的应用,解题时注意:角平分线上的点到角两边的距离相等. 7.如图,在ABC 中,90ACB ∠=︒,BE CE ⊥于点E ,AD CE ⊥于点D ,请你添加一个条件__________,使BEC CDA ≌(填一个即可).【答案】AC BC =(答案不唯一)【分析】两个三角形全等已具备的条件是:90ADC CEB ∠=∠=︒,ACD CBE ∠=∠,根据三角形全等的判定方法即可确定添加的条件. 【详解】解:添加的条件是AC BC =, BE CE ⊥,AD CE ⊥,90BEC ADC ∴∠=∠=︒,90BCE CBE ∴∠+∠=︒ ,90ACB ACD ECB ∠=∠+∠=︒,ACD CBE ∴∠=∠,在BEC ∆和CDA ∆中, 90BEC ADC ACD CBEAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()BEC CDA AAS ∴∆≅∆.故答案为:AC BC =(答案不唯一).【点睛】本题考查了全等三角形的判定,掌握全等三角形的判定定理是解决问题的关键.三、解答题8.如图,E 、F 分别是矩形ABCD 对角线上的两点,且BE DF =.求证:AE CF =.【答案】见解析;【分析】根据矩形ABCD 的性质得出AB CD =,ABE CDF ∠=∠ ,再根据BE DF = ,用SAS 可直接证明出ABE CDF ≅,即可证明出AE CF = . 【详解】证明:ABCD 是矩形, ∴ AB CD = ,ABE CDF ∠=∠,在ABE △和CDF 中AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩ ∴ABE CDF ≅()SAS ,AE CF ∴= .【点睛】本题主要考查了矩形的性质,全等三角形性质和判定,熟练掌握矩形的性质和全等三角形的判定是解决问题的关键.等腰三角形(提升测评)一、单选题1.如图,点D 、E 分别为①ABC 的边AB 、AC 的中点,点F 在DE 的延长线上,CF ∥BA ,若①ADE 的面积为2,则四边形BCFD 的面积为( )A .10B .8C .6D .4【答案】B【分析】根据三角形中位线定理得到DE ∥BC ,DE =12BC ,证明ADEABC ;根据相似三角形的性质计算(相似三角形的面积比等于相似比的平方),可求得S ABC 的面积;根据三角形全等的判定和性质定理,证明ADE ≌CFE ,可得S ADE =S CFE ,从而可得S 四边形BCFD = S ABC 即可. 【详解】解:①D ,E 分别是ABC 的边AB ,AC 的中点 ①DE 是ABC 的中位线 ①AE =CE ,DE ∥BC ,DE =12BC ①ADEABC①S ADE =21()2ABCS①S ADE =2 ①S ABC =8 又①CF ∥BA ①∠A=∠FCE在ADE 和CFE 中,A FCE AE CEAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩①ADE ≌CFE (ASA ) ①S ADE =S CFE①S ADE + S 四边形BCED =S CFE +S 四边形BCED ①S 四边形BCFD = S ABC =8故选:B.【点睛】本题考查的是三角形中位线定理、相以三角形的判定和性质,全等三角形的判定与性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.2.如图,Rt①ABC中,①C=90°,BD平分①ABC交AC于点D,点E为AB的中点,若AB=12,CD =3,则①DBE的面积为()A.10B.12C.9D.6【答案】C【分析】如图:过D作DF①AB于F,然后根据角平分线的性质可得DF=CD=3,然后再根据中点的定义求得BE的长,最后根据三角形的面积公式求解即可.【详解】解:如图:过D作DF①AB于F,①①C=90°,BD平分①ABC交AC于点D,①DF=CD=3①点E为AB的中点,AB=12①BE=12AB=6①①DBE的面积为1163922BE DF=⨯⨯=.故选:C.【点睛】本题主要考查了角平分线定理、中点的定义、三角形的高等知识点,作出①DBE的高并运用角平分线定理求出成为解答本题的关键.3.如图,Rt①ABC中,①C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=5,P为AB上一动点,则PD的最小值为()A .2B .3C .4D .5【答案】D【分析】当DP ①AB 时,根据垂线段最短可知,此时DP 的值最小.再根据角平分线的性质定理可得DP =CD 解决问题;【详解】解:当DP ①AB 时,根据垂线段最短可知,此时DP 的值最小. 由作图可知:AE 平分①BAC , ①①C =90°, ①DC ①AC , ①DP ①AB , ①DP =CD =5, ①PD 的最小值为5, 故选:D .【点睛】本题考查角平分线的性质定理,垂线段最短,基本作图等知识,解题的关键是学会利用垂线段最短解决最短问题.4.如图,在正方形ABCD 中,E ,F 分别为BC ,CD 的中点,点G 在CD 边上,GAE BAE ∠=∠,AG交BF 于点H ,连接,,EH EG CH .下列结论:①AHE BCF △≌△;①GE BF ∥;①sin ABF ∠=①14GCH ABH S S =△△,其中正确的结论有( )A .4个B .3个C .2个D .1个.【答案】B【分析】先证明①AHE ①①BCF (AAS ),即可判断①,由三角形的中位线定理可证GE BF ,即可判断①,由勾股定理可求BF 的长,即可求sin①ABF =sin①BFC ,即可判断①,由相似三角形的性质可求FH ,CH ,AO 的长,即可求出16GCHABHSS,即可判断①.【详解】解:如图,设BF 与AE 的交点为O ,设AB =4a ,①四边形ABCD 是正方形,①AB =BC =CD =AD =4a ,①ABC =①BCD =90°, ①E ,F 分别为BC ,CD 的中点, ①CF =DF =2a =CE =BE , ①①ABE ①①BCF (SAS ),①①BAE =①CBF ,BF =AE ,①AEB =①BFC , ①①ABF +①CBF =90°=①ABF +①BAE , ①①AOB =90°=①AOH , 又①①BAE =①GAE ,AO =AO , ①①AOH ①①AOB (ASA ), ①AH =AB ,①AOB =①AOH =90°, ①AE 垂直平分BH ,①BE =EH ,①ABE =①AHE =90°,①①AHE =①BCF =90°,AH =AB =BC ,①GAE =①BAE =①BCF , ①①AHE ①①BCF (AAS ),故①正确; ①AH =AB , ①①AHB =①ABH , ①AB CD , ①①ABF =①CFB ,①①CFB =①AHB =①CHF , ①FG =GH , ①HE =BE =CE ,①①CHE =①ECH ,①EHB =①EBH ,①①CHE +①ECH +①EHB +①EBH =2①CHE +2①EHB =180°, ①①BHC =①CHE +①EHB = 90°, ①①GHC =①GCH , ①CG =GH , ①FG =GC =GH =a , 又①CE =BE , ①GE BF ,故①正确;①BF ==,①sin①ABF =sin ①BFC =BC BF ==, 故①正确;①①CHF =①BCF =90°,①CFH =①CFB , ①①CFH ①①BFC , ①CF CH FHBF BC CF == ,42CH FHa a ==,①CH =,FH =,①BH =,①sin ①ABF =AO AB ,①AO =, ①FG =GC ,①211122225GCHFCHS S a ==⨯=,①21132225ABHSAO BH a =⨯⨯==, ①16GCHABHSS=,故①错误,故选:B .【点睛】本题是四边形综合题,考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定和性质,锐角三角函数,勾股定理,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.二、填空题5.如图,在边长为4的正方形ABCD 中,点E 、F 分别是边BC 、CD 上的动点.且BE CF =,连接BF 、DE ,则BF DE +的最小值为______.【答案】【分析】连接AE ,利用ABE BCF △△≌转化线段BF 得到BF DE AE DE +=+,则通过作点A 关于BC 的对称点H ,连接DH 交BC 于点E ,利用勾股定理求出DH 的长即可. 【详解】解:连接AE ,如图1, 四边形ABCD 是正方形,AB BC ∴=,90ABE BCF ∠∠==︒,又BE CF =,ABE ∴①(BCF SAS ). AE BF ∴=.所以BF DE +最小值等于AE DE +最小值. 作点A 关于BC 的对称点H 点,如图2, 连接BH ,则A 、B 、H 三点共线,连接DH ,DH 与BC 的交点即为所求的E 点. 根据对称性可知AE HE =, 所以AE DE DH +=.在Rt ADH中,DH=∴+最小值为BF DE故答案为:.【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质、最短距离问题,一般求两条线段最短距离问题,都转化为一条线段.6.正方形ABCD的边长为4,E为AD的中点,连接CE,过点B作BF CE⊥交CD于点F,垂足为G,则EG=______.【分析】先证明①BFC①①CED,得到DE=CF=2,CE=BF,利用勾股定理可求BF的长,由面积法可求EG.【详解】解:正方形ABCD的边长为4,E为AD的中点,∠=∠=︒,DE=2,BCD ADC∴==,90AD CD BC∴∠+∠=︒,90DCE DEC⊥,BF CE①①CGF=90°,DCE CFB∴∠+∠=︒,90∴∠=∠,BFC DEC∴△①CEDBFC△(AAS),2DE CF ∴==,CE BF =,BF ∴=CE ∴=1122BFCSBC CF BF CG =⨯⨯=⨯⨯,42∴⨯=,CG ∴,①EG =CE -CG【点睛】此题考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造全等三角形是解题的关键.三、解答题7.如图,在矩形ABCD 中,BAD ∠的平分线交BC 于点E ,交DC 的延长线于点F ,点G 为EF 的中点,连接BD 、DG .(1)试判断ECF △的形状,并说明理由; (2)求BDG ∠的度数.【答案】(1)ECF △是等腰直角三角形,理由见解析 (2)45°【分析】(1)根据矩形的性质和角平分线的定义及平行线的性质证得45CEF F ∠=∠=︒,90ECF BCD ∠=∠=︒,再根据等角对等边得到EC FC =即可得到结论;(2)根据矩形性质和等腰直角三角形的性质证得BE CD =,DCG BEG ∠=∠,CG EG ,再根据全等三角形的判定与性质证明DCG BEG ≌△△得到DG BG =,DGC BGE ∠=∠,则有90BGD EGC ∠=∠=︒,进而求解即可.(1)解:ECF △是等腰直角三角形;理由如下:①四边形ABCD 是矩形,①AD BC ∥,AB CD ∥,90DAB ABC BCD ∠=∠=∠=︒,①DAE CEF ∠=∠,BAE F ∠=∠.①AE 平分BAD ∠,①45DAE BAE ∠=∠=︒,①45CEF F ∠=∠=︒,①EC FC =.又①90ECF BCD ∠=∠=︒,①ECF △是等腰直角三角形;(2)解:①四边形ABCD 是矩形,①AB CD =,AD BC ∥,①45BEA BAE ∠=∠=︒①AB BE =,即BE CD =.①EC FC =,90ECF ∠=︒,点G 为EF 的中点, ①12CG EF EG ==,1452ECG ECF ∠=∠=︒,90EGC ∠=︒, ①9045135DCG ∠=︒+︒=︒.①18045135BEG ∠=︒-︒=︒,①DCG BEG ∠=∠.在DCG △和BEG 中,DC BE DCG BEG CG EG =⎧⎪∠=∠⎨⎪=⎩,①()DCG BEG SAS △≌△,①DG BG =,DGC BGE ∠=∠,①90BGD EGC ∠=∠=︒.又①DG BG =,①BGD △是等腰直角三角形①45BDG ∠=︒.【点睛】本题考查矩形的性质、等腰直角三角形的判定与性质、直角三角形的斜边中线性质、全等三角形的判定与性质、平行线的性质、角平分线的定义等知识,熟练掌握矩形的性质和等腰直角三角形的判定与性质,证明DCG BEG ≌△△是解答的关键. 8.如图,在四边形ABCD 中,点E 在边AB 上,=AD DE ,CE AD DE BC ∥,∥,作BF CD ∥交线段DE 于点F ,连接AF ,求证:ΔΔDAF EDC ≅.【答案】证明见解析【分析】根据题意得到四边形BCDF 是平行四边形,根据平行四边形的性质得到DF BC =,根据平行线的性质及等腰三角形的性质推出=DF CE ,即可利用SAS 证明ΔΔDAF EDC ≅.【详解】∥DE BC ,BF CD ∥,∴四边形BCDF 是平行四边形,=DF BC ∴,①CE AD ∥,=DAE CEB ∴∠∠,ADF DEC ∠=∠,①∥DE BC ,=DEA CBE ∴∠∠,AD DE =,=DAE DEA ∴∠∠,=CEB CBE ∴∠∠,=CE BC ∴,=DF CE ∴,在ΔDAF 和EDC ∆中,===AD DE ADF DECDF CE ∠∠⎧⎪⎨⎪⎩,ΔΔ()DAF EDC SAS ∴≅.【点睛】此题考查了平行四边形的判定与性质、全等三角形的判定,熟记平行四边形的判定与性质是解题的关键.。
等腰三角形典型题解析

B
E
∴△ABC≌△AED(SAD) ∴AC=AD(全等三角形的对应边相等)
C FD
又∵△ACD 中 AF 是 CD 边的中线(已知)
燕园教育辅导中心
∴AF⊥CD(等腰三角形底边上的高和底边上的中线互相重合)
三、练习
(一)、选择题
1.等腰三角形的对称轴是( )
A.顶角的平分线
B.底边上的高
C.底柱 BD、DE 要多长?
B D
以发现在 Rt△AED 与 Rt△ACB 中,由于∠A=30°, A E C
1
1
AB,又由 D 是 AB 的中点,所以 DE= AB.
2
4
[例]等腰三角形的底角为 15°,腰长为 2a,求腰上的高.
分析:观察图形可
1
所 以 DE= AD, BC=
燕园教育辅导中心
A D
E
B
C
答案: 10.60°或 120° 11.∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°, ∴在 Rt△ADC 中 CD=2AD, ∵∠BAC=120°,∴∠BAD=120°-90°=30°, ∴∠B=∠BAD,∴AD=BD,∴BC=3AD 12.①∵∠ACB=∠DCE=60°,
⊥CD.
分析:要证明 AF⊥CD,而点 F 是 CD 的中点,联想到这是等腰三角形特有的性质,于是连接 AC、
AD,证明 AC=AD,利用等腰三角形“三线合一”的性质得到结论.
在△ABC 和△AED 中
证 明 : 连 接 AC、 AD A
AB AE(三 三 ) ABC AED(三 三 ) BC ED(三 三 )
等边三角形
一、复习知识要点
1.三条边都相等的三角形叫做等边三角形,也叫做正三角形.
专题05 等腰、等边三角形压轴真题(解析版)-初中数学七年级上学期重难点题型分类高分必刷题(人教版)

专题05 高分必刷题-等腰三角形、等边三角形压轴题真题(解析版)题型一:等腰三角形、等边三角形中的动点问题1.如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,△BPD与△CQP是否全等?请说明理由;(2)若点P、Q两点分别从B、A两点同时出发,△CPQ的周长为16cm,设运动时间为t,问:是否存在某一时刻t,使得△CPQ是等腰三角形?如存在,请求出t的值,若不存在,请说明理由.【解答】解:(1)∠CMQ=60°不变.∵等边三角形中,AB=AC,∠B=∠CAP=60°,又由条件得AP=BQ,∴△ABQ≌△CAP(SAS),∴∠BAQ=∠ACP,∴∠CMQ=∠ACP+∠CAM =∠BAQ+∠CAM=∠BAC=60°.(2)设时间为t,则AP=BQ=t,PB=4﹣t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得4﹣t=2t,t=;②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),t=;∴当第秒或第秒时,△PBQ为直角三角形.(3)∠CMQ=120°不变.∵在等边三角形中,BC=AC,∠B=∠CAP=60°∴∠PBC=∠ACQ=120°,又由条件得BP =CQ,∴△PBC≌△QCA(SAS)∴∠BPC=∠MQC又∵∠PCB=∠MCQ,∴∠CMQ=∠PBC=180°﹣60°=120°2.如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)何时△PBQ是直角三角形?(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.【解答】解:(1)∠CMQ=60°不变.∵等边三角形中,AB=AC,∠B=∠CAP=60°,又由条件得AP=BQ,∴△ABQ≌△CAP(SAS),∴∠BAQ=∠ACP,∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.(2)设时间为t,则AP=BQ=t,PB=4﹣t,①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得4﹣t=2t,t=;②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),t=;∴当第秒或第秒时,△PBQ为直角三角形.(3)∠CMQ=120°不变.∵在等边三角形中,BC=AC,∠B=∠CAP=60°∴∠PBC=∠ACQ=120°,又由条件得BP=CQ,∴△PBC≌△QCA(SAS)∴∠BPC=∠MQC又∵∠PCB=∠MCQ,∴∠CMQ=∠PBC=180°﹣60°=120°3.已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB 向点B运动.(1)如图1,设点P的运动时间为t(s),那么t为何值时,△PBC是直角三角形;(2)若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.①如图2,设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?②如图3,连接PC,请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.【解答】解:(1)当△PBC是直角三角形时,∠B=60°,∠BPC=90°,所以BP=1.5cm,所以t=,(2)①∵∠DCQ=120°,当△DCQ是等腰三角形时,CD=CQ,∴∠PDA=∠CDQ=∠CQD=30°,∵∠A=60°,∴AD=2AP,∴2t+t=3,解得t=1(s);②相等,如图所示:作PE垂直AD,QG垂直AD延长线,则PE∥QG,∴∠G=∠AEP,在△EAP和△GCQ,,∴△EAP≌△GCQ(AAS),∴PE=QG,∴△PCD和△QCD同底等高,所以面积相等.4.如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于A(a,0)、B(0,b)两点,且a,b满足(a﹣b)2+|a﹣4t|=0,且t>0,t是常数.直线BD平分∠OBA,交x轴于D 点.(1)若AB的中点为M,连接OM交BD于N,求证:ON=OD;(2)如图2,过点A作AE⊥BD,垂足为E,猜想AE与BD间的数量关系,并证明你的猜想;(3)如图3,在x轴上有一个动点P(在A点的右侧),连接PB,并作等腰Rt△BPF,其中∠BPF=90°,连接F A并延长交y轴于G点,当P点在运动时,OG的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.【解答】(1)证明:∵直线AB分别交x轴、y轴于A(a,0)、B(0,b)两点,且a,b满足(a﹣b)2+|a﹣4t|=0,且t>0,∴a=b=4t,当x=0时,y=4t,当y=0时,﹣x+4t=0,解得x=4t,∴点A、B的坐标是A(4t,0),B(0,4t),∴△AOB是等腰直角三角形,∵点M是AB 的中点,∴OM⊥AB,∴∠MOA=45°,∵直线BD平分∠OBA,∴∠ABD=∠ABO=22.5°,∴∠OND=∠BNM=90°﹣∠ABD=90°﹣22.5°=67.5°,∠ODB=∠ABD+∠BAD=22.5°+45°=67.5°,∴∠OND=∠ODB,∴ON=OD(等角对等边);(2)答:BD=2AE.理由如下:延长AE交BO于C,∵BD平分∠OBA,∴∠ABD=∠CBD,∵AE⊥BD于点E,∴∠AEB=∠CEB=90°,在△ABE≌△CBE中,,∴△ABE≌△CBE(ASA),∴AE=CE,∴AC=2AE,∵AE⊥BD,∴∠OAC+∠ADE=90°,又∠OBD+∠BDO=90°,∠ADE=∠BDO(对顶角相等),∴∠OAC=∠OBD,在△OAC与△OBD中,,∴△OAC≌△OBD(ASA),∴BD=AC,∴BD=2AE;(3)OG的长不变,且OG=4t.过F作FH⊥OP,垂足为H,∴∠FPH+∠PFH=90°,∵∠BPF=90°,∴∠BPO+∠FPH=90°,∴∠FPH=∠BPO,∵△BPF是等腰直角三角形,∴BP=FP,在△OBP与△HPF中,,∴△OBP≌△HPF(AAS),∴FH=OP,PH=OB=4t,∵AH=PH+AP=OB+AP,OA=OB,∴AH=OA+AP=OP,∴FH=AH,∴∠GAO =∠F AH=45°,∴△AOG是等腰直角三角形,∴OG=OA=4t.5.如图,在平面直角坐标系中,点O为原点,△OAB为等边三角形,P、Q分别为AO、AB边上的动点,点P、点Q同时从点A出发,且当其中一点停止运动时,另一点也立即停止运动;若P以2个单位长度每秒的速度从点A向终点O运动,点Q以3个单位长度每秒的速度从点A向终点B运动,设运动时间为t,已知点A坐标为(a,b),且满足(a﹣6)2+|a﹣b|=0.(1)求A点坐标;(2)如图1,连接BP、OQ交于点C,请问当t为何值时,∠OCP=60°;(3)如图2,D为OB边上的中点,P,Q在运动过程中,D,P,Q三点是否能构成使∠PDQ =120°的等腰三角形,若能,求运动时间t并直接写出四边形APDQ的面积:若不能,请说明理由.【解答】解:(1)∵(a﹣6)2+|a﹣b|=0,又∵(a﹣6)2,≥0,|a﹣b|≥0,∴a=6,b=6∴点A(6,6).(2)如图1中,∵△AOB是等边三角形,点A(6,6),∴AO=BO=AB=12,∠AOB=∠ABO=60°=∠A,∵∠OCP=60°=∠AOB,∴∠AOB=∠QOB+∠AOQ=∠QOB+∠PBO=∠PCO,∴∠AOQ=∠PBO,且AO=BO,∠A=∠AOB,∴△AOQ≌△OBP(ASA),∴OP=AQ,∴12﹣2t=3t∴t=2.4∴当t=2.4时,∠OCP=60°.(3)如图2中,过点D作DF⊥AO,DE⊥AB,连接AD,∵△ABO是等边三角形,D是OB中点,点A(6,6),∴OD=BD=6,∠AOB=∠ABO =60°,AD=6,又∵∠DFO=∠DEB=90°,∴△ODF≌△BDE(AAS),∴OF=BE,DF=DE,∵AO=AB,∴AO﹣OF=AB﹣BE,∴AF=AE,∵DF=DE,PD=DQ,∴Rt△DFP≌Rt△DEQ(HL),∴PF=EQ,∵OD=6,∠AOD=60°,∠DFO=90°,∴∠ODF=30°∴OF=3,DF=OF=3,∴AF=AO﹣OF=9=AE,BE=OF=3,∵AP+AQ=AP+AE+EQ=AP+PF+AE=AF+AE=2AF,∴2t+3t=18∴t=3.6,∴当t=,3.6时,D,P,Q三点是能构成使∠PDQ=120°的等腰三角形,∵Rt△DFP≌Rt△DEQ,∴S△DFP=S△DEQ,∴S四边形APDQ=S四边形AFDQ=S△AOB﹣2S△OFD=×12×6﹣2××3×3=27.6.如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,点C、D在x 正半轴上.(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE是△ABC的两条角平分线,且BD、CE 交于点F,直接写出CF的长6.(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接QD并延长,交y轴于点P,当点C运动到什么位置时,满足PD=DC?请求出点C的坐标;(3)如图,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.【解答】解:(1)作∠DCH=10°,CH交BD的延长线于H,∵∠BAO=60°,∴∠ABO=30°,∴AB=2OA=6,∵∠BAO=60°,∠BCO=40°,∴∠ABC=180°﹣60°﹣40°=80°,∵BD是△ABC的角平分线,∴∠ABD=∠CBD=40°,∴∠CBD=∠DCB,∠OBD=40°﹣30°=10°,∴DB=DC,在△OBD和△HCD中,,∴△OBD≌△HCD(ASA),∴OB=HC,在△AOB和△FHC中,,∴△AOB≌△FHC(ASA),∴CF=AB=6,故答案为:6;(2)∵△ABD和△BCQ是等边三角形,∴∠ABD=∠CBQ=60°,∴∠ABC=∠DBQ,在△CBA和△QBD中,,∴△CBA≌△QBD(SAS),∴∠BDQ=∠BAC=60°,∴∠PDO=60°,∴PD=2DO=6,∵PD=DC,∴DC=9,即OC=OD+CD=12,∴点C的坐标为(12,0);(3)如图3,以OA为对称轴作等边△ADE,连接EP,并延长EP交x轴于点F.由(2)得,△AEP≌△ADB,∴∠AEP=∠ADB=120°,∴∠OEF=60°,∴OF=OA=3,∴点P在则OP的最小值为.直线EF上运动,当OP⊥EF时,OP最小,∴OP=OF=,7.等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E.(1)如图(1),已知C点的横坐标为﹣1,直接写出点A的坐标;(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB =∠CDE;(3)如图(3),若点A在x轴上,且A(﹣4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连接CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.【解答】解:(1)如图(1),过点C作CF⊥y轴于点F,∵CF⊥y轴于点F,∴∠CF A=90°,∠ACF+∠CAF=90°,∵∠CAB=90°,∴∠CAF+∠BAO=90°,∴∠ACF=∠BAO,在△ACF 和△ABO中,,∴△ACF≌△ABO(AAS),∴CF=OA=1,∴A(0,1);(2)如图2,过点C作CG⊥AC交y轴于点G,∵CG⊥AC,∴∠ACG=90°,∠CAG+∠AGC=90°,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∴∠AGC=∠ADO,在△ACG和△ABD中,,∴△ACG≌△ABD(AAS),∴CG=AD=CD,∠ADB=∠G,∵∠ACB=45°,∠ACG=90°,∴∠DCE=∠GCE=45°,在△DCE和△GCE中,,∴△DCE≌△GCE(SAS),∴∠CDE=∠G,∴∠ADB=∠CDE;(3)BP的长度不变,理由如下:如图(3),过点C作CE⊥y轴于点E.∵∠ABC=90°,∴∠CBE+∠ABO=90°.∵∠BAO+∠ABO=90°,∴∠CBE=∠BAO.∵∠CEB=∠AOB=90°,AB=AC,∴△CBE≌△BAO(AAS),∴CE=BO,BE=AO=4.∵BD=BO,∴CE=BD.∵∠CEP=∠DBP=90°,∠CPE=∠DPB,∴△CPE≌△DPB(AAS),∴BP=EP=2.8.如图,在△ABC中.AB=AC,点E在线段BC上,连接AE并延长到G,使得EG=AE,过点G作GD∥BA分别交BC,AC于点F,D.(1)求证:△ABE≌△GFE;(2)若GD=3,CD=1,求AB的长度;(3)过点D作DH⊥BC于H,P是直线DH上的一个动点,连接AF,AP,FP,若∠C=45°,在(2)的条件下,求△AFP周长的最小值.【解答】(1)证明:如图1中,∵GD∥AB,∴∠B=∠EFG,在△ABE和△GFE中,,∴△ABE≌△GFE(AAS).(2)解:如图1中,∵AB=AC,∴∠B=∠ACB,∵DF∥AB,∴∠DFC=∠B,∴∠DFC =∠DCF,∴DC=DF=1,∵DG=3,∴FG=DG﹣DF=2,∵△ABE≌△GFE,∴AB=GF=2.(3)解:如图2中,∵AB=AC=2,∴∠B=∠C=45°,∴∠BAC=90°,∵AB∥FD,∴∠FDC=∠BAC=90°,即FD⊥AC∵AC=AB=2,CD=1,∴DA=DC,∴F A=FC,∴∠C=∠F AC=45°,∴∠AFC=90°,∴DF=DA=DC=1,∴AF=,∵DH⊥CF,∴FH=CH,∴点F与点C关于直线PD对称,∴当点P与D重合时,△P AF的周长最小,最小值=△ADF的周长=2+.9.如图,在平面直角坐标系中,点O为坐标原点,点A(0,3)与点B关于x轴对称,点C (n,0)为x轴的正半轴上一动点.以AC为边作等腰直角三角形ACD,∠ACD=90°,点D在第一象限内.连接BD,交x轴于点F.(1)如果∠OAC=38°,求∠DCF的度数;(2)用含n的式子表示点D的坐标;(3)在点C运动的过程中,判断OF的长是否发生变化?若不变求出其值,若变化请说明理由.【解答】解:(1)∵∠AOC=90°,∴∠OAC+∠ACO=90°,∵∠ACD=90°,∴∠DCF+∠ACO=90°,∴∠DCF=∠OAC,∵∠OAC=38°,∴∠DCF=38°;(2)如图,过点D作DH⊥x轴于H,∴∠CHD=90°∴∠AOC=∠CHD=90°,∵等腰直角三角形ACD,∠ACD=90°∴AC=CD,由(1)知,∠DCF=∠OAC,∴△AOC≌△CHD (AAS),∴OC=DH=n,AO=CH=3,∴点D的坐标(n+3,n);(3)不会变化,理由:∵点A(0,3)与点B关于x轴对称,∴AO=BO,又∵OC⊥AB,∴x轴是AB垂直平分线,∴AC=BC,∴∠BAC=∠ABC,又∵AC=CD,∴BC=CD,∴∠CBD=∠CDB,∵∠ACD=90°,∴∠ACB+∠DCB=270°,∴∠BAC+∠ABC+∠CBD+∠CDB=90°,∴∠ABC+∠CBD=45°,∵∠BOF=90°,∴∠OFB=45°,∴∠OBF=∠OFB=45°,∴OB=OF=3,∴OF的长不会变化.题型二:等腰三角形、等边三角形综合类压轴题10.(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.①∠AEB的度数为②猜想线段AD,BE之间的数量关系为:,并证明你的猜想.(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请求出∠AEB的度数及线段CM,AE,BE之间的数量关系.【解答】解:(1)①∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB =∠DCE=60°,∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE,∴∠CEB=∠CDA=120°,∴∠AEB=60°,故答案为:60°;②AD=BE,证明:∵△ACD≌△BCE,∴AD=BE,故答案为:AD=BE;(2)∠AEB=90°,AE﹣BE=2CM,证明:∵△DCE是等腰直角三角形,CM是中线,∴CM=DM=EM=DE,在△ACD和△BCE中,,∴△ACD≌△BCE,∴∠CDA=∠CEB,∵∠CDA=135°,∴∠AEB=135°﹣45°=90°,∴BE=AD,∴AE﹣AD=DE=2CM,∴AE﹣BE=2CM.11.如图1,已知△ABC和△EFC都是等边三角形,且点E在线段AB上.(1)求证:BF∥AC;(2)过点E作EG∥BC交AC于点G,试判断△AEG的形状并说明理由;(3)如图2,若点D在射线CA上,且ED=EC,求证:AB=AD+BF.【解答】(1)证明:∵△ABC和△EFC都是等边三角形,∴∠A=∠ABC=∠ACB=∠ECF=60°,AC=BC,CE=FC,∴∠ACE=∠BCF,在△ACE与△FCB中,,∴△ACE≌△FCB(SAS),∴∠A=∠CBF=60°,∵∠ABC=60°,∴∠A+∠ABC+∠CBF=180°,∴∠A+∠ABF=180°,∴AC∥BF;(2)解:△AEG是等边三角形,理由如下:如图1所示:∵△ABC是等边三角形,∴∠A =∠ABC=∠ACB=60°,∵EG∥BC,∴∠AEG=∠ABC=60°,∠AGE=∠ACB=60°,∴∠A=∠AEG=∠AGE=60°,∴△AEG是等边三角形;(3)证明:如图2,过E作EM∥BC交AC于M,则∠AEM=∠ABC=60°,∠AME=∠ACB =60°,∵∠A=∠ABC=∠ACB=60°,∴∠A=∠AEM=∠AME=60°,∴△AEM是等边三角形,∴AE=EM=AM,∴∠DAE=∠EMC=120°,∵DE=CE,∴∠D=∠MCE,在△ADE和△MCE中,,∴△ADE≌△MCE(AAS),∴AD=CM,∴AC=AM+CM,由(1)得△ACE≌△FCB,∴BF=AE,∴BF=AM,∴AC=BF+AD,∴AB=AD+BF.12.已知:△ABC为等边三角形,点E为射线AC上一点,点D为射线CB上一点,AD=DE.(1)如图1,当E在AC的延长线上且CE=CD时,求证:BD=CD;(2)如图2,当E在AC的延长线上时,AB+BD等于AE吗?请说明理由;(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE 的数量关系,并证明.【解答】(1)证明:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠B=∠ACB=60°,∵CD=CE,∴∠CDE=∠E,∵∠ACD=∠CDE+∠E=60°,∴∠E=30°,∵DA=DE,∴∠DAC=∠E =30°,∵∠BAC=60°,∴∠DAB=∠CAD,∵AB=AC,∴BD=DC;(2)结论:AB+BD=AE,理由如下:如图2,在AB上取BH=BD,连接DH,∵BH=BD,∠B=60°,∴△BDH为等边三角形,AB﹣BH=BC﹣BD,即AH=DC,∴∠BHD=60°,BD=DH,∵AD=DE,∴∠E=∠CAD,∴∠BAC﹣∠CAD=∠ACB﹣∠E,即∠BAD=∠CDE,∵∠BHD=60°,∠ACB=60°,∴180°﹣∠BHD=180°﹣∠ACB,即∠AHD=∠DCE,在△AHD和△DCE,,∴△AHD≌△DCE(AAS),∴DH=CE,∴BD=CE,∴AE=AC+CE=AB+BD;(3)AB=BD+AE;如图3,在AB上取AF=AE,连接DF,∵△ABC为等边三角形,∴∠BAC=∠ABC=60°,∴△AFE是等边三角形,∴∠F AE=∠FEA=∠AFE=60°,∴EF∥BC,∴∠EDB=∠DEF,∵AD=DE,∴∠DEA=∠DAE,∴∠DEF=∠DAF,在△AFD和△EFD中,,∴△AFD≌△EFD(SSS),∴∠ADF=∠EDF,∠DAF=∠DEF,∴∠FDB=∠EDF+∠EDB,∠DFB=∠DAF+∠ADF,∵∠EDB=∠DEF,∴∠FDB=∠DFB,∴DB=BF,∵AB=AF+FB,∴AB=BD+AE.13.已知△ABC为等边三角形,取△ABC的边AB,BC中点D,E,连接DE,如图1,易证△DBE为等边三角形,将△DBE绕点B顺时针旋转,设旋转的角度∠ABD=α,其中0<α<180°.(1)如图2,当α=30°,连接AD,CE,求证:AD=CE;(2)在△DBE旋转过程中,当α超过一定角度时,如图3,连接AD,CE会交于一点,记交点为点F,AD交BC于点P,CE交BD于点Q,连接BF,请问BF是否会平分∠CBD?如果是,求出α,如果不是,请说明理由;(3)在第(2)问的条件下,试猜想线段AF,BF和CF之间的数量关系,并说明理由.【解答】证明:(1)∵△ABC,△DBE都是等边三角形,∴AB=BC,BD=BE,∠ABC=∠DBE=60°,∴∠ABD=∠CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴AD=CE;(2)不存在,理由如下:如图3,过点B作BN⊥AD于N,过点B作BH⊥CE于H,∵△ABC,△DBE都是等边三角形,∴AB=BC,BD=BE,∠ABC=∠DBE=60°,∴∠ABD =∠CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴AD=CE,S△ABD=S△CBE,∠BAD=∠BCE,∴×AD×BN=×CE×BH,∴BN=BH,又∵BF=BF,∴Rt△BFN≌Rt△BFH(HL),∴∠AFB=∠EFB,∵∠BAD=∠BCE,∠CPF=∠APB,∴∠AFC=∠ABC=60°,∴∠AFB =∠EFB=60°,∴∠CFB=∠DFB=120°,当BF平分∠CBD时,则∠CBF=∠DBF,∴∠BCF=180°﹣∠CBF﹣∠CFB=180°﹣∠DBF﹣∠DFB=∠ADB,∴∠DAB=∠ADB,∴AB =DB,与题干DB=BC=AB相矛盾,∴BF不会平分∠CBD;(3)AF=CF+BF,理由如下:如图4,在AF上截取MF=BF,连接BM,∵∠AFB=60°,MF=FB,∴△MFB是等边三角形,∴MB=BF,∠MBF=∠ABC=60°,∴∠ABM=∠CBF,在△ABM和△CBF中,,∴△ABM≌△CBF(SAS),∴AM=CF,∵AF=AM+MF,∴AF=CF+BF.14.如图1,△ABC为等腰三角形,∠ABC=90°,点P在线段BC上(不与B、C重合),以点A为直角顶点作等腰直角△P AQ,且点Q在AP的左下方,过点Q作QE⊥AB于点E.(1)求证:△P AB≌△AQE;(2)连接CQ交AB于M,若PC=2PB,求的值.(3)如图2,过点Q作QF⊥AQ于AB的延长线于点F,过P点作DP⊥AP交AC于点D,连接DF,当点P在线段BC上运动时(不与B,C重合),式子的值会变化吗?若不变,求出该值;若变化,请说明理由.【解答】(1)证明:∵△ACB为等腰三角形,∠ABC=90°,△P AQ是等腰直角三角形,QE⊥AB于E.∴AP=AQ,∠ABP=∠QEA=90°,∠QAE+∠BAP=∠BAP+∠APB=90°,∴∠QAE=∠APB,在△P AB和△AQE中,,∴△P AB≌△AQE(AAS);(2)解:∵△P AB≌△AQE,∴AE=PB,∵AB=CB,∴QE=CB.在△QEM和△CBM 中,,∴△QEM≌△CBM(AAS),∴ME=MB,∵AB=CB,AE=PB,PC=2PB,∴BE=PC,∵PC=2PB,∴PC=2MB,∴=2;(3)解:式子的值不会变化,理由如下:过A作HA⊥AC交QF于点H,如图2所示:∵QA⊥AP,HA⊥AC,AP⊥PD,⊥⊥QAH+⊥HAP=⊥HAP+⊥P AD=90°,⊥AQH=⊥APD=90°,⊥⊥QAH=⊥P AD,⊥⊥P AQ为等腰直角三角形,⊥AQ=AP,在⊥AQH和⊥APD中,,⊥⊥AQH⊥⊥APD(ASA),⊥AH=AD,QH=PD,⊥HA⊥AC,⊥BAC=45°,⊥⊥HAF=⊥DAF,在⊥AHF和⊥ADF中,,⊥⊥AHF⊥⊥ADF(SAS),⊥HF=DF,⊥===1.15.如图1,在平面直角坐标系中,点A在y轴上,点B在x轴上,AB=AC,⊥BAC=90°,CM⊥y轴,交y轴于点M.(1)求证⊥ABO=⊥CAM;(2)如图2,D,E为y轴上的两个点,BD=BE,BD⊥BE,求⊥CEM的度数;(3)如图3,⊥P AQ是等腰直角三角形,⊥P AQ为顶角,点Q在x轴负半轴上,连接CB,交y轴于点H,AC与x轴交于点G,连接PC,交AQ于点K,交x轴于点N,若CN=CM,NG=3,HM=2,求GH.【解答】(1)证明:⊥⊥BOA=90°,⊥⊥BAO+⊥ABO=90°,又⊥⊥BAC=⊥BAO+⊥CAM=90°,⊥⊥ABO=⊥CAM;(2)解:⊥CM⊥y轴,⊥⊥AMC=⊥BOA=90°,⊥AB=AC,⊥ABO=⊥CAM,⊥⊥AMC⊥⊥BOA (AAS),⊥CM=AO,AM=BO,⊥BD=BE,BD⊥BE,⊥⊥BDE是等腰直角三角形,⊥⊥BDE=⊥BED =45°,⊥EBO=⊥DBE=45°,⊥⊥EBO=⊥BEO,⊥BO=EO=AM,⊥EO﹣OM=AM﹣OM,⊥EM=AO=CM,⊥⊥CME是等腰直角三角形,⊥⊥CEM=45°;(3)解:⊥AB=AC,⊥BAC=90°,⊥⊥ACB=45°,⊥⊥P AQ是等腰直角三角形,⊥P A=QA,⊥P AQ=⊥CAB=90°,⊥⊥P AQ+⊥QAC=⊥CAB+⊥QAC,即⊥P AC=⊥QAB,⊥AC=AB,⊥⊥P AC⊥⊥QAB(SAS),⊥⊥APC=⊥AQB,⊥⊥AKP=⊥QKN,⊥⊥QNK=⊥P AK=90°,⊥CM⊥y 轴,⊥CM⊥NO,⊥⊥NCM=⊥KNO=90°,在ON的延长线上截取NI=MH,连接CI,如图3所示:⊥CN=CM,⊥CNI=⊥CMH=90°,⊥⊥CNI⊥⊥CMH(SAS),⊥⊥NCI=⊥MCH,CI=CH,⊥⊥NCG+⊥NCI=⊥NCG+⊥MCH=⊥NCM﹣⊥GCH=90°﹣45°=45°=⊥GCH=⊥GCI,⊥⊥GCI⊥⊥GCH(SAS),⊥GI=GH,⊥GI=IN+NG=HM+NG=2+3=5,⊥GH=5.16.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt⊥ABC,(1)求C点的坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,P A为腰作等腰Rt⊥APD,过D作DE⊥x轴于E点,求OP﹣DE的值;(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt⊥FGH,始终保持⊥GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:⊥m﹣n为定值;⊥m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.【解答】解:(1)过C作CM⊥x轴于M点,如图1,⊥CM⊥OA,AC⊥AB,⊥⊥MAC+⊥OAB =90°,⊥OAB+⊥OBA=90°则⊥MAC=⊥OBA在⊥MAC和⊥OBA中,则⊥MAC⊥⊥OBA(AAS),则CM=OA=2,MA=OB=4,则点C的坐标为(﹣6,﹣2);(2)过D作DQ⊥OP于Q点,如图2,则OP﹣DE=PQ,⊥APO+⊥QPD=90°⊥APO+⊥OAP=90°,则⊥QPD=⊥OAP,在⊥AOP和⊥PDQ中,则⊥AOP⊥⊥PDQ(AAS),⊥OP﹣DE=PQ=OA=2;(3)结论⊥是正确的,m+n=﹣4,如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T 点,则FS=FT=2,⊥FHS=⊥HFT=⊥FGT,在⊥FSH和⊥FTG中,则⊥FSH⊥⊥FTG(AAS),则GT=HS,又⊥G(0,m),H(n,0),点F坐标为(﹣2,﹣2),⊥OT═OS=2,OG=|m|=﹣m,OH=n,⊥GT=OG﹣OT=﹣m﹣2,HS=OH+OS=n+2,则﹣2﹣m=n+2,则m+n=﹣4.17.如图,四边形OABC的位置在平面直角坐标系中如图所示,且A(0,a),B(b,a),C(b,0),又a,b满足﹣+b2+4b+8=0,点P在x轴上且横坐标大于b,射线OD是第一象限的一条射线,点Q在射线OD上,BP=PQ.并连接BQ交y轴于点M.(1)求点A,B,C的坐标为A、B、C.(2)当BP⊥PQ时,求⊥AOQ的度数.(3)在(2)的条件下,若点P在x轴的正半轴上,且OP=3AM,试求点M的坐标.【解答】解:(1)⊥﹣+b2+4b+8=0,⊥﹣+(b﹣4)2=0,⊥a=4,b=4,⊥A(0,4),B(﹣4,4),C(﹣4,0),故答案为(0,4),(﹣4,4),(﹣4,0);(2)由(1)知,A(0,4),B(﹣4,4),C(﹣4,0),⊥AB=BC=OC=OA=4,⊥四边形OABC是菱形,⊥⊥AOC=90°,⊥菱形OABC是正方形,过点Q作QN⊥x轴于N,⊥⊥PNQ =90°,⊥⊥QPN+⊥PQN=90°,⊥BP⊥BQ,⊥⊥BPQ=90°,⊥⊥BPC+⊥QPN=90°,⊥⊥PQN =⊥BPC,由(1)知,B(﹣4,4),C(﹣4,0),⊥BC=4,BC⊥x,⊥⊥BCP=⊥PNQ=90°,在⊥BCP和⊥PNQ中,,⊥⊥BCP⊥⊥PNQ(AAS),⊥CP=QN,BC=PN,⊥OC=PN=4,⊥当点P在x轴负半轴时,如图1、OC=CP+OP,PN=OP+ON,⊥CP=ON,⊥CP=QN,⊥ON=QN,⊥⊥PNQ=90°,⊥⊥QON=45°,⊥⊥AOQ=45°,⊥当点P在x轴正半轴时,如图2、OC=CP﹣OP,PN=ON﹣OP,⊥CP=ON,⊥CP=QN,⊥ON=QN,⊥⊥PNQ=90°,⊥⊥QON=45°,∴∠AOQ=45°,即:∠AOQ=45°;(3)如图2,过点Q作QN⊥x轴于N,设P(m,0)(m>0),∵OP=3AM,∴AM=OP =m,∴M(0,m+4),∵点B(﹣4,4),∴直线BM的解析式为y=mx+m+4,由(2)知,PN=OC=4,∴N(m+4,0),∴Q(m+4,m+4),∵点Q在直线BM上,∴m(m+4)+m+4=m+4,∴m=0(舍)或m=4,∴M(0,).。
等腰三角形典型例题
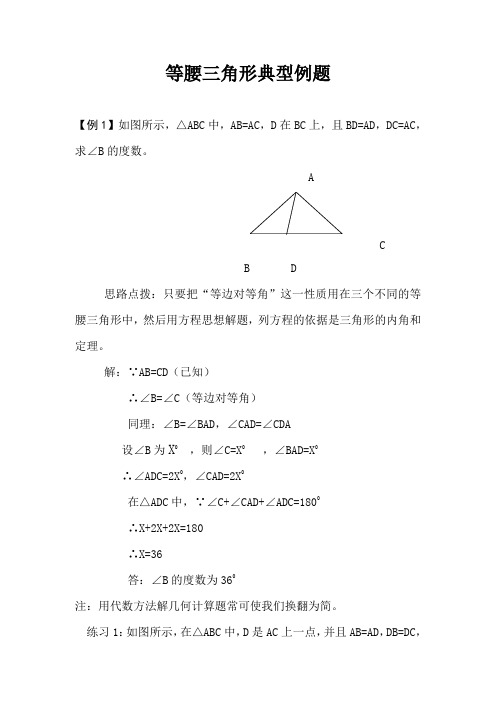
等腰三角形典型例题【例1】如图所示,△ABC中,AB=AC,D在BC上,且BD=AD,DC=AC,求∠B的度数。
ACB D思路点拨:只要把“等边对等角”这一性质用在三个不同的等腰三角形中,然后用方程思想解题,列方程的依据是三角形的内角和定理。
解:∵AB=CD(已知)∴∠B=∠C(等边对等角)同理:∠B=∠BAD,∠CAD=∠CDA设∠B为X0,则∠C=X0,∠BAD=X0∴∠ADC=2X0,∠CAD=2X0在△ADC中,∵∠C+∠CAD+∠ADC=1800∴X+2X+2X=180∴X=36答:∠B的度数为360注:用代数方法解几何计算题常可使我们换翻为简。
练习1:如图所示,在△ABC中,D是AC上一点,并且AB=AD,DB=DC,若∠C=290,则∠A=___练习2:如图在△ABC 中,AB=AC,点D 在AC 上,且BD=BC=AD,求△ABC 各角的度数?【例2】如图所示,在△ABC 中,AB=AC ,O 是△ABC 内一点,且OB=OC 。
求证:AO ⊥BC思路点拨:要证AO ⊥BC ,即证AO是等腰三角形底边上的高,根据三线合一定理,只要先证AO 是顶角的平分线即可。
B证明:延长AO 交BC 于DAB=AC (已知) 在△ABO 和△ACO 中 OB=OC (已知) AO=AO(公共边) ∴△ABO ≌△ACO (SSS ) ∴∠BAO=∠CAO即∠BAD=∠CAD (全等三角形的对应角相等)∴AD ⊥BC ,即AO ⊥BC (等腰三角形顶角的平分线与底边上的高互相重合)评注:本题用两次全等也可达到目的.。
练习:如图所示,点D 、E 在△ABC 的边BC 上,AB=AC ,AD=AE 求证:BD=CE【例3】求证等腰三角形底边上任一点到两腰的距离之和等于一腰上C的高。
思路点拨:本题为文字题,文字题必须按下列步骤进行:(1)根据题意画出图形;(2)根据图形写出“已知”、“求证”;(3)写出证明过程。
等腰三角形知识点+经典例题

等腰三角形知识点+经典例题等腰三角形知识点+经典例题等腰三角形是一种特殊的三角形,它具有两条边相等的性质。
在几何学中,等腰三角形有着独特的特点和应用。
本文将介绍等腰三角形的基本性质和解题技巧,并通过经典例题加深对该知识点的理解。
一、等腰三角形基本性质1. 两边相等:等腰三角形的两条边长相等,通常表示为AB = AC。
2. 两底角相等:等腰三角形的两个底角(即底边两侧的角)相等,通常表示为∠B = ∠C。
3. 对顶角平分底边:等腰三角形的对顶角(即顶点处的角)平分底边,即顶角的平分线与底边相等和垂直。
4. 底角是钝角:当等腰三角形的顶角大于90度时,底角为钝角。
二、等腰三角形的特殊性质1. 高线重合:等腰三角形的高线与底边重合,且高线上的高度等于底边的中线和中线的一半。
2. 内切圆:等腰三角形的内切圆与底边相切,且圆心在高线上。
3. 外接圆:等腰三角形的外接圆的圆心位于底边的中点,且外接圆的半径等于底边长度的一半。
三、等腰三角形的解题技巧1. 利用等腰三角形的两边相等性质,可在题目中找到相等的边长,进而推导其他角度和边长的关系。
2. 利用等腰三角形的两底角相等性质,可在题目中找到已知角度与未知角度的关系,从而推导解题过程。
3. 利用等腰三角形的对顶角平分底边性质,和底角是钝角的特点,可应用角平分线定理解题。
四、经典例题例题1:在等腰三角形ABC中,AB = AC = 6cm,∠B = 60°,求角A的度数和三角形的面积。
解析:由于AB = AC,可知三角形ABC是等腰三角形。
又∠B =∠C = 60°,由等腰三角形的两底角相等性质可得∠A = 180° - 2∠B = 60°。
三角形ABC的三个角度均为60°,是等边三角形。
根据等边三角形的性质,三角形ABC的面积为√3/4 * AB^2 = √3/4 * 6^2 = 9√3 cm^2。
例题2:在等腰三角形ABC中,AB = AC = 8cm,∠A = 100°,求顶角B的度数和三角形的周长。
七年级数学下册专题第13讲等腰三角形重点、考点知识总结及练习

专题 第13讲等腰三角形知识点1 等腰三角形的相关概念---分类讨论求边角的值1.等腰三角形的两个腰相等,两个底角也相等.2.直角三角形30°的角所对的直角边等于斜边的一半.【典例】1.若等腰三角形一腰上的高等于腰长的一半,求此三角形的底角.【解析】解:①如下图,当高在三角形内部时,12BD AB =,∴∠A=30°,∴∠ABC=∠ACB=75°,②如下图,当高在三角形外部时,12BD AB =,则∠BAD=30°,∴∠BAC=150°,∴∠ABC=∠ACB=15°,所以此三角形的底角等于75°或15°.【方法总结】本题考查了等腰三角形的性质,以及含特殊角的直角三角形,熟记三角形的高相对于三角形的三种位置关系(三角形内部,三角形的外部,三角形的边上),解题时注意需要分类讨论.2.如果一等腰三角形的周长为27,且两边的差为12,求这个等腰三角形的腰长.【解析】解:设等腰三角形的腰长为x,则底边长为x﹣12或x+12,当底边长为x﹣12时,根据题意,得2x+x﹣12=27,解得x=13,∴腰长为13,此时底边长为13-12=1,满足三角形的两边之和大于第三边,两边之差小于第三边,当底边长为x+12时,根据题意,得2x+x+12=27,解得x=5,此时底边长为5+12=17,因为5+5<17,所以构不成三角形,故这个等腰三角形的腰的长为13.【方法总结】已知等腰三角形的周长和两边之差来求等腰三角形的底或腰时,我们需要分类讨论,分为两种情况:一种是“腰-底=某个值”,第二种是“底-腰=某个值”,可将底或腰设为未知数,再根据等腰三角形的周长列出方程,求出三边以后根据三角形的三边关系进行验证,选择合理的数值.【随堂练习】1.(2017秋•洛阳期末)若等腰三角形的一个内角比另一个内角大30°,则这个等腰三角形的顶角的度数为_____.【解答】解:在△ABC中,设∠A=x,∠B=x+30°,分情况讨论:当∠A=∠C为底角时,2x+(x+30°)=180°,解得x=50°,顶角∠B=80°;当∠B=∠C为底角时,2(x+30)+x=180°,解得x=40°,顶角∠A=40°.故这个等腰三角形的顶角的度数为80°或40°.故答案为:80°或40°.2.(2017秋•襄州区期末)在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则该等腰三角形的底边长为______.【解答】解:根据题意,①当15是腰长与腰长一半时,AC+AC=15,解得AC=10,所以底边长=12﹣×10=7;②当12是腰长与腰长一半时,AC+AC=12,解得AC=8,所以底边长=15﹣×8=11.所以底边长等于7或11.故答案为:7或11.3.(2017秋•枣阳市期末)一个等腰三角形的周长为20,一条边的长为6,则其两腰之和为______.【解答】解:①底边长为6,则腰长为:(20﹣6)÷2=7,所以另两边的长为7,7,能构成三角形,7+7=14;②腰长为6,则底边长为:20﹣6×2=8,能构成三角形,6+6=12.故答案为:12或144.(2017秋•诸暨市期末)已知等腰三角形的周长为8,其中一边长为2,则该等腰三角形的腰长为_____.【解答】解:①2是腰长时,底边为:8﹣2×2=4,三角形的三边长分别为2、2、4,∵2+2=4,∴不能组成三角形,②2是底边长时,腰长为:×(8﹣2)=3,三角形的三边长分别3、3、2,能组成三角形,综上所述,该等腰三角形的腰长是3.故答案为:3.5.(2018春•李沧区期中)若等腰三角形一腰上的高与另一腰的夹角为48°,则其顶角度数为_______°.【解答】解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+48°=138°;②如图1,当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣48°=42°.故答案为:42或138.6.(2018春•邗江区期中)已知等腰三角形的一条边等于4,另一条边等于9,那么这个三角形的第三边是_____.【解答】解:当4为底时,其它两边都为9,4、9、9可以构成三角形;当4为腰时,其它两边为4和9,因为4+4=8<9,所以不能构成三角形.故答案为:9.知识点2 等腰三角形的性质---边角关系等腰三角形的两底角相等(简称“等边对等角”),即在△ABC,AB=AC,可得∠B=∠C.【典例】1.如图,在△ABC中,∠ACB=90°,AD=AC,BE=BC,求∠DCE的大小.【解析】解:设∠ACE=x,∠ECD=y,∠DCB=z,∵BC=BE,+,∴∠CED=∠ECB=y z∵AC=AD,+,∴∠ADC=∠ACD=x y+-,在△CDB中,∠B=x y z+-,在△ACE中,∠A=y z x在△ABC中,∠ACB=90°,+-++-=90°,∴∠A+∠B=90°,即x y z y z x∴2y=90°,解得y=45°.于是∠DCE=45°.【方法总结】本题考查了等腰三角形的性质,解答此题的关键是建立起各角之间的关系,结合图形列出方程进行解答.2.如图,在△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC 与△EBC的周长分别是40,24,求AB的长.【解析】解:∵DE是AB的垂直平分线,∴AE=BE,∵△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,∴△ABC的周长﹣△EBC的周长=(AB+AC+BC)-(AC+BC)=AB,∴AB=40﹣24=16.【方法总结】本题考查了等腰三角形的性质和垂直平分线上的性质,根据垂直平分线上的点到线段两端点的距离相等,得出相等的线段,把三角形的周长表示出来,再利用相等的线段进行转化求解. 【随堂练习】1.(2017春•成华区期末)如图△ABC中,AB=AC,点E、D、F分别是边AB、BC、AC边上的点,且BE=CD,CF=BD.若∠EDF=50°,则∠A的度数为_____.【解答】解:∵AB=AC,∴∠B=∠C,在△BDE与△CEF中,∴△BDE≌△CFE.∴∠BDE=∠CFD,∵∠EDF=50°,∴∠BDE+∠CDF=∠CDF+∠CFD=130°,∴∠C=50°∵AB=AC,∴∠C=∠B=50°,∴∠A=180°﹣50°﹣50°=80°,故答案为:80°.2.(2017秋•浦东新区校级期末)如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数.【解答】解:设∠EDC=x,∠B=∠C=y,∠AED=∠EDC+∠C=x+y,又因为AD=AE,所以∠ADE=∠AED=x+y,则∠ADC=∠ADE+∠EDC=2x+y,又因为∠ADC=∠B+∠BAD,所以2x+y=y+30,解得x=15.所以∠EDC的度数是15°.知识点3等腰三角形的性质---三线合一等腰三角形底边上的高线、中线及顶角平分线重合.例:已知△ABC是等腰三角形,AB=AC,①AD⊥BC ②BD=CD ③AD平分∠BAC,上述三个条件,任意满足一个,可得到另外两个.即①⇒②,③;②⇒①,③;③⇒①,②.【典例】1.如图,在△ABC中,AB=AC,AD是BC边上的中线,E是AC 边上的一点,且∠CBE=∠CAD.求证:BE⊥AC.【解析】证明:∵AB=AC,AD是BC边上的中线,∴AD⊥BC,∴∠CAD+∠C=90°,又∵∠CBE=∠CAD,∴∠CBE+∠C=90°,∴∠BEC=90°,即BE⊥AC.【方法总结】本题主要是利用等腰三角形的三线合一,根据三线合一的性质可知,等腰三角形底边上的中线也是底边的高线.注:等腰三角形常作的辅助线是,过顶角的顶点向底边作垂线,再利用三线合一得到一些相等的关系式,当题目中给出等腰三角形底边上的中点时,常常将等腰三角形的顶角顶点和它直接相连.【随堂练习】1.(2017秋•莘县期末)如图,在等腰三角形△ABC中,AB=AC,BD平分∠ABC,在BC的延长线上取一点E,使CE=CD,连接DE,求证:BD=DE.【解答】证明:∵AB=AC∴∠ABC=∠ACB,∵BD平分∠ABC,∵CD=CE,∴∠E=∠CDE,∵∠ACB=∠E+∠CDE,∴∠E=∠ACB,∴∠E=∠DBE,∴BD=DE.2.(2017秋•东城区期末)如图,在△ABC中,AB=AC,AD⊥于点D,AM是△ABC的外角∠CAE的平分线.(1)求证:AM∥BC;(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.【解答】证明:(1)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD=.∵AM平分∠EAC,∴∠EAM=∠MAC=.∴∠MAD=∠MAC+∠DAC==.∵AD⊥BC∴∠ADC=90°∴AM∥BC.(2)△ADN是等腰直角三角形,理由是:∵AM∥AD,∴∠AND=∠NDC,∵DN平分∠ADC,∴∠ADN=∠NDC=∠AND.∴AD=AN,∴△ADN是等腰直角三角形.知识点4等腰三角形的判定与性质1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(简称“等角对等边”).2.等腰三角形的两个底角相等(简称“等边对等角”).3. 等腰三角形底边上的高线、中线及顶角平分线重合.【典例】1.如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC是等腰三角形,则符合条件是点C共有_______ 个.【答案】9【解析】解:①以AB作为等腰三角形的底边,则符合条件的C一定在线段AB的垂直平分线上,且处于格点上,图中红线上的点,共5个;②以AB作为等腰三角形的一个腰,当点A是等腰三角形的顶角顶点时,符合条件的点在紫色线上,共有2个,当点B是等腰三角形的顶角顶点时,符合条件的点在蓝色线上,共有2个,综合①②可知,符合条件的点C共有9个.故答案是:9.【方法总结】本题考查的等腰三角形的判定,利用的是数形结合思想,当已知两个格点找寻第三个格点时,需要分类讨论,将这条边作为底和作为腰时可以构建的等腰三角形的个数之和,即为所求的点的个数.2.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB 以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____________s时,△POQ是等腰三角形.【答案】10或103【解析】解:当PO=QO时,△POQ是等腰三角形;如图1所示:当P点在O的左侧时,∵PO=AO﹣AP=10﹣2t,OQ=1t∴当PO=QO时,10﹣2t=t;解得t=103时,△POQ是等腰三角形;即当t=103如图2所示:当P点在O的右侧,△POQ是等腰三角形,∵∠BOC=60°,∴△POQ是等边三角形,∴PO=QO=PQ∵PO=AP﹣AO=2t﹣10,OQ=1t;∴2t﹣10=t;解得t=10;故答案为:10或10.3【方法总结】本题主要考查了等腰三角形的性质,由等腰三角形的两个腰相等得出方程是解决问题的关键,注意本题分类讨论时,由于∠POQ=60°,可得出△POQ是等边三角形,再根据PO=QO进行求解.3.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.(1)求证:DE=CE.(2)若∠CDE=35°,求∠A的度数.【解析】证明:(1)∵CD是∠ACB的平分线,∴∠BCD=∠ECD.∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.(2)解:∵∠ECD=∠EDC=35°,∴∠ACB=2∠ECD=70°.∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=180°﹣70°﹣70°=40°.【方法总结】本题主要考查的是“平行+角分线” 模型,在之后学习菱形证明题时也会用到,需记牢.模型如下:如图所示,①∠1=∠2;②AC∥BD;③AB=AC(△ABC是等腰三角形)上述条件任意两个成立则第三个也成立.即①②⇒③;①③⇒②;②③⇒①.【随堂练习】1.(2018•安徽模拟)如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分別交AB、AC于点E、F,若EF=2DF,则AB的长为()A.4 B.6 C.8 D.10【解答】解:如图,延长AD,BC交于点G,∵BD平分∠ABC,AD⊥BD于点D,∴∠BAD=∠G,∴AB=BG,∴D是AG的中点,又∵DE∥BG,∴E是AB的中点,F是AC的中点,∴DE是△ABG的中位线,EF是△ABC的中位线,∴EF=BC=2,又∵EF=2DF,∴DF=1,∴DE=3,∴BG=2DE=6,∴AB=6,故选:B.2.(2018•河东区二模)如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为_____.【解答】解:过E作EG∥AB,交AC于G,则∠BAE=∠AEG,∵AE平分∠BAC,∴∠BAE=∠CAE,∴∠CAE=∠AEG,∴AG=EG,同理可得,EF=CF,∵AB∥GE,BC∥EF,∴∠BAC=∠EGF,∠BCA=∠EFG,∴△ABC∽△GEF,∵∠ABC=90°,AB=6,BC=8,∴AC=10,∴EG:EF:GF=AB:BC:AC=3:4:5,设EG=3k=AG,则EF=4k=CF,FG=5k,∵AC=10,∴3k+5k+4k=10,∴k=,∴EF=4k=.故答案为:.3.(2017春•平南县期中)如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=______.【解答】解:在Rt△ABC中,∠C=90°,∵BD=DC,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴AD=DC=5,故答案为5.综合运用1. 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有________个.【答案】2【解析】解:如上图:分情况讨论.①AB为等腰△ABC底边时,符合△ABC为等腰三角形的C点有4个;②AB为等腰△ABC其中的一条腰时,符合△ABC为等腰三角形的C点有4个.因为S△ABC=1.5,所以满足条件的格点C只有两个,如图中蓝色的点.故答案为:2.2.如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE其中正确的结论有_________.【答案】①④【解析】解:①∵D是BC的中点,AB=AC,∴AD⊥BC,故①正确;②∵虽然AC=CE,F在AE上,但F点不一定是AE的中点,∴无法证明CF⊥AE,故②错误;③由②可知,CF不一定垂直于AE,则无法证明∠1=∠2,故③错误;21④∵D 是BC 的中点,∴BD=DC ,∵AB=CE ,∴AB+BD=CE+DC=DE ,故④正确.故其中正确的结论有①④.故答案为:①④.3.如图,△ABC 中,AB=AC ,D 是BC 的中点,E 、F 分别是AB 、AC 上的点,且AE=AF ,求证:DE=DF .【解析】证明:连接AD ,∵AB=AC ,D 是BC 的中点,∴∠EAD=∠FAD ,在△AED 和△AFD 中,AE AF EAD FAD AD AD =⎧⎪=⎨⎪=⎩∠∠,∴△AED ≌△AFD (SAS ),∴DE=DF .4.如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.(1)求∠B的度数,并判断△ABC的形状;(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.【解析】解:(1)∵DE⊥AC于点E,∴∠AED=90°,∵∠D=20°,∴∠CAD=90°-∠D =90°-20°=70°,∵AD∥BC,∴∠C=∠CAD=70°,∵∠BAC=70°,∴∠BAC=∠C,∠B=180°-∠BAC- ∠C =40°,∴AB=AC,∴△ABC是等腰三角形.(2)∵延长线段DE恰好过点B,DE⊥AC,∴BD⊥AC,23∵△ABC 是等腰三角形,∴DB 是∠ABC 的平分线.5.已知等腰三角形△ABC ,AB=AC ,一腰上的中线把这个三角形的周长分成12和15两部分,求这个三角形的三边长.【解析】解:如图,在△ABC 中,AB=AC ,且AD=BD .设AB=AC=x ,BC=y ,(1)当AC+AD=15,BD+BC=12时, 根据题意得,152x x +=,122x y +=, 解得x=10,y=7.(2)当AC+AD=12,BC+BD=15时, 根据题意得,122x x +=,152x y +=, 解得x=8,y=11,故得这个三角形的三边长分别为10,10,7或8,8,11.6.如图,O 是△ABC 的∠ABC ,∠ACB 的角平分线的交点,OD ∥AB 交BC 于D ,OE ∥AC 交BC 于E ,若BC=16,求△ODE 的周长.【解析】解:∵BO平分∠ABC,∴∠ABO=∠DBO,又OD∥AB,∴∠ABO=∠DOB,∴∠DBO=∠DOB,∴OD=BD,同理OE=CE,∵BC=16,则△ODE的周长为:OD+DE+OE=BD+DE+EC=BC=16.。
等腰三角形的性质经典练习题易错易考(重点中学精品)

等腰三角形性质:1、若等腰三角形的底角等于︒15,则顶角等于2、若等腰三角形的一个角为︒50,则其他两个角的度数为 ; 若一个角为︒100,则其他两个角为3、若等腰三角形的顶角为︒n ,则底角为4、如图,在ABC ∆中,AC AB =,点D 在AC 上,且AD BC BD ==,则A ∠的度数为5、如图,BC AD //,AC AB =,︒=∠80BAC ,则=∠B ,=∠DAC6、如图,在ABC ∆中,C B ∠=∠,BC FD ⊥,AB DE ⊥,︒=∠158AFD ,则=∠EDF7、如图,ABC ∆中,AC AB =,E 为BC 中点,AC BD ⊥于D ,若︒=∠20EAC ,则=∠DBC ,=∠ABD 8、如图,等边ABC ∆中,CE BD =,AD 、BE 相交于P ,则=∠APE9、等腰三角形一腰上的高与另一腰的夹角为︒30,它的腰长为a ,则底边上的高为10、如上图,在ABC ∆中,D 、E 是BC 上两点,并且BD AB =,EC AC =,若︒=∠100BAC ,则=∠DAE11、若等腰三角形的两边a 、b ,满足0)1132(22=-+++-b a b a ,则此等腰三角形的周长为12、等腰三角形的一个底角的补角( )A.可以是钝角B. 可以是锐角C. 可以是直角D. 只能是钝角13、等腰三角形的一个底角的余角( )A.顶角B. 顶角的一半C. 顶角的两倍D. 一腰上的高与另一腰的夹角14、下列命题为假命题的是( )A.等腰三角形顶角的外角平分线与底边平行B.等腰三角形的高、中线、角平分线互相重合C.有一角为︒150且有一腰相等的两个三角形全等D.等腰三角形的底边不可以是腰的二倍15、如图,在ABC ∆中AC AB =,BD BC =, EB DE AD ==,=∠A16、等腰三角形一边长等于4,一边长等于9,它的周长为17、如图,ABC ∆中,BC AC =,AD 是BC 边上的高,AE 是BAC ∠的平分线,︒=∠48EAD ,则为=∠ACD18、如图,ABC ∆中,AC AB =,AD 和BE 是高,它们相交于点H ,且BE AE =,求证:BD AH 2=19、在等边ABC ∆中,D 、E 分别为AB 、BC 上的点,且BE AD =,AE 、CD 相交于点F ,CD AG ⊥于G ,求证:FG AF 2=20、在ABC ∆中,BAC ∠的平分线与BC 边的垂直平分线相交于点P ,过点P 作AB 、AC 的垂线,垂足分别为M 、N ,求证:CN BM =21、在ABC ∆中,AD 平分BAC ∠,AC DE //交AB 于E ,EF 平分AED ∠交BC 延长线于F ,求证:B CAF ∠=∠22、在ABC ∆中,︒=∠90ACB ,CB CA =,AB CD ⊥于D ,CE 平分BCD ∠交AB 于E ,AF 平分CAD ∠交CD 于F ,求证:BC EF //23、已知:AD AB =,CE AE ⊥于点E ,AE 平分BAC ∠,求证:AC AB AE +=2等腰三角形性质答案:1、︒1502、︒50和︒80,︒65和︒65;︒40和︒403、2180︒-︒n 4、︒36 5、︒50,︒506、︒687、︒20,︒50 8、︒60 9、a 21(钝角三角形)或a 23(等边三角形)10、︒40 11、7 12、D 13、B 14、B 15、︒4516、22 17、︒56 第19题:易证CAE ∆≌BCD ∆,BCD CAE ∠=∠∴,由等边三角形知, CAE ACD DCB ACD ACB ∠+∠=∠+∠=︒=∠60,∴︒=∠60AFG , ︒=∠30FAG ,ΘCD AG ⊥,在∆Rt 中,︒30角所对的边是斜边的一半 ∴FG AF 2=第20题:线段垂直平分线上的点到线段两端距离相等;角平分线上的点到角的两边距离相等,连结PB 、PC ,易得PC PB =,PN PM =,由HL 定理 得CN BM =第21题:AD Θ平分BAC ∠,CAD EAD ∠=∠∴AC DE //Θ,EDA CAD ∠=∠∴,EDA EAD ∠=∠∴,EA ED =∴ ΘEF 平分AED ∠,由三线合一知,EF 垂直平分AD ,FA FD =∴ADF FAD ∠=∠∴,CAD FAC FAD ∠+∠=∠,BAD B ADF ∠+∠=∠ 而BDA CAD ∠=∠,∴B CAF ∠=∠第22题:Θ︒=∠90ACB ,CB CA =,∴︒=∠=∠45B CAB ΘAB CD ⊥于D ,∴DB CD =,︒=∠=∠45B DCB ΘCE 平分BCD ∠,∴︒=∠=∠5.22ECB DCE ΘAF 平分CAD ∠,∴︒=∠5.22CAF ,易证CAF ∆≌BCE ∆,∴EB CF = ∴DE FD =,∴︒=∠=∠45B FED ,∴BC EF //第23题:延长AB 至F ,使AC BF =;延长AE 至M ,使AE AM 2=;连结CM ,易证CM AC =,CME CAE ∠=∠;AE Θ平分BAC ∠ ∴BAD CAE ∠=∠,BAD CAM ∠=∠∴,CM AF //∴,又CM AC BF ==Θ,∴四边形BFMC 为平行四边形,FM BC //∴, AD AB =Θ, ADB ABD ∠=∠∴,FM BC //Θ, AMF F ∠=∠∴ AM AF =∴,∴AC AB AE +=2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形典型题一、求度数类题目(主要以等边对等角、等角对等边为设未知数依据,将所有角用按x的未知数表示后,再找等量关系)1. 如图,△ABC中,AB=AC,BC=BD,AD=DE=EB,求∠A的度数。
2.如图,CA=CB,DF=DB,AE=AD,求∠A的度数3. 如图,△ABC中,AB=AC,D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,求∠AFD的度数4. 如图,△ABC中,AB=AC,BC=BD=ED=EA,求∠A的度数CDC5. 如图,△ABC 中,AB=AC ,D 在BC 上, ∠BAD=30°, 在AC 上取点E ,使AE=AD ,求∠EDC 的度数6. 如图,△ABC 中,∠C=90°,D 为AB 上一点,作DE ⊥BC 于E ,若BE=AC,BD=21,DE+BC=1, 求∠ABC 的度数7. 如图,△ABC 中,AD 平分∠BAC ,若AC=AB+BD 求∠B :∠C 的值8. 如图,△ABC 中,∠ABC,∠CAB 的平分线交于点P ,过点P 作DE ∥AB ,分别交BC 、AC 于点D 、E 求证:DE=BD+AECBADEP DD9. 如图,△DEF中,∠EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的大小关系10. 如图,△ABC中,∠B=60°,角平分线AD、CE交于点O求证:AE+CD=AC11. 如图,△ABC中,AB=AC, ∠A=100°,BD平分∠ABC,求证:BC=BD+AD12. 如图,△ABC中,AB=AC,D为△ABC外一点,且∠ABD=∠ACD =60°求证:CD=AB-BDADF EBOABCDEFACFABCEF13.已知:如图,AB=AC=BE ,CD 为△ABC 中AB 边上的中线求证:CD=21CE14. 如图,△ABC 中,∠1=∠2,∠EDC=∠BAC 求证:BD=ED15. 如图,△ABC 中,AB=AC,BE=CF,EF 交BC 于点G 求证:EG=FG16. 如图,△ABC 中,∠ABC=2∠C ,AD 是BC 边上的高,B 到点E ,使BE=BD 求证:AF=FCAB DFECE CA BDE 1 2FF17. 如图,△ABC 中,AB=AC,AD 和BE 两条高,交于点H ,且AE=BE 求证:AH=2BD18. 如图,△ABC 中,AB=AC, ∠BAC=90°,BD=AB, ∠ABD=30° 求证:AD=DC19. 如图,等边△ABC 中,分别延长BA 至点E ,延长BC 至点D ,使AE=BD 求证:EC=ED20. 如图,四边形ABCD 中,∠BAD+∠BCD=180°,AD 、BC 的延长线交于点F ,DC 、AB 的延长线交于点E ,∠E 、∠F 的平分线交于点H 求证:EH ⊥FHBDABBCDFADCF HG 12 M二、等腰三角形的性质及判定一、选择题1.等腰直角三角形的一个底角的度数是( )A .30°B .45°C .60°D .90°2、如图,AB AC BD BC ==,,若40A ∠=,则ABD ∠的度数是( )A .20B .30C .35D .403.如图,在Rt △ABC 中,AB =AC ,AD ⊥BC ,垂足为D .E 、F 分别是CD 、AD 上的点,且CE =AF .如果∠AED =62º,那么∠DBF =( )A .62ºB .38ºC .28ºD .26º4、如图,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,则∠A 等于( )A 、30oB 、40oC 、45oD 、36o5、如图,已知O 是四边形ABCD 内一点,OA =OB =OC ,∠ABC =∠ADC =70°,则∠DAO+∠DCO 的大小是( ) A .70° B .110 C .140° D .150°6.如图,等边△ABC 的边长为3,P 为BC 上一点,且BP =1,D 为AC 上一点,若∠APD =60°,则CD 的长为( )A .32B .23C .12D .347、某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( )A .9cmB .12cmC .15cmD .12cm 或15cm二、填空题8. 如图,在△ABC 中,AB =AC ,与∠BAC 相邻的外角为80°,则∠B =____________.AD CPB60°BCOA9.如图,在Rt △ABC 中,∠ACB =90°,∠BAC 的平分线AD 交BC 于点D ,DE ∥AC ,DE 交AB 于点E ,M 为BE 的中点,连结DM . 在不添加任何辅助线和字母的情况下,图中的等腰三角形是 .(写出一个即可)10.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于一点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:①AD=BE ; ②PQ ∥AE ; ③AP=BQ ;④DE=DP ;⑤∠AOB=60°.恒成立的有________(把你认为正确的序号都填上).11、一个等腰三角形的一个外角等于110︒,则这个三角形的三个角应该为 。
12、如图,在ABC △中,点D 是BC 上一点,80BAD ∠=°,AB AD DC ==,则C ∠= 度.三、解答题13、如图,在ABC △中,40AB AC BAC =∠=,°,分别以AB AC ,为边作两个等腰直角三角形ABD 和ACE ,使90BAD CAE ∠=∠=°.(1)求DBC ∠的度数;(2)求证:BD CE =.14.如图所示,∠BAC =∠ABD ,AC =BD ,点O 是AD 、BC 的交点,点E 是AB 的中点.试判断OE 和AB 的位置关系,并给出证明.15、如图,已知△ABC 为等边三角形,点D 、E 分别在BC 、AC 边上,且AE=CD , AD 与BE 相交于点F .(1)求证:ABE ∆≌△CAD ; (2)求∠BFD 的度数.16、如图,在边长为4的正三角形ABC 中,AD ⊥BC 于点D ,以AD 为一边向右作正三角形ADE 。
(1)求△ABC 的面积S ;(2)判断AC 、DE 的位置关系,并给出证明。
17、(2008·龙岩中考)如图,∠A =36°,∠DBC =36°,∠C =72°,找出图中的一个等腰三角形,并给予证明.我找的等腰三角形是: .三、线段的垂直平分线的性质一、选择题1、如图,在Rt ABC △中,90=∠B ,ED 是AC 的垂直平分线,交AC 于点D ,交BC 于点E .已知10=∠BAE ,则C ∠的度数为( )A .30 B .40 C .50 D .602、如图,AC =AD ,BC =BD ,则有( )A .AB 垂直平分CD B .CD 垂直平分ABC .AB 与CD 互相垂直平分 D .CD 平分∠ACB3、如图,等腰△ABC 的周长为21,底边BC = 5,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则△BEC 的周长为( )A .13B .14C .15D .16ADE二、填空题4、如图,在△ABC 中,BC 边上的垂直平分线DE 交边BC 于点D ,交边AB 于点E ,若△EDC 的周长为24,△ABC 与四边形AEDC 的周长之差为12,则线段DE 的长为 ;5、在△A BC 中,AB =AC ,AB 的垂直平分线与AC 所在的直线相交所得到锐角为50°,则∠B 等于_____________度.6、如图,AB=AC ,,AB 的垂直平分线交BC 于点D ,那么;7、如图,Rt △ABC 中,90B ∠=︒,3AB =cm ,5AC =cm .将△ABC 折叠,使点C 与A 重合,得折痕DE ,则△ABE 的周长 = cm .8、如图,50ABC AD ∠=,垂直平分线段BC 于点D ABC ∠,的平分线BE 交AD 于点E ,连结EC ,则AEC ∠的度数是 .三、解答题9、如图所示,在Rt ABC △中,9030C A ∠=∠=°,°.(1)尺规作图:作线段AB 的垂直平分线l (保留作图痕迹,不写作法);(2)在已作的图形中,若l 分别交AB AC 、及BC 的延长线于点D E F 、、,连结BE . 求证:2EF DE =.10、作图证明如图,在ABC △中,作ABC ∠的平分线BD ,交AC 于D ,作线段BD 的垂直平分线EF ,分别交AB 于E ,交BC 于F ,垂足为O ,连结DF .在所作图中,寻找一对全等三角形,并加以证明.(不写作法,保留作图痕迹)11、已知:如图,ABC △中,45ABC ∠=°,CD AB ⊥于D ,BE 平分ABC ∠,且BE AC ⊥于E ,与CD 相交于点F H ,是BC 边的中点,连结DH 与BE 相交于点G . (1)求证:BF AC =; (2)求证:12CE BF =; (3)CE 与BG 的大小关系如何?试证明你的结论.四、中考真题(学完勾股定理、实数之后可做)一、选择题 1.(浙江宁波) 在△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别是△ABC 、△BCD 的角平分线, 则图中的等腰三角形有( )(A)5个 (B)4个 (C)3个 (D)2个 2.(浙江义乌)直线CD 是线段AB 的垂直平分线,P 为直线CD 上的一点,已知线段PA =5,则线段PB 的长度为( )A .6B .5C .4D .33.(江苏无锡)下列性质中,等腰三角形具有而直角三角形不一定具有的是 ( )A .两边之和大于第三边B .有一个角的平分线垂直于这个角的对边C .有两个锐角的和等于90°D .内角和等于180° 4.(黄冈)如图,过边长为1的等边△ABC 的边AB 上一点P , 作PE ⊥AC 于E ,Q 为BC 延长线上一点,当PA =CQ 时,连PQ 交 AC 边于D ,则DE 的长为( ) A .13 B .12 C .23D .不能确定5.(山东烟台)如图,等腰△ ABC 中,AB=AC ,∠A=20°。
