层次分析法课后作业
层次分析法作业
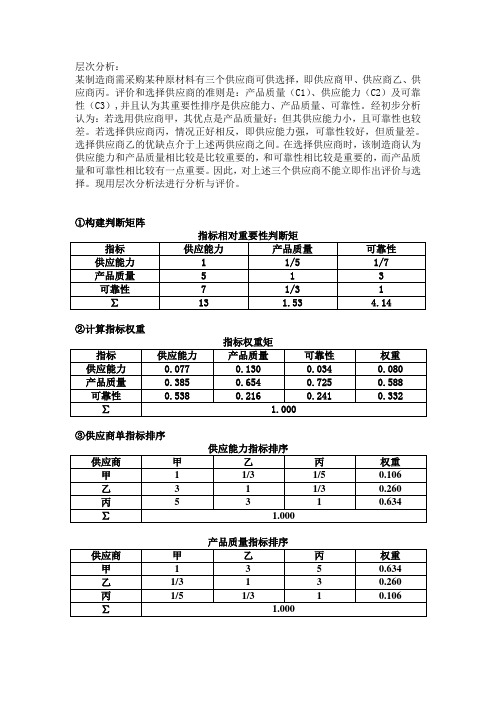
层次分析：某制造商需采购某种原材料有三个供应商可供选择，即供应商甲、供应商乙、供应商丙。
评价和选择供应商的准则是：产品质量（C1）、供应能力（C2）及可靠性（C3）,并且认为其重要性排序是供应能力、产品质量、可靠性。
经初步分析认为：若选用供应商甲，其优点是产品质量好；但其供应能力小，且可靠性也较差。
若选择供应商丙，情况正好相反，即供应能力强，可靠性较好，但质量差。
选择供应商乙的优缺点介于上述两供应商之间。
在选择供应商时，该制造商认为供应能力和产品质量相比较是比较重要的，和可靠性相比较是重要的，而产品质量和可靠性相比较有一点重要。
因此，对上述三个供应商不能立即作出评价与选择。
现用层次分析法进行分析与评价。
①构建判断矩阵指标相对重要性判断矩指标供应能力产品质量可靠性供应能力 1 1/5 1/7产品质量 5 1 3可靠性7 1/3 1 ∑13 1.53 4.14②计算指标权重指标权重矩指标供应能力产品质量可靠性权重供应能力0.077 0.130 0.034 0.080 产品质量0.385 0.654 0.725 0.588 可靠性0.538 0.216 0.241 0.332 ∑ 1.000③供应商单指标排序供应能力指标排序供应商甲乙丙权重甲 1 1/3 1/5 0.106乙 3 1 1/3 0.260丙 5 3 1 0.634∑ 1.000产品质量指标排序供应商甲乙丙权重甲 1 3 5 0.634乙1/3 1 3 0.260丙1/5 1/3 1 0.106∑ 1.000可靠性指标排序供应商甲乙丙权重甲 1 1/3 1/5 0.106 乙 3 1 1/3 0.260 丙 5 3 1 0.634 ∑ 1.000④供应商总排序供应商指标供应能力（0.080）产品质量（0.588）可靠性（0.332）总权重甲0.106 0.634 0.106 0.416 乙0.260 0.260 0.260 0.260 丙0.634 0.106 0.634 0.324经过计算，应该优先选择供应商甲。
现代汉语课后练习答案二zt
现代汉语课后练习答案二 zt第五节练习(P208)一、用层次分析法分析下列短语;二、下面的切分哪个才是正确的?请运用层次分析的三原则作出解释。
1、割断中国的历史/割断皮带的刀子前面一句的b组切分是正确的。
后面一句的a组切分是正确的。
这是三原则中的意义原则在起作用。
否则就不合愿意了。
2、去了一趟美国/去了一层外壳前面一句的切分a组是正确的，后面一组的切分b组是正确的。
这是三原则中的结构原则在起作用。
因为其它切分出来的单位不是合法的结构体。
3、小张看中的皮鞋/小张最好的皮鞋前面一句的切分a组是正确的，后面一组的切分b组是正确的。
这是三原则中的功能原则。
因为"看中的皮鞋"是名词性的结构，不能和小张构成主谓搭配。
后面的一句"小张最好"不能和皮鞋搭配，只能是"最好的皮鞋"和小张构成偏正结构。
4、很解决问题/很喜欢唱歌第一个句子b组是正确的。
第二个句子a组是正确的。
符合三原则中的结构原则和功能原则。
5、直接回答问题/救了他的孩子这两个句子的两种切分都是成立的。
第一个句子的"直接"既可以修饰"回答问题"，也可以修饰"回答";后一个句子可以是"救了""他的孩子"是述宾结构，也可以是"救了他"和"孩子"是偏正结构。
即"孩子救了他"。
分别符合三个原则。
6、没有买票的/越发显得精神第一个句子的两种切分都是正确的。
符合三原则的功能和结构原则。
后面的句子中b组的切分是正确的。
因为a种切分违反了功能原则。
三、用层次分析法分化下列的歧义短语:思考题一、层次分析法对分化类似"修路"、"汽车医院"、"连校长都不认识"、"大衣裹得严严的"这样的歧义有作用吗?层次分析法对分化类似"修路"、"汽车医院"、"连校长都不认识"、"大衣裹得严严的"这样的歧义没有作用。
现代汉语语法学第七章关于层次分析法及有关问题
（一）句法组合的层次性 （二）层次分析法 （三）对汉语一些特殊结构的处 理 （四）广义同构和狭义同构 （五） 对两种分析法的评论 1、中心词分析法
（1）基本原则
①句子分析就是分析一个句子（单句） 的句子成分。句子成分有六种——主语、 谓语、宾语、定语、状语、补语。 ②词与句子成分发生直接关系，短语 中只有联合短语和主谓短语可以直接充当 句子成分。
（2）局限性： ①层次分析法无法揭示句法结 构内部的深层语义关系。例如： 鸡不吃了 |_||_____| 主谓关系 |_||_| 状中关系 ②不易于归纳句型，对长句较 难检查出毛病。
（4）中心词分析法的局限性： ①应用范围有限。 ②忽视句法构造的层次性。 ③语义理解容易偏差 。 ④ 短语在句中的位置没有了。
一、句法组合的层次性 二、层次分析法 三、对汉语一些特殊结构的处理 四、对两种分析法的评论 1、中心词分析法 2、层次分析法
（1）优越性： ①注意到了句子构造的层次 性； ②有效地分化了歧义句； ③有一贯性。
一、现代汉语句法结构的基本类型 二、句法结构的扩展和替换 三、句法结构的层次性和层次分析法
（一）句法结构的层次性 一个句法结构是由若干个词组成 的一个序列，这个序列表面上呈线性 状态。其实，它的内部组织是有层次 性的。它是由小到大，有密到疏，有 层次地进行组合的。句法结构的这种 一层一层地组合起来的特点，就是句 法结构的层次性。
（一）句法组合的层次性 （二）层次分析法 1、什么是层次分析法 层次分析法就是逐层顺次找出某一语言 片断（包括短语和句子）的直接组成成分的 一种方法。又叫直接组成成分分析） 我们利用层次分析法把一个语言片段分 出许许多多的大小不同的片段，如果把一个 大片断包含的小片断叫做“成分”；小片断合 成的大片断叫做“组合”。
导学案答案：第二讲 短语与层次分析法
第二讲 短语与层次分析法【学习目标】1.知识目标：了解和掌握短语结构类型与层次分析法相关知识。
2.能力目标：①能够正确判断短语的结构类型；②能够运用层次分析法分析短语和单句。
3.情感、态度、价值观目标：通过该讲的学习使学生深入了解现代汉语短语的结构与层次，为提高学生个人母语素养以及他们日后正确传授语言知识奠定基础。
【重点和难点】1.短语结构类型。
2.层次分析法。
【学法指导】1.课前阅读纸质教材《现代汉语》下册44页-57页，并完成后面的预习要求。
2.通过课中学习和讨论，梳理该讲内容。
3.课后进行总结，构建知识体系。
【课前预习】一、指出下列短语的类型1.住了一年（述补）2.予以严厉批评（述宾）3.洗刷干净（述补）4.知道底细（述宾）5.阳光灿烂（主谓）6.进来歇一下（连谓）7.文化教育（偏正/联合）8.分析研究（联合）9.坚强无比（述补）10.他中等身材（主谓） 11.凯歌阵阵（主谓） 12.他去比较适合（主谓）13.态度和蔼（主谓） 14.富裕起来（述补） 15.硕果累累（主谓）16.热爱家乡（述宾） 17.十分壮丽（偏正） 18.喜欢清静（述宾）19.走了一个（述宾） 20.通知你所认识的（述宾） 21.坚持下去（述补） 22.读了三遍（述补） 23.吃得很饱（述补） 24.病虫害防治（偏正）25.我们大家（同位） 26.有人找你（兼语） 27.你们几位（同位） 28.互相支援（偏正） 29.船长老李（同位） 30.活跃学术气氛（述宾）31.独立思考（偏正） 32.禁止大声喧哗（述宾） 33.体育运动（偏正） 34.春秋两季（同位） 35.研究水平（偏正） 36.高兴得很（述补）37.“山”这个字（同位） 38.进京告状（连谓） 39.写文章做演说（联合）40.无比坚强（偏正） 41.伟大事业（偏正） 42.鼓励他学好功课（兼语）43.国庆节那天（同位） 44.战斗英雄黄继光（同位） 45.叫河水让路（兼语）46.迅速发展（偏正） 47.痛快极了（述补） 48.非常谦虚（偏正）49.摔交这种运动（同位） 50.称她为师姐（兼语） 51.史密斯先生（同位）52.打电话报警（连谓） 53.请他做东（兼语） 54.有决心搞好工作（连谓）55.出去闲逛（连谓） 56.使人聪明（兼语）二、下列短语都是多义短语，试用层次分析法分析它们内部结构层次和结构关系的不同。
层次分析法例题及答案
1.744537635
.5163904
2018
680
626.2267776
605.4918067
20.73497088
646.9617485
31.10245632
678.0642048
709.1666611
740.2691174
771.3715738
802.4740301
年份
一次
672.4387174
704.9863578
737.5339981
年份
一次
二次
at
bt
预测值
C
2011
461
480
480
0
480
0
2012
478
468.6
473.16
-4.56
464.04
-6.84
2013
501
474.24
473.808
0.432
474.672
0.648
2014
548
490.296
2014
446
390.7866667
369.1866667
21.6
412.3866667
32.4
2015
486
423.9146667
402.0234667
21.8912
445.8058667
32.8368
2016
518
461.1658667
437.5089067
23.65696
484.8228267
35.48544
2017
547
495.2663467
472.1633707
关于层次分析法的例题与解
旅游业发展水平评价问题摘要为了研究比较两个旅游城市Q、Y的旅游业发展水平，建立层次分析法]3[数学模型，对两个旅游城市Q、Y的旅游业发展水平进行了评价.首先，通过对题目中的图1、表1进行了分析与讨论，根据层次分析法，建立了目标层A、准则层B和子准则层C、方案层D四个层次，通过同一层目标之间的重要性的两两比较，得出判断矩阵,利用]1[MATLAB编程对每个判断矩阵进行求解.其次,用MATLAB软件算出决策组合向量，再比较决策组合向量的大小，由“决策组合向量最大”为目标,得出城市Y的决策组合向量为0.4325，城市Q组合向量为0.5675.最后，通过城市Q旅游业发展水平与旅游城市Y旅游业发展水平的决策组合向量比较，得出城市Q的旅游业发展水平较高.关键词层次分析法MATLAB旅游业发展水平决策组合向量1.问题重述本文要求分析QY,两个旅游城市旅游业发展水平,并且给出了两个城市各方面因素的对比，如城市规模与密度，经济条件，交通条件，生态环境条件，宣传与监督，旅游规格，空气质量，城市规模，人口密度，人均GDP，人均住房面积，第三产业增加值占GDP比重，税收GDP，外贸依存度，市内外交通，人均拥有绿地面积，污水集中处理率，环境噪音，国内外旅游人数，理赔金额，立案数量，A级景点数量，旅行社数量，星级饭店数量.建立数学模型进行求解.2.问题分析本文要求分析QY,两个城市的分析Y,两个旅游城市旅游业发展水平，在对Q中，发现需要考虑因素较多，第一、城市规模与密度，包括城市规模与人口密度.第二、经济条件，包括外贸依存度，人均GDP，人均住房面积，第三产业增加值占GDP比重，税收GDP.第三、交通条件，包括市内外交通.第四，生态环境条件包括空气质量，人均绿地面积，污水处理能力，环境噪音.第五、宣传与监督，包括国内外旅游人数，游客投诉立案件数.第六、旅游规格，包括A级景点个数，旅行社个数，星级饭店个数，这就涉及到层次分析法来估算各个指标的权重，评出最优方案.具体内容如下：（1）本文选择了对QY,两个旅游城市旅游业发展水平有影响的19个指标作为评价要素,指标规定如下：城市规模：城市的人口数量.人口密度：单位面积土地上居住的人口数.是反映某一地区范围内人口疏密程度的指标.人口影响城市规模.人口密度越大城市规模也就越大.人均GDP：即人均国内生产总值.人均城建资金：即用于城市建设的资金总投入.第三产业增加值：增加值率指在一定时期内单位产值的增加值.即第三产业增加值越高越能带动城市经济的发展.税收GDP：税收是国家为实现其职能，凭借政治权力，按照法律规定，通过税收工具强制地、无偿地征收参与国民收入和社会产品的分配和再分配取得财政收入的一种形式.外贸依存度：即城市对于外贸交易的依赖程度.市内交通：即城市市区交通情况.市外交通：即城市郊区交通情况.市内交通与市外交通对于城市交通条件具有同等的重要性.空气质量：即城市总体空气质量情况.空气质量越好对于城市生态环境就越好.人均绿地面积：即反应城市绿化面积以及人口密度的比值关系.污水处理能力：城市污水处理水平.环境噪音：城市环境噪音情况.国内外旅客人数：国内外来旅客一年总人数.人数越多说明宣传与监督就越好.理赔金额：即立案后需要赔付的资金数.立案件数：即在旅游时发生违法事件后公安部立案的件数.A 级景点数量：即A 级景点的个数.A 级景点越多,越能带动旅行社数量以及星级饭店数量,则旅游规格越大.旅行社数量：即旅行社的个数.星级饭店数量：即星级饭店在旅游景点的个数.（2）用层次分析法建立模型，根据判断矩阵，利用MATLAB 软件，算出每个判断矩阵的特征向量W 、最大特征根c 、一次性指标CI ，再结合随机一次性指标，得出每个指标的特征向量.（3）用（2）得出的数据，运用MATLAB 软件算出两个城市的决策组合向量，做比较.3.模型假设1.假设两个城市Q 、Y 的人口流动不大.2.假设两个城市Q 、Y 的各项指标短期内不会发生太大的改变.4.符号说明A : 表示目标层；j B : 表示准则层第j 个指标的名称)6,,2,1( =j ；i C : 表示子准则层第i 个指标的名称()19,,2,1 =i ； q D : 表示方案层第q 个指标的名称()2,1=q ；1w : 表示准则层对目标层的特征向量组成的矩阵； 2w : 表示子准则层对准则层的特征向量组成的矩阵； 3w : 表示方案层对子准则层的特征向量组成的矩阵；CI : 表示一次性指标；CR : 表示随机一次性指标； Z : 表示决策组合向量.5.模型建立与求解5.1 根据层次分析法分析以及题目中的图1可以建立如下表5-1的层次分析结构，并构造两两比较判断矩阵在递阶层次结构中，设上一层元素B 为准则层，所支配的下一层元素为1C ……19C ，要确定元素1C ……n C 对于准则层B 相对的重要性即权重，可分为两种情况：（1）如果1C 2C ……n C 对B 的重要性可定量，其权重可直接确定； （2）如果问题复杂，1C 2C ……n C 对B 的重要性无法直接定量，而是一些定性的，确定权重用两两比较方法.（3）其方法是，对于准则层C ，元素i C 和j C 哪一个更重要，重要多少，按1-9比例标度对重要性程度赋值.表5-2中列出了1-9标度的含义.对于准则B ，n 个元素之间相对重要性的比较得到一个两两比较判断矩阵P =()mxn ij P ，表示其中ij P 表示i P 和j P 对B 的影响之比，显然ij P >0，ij P =ijP 1，ij P =1，由ij P 的特点，P 称为正互反矩阵.通过两两判断矩阵用方根法求出他们的最大特征根和特征向量，求法如下： 1. 判断矩阵每一行元素的乘积，其中ij n1j 1p m =∏=，i =1,2…,n .2. 计算i m 的n 次方根_i w ，_i w =n i m .3. 对向量Tn w w w ⎪⎭⎫ ⎝⎛=__1,...,归一化，即∑==n j ji w 1__i w w ，则Tn w w w ⎪⎭⎫⎝⎛=__1,.为所求的特征向量.4. 计算判断矩阵的最大特征跟max λ，()∑==n1max i iinw pw λ，式中()i pw 表示pw 的第i 个元素.5. 定义⎪⎭⎫ ⎝⎛--=1max n n CI CI λ为矩阵A 的一致性指标，为了确定A 的不一致性程度的容许范围，需要找出衡量A 的一致性指标CI 的标准.引入随机一致性指标RI .平均随机一致性指标RI 是这样得到的；对于固定的n ，随机构造正互反矩阵A ，其中ij a 是从1，2，……9,91......31,21中随机抽取的，这样的A 是最不一致的，取充分大的样子（500个样本）得到A 的最大特征跟的平均值max λ，定义⎪⎭⎫ ⎝⎛--=1max n n RI λ，对于不同的n 得出随机一致性指标RI 的数值如下表5-3表中n =1,2时RI =0，是因为1,2阶的正互反矩阵总是一致阵.令RICICR =，称CR 为一致性比率，当CR <0.1时，本文认为判断矩阵具有满意的一致性，否则就需要调整判断矩阵，使之具有满意的一致性.最后通过计算得出下表5-4（其中n B 表示准则层的特征向量中的第n 个数值，in C 表示指标层的特征向量第n 个准则对第j 个指标的数值）层次总排序一致性检验的方法j n1CI c CI j j ∑==j n 1c RI RI j j ∑==RICI CR =若1.0CR时，所以认为判断矩阵具有满意的一致性，否则就需要调整判断.矩阵，使之具有满意的一致性.5.2根据层次分析法求出各个指标的权重依据题目中的表1分析，对本题做出其中一种假设：（1）经济条件和交通条件重要性相当，生态环境条件最重要，旅游规格、宣传与监督、城市规模与密度依次次之.（2）在城市规模与密度中，城市人口比人口密度重要一点.（3）在经济条件中，第三产业增加值GDP第一重要，其次是人均GDP，税收GDP、外贸依存度、人均城建资金依次次之.（4）在交通条件中，市内交通和市外交通的重要性相当.（5）在生态环境条件中，空气质量第一重要，其次是人均绿地面积，污水处理能力、环境噪音依次次之.（6）在宣传与监督中，国内外旅游人数第一重要，理赔金额、游客投诉立案件数重要性相当.（7）在旅游规格中，A级景点个数第一重要，星级饭店个数、旅行社个数依次次之.（8）对于城市规模，城市Q比城市Y的重要性小一些；对于人口密度，城市Y比城市Q的重要性明显重要；对于人均GDP，城市Q比城市Y的重要性稍重要；对于人均城建资金，城市Q比城市Y的重要性稍微重要；对于第三产业增加值GDP，城市Q比城市Y的重要性小一些；对于税收GDP，城市Q比城市Y的重要性稍小一点；对于外贸依存度,城市Q比城市Y的重要性稍重要；对于市内交通，城市Y比城市Q的重要性稍重要一点；对于市外交通，城市Y比城市Q的重要性比稍重要小一点；归于空气质量，城市Q比城市Y的重要性相当；对于人均绿地面积，城市Y比城市Q的重要性稍重要；对于污水处理能力，城市Y比城市Q的重要性稍重要一些；对于环境噪音，城市Q比城市Y的重要性相当；对于国内外旅游人数，城市Q比城市Y的重要性稍重要；对于理赔金额，城市Q比城市Y的重要性稍重要一些；对于游客投诉立案件数，城市Q比城市Y的重要性稍重要；对于A级景点个数，城市Y比城市Q的重要性稍重要小一些；对于旅行社个数，城市Y比城市Q的重要性稍重要小一些；对于星级饭店个数，城市Q比城市Y的重要性相当.根据上述分析，按1-9比例标度对准则层对目标层、子准层对准则层、目标层对子准则层的重要程度进行赋值，构造准则层对目标层的判断矩阵、子准则层对准则层的判断矩阵、方案层对子准则层的判断矩阵.准则层()6,,2,1 =j B j 对目标层A 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=12312121321141313123412252321114232111431215141411A 利用MATLAB 软件(附录1)求得 最大特征值0719.6m ax =λ特征向量⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1219.00753.03422.02057.02057.00492.01w一致性检验比率1.00116.0<=CR所以矩阵满足一致性检验.子准则层21,C C 对准则层1B 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=131311B利用MATLAB 软件(附录2)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 子准则层76543,,,,C C C C C 对准则层2B 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=121412312131321431522131511413221412B 利用MATLAB 软件(附录3)求得 最大特征值0681.5m ax =λ特征向量⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0973.01599.04185.00618.02625.0w一致性检验比率1.00152.0<=CR所以矩阵满足一致性检验.子准则层98,C C 对准则层3B 的判断矩阵⎥⎦⎤⎢⎣⎡=11113B 利用MATLAB 软件(附录4)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 子准则层13121110,,,C C C C 对准则层4B 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1121311121312212133214B 利用MATLAB 软件(附录5)求得最大特征值0104.4m ax =λ特征向量⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1409.01409.02628.04554.0w 一致性检验比率1.00038.0<=CR所以矩阵满足一致性检验.子准则层161514,,C C C 对准则层5B 的判断矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1221211212215B 利用MATLAB 软件(附录6)求得最大特征值0536.3m ax =λ特征向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3108.01958.04934.0w 一致性检验比率1.00462.0<=CR所以矩阵满足一致性检验.子准则层191817,,C C C 对准则层6B 的判断矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1221211312316B 利用MATLAB 软件(附录7)求得最大特征值0092.3m ax =λ特征向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2970.01634.05396.0w 一致性检验比率1.00079.0<=CR所以矩阵满足一致性检验.方案层对子准则层的判断矩阵 方案层21,D D 对子准则层1C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=122111C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层2C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=155112C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎢⎣=1667.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层3C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=133113C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层4C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=144114C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层5C 的判断矩阵：⎥⎥⎦⎤⎢⎢⎣⎡=122115C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎢⎣=3333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层6C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=133116C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层7C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=141417C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层8C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=155118C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎢⎣=8333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层9C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=122119C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层10C 的判断矩阵⎥⎦⎤⎢⎣⎡=111110C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层11C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1313111C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=7500.02500.0w因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层12C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1414112C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2000.08000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层13C 的判断矩阵⎥⎦⎤⎢⎣⎡=111113C 利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层14C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331114C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验.2115⎥⎥⎦⎤⎢⎢⎣⎡=1441115C 利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层16C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331116C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层17C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331117C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验.2118⎥⎥⎦⎤⎢⎢⎣⎡=1221118C 利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子19C 的判断矩阵： ⎥⎦⎤⎢⎣⎡=111119C 利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 通过准则层()6,,2,1 =j B j 对目标层A 的判断矩阵、子准则层()19,,2,1 =i C i 对准则层()6,,2,1 =j B j 的判断矩阵得出特征向量，建立层次总表5-5层次总排序一致性检验如下:0073.061==∑=j j j CI B CI65274.0j 61j j ==∑=RI B RI0111.065274.00073.0===RI CI CR 由于1.00111.0<=CR ,所以认为层次总排序的结果具有满意的一致性，因此不需要重新调整判断矩阵的元素取值.5.3 利用MATLAB 进行决策组合向量的运算（附录9）⋅⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⋅⋅=Tw w w Z 2970.0001634.0000005396.00000003108.0000001958.0000004934.00000001409.0000001409.0000002628.0000004554.00000005000.0000005000.00000000973.0000001599.0000004185.0000000618.0000002625.00000002500.0000007500.0132⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡5000.05000.06667.03333.06667.03333.02500.07500.08000.02000.02500.07500.05000.05000.02000.08000.07500.02500.05000.05000.06667.03333.01667.08333.08000.02000.02500.07500.06667.03333.02000.08000.02500.07500.08333.01667.03333.06667.0⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅1219.00753.03422.02057.02057.00492.0 Z ⎥⎦⎤⎢⎣⎡=5675.04325.0 比较Z 值大小可知，12Z Z >,表明城市Q 的旅游发展也水平最高，城市Y 的旅游业发展水平次之，所以城市Q 的旅游发展也水平高.6模型的评价优点：(1) 本文选择了计算比较简单的层次分析法，经过计算得到了相应的综合发展旅游业的估计值，为城市旅游业的发展提供了依据.(2) 使用了MATLAB 软件，减少了计算工作量，大大降低了运算的困难.缺点：判断的结果具有一定的主观性，不能比较切实的结合当地的具体情况，做出科学的决策方案.7参考文献[1] 姜启源等，数学建模（第四版）北京:高等教育出版社.2011年[2] 马莉，数学实验与建模，北京:清华大学出版2010年[3] 王莲芬，层次分析法引论，北京:中国人民大学出版社，1990年附录：附录1x=[1 1/4 1/4 1/5 1/2 1/3;4 1 1 1/2 3 2;4 1 1 1/2 3 2;5 2 2 1 4 3;2 1/3 1/3 1/4 1 1/2;3 1/2 1/2 1/3 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-6)/5 %一致性指标CR=CI/1.24 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =6.0719W =0.04920.20570.20570.34220.07530.1219B =0.04670.21410.21410.29180.08810.1452CI =0.0144CR =0.0116C =0.2146附录2：>> x=[1 3;1/3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250附录3：x=[1 4 1/2 2 3;1/4 1 1/5 1/3 1/2;2 5 1 3 4;1/2 3 1/3 1 2;1/3 2 1/4 1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-5)/4 %一致性指标CR=CI/1.12 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =5.0681W =0.26250.06180.41850.15990.0973B =0.27340.05940.36640.18730.1135CI =0.0170CR =0.0152C =0.2698附录4：x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000附录5：x=[1 2 3 3;1/2 1 2 2;1/3 1/2 1 1;1/3 1/2 1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-4)/3 %一致性指标CR=CI/0.90 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =4.0104W =0.45540.26280.14090.1409B =0.43950.27870.14090.1409CI =0.0035CR =0.0038C =0.3131附录6：x=[1 2 2;1/2 1 1/2;1/2 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-3)/2 %一致性指标CR=CI/0.58 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =3.0536W =0.49340.19580.3108B =0.46060.18790.3515CI =0.0268CR =0.0462C =0.3733附录7：x=[1 3 2;1/3 1 1/2;1/2 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-3)/2 %一致性指标CR=CI/0.58 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =3.0092W =0.53960.16340.2970B =0.51990.16200.3181CI =0.0046CR =0.0079C =0.4015附录8：% 目标层Q,Y对子准则层C1的赋值>> x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C2的赋值x=[1 5;1/5 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.83330.1667B =0.83330.1667CI =CR =NaNC =0.7222End% 目标层Q,Y对子准则层C3的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C4的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.80000.2000B =0.80000.2000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C5的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.66670.3333B =0.66670.3333CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C6的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C7的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.20000.8000B =0.20000.8000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C8的赋值x=[1 5;1/5 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.16670.8333B =0.16670.8333CI =CR =NaNC =0.7222End% 目标层Q,Y对子准则层C9的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C10的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =NaNC =0.5000% 目标层Q,Y对子准则层C11的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.25000.7500B =0.25000.7500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C12的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =W =0.80000.2000B =0.80000.2000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C13的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000% 目标层Q,Y对子准则层C14的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C15的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.20000.8000B =0.20000.8000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C16的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C17的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C18的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C19的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000附录9：% 最终组合权向量：x=[0.75 0 0 0 0 0;0.25 0 0 0 0 0;0 0.2625 0 0 0 0;0 0.0618 0 0 0 0;0 0.4185 0 0 0 0;0 0.1599 0 0 0 0;0 0.0973 0 0 0 0;0 0 0.5 0 0 0;0 0 0.5 0 0 0;0 0 0 0.4554 0 0;0 0 0 0.2628 0 0;0 0 0 0.1409 0 0;0 0 0 0.1409 0 0;0 0 0 0 0.4934 0;0 0 0 0 0.1958 0;0 0 0 0 0.3108 0;0 0 0 0 0 0.5396;0 0 0 0 0 0.1634;0 0 0 0 0 0.2970]x =0.7500 0 0 0 0 00.2500 0 0 0 0 00 0.2625 0 0 0 00 0.0618 0 0 0 00 0.4185 0 0 0 00 0.1599 0 0 0 00 0.0973 0 0 0 00 0 0.5000 0 0 00 0 0.5000 0 0 00 0 0 0.4554 0 00 0 0 0.2628 0 00 0 0 0.1409 0 00 0 0 0.1409 0 00 0 0 0 0.4934 00 0 0 0 0.1958 00 0 0 0 0.3108 00 0 0 0 0 0.53960 0 0 0 0 0.16340 0 0 0 0 0.2970y=[0.0492;0.2057;0.2057;0.3422;0.0753;0.1219]y =0.04920.20570.20570.34220.07530.1219z=x*y运算结果：z =0.03690.01230.05400.01270.08610.03290.02000.10290.10290.15580.08990.04820.04820.03720.01470.02340.06580.01990.0362a=[0.3333 0.8333 0.75 0.2 0.3333 0.75 0.2 0.1667 0.3333 0.5 0.25 0.8 0.5 0.75 0.2 0.75 0.3333 0.3333 0.5;0.6667 0.1667 0.25 0.8 0.6667 0.250.8 0.8333 0.6667 0.5 0.75 0.2 0.5 0.25 0.8 0.25 0.6667 0.6667 0.5]a =Columns 1 through 70.3333 0.8333 0.7500 0.2000 0.3333 0.7500 0.20000.6667 0.1667 0.2500 0.8000 0.6667 0.2500 0.8000Columns 8 through 140.1667 0.3333 0.5000 0.2500 0.8000 0.5000 0.75000.8333 0.6667 0.5000 0.7500 0.2000 0.5000 0.2500Columns 15 through 190.2000 0.7500 0.3333 0.3333 0.50000.8000 0.2500 0.6667 0.6667 0.5000c=a*z运算结果：c =0.43250.5675。
层次分析法作业
一．问题重述研究“美丽河南”的综合评价体系。
[提示：采用绝对美丽和相对美丽的方式，从多个方面给出指标体系，并给出相应的权重（说明给出权重的依据或方法）]。
二．问题分析河南，古称中原，简称“豫”，地处中国中东部，黄河中下游，省会郑州，因省域大部分位于黄河以南，故名河南，与山东、河北、山西、陕西、湖北、安徽接壤。
河南是华夏文明和中华民族的核心发祥地，华夏历史文化的中心，先后有20多个朝代建都或迁都于此，数千年来是中国的政治、经济、文化中心，诞生了洛阳、开封、安阳、郑州等中华古都。
问题要求采用绝对美丽和相对美丽的方式，从多个方面给出指标体系，并给出相应的权重。
故考虑运用层次分析法建立模型，首先建立层次结构模型，其次构造成对比较矩阵，最后分别计算单排序权向量和总排序权向量并做一致性检验。
二．模型假设1.假设我们所统计和分析的规律都是客观真实的。
2.在数据计算的过程中，假设误差在合理的范围之内，对数据结果的影响可以忽略。
四．符号说明符号定义与说明A，B，C 成对比较矩阵ω权向量λ特征根CI 一致性指标绝对RI 随机一致性指标CR 一致性比率五．模型的建立与求解5.1 建模，分析层次结构其中，Z 表示“美丽河南”城市评判，和分别表示绝对美丽和相对美丽，,，分别表示空气质量，旅游景点数目和市民幸福指数，市民素质，人均GDP 。
5.2 构造成对比较矩阵其中，准则层Ｂ对目标层Ａ的成对比较矩阵：；子准则层Ｃ对准则层Ｂ的成对比较矩阵：;方案层D 对子准则层C 的成对比较矩阵：111/21/3211/2321C 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫;21321/311/31/231C 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫;311/91/291521/51C 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫; 411/5151411/41C 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫;511/7171511/51C 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫5.3确定权重经Matlab 编程计算确定准则层B 对目标层A 的权向量(2)(0.6667,0.3333)T w =，且A 为一致阵，满足(2)2,0CI l ==,一致性检验通过。
《现代汉语通论》语法_课后作业答案[1]1
![《现代汉语通论》语法_课后作业答案[1]1](https://img.taocdn.com/s3/m/7ac2b95dff00bed5b9f31d65.png)
172页第四章第一节练习题一、汉语语法的总特点是什么？举例说明汉语语法的四个主要特点。
语言中用来表示语法关系、表现语法意义的语法手段有多种多样，重要的有：形态变化、词序变化、虚词运用等等。
有的语言偏重于形态变化，例如法语、俄语；有的语言偏重于词序变化和虚词运用，例如汉语。
汉语的特点是在跟印欧语的比较中表现出来的。
它的总特点是：不依赖于严格意义的形态变化，而主要借助于语序、虚词等其他的语法手段来表示语法关系和语法意义。
这一总特点具体表现在以下四个方面：1．语序的变化对语法结构和语法意义起重大影响。
例如：“名词+动词/形容词”构成“主谓结构”，词序一变化，“动词+名词”就构成了“述宾结构”，“形容词+名词”就构成了偏正结构。
例如：我们同意(主谓关系)--同意我们（述宾关系）衣服干净（主谓关系）--干净衣服（偏正关系）2．词的运用对语法结构和语法意义有重要作用。
汉语里的虚词十分丰富，作用也特别的重要。
例如：某些句法结构有没有虚词，结构关系和语义会发生很大的变化。
如“爸爸妈妈”和“爸爸的妈妈”意思不同。
3．语词类跟句法成分之间不存在简单的一一对应的关系。
在印欧语里，词类和句法成分之间往往存在着一种简单的对应关系。
但是在汉语里，词类跟句法成分之间的关系就比较复杂，除了副词只能做状语，属于一对一之外，其余的都是一对多，即一种词类可以做多种句法成分。
例如：名词主要做主语宾语，但有时也可以做定语、谓语等。
4．短语的结构跟句子的结构以及词的结构基本一致。
例如：结构类型短语词句子联合哥哥弟弟兄弟团结，团结，在团结。
偏正牛皮箱子皮箱伟大的人民！述宾管理家务管家欢迎新同学。
述补说得明白说明高兴得跳起来。
主谓年纪轻年轻我们上课。
二、请以“不怕辣”、“辣不怕”和“怕不辣”为例，说明汉语语法语序变化的特点。
语序是汉语句法结构中的一个主要的表达手段，同样的词排列顺序不同，句法结构关系也不同，所表达的意义也有所不同，例如：“不怕辣”、“辣不怕”和“怕不辣”三个词：不、怕、辣，排列的语序不同，其结构关系分别是：述宾结构、主谓结构、述宾结构。
层次分析法例题
二、AHP 求解层次分析法（Analytic Hierarchy Process ）是一种定量与定性相结合的多目标决策分析法，将决策者的经验给予量化，这在对目标（因素）结构复杂且缺乏必要数据的情况下较为实用。
（一）、建立递阶层次结构目标层：最优生鲜农产品流通模式。
准则层：方案的影响因素有：1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层：设三个方案分别为：1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构（二）、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵，引入1～9的标度，见表3—1.目标层：准则层：方案层：表3—1 标度值为了构造判断矩阵，作者对6个专家进行了咨询，根据专家和作者的经验，四个准则下的两两比较矩阵分别为：（三）、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素，排出评比的次序，这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量，经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值，这一过程称为层次单排序。
能否确认层次单排序，需要进行一致性检验，所谓一致性检验是指对A确定不一致的允许范围。
a，则λ比n 大的越多，A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量，其不一致程度越大，引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验：max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值，n 是比较矩阵的阶数。
语言学概论课后作业语法部分
C、可以插如别的成份 D、可以作为一个单位出现。
4、“老朋友”作为语法单位属于:
A、实词 B、虚词
C、固定词组 D、自由词组
5、下列各组词中全都属于复合词的一组是：
A、大学、人民、（英）reader
A．The newspaper is reading by John.
B．The newspaper is by John reading.
C．The newspaper is being read by John.
D．The newspaper is being readed by John.
A、动宾 B、偏正
C、动词 D、联合
16．以下概念属于组合关系的是:
A、主谓 B、形容词
C、宾语 D、单纯词
17．下列语言单位都属于词的是:
A、语言、饭菜、（英语）classsroom（教室）、（俄语）книга（书）
B、劳动、进步、（英语）light -wave（光波）、（日语）わたくし（我）
D． 折断了猎人的枪
26．英语动词"be"有八种变化形式，下列句子中，只有_____使用正确。
A． He be good child.
B． I am a teacher.
C． They is peasant.
D． You was workers.
27．下列句子符合英语语法规则的是:
D、走-走走 看-看看
20．下列说法不正确的一项是:
A． 组合规则为句子的生成提供了无数的可能
B． 聚合规则为句子的生成提供了无数的可能
C． 我们日常使用语言离不开语法规则
黄伯荣版现代汉语下册课后习题答案
⑥这个特别恶狠狠的抢劫犯，终于被刑警逮捕了。 形容词“恶狠狠”不能加程度副词，“特别”应删。
第五章 语法
思考和练习三
一、划分汉语实词、虚词的依据是什么？
两者的不同主要是：实词意义比较实在，有词汇 意义，能充当句法成分；虚词则相反，意义较虚，只 有语法意义，不单独充当句法成分。
二、用“△”号把下面一段话里的虚词标出来，然后列 一个虚词表，把它们的大类小类分别填在表里。（重复 的可只写一个，并用数码表示重复的次数）
六、举例说明一般的句法成分是如何配对的。
一般句法成分有八个。每—个成分都是在同一层次上 跟另一成分发生直接关系，因而配成一对，即：
主语——谓语：
差距‖很大
动语——宾语：
学
状语——状语中心语：〔明显〕回落
这两例中，用中心词分析法分析出的主语是一个词 （名词），谓语也只是一个词（动词）；用层次分析法分 析出的主语则是一个短语（名词性短语），谓语也是一个
四、为什么说研究语法要注意民族特点。
不同民族的语言，既有共性又各有个性，如果忽视民 族语言的个性或特点，就不能深入认识一种语言的语法结 构规律。例如对汉语，要研究“把”字句和“被”字句， 不能只满足于说明哪是主语、哪是谓语、哪是状语等，还 要指出它的结构特点、构成条件和所表示的语法意义，还 要了解“把家回、被他打”这些说法的语用条件，这样才 能研究好、掌握好汉语语法。
形容词 热烈 透彻 充分 乌蓝 区别词 初步 数词 一 量词 双 个 片 副词 刚刚 即将 务必 还 没有 就 决 代词 这 我们 你们 什么
三、给下列各词分别归类。
①热爱（动词）、可爱（形容词） ②答案（名词）、答应（动词） ③战争（名词）、作战（动词） ④非常（副词）、平常（形容词） ⑤青年（名词）、年轻（形容词） ⑥坚决（形容词）、决心（名词）
层次分析法实例
• 一切伟大的劳动成果都值得爱惜和尊重
主
‖
谓
定） 中
状〕 中
定） 中
动｜ 宾
定）中
联+合
精品课件
小王劝你别去 主‖ 谓
兼语
动｜宾
主‖谓
状〕中
（从大到小的层次分析法）
• 战斗在硝烟弥漫的前沿阵地上
中〈
补
Hale Waihona Puke 介词短语方位短语定） 中
主‖谓 定 ）中
连长马上返回军部开会 主‖ 谓 状〕 中 连 ┊谓 动｜宾
• 复杂短语切分的十六字口诀：
• 以动为心（先找出短语的中心——动词） • 先切动前（先找主、状） • 再切动后（后找宾、补） • 先远后近（多个状语或动后有多个成分）
精品课件
（从大到小的层次分析法）
• 我国人民的物质文化生活水平 定） 中
定）中
定 ）中 定 ）中 联+合
• 世界上第一个发明针灸的国家
• 写出 更多更好的作品
分析研究一下材料
•
动｜
宾
动
｜ 宾 精品课件
• 谁是最可爱的人 做 一个有理想有作为的青年
• 主‖
谓
宾
动｜
•
动｜ 宾
中
定）
•
定 ）中
量短
定
）中
•
状〕中
联＋合
精品课件
•
一种新式的炊具电磁炉
•
同
=位
•
定） 中
•
量短 定 ） 中
精品课件
• 世界珍贵稀有动物熊猫的故乡中国
•
同
=位
•
语法上不能搭配）
精品课件
• ③ 切分出来的各个成分在语义上的搭配必须跟 整个组合（即与它所在的更高一级的语言单位） 的原意相符。如： 咸/鸭蛋 咸鸭/蛋※
层次分析法练习
1．对下列短语作层次分析，如果有歧义，要作不同的分析。
(1)要求我们班明天去主楼开会(2)访问台湾归来的科学家(3)咬死了猎人的狗(4)他的哥哥和妹妹的朋友(5)三个报社的记者和编辑(6)看打乒乓球的中小学生(7)校办工厂幼儿园(8)看望陈老师的学生(9)打死老虎(10)爸爸和妈妈的同事(11)我们三个一组2．用层次分析法分析下列词组(1)恢复和发扬母校的优良传统(2)母亲那布满皱纹的慈祥的脸(3)牺牲在这块土地上的烈士(4)处理好工作、学习二者的关系(5)用中国乐器演奏的西洋乐曲(6)积极地培育和正确地使用人才(7)一位优秀的小学低年级语文教师(8)那些充满幻想的诗句(9)交给连长一份秘密文件(10)发明能打出乐谱的打字机的人(11)周密的调查能解决问题(12)在人才集中的研究机关工作(13)把这个问题讲得又深又透(14)教室里有两个人在交谈(15)为国家和人类作出重大贡献的科学工作者(16)派他到镇上看一下市场情况(17)矿山建设者的豪迈誓言(18)不能磨灭的深刻印象(19)写出更多更好的作品(20)分析研究以下材料(21)严格控制基本建设的规模(22)选他当人民代表(23)请他到北京参加科学讨论会(24)谁是最可爱的人(25)夏天和冬天温差都很大(26)世界珍惜动物熊猫的故乡中国(27)浓浓的长长的眉毛和一双不大不小的眼睛(28)在我们读书的教室里(29)那个特别红的让他拿走了(30)沿走廊走过去往右拐就到了(31)去图书馆借讲法律的书(32)命令部队迅速占领制高点阻击敌人(33)老师叫你去办公室交语法作业(35)扮成一个看山林的人(36)请你陪小李上街买东西(37)刚刚打扫完教室的王芳(38)气氛紧张的会议室里(39)对国内外旅游者有着极大的吸引力(40)选你当组长最合适。
全体同学都做完了语法作业层次分析法
全体同学都做完了语法作业层次分析法本文主要讨论如何使用层次分析法来识别全体同学都完成了语法作业的情况。
首先，本文介绍了层次分析法的基本概念，然后讨论了利用这一方法识别全体同学完成作业的具体实施方法。
在结论部分，本文进一步讨论了层次分析法对学校教育效率的提升作用。
第一部分次分析法基础层次分析法是一种系统分析方法，是一种量化技术，用于中层管理者来分析复杂的问题，以识别出大型组织中存在的致命性问题，以及组织中可能出现的问题。
它把复杂的问题拆分成一系列子问题，用定量和定性数据对其进行分析，从而找出系统中存在的问题，提出改进措施。
层次分析法的基本步骤是：首先，将复杂的问题拆分成一系列子问题，然后用定量和定性数据对它们进行分析，最后用这一分析结果来识别出系统中存在的问题，并计算出它们的优先级，从而推出最佳的解决方案。
第二部分体同学完成作业的层次分析层次分析法可以用来识别全体同学都完成了语法作业的情况。
这一过程可以分为以下几个步骤。
第一步，进行完整性评估。
这一步骤旨在让老师能够识别出班级中有多少学生完成了语法作业。
可以通过剔除其他项目来鉴别学生完成语法作业的情况，以及对完成了语法作业的学生进行统计，来评估班级中全部学生完成了语法作业的情况。
第二步，进行质量评估。
在这一步中，老师可以用定量和定性数据来评估各个学生完成了语法作业的质量。
可以使用范围、平均值、方差等量化技术，以及复杂件技术来对语法作业的质量进行评估。
第三步，采取改进措施。
在这一步中，老师可以根据分析结果，采取不同的改进措施来提高学生完成语法作业的质量。
例如，老师可以采取定期讨论、定期评估等方式来提高学生完成语法作业的质量。
第三部分次分析法对学校教育效率的提升作用层次分析法不仅可以用来识别全体同学完成语法作业的情况，它也可以用来提高学校教育效率。
在系统管理方面，层次分析法可以帮助教育机构更好地规划教学大纲，确定课程质量要求，以及提高教学管理效率。
此外，层次分析法也可以用来检查和完善教学评估系统，以确保学生受到有效的评估和详细的反馈，从而提高学校的教学质量。
全体同学都做完了语法作业层次分析法
全体同学都做完了语法作业层次分析法在汉语言中，语法作业层次分析法是一种有效的语言学习方法，尤其是在汉语语法概念以及汉语句子结构上，它能够帮助学习者更容易理解汉语的语法构成以及汉语句子的结构，这有助于学习者更好地理解汉语，尤其是针对汉语句子结构方面的理解。
语法作业层次分析法是一种逐步分析语法结构和句子结构的方法，它有助于学习者熟悉语法结构概念，逐步了解句子结构，从而提高其理解能力。
语法作业层次分析法通常被称为“语法研究”，它是逐步了解语法结构的一种方法。
首先，学习者应该从语言的最基本的部分开始，比如说词语、句子等，并逐步了解语言结构构成的内容，再逐步了解语法结构的演变，最后，可以更好地理解句子的结构，从而提高对语言的理解能力。
通过语法作业层次分析法，学习者可以更容易地理解语法构成，从而更好地了解语言结构和句子结构，从根本上提高自己的语言理解能力。
在汉语句子中，“主语-谓语-宾语”的结构是最基本的，如果学习者掌握了这个基本的句子结构，对其它相对复杂的句子结构也会更加熟悉，这也是“语法作业层次分析法”所体现出来的。
再次，通过语法作业层次分析法，学习者可以更好地认识到句子的特点，也就是句子中的每个部分所承担的含义以及目的。
由于每个句子都是由不同部分组成的，所以学习者了解每个部分所承担的意义和功能就非常重要，将这些语法结构清楚地拆分出来，分析每一部分的成分，可以帮助学习者更好地理解句子的结构。
最后，语法作业层次分析法还有助于学习者掌握句子的特点，其中包括句子的正确发音、句子的正确格式等，这些可以帮助学习者掌握句子的语音特点，从而更好地理解句子的意思及其结构。
综上所述，语法作业层次分析法是一种有效的汉语语法学习方法，它帮助学习者更容易理解汉语的语法构成以及汉语句子的结构，有助于学习者更好地理解汉语，从而提高自己的汉语水平。
“语法作业层次分析法”是一种逐步分析语法结构和句子结构的方法，它能够帮助学习者更容易理解语言结构的构成，掌握句子的特点，从而更好地理解汉语句子的结构及其变化。
我们在教室写完了作业。用层次法分析
我们在教室写完了作业。
用层次法分析
1、第一层次：能够认真落实、出色的完成老师布置的各项作业，并且能够深入研究与思考作业中的困惑和问题，同时还会有安排紧凑的、严密的学习计划，与老师的安排相辅相成，共同促进深度的学习，有一种不解决问题誓不罢休的心态，自律性强，懂的珍惜学习时间，能够高效学习。
2、第二层次：及时查看老师布置的作业，基本能完成各项作业、缺乏深度思考，关于自己的学习计划有自己的想法但是落实不够到位，有自律性，但不够强，面对自己的一些难点、疑点有所妥协，能有效学习但不高效，时间观念有点欠缺。
3、第三层次：面对各项作业都尽量去做，做不完或者不会做的就随便应付一下，没有自己的思考，没有自己的学习计划，没有自律性，存在无效学习，没有时间观念。
4、第四层次：作业马虎应付，随便做一下甚至不做作业，没有主动学习，谈不上自己的学习计划，自律性差，谈不上自己的思考，学习比较随便，从不考虑学习效率和质量。
01短语层次及句子成分分析练习答案
4
六、指出下面句子的定语、状语是用什么词语充当的(短语指出结构类)。 ①他拿<来>(一件)(崭新)的(白色)(府绸)衬衫。(量词短语·形容词·名词·名词) ②国家保护(公民)的(合法收入、储蓄、房屋和其他生活资料的)所有权。(名词·联合短语) 按:这句应为一个定语。 ③(我们的)国家进入了(新)的(历史)时期。(代词·形容词·名词) ④这是(一件)(刚买来)的(呢子)大衣。(量词短语·偏正短语·名词) ⑤他[用胳膊][轻轻]地触着我，眼睛[却][仍然][在][兴奋]地望着外面。 (介词短语·形容词·副词·副词·副词·形容词) ⑥宏儿听得(这)话，[便]来招水生，水生[却][松松爽爽][同他][一路]出去。 (副词·副词·形容词·介词短语·副词) 七、定语是说明性质、领属、数量等等的，试指出下面句子里每个定语所表示的语义类别以及是描写 性的还是限制性的。 ①(我们)的祖国[多么]壮丽！(事物的领有者／限制性) ②(昨天)的报纸有(个)(好)消息。(时间·数量·性状／限制性·限制性·限制性) ③(西湖)的风景非常美。(处所／限制性) ④前面是(一片)(绿油油)的田野。(数量·性状／限制性·描写性) ⑤他是(一个)(勇敢)的人。(数量·性状／限制性·限制性) ⑥(四个)战士[都]来了。(数量／限制性) ⑦(铜)茶壶放<在桌子上>。(质料／限制性) ⑧(那件)衣服[已经]晒<干>了。(指量／限制性) 八、下面句子里的状语，哪些既可以放在主语后，又可以移到主语前？哪些只适宜于放在主语前？哪 些不能放在主语前？ ①[在敌国，在暴君的掌握之中]，我[也]不怕不惊。 状语“在敌国，在暴君的掌握之中”分别表处所、范围，可以移到主语后。只是状语比较长，而要突 出状语所表达的意思，最好放在句首。 ②[早在十六七世纪之交]，(西方)的(一些)(自然科学)知识[已经]传播<到>中国。 状语“早在十六七世纪之交”表时间，可以移到主语后。状语“已经”也是表时间的，不过这个副词 只能用在动词前，不能移到主语前。 ③[根据一些地方的调查]，[五十年代]，(从事农业生产)的劳力[约]占 95％以上。 句中有两个状语，每一个都有可能移到主语后，但是这一句的状语较长，为了句子结构的紧凑，状语 不宜移动。
层次分析法例题
某物流企业需要采购一台设备,在采购设备时需要从功能、价格与可维护性三个角度进行评价,考虑应用层次分析法对3个不同品牌的设备进行综合分析评价和排序,从中选出能实现物流规划总目标的最优设备,其层次结构如下图所示;以A 表示系统的总目标,判断层中1B 表示功能,2B 表示价格,3B 表示可维护性;1C ,2C ,3C 表示备选的3种品牌的设备;解题步骤：1、标度及描述人们定性区分事物的能力习惯用5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就得到9个数值,即9个标度;为了便于将比较判断定量化,引入1～9比率标度方法,规定用1、3、5、7、9分别表示根据经验判断,要素i 与要素j 相比：同样重要、稍微重要、较强重ij a ij =1/a ji ；a ii =1； i,j=1,2,…,n目标层判断层 方案层 图 设备采购层次结构图显然,比值越大,则要素i 的重要度就越高;2、构建判断矩阵A判断矩阵是层次分析法的基本信息,也是进行权重计算的重要依据; 根据结构模型,将图中各因素两两进行判断与比较,构造判断矩阵：●判断矩阵B A -即相对于物流系统总目标,判断层各因素相对重要性比较如表1所示；●判断矩阵C B -1相对功能,各方案的相对重要性比较如表2所示； ●判断矩阵C B -2相对价格,各方案的相对重要性比较如表3所示； ●判断矩阵C B -3相对可维护性,各方案的相对重要性比较如表4所 示;B A -C B -1C B -3一般来讲,在AHP 法中计算判断矩阵的最大特征值与特征向量,必不需要较高的精度,用求和法或求根法可以计算特征值的近似值;●求和法1将判断矩阵A 按列归一化即列元素之和为1：b ij = a ij /Σa ij ； 2将归一化的矩阵按行求和：c i =Σb ij i=1,2,3….n ； 3将c i 归一化：得到特征向量W =w 1,w 2,…w n T ,w i =c i /Σc i ,W 即为A 的特征向量的近似值； 4求特征向量W 对应的最大特征值： ●求根法1计算判断矩阵A 每行元素乘积的n 次方根；nnj iji aw ∏==1i =1, 2, …,n2将i w 归一化,得到∑==ni iii ww w 1；W =w 1,w 2,…w n T 即为A 的特征向量的近似值；3求特征向量W 对应的最大特征值：1判断矩阵B A -的特征根、特征向量与一致性检验 ①计算矩阵B A -的特征向量;计算判断矩阵B A -各行元素的乘积i M ,并求其n 次方根,如3223111=⨯⨯=M ,874.0311==M W ,类似地有,466.2322==M W ,464.0333==M W ;对向量Tn W W W W ],,,[21 =规范化,有类似地有684.02=W ,122.03=W ;所求得的特征向量即为： ②计算矩阵B A -的特征根类似地可以得到948.12=AW ,3666.03=AW ; 按照公式计算判断矩阵最大特征根： ③一致性检验;实际评价中评价者只能对A 进行粗略判断,这样有时会犯不一致的错误;如,已判断C 1比C 2重要,C 2比C 3较重要,那么,C 1应该比C 3更重要;如果又判断C 1比C 3较重要或同等重要,这就犯了逻辑错误;这就需要进行一致性检验;根据层次法原理,利用A 的理论最大特征值λmax 与n 之差检验一致性; 一致性指标：计算002.0133004.31max =--=--=n nCI λ<,1.0003.0<==RI CI CR ,查同阶平均随机一致性指标表5所示知58.0=RI ,一般认为CI<、 CR<时,判断矩阵的一致性可以接受,否则重新两两进行比较;1类似于第1步的计算过程,可以得到矩阵C B -1的特征根、特征向量与一致性检验如下：T W ]637.0,258.0,105.0[=,039.3max =λ,1.0033.0<=CR3判断矩阵C B -2的特征根、特征向量与一致性检验类似于第1步的计算过程,可以得到矩阵刀：—C 的特征根、特征向量与一致性检验如下：T W ]075.0,333.0,592.0[=,014.3max =λ,1.0012.0<=CR 4判断矩阵C B -3的特征根、特征向量与一致性检验类似于第1步的计算过程,可以得到矩阵C B -3的特征根、特征向量与一致性检验如下：T W ]785.0,066.0,149.0[=,08.3max =λ,1.0069.0<=CR 4、层次总排序获得同一层次各要素之间的相对重要度后,就可以自上而下地计算各级要素对总体的综合重要度;设二级共有m 个要素c 1, c 2,…,c m ,它们对总值的重要度为w 1, w 2,…, w m ；她的下一层次三级有p 1, p 2,…,p n 共n 个要素,令要素p i 对c j 的重要度权重为v ij ,则三级要素p i 的综合重要度为：方案C 1的重要度权重=×+×+×= 方案C 2的重要度权重=×+×+×=方案C 3的重要度权重=×+×0. 075+×=依据各方案综合重要度的大小,可对方案进行排序、决策; 层次总排序如表6所示;由表5可以看出,3种品牌设备的优劣顺序为：1C ,3C ,2C ,且品牌1明显优于其他两种品牌的设备;。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一步：自上而下，先求判断矩阵A的最大特征 根与特征向量。
AW W 自变量 W -W
1 5
1 2 1 / 4 1 / 3 1 / 3
1/ 2 4 1 7 1/ 7 1 1/ 5 2 1/ 5 3
3 5 5 1 / 2 1 / 3 1 1 1 1 3
（2）平均随机性一致指标RI：
n 1 2 3 4 5
根据矩阵理论可知：所有 aii=1的矩阵A n 有 ，当矩阵具有完全一致
i 1
i
n
max 性时，1 ,其余特征根为0；矩 阵A具有不完全一致性时，有 1 max n ，用最大特征根以外的 其余特征根的负平均值作为度量判断 矩阵偏离一致性的指标，即：CI
5
7 9
表示两个元素相比，前者比后者明显重要
表示两个元素相比，前者比后者极其重要 表示两个元素相比，前者比后者强烈重要
2，4，6，8 表示上述相邻判断的中间值
倒数：若元素i和元素j的重要性之比为aij,那么元素j与元 素i的重要性之比为aji=1/aij 对于要比较的因子而言，你认为一样重要就是 1:1 ，强烈重 要就是9:1，也可以取中间数值 6:1等，两两比较，把数值填入， 并排列成判断矩阵（判断矩阵是对角线积是 1的正反矩阵即可）。
0.559 0.082 0.429 0.633 0.166 0.277 0.236 0.429 0.193 0.166 0.129 0.682 0.142 0.175 0.668
（5）层次总排序
各个方案优先程度的排序向量为：
各规则层的特 征向量
0.263 0.595 0.082 0.429 0.633 0.166 0.475 0.300 ( 3) ( 2 ) 0.277 0.236 0.429 0.193 0.166 0.055 0.246 W W W 0.129 0.682 0.142 0.175 0.668 0.099 0 . 456 0.110
P2
0.429 0.429 0.142
P3
0.633 0.193 0.175 0.166 0.166 0.668
（2）构造判断矩阵
通过相互比较确定各准则对于目标的权重，即构造判断矩 阵。在层次分析法中，为使矩阵中的各要素的重要性能够进行 定量显示，引进了矩阵判断标度（1～9标度法） : 标度 含义 1 3 表示两个元素相比，具有同样的重要性 表示两个元素相比，前者比后者稍重要
利用层次结构图绘出从目标层到方案层的计算结果：
选择旅游地
0.263 景 色 0.475 费 用 0.055 居 住 0.099 饮 食 0.110 旅 途
P1
0.595 0.277 0.129 0.082 0.236 0.682
i 1
a. 将A的每一列向量归一化得： ij
n
利用判断矩阵计算各因素C对目标层Z的权重（权系数） n ~ w a /a
ij i 1 ij
j 1 T ~ ~ ~ w w / w , w ( w , w ,..., w ) c. 将 wi 归一化 i 1 2 i i n ，即为近似特征根（权向量）
（4）一致性检验
1 2 A 1 / 4 1 / 3 1 / 3 1/ 2 4 1 7 1/ 7 1 1/ 5 2 1/ 5 3 3 5 5 1 / 2 1/ 3 1 1 1 1 3
a14 3, a43 2
a13 a14a43 3 2 6.
基本概念
什么是权重（权系数）？ 在决策问题中，通常要把变量Z表示成变量 x1，x2，… ，xn 的线性组合： z w x + w x + L + w x
n
其中 w i 0 , w i . 1 则 标Z的权重， i 1
1 1
2
2
n
n
n
w 1 , w 2 ,..., w
T
叫各因素对于目
max 5.073 前述计算得到了最大特征跟：
CI
max - n
n -1
5.073 - 5 0.01825 5 -1
查表知平均随机一致性指标RI，从而可检验矩阵一致性：
CR CI 0.01825 0.016295 0.1 RI 1.12
同理，对于第二层次的景色、费用、居住、饮食、旅途五 个判断矩阵的一致性检验均通过。
W1 W2 W3 W4 W5
W1
W2 W3 W4 W5
表示准 则重要 性次序 权值 （和为1）
max 5.073 对应于 max 的正规化的特征向量为：
W (0.263 ,0.475 ,0.055 ,0.099,0.110)T
第三步，算出 B2 , B3 , B4 , B5 的最大特征值分别为：
max(2) 3.002, max(3) 3,
所对应的特征向量分别为：
max(4) 3.009,
max(5) 3.
W2( 3)
0.082 0.429 0.633 0.166 ( 3) ( 3) ( 3) 0.236 W3 0.429, W4 0.193, W5 0.166. 0.682 0.142 0.175 0.668
1 Aw 1 / 2 1 / 6
2
1
1/ 4
6 4 1
0 . 587 0 . 324 0 . 089
1 . 769 0 . 974 0 . 268
判断矩阵的一致性检验 判断矩阵通常是不一致 的，但是为了能用它的对应 于特征根的特征向量作为被 比较因素的权向量，其不一 致程度应在容许的范围内 . 如 何确定这个范围？ max- n CI （1）一致性指标： n-1
n ( )i 1 d. 计算 Aw n i 1 wi
，作为最大特征根的近似值。
0.6 0.615 0.545 按行求和 0 . 3 0 . 308 0 . 364 0.1 0.077 0.091 1.760 0 . 972 0.268
w ( w1
,
w2 ,..., wn )
叫权向量.
注意， X1，X2，… ，Xn中有的不是基数变量， 而有可能是序数变量如舒适程度或积极性 之类。
设想： 把一块单位重量的石头砸成n块小石块
小石块W1 小石块W2 … 小石块Wn
~ w ~ ~ b. 对 wij 按行求和得：w i ij n
相对于居住
P P 1 2 P 1 1 1 B3 P2 1 1 P3 1 / 3 1 / 3 P 3 3 3 ` 1
相对于饮食
P 1 P 2 P 3
相对于旅途
P 1 P 2 P 3
P 3 4 1 1 B4 P2 1 / 3 1 1 P3 1 1 / 4 1 `
P 1 1/ 4 1 1 B5 P2 1 1 1 / 4 P3 4 4 1
（3）层次单排序
所谓层次单排序是指，对于上一层某因素而言，本层次 各因素的重要性的排序。 具体计算是：对于判断矩阵B，计算满足 BW maxW 的 特征根与特征向量。
max 的正规化 W 为对应于 式中 max 为 B 的最大特征根， W 的分量i 即是相应元素单排序的权值。 的特征向量，
3 0.587 0.324 0.089
得到排序结果：w=(0.588,0.322,0.090)T, max=3.009
矩阵与向量的乘积计算：
a11 AW a 21 a31 a12 a 22 a32 a13 W1 a 23 W2 a33 W3
AW1 a11 W1 + a12 W2 + a13 W3 AW2 a 21 W1 + a 22 W2 + a 23 W3 AW3 a31 W1 + a32 W2 + a33 W3
层次分析法例题
层次分析法的基本思路：先分解后综合
整理和综合人们的主观判断，使定性分析与定量分析 有机结合，实现定量化决策。 首先将所要分析的问题层次化，根据问题的性质和要 达到的总目标，将问题分解成不同的组成因素，按照因素 间的相互关系及隶属关系，将因素按不同层次聚集组合， 形成一个多层分析结构模型，最终归结为最低层（方案、 措施、指标等）相对于最高层（总目标）相对重要程度的 权值或相对优劣次序的问题。
n
CI=0 时A一致； CI 越大，A的不一致性程度 越严重。
6 7 8 9 10 11
RI
0
0
0.58 0.90 1.12 1.24
1.32 1.41
1.45
1.49 1.51
（3）一致性比率（用于确定A的不一致性的容许范围） CI 当CR<0.1时，A的不一致性程度在容许范围 CR RI 内，此时可用A的特征向量作为权向量。
常 规 思 维 过 程
确定这些准则在你心目中各占的比重多大；
就每一准则将三个地点进行对比；
将这两个层次的比较判断进行综合，作出选择。
利用层次结构图绘出从目标层到方案层的计算结果：
选择旅游地
0.263 景 色 0.475 费 用 0.055 居 住 0.099 饮 食 0.110 旅 途
P1
0.595 0.277 0.129 0.082 0.236 0.682
用AHP分析问题大体要经过以下五个步骤：来自（1） 建立层次结构模型；