抛物线焦点弦的弦长公式.pdf
抛物线焦点弦

抛物线焦点弦
抛物线的焦点弦是:焦点弦长就是两个焦半径长之和。
焦半径长可以用该点的横坐标来表示,与纵坐标无关。
由于焦点弦经过焦点,其方程式可以由其斜率唯一确定,很多问题可以转化为对其斜率范围或取值的讨论。
相关简介:
在抛物线y²=2px中,弦长公式为d=p+x1+x2。
若直线AB的倾斜角为α,则|AB|=2p/sin²α。
y²=2px或y²=-2px时,x1x2=p²/4,y1y2=-p²。
x²=2py或x²=-2py 时,y1y2=p²/4,x1x2=-p²。
焦点弦是指椭圆、双曲线或者抛物线上经过一个焦点的弦,是指同一条圆锥曲线或同一个圆上两点连接而成的线段。
焦点弦是由两个在同一条直线上的焦半径构成的。
焦半径是由一个焦点引出的射线与椭圆或双曲线相交形成的。
而由于椭圆或双曲线上的点与焦点之间的距离(即焦半径长)可以用椭圆或双曲线离心率和该点到对应的准线之间的距离来表示。
抛物线焦点弦性质

抛物线焦点弦性质
抛物线焦点弦性质:焦点弦长就是两个焦半径长之和。
焦半径长可以用该点的横坐标来表示,与纵坐标无关。
由于焦点弦经过焦点,其方程式可以由其斜率唯一确定,很多问题可以转化为对其斜率范围或取值的讨论。
在抛物线y²=2px中,弦长公式为d=p+x1+x2。
若直线AB的倾斜角为α,则|AB|=2p/sin²α。
y²=2px或y²=-2px时,x1x2=p²/4,y1y2=-p²。
x²=2py或x²=-2py时,y1y2=p²/4,x1x2=-p²。
焦点弦是指椭圆、双曲线或者抛物线上经过一个焦点的弦,是指同一条圆锥曲线或同一个圆上两点连接而成的线段。
焦点弦是由两个在同一条直线上的焦半径构成的。
焦半径是由一个焦点引出的射线与椭圆或双曲线相交形成的。
而由于椭圆或双曲线上的点与焦点之间的距离(即焦半径长)可以用椭圆或双曲线离心率和该点到对应的准线之间的距离来表示。
抛物线弦长公式
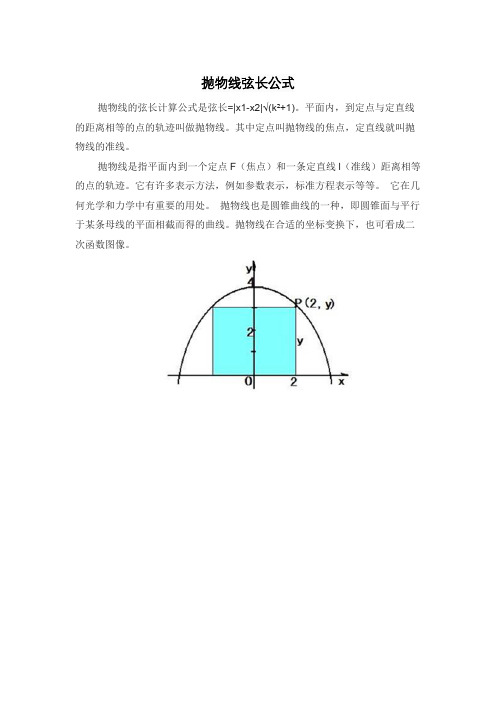
抛物线弦长公式
抛物线的弦长计算公式是弦长=|x1-x2|√(k²+1)。
平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。
其中定点叫抛物线的焦点,定直线就叫抛物线的准线。
抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨迹。
它有许多表示方法,例如参数表示,标准方程表示等等。
它在几何光学和力学中有重要的用处。
抛物线也是圆锥曲线的一种,即圆锥面与平行于某条母线的平面相截而得的曲线。
抛物线在合适的坐标变换下,也可看成二次函数图像。
抛物线焦点弦长公式推导过程

抛物线焦点弦长公式推导过程抛物线焦点弦长公式是指在一个抛物线上,通过焦点的弦长的长度公式。
推导过程如下:假设抛物线的方程为 y = ax^2,其中 a 是常数,焦点坐标为(0, p)。
1. 假设抛物线上一点为 P(x,y),则有 y = ax^2。
2. 然后,我们将 P 点到焦点的距离表示为 d,可以通过几何关系得到:d = sqrt(x^2 + (y-p)^2)3. 我们还可以通过另一种方式计算 d,即利用抛物线焦点的特性:焦点到抛物线上任意一点 P 的距离等于 P 点到抛物线的准线的距离。
因此,我们可以将 d 表示为:d = |y - p| / (2a)4. 将步骤 1 的方程代入步骤 3 的公式中,得到:d = |ax^2 - p| / (2a)5. 再次利用绝对值的性质,我们可以将式子转化为两种情况:当 ax^2 > p 时,d = (ax^2 - p) / (2a) = x^2 / (2a) - p / (2a)当 ax^2 < p 时,d = (p - ax^2) / (2a) = p / (2a) - x^2 / (2a)6. 接下来,我们考虑通过这个弦长公式来求抛物线上两点 A 和 B 之间的弦长。
假设点 A 的坐标为 (x1, y1),点 B 的坐标为 (x2, y2)。
首先,我们需要求出抛物线焦点到直线 AB 的距离 h。
h = (|y1 - p| + |y2 - p|) / 2将步骤 4 中的公式代入上面的式子,可得:h = |x1^2 - x2^2| / (4a)7. 然后,我们可以通过勾股定理计算出弦长 L:L = sqrt((x2 - x1)^2 + h^2)将步骤 6 中的 h 公式代入上面的式子,可得:L = sqrt((x2 - x1)^2 + (|x1^2 - x2^2| / (4a))^2)8. 最后,我们可以将步骤 5 中的两种情况代入上面的公式中,得到抛物线焦点弦长公式:当 ax1^2 > p 且 ax2^2 > p 时,L = sqrt((x2 - x1)^2 + ((x1^2 - x2^2) / (4a))^2) 当 ax1^2 < p 且 ax2^2 < p 时,L = sqrt((x2 - x1)^2 + ((x2^2 - x1^2) / (4a))^2) 至此,我们就成功推导出了抛物线焦点弦长公式。
(完整版)抛物线的焦点弦_经典性质及其证明过程
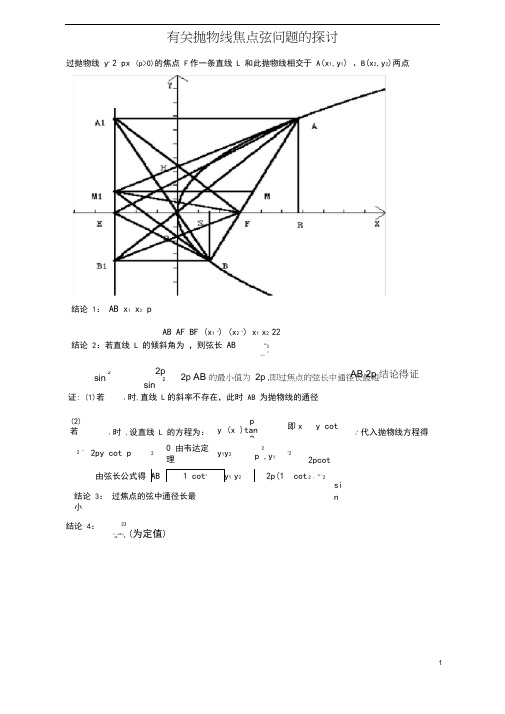
有关抛物线焦点弦问题的探讨过抛物线 y 22 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A (x 1,y 1) 、B (x 2,y 2)两点结论 1: AB x 1 x 2 pAB AF BF (x 1 p) (x 2 p) x 1 x 2 22结论 2:若直线 L 的倾斜角为 ,则弦长 AB 2p 2sin2结论 4:23S ABoAB p8(为定值)(2)若2时 ,设直线 L 的方程为: py (x )tan2 即xy cot2p代入抛物线方程得2 y2py cot p 2 0 由韦达定理y 1y 2 2 p ,y 1y22pcot2 )2p )2由弦长公式得 AB 1 cot 2y 1 y 2 2p(1 cot证: (1)若2时,直线 L 的斜率不存在,此时 AB 为抛物线的通径si n结论 3: 过焦点的弦中通径长最小 AB 2p 结论得证 2sin2p 2sin2p AB 的最小值为 2p ,即过焦点的弦长中通径长最短同理 B 1FOB 1FBA 1FB 1 90A 1FB 1 F2结论 8:(1)AM 1 BM 1 (2)M 1F AB (3) M 1F AF BF(4)设 AM 1 与 A 1F 相交于 H ,M 1B 与 FB 1相交于 Q 则M 1,Q ,F ,H 四点共圆 (5) AM 12M 1B 24M 1M 2证:由结论( 6)知 M 1 在以 AB 为直径的圆上 AM 1 BM 1A 1FB 1为直角三角形, M 1 是斜边 A 1 B 1 的中点A 1M 1 M 1F M1FA 1M1A 1FAA 1F AFA 1AA 1FFA 1MAA 1M190AFA 1A1FM190M 1FABM 1F2AFBFAM 1BM 1 AM1B 90又 A 1FB 1FA 1FB 1 90 所以 M 1,Q , F,H 四点共圆, AM 1 2M 1B 2AB 22 2 2 2AF BF 2AA 1 BB 1 22MM 1 24MM 1 2结论 9: (1) A 、O 、B 1 三点共线 ( 2)B ,O ,A 1 三点共线(3)设直线 AO 与抛物线的准线的交点为 B 1,则 BB 1平行于 X 轴( 4)设直线 BO 与抛物线的准线的交点为 A 1,则 AA 1平行于 X 轴S OAB SOBF1S 0AFOFBF 1sin 2OF AF sin OF 2S OABAB结论 5: (1) 证x 1AFP 3y 1y 22y1 2p ,x 2BF 2p 2sinOF AB sinp22psin2 sin 22 p2sin(2) x 1x 2=2 y22px 1x 2(y 1y 2)24P 2P 2结论 6:以 AB 证:设 M 为 AB 的中点,过 A 点作准线的垂线 过 M 点作准线的垂线 MM 1,由梯形的中位线性质和抛物线的定义知 为直径的圆与抛物线的准线相切AA 1, 过 B 点作准线的垂线 BB 1,MM 1结论 7:连接 A 1F 、 AA 1 AF,AA 1 BB 1 AF BF22B 1 F 则 A 1FAA 1F B 1FAB 2故结论得证AFA 1 AA 1 //OF AA 1FA 1FO A 1FO A 1FA41E,因为直线 L 的倾斜角为证:因为 k oAy1 x1y12 y12p,k oBoB 1y 11y2 p2y2,而 y 1y 2 p2 p2p2所以 k oA2p2 p y22y 2 pk oB 1所以三点共线。
抛物线的焦点弦公式

抛物线的焦点弦公式
抛物线的焦点弦公式是抛物线的一个重要的数学概念,这个概念在研究动力学、设计机器以及物理分析等方面有重要的意义。
抛物线可以用焦点弦公式表达,即直线弦长等于2倍小数点到顶点的距离。
为了更加清楚地表达这一概念,我们先来看看抛物线的几何特性,抛物线的定义为一条由原点出发的双曲线,它的端点可以是一个极值点,到极值点的距离叫做焦点弦。
这个焦点弦的长度可以用焦点弦公式来表达:
焦点弦公式为:弦长等于2倍小数点到顶点的距离。
其中,顶点用(h,k)表示,h和k分别代表x轴和y轴的坐标值;焦点弦公式
可以简单地用距离公式表示出:D = √((x–h)^2+(y–k)^2)。
有了这条焦点弦公式,我们就可以轻松地解决很多抛物线的问题,例如找出抛物线的最高点以及整条抛物线右侧的总长度等等。
甚至,可以使用抛物线的焦点弦公式证明一些重要的数学定理。
总的来说,抛物线的焦点弦公式是一个重要的数学概念,它不仅可用于解决抛物线的数学问题,而且也可应用于不同的领域,以期达到更好的精确度,研究出更多新奇的数学定理。
抛物线垂直于焦点的弦长公式

抛物线垂直于焦点的弦长公式抛物线垂直于焦点的弦长公式是指,当一条直线与抛物线垂直时,它所截取的弦长与焦距的关系。
这个公式在数学中有着广泛的应用,特别是在物理学和工程学中。
我们需要了解什么是抛物线。
抛物线是一种二次曲线,它的形状类似于一个开口朝上或朝下的碗。
抛物线有一个焦点和一个直线,这个直线被称为抛物线的准线。
焦点和准线是抛物线的两个重要特征,它们决定了抛物线的形状和性质。
当一条直线与抛物线垂直时,它所截取的弦长与焦距的关系可以用以下公式表示:L = 2f√(1 + m^2)其中,L表示弦长,f表示焦距,m表示直线的斜率。
这个公式的推导过程比较复杂,我们不在这里详细讲解。
但是,我们可以通过一个例子来理解这个公式的应用。
假设有一个抛物线,它的焦距为4,准线为x轴,方程为y = x^2。
现在有一条直线,它与抛物线垂直,且过抛物线上的点(2,4)。
我们需要求出这条直线所截取的弦长。
我们需要求出这条直线的斜率。
由于这条直线与抛物线垂直,所以它的斜率为-1/m,其中m为抛物线在点(2,4)处的斜率。
抛物线在点(2,4)处的斜率为4,因此这条直线的斜率为-1/4。
接下来,我们可以将这些值代入公式中,得到:L = 2×4√(1 + (-1/4)^2) ≈ 8.944因此,这条直线所截取的弦长约为8.944。
这个例子展示了抛物线垂直于焦点的弦长公式的应用。
这个公式在物理学和工程学中有着广泛的应用,特别是在光学和声学中。
例如,在光学中,我们可以用这个公式来计算透镜的焦距;在声学中,我们可以用这个公式来计算声波的传播距离。
抛物线垂直于焦点的弦长公式是一个重要的数学公式,它在物理学和工程学中有着广泛的应用。
通过这个公式,我们可以计算出一条直线与抛物线垂直时所截取的弦长与焦距的关系,从而更好地理解和应用抛物线的性质。
抛物线焦点弦性质很全
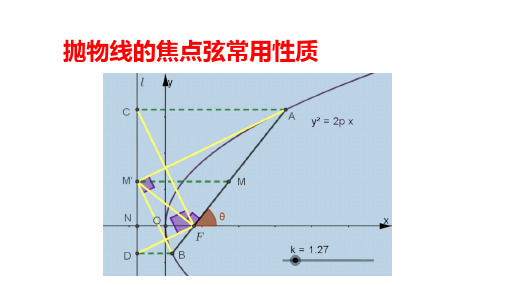
五、 CFD 900
CFO FCA AFC DFO FDB BFD CFO DFO AFC BFD 即有CFD AFC BFD
CFD 900
六、抛物线的焦点三角形的面积公式
S AOB
p2
2sin
S AOB
SAOF
SBOF
1 2
OF
y1
1 OF 2
y2
1 2 OF y1 y2
kMA kMB
2 py1 y12 p2
2 py2 y22 p2
kMA kMB
2 py1 y12 y1 y2
2 py2 y22 y1 y2
0
kMA kMB
MA, MB的倾斜角互补,即 AMF BMF
设:x my p ,代入y2 2 px可得
F
2
y1 y2 2 pm, y1 y2 p2
y1 y2 y1 y2 2 4 y1 y2 2 p m2 1
又k AB
tan
1 m
, 则m
1
tan
y1 y2 2 p
1
tan 2
1
2p
sin
SAOB
1 2
OF
y1 y2
1 p 2p
(1)若焦点在 x轴上,则 x1x2
p2 4
, y1 y2
p2
(2)若焦点在 y轴上,则 y1 y2
p2 4
, x1x2
p2
四、以抛物线的焦点弦为直径的圆与准线
证明:
MM1
1 2 ( AA1
BB1 )
1 ( AF BF ) 2
1 AB 2
即有:AM1B 900
引申:以焦半径为直径的圆与y轴相切(学生完成)
2 2 sin
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的两种表达式不一样,为了统一这两种不同的表达式,只须作很小的改动即可。现将改动陈 述于下:
y (3)已知:抛物线的方程为 2 = 2 px ( p 0) ,过焦点 F 的弦 AB 交抛物线于 A ,B
两点,且弦 AB 与抛物线的对称轴的夹角为 ,求弦 AB 的长。
学海无涯
解:由题意可设直线 AB 的方程为 y = k(x − p ) ( ) 将其代入抛物线方程整理得:
x2
− 2 pkx−
p2
=
0, 从而
x1 +
x2
=
2 pk, x1 x2
=Байду номын сангаас
−
p2 ,
弦长为:| AB |=
1+ k2
(x1+
x2)2
−
4
x1
x2
=
2p
(cos
)2
= 0,cos = 1,| AB |= 2p ,即为通径。
y x 而
2
= −2 px 与(1)的结果一样,
2 = −2 py 与(2)的结果一样,但是(1)与(2)
x (2)已知:抛物线的方程为 2 = 2 py( p 0) ,过焦点的弦 AB 交抛物线于 A,B 两点,
直线 AB 倾斜角为 ,求弦 AB 的长。
x y x y 解:设 A,B 的坐标为 ( , ),( , ) ,斜率为 k (k = tan ) ,而焦点坐标为 (0, p ) ,
11
22
2
故 AB 的方程为 y − p = kx,将其代入抛物线的方程整理得: 2
y 而 2 = −2 px 与(3)的结果一样
x 同理:(4)已知:抛物线的方程为 2 = 2 py( p 0) ,过焦点的弦 AB 交抛物线于 A,B
两点,直线 AB 与抛物线的对称轴的夹角为 ,求弦 AB 的长。
x y x y 解:设 A,B 的坐标为 ( , ),( , ) ,若倾斜角为 ,斜率为 k,
p
k2 + k2
2
p
,
x1
x2
=
p2
4
| AB |= 1 + k 2 ( x1+ x 2)2 − 4 x1 x2
=
1 + (tan )2
(
p
k
2
+
2
2
p)
−
p2 k 4
k4
=
2p
(sin )2
而
sin
=
sin
, sin(
−)
=
sin
,故 |
AB
|=
2p
(sin
)2
;
当 = 时, sin = 1,|AB|=2p.即为通径。 2
当倾斜角 ,则 = − , cos = cos( − ) = sin ;
2
2
2
学海无涯
当倾斜角 , 则 = + , cos = cos( + ) = −sin
2
2
2
所以| AB |= 2 p 恒成立。
(sin )2
当 = 时, sin = 1,|AB|=2p.即为通径。 2
11
22
则 k = tan ,而焦点坐标为 (0, p ) , 2
故 AB 的方程为 y − p = kx,将其代入抛物线的方程整理得: 2
x2
− 2 pkx−
p2
=
0, 从而
x1 +
x2
=
2 pk, x1 x2
=
−
p2 ,
弦长为:| AB |=
1+ k2
(x1+
x2)2
−
4
x1
x2
=
2p
(cos
)2
学海无涯
关于抛物线焦点弦的弦长公式
在高中教材第八章中有关于已知倾斜角的焦点弦,求焦点弦的弦长的问题,其中只介绍 了开口向右时的焦点弦的长度计算问题:
y (1)已知:抛物线的方程为 2 = 2 px ( p 0) ,过焦点 F 的弦 AB 交抛物线于 A B 两点,
且弦 AB 的倾斜角为 ,求弦 AB 的长。
解:由题意可设直线 AB 的方程为 y = k(x − p ) ( ) 将其代入抛物线方程整理得:
2
2
4 k 2 x2 − (4 p k 2 + 8 p)x + p2 k 2 = 0 ,且 k = tan
x y x y 设 A,B 两点的坐标为 (
,
1
),( ,
1
2
)
2
则: x1+ x2 =
p
k2 + k2
2
p
,
x1
x2
=
p2
4
| AB |=
1+ k2
(x1+
x 2)2
−
4
x1
x2
=
2p
(sin
)2
当 = 时,斜率不存在, sin = 1,|AB|=2p.即为通径 2
而如果抛物线的焦点位置发生变化,则以上弦长公式成立吗?这只能代表开口向右时的 弦长计算公式,其他几种情况不尽相同。 现在我们来探讨这个问题。
2
2
4k2 x2 − (4 p k2 + 8 p)x + p2 k2 = 0 ,
若倾斜角 ,则 = , k = tan = tan ; 2
若倾斜角 , 则 = −, k = tan = tan( −) 。 2
x y x y 设 A,B 两点的坐标为 (
,
1
), (
1
,
2
)
2
则: x1+ x2 =
x 而 2 = −2 py 与(4)的结果一样。
故只要直线 AB 与抛物线的对称轴的夹角为 ,那么不论抛物线的开口向上,向下,向 左还是向右,过焦点的弦的弦长都可以用一个公式表示,即| AB |= 2 p 。这个公式
(sin )2
包含了抛物线的四种开口形式,没有了因为开口不同而导致的公式不同,便于记忆,便于应 用,是一个很好的弦长公式,这里推荐给大家使用。
