8.1变参数模型
电机学变压器的运行原理(空载、负载、数学模型)

第8章 变压器
28
2、T型等效电路 T型等效电路的形成过程,见下图。
I&1 R1
X 1
R2
I&0
Rm
U&1
E&2 E&1E&2 E&1
E&2
Xm
X 2 I&2
U&2
Z L
T型等效电路的形成过程
第8章 变压器
29
Γ型等效电路
对于电力变压器,一般 I1NZ1<0.08U1N,且 I1NZ1 与 -E1是相量相加,因此可将励磁支路前移与电源并 联,得到Γ型等效电路。
1、空载电流的波形
电网电压为正弦波,铁 心中主磁通亦为正弦波。若 铁心不饱和(Bm < 1.3T), 空载电流 i0 也是正弦波。
电力变压器,Bm= 1.4T ~1.73T,铁心都是饱和的 。其励磁电流呈尖顶波,除 基波外,还有较强的三次谐 波和其它高次谐波。
第8章 变压器
11
2、空载电流与主磁通的相量关系
问题:一般电力变压器 的变比 k 较大,一、二 次侧的电压、电流差别
很大,计算不便,画相
量图更加困难。因此,
下面介绍分析变压器的 一个重要方法——等效 电路、折算。
第8章 变压器
19
四、绕组归算(折算)及数学模型
所谓把二次侧折算到一次侧,就是用一个匝数为N1 的等效绕组,去替代变压器匝数为N2二次侧绕组,折 算后的变压器变比 N1/ N1=1 。
第8章 变压器
30
4、简化等效电路和相量图
对于电力变压器,由于 I0<0.03I1N,故在分析变压器满载及负 载电流较大时,可以近似地认为 I0=0,将励磁支路断开,等效电 路进一步简化成一个串联阻抗,如图所示。
第八章随机解释变量和滞后变量模型

拟合的样本回归线 高估截距项,而低 估斜率项。
对一元线性回归模型:
Yt 0 1 X t t
OLS估计量为
ˆ 1
x y x
t 2 t
t
1
x x
t 2 t
t
随机解释变量X与随机项的关系不同,参 数OLS估计量的统计性质也会不同。
1、如果X与相Leabharlann 独立,得到的参数估计量 仍然是无偏、一致估计量。
2的证明中已得到 注意: 如果模型中带有滞后被解释变量作为解释变量, 则当该滞后被解释变量与随机误差项同期相关时, OLS估计量是有偏的、且是非一致的。
即使同期无关,其OLS估计量也是有偏的,因为 此时肯定出现异期相关。
(三)实际经济问题中的随机解释变量问题 在实际经济问题中,经济变量往往都具 有随机性。
8.2.3 滞后变量模型
以滞后变量作为解释变量,就得到滞后变量模型。 它的一般形式为:
Yt 0 1Yt 1 2Yt 2 qYt q 0 X t 1 X t 1 s X t s t
q,s:滞后时间间隔 自回归分布滞后模型 ( autoregressive distributed lag model, ADL):既含有Y对自身滞后变量的回归, 还包括着X分布在不同时期的滞后变量 有限自回归分布滞后模型:滞后期长度有限 无限自回归分布滞后模型:滞后期无限,
第八章 随机解释变量和滞后变量模型
内容安排
8.1 随机解释变量 8.2 滞后变量模型 8.3 实验操作
8.1 随机解释变量 一、随机解释变量的存在与后果
(一)随机解释变量
对于模型
Yi 0 1Y1i 2 X 2i k X ki i
苏亚星多媒体教学网软件V8.1 (电子教室版) 用户手册

目录第一章:系统概述 (4)1-1性能特点 (4)1-2主要功能 (5)1-2使用环境要求 (8)第二章:安装与启动 (9)2-1 TCP/IP协议设置参考 (9)2-2系统安装 (11)安装注意: (11)安装中心服务器 (11)安装管理机 (18)安装教师机 (23)安装学生机 (28)2-3卸载 (33)第三章:中心服务管理器程序使用 (34)第四章:管理机程序使用 (35)4-1班级模型编辑器使用 (35)4-2管理机使用 (39)第五章:教师机程序使用 (42)5-1教师机界面 (42)5-2教师机功能列表 (43)5-3教师机基本操作 (43)5-4主菜单操作 (44)5-5主功能操作 (64)5-6辅助功能操作 (66)第六章:学生机程序使用 (71)第七章: 常见问题 (76)前言首先感谢您选用苏亚星公司的苏亚星多媒体教学网V8.1(以下简称AsiaStar 8.1)。
近几年,在教育部、各地教委和学校的共同推动下,多媒体教学网的应用得到迅速普及,目前已成为电脑教室的标准配备,可以说,电脑室没有配备多媒体教学网,就像传统教室没有黑板一样。
多媒体教学网是充分利用计算机及网络技术,结合现代教育思想,为学校各学科提供一种计算机教学辅助工具,实现和优化了传统教学中老师与学生、学生与学生之间的交流活动,发挥学生学习的主动性与参与性,改善教学手段与学习方法。
苏亚星多媒体教学网 V8.1是苏亚星公司在V7.1的基础上,数十位软件工程师历时三年多,精心打造的一款全新的多媒体教学网软件。
它不仅继承了V7.1的优点,吸纳了全国五万多所学校老师的反馈建议;同时也采用了多项苏亚星独创的新技术。
它的功能规划全面实用,充分考虑了各学科老师在课堂教学中的实际需要,实现了多小组、多班级、多机房、多老师、多学科、多环节及多功能的灵活应用,广泛适用于各类学校及培训机构的计算机辅助教学。
苏亚星多媒体教学网V8.1的全面应用,必将引领一场计算机辅助教学的革命。
arch模型
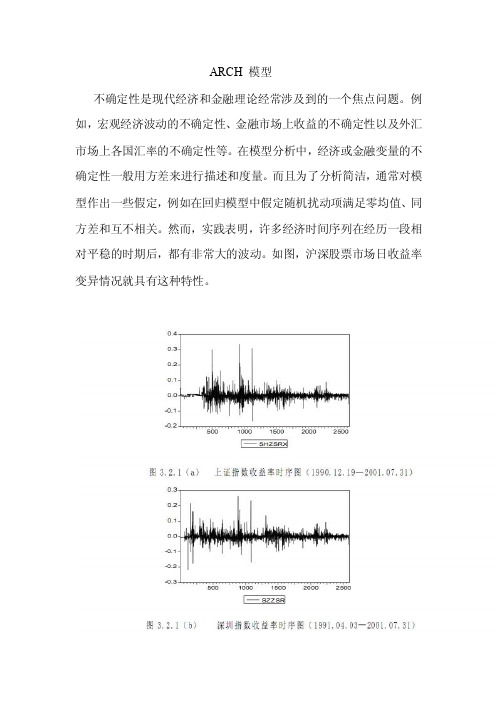
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
8系统辨识原理及辨识模型简介

(3) 参数模型估计 在系统辨识工具箱中包括多种参数模型估计的函数,它们 都具有共同的命令结构。 m = function(Data,modstruc) m = ... function(Data,modstruc,'Property1',Value1,…'PropertyN',Valu eN) 变量Data是包括输入输出序列的iddata对象,而modstruc 说明了被估计模型的特定结构。模型估计的结果返回到变 量m中,它是存放了多种信息的模型对象。在大多数情况 使用时可以不必考虑对象的细节重要输入模型名称m就可 以了。若查看m的简要信息输入present(m),通过get(m)则 可以得到更为详细的参数信息,参数值仍然可以采用圆点 引用的形式得到,例如m.par返回的就是估计参数。 函数调用(...,'Property1', Value1,...,'PropertyN',ValueN)的参 数影响着模型结构及估计算法。
(5) AR 模型 对于单个输出信号,ARX模型的特例就是AR模型
A(q) y(t ) e(t )
(8.10)
arx命令同样可以应用在此特例上:m = arx(y,na),但是对于标量信号, 可以通过如下命令可以有更多的选择:m = ar(y,na) 通过对参数的设置可以选择参数估计的最小二乘类方法,包括Burg机遇 网格的方法、几何网格的方法、Yule-Walker方法以及修正的协方差法。 相关格式内容可通过“help ar ”命令得到。
(8.12)
定义式(8.11)离散模型的语法结构为:m= idss(A,B,C,D,K,X0,'Ts',T),若令 T=0,则表 示连续时间模型(见式 8.12)即:m=idss(A,B,C,D,Kt,X0,'Ts',0)
第8章 虚拟变量模型

效应。
8.1.3 虚拟变量作为因变量的情况
1、因变量为虚拟变量的回归模型
• 虚拟变量作为因变量的模型也称定性响应模型,既可 以包括二值变量模型(也称二分选择模型),也包括 多分选择模型。我们重点讨论二值变量模型。
• 模型举例: 一个大学毕业生是否会被一个不错的MBA项目录取, 取决于其学习成绩、GMAT分数和其它因素。 一位成年男子是否就业取决于总体失业率、平均工资 率、受教育程度和家庭收入等因素。
其中:
1
yi
{ 0
已购买汽车 未购买汽车
且假定E(ui ) 0
1.2 Y
1.0
0.8
0.6
0.4
0.2
0.0 X
-0.2 280 300 320 340 360 380 400 420
对于给定的xi ,E(yi / xi ) 0 1xi
设pi表示yi 1的概率,则1 pi表示yi 0的概率 E(yi / xi ) pi 1 (1 pi) 0 pi 可见,该模型描述了随着收入的变动, 第i个家庭 购买汽车的概率变动情况。
b0 + b1xt + ut , (D = 0)
Y
yt =
b0 + (b1 + b2) xt + ut , (D = 1)
男
女
t
0
3、一般方式
直接以加法和乘法方式引入虚拟变量。 可建立如下模型:
yt = b0 + b1 xt + b2 D + b3 xt D + ut ,
其中 xt 为定量变量;D 为定性变量。当 D = 0 或 1 时,上述模
yt =
计量经济学课件5

8.5 应用
Enter键后,回归系数估计及标准误和残差保存于080101.dta中,stata结果显示 :
这里有一段被删除 由于目的是为了对各个体的残差平方进行计算求和,思路是现根据估计参数进 行计算拟合值,然后实际值减去拟合值,从而得到残差,最后对残差进行平方 求和。在Stata中的command窗口中输入如下命令: merge m:1 state using “D:\stata16\shuju\chap08\080101.dta” /*将分组回归的结 果合并到原始数据文件中,同时注意路径是英文下双引号*/ gen mhat=_b_cons+_b_beertax*beertax /*mhat是回归预测值,该步是进行拟 合值拟合*/ gen resid=mrall-mhat egen SSR=sum(resid^2) /*对所有残差平方和进行求和*/ Enter键后,可见数据编辑器中有S1(SSR)的求解结果:
df
MS Number of obs =
F(1, 334)
=
1 1.0169e-07 Prob > F
=
334 2.9565e-09 R-squared
=
Adj R-squared =
335 3.2512e-09 Root MSE
=
336 34.39 0.0000 0.0934 0.0906 5.4e-05
8.1 面板数据模型概述
对于情形1,称为无个体影响的不变系数模型,其在横截面上无个体影 响、无结构变化,可由普通最小二乘法估计给出a和b的一致有效估计, 即相当于多个时期的截面数据放在一起作为样本数据。对于情形2,称 为变截距模型,由于在横截面上存在个体影响,而不存在结构性的变化 ,同时又考虑到个体差异影响是否在模型中被忽略,因此还可将模型进 一步分为固定效应影响和随机效应影响两种情况。对于情形3,称为变 系数模型,除了存在个体影响外,在横截面上还存在结构变化,因此结 构参数在不同横截面单位上是不同的。
RT-LAB中文使用手册

RT-LAB8.1版用户手册介绍1.1关于RT-LABRT-LAB是一个分布式实时平台,它能够在很短的时间内、以很低的花费,通过对进行工程仿真或者是对实物在回路的实时系统建立动态模型,使得工程系统的设计过程变的更加简单。
他的可测量性使得开发者能够把计算机使用到任何需要他的地方;充分的灵活性使得它能够应用于最复杂的仿真和控制问题,而不论是应用于实时硬件在回路还是快速模型,控制和测试中。
为了达到理想的性能,RT-LAB为分布式网络下分立目标机对高度复杂的模型进行仿真、通过超低反应时间通讯,提供了丰富的工具。
此外,RT-LAB的模型化设计使得用户仅仅提供应用所需的模型就能完成经济的系统、最小化经济要求、并满足用户的价格目标。
这在大量的嵌入式应用中尤其显得重要。
1.2主要特征完全集成MATLAB/Simulink,以及MATRIXx/SystemBuild所有为RT-LAB准备的模型都能够在已有的动态系统模型环境中完成,通过使用这些工具,用户的经验也会相应的提高。
分布式处理的专业化块设计,内部节点通讯以及信号I/ORT-LAB提供的工具能够方便的把系统模型分割成子系统,使得在目标机上能够并行处理(标准的PC上可以运行QNX实时操作系统,或者RedHawk Linux)。
通过这种方法,如果你不能在单处理器上运行实时模型,RT-LAB提供多个处理器共享一个负载的方法来实现的。
完全集成第三方建模环境以及用户代码库RT-LAB支持StateFlow,StateMate,CarSimRT,GT-PowerRT,AMESim,Dymola的模型,以及C,C++,FORTRAN的合法代码。
丰富的API为开发自己的在线应用使用诸如LabVIEW、C、C++、Visual Basic、TestStand、Python and 3D virtual reality等工具可以轻松的创建定制的功能和自动测试界面。
非定制技术RT-LAB是第一个完全可测量的仿真和控制包,使得你能够分割模型,并在标准PC,PC/104s 或者SMP(对称式多处理器)组成的网络上并行运行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⒉ 参数随某一变量作规律性变化,同时受 随机因素影响
t pt t
t pt t
• 将原模型转换为具有异方差性的多元线性模型。
yt pt xt pt xt t t t t xt
• 可以采用经典线性计量经济学模型中介绍的 估计方法,例如加权最小二乘法等方法很方 便地估计参数。
t 0 1 pt t 0 1 pt
1 t n0 n0 t n
pt 0 pt 1
• 在实际经济问题中,往往表示某项政策的实施 在某一时点上发生了变化。 • 这类变参数模型的估计,分3种不同情况。
(1)n0已知
• 可以分段建立模型,分段估计模型(CHOW 方法)
0.2645 0.0474 X Y 1 1 175017 Y . 015045 . X2 2
(2)n0未知 • n0未知,但
Var ( 1t ) Var ( 2t )
一般可以选择不同的n0 ,进行试估计,然后 从多次试估计中选择最优者。选择的标准是使得 两段方程的残差平方和之和最小。 • n0未知,且
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
Chow Test
Chow Breakpoint Test: 1972 F-statistic Log likelihood ratio 5.091499 Probability 9.833988 Probability 0.007321 0.023282
ˆ 1.7502 0.1505X 1.4843 Y D 0.1034 ( DX )
0.2659 0.0471 X Y 1 1 17502 Y . 01505 . X2 2
分 段
(1964 1972) (1973 1981)
(1964 1972) (1973 1981)
第八章
扩展的单方程计量经济学模型
§8.1 变参数线性单方程计量经济学模型 §8.2 非线性单方程计量经济学模型 §8.3 二元离散选择模型 *§8.4 平行数据计量经济学模型
§8.1 变参数单方程计量经济学模型
一、确定性变参数模型
*二、随机变参数模型
说明
• 常参数模型与变参数模型。真正的常参数模型只 存在于假设之中,变参数的情况是经常发生的。
Var ( 1t ) Var ( 2 t )
将n0看作待估参数,用最大或然法进行估计。
*二、随机变参数模型
⒈ 参数在一常数附近随机变化
t t t t
• 将原模型转换为具有异方差性的模型,而且 已经推导出随机误差项的方差与解释变量之 间的函数关系。
• 可以采用经典线性计量经济学模型中介绍的 估计方法,例如加权最小二乘法等方法很方 便地估计参数。 • 一种普遍的形式是1968年提出的的变参数 Hildreth-Houck模型 。
Chow 检验
H 0 : 分段参数估计量相等 H1 : 分段参数估计量不等
( SSE SSE 1 SSE 2 ) /(k 1) F ( SSE 1 SSE 2 ) /(n 2(k 1))
例8.1.1 数据
save 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 0.36 0.21 0.08 0.2 0.1 0.12 0.41 0.5 0.43 0.59 0.9 0.95 0.82 1.04 1.53 1.94 1.99 income 8.8 9.4 10 10.6 11 11.9 12.7 13.5 14.3 15.5 16.7 17.7 18.6 19.7 21.1 22.8 25.2
• 模型参数是变量,但不是随机变量,而是确定性 变量,称为确定性变参数模型。 • 模型参数不仅是变量,而且是随机变量,称为随 机变参数模型。 • 内容广泛,本节仅讨论最简单的变参数模型。
一、确定性变参数模型
⒈参数随某一个变量呈规律性变化
yt t t xt t
yt 0 1 pt 0 xt 1 pt xt t
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
1964-1980 估计结果
Dependent Variable: SAVE Method: Least Squares Date: 09/18/04 Time: 17:58 Sample: 1964 1980 Included observations: 17 Variable C INCOME R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient -1.077779 0.117504 0.904908 0.898568 0.195265 0.571924 4.709730 0.851219 Std. Error 0.157422 0.009835 t-Statistic -6.846443 11.94745 Prob. 0.0000 0.0000 0.715882 0.613107 -0.318792 -0.220767 142.7416 0.000000
3.80(1%显著性水平)<5.09<6.70(5%显著性 水平),在0.023的显著性水平下拒绝H0。
• 也可以引入虚变量,建立一个统一的模型 (Gujarati方法)
yt 0 1 Dt 0 xt 1 Dt xt t
1 t n0 n0 t n D 1 D0
t 0 1 pt t 0 1 pt
• 实际经济问题中的实例:具有经济意义的参数受 某一因素的影响。
• 模型的估计
p为确定性变量,与随机误差项不相关,可 以用OLS方法估计,得到参数估计量。
可以通过检验α1、β1是否为0来检验变量p是 否对α、β有影响。
⒉参数作间断性变化
⒊ 自适应回归模型
t t 1 t 1 E ( t ) 0
Var (t ) 2
t
• 由影响常数项的变量具有一阶自相关性所引起。 • 是实际经济活动中常见的现象。
• 采用广义Biblioteka 小二乘法(GLS)估计模型参数 。
例8.1.1 散点图
2.5
2.0
1.5
SAVE
1.0
0.5
0.0 5 10 15 20 25 30
INCOME
1964-1972 估计结果
Dependent Variable: SAVE Method: Least Squares Date: 09/15/04 Time: 22:22 Sample: 1964 1972 Included observations: 9 Variable C INCOME R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient -0.266249 0.047028 0.309194 0.210507 0.141245 0.139650 5.975825 1.130344 Std. Error 0.305353 0.026569 t-Statistic -0.871940 1.770053 Prob. 0.4121 0.1200 0.267778 0.158964 -0.883517 -0.839689 3.133086 0.120027
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
1973-1980 估计结果
Dependent Variable: SAVE Method: Least Squares Date: 09/15/04 Time: 22:25 Sample: 1973 1980 Included observations: 8 Variable C INCOME R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient -1.846345 0.155949 0.908410 0.893145 0.173501 0.180615 3.811805 1.670473 Std. Error 0.402197 0.020216 t-Statistic -4.590648 7.714237 Prob. 0.0037 0.0002 1.220000 0.530768 -0.452951 -0.433091 59.50946 0.000249
