时变参数的状态空间模型
合集下载
第1章 控制系统的状态空间表达式
§1－1 状态空间变量及状态空间表达式
三. 状态空间 以状态变量为坐标轴所构成的空间为状态空间。
x2
x
x1
x3
●系统任一时刻的状态均可表示为状态空间中的一个点。 ●系统状态随时间变化的过程，在状态空间中描绘出一条轨迹，称为
. 状态轨迹。
§1－1 状态空间变量及状态空间表达式
四. 状态方程 由系统状态变量构成的描述系统动态过程的一阶微分方程组称为 系统的状态方程 。 ●状态方程用于描述系统输入引起系统状态变化的动态过程 。
K1 Kp
u
K1 Kp
＋
K1
Kp
x6
x6
＋
x5
x5
1 x4 J1
x3
x3
Kn
＋
x4
§1－3 状态空间表达式的建立（一）
由以上方框图可知：x1 x 2 x2 x3
状态方程：
x4 x5 x6
J2 x4 Kb K n x4 Kp Kp 1 1 x3 x4 x5 x6 J1 J1 J1 J1 K1 x4 K1 x6 K1 K1 K1 x1 x6 u Kp Kp Kp
ቤተ መጻሕፍቲ ባይዱ
1 K p K1 s
＋
故：
K p s K1 s
K1
Kp
＋
§1－3 状态空间表达式的建立（一）
一.从系统方框图出发建立状态空间表达式
1 J1
J2 Kb
J 2S 2
Kn s
Kn
Kb
1 J1s
§1－3 状态空间表达式的建立（一）
线性系统理论 第2章 线性系统的状态空间描述
D(k )
u(k )
H (k )
x(k 1)
x(k )
单位延迟
C (k )
y(k )
G (k )
7/7,11/50
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x, u, t ) y g ( x, u, t )
向量函数
g1 ( x, u, t ) f1 ( x, u, t ) g ( x, u , t ) f ( x, u , t ) ，g ( x, u, t ) 2 f ( x, u , t ) 2 g q ( x, u , t ) f n ( x, u , t )
和t≥t0 各时刻的任意输入变量组 u1 (t ),u2 t ,, u p (t ) 那么系统的任何一个内部变量在t≥t0各时刻的运动行为也就随之而完全确定
3/4,3/50
(2).状态变量组最小性的物理特征： 少一个不行，多一个没用 (3). 状态变量组最小性的数学特征：极大线性无关变量组 (4). 状态变量组的不唯一性 ：任意
1/18,14/50
结论1
给定单输入,单输出线性时不变系统的输入输出描述,
y ( n) an1 y ( n1) a1 y (1) a0 y bmu ( m) bm1u ( m1) b1u (1) b0u
Y (s) bm s m bm1 s m1 b1 s1 b0 g ( s) U ( s) s n an1 s n1 a1 s a0
时变系统和时不变系统
f f ( x, u ) 若向量f,g不显含时间变量t,即 g g ( x, u )
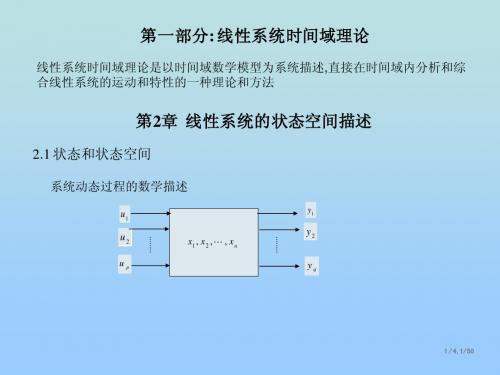
u(k )
H (k )
x(k 1)
x(k )
单位延迟
C (k )
y(k )
G (k )
7/7,11/50
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x, u, t ) y g ( x, u, t )
向量函数
g1 ( x, u, t ) f1 ( x, u, t ) g ( x, u , t ) f ( x, u , t ) ，g ( x, u, t ) 2 f ( x, u , t ) 2 g q ( x, u , t ) f n ( x, u , t )
和t≥t0 各时刻的任意输入变量组 u1 (t ),u2 t ,, u p (t ) 那么系统的任何一个内部变量在t≥t0各时刻的运动行为也就随之而完全确定
3/4,3/50
(2).状态变量组最小性的物理特征： 少一个不行，多一个没用 (3). 状态变量组最小性的数学特征：极大线性无关变量组 (4). 状态变量组的不唯一性 ：任意
1/18,14/50
结论1
给定单输入,单输出线性时不变系统的输入输出描述,
y ( n) an1 y ( n1) a1 y (1) a0 y bmu ( m) bm1u ( m1) b1u (1) b0u
Y (s) bm s m bm1 s m1 b1 s1 b0 g ( s) U ( s) s n an1 s n1 a1 s a0
时变系统和时不变系统
f f ( x, u ) 若向量f,g不显含时间变量t,即 g g ( x, u )
1.控制系统的状态空间模型
Chapter1控制系统的状态空间模型1.1 状态空间模型在经典控制理论中，采用n 阶微分方程作为对控制系统输入量)(t u 和输出量)(t y 之间的时域描述，或者在零初始条件下，对n 阶微分方程进行Laplace 变换，得到传递函数作为对控制系统的频域描述，“传递函数”建立了系统输入量)]([)(t u L s U =和输出量)]([)(t y L s Y =之间的关系。
传递函数只能描述系统的外部特性，不能完全反映系统内部的动态特征，并且由于只考虑零初始条件，难以反映系统非零初始条件对系统的影响。
现代控制理论是建立在“状态空间”基础上的控制系统分析和设计理论，它用“状态变量”来刻画系统的内部特征，用“一阶微分方程组”来描述系统的动态特性。
系统的状态空间模型描述了系统输入、输出与内部状态之间的关系，揭示了系统内部状态的运动规律，反映了控制系统动态特性的全部信息。
1.1.1 状态空间模型的表示法例1-1（6P 例1.1.1） 如下面RLC （电路）系统。
试以电压u 为输入，以电容上的电压C u 为输出变量，列写其状态空间表达式。
例1-1图 RLC 电路图解：由电路理论可知，他们满足如下关系⎪⎩⎪⎨⎧==++)(d )(d )()()(d )(d t i t t u C t u t u t Ri t t i L C C 经典控制理论：消去变量)(t i ，得到关于)(t u C 的2=n 阶微分方程：)(1)(1d )(d d )(d 22t u LCt u LC t t u L R t t u C C C =++ 对上述方程进行Laplace 变换：)()()2(20202s U s U s s C ωωζ=++得到传递函数：202202)(ωζω++=s s s G ，LC10=ω，L R 2=ζ 现代控制理论：选择⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛)()(21t u t i x x C 流过电容的电流)(t i 和电容上的电压)(t u C 作为2个状态变量，2=n （2个储能元件）；1个输入为)(t u ，1=m ；1个输出C u y =，1=r 。
控制理论(状态空间表达式)课件
为状态矢量．
x1(t)
x (t)
x
2
(
t
)
x
n
(t
)
x (t) x 1 (t) x 2 (t)
x n (t)T
三.状态空间
以状态变量 x1, x2,
空间，称为状态空间．
xn 为坐标轴所构成的n维
四. 状态方程
由系统的状态变量构成的一阶微分方程组称为
系统的状态方程．
五. 输出方程
在指定系统输出的情况下,该输出与状态变量间 的函数关系式,称为系统的输出方程.
式中 e 为反电动势； K a , K b 转矩常数和反电动势常数．
整理得：
di R i Kb 1 u dt L L L
d Ka i B
dt J J
把 x1i,x2 代入，有
x1 x2
RL Ka
J
Kb L
B J
xx12
1 Lu
0
若指定角速度为输出，则
y x2 0
1xx12
【例1-2】 RLC电路如下图所示. 以ei作为系统的 控制输入u(t)，eo作为系统输出y(t)。建立系统的 动态方程。
解: 该R-L-C电路有两个独立的储能元件L和C，可以取 电容C两端电压和流过电感L的电流 作为系统的两个状 态变量，分别记作x1和x2。根据基尔霍夫电压定律和 R、L、C元件的电压电流关系，可得到下列方程：
出变量与状态变量之间的关系，Dmxr矩阵称
为直接传递矩阵，表示了控制向量U直接转
移到输出变量Y的转移关系。
和经典控制理论类似，可以用方块图表示系统信 号的传递关系．
将状态方程表示的系统动态方程用方块图表示为 如图所示。系统有两个前向通道和一个状态反馈回路 组成，其中D通道表示控制输入U到系统输出Y的直接 转移。
状态空间表达式
（28） 状态空间方程实现非唯一，书p28, 图1.16b求得其对应的传递函数为： （29）
为求得 令式（29）与式（26）相等，通过对 多项式系数的比较得： 故得： （30）
也可将式(30)写成式(31)的形式，以便记忆。 （31）
将上图a的每个积分器输出选作状念变最，如图所示，得这种结构下的 状态空间表达式：
解：
→
→
u
y
－
＋
例： 解： 比例积分环节： → → u y ＋
例：
解：
综合惯性环节、积分环节模拟结构图得：
u
y
－
＋
u
y
解：选积分器的输出为状态变量得：
u
y
状态方程：
输出方程：
状态空间表达式
1.3.2 从系统的机理出发建立状态空间表达式
一般常见的控制系统，按其能量属性，可分为电气、机械、机电、气动 液压、热力等系统。根据其物理规律，如基尔霍夫定律、牛顿定律、能量守 恒定律等，即可建立系统的状态方程。当指定系统的输出时，很容易写出系 统的输出方程。
同一系统，经非奇异变换后，得：
其特征方程为：
（44）
1.5.2 系统特征值的不变性及系统的不变量
1.系统特征值
式(43)与式(44)形式虽然不同，但实际是相等的，即系统的非奇异变换，其特征值是不变的。可以证明如下：
将特征方程写成多项式形式 由于特征 值全由特征多项式的系数 唯一确定，而特征值 经非奇异变换是不变的，那么这些系统 也是不变 的量。所以称特征多项式的系数为系统的不变量。
(3)有共轭复根时，以四阶系统其中有一对共轭复根为例，即 此时
1.6 从状态空间表达式求传递函数阵
1.6.1 传递函数(阵)
状态和状态空间模型
x2 x(t0)
x (t1)
x (t2)
x (t) x1 图2-2 二维空间的状态轨线
➢ 随着时间的推移,状态不断地变化,tt0各瞬时的状态在状 态空间构成一条轨迹,它称为状态轨线。
➢ 状态轨线如图2-2所示。
系统的状态空间模型
• 状态空间模型是应用状态空间分析法对动 态系统所建立的一种数学模型,它是应用现 代控制理论对系统进行分析和综合的基础。
– 最小变量组。即描述系统状态的变量组的各分 量是相互独立的。
• 减少变量,描述不全。
• 增加则一定存在线性相关的变量,冗余的变量,毫无必 要。
• 若要完全描述n阶系统,则其最小变量组必须
由n个变量(即状态变量)所组成,一般记这n
个状态变量为x1(t),x2(t), …,xn(t).
– 若以这n个状态变量为分量,构成一个n维变量向
C为mn维的输出矩阵;
D为mr维的直联矩阵(前馈矩阵,直接转移矩阵)。
• 状态空间模型的意义,有如下讨论:
– 状态方程描述的是系统动态特性,
• 其决定系统状态变量的动态变化。
– 输出方程描述的是输出与系统内部的状态变量的 关系。
– 系统矩阵A表示系统内部各状态变量之间关联情况,
• 它主要决定系统的动态特性。
其中各矩阵为时间t的函数,随时间变化而变化。
系统的状态空间模型(10/11)
4. 线性定常系统
x Ax Bu
y
Cx
Du
为简便,常将线性时变系统的状态空间模型简记为 (A(t),B(t),C(t),D(t)).
➢ 类似地,线性定常系统的状态空间模型亦可简记为
(A,B,C,D).
➢ 几种简记符的意义:
状态空间分析法
对复杂的时变、非线性、多输入－多输出系统的问题， 需要用对系统内部进行描述的新方法——状态空间分析法。
4
§1-1 状态变量及状态空间表达式
一、状态
状态:动态系统的状态粗略地说就是指系统的过去、现在和 将来的运动状况。精确地说，状态需要一组必要而充分的 数据来说明。
二、状态变量
状态变量：足以完全确定系统运动状态的一组最小（内部） 变量。
y(t) Cx(t) Du(t)
11
§1-1 状态变量及状态空间表达式
例：
R
方法二： 令x1(t)= uc(t)
u(t)
x1
(
t
)
x 2
(
t
)
x1(t)
yx2((tt ))
Lxx1C21((xt1t)(0L)tL1)iC(RLt)1xC12RL(ut )0c(t)Lxx1Cxx12 ((12uLLitt((((Ct))ttti))())utc)(tC)0L1RuRciC((uttux)()ct2(()t t)u)=cu(cut()tc)(t)uu((tt))
四、状态空间 以状态变量x1(t), x2(t) , x3(t) , … , xn(t)为坐标轴
所构成的 n 维空间，称为状态空间。 在特定时刻t，状态向量x (t) = [x1(t) , … , xn(t)]T
在状态空间中是一点 。随着时间的推移，状态向量 x (t) 在状态空间中描绘出一条轨迹，称为状态轨迹。
x1
(
t
)
x2
(
t
)
0
1
L
4
§1-1 状态变量及状态空间表达式
一、状态
状态:动态系统的状态粗略地说就是指系统的过去、现在和 将来的运动状况。精确地说，状态需要一组必要而充分的 数据来说明。
二、状态变量
状态变量：足以完全确定系统运动状态的一组最小（内部） 变量。
y(t) Cx(t) Du(t)
11
§1-1 状态变量及状态空间表达式
例：
R
方法二： 令x1(t)= uc(t)
u(t)
x1
(
t
)
x 2
(
t
)
x1(t)
yx2((tt ))
Lxx1C21((xt1t)(0L)tL1)iC(RLt)1xC12RL(ut )0c(t)Lxx1Cxx12 ((12uLLitt((((Ct))ttti))())utc)(tC)0L1RuRciC((uttux)()ct2(()t t)u)=cu(cut()tc)(t)uu((tt))
四、状态空间 以状态变量x1(t), x2(t) , x3(t) , … , xn(t)为坐标轴
所构成的 n 维空间，称为状态空间。 在特定时刻t，状态向量x (t) = [x1(t) , … , xn(t)]T
在状态空间中是一点 。随着时间的推移，状态向量 x (t) 在状态空间中描绘出一条轨迹，称为状态轨迹。
x1
(
t
)
x2
(
t
)
0
1
L
《现代控制理论》课后习题答案
=
3 2
， c2
=
2s + 5 lim s→−3 s + 1
=
1 2
。
从输入通道直接到输出通道上的放大系数 d = 1，由此可得:
⎡ x1
⎢ ⎣
x 2
⎤ ⎥ ⎦
=
⎡− 1
⎢ ⎣
0
0⎤ − 3⎥⎦
⎡ ⎢ ⎣
x1 x2
⎤ ⎥ ⎦
+
⎡1⎤ ⎢⎣1⎥⎦u
y
=
⎡ ⎢⎣
3 2
1 2
⎤ ⎥⎦
⎡ ⎢ ⎣
x1 x2
u
d
d
b2
dt
dt
d
b1
m
dt
b0
因此，两个环节调换后的系统状态变量图为
u
d
d
b2
dt
dt
d
b1
dt
b0
m
−∫
−∫
y −∫
a0
a1
a2
进一步简化，可得系统状态变量图为 u
b0
b1
b2
− ∫ x1
− ∫ x2
− ∫ x3 y
a0
a1
a2
3
取 y = x3 ， y = x2 ， y = x1 ，可以得到两个环节调换后的系统的状态空间模型为
a(s)
1 a(s)
=
s3
+
1 a2s2 +
a1s
+
a0
， b(s)
=
b2 s 2
+ b1s
+ b0
。
2
由于 s−3 y 相当于对 y 作 3 次积分，故 y = 1 可用如下的状态变量图表示： m a(s)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则
当然，也可以扩展为AR(P)
• 货币政策工具对货币供给的时变效力
量测方程
状态方程
量测方程：
1.方程右端不能包含两侧变量的当期和未来值； z=sv1+sv2*x1+c(3)*z(1)+c(1)+[var=exp(c(2))] 2.量测方程必须是同期状态向量的线性方程。 @signal y=sv1*sv2*x1+[var=exp(c(2))] 3.量测方程可以包含外生变量和未知参数，也可以使这些元 素的非线性形式； Z=c(1)+sv1+sv2*x1+sv3*x2+[var=exp(c(2))] 4.可以包含误差或误差方差指定选项，如果不包含，则方程 是确定性的。
给误差方差和误差协方差 赋值
IF 误差项被命名，但没有对应的@evar赋值，则方差或协方差默认为NA或0
Ename语句定义的误差项只能存在于@evar赋值语句中，不能进入状态或量测方程
状态方程： 1.每一个状态方程具有唯一的因变量名，不允许使用表达式 @state exp(sv1)=sv1(-1)+[var=exp(c(3))] 2.状态方程中不能包含因变量及其超前、滞后变量。 3.状态方程中可以包含外生变量和未知参数，也可以是非线 性的； 4.每一个状态方程必须是状态变量一期滞后的线性方程。非 线性、同期、超前或多期滞后将导致错误信息。 @state sv2=log(sv2(-1))+[var=exp(c(3))] @state sv3=c(1)+c(2)*sv3(-2)+))+[var=exp(c(3))]
动态预测/平滑预测/n期向前预测
如果量测方程的因变量是一个表达式，EVIEWS只提供变大时的预测， 如果量测变量是log(y)，则只预测y的对数。
时变参数的状态空间模型(入门)
多变量时 间序列
第一、将不可观测的变量并入可观测模型并与其一起得到估 计结果； 第二、通过强有力的迭代算法——卡尔曼滤波来估计。
可以估计单变量和多变量的ARMA模型，马尔科夫转 换模型和变参数模型。
内部系统
输入
输出
一般情况
不可观测
随时间的改变而改变，体现了因变量和 自变量之间关系的改变
Z=c(1)+sv1+sv2*x1+sv3*x2+[var=exp(c(2))]
Y=c(1)++sv1*x1+[ename=e1] @state sv1=sv1(1)+[ename=el]
用 ename给残差序列命名
@evar cov(e1,e2)=c(2)
@evar var(e1)=exp(c(3)) @evar var(e2)=exp(c(4)*x)
当然，也可以扩展为AR(P)
• 货币政策工具对货币供给的时变效力
量测方程
状态方程
量测方程：
1.方程右端不能包含两侧变量的当期和未来值； z=sv1+sv2*x1+c(3)*z(1)+c(1)+[var=exp(c(2))] 2.量测方程必须是同期状态向量的线性方程。 @signal y=sv1*sv2*x1+[var=exp(c(2))] 3.量测方程可以包含外生变量和未知参数，也可以使这些元 素的非线性形式； Z=c(1)+sv1+sv2*x1+sv3*x2+[var=exp(c(2))] 4.可以包含误差或误差方差指定选项，如果不包含，则方程 是确定性的。
给误差方差和误差协方差 赋值
IF 误差项被命名，但没有对应的@evar赋值，则方差或协方差默认为NA或0
Ename语句定义的误差项只能存在于@evar赋值语句中，不能进入状态或量测方程
状态方程： 1.每一个状态方程具有唯一的因变量名，不允许使用表达式 @state exp(sv1)=sv1(-1)+[var=exp(c(3))] 2.状态方程中不能包含因变量及其超前、滞后变量。 3.状态方程中可以包含外生变量和未知参数，也可以是非线 性的； 4.每一个状态方程必须是状态变量一期滞后的线性方程。非 线性、同期、超前或多期滞后将导致错误信息。 @state sv2=log(sv2(-1))+[var=exp(c(3))] @state sv3=c(1)+c(2)*sv3(-2)+))+[var=exp(c(3))]
动态预测/平滑预测/n期向前预测
如果量测方程的因变量是一个表达式，EVIEWS只提供变大时的预测， 如果量测变量是log(y)，则只预测y的对数。
时变参数的状态空间模型(入门)
多变量时 间序列
第一、将不可观测的变量并入可观测模型并与其一起得到估 计结果； 第二、通过强有力的迭代算法——卡尔曼滤波来估计。
可以估计单变量和多变量的ARMA模型，马尔科夫转 换模型和变参数模型。
内部系统
输入
输出
一般情况
不可观测
随时间的改变而改变，体现了因变量和 自变量之间关系的改变
Z=c(1)+sv1+sv2*x1+sv3*x2+[var=exp(c(2))]
Y=c(1)++sv1*x1+[ename=e1] @state sv1=sv1(1)+[ename=el]
用 ename给残差序列命名
@evar cov(e1,e2)=c(2)
@evar var(e1)=exp(c(3)) @evar var(e2)=exp(c(4)*x)