《探索直线平行的条件一》导学案
北师大版数学七年级下册2.2《探索直线平行的条件》教案1

北师大版数学七年级下册2.2《探索直线平行的条件》教案1一. 教材分析《探索直线平行的条件》是北师大版数学七年级下册第2章第2节的内容。
本节课主要让学生通过探索活动,掌握直线平行的条件,理解平行线的性质,并能运用这些性质解决一些简单问题。
本节课的内容是学生进一步学习几何知识的基础,对于培养学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析学生在学习本节课之前,已经学习了直线、射线、线段的基本概念,对图形的基本性质有所了解。
但是,对于直线平行的条件和平行线的性质,学生可能还比较陌生。
因此,在教学过程中,需要引导学生通过探索活动,自主发现和总结直线平行的条件和平行线的性质。
三. 教学目标1.理解直线平行的条件,掌握平行线的性质。
2.能够运用直线平行的条件和平行线的性质解决一些简单问题。
3.培养学生的空间想象能力和逻辑思维能力。
四. 教学重难点1.教学重点:直线平行的条件,平行线的性质。
2.教学难点:直线平行的条件的推导,平行线的性质的理解和运用。
五. 教学方法采用问题驱动的教学方法,引导学生通过探索活动,自主发现和总结直线平行的条件和平行线的性质。
在教学过程中,注重学生的主体地位,鼓励学生积极参与,培养学生的动手能力和思维能力。
六. 教学准备1.准备一些直线和平行线的模型,用于直观展示直线平行的条件和平行线的性质。
2.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用直尺和三角板,展示一些直线和平行线,引导学生观察和思考:什么是直线?什么是平行线?直线和平行线有哪些性质?2.呈现(10分钟)呈现一些直线平行的例子,引导学生观察和思考:这些直线为什么是平行的?直线平行有哪些条件?3.操练(10分钟)让学生分组合作,利用直尺和三角板,尝试画出一些平行线,并总结直线平行的条件。
4.巩固(10分钟)让学生独立完成一些关于直线平行的练习题,巩固所学知识。
5.拓展(10分钟)引导学生思考:平行线除了具有直线平行的条件外,还有哪些性质?让学生通过探索活动,发现和总结平行线的性质。
2.2.2探索直线平行的条件(教案)

四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是“探索直线平行的条件”这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过两条直线看起来永远不会相交的情况?”比如,铁轨或者操场的跑道。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索直线平行的奥秘。
c.逻辑推理能力的培养:在探索直线平行条件的过程中,学生需要运用逻辑推理来理解为何这些条件能证明直线平行。
突破方法:通过小组讨论、问题驱动的教学方法,鼓励学生提出假设、进行验证、总结规律,从而培养他们的逻辑推理能力。
d.数学语言的准确表达:学生需要学会使用准确的数学语言描述直线平行的条件,这对于他们的数学表达和交流能力是一个挑战。
在总结回顾环节,大多数学生能较好地掌握直线平行的判定条件,但也有少数学生表示还存在疑问。为了确保每个学生都能跟上教学进度,我计划在课后对这部分学生进行个别辅导,解答他们的疑问,巩固所学知识。
二、核心素养目标
本节课的核心素养目标致力于培养学生的几何直观、逻辑推理和数学建模能力:
1.通过观察和操作几何图形,培养学生识别同位角、内错角、同旁内角的能力,增强几何直观。
2.引导学生运用逻辑推理,探究直线平行的条件,理解同位角相等、内错角相等、同旁内角互补与直线平行之间的关系。
3.培养学生运用数学语言表达几何图形关系,建立数学模型,解决实际问题,提升数学建模能力。
重点难点解析:在讲授过程中,我会特别强调同位角相等、内错角相等、同旁内角互补这三个重点。对于难点部分,我会通过图形示例和逐步引导来帮助大家理解。
《探索直线平行的条件》教案

《探索直线平行的条件》优秀教案第一章:引言1.1 教学目标:让学生了解直线平行的概念及实际应用。
激发学生对探索直线平行条件的兴趣。
1.2 教学内容:直线平行的定义及实例。
直线平行的实际应用场景。
1.3 教学方法:通过图片、实例等方式引入直线平行的概念。
引导学生思考直线平行的实际应用场景。
1.4 教学步骤:1. 引入直线平行的概念,引导学生理解直线平行的定义。
2. 展示直线平行的实例,让学生通过观察和分析来理解和记忆直线平行的特征。
3. 引导学生思考直线平行的实际应用场景,如交通运输、建筑设计等,激发学生对直线平行的兴趣。
第二章:直线平行的判定2.1 教学目标:让学生掌握直线平行的判定方法。
培养学生运用判定方法解决实际问题的能力。
2.2 教学内容:直线平行的判定方法。
判定方法的证明和解释。
2.3 教学方法:通过几何图形和实例来引导学生理解和记忆直线平行的判定方法。
通过证明和解释来说明判定方法的合理性。
2.4 教学步骤:1. 引导学生回顾直线平行的定义,复习相关知识。
2. 引入直线平行的判定方法,让学生通过观察和分析几何图形来理解和记忆判定方法。
3. 通过证明和解释来说明判定方法的合理性,帮助学生深入理解判定方法。
第三章:直线平行的性质3.1 教学目标:让学生掌握直线平行的性质。
培养学生运用性质解决实际问题的能力。
3.2 教学内容:直线平行的性质。
性质的证明和解释。
3.3 教学方法:通过几何图形和实例来引导学生理解和记忆直线平行的性质。
通过证明和解释来说明性质的合理性。
3.4 教学步骤:1. 引导学生回顾直线平行的判定方法,复习相关知识。
2. 引入直线平行的性质,让学生通过观察和分析几何图形来理解和记忆性质。
3. 通过证明和解释来说明性质的合理性,帮助学生深入理解性质。
第四章:直线平行的应用4.1 教学目标:让学生学会运用直线平行的条件解决实际问题。
培养学生的实际问题解决能力。
4.2 教学内容:直线平行的条件在实际问题中的应用。
《探索直线平行的条件》教案

《探索直线平行的条件》优秀教案一、教学目标1. 让学生理解直线平行的概念,掌握直线平行的条件。
2. 培养学生运用几何知识解决实际问题的能力。
3. 提高学生逻辑思维能力和团队协作能力。
二、教学内容1. 直线平行的定义2. 直线平行的条件3. 平行线的性质4. 平行线的判定5. 直线平行在实际问题中的应用三、教学重点与难点1. 教学重点:直线平行的概念、条件、性质和判定。
2. 教学难点:直线平行条件的推理和证明。
四、教学方法1. 采用问题驱动法,引导学生主动探索直线平行的条件。
2. 利用几何画板软件,直观展示直线平行的过程,增强学生直观感知。
3. 组织小组讨论,培养学生团队协作能力和口头表达能力。
4. 运用例题讲解,让学生在实践中掌握直线平行的应用。
五、教学准备1. 教学课件:包括直线平行的图片、动画、例题等。
2. 几何画板软件:展示直线平行的过程。
3. 练习题:巩固直线平行的知识和应用。
4. 小组讨论卡片:分配给各小组,用于记录讨论成果。
教案一、导入新课1. 展示生活中常见的平行现象,如的道路、书本排版等。
2. 引导学生思考:这些平行现象背后有什么共同的规律?3. 引入本节课的主题:《探索直线平行的条件》。
二、自主学习1. 让学生阅读教材,了解直线平行的定义。
三、课堂讲解1. 讲解直线平行的条件,引导学生通过几何画板软件直观展示。
2. 利用几何画板软件,展示直线平行的过程,引导学生观察、思考。
3. 讲解平行线的性质,如同位角相等、内错角相等等。
4. 讲解平行线的判定方法,如同位角相等、内错角相等等。
四、巩固练习1. 让学生运用几何画板软件,自主探究直线平行的条件。
2. 学生完成练习题,教师点评并讲解答案。
五、小组讨论1. 发放小组讨论卡片,让学生分组讨论直线平行的应用。
六、课堂小结2. 强调直线平行在实际问题中的应用。
七、作业布置1. 让学生完成课后练习题,巩固直线平行的知识。
2. 选择一道实际问题,运用直线平行的知识解决。
7.1探索直线平行的条件(1)(教案)

(3)
(4)
2
1 1 1
7c 5 1 c c 1 2 1 6 1 c
1 1 b 1
(5)结论:同位角相等,两直线平行。
1
汤庄桥中学七年级备课组
二、学会应用: 例 1、如图,∠1 和∠2 是同位角的是(
)
1 1 2
1
1
2
2பைடு நூலகம்2
板 块 二:学 会运用 同位角
A B C D 例3、如图直线 a.b 被 c 所截∠1=35°,∠2=145°。问直线 a 与 b 平行吗?
板块
教师活动的问题串设计 一、 (1)利用三角板和直尺画平行线:
c 1 a 1 a 1 a 1
学生活动串设 计
目标达成及 反馈串设计
1 1 1 b 2 b 2 2 1 1 1 c 1 1 1 1 1 c 1 1 1 1 1 1 1 1 1 1 1 1 1 (2)观察:∠1 与∠2 相等时,所画的直线 1 a、b 是否平行? 板 块 一:初 次接触 同位角 及同位 角的用 途
1
a
2 c
b
1、如图(1),直线 AB、CD 被直线 AE 所截,∠A 和______是 同位角。 2、 如图 (2) ∠3 和∠9 是直线________、 , _______被直线_______ 所截而成的______角;∠6 和∠9 是直线_____、______被直线 ________所截而成的_______角。
1 1 1
1 1 1
1
1 b 1 1 1 1 1 1
(3)探索:∠1 与∠2 不相等,所画的直线 a、b 平行吗?
c 1 2 1 3 a 1 b 1 4 1 a 1
1 8 1 c 1 1 1 1 1 1 1 1 1 1 1 1 定义:两条直线 a、b 被第三条直线所截而成的 8 个角中,像∠1 1 1 与∠2 这样的一对角称为同位角。 (4)猜想:图中还有其它的同位角吗?
探索直线平行的条件(1)
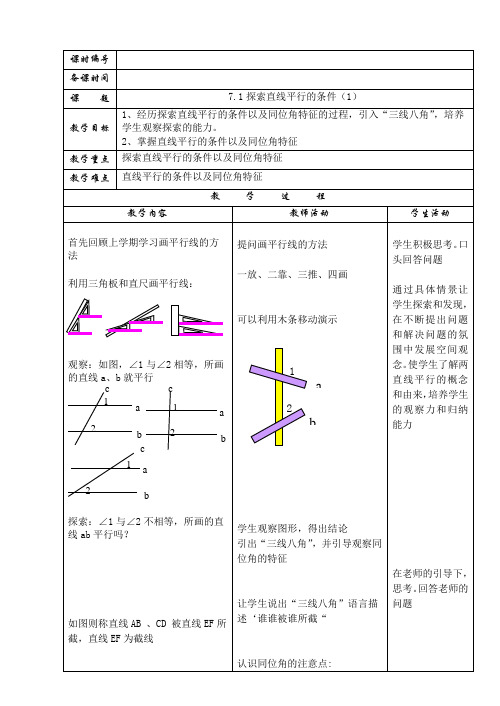
2、如图 2,∠C=31°,当∠ABE= 度时,就能使 BE//CD.
解:(1)AB∥CD 因为∠1 与∠C 是 ABCD 被 A C 截成的同位角, 且∠1 =∠C 所以 AB∥CD (2)AB∥CD. 因为∠2 与∠C 是 BDAC 被 CD 截成 的同位角 且∠2=∠C 所以 AC∥BD 情境创设 1、 2、
图2
3、如图 3,直线 a、b 被直线 c 所 截,∠1=35°,∠2=145°,问: 直线 a 与 b 平行吗? 认真听讲, 注意格 式
图3
例 1:„„
例 2:„„
习题 „„
板书设计
„„ „„
„„ „„
„„ „„
作业布置 课后随笔 通过学生操作---观察---猜想---探索平行线条件的过程,激发学生积极参与的 兴趣,掌握平行线的识别方法,调动学生学习几何的积极性,培养合情说理的 能力。 “三线八角”的语言描述必须要加强训练,让学生要多说才行。
课时编号 备课时间 课 题 7.1 探索直线平行的条件(1) 1、经历探索直线平行的条件以及同位角特征的过程,引入“三线八角” ,培养 学生观察探索的能力。 2、掌握直线平行的条件以及同位角特征 探索直线平行的条件以及同位角特征 直线平行的条件以及同位角特征 教 教学内容 首先回顾上学期学习画平行线的方 法 利用三角板和直尺画平行线: 学 过 程 学生活动 学生积极思考。 口 头回答问题 通过具体情景让 学生探索和发现, 在不断提出问题 和解决问题的氛 围中发展空间观 念。 使学生了解两 直线平行的概念 和由来, 培养学生 的观察力和归纳 能力
教学目标 教学重点 教学难点
教师活动 提问画平行线的方法 一放、二靠、三推、四画
可以利用木条移动演示
观察:如图,∠1 与∠2 相等,所画 的直线 a、b 就平行 c 2 b
《探索直线平行的条件》教案

《探索直线平行的条件》优秀教案第一章:引言1.1 课程背景本节课旨在引导学生探索直线平行的条件,通过观察、思考、交流等活动,让学生理解直线平行的概念,掌握判断直线平行的方法,为后续学习几何知识打下基础。
1.2 教学目标1. 了解直线平行的概念;2. 掌握判断直线平行的方法;3. 培养观察、思考、交流能力。
1.3 教学重难点1. 直线平行的概念;2. 判断直线平行的方法。
第二章:直线平行的概念2.1 教学内容通过观察生活中实例,引导学生认识直线平行的概念,理解直线平行的特点。
2.2 教学方法采用直观演示、小组讨论的教学方法,让学生在观察、思考中掌握直线平行的概念。
2.3 教学步骤1. 展示生活中的实例,引导学生观察直线平行的特点;2. 引导学生思考直线平行的定义;3. 组织小组讨论,让学生交流直线平行的理解;4. 总结直线平行的概念及特点。
第三章:判断直线平行的方法3.1 教学内容本节课引导学生学习判断直线平行的方法,包括平行公理、平行线的性质等。
3.2 教学方法采用讲解、示范、练习的教学方法,让学生在理解判断直线平行的方法的基础上,能够独立进行判断。
3.3 教学步骤1. 讲解平行公理及其实际意义;2. 示范判断直线平行的方法;3. 组织学生进行练习,巩固判断方法;4. 引导学生总结判断直线平行的关键点。
第四章:直线平行的应用4.1 教学内容本节课让学生学会运用直线平行的知识解决实际问题,提高学生的应用能力。
4.2 教学方法采用案例分析、小组合作的方法,让学生在解决实际问题中,巩固直线平行的知识。
4.3 教学步骤1. 展示实际问题,引导学生运用直线平行的知识进行分析;2. 组织小组合作,让学生共同探讨解决问题的方法;3. 分析、评价小组成果,总结直线平行在实际问题中的应用;4. 进行课堂练习,巩固所学知识。
第五章:总结与拓展5.1 教学内容本节课对本节课内容进行总结,引导学生思考直线平行在几何学中的重要性,并进行拓展学习。
初一数学导学案

课题:探索直线平行的条件班级 姓名学习目标:1.认识同位角。
2.会用同位角相等判断两直线平行。
预习案:1 有十五分钟左右的时间,阅读探究课本63—65页的基础知识2 思考教材设置的问题,然后结合课本的基础知识,完成预习自测3 将预习中不能结局的问题标记出来 相关知识: 1、了解三线八角。
2、什么是同位角?3、如何画平行线并说明其道理。
教材助读:1.在同一平面内__________________的两条直线叫做平行线。
2.图1、2中的直线平行吗?你是怎样判断的?(1) (2) 预习自测:1.结合右图,当∠1= 时,a 1∥a 2当∠3= 时,a 1∥a 2。
2.如图, 请你说一说∠1与∠2是哪两条直线被哪条直线截成的同位角?3.如图,直线a 、b 被直线c 所截∠1=35º,∠2=145º,问直线a 、b 平行吗?为什么?a b c 2 11 c ba 23我的疑问:请将你预习中未能解决的问题和有疑问的问题写下来,等待课堂上与老师和同学探究解决。
质疑探究: 活动一、 如图,3根硬纸条相交成∠1、∠2,固定硬纸条b 、c ,转动硬纸条a 。
活动思考:(1)在硬纸条a 转动过程中,∠2的大小发生了变化,随之它也带动了哪条直线的位置发生变化?(2)当∠1与∠2的大小满足什么关系时,硬纸条a 与硬纸条b 平行?我们可以发现:要使图中直线a//b ,必须满足 条件。
(3)若图中∠1与∠2不相等时,硬纸条a 与硬纸条b 平行?我发现了 。
活动二、下列图形中,两条直线a 、b 被第三条直线c 所截而得到的∠1和∠2在位置上有什么关系?(提示:∠1和∠2在两条直线a 、b 的哪一侧?又在第三条直线c 的哪个方向呢?) (1)位置关系:(2)你还能找出类似的一组角吗?(3)辨一辨;如图∠1和∠2是同位角的是( )三、应用实践:1.如图所示:∠1=∠C 、∠2=∠C 请你找出图中互相平行的直线,并说明理由1 2 1 2 211 2 b a c12ba c21 A B C D21A B C D2.如右图,∠1=∠2=55°,∠3等于多少度?直线AB, CD平行吗?说说你的理由?四、盘点收获:六、有奖征答:如图,已知直线AB、CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ//NP,为什么?123ABCDF EGHB1AEMQP。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探索直线平行的条件一
【学习目标】1、会找同位角(“F 型”);
2、掌握平行线公理1及平行线的传递性 ;
3、掌握判定直线平行的条件并能解决一些问题
【学习重点】1、会认各种图形下的“三线八角”中的同位角;
2、掌握直线平行的条件是“同位角相等,两直线平行”
【学习过程】 一、知识预备
1、在同一平面内,两条直线的位置关系有 和 ,不相交的两条直线叫 ;
2、如图,①是由直线 和直线______被第三条直线_______所截而成的 角;
②∠7与∠8是由直线 和直线______被第三条直线_______所截而成的 角;
你还能找到其它的同位角吗?它们都有怎样的特征? 二、知识研究
(一)、同位角的特征(简称“三线八角”)如下表: 基本图形
角的名称
位置特征
图形结构特征
基础达标练习:
1、下列图中,∠1和∠2哪些是同位角?那些不是?
12∠∠与_2
_1
( ) ( )
( ) ( ) 2、分别找出图1和图2当中的同位角。
(1) (2)
(二)平行线的判定:
平行判定1:两条直线被第三条直线所截,如果同位角 ,那么这两条直线 。
简称: (公理) 如图,可表述为:
∵ ( ) ∴ ( )
学以致用:如图,一张纸上画有a 、b 两条线段,请你设计一个方案,判断这两条线段是否平行?
2
1E
D C
B
A
F
E
D C B
A
2
1
如图,直线AB 外有两点P 、Q.(1)你能过点P 画一条直线与直线AB 平行吗?这样的直线还能画吗?
2、平行线公理:过直线外一点有 条直线与这条直线平行。
3、平行线的传递性: 几何语言:(如图)
∵ a b ∴ c
三、知识运用 (一)基础达标 1、如图
(1)(已知)
12∠=∠d
c
b
a
3
2
1
m
n
a
b
140度
40度
40度
3
2
1
F
A
B
C
D
E
∴ ∥ ( ) (2)(已知)
∴ ∥ ( ) 2、如图,∠1 = ∠2 = 55°, ∠3等于多少
度?
直线AB 、CD 平行吗? 说明你的理由。
3、写出图中互相平行直线,并说明理由。
四、课堂反思:今天,你学习了什么知识?你还有哪些疑惑?
23∠=∠
五、牛刀小试
1.如图,∠1与∠2不能构成同位角的图形是[ ]
2.如图, ∠1=70°,在给出的下列条件中,能判定AB ∥ CD 的条件的是( )
(A )∠2= 70° (B ) ∠3= 110° ( C )∠4= 70° (D )∠5= 70° 3.如图,∠1=65°,∠B =65°,可以判断__ ∥____,理由是_________________.
4.∠3=30°,当∠ABE =______时,就能使 BE ∥CD ?
第2题图 第3题图 第4题图
3
E
D
C
B
A
1
D
C
B
A
D
C
B
A 54
3
21。
