轮系 渐开线 (公开课专用)
机械基础 教学最好的PPT 渐开线齿轮 (公开课专用)

至此,可以给分度圆一个完整的定义:分度圆是设计齿轮时
给定的一个圆,该圆上的模数m和压力角α均为标准值。
第8章 齿 轮 传 动 9. 齿顶高、 齿根高和全齿高
如图8-9所示,轮齿被分度圆分为两部分,轮齿在分度圆和
8.3 渐开线齿轮各部分的名称及尺寸
8.3.1 渐开线齿轮各部分的名称
图8-9 齿轮各部分的尺寸和符号
第8章 齿 轮 传 动 1. 齿数
在齿轮整个圆周上轮齿的总数称为该齿轮的齿数,用z表示。
2. 齿顶圆
过齿轮所有轮齿顶端的圆称为齿顶圆,用ra和da分别表示其
半径和直径。 3. 齿槽宽 齿轮相邻两齿之间的空间称为齿槽,在任意圆周上所量得 齿槽的弧长称为该圆周上的齿槽宽,以ei表示。
速度分量应相等,否则两齿廓将互相压入或分离, 因而
vK1cosαK1=vK2cosαK2
第8章 齿 轮 传 动
即
ω1O1K cosαK1=ω2O2K cosαK2
故齿轮传动的瞬时转动比为
1 O2 K cos K 2 rb 2 i 2 O1K cos K 1 rb1
(8-3)
由于渐开线齿轮的两基圆半径rb1 ,rb2 不变,所以渐开线齿 廓在任意点接触(如图8-7中的K1位置),两齿轮的瞬时传动比 恒定,且与基圆半径成反比,因此满足齿轮传动的第一个基本 要求。
点的曲率中心,线段NK是渐开线上K点的曲率半径。
(3) 作用于渐开线上K点的正压力FN方向(法线方向)与点K的 速度vK 方向所夹的锐角αK 称为渐开线在K点的压力角,由图8-5
可知
rb cos K rK
渐开线齿轮

渐开线齿轮
什么是渐开线?
所谓渐开线顾名思义的说,那就是它上面的点逐渐离开一个固定点(基圆的圆心)的曲线。
如果你把一条线缠绕在一个圆柱上,线的末端固定在一个笔头上,让笔头牵着线逐渐取开圆柱并画下痕迹,那么这个痕迹就是一个渐开线。
从你这样画图的轨迹中你可以看到,这实际上是一条直线在一个圆上滚动的时候直线上的一个的的运动轨迹。
另外,类似的还有摆线,摆线就是一个圆在一条直线或曲线上滚动时圆上的一个点随圆滚动时的运动轨迹。
在实际应用中,渐开线和摆线主要用来设计齿轮、齿条的形状,因为齿轮、齿条的工作方式都是“滚动”,所以这两种曲线才是它们最合适的运动轨迹……
渐开线圆柱齿轮是齿轮中的一种。
齿轮的齿形由渐开线和过渡线组成时,便被称为渐开线齿轮。
因渐开线具有众多优点,是应用最广的一种齿轮曲线。
齿形有多种形式,其中以渐开线齿形最为常见。
渐开线齿形常用的加工方法有两大类,即成形法和展成法。
齿轮基础渐开线的形成概要ppt课件

由于O2 、O1为定点,故P必为一个定点。 o1
节圆: r’1 r’2
r’1
ω1
两节圆相切于P点,且两轮节点处
速度相同,故两节圆作纯滚动。 a
中心距: a=r’1+r’2 共轭齿廓:一对能实现预定传动
比(i12=ω1/ω2)规律 的 啮合齿廓。
节圆
n
k
作者:潘存云教授
P n
ω2 r’2
o2
2.齿廓曲线的选择
或rb=rcosα,
对于分度圆大小相同的齿轮,
d =dcosα 如果α不同,则基圆大小将不
b
同,因而其齿廓形状也不同。
α是决定渐开线齿廓形状的一个重要参数。
规定标准值:α=20° 某些场合采用α=14.5°、15°、22.5°、25° 如航空齿轮。
由d=mz知:m和z一定时,分度圆是一个大小唯一确 定的圆。
K 作者:潘存云教授 K’ P C2 C1
为定直线。
rb2
两轮中心连线也为定直线,故交
ω2
点P必为定点。在位置K’时同样有此结论。
O2
i12=ω1/ω2=O2P/ O1P=const
要使两齿轮作定传动比
传动,则两轮的齿廓无
工程意义:i12为常数可减少因速度变化所
论在任何位置接触,过 接触点所作公法线必须
设计和检验齿轮时,常需要知道某些圆上的齿厚。
一般表达式: si=CC=riφ
sa
φ=∠BOB-2∠BOC =(s/r) - 2(θi-θ)
C si C
B
sB
=(s/r)-2( invαi-invα) Si=riφ
A N
sb
A
=(sri/r)-2ri(invαi-invα)(9-7) 其中:αi=arccos(rb/ri)
渐开线直齿圆柱齿轮

rb rK
(10-1)
由此可见,渐开线上各点的压力角是不同的,向径rK越大,则压力角
αK越大;渐开线起始点A处向径rK =rb,即基圆上的压力角等于零。
返回
机械设计基础
Machine Design Foundation
2.渐开线方程 由图10-2a并由渐开线性质可推得:
渐开线直齿圆柱齿轮
上式表明,展角θK压力角αK而变化,称θK为压力角αK的渐开线
作为尺寸计算的基准,称该圆为齿轮的分度圆,其半径和直径分别
用r和d表示。一般将分度圆上的齿距、齿厚和齿槽宽简称为齿距、齿
厚和齿槽宽,分别用p、s和e表示,因此,p=s+e。
齿顶圆与分度圆之间的径向高度称为齿顶高,用ha表示;分度 圆与齿根圆之间的径向高度称为齿根高,用hf表示。齿顶圆与齿根圆 之间的径向高度称为齿高,用h表示。显然,h =ha+hf。
1.发生线沿基圆滚过的长度,等于基圆上被滚过的一段弧长,
即
。
2.渐开线上任一点K的法线始终与基圆相切。
3.渐开线上各点的曲率半径不同。渐开线上离基圆越远的点,
其曲率半径越大;离基圆越近的点,其曲率半径越小;在基圆上,
其曲率半径为零。
4.渐开线的形状取决于基圆的大小。如图10-2b所示,基圆半
径越小,其渐开线越弯曲;基圆半径越大,其渐开线越平直;当基
于是
m p
d= m z
(10-4) (10-5)
齿轮的模数在我国已经标准化了,见表10-1。
表10-1 标准模数系列值
注:1.优先采用第一系列,其次为第二系列,括号内的模数尽可能不用。 2.对斜齿轮,该表所示为法面模数。
返回
机械设计基础
渐开线齿轮详解PPT课件

渐开线齿轮参数测定
3.齿顶高系数ha*、顶隙系数c*测定
通过测量齿根圆直径df,可定ha*和c*。 若测出df值,则由齿轮的几何关系知:
h f m h a * c * x d d f/2
式中ha*和c*为未知,可分别用正常齿制ha* =1,c* =0.25,短齿制 ha* =0.8,c* =0.3两组标准值代入上式,取最接近hf的一组ha*和c*, 即为所求值。
渐开线齿轮 参数测定
渐开线齿轮参数测定
一、实验目的
1.培养学生运用所学知识解决齿轮参数测定这一 生产实际问题的动手能力 。
2.初步掌握齿轮参数的基本测定方法,进一步巩 固有关齿轮方面的基本知识 。
渐开线齿轮参数测定
二、实验内容和工具
1.实验内容:测定一个奇数齿轮和一个偶数 齿轮的几何参数(m、α、ha*、c*、x),并判 定齿轮为标准齿轮还是变位齿轮。
W k m [2 .95 (k 2 0 .5 )1 0 .0z 1 ] 4 kz0.50.11z 10.5 9
渐开线齿轮参数测定
W k(k1)P bSb
W k1kbPSb
W k1W kPb
P b P co sm cos
m P b W k1W k
cos
cos
式中的α可能是20°,也可能是15°(我国常用的是20°)。 分别用15°和20°代入上式,算出两个模数,其模数最接近标 准模数值的一组m和α,即为所求齿轮的模数和压力角。
渐开线齿轮参数测定
四、实验步骤
1.直接计数齿轮的齿数; 2.测量Wk、Wk+1和df,对每一个尺寸应测量三次,取其 平均值为测量数据; 3.利用公式计算m、α、x、ha*和c*。
渐开线齿轮参数测定
齿轮渐开线方程图解
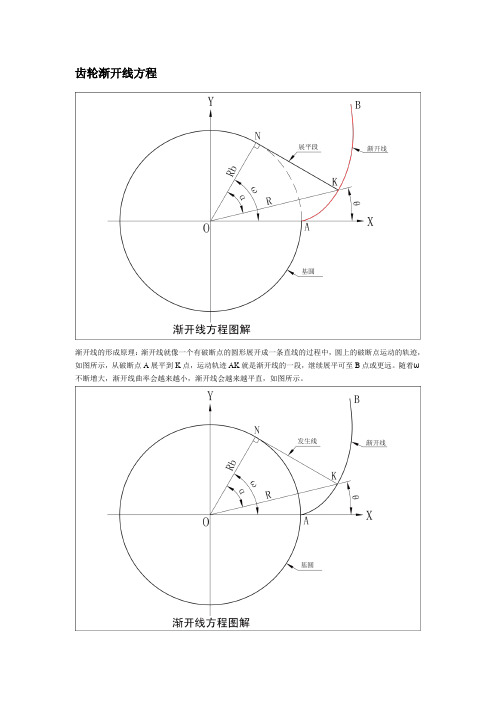
齿轮渐开线方程渐开线的形成原理:渐开线就像一个有破断点的圆形展开成一条直线的过程中,圆上的破断点运动的轨迹,如图所示,从破断点A展平到K点,运动轨迹AK就是渐开线的一段,继续展平可至B点或更远。
随着ω不断增大,渐开线曲率会越来越小,渐开线会越来越平直,如图所示。
渐开线方程的推理过程:如图所示,圆O为渐开线AB的基圆,半径为Rb,K为渐开线AB上的任一点;展平段KN为渐开线AB的发生线。
根据渐开线形成的原理可知,NO⊥NK,NK= N⌒A, ONK构成一个直角三角形。
以下过程将滚动角α(rad)作为已知变量进行推导:根据渐开线的形成原理可得N⌒A = NK,圆心角ω所对应的弧长:N⌒A =Rb*ω* PI /180, R=Rb/COS(α)。
先计算出OK与OX的夹角θ,根据渐开线函数公式θ=TAN(α)-α。
因为TAN(α)是N⌒A与Rb之比,相当于弧度值,所以此时α应换算为弧度值。
用PRO/E绘制方程曲线时,应将其转换为十进制角度。
即:θ=TAN(α)*180/PI-α,在PRO/E极坐标表示的方程中,θ用THETA表示。
A. 设α为压力角参数,将α用个人习惯的字母符号代替,如FAI。
设定一个参数值,如45°,即可写成:1. 压力角为参数“极坐标”表示的渐开线方程:FAI=T*45Rb=DB/2R=Rb/COS(FAI)THETA=TAN(FAI)*180/PI-FAIZ=0以上方程式是以压力角∠α作为变量参数。
若想使渐开线的长度控制在齿轮外径DW以内,就必须使渐开线K点与齿轮外径DW的边缘共线约束,可用∠α来控制。
因为齿轮的外径等于2*R=DW,基圆直径等于2*Rd=DB,渐开线K点与R的端点重合。
所以∠α应等于DB/DW的反余弦函数,即:∠α=ACOS(DB/DW),此角就可使渐开线K点落在齿顶圆边缘的位置。
将其作为变量代入方程,即可写成:2. 齿顶圆压力角为参数控制的“极坐标”表示的渐开线方程A:以ACOS(DB/DW)作为已知变量进行推导,方程如下:FAI=T*ACOS(DB/DW)Rb=DB/2R=Rb/COS(FAI)THETA=TAN(FAI)*180/PI-FAIZ=0如果方程式是以滚角∠ω作为变量参数。
渐开线的形成PPT课件

§4—4 齿轮各局部名称及 渐开线标准齿轮的根本尺寸
一、齿轮各局部名称
二、齿轮的根本参数 三、齿条的根本参数
四、标准直齿圆柱齿 轮几何尺寸计算
一、齿轮各局部名称和符号
rk
齿顶圆da 齿槽 齿根圆df
在任意圆上rk 齿槽宽ek 齿厚SK 齿距PK=eK+SK
分度圆d
齿顶高ha
齿根高hf
全齿高h 基圆db
第四章 齿轮机构
本章要求 §4—1 齿轮机构的特点和类型 §4—2 齿廓实现定角速比传动的条件 §4—3 渐开线齿廓 §4—4 齿轮各局部名称及渐开线标准
齿轮的根本尺寸
§4—5 渐开线标准齿轮的啮合 §4—6 渐开线齿轮的切齿原理 §4—7 根切、最少齿数及变位齿轮 §4—8 平行轴斜齿轮机构 §4—9 圆锥齿轮机构
k1k1 pb1
k 2 k 2 pb 2
pb1 pb2
如左图所示为一对渐开 线齿轮啮合的状况。设前一 对齿轮在K点接触,后一对齿 轮在K”点接触。
为使前后两轮齿能同时 在啮合线上接触,必需使法 向齿距K1K”1 = K2K”2, 否则
假设K1K”1 > K2K”2 ,传动中断。
假设K1K”1 < K2K”2 ,两轮可能 卡住。
一对齿轮的传动比为:
in 11d2 db2d2z2 n 2 2 d1 db1 d1 z1
二、标准中心距
齿轮传动时,一轮 节圆上的齿槽宽与另一 轮节圆上的齿厚之差称 为齿侧间隙。
标准齿轮的分度圆 齿厚等于其齿槽宽,因 此一对标准齿轮啮合时, 只要是两分度圆相切, 就可以确保齿轮无侧隙 啮合传动。
顶隙 c= c * m
c
'
齿顶高 ha = ha*m 齿根高 hf= (ha* +c *) m 全齿高 h= ha + hf
汽车机械基础课件 任务二 渐开线直齿圆柱齿轮传动

四、渐开线直齿圆柱齿轮的啮合传动
(二)渐开线齿轮传动的重合度 一对轮齿的实际啮合过程为:当一对轮齿开始啮合时,主动轮的齿根推动从动轮的 齿顶;当一对轮齿脱离啮合时,主动轮的齿顶推动从动轮的齿根,如图
五、渐开线齿轮的加工方法与根切
(一)渐开线齿轮的加工方法 齿轮的切齿方法就其原理来说可概括为仿形法和展成法两种。
则相啮合两齿廓的形状应满足条件: 过齿廓任一 啮合点的公法线,都要与两轮连心线交于 相应的瞬时 啮合节点。
因此,要使齿轮的传动比为定值,一对齿轮的齿廓 曲线应满足的条件是:无论两齿廓在何处接触,过啮 合点所作的公法线必须与两轮连心线交于一定点。
二、渐开线齿轮的齿廓及传动比
理论上,能满足齿廓啮合基本定律的曲线有很多。但考虑到设计、制造、使用 和检测等各种因素,工程上只用少数几种曲线作为齿廓曲线,如渐开线、摆线、 圆弧和抛物线等。其中应用最广的是渐开线。
三、渐开线标准直齿圆柱齿轮的主要参数及几何计算
(一)齿轮各部分的名称和符号
齿顶圆:连接各轮齿齿顶的圆,其直 径用da表示。 齿槽:相邻两齿之间的空间。 齿根圆:过齿槽底部连成的圆,其直 径用df表示。 齿厚:任意直径dk的圆周上,轮齿两 侧齿廓之间的弧长,用sk表示; 齿槽宽:齿槽两侧齿廓之间的弧长, 用ek表示; 齿距:相邻两齿同侧齿廓之间的弧长, 用pk表示。 显然,pk=sk+ek。
三、渐开线标准直齿圆柱齿轮的主要参数及几何计算
(一)齿轮各部分的名称和符号
在直径为dk的圆周长为pkz, 同时又等于πdk,即
为了便于设计、制造及互换使用, 将齿轮某一圆周上的比值规定为标 准值(整数或较完整的有理数),并 使该圆上的齿廓压力角也为标准值, 这个圆称为分度圆,其直径用d表 示。分度圆上的压力角用表示,我 国规定的标准压力角为20°。分度 圆上的齿距用p表示,p与π的比值 称为分度圆上的模数,简称模数, 用m(㎜)表示,即m=,m越大,p 越大,轮齿的尺寸也越大,齿轮承 受载荷的能力也越高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A 处的曲率半径为0 KB 为渐开线在K点的法线,并与基圆相切
3.渐开线的形状取决于基圆的大小 rb↑→∞,渐开线→直线;
4. 基圆内无渐开线
• 问题1:G1、G3为同一基圆上所生成的两条同向渐
开线,试问
K1 K
和
K1' K 3' 有何关系?
K1 K 3 K K
' 1
' 3
5.同一基圆上所生成的两条
4.3 渐开线齿廓
4.3.1 渐开线的形成
直线BK沿半径为rb的 圆作纯滚动时,直线上任 意一点K的轨迹称为该圆 的渐开线。该圆称为渐
开线的基圆
rb—基圆半径; BK—渐开线发生线
θ K—渐开线上K点的展角
4.3.2 渐开线的性质
1.渐开线的发生线展直前后长度不变;
弧AB KB
K
2. B 是渐开线K点处的曲率中心,BK 是曲率半径;
同向渐开线为法向等距曲线。
2.接触点的轨迹是直线─啮合线;
3.作用力的方向始终沿啮合线; 4.中心距变动,啮合线变化; 5.存在相对滑动,导致摩擦磨损。
