第十一讲
第11讲——社区服务概述

第十一讲——社区服务的概述随着我国社会主义市场经济体制的建立和改革开放的进一步深化,城市社会服务在社会与经济生活中作用越来越重要,它已成为促进社会与经济协调、持续发展,促进社会进步的一个重要组成部分。
为了适应形势的要求,更好地加强社区服务工作,就要把握其内涵、原则,了解其发展过程、一般特征等。
第一节社区服务的概念一、社会服务的由来“社区服务”一词在国外有的称为“社区照顾”。
一般地讲,社区服务是指在政府的指导下,发动社区成员,通过互助性的社会服务,就地解决本地区的社会问题。
其目的是,协调人际关系,缓解社会矛盾,为社区居民分忧解愁,创造一个和谐、良好的社会环境,促进物质文明和精神文明建设。
社区服务,是伴随着经济发展和社会进步而发展起来的,是工业化、城市化、社会化大生产和社会分工专业化的产物。
社区服务,概括起来讲,有以下特征:一是资金采取政府补助、社会集资、个人捐赠、适当收费相结合的办法解决。
二是组织形式采取政府机构与民间机构相结合,政府指导和民间机构的创造性相结合,专业服务人员与志愿人员、社区居民互相服务相结合。
三是服务设施齐全,按社区的实际需要,合理布局。
四是服务项目以社区居民社会生活需要为目标,福利性与服务性相结合,内容广泛,方式灵活。
五是由点到面,形成社区服务的工作系统与服务网络。
社区服务,毕竟与经济基础有密切的联系,在各国经济发展不相同的情况下,社区服务发展差异是很大的,但有一点是相同的,社区服务减轻了财政压力,在满足社会需求方面具有其特殊的优越性和活力,因而使得社区服务在世界各国日益受到重视,并不断丰富和发展。
二、我国的社区服务1.社区服务兴起的背景建国初期,城市居民委员会开展的尊老爱幼,扶困助残,教育失足青少年,进行一些便民活动等,是我国最早的社会服务的雏形。
党的十一届三中全会提出以经济建设为中心,解放生产力,从根本上改变贫穷、落后的面貌。
最主要的措施是改革开放,推动城市社会结构的变革,给计划经济体制下的社会福利体制带来一系列的冲击。
关于张桂梅第十一讲观后感

关于张桂梅第十一讲观后感
在听完张桂梅思政大讲堂第十一讲后,我深感震撼。
这次讲堂以“科技的力量”为主题,结合了张桂梅同志及其他科技工作者的真实经历和故事,让我对科技的力量有了更深入的理解。
我为科技在社会发展中的巨大作用所折服。
从讲堂中,我了解到科技不仅在提高生产效率、改善生活质量方面发挥了巨大作用,还在推动社会进步、增强国家竞争力方面发挥了不可或缺的作用。
尤其是在当今这个信息爆炸的时代,科技的发展更是日新月异,它不断地改变着我们的思维方式和生活方式。
我对科技工作者的敬意油然而生。
他们默默无闻,用自己的智慧和汗水推动着科技的进步,为社会的发展做出了巨大的贡献。
他们的奋斗精神,不仅值得我们学习和尊敬,更应该得到社会的认可和支持。
我对科技伦理的重要性有了更深刻的认识。
科技的发展无疑带来了巨大的便利,但同时也带来了一些伦理问题。
如何在利用科技的同时,保障人民的权益、维护社会的公平正
义,是一个值得深入思考的问题。
这次讲堂让我受益匪浅。
我相信,只要我们能够正确地认识和利用科技的力量,就一定能够推动社会的进步和发展。
同时,我们也应该更加关注和支持科技工作者,为他们的奋斗精神点赞,为他们的成就喝彩。
第11讲 并项求和法

第十一讲 并项求和法并项求和法:一个数列的前n 项和中,可两两结合求解,则称之为并项求和. 形如()()1nn a f n =-类型,可采用两项合并求解.例如, 22222210099989721n S =-+-++-()()()100999897215050=++++++=. 例1.已知数列{}n a 的前n 项和是n S ,且()21n n S a n =-∈*N . (1)求数列{}n a 的通项公式;(2)令2log n n b a =,求数列(){}21n n b -前2n 项的和T . 【答案】(1) 12n n a ;(2)()21T n n =-. 【解析】(1)由112121n n n n S a S a --=-⎧⎨=-⎩得()*12N ,1n n a a n n -=∈≥, 于是{}n a 是等比数列.令1n =得11a =,所以12n n a -=.(2)122log log 21n n n b a n -===-,于是数列{}n b 是首项为0,公差为1的等差数列.2222221234212n n T b b b b b b -=-+-+--+ 123212n n b b b b b -=+++++,所以()()221212n n T n n -==-.例2.已知{}n a 是公差不为零的等差数列,413a =,且1a ,2a ,7a 成等比数列.(1)求数列{}n a 的通项公式;(2)设()11n n n b a +=-,数列{}n b 的前n 项和为n T ,求2019T .【答案】(1)43n a n =-(2)4037 【解析】(1)设{}n a 的公差为d ,因为1a ,2a ,7a 成等比数列,所以2217a a a =,可得()()21116a d a a d +=+,0d ≠,得14d a =,又41133a a d ==+,可得11a =,4d =,所以43n a n =-.(2)()()()111143n n n n b a n ++=-=--,2019122019T b b b =++⋅⋅⋅+()()()15913806580698073=-+-+⋅⋅⋅+-+()4100980734037=-⨯+=.例3.已知数列{}n a 的前n 项和22n S n n =-,*n N ∈.(1)求数列{}n a 的通项公式;(2)若()1nn n b a =-,求数列{}n b 的前n 项和n T . 【答案】(1)43n a n =-,*n N ∈(2)2,21,n n n T n n ⎧=⎨-+⎩为偶数为奇数 【解析】(1)由22n S n n =-,当2n ≥时,()()221221143n n n a S S n n n n n -⎡⎤=-=-----=-⎣⎦, 当1n =时,111a S ==,而4131⨯-=,所以数列{}n a 的通项公式43n a n =-,*n N ∈.(2)由(1)可得()()()1143n n n n b a n =-=--,当n 为偶数时,()159131743n T n =-+-+-++-422n n =⨯=,当n 为奇数时,1n +为偶数,()()11214121n n n T T b n n n ++=-=+-+=-+. 综上,2,21,n n n T n n ⎧=⎨-+⎩为偶数为奇数.课后练习:1.(2016天津高考)已知{}n a 是等比数列,前n 项和为()n S n *∈N ,且6123112,63S a a a -==.(Ⅰ)求{}n a 的通项公式;(Ⅱ)若对任意的,b n n N ∈*是2log n a 和21log n a +的等差中项,求数列(){}21nn b-的前2n 项和.【解析】(Ⅰ)解:设数列}{n a 的公比为q , 由已知有2111211q a q a a =-,解得1,2-==q q ,又由616(1)631aq S q -==-知1-≠q , 所以6321)21(61=--a ,解得11=a ,所以12-=n n a . (Ⅱ)解:由题意得2211(log log )2n n n b a a +=+1221(log 2log 2)2n n -=+12n =-,即数列}{n b 是首项为21,公差为1的等差数列.设数列})1{(2n n b -的前n 项和为n T ,则22222221234212()()()n n n T b b b b b b -=-++-++⋅⋅⋅+-+122n b b b =++⋅⋅⋅+122()2n n b b +=22n = 所以数列})1{(2n n b -的前2n 项和为22n .2.(2018山西省适应性考试)已知等比数列{}n a 中,0n a >,1164a =,n a 1-11+n a =22+n a ,*n ∈N .(1)求{a n }的通项公式;(2)设22(1)(log )n n n b a =-⋅,求数列{b n }的前2n 项和T 2n . 解:(1)设等比数列{a n }的公比为q ,则q >0. 因为n a 1-11+n a =22+n a ,所以111-n q a -n q a 11=112+n qa ,因为q >0,解得q =2.所以a n =641×2n -1=2n -7,n ∈N*.(2)b n =(-1)n log 22a n =(-1)n log 222n -7=(-1)n (n -7) 2.(3)设c n =n -7,则b n =(-1)n (c n ) 2.T 2n =b 1+ b 2+ b 3+ b 4+…+ b 2n -1 + b 2n=-c 1 2+ c 2 2- c 3 2+ c 4 2+…- c 2n -1 2+ c 2n 2=(-c 1+ c 2)(c 1+ c 2)+(-c 3+ c 4)(c 3+ c 4)+…+(-c 2n -1+ c 2n )(c 2n -1+ c 2n ) = c 1+ c 2+c 3+ c 4+…+c 2n -1+ c 2n =2[6(27)]2n n -+-=2(213)213n n n n -=-.。
第11讲向量组的秩与向量空间

4 例 .在R 中取定一组基a1,a2 , a3,再取一个新基 b1, b2 , b3,记A = (a1,a2 ,a3 ),B = (b1, b2 ,b3 ),求用 a1,a2 ,a3表示b1,b2 , b3的表示式(基变换公式),并 求向量在两个基中的坐标之间的关系式(坐标 变换公式). Q 解: (a1, a2 , a3 ) = (e1, e2 ,e3 )A , ∴(e1,e2 , e3 ) = (a1, a2 , a3 )A−1, 又(b1, b2 ,b3 ) = (e1,e2 , e3 )B ∴(b1, b2 , b3 ) = (a1, a2 , a3 )A−1B ( 即基变换公式为: b1, b2 , b3 ) = (a1, a2 , a3 )P 其中P = A−1B.
1.定义:在向量空间V 1.定义:在向量空间 中,如果存在 n 个元素 定义 a1,a2,…,an满足: 满足: 1)a1,a2,…,an线性无关; 线性无关; 2)V 中任一元素 a 总可由 1,a2,…,an线性表示, 总可由a 线性表示, 那么, 就称为向量空间V 的一个基, 那么, a1,a2,…,an就称为向量空间 的一个基, 称为向量空间V 的维数. 基中元素的个数 n 称为向量空间 的维数 维向量空间, 维数为 n 的向量空间称为 n 维向量空间,记 作Vn。
3
设向量x在旧基和新基中的坐标分别是: (y1, y2 , y3 )T,(x1, x2 , x3 )T,即有 y1 x1 x = (a1, a2 ,a3 ) y2 ,x = (b1, b2 ,b3 ) x2 y x 3 3 y1 x1 y1 x1 故:A y2 = B x2 ⇒ y2 = A−1B x2 y x y x 3 3 3 3 y1 x1 y2 = P x2 即 y x 3 3
第11讲 切比雪夫不等式与大数定律

第11讲 切比雪夫不等式与大数定律教学目的:1.使学生理解切比雪夫不等式与大数定律的内涵。
2.使学生会用切比雪夫不等式及大数定律解决实际问题。
教学重点:使学生理解切比雪夫不等式与大数定律的内涵。
教学难点:使学生理解切比雪夫不等式与大数定律的统计意义。
教学学时:2学时 教学过程:第三章 随机变量的数字特征§3.5 切比雪夫不等式与大数定律1.切比雪夫(Chebyshev )不等式我们知道方差)(X D 是用来描述随机变量X 的取值在其数学期望)(X E 附近的离散程度的,因此,对任意的正数ε,事件ε≥-)(X E X 发生的概率应该与)(X D 有关,而这种关系用数学形式表示出来,就是下面我们要学习的切比雪夫不等式。
定理1 设随机变量X 的数学期望)(X E 与方差)(X D 存在 ,则对于任意正数ε,不等式2)(])([ εεX D X E X P ≤≥- (1)或2)(1])([ εεX D X E X P -≥<- (2)都成立。
不等式(1)和(2)称为切比雪夫不等式。
下面只对连续随机变量情形证明不等式(1)和(2)。
证 设随机变量X 的密度函数为)(x f ,则有⎰≥-=≥-εε)()(])([ X E x dx x f X E X P ≤⎰≥--εε)(22)()]([X E x dxx f X E x222)()()]([1εεX D dx x f X E x =-≤⎰+∞∞-由于ε≥-)(X E X 与ε<-)(X E X 是对立事件,故有2)(1])([1])([ εεεX D X E X P X E X P -≥≥--=<-切比雪夫不等式给出了在随机变量X 的分布未知的情况下,只利用X 的数学期望和方差即可对X 的概率分布进行估值的方法,这就是切比雪夫不等式的重要性所在。
例1 已知正常男性成人血液中,每毫升含白细胞数的平均值是7300,均方差是700,利用切比雪夫不等式估计每毫升血液含白细胞数在9400~5200之间的概率。
第11讲 空间中垂直关系的判定与性质
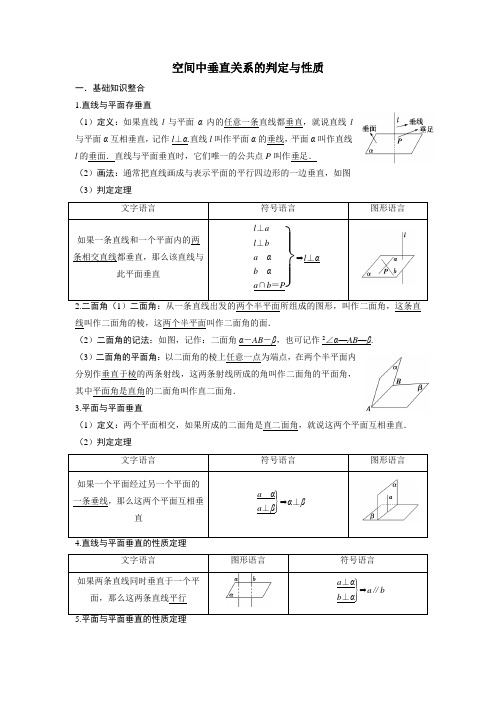
空间中垂直关系的判定与性质一.基础知识整合1.直线与平面存垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直,记作l ⊥α.直线l 叫作平面α的垂线,平面α叫作直线l 的垂面.直线与平面垂直时,它们唯一的公共点P 叫作垂足.(2)画法:通常把直线画成与表示平面的平行四边形的一边垂直,如图(3)判定定理 ⎭⎪⎬⎪⎫l ⊥a l ⊥b a αb αa ∩b =P ⇒l ⊥α从一条直线出发的两个半平面所组成的图形,叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.(2)二面角的记法:如图,记作:二面角α-AB -β,也可记作2∠α—AB —β.(3)二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角,其中平面角是直角的二面角叫作直二面角.3.平面与平面垂直(1)定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理⎭⎪⎬⎪⎫a αa ⊥β⇒α⊥β符号语言⎭⎪⎬⎪⎫α⊥βα∩β=l a αa ⊥l ⇒a ⊥β 题型一:线面垂直的判定 例1:如图所示,在Rt △ABC 中,∠B =90°,且S 为所在平面外一点,满足SA =SB =SC .D为AC 的中点.求证:SD ⊥平面ABC .证明:∵在Rt △ABC 中,∠B =90°,且D 为AC 的中点,∴BD =AD =DC .又∵SA =SB =SC ,SD为公共边,∴△SBD ≌△SAD ≌△SCD , ∴∠SDB =∠SDA =∠SCD =90°,∴SD ⊥AD ,SD ⊥BD ,∵AD ∩BD =D ,∴SD ⊥平面ABC .变式训练1:如图,已知AB 是⊙O 的直径,C 是圆周上不同于A ,B 的点,P A ⊥⊙O 所在的平面,AF ⊥PC 于F ,求证:BC ⊥平面PAC .证明:因为AB 为⊙O 的直径,所以BC ⊥AC .因为P A ⊥平面ABC ,BC平面ABC ,所以P A ⊥BC .因为P A ∩AC =A ,所以BC ⊥平面P AC .题型二:面面垂直的判定例2:已知四面体ABCD 的棱长都相等,E ,F ,G ,H 分别为AB ,AC ,AD ,BC 的中点.求证:平面EHG ⊥平面FHG .证明:如图,取CD 的中点M ,连接HM ,MG ,FM ,则四边形MHEG为平行四边形.连接EM 交HG 于O ,连接FO .在△FHG 中,O 为HG的中点,且FH =FG ,所以 FO ⊥HG .同理可证FO ⊥EM .又HG ∩EM =O ,所以FO ⊥平面EHMG .又FO 平面FHG ,所以平面EHG ⊥平面FHG .变式训练2:如图,在空间四边形ABDC中,AB =BC ,CD =DA ,E 、F 、G 分别为CD 、DA 和对角线AC 的中点.:求证:平面BEF ⊥平面BDG .证明:∵AB =BC ,CD =AD ,G 是AC 的中点,∴BG ⊥AC ,DG ⊥AC ,又EF ∥AC ,∴EF ⊥BG ,EF ⊥DG .∴EF ⊥平面BGD .∵EF 平面BEF ,∴平面BDG ⊥平面BEF .题型三:垂直关系的综合应用例3:如图,在三棱锥P —ABC 中,P A ⊥底面ABC ,P A =AB ,∠BCA=90°.点D ,E 分别在棱PB ,PC 上,且DE ∥BC .(1)求证:BC ⊥平面P AC ;(2)是否存在点E 使得二面角A —DE —P 为直二面角?并说明理由.证明:(1)∵P A ⊥底面ABC ,∴P A ⊥BC .又∠BCA =90°,∴AC ⊥BC .又P A ∩AC =A ,∴BC ⊥平面P AC .(2)存在点E 使得二面角A —DE —P 为直二面角.由(1)知BC ⊥平面P AC ,又∵DE ∥BC ,∴DE ⊥平面P AC .又∵AE 平面P AC ,PE 平面P AC ,∴DE ⊥AE ,DE ⊥PE .∴∠AEP 为二面角A —DE —P 的平面角.又∵P A ⊥底面ABC ,∴P A ⊥AC .∴∠P AC =90°.∴在棱PC 上存在一点E ,使得AE ⊥PC .这时,∠AEP =90°.故存在点E 使得二面角A —DE —P 是直二面角.变式训练3:如图所示,P A ⊥平面ABC ,AC ⊥BC ,AB =2,BC =2,PB =6,求二面角P —BC —A 的大小.解:∵P A ⊥平面ABC ,BC 平面ABC ,∴P A ⊥BC .又AC ⊥BC ,P A ∩AC =A ,∴BC ⊥平面P AC .又PC 平面P AC ,∴BC ⊥PC .又BC ⊥AC ,∴∠PCA 为二面角P —BC —A 的平面角.在Rt △PBC 中,∵PB =6,BC =2,∴PC =2.在Rt △ABC 中,∵AB =2,BC =2,∴AC = 2.∴在Rt △P AC 中,cos ∠PCA =22,∴∠PCA=45°,即二面角P —BC —A 的大小为45°.题型四:线面垂直性质定理的应用例4:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC 上,且EF ⊥A 1D ,EF ⊥AC .求证:EF ∥BD 1.证明:如图所示,连接AB 1、B 1C 、BD .∵DD 1⊥平面ABCD ,AC 平面ABCD .∴DD 1⊥AC .又∵AC ⊥BD ,且BD ∩DD 1=D ,∴AC ⊥平面BDD 1. ∵BD 1平面BDD 1,∴BD 1⊥AC .同理可证BD 1⊥B 1C .∴BD 1⊥平面AB 1C .∵EF ⊥A 1D ,A 1D ∥B 1C ,∴EF ⊥B 1C .又EF ⊥AC ,且AC ∩B 1C =C ,∴EF ⊥平面AB 1C ,∴EF ∥BD 1.变式训练3:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC上,且EF ⊥A 1D ,EF ⊥AC .若G 是AB 的中点,则E 在A 1D 上什么位置时,能使EG ⊥平面AB1C?解:若EG⊥平面AB1C,因为BD1⊥平面AB1C,所以EG∥BD1.因为G为AB的中点,所以E为AD1的中点,即E为A1D的中点时,EG⊥平面AB1C.题型五:面面垂直性质定理的应用例5:已知平面P AB⊥平面ABC,平面P AC⊥平面ABC,求证:P A⊥平面ABC.证明:如图所示,在BC上任取一点D,作DF⊥AC于F,DG⊥AB于G,∵平面P AC⊥平面ABC,且平面P AC∩平面ABC=AC,∴DF⊥平面P AC,又∵P A平面P AC,∴DF⊥P A,同理DG⊥P A,又∵DF∩DG=D且DF平面ABC,DG平面ABC,∴P A⊥平面ABC.变式训练5:如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=22,M为BC的中点.求证:AM⊥PM.证明:如图连接AP.矩形ABCD中,AD⊥DC,BC⊥DC,又∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,∴AD⊥平面PDC,BC⊥平面PDC,又∵PD平面PDC,PC平面PDC,∴AD⊥PD,BC⊥PC,在Rt△P AD和Rt△PMC中,易知AP2=AD2+PD2=(22)2+22=12,PM2=PC2+MC2=22+(2)2=6,又∵Rt△ABM中,AM2=AB2+BM2=22+(22)2=6,∴AP2=PM2+AM2,∴AM⊥PM.题型六:垂直关系的综合应用例6:如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,F A=FE,∠AEF=45°.(1)求证:EF⊥平面BCE;(2)设线段CD、AE的中点分别为P,M,求证:PM∥平面BCE.证明:(1)因为平面ABEF⊥平面ABCD,BC平面ABCD,BC⊥AB,平面ABEF∩平面ABCD =AB,所以BC⊥平面ABEF.所以BC⊥EF.因为△ABE为等腰直角三角形,AB=AE,所以∠AEB=45°.又因为∠AEF =45°,所以∠FEB =90°,即EF ⊥BE .因为BC 平面BCE ,BE 平面BCE ,BC ∩BE =B ,所以EF ⊥平面BCE .(2)取BE 的中点N ,连接CN ,MN ,则MN 綊12AB 綊PC ,所以PMNC 为平行四边形.所以PM ∥CN . 因为CN 在平面BCE 内,PM 不在平面BCE 内,所以PM ∥平面BCE .变式训练6:如图,四棱锥S -ABCD 中,SD ⊥平面ABCD ,AB ∥DC ,AD ⊥DC ,AB =AD=1,SD =2,BC ⊥BD ,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(1)证明:DE ⊥平面SBC ;(2)证明:SE =2EB .证明:(1)连接BD ,∵SD ⊥平面ABCD ,故BC ⊥SD ,又∵BC ⊥BD ,BD ∩SD =D ,∴BC ⊥平面BDS ,∴BC ⊥DE . 作BK ⊥EC ,K 为垂足,因平面EDC⊥平面SBC ,故BK ⊥平面EDC ,BK ⊥DE . 又∵BK 平面SBC ,BC 平面SBC ,BK ∩BC =B ,∴DE ⊥平面SBC .(2)由(1)知DE ⊥SB ,DB =2AD = 2.∴SB =SD 2+DB 2=6,DE =SD ·DB SB =233,EB =DB 2-DE 2=63,SE =SB -EB =263,∴SE =2EB . 三.方法规律总结1.线面垂直的判定定理是证明线面垂直的主要方法,证明的关键是在平面内找到两条相交直线与已知直线垂直.2.在证明面面垂直时,一般方法是从一个平面内寻找另一个平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决(所作辅助线要有利于题目的证明),即由线面垂直证面面垂直.3.空间中线线、线面、面面之间的垂直关系可以相互转化,其转化关系如下:4.会用线面垂直的性质定理证明平行问题,用面面垂直的性质定理证明垂直问题.四:课后练习作业一、选择题1.设l、m为不同的直线,α为平面,且l⊥α,下列为假命题的是(B) A.若m⊥α,则m∥l B.若m⊥l,则m∥αC.若m∥α,则m⊥l D.若m∥l,则m⊥α【解析】A中,若l⊥α,m⊥α,则m∥l,所以A正确;B中,若l⊥α,m⊥l,则m∥α或mα,所以B错误;C中,若l⊥α,m∥α,则m⊥l,所以C正确;若l⊥α,m∥l,则m⊥α,所以D正确.2.在正方体ABCD—A1B1C1D1中,与AD1垂直的平面是(A)A.平面A1DCB1 B.平面DD1C1C C.平面A1B1C1D1D.平面A1DB【解析】连接A1D、B1C,由ABCD—A1B1C1D1为正方体可知,AD1⊥A1B1,AD1⊥A1D.故AD1⊥平面A1DCB1.3.如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是(C)A.BC∥平面PDF B.DF⊥平面P AEC.平面PDF⊥平面ABC D.平面P AE⊥平面ABC【解析】由题意知BC∥DF,且BC⊥PE,BC⊥AE.∵PE∩AE=E,∴BC⊥平面P AE,∴BC∥平面PDF成立,DF⊥平面P AE成立,平面P AE⊥平面ABC也成立.4.设α、β是两个不同的平面,l是一条直线,以下命题正确的是(C) A.若l⊥α,α⊥β,则lβB.若l∥α,α∥β,则lβC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β【解析】A错,可能l∥β;B错,可能l∥β;C正确;D错,不一定l⊥β.5.设平面α⊥平面β,且α∩β=l,直线aα,直线bβ,且a不与l垂直,b不与l垂直,那么a与b (B)A.可能垂直,不可能平行B.可能平行,不可能垂直C.可能垂直,也可能平行D.不可能垂直,也不可能平行【解析】当a,b都平行于l时,a与b平行,假设a与b垂直,如图所示,由于b与l不垂直,在b上任取一点A,过点A作b′⊥l,∵平面α⊥平面β,∴b′⊥平面α,从而b′⊥a,又由假设a⊥b易知a⊥平面β,从而a⊥l,这与已知a不与l垂直矛盾,∴假设不正确,a与b不可能垂直.6.空间四边形ABCD,若AB、AC、AD与平面BCD所成角相等,则A点在平面BCD的射影是△BCD的(A)A.外心B.内心C.重心D.垂心【解析】设A点在平面BCD内的射影为O.可知,△OAB≌△OAC≌△OAD.∴OB=OC=OD,∴点O为外心.7.下列说法中正确命题的个数为(B)①如果直线l与平面α内的无数条直线垂直,则l⊥α;②如果直线l不垂直于α,则α内没有与l垂直的直线;③如果一条直线与平面内的一条直线垂直,则该直线与此平面必相交;④如果一条直线和平面的一条垂线垂直,该直线必在这个平面内;⑤如果一条直线和一个平面垂直,该直线垂直于平面内的任一直线.A.0B.1C.2D.3【解析】如图(1)所示,l与α相交(不垂直),此时也有无数条直线与l垂直.故①②错误;如图(2)所示,l与α平行,此时平面内也存在无数条直线与l垂直,故③④错误;如图(3)所示,直线l与平面α的垂线m垂直,但l不在平面α内;由线面垂直的定义可知,⑤正确.8.如图,在正方形ABCD中,E、F分别为边BC,CD的中点,H是EF的中点,现沿AE、AF,EF把这个正方形折成一个几何体,使B、C、D三点重合于点G,则下列结论中成立的是(A)A.AG⊥平面EFG B.AH⊥平面EFGC.GF⊥平面AEF D.GH⊥平面AEF【解析】∵AG⊥GF,AG⊥GE,GF∩GE=G,∴AG⊥平面EFG.9.如图,在四边形ABCD中,AD∥BC,AB=AD,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列命题正确的是(B)A.平面ADC⊥平面BDCB.平面ABD⊥平面ABCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC【解析】在图①中,∵∠BAD=90°,AD=AB,∴∠ADB=∠ABD=45°.∵AD∥BC,∴∠DBC=45°.又∵∠BCD=45°.∴∠BDC=90°,即BD⊥CD.在图②中,此关系仍成立.∵平面ABD⊥平面BCD,∴CD⊥平面ABD.∵BA平面ADB,∴CD⊥AB.∵BA⊥AD,∴BA⊥平面ACD.∵BA平面ABC,∴平面ABC⊥平面ACD.10.如图,在正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1上运动,并且总保持AP⊥BD1,则动点P在(A)A.线段B1C上B.线段BC1上C.BB1中点与CC1中点的连线上D.B1C1中点与BC中点的连线上【解析】连接AC,B1C,AB1,由线面垂直的判定可知BD1⊥平面AB1C.若AP平面AB1C,则AP⊥BD1.这样只要P在B1C上移动即可.二、填空题11.如图,在正方体ABCD—A1B1C1D1中,平面ACD1与平面BB1D1D的位置关系是________.垂直D⊥平面ABCD,AC平面【解析】∵ABCD是正方形,∴AC⊥BD.又∵DABCD,∴D1D⊥AC.∵D1D∩DB=D,∴AC⊥平面BB1D1D.∵AC平面ACD1,∴平面ACD1⊥平面BB1D1D.12.如图所示,已知P A⊥平面α,PB⊥平面β,垂足分别为A、B,α∩β=l,∠APB=50°,则二面角α-l-β的大小为________.130°【解析】如图,设平面P AB∩l=O,连接AO,BO,AB,∵P A⊥α,lα,∴P A⊥l.同理PB⊥l,而PB∩P A=P,∴l⊥平面P AB,∴l⊥AO,l⊥BO,∴∠AOB即为二面角α-l-β的平面角.结合图形知∠AOB+∠APB=180°,∴∠AOB=130°.13.如图,已知平面α⊥平面β,在α与β的交线l上,取线段AB=4,AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=3 cm,BD=12 cm,则CD=______.13 cm【解析】连接BC.因为平面α⊥平面β,且α∩β=l,又因为BD平面β,且BD⊥l,所以BD⊥平面α.又∵BC平面α,∴BC⊥BD.所以△CBD也是直角三角形.在Rt △BAC 中,BC =32+42=5.在Rt △CBD 中,CD =52+122=13.所以CD 长为13 cm.14.α,β是两个不同的平面,m ,n 是平面α与β之外的两条不同直线,给出四个论断:①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________.若①③④,则②(或若②③④,则①)【解析】利用面面垂直的判定,可知①③④⇒②为真;利用面面垂直的性质,可知②③④⇒①为真.15.如图平面ABC ⊥平面BDC ,∠BAC =∠BDC =90°,且AB =AC =a ,则AD =_______a【解析】如图所示,取BC 的中点E ,连接ED ,AE ,∵AB =AC ,∴AE ⊥BC ,∵平面ABC ⊥平面BDC .∴AE ⊥平面BDC ,∴AE ⊥ED .在Rt △ABC 和Rt △BCD 中,AE =ED =12BC =22a ,∴在Rt △AED 中,AD =AE 2+ED 2=a .三、解答题16.如图所示,AB 是圆O 的直径,P A 垂直于圆O 所在的平面,M 是圆周上任意一点,AN ⊥PM ,垂足为N .求证:AN ⊥平面PBM .证明:设圆O 所在的平面为α,∵P A ⊥α,且BM α,∴P A ⊥BM .又∵AB 为⊙O 的直径,点M 为圆周上一点,∴AM ⊥BM ,∵直线P A ∩AM =A ,∴BM ⊥平面P AM .又AN 平面P AM ,∴BM ⊥AN .这样,AN 与PM ,BM 两条相交直线垂直.故AN ⊥平面PBM .17.如图所示,过S 引三条长度相等但不共面的线段SA ,SB ,SC 且∠ASB =∠ASC =60°,∠BSC =90°.求证:平面ABC ⊥平面BSC .【证明】(法一)取BC 的中点D ,连接AD ,SD .∵∠ASB =∠ASC ,且SA =SB=AC ,∴AS =AB =AC .∴AD ⊥BC .又△ABS 是正三角形,△BSC 为等腰直角三角形,∴BD =SD .∴AD 2+SD 2=AD 2+BD 2=AB 2=AS 2.由勾股定理的逆定理,知AD ⊥SD .又∵SD ∩BC =D ,∴AD⊥平面BSC .又AD 平面ABC ,∴平面ABC ⊥平面BSC .(法二)同法一证得AD ⊥BC ,SD ⊥BC ,则∠ADS 即为二面角A —BC —S 的平面角.∵∠BSC =90°,令SA =1,则SD =22,AD =22,∴SD 2+AD 2=SA 2.∴∠ADS =90°.∴平面ABC ⊥平面BSC .18.如图,在三棱锥S -ABC 中,SA ⊥平面ABC ,AB ⊥BC ,DE 垂直平分SC ,分别交AC 、SC 于D 、E ,且SA =AB =a ,BC =2a .(1)求证:SC ⊥平面BDE ;(2)求平面BDE 与平面BDC 所成二面角的大小.(1)证明:∵SA ⊥平面ABC ,又AB 、AC 、BD 平面ABC ,∴SA ⊥AB ,SA ⊥AC ,SA ⊥BD ,∴SB =SA 2+AB 2=2a .∵BC =2a ,∴SB =BC .∵E 为SC 的中点,∴BE ⊥SC .又DE ⊥SC ,BE ∩DE =E ,∴SC ⊥平面BDE .(2)由(1)及BD 平面BDE ,得BD ⊥SC .又知BD ⊥SA ,∴BD ⊥平面SAC .∴BD ⊥AC 且BD ⊥DE .∴∠CDE 为平面BDE 与平面BDC 所成二面角的平面角.∵AB ⊥BC ,AC =AB 2+BC 2=3a .∴Rt △SAC中,tan ∠SCA =SA AC =33,∴∠SCA =30°.∴∠CDE =60°,即平面BDE 与平面BDC 所成二面角为60°.19.如图,已知三棱锥A BPC -中,AP PC ⊥,AC BC ⊥,M为AB 中点,D 为PB 中点,且PMB ∆为正三角形.(1)求证:DM APC ∥平面;(2)求证:ABC APC ⊥平面平面.证明:(1)∵M 为AB 中点,D 为PB 中点,∴MD //AP ,又MD不在平面APC 上,∴MD //平面APC.(2)∵△PMB 为正三角形,又D 为PB 中点. ∴MD ⊥PB .又由(1)知MD //A P , ∴AP ⊥PB . 又AP ⊥PC , 且PB ∩PC =P ,∴AP ⊥平面PBC , ∴AP ⊥BC , 又∵AC ⊥BC , 且AP ∩AC =A ∴BC ⊥平面APC , 又BC 在平面ABC 内,∴平面ABC ⊥平面APC .20.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M 是AB 上一点,N 是A 1C 的中 点,MN ⊥平面A 1DC .求证:(1)MN ∥AD 1;(2)M 是AB 的中点.证明:(1)∵ADD 1A 1为正方形,∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1,AD 1平面ADD 1A 1,∴CD ⊥AD 1.∵A 1D ∩CD =D ,∴AD 1⊥平面A 1DC .又∵MN ⊥平面A 1DC ,∴MN ∥AD 1. MD B P C A(2)连接ON ,在△A 1DC 中,A 1O =OD ,A 1N =NC .∴ON 綊12CD 綊12AB ,∴ON ∥AM .又∵MN ∥OA ,∴四边形AMNO 为平行四边形,∴ON =AM .∵ON =12AB ,∴AM =12AB ,∴M 是AB 的中点. 21.如图所示,P 是四边形ABCD 所在平面外一点,ABCD 是∠DAB =60°且边长为a 的菱形,侧面P AD 为正三角形,其所在平面垂直于底面ABCD .(1)若G 为AD 边的中点,求证:BG ⊥平面P AD ;(2)求证:AD ⊥PB .证明:(1)连接PG ,BD .由题知△P AD 为正三角形,G 是AD 的中点,∴PG ⊥AD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,PG 平面P AD ,∴PG ⊥平面ABCD ,∴PG ⊥BG .又∵四边形ABCD 是菱形且∠DAB =60°,∴△ABD 是正三角形,∴BG ⊥AD .又AD 平面P AD ,PG 平面P AD ,且AD ∩PG =G ,∴BG ⊥平面P AD .(2)由(1)可知BG ⊥AD ,PG ⊥AD .又BG 平面PBG ,PG 平面PBG ,且BG ∩PG =G ,AD ⊥平面PBG ,∴AD ⊥PB .。
第十一讲—空间群(3)

点群
三 斜 1(C1), 1(Ci)
布拉菲点阵
P
2(C2)或2(m)
单 斜 2(C2), m(C1h), 2/m(C2h)
两个2(C2)或2(m) 正 交 222(D2), mm2(C2v), mmm(D2h)
P, B P, C, I, F
4(C4)或4(S43) 3(C3)或3(S65) 6(C6)或6(S35)
2或2沿a、b和a+b 2或2a、b和a+b 2或2沿a、b和a+b 2或2a、b和a+b
62m (Li63L23P)
y
y
x
x
6m2 (Li63P3L2)
P3m1 (C31v, No. 156)
+
+
,
,++
,
+
+
,
,++
,
P31m (C32v, No. 157)
+
+
+
+
+
+
,
,++
,
+
+
,
,++
,
{R|} {R|t}、 {1|tn}、 {R|0} 、
点式空间群:由全部作用于同一个公共点
上的对称操作完全确定,或者说仅由点对称操 作和平移对称操作组合而产生。
۞ 螺旋轴或滑移面不是其基本操作。
۞ 点式空间群在单胞中一定至少有一个位置具有与
空间群点群相同的位置对称性
点对称条件
1(E)或1(i)
晶系
俯视图(单胞): (左)一般等效点位置 (右)对称元素分布
第11讲 流域产沙与输沙

右图中,有Ⅰ、Ⅱ
两组沙样,试比较一 下两种沙样的区别。 沙样Ⅰ的组成要粗些、均匀些;沙 样Ⅱ的组成要细些、不均匀些。
6.2.2 泥沙的比重和容重
1.泥沙的比重(γs)
泥沙样品中各个颗粒的实有重量之和(Ws)与所有沙粒的 实际体积(无孔隙的体积,V)之比,也就是无孔隙的单位 体积的泥沙样品的重量,称为泥沙的比重(g/cm3)。
就较严重,进入江河的泥沙量就多。
(一)层状侵蚀(片蚀)
(二)沟状侵蚀(沟蚀)
(三)陷穴侵蚀 (四)滑坡
层状侵蚀(片蚀)
雨滴将坡地上的土壤或其他地表物质的颗粒溅起,
落下的颗粒相对疏松且在坡地的下部相对较多。层
状的漫流出现后,可将这些松散的颗粒移动,坡地
表面均匀地遭受剥蚀,这就是层状侵蚀,又称片蚀
水流有层流和紊流两种状态。
(1)层流 层流——在岩石空隙中渗流时,水的质点作有秩序、平行而互
不混杂的流动。
层流示意图
(2)紊流 紊流——在岩石空隙中渗流时,水的质点作无秩序、互相混 杂、互相碰撞的流动。
水作紊流运动时,水流所受到的阻力比层流状态大,消耗的 能量较多。
若水流处于层流状态,泥沙的水力粗度公式变为:
流域产沙与输沙
引言
什么是泥沙? 随河水运动和组成河床的松散固体颗粒,叫做泥 沙。随水流运动的泥沙,又称固体径流。 河流泥沙是重要的水文现象之一。河流泥沙对于 河流水情及河流的变迁有着重要的影响,防洪、 航运、灌溉、发电、港口码头等水利工程的建设 都必须考虑河流泥沙问题。
黄河泥沙
6.1 河流的泥沙的来源
s W s V
泥沙的比重随沙粒的成分而变,变化范围不大,大致在 2.60-2.70g/cm3之间。实际应用上,取其平均值2.65g/cm3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西学东渐风吹起,一时众人都向西
传教士们对中国文化的否定性认识
与明末耶稣会修士不同的是,晚清来华的更正教传教士的主要传教对象是社会上的低下阶层。
这除了导致整个传教策略都带着慈善性质外,也影响了他们对中国的看法。
生活在社会的基层中间,接触到的绝大部分是中国社会和文化的黑暗面:愚昧迷信的风俗(庙宇林立,满街偶像)、残忍荒谬的行为(缠足、杀婴、蓄婢……)、环境污秽、卫生恶劣、盲目无知、故步自封,还有政治贪污腐败、司法不公正、教育泯灭个性等等。
这些现象构成了传教士笔记和书信中有关中国的主要素描。
无疑,在17世纪的中国亦存在着同样的情况,利玛窦等耶稣会士的笔下也有类似的记述。
但是与此同时,利玛窦等人却又在研读传统儒家的典籍及与一些士大夫的交往中,发现中国理性和理想的一面,因此他们对中国有较平衡公允的评价。
更正教的传教士接触的既全是黑暗的一面,兼且又以“异教主义”来一笔抹煞传统中国的道德伦理价值,所以他们对中国的评价,自然是一面倒地予以否定了。
(上图为1900年天足会印发《劝释缠脚论》
当然其中也有少数例外的,如理雅各便是一出色的汉学家,将不少传统典籍翻译成英文,对中国文化引入西方做了相当的贡献。
不过这样的人委实只是极少数。
即使是一些有兴趣研究中国的传教士,包括19世纪中叶在香港及上海成立的英国皇家亚洲学会支会(Branches of the Royal Asiatic Society)的成员,其实都只是欲以“中国通”自居,企图全面了解这个古老的异教文化而已。
在他们的论著中,极少带着肯定或欣赏的态度。
(人群聚集的西式教堂,时间不详)
要富强先信教
基于这种文化上的偏见,传教士在传福音之余,也积极要帮助中国人洗除异教主义文化的影响。
传教学校在此扮演了重要的角色。
儿童在进校后,除了学习西方的文化和科学的课程(如前所说,连历史、地理也是有关欧洲的)外,他们亦会有系统地接受西方的伦理道德和生活习惯,包括家务料理及育婴常识(限于女校)。
为了防范学生过早结婚、或被家庭强行许配给异教徒,学校更会与家长订约,学生的婚配由学校代为做主,违约者将要被迫缴回过去学校给予家长的全部金钱津贴(在19世纪此种订约制度非常普遍,尤以女校为甚)。
如此学生的升学、就业以至婚配,都是在传教士安排的传教事业系统之内。
基督徒成了与社会脱节的独特群体(早在1830年代,便已有传教学校的中国学生表示,担心他们在离校后会“迷失”)。
大部分的传教士,都认定了西洋文化就是基督教文化,西洋社会和科技知识的进步,和基督教信仰是不能分割的。
所以中国若要西化(Westernized,即近代化),就必须首先“基督教化”(Christianized)。
不过他们多数仅将这个想法实现于已有的信徒群体,如为信徒提供西化教育,避免受异教主义沾染等。
传教士认为,改变中国人的信仰(基督教化)远较改变他们的思想文化为迫切及优先,虽然在若干程度上两者是息息相关的。
推动中国社会西化变革
但是在主后1860年以后,却有部分传教士认为,基督教在中国传播的种种困难,主要是因着整个文化的环境都是被异教所笼罩。
因此若不改变社会和文化的土壤,要国人大量地皈依,还是不可能的事。
这些传教士既
认为西化中国是基督教化中国的先决条件,他们遂投身于协助中国西化改革的运动中。
恰好在这个时候,中国在与西洋列强接战遭遇到连番挫败,被迫签订种种丧权辱国的不平等条约,甚至在主后1860年英法联军一役中,连皇城都被蹂躏,皇帝也被迫蒙尘后,政府的高层官员终于承认中国在军事和技术上有所不如,需要向外国学习。
于是在以恭亲王奕訢为首的满汉大臣领导下,开始了以富国强兵为目标的西化改革运动,史称“自强运动”。
中国要进行西化改革,面对的其中一个困难是西学人才难求。
因为在当时期,中国人通晓西洋语言和科技的人极其罕有,要派遣人员出洋学习又旷日弥久,非一朝一夕可办。
至于在华的外国人,有能力而又愿意协助中国引进西洋知识的也并不多,商人和领事都很少会作此考虑,唯一可资利用的便是传教士。
至于为什么有传教士愿意暂时性地放弃传教工作,投身于协助中国改革的客卿行列中呢?原因是相当个别性的。
有学者认为这是基于传教士的不同的神学思想,“基要派”和“保守派”的传教士只着重拯救灵魂,对政治漠不关心;而“社会派”及“自由派”的则本着人道主义精神,提供医疗、教育等服务,并协助中国进行改革。
这个解释对20世纪尚可适用,在此时期却未免与事实相距甚遥了。
一方面几乎所有来华的差会都提供不同程度的教育和医疗服务,但并非都只本着人道主义精神,更不必然协助中国改革。
另一方面(更重要的是)晚清倡导西化改革最力的传教士,在来华之初几都投身于直接布道工作,他们的转变与其说是受到欧美神学思潮的影响,不若说是被中国的经验和体会导引他们反省的结果。
事实上,不少传教士的转变是机缘巧合的。
例如林乐知(Young J. Allens)原隶属美南监理会(Methodist Episcopal Church, South)。
在主后1860年代初因美国发生南北战争,南部的监理会无力支持侮外传教士,林乐知一家生活陷于困境,才不得已在主后1864年加入上海广方言馆担任西学教习。
李提摩太则是在主后1870年代末期参与华北五省的旱灾救灾工作时,结纳了不少政府官员,才认定协助中国西化改革是福音化中国的重要途径。
他如丁韪良(W.A.P.Martin)、花之安(Ernst Faber)……等皆是在中国工作了一段日子后才改变他们的传教方向。
唯一较为例外的是傅兰雅(John Fryer)。
他一开始便是以教育传教士的身份来华,并且很快便由传教学校跳到中国官办学堂这个更具战略性意义的教育机构。
这些传教士,不少直接加入中国政府的洋务机构,从事教育及翻译的工作。
例如丁韪良任北京同文馆及京师大学堂总教习前后共29年,傅兰雅在江南制造局翻译馆任职28年等。
他们运用兼通中外语言及对西学有相当认识的专长,翻译了大量西洋书籍。
虽然这些书籍的使用量和影响并不见得理想,但正如同文馆等西学机构实际地栽培出来的西学人才并不很多一样,背后是反映了中国在西化改革的过程中许多复杂的问题,而这些问题都与传教士本身的努力无关。
反倒从另一个角度看,在翻译及引进西洋科技的过程中,一些曾协助传教士工作的中国人,都成了第一批近代的科学家,如徐寿、徐建寅、华衡芳、应祖锡等。
他们之接触及学习西洋科技,并非是造就自官办西学堂,却是直接受到传教士的影响。
这样足可证明传教士在传播西洋科技知识的作用。
除了协助中国政府的洋务机构外,传教士也主动地向国人介绍西洋科
技知识,并鼓吹中国西化改革。
例如傅兰雅于主后1876年联同一些中外人士,成立了上海格致书院。
这是一个向民众推广西洋科技的机构,工作包括展览新式机器、开办格致课程、举办以倡导西学为题的征文比赛等。
对当时中国变革具有重要影响的,还是前面已经提到的《万国公报》和广学会。
思考与评论——基督教化必先西化?
1.为什么传教士会对中国文化有否定性的认识?
2.基督教与中国社会政治、经济变革有何关系?。
