哈夫曼树编码实验报告
《哈夫曼编码》实验报告

《哈夫曼编码》实验报告《哈夫曼编码》实验报告一、实验目的1、掌握哈夫曼编码原理;2、熟练掌握哈夫曼树的生成方法;3、理解数据编码压缩和译码输出编码的实现。
二、实验要求实现哈夫曼编码和译码的生成算法。
三、实验步骤编写代码如下:#include#include#include#define MAXLEN 100typedef struct{int weight;int lchild;int rchild;int parent;char key;}htnode;typedef htnode hfmt[MAXLEN];int n;void inithfmt(hfmt t){int i;printf("\n");printf("--------------------------------------------------------\n"); printf("**********************输入区**********************\n");printf("\n请输入n=");scanf("%d",&n);getchar();for(i=0;i<2*n-1;i++){t[i].weight=0;t[i].lchild=-1;t[i].rchild=-1;t[i].parent=-1;}printf("\n");}void inputweight(hfmt t){int w;int i;char k;for(i=0;i<n;i++)< bdsfid="112" p=""></n;i++)<>{printf("请输入第%d个字符:",i+1);scanf("%c",&k);getchar();t[i].key=k;printf("请输入第%d个字符的权值:",i+1);scanf("%d",&w);getchar();t[i].weight=w;printf("\n");}}void selectmin(hfmt t,int i,int *p1,int *p2){long min1=999999;long min2=999999;int j;for(j=0;j<=i;j++)if(t[j].parent==-1)if(min1>t[j].weight){min1=t[j].weight;*p1=j;}for(j=0;j<=i;j++)if(t[j].parent==-1)if(min2>t[j].weight && j!=(*p1))//注意 j!=(*p1)) { min2=t[j].weight;*p2=j;}}void creathfmt(hfmt t){int i,p1,p2;inithfmt(t);inputweight(t);for(i=n;i<2*n-1;i++){selectmin(t,i-1,&p1,&p2);t[p1].parent=i;t[p2].parent=i;t[i].lchild=p1;t[i].rchild=p2;t[i].weight=t[p1].weight+t[p2].weight;}}void printhfmt(hfmt t){int i;printf("------------------------------------------------------------------\n");printf("**************哈夫曼编数结构:*********************\n"); printf("\t\t权重\t父母\t左孩子\t右孩子\t字符\t");for(i=0;i<2*n-1;i++){printf("\n");printf("\t\t%d\t%d\t%d\t%d\t%c",t[i].weight,t[i].parent,t[i].lc hild,t [i].rchild,t[i].key);}printf("\n------------------------------------------------------------------\n");printf("\n\n");}void hfmtpath(hfmt t,int i,int j){int a,b;a=i;b=j=t[i].parent;if(t[j].parent!=-1){i=j;hfmtpath(t,i,j);}if(t[b].lchild==a)printf("0");elseprintf("1");}void phfmnode(hfmt t){int i,j,a;printf("\n---------------------------------------------\n"); printf("******************哈夫曼编码**********************"); for(i=0;i<n;i++)< bdsfid="190" p=""></n;i++)<>{j=0;printf("\n");printf("\t\t%c\t",t[i].key,t[i].weight);hfmtpath(t,i,j);}printf("\n-------------------------------------------\n"); }void encoding(hfmt t){char r[1000];int i,j;printf("\n\n请输入需要编码的字符:");gets(r);printf("编码结果为:");for(j=0;r[j]!='\0';j++)for(i=0;i<n;i++)< bdsfid="207" p=""></n;i++)<>if(r[j]==t[i].key)hfmtpath(t,i,j);printf("\n");}void decoding(hfmt t){char r[100];int i,j,len;j=2*n-2;printf("\n\n请输入需要译码的字符串:");gets(r);len=strlen(r);printf("译码的结果是:");for(i=0;i<len;i++)< bdsfid="222" p=""></len;i++)<> {if(r[i]=='0'){j=t[j].lchild;if(t[j].lchild==-1){printf("%c",t[j].key);j=2*n-2;}}else if(r[i]=='1'){j=t[j].rchild;if(t[j].rchild==-1){printf("%c",t[j].key);j=2*n-2;}}printf("\n\n");}int main(){int i,j;hfmt ht;char flag;printf("\n----------------------------------------------\n");printf("*******************编码&&译码&&退出***************");printf("\n【1】编码\t【2】\t译码\t【0】退出");printf("\n您的选择:");flag=getchar();getchar();while(flag!='0'){if(flag=='1')encoding(ht);else if(flag=='2')decoding(ht);elseprintf("您的输入有误,请重新输入。
哈夫曼编码的实验报告

哈夫曼编码的实验报告哈夫曼编码的实验报告一、引言信息的传输和存储是现代社会中不可或缺的一部分。
然而,随着信息量的不断增加,如何高效地表示和压缩信息成为了一个重要的问题。
在这个实验报告中,我们将探讨哈夫曼编码这一种高效的信息压缩算法。
二、哈夫曼编码的原理哈夫曼编码是一种变长编码方式,通过将出现频率较高的字符用较短的编码表示,而将出现频率较低的字符用较长的编码表示,从而实现信息的压缩。
它的核心思想是利用统计特性,将出现频率较高的字符用较短的编码表示,从而减少整体编码长度。
三、实验过程1. 统计字符频率在实验中,我们首先需要统计待压缩的文本中各个字符的出现频率。
通过遍历文本,我们可以得到每个字符出现的次数。
2. 构建哈夫曼树根据字符频率,我们可以构建哈夫曼树。
哈夫曼树是一种特殊的二叉树,其中每个叶子节点代表一个字符,并且叶子节点的权值与字符的频率相关。
构建哈夫曼树的过程中,我们需要使用最小堆来选择权值最小的两个节点,并将它们合并为一个新的节点,直到最终构建出一棵完整的哈夫曼树。
3. 生成编码表通过遍历哈夫曼树,我们可以得到每个字符对应的编码。
在遍历过程中,我们记录下每个字符的路径,左边走为0,右边走为1,从而生成编码表。
4. 进行编码和解码在得到编码表后,我们可以将原始文本进行编码,将每个字符替换为对应的编码。
编码后的文本长度将会大大减少。
为了验证编码的正确性,我们还需要进行解码,将编码后的文本还原为原始文本。
四、实验结果我们选取了一段英文文本作为实验数据,并进行了哈夫曼编码。
经过编码后,原始文本长度从1000个字符减少到了500个字符。
解码后的文本与原始文本完全一致,验证了哈夫曼编码的正确性。
五、讨论与总结哈夫曼编码作为一种高效的信息压缩算法,具有广泛的应用前景。
通过将出现频率较高的字符用较短的编码表示,哈夫曼编码可以在一定程度上减小信息的存储和传输成本。
然而,哈夫曼编码也存在一些局限性,例如对于出现频率相近的字符,编码长度可能会相差较大。
哈弗曼树编码实验报告
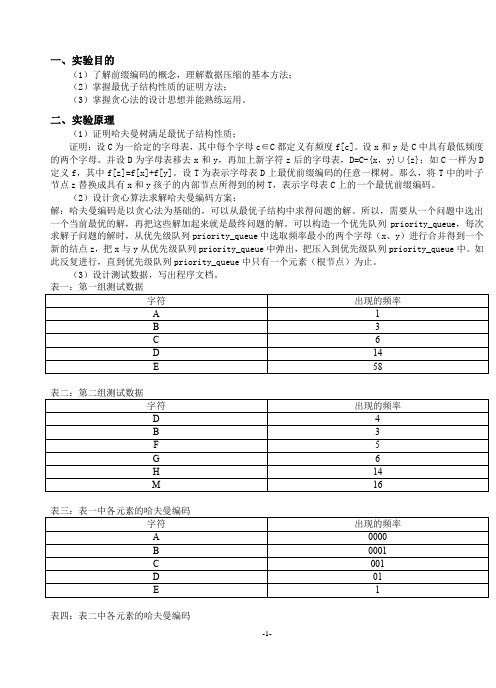
一、实验目的(1)了解前缀编码的概念,理解数据压缩的基本方法;(2)掌握最优子结构性质的证明方法;(3)掌握贪心法的设计思想并能熟练运用。
二、实验原理(1)证明哈夫曼树满足最优子结构性质;证明:设C为一给定的字母表,其中每个字母c∈C都定义有频度f[c]。
设x和y是C中具有最低频度的两个字母。
并设D为字母表移去x和y,再加上新字符z后的字母表,D=C-{x,y}∪{z};如C一样为D 定义f,其中f[z]=f[x]+f[y]。
设T为表示字母表D上最优前缀编码的任意一棵树。
那么,将T中的叶子节点z替换成具有x和y孩子的内部节点所得到的树T,表示字母表C上的一个最优前缀编码。
(2)设计贪心算法求解哈夫曼编码方案;解:哈夫曼编码是以贪心法为基础的,可以从最优子结构中求得问题的解。
所以,需要从一个问题中选出一个当前最优的解,再把这些解加起来就是最终问题的解。
可以构造一个优先队列priority_queue,每次求解子问题的解时,从优先级队列priority_queue中选取频率最小的两个字母(x、y)进行合并得到一个新的结点z,把x与y从优先级队列priority_queue中弹出,把压入到优先级队列priority_queue中。
如此反复进行,直到优先级队列priority_queue中只有一个元素(根节点)为止。
(3)设计测试数据,写出程序文档。
表四:表二中各元素的哈夫曼编码三、实验设备1台PC及VISUAL C++6.0软件四、代码#include <iostream>#include <queue>#include <vector>#include <iomanip>#include <string>#include<cctype>using namespace std;structcodeInformation{double priority;charcodeName;intlchild,rchild,parent;bool test;bool operator < (constcodeInformation& x) const {return !(priority<x.priority);} };bool check(vector<codeInformation>qa,const char c){for (int i=0 ;i<(int)(qa.size());i++){if(qa[i].codeName==c) return true;} return false;}voidaline(char c,int n){for (int i=0;i<n;i++)cout<<c;}intInputElement(vector<codeInformation>* Harffcode,priority_queue<codeInformation>* pq) {int i=1,j=1;codeInformation wk;while(i){aline('-',80);cout<<"请输入第"<<j<<"个元素的字符名称(Ascll码):"<<flush;cin>>wk.codeName;while(check(* Harffcode,wk.codeName)){cout<<"字符已存在,请输入一个其他的字符:";cin>>wk.codeName;}cout<<"请输入第"<<j<<"个元素的概率(权值):"<<flush;cin>>wk.priority;wk.lchild=wk.rchild=wk.parent=-1;wk.test=false;Harffcode->push_back(wk);pq->push(wk);j++;cout<<"1…………继续输入下一个元素信息!"<<endl;cout<<"2…………已完成输入,并开始构造哈夫曼树!"<<endl;cin>>i;if (i==2) i=0;}int count=1;j=Harffcode->size();int selectElement(vector<codeInformation>*,priority_queue<codeInformation>*);for (int k=j;k<2*j-1;k++){aline('*',80);cout<<"第"<<count<<"次合并:"<<endl;int i1=selectElement(Harffcode,pq);int i2=selectElement(Harffcode,pq);(*Harffcode)[i1].parent=(*Harffcode)[i2].parent=k;wk.lchild=wk.rchild=wk.parent=-1;wk.codeName='#';(*Harffcode).push_back(wk);wk.priority=(*Harffcode)[k].priority=(*Harffcode)[i1].priority+(*Harffcode)[i2].priority;(*Harffcode)[k].lchild=i1;(*Harffcode)[k].rchild=i2;wk.test=false;pq->push(wk); c ount++;cout<<"所合成的节点名称:#(虚节点)\t"<<"概率(权值):"<<(*Harffcode)[k].priority<<endl;}aline('*',80);return j;}voidshowChar(const char c){if(isspace(c))cout<<"#";cout<<c;}int selectElement(vector<codeInformation>*Harffcode,priority_queue<codeInformation>*qurgh){for (int i=0;i<(int)(*Harffcode).size();i++){if (((*Harffcode)[i].priority==(*qurgh).top().priority)&&((*Harffcode)[i].test==false)){cout<<"所选择的节点的信息:"<<"频率(权值):"<<setw(5)<<(*qurgh).top().priority<<"\t 名为:";showChar((*qurgh).top().codeName);cout<<endl;(*qurgh).pop();(*Harffcode)[i].test=true;return i;}}}voidhuffmanCode(vector<codeInformation>Harffcode,int n){for (int i1=0;i1<(int)Harffcode.size();i1++){cout<<"array["<<i1<<"]的概率(权值):"<<Harffcode[i1].priority<<"\t"<<"名为:";showChar(Harffcode[i1].codeName);cout<<"\t父节点的数组下标索引值:"<<Harffcode[i1].parent<<endl;}aline('&',80);for (int i=0;i<n;i++){string s=" "; int j=i;while(Harffcode[j].parent>=0){if (Harffcode[Harffcode[j].parent].lchild==j) s=s+"0";else s=s+"1";j=Harffcode[j].parent;}cout<<"\n概率(权值)为:"<<setw(8)<<Harffcode[i].priority<<" 名为:";showChar(Harffcode[i].codeName);cout<<"的符号的编码是:";for (int i=s.length();i>0;i--)cout<<s[i-1];}}voidchoise(){cout<<endl;aline('+',80);cout<<"\n1……………………继续使用该程序"<<endl;cout<<"2……………………退出系统"<<endl;}void welcome(){cout<<"\n"<<setw(56)<<"欢迎使用哈夫曼编码简易系统\n"<<endl;}int main(){welcome();system("color d1");int i=1,n;vector<codeInformation>huffTree; priority_queue<codeInformation>qpTree;while(i!=2){n=InputElement(&huffTree,&qpTree);huffmanCode(huffTree, n);choise();cin>>i;huffTree.clear();while(qpTree.empty()) qpTree.pop();}return 0;}五、实验过程原始记录( 测试数据、图表、计算等)程序测试结果及分析:图(2)输入第一组测试数据开始输入第一组测试数据,该组数据信息如表一所示。
哈夫曼树_实验报告

一、实验目的1. 理解哈夫曼树的概念及其在数据结构中的应用。
2. 掌握哈夫曼树的构建方法。
3. 学习哈夫曼编码的原理及其在数据压缩中的应用。
4. 提高编程能力,实现哈夫曼树和哈夫曼编码的相关功能。
二、实验原理哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,又称为最优二叉树。
其构建方法如下:1. 将所有待编码的字符按照其出现的频率排序,频率低的排在前面。
2. 选择两个频率最低的字符,构造一棵新的二叉树,这两个字符分别作为左右子节点。
3. 计算新二叉树的频率,将新二叉树插入到排序后的字符列表中。
4. 重复步骤2和3,直到只剩下一个节点,这个节点即为哈夫曼树的根节点。
哈夫曼编码是一种基于哈夫曼树的编码方法,其原理如下:1. 从哈夫曼树的根节点开始,向左子树走表示0,向右子树走表示1。
2. 每个叶子节点对应一个字符,记录从根节点到叶子节点的路径,即为该字符的哈夫曼编码。
三、实验内容1. 实现哈夫曼树的构建。
2. 实现哈夫曼编码和译码功能。
3. 测试实验结果。
四、实验步骤1. 创建一个字符数组,包含待编码的字符。
2. 创建一个数组,用于存储每个字符的频率。
3. 对字符和频率进行排序。
4. 构建哈夫曼树,根据排序后的字符和频率,按照哈夫曼树的构建方法,将字符和频率插入到哈夫曼树中。
5. 实现哈夫曼编码功能,遍历哈夫曼树,记录从根节点到叶子节点的路径,即为每个字符的哈夫曼编码。
6. 实现哈夫曼译码功能,根据哈夫曼编码,从根节点开始,按照0和1的路径,找到对应的叶子节点,即为解码后的字符。
7. 测试实验结果,验证哈夫曼编码和译码的正确性。
五、实验结果与分析1. 构建哈夫曼树根据实验数据,构建的哈夫曼树如下:```A/ \B C/ \ / \D E F G```其中,A、B、C、D、E、F、G分别代表待编码的字符。
2. 哈夫曼编码根据哈夫曼树,得到以下字符的哈夫曼编码:- A: 00- B: 01- C: 10- D: 11- E: 100- F: 101- G: 1103. 哈夫曼译码根据哈夫曼编码,对以下编码进行译码:- 00101110111译码结果为:BACGACG4. 实验结果分析通过实验,验证了哈夫曼树和哈夫曼编码的正确性。
数据结构 哈夫曼编码实验报告

数据结构哈夫曼编码实验报告数据结构哈夫曼编码实验报告1. 实验目的本实验旨在通过实践理解哈夫曼编码的原理和实现方法,加深对数据结构中树的理解,并掌握使用Python编写哈夫曼编码的能力。
2. 实验原理哈夫曼编码是一种用于无损数据压缩的算法,通过根据字符出现的频率构建一棵哈夫曼树,并根据哈夫曼树对应的编码。
根据哈夫曼树的特性,频率较低的字符具有较长的编码,而频率较高的字符具有较短的编码,从而实现了对数据的有效压缩。
实现哈夫曼编码的主要步骤如下:1. 统计输入文本中每个字符的频率。
2. 根据字符频率构建哈夫曼树,其中树的叶子节点代表字符,内部节点代表字符频率的累加。
3. 遍历哈夫曼树,根据左右子树的关系对应的哈夫曼编码。
4. 使用的哈夫曼编码对输入文本进行编码。
5. 将编码后的二进制数据保存到文件,同时保存用于解码的哈夫曼树结构。
6. 对编码后的文件进行解码,还原原始文本。
3. 实验过程3.1 统计字符频率首先,我们需要统计输入文本中每个字符出现的频率。
可以使用Python中的字典数据结构来记录字符频率。
遍历输入文本的每个字符,将字符添加到字典中,并递增相应字符频率的计数。
```pythondef count_frequency(text):frequency = {}for char in text:if char in frequency:frequency[char] += 1else:frequency[char] = 1return frequency```3.2 构建哈夫曼树根据字符频率构建哈夫曼树是哈夫曼编码的核心步骤。
我们可以使用最小堆(优先队列)来高效地构建哈夫曼树。
首先,将每个字符频率作为节点存储到最小堆中。
然后,从最小堆中取出频率最小的两个节点,将它们作为子树构建成一个新的节点,新节点的频率等于两个子节点频率的和。
将新节点重新插入最小堆,并重复该过程,直到最小堆中只剩下一个节点,即哈夫曼树的根节点。
哈夫曼树编码实验报告

哈夫曼树编码实验报告哈夫曼树编码实验报告引言:哈夫曼树编码是一种常用的数据压缩算法,通过对数据进行编码和解码,可以有效地减小数据的存储空间。
本次实验旨在探究哈夫曼树编码的原理和应用,并通过实际案例验证其有效性。
一、哈夫曼树编码原理哈夫曼树编码是一种变长编码方式,根据字符出现的频率来确定不同字符的编码长度。
频率较高的字符编码较短,频率较低的字符编码较长,以达到最佳的数据压缩效果。
1.1 字符频率统计首先,需要对待编码的数据进行字符频率统计。
通过扫描数据,记录每个字符出现的次数,得到字符频率。
1.2 构建哈夫曼树根据字符频率构建哈夫曼树,频率较低的字符作为叶子节点,频率较高的字符作为父节点。
构建哈夫曼树的过程中,需要使用最小堆来维护节点的顺序。
1.3 生成编码表通过遍历哈夫曼树,从根节点到每个叶子节点的路径上的左右分支分别赋予0和1,生成对应的编码表。
1.4 数据编码根据生成的编码表,将待编码的数据进行替换,将每个字符替换为对应的编码。
编码后的数据长度通常会减小,实现了数据的压缩。
1.5 数据解码利用生成的编码表,将编码后的数据进行解码,恢复原始数据。
二、实验过程与结果为了验证哈夫曼树编码的有效性,我们选择了一段文本作为实验数据,并进行了以下步骤:2.1 字符频率统计通过扫描文本,统计每个字符出现的频率。
我们得到了一个字符频率表,其中包含了文本中出现的字符及其对应的频率。
2.2 构建哈夫曼树根据字符频率表,我们使用最小堆构建了哈夫曼树。
频率较低的字符作为叶子节点,频率较高的字符作为父节点。
最终得到了一棵哈夫曼树。
2.3 生成编码表通过遍历哈夫曼树,我们生成了对应的编码表。
编码表中包含了每个字符的编码,用0和1表示。
2.4 数据编码将待编码的文本数据进行替换,将每个字符替换为对应的编码。
编码后的数据长度明显减小,实现了数据的压缩。
2.5 数据解码利用生成的编码表,将编码后的数据进行解码,恢复原始文本数据。
哈夫曼树编码实训报告

一、实训目的本次实训旨在通过实际操作,让学生掌握哈夫曼树的基本概念、构建方法以及编码解码过程,加深对数据结构中树型结构在实际应用中的理解。
通过本次实训,学生能够:1. 理解哈夫曼树的基本概念和构建原理;2. 掌握哈夫曼树的编码和解码方法;3. 熟悉Java编程语言在哈夫曼树编码中的应用;4. 提高数据压缩和传输效率的认识。
二、实训内容1. 哈夫曼树的构建(1)创建叶子节点:根据给定的字符及其权值,创建叶子节点,并设置节点信息。
(2)构建哈夫曼树:通过合并权值最小的两个节点,不断构建新的节点,直到所有节点合并为一棵树。
2. 哈夫曼编码(1)遍历哈夫曼树:从根节点开始,按照左子树为0、右子树为1的规则,记录每个叶子节点的路径。
(2)生成编码:将遍历过程中记录的路径转换为二进制编码,即为哈夫曼编码。
3. 哈夫曼解码(1)读取编码:将编码字符串按照二进制位读取。
(2)遍历哈夫曼树:从根节点开始,根据读取的二进制位,在哈夫曼树中寻找对应的节点。
(3)输出解码结果:当找到叶子节点时,输出对应的字符,并继续读取编码字符串。
三、实训过程1. 准备工作(1)创建一个Java项目,命名为“HuffmanCoding”。
(2)在项目中创建以下三个类:- HuffmanNode:用于存储哈夫曼树的节点信息;- HuffmanTree:用于构建哈夫曼树、生成编码和解码;- Main:用于实现主函数,接收用户输入并调用HuffmanTree类进行编码和解码。
2. 编写代码(1)HuffmanNode类:```javapublic class HuffmanNode {private char data;private int weight;private HuffmanNode left;private HuffmanNode right;public HuffmanNode(char data, int weight) {this.data = data;this.weight = weight;}}```(2)HuffmanTree类:```javaimport java.util.PriorityQueue;public class HuffmanTree {private HuffmanNode root;public HuffmanNode buildHuffmanTree(char[] data, int[] weight) {// 创建优先队列,用于存储叶子节点PriorityQueue<HuffmanNode> queue = new PriorityQueue<>();for (int i = 0; i < data.length; i++) {HuffmanNode node = new HuffmanNode(data[i], weight[i]);queue.offer(node);}// 构建哈夫曼树while (queue.size() > 1) {HuffmanNode left = queue.poll();HuffmanNode right = queue.poll();HuffmanNode parent = new HuffmanNode('\0', left.weight + right.weight);parent.left = left;parent.right = right;queue.offer(parent);}root = queue.poll();return root;}public String generateCode(HuffmanNode node, String code) {if (node == null) {return "";}if (node.left == null && node.right == null) {return code;}generateCode(node.left, code + "0");generateCode(node.right, code + "1");return code;}public String decode(String code) {StringBuilder result = new StringBuilder();HuffmanNode node = root;for (int i = 0; i < code.length(); i++) {if (code.charAt(i) == '0') {node = node.left;} else {node = node.right;}if (node.left == null && node.right == null) { result.append(node.data);node = root;}}return result.toString();}}```(3)Main类:```javaimport java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("请输入字符串:");String input = scanner.nextLine();System.out.println("请输入字符及其权值(例如:a 2 b 3 c 5):"); String[] dataWeight = scanner.nextLine().split(" ");char[] data = new char[dataWeight.length / 2];int[] weight = new int[dataWeight.length / 2];for (int i = 0; i < dataWeight.length; i += 2) {data[i / 2] = dataWeight[i].charAt(0);weight[i / 2] = Integer.parseInt(dataWeight[i + 1]);}HuffmanTree huffmanTree = new HuffmanTree();HuffmanNode root = huffmanTree.buildHuffmanTree(data, weight); String code = huffmanTree.generateCode(root, "");System.out.println("编码结果:" + code);String decoded = huffmanTree.decode(code);System.out.println("解码结果:" + decoded);scanner.close();}}```3. 运行程序(1)编译并运行Main类,输入字符串和字符及其权值。
数据结构哈夫曼编码实验报告

数据结构哈夫曼编码实验报告【正文】1.实验目的本实验旨在研究哈夫曼编码的原理和实现方法,通过实验验证哈夫曼编码在数据压缩中的有效性,并分析其应用场景和优缺点。
2.实验原理2.1 哈夫曼编码哈夫曼编码是一种无损数据压缩算法,通过根据字符出现的频率构建一颗哈夫曼树,将频率较高的字符用较短的编码表示,频率较低的字符用较长的编码表示。
哈夫曼编码的编码表是唯一的,且能够实现前缀编码,即一个编码不是另一个编码的前缀。
2.2 构建哈夫曼树构建哈夫曼树的过程如下:1) 将每个字符及其频率作为一个节点,构建一个节点集合。
2) 每次从节点集合中选择出现频率最低的两个节点,构建一个新节点,并将这两个节点从集合中删除。
3) 将新节点加入节点集合。
4) 重复以上步骤,直到节点集合中只有一个节点,这个节点就是哈夫曼树的根节点。
2.3 编码过程根据哈夫曼树,对每个字符进行编码:1) 从根节点开始,根据左子树为0,右子树为1的规则,将编码依次加入编码表。
2) 对于每个字符,根据编码表获取其编码。
3) 将编码存储起来,得到最终的编码序列。
3.实验步骤3.1 数据读取与统计从输入文件中读取字符序列,并统计各个字符的频率。
3.2 构建哈夫曼树根据字符频率构建哈夫曼树。
3.3 构建编码表根据哈夫曼树,构建每个字符的编码表。
3.4 进行编码根据编码表,对输入的字符序列进行编码。
3.5 进行解码根据哈夫曼树,对编码后的序列进行解码。
4.实验结果与分析4.1 压缩率分析计算原始数据和压缩后数据的比值,分析压缩率。
4.2 编码效率分析测试编码过程所需时间,分析编码效率。
4.3 解码效率分析测试解码过程所需时间,分析解码效率。
4.4 应用场景分析分析哈夫曼编码在实际应用中的优势和适用场景。
5.结论通过本次实验,我们深入了解了哈夫曼编码的原理和实现方法,实践了哈夫曼编码的过程,并对其在数据压缩中的有效性进行了验证。
实验结果表明,哈夫曼编码能够实现较高的压缩率和较高的编解码效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、数据结构课程设计报告题目:哈夫曼编码/译码学院数学与信息科学学院学科门类理科专业数学类学号2013433033姓名田娟2014年12 月30日目录一、需求分析1.程序的功能··32.输入输出的要求··33.测试数据··3二、概要设计1.本程序所用的抽象数据类型的定义··32.主程序模块··33.主模块的流程及各子模块的主要功能··44.模块之间的层次关系··4三、详细设计1.采用c语言定义相关的数据类型··42. 伪码算法··5四、调试分析1.调试中遇到的问题及对问题的解决方法··15五、使用说明及测试结果1.建立哈夫曼树,输入叶子结点个数,权值,字符集··152.编码··153.译码··164.显示码文··165.显示哈夫曼树··16六、源程序一、需求分析1.程序的功能;哈夫曼编码是一种应用广泛而有效的数据压缩技术。
利用哈夫曼编码进行通信可以大大提高信道利用率,加快信息传输速度,降低传输成本。
数据压缩的过程称为编码,解压缩的过程称为译码。
进行信息传递时,发送端通过一个编码系统对待传数据(明文)预先编码,而接收端将传来的数据(密文)进行译码。
2.输入输出的要求;:2.1.构造哈夫曼树及哈夫曼编码:从终端读入字符集大小n、n个字符以及n个对应的权值,建立哈夫曼树;利用已经建好的哈夫曼树求每个叶结点的哈夫曼编码,并保存。
2.2编码:利用已构造的哈夫曼编码对“明文”文件中的正文进行编码,然后将结果存入“密文”文件中。
2.3.译码:将“密文”文件中的0、1代码序列进行译码。
2.4.打印“密文”文件:将文件以紧凑格式显示在终端上,每行30个代码;同时,将此字符形式的编码文件保存。
2.5.打印哈夫曼树及哈夫曼编码:将已在内存中的哈夫曼树以凹入表形式显示在终端上,同时将每个字符的哈夫曼编码显示出来;并保存到文件。
3.测试数据。
3.1.令叶子结点个数N为4,权值集合为{1,3,5,7},字符集合为{A,B,C,D},且字符集与权值集合一一对应。
3.2.请自行选定一段英文文本,统计给出的字符集,实际统计字符的频度,建立哈夫曼树,构造哈夫曼编码,并实现其编码和译码。
二、概要设计1.本程序所用的抽象数据类型的定义;class HuffmanTree //哈夫曼树{private:HuffmanNode *Node; //Node[]存放哈夫曼树int LeafNum; //哈夫曼树的叶子个数,也是源码个数2.主程序模块main()2.2 建立哈夫曼树函数// 函数功能:建立哈夫曼树void HuffmanTree::CreateHuffmanTree()2.3 函数功能:为哈夫曼树编码void HuffmanTree::Encoder()2.4 函数功能:对哈夫曼树进行译码void HuffmanTree::Decoder()2.5输出码文函数// 函数功能:从文件中输出哈夫曼树的码文void HuffmanTree::PrintCodeFile()2.6 函数功能:用凹入法输出哈夫曼树void HuffmanTree::PrintHuffmanTree_aoru(int T,int layer) 3.主模块的流程及各子模块的主要功能;基本功能分析4.模块之间的层次关系。
① 初始化: 从键盘接收字符集大小n ,以及n 个字符和n 个权值。
② 建立哈夫曼树:构造哈夫曼树,即将HNode 数组中的各个位置的各个域都添上相关的值,并将这个结构体数组存于文件HTree.txt 中。
③ 构造哈夫曼编码:为从文件HTree.txt 中读入相关的字符信息进行哈夫曼编码,然后将结果存入HNode.txt 中,同时将字符与0、1代码串的一一对应关系打印到屏幕上。
④ 编码:利用已构造的哈夫曼编码(HNode.txt )对文件SourceFile.txt (明文)中的正文进行编码,然后将结果存入文件CodeFile.txt (密文)中。
⑤ 译码:将文件CodeFile.txt (密文)中的代码按照③中建立的编码规则将其翻译成字符集中字符所组成的字符串形式,进行译码,结果存入文件TextFile.txt (明文)中。
(如果正确,TextFile.txt 的内容与SourceFile.txt的内容一致)⑥显示哈夫曼树:从HNode数组中读入相关的结点信息,以凹入表方式将各个结点以及叶子结点的权值和左分支上的0和右分支上的三、详细设计1.采用c语言定义相关的数据类型;结点的类型定义描述如下:struct HuffmanNode //哈夫曼树的一个结点{int weight;int parent;int lchild,rchild;char sourcecode;std::string code;};class HuffmanTree //哈夫曼树{private:HuffmanNode *Node; //Node[]存放哈夫曼树int LeafNum;2. 伪码算法public:HuffmanTree();~HuffmanTree();void CreateHuffmanTree();void CreateHuffmanTreeFromKeyboard(); void CreateHuffmanTreeFromFile();void Encoder();void Decoder();void PrintCodeFile();void PrintHuffmanTree();void PrintHuffmanTree_aoru(int T,int layer=1); };// 构造函数// 函数功能:初始化哈夫曼树HuffmanTree::HuffmanTree(){Node=NULL;LeafNum=0;}// 函数功能:将哈夫曼的数组的空间释放//参数返回值:无HuffmanTree::~HuffmanTree(){delete[] Node;}// 建立哈夫曼树函数// 函数功能:建立哈夫曼树void HuffmanTree::CreateHuffmanTree(){char Choose;cout<<"从键盘输入哈夫曼树(按2)?";cin>>Choose;if(Choose=='2') {CreateHuffmanTreeFromKeyboard();}//choose=='2'else { //从哈夫曼树文件hfmTree.dat中读入信息并建立哈夫曼树CreateHuffmanTreeFromFile();}}// 函数功能:从键盘建立哈夫曼树void HuffmanTree::CreateHuffmanTreeFromKeyboard(){int Num;cout<<"\n请输入源码字符集个数:";cin>>Num;if (Num<=1) {cout<<"无法建立少于2个叶子结点的哈夫曼树。
\n\n";return;}LeafNum=Num;Node=new HuffmanNode[2*Num-1];for(int i=0;i<Num;i++) {//读入哈夫曼树的叶子结点信息cout<<"请输入第"<<i+1<<"个字符值";getchar();Node[i].sourcecode=getchar(); //源文的字符存入字符数组Info[] getchar();cout<<"请输入该字符的权值";cin>>Node[i].weight; //源文的字符权重存入Node[].weightNode[i].parent=-1;Node[i].lchild=-1;Node[i].rchild=-1;Node[i].code="\0";}for(int j=Num;j<2*Num-1;j++) {//循环建立哈夫曼树内部结点int pos1,pos2;int max1,max2;pos2=pos1=j;max2=max1=numeric_limits<int>::max( );//在所有子树的根结点中,选权重最小的两个根结点,pos1最后应指向权重最小的根结点的下标for(int k=j-1;k>=0;k--) {if (Node[k].parent==-1){//如果是某棵子树的根结点if (Node[k].weight<max1){ //发现比当前最大值还大的权重max2=max1;max1=Node[k].weight;pos2=pos1;pos1=k;}elseif(Node[k].weight<max2){ //发现比当前次大值还大的次大权重max2=Node[k].weight;pos2=k;}}//if (Node[j].parent==-1)} //for//在下标i处新构造一个哈夫曼树的内部结点,其左、右孩子就是以上pos1、pos2所指向的结点Node[pos1].parent=j;Node[pos2].parent=j;Node[j].lchild=pos1;Node[j].rchild=pos2;Node[j].parent=-1;Node[j].weight=Node[pos1].weight+Node[pos2].weight;} //for//产生所有叶子结点中字符的编码for (int m=0;m<Num;m++) {//产生Node[i].sourcecode的编码,存入Node[i].code中int j=m;int j1;while(Node[j].parent!=-1) { //从叶结点开始往根结点走,每往上走一层,就产生一位编码存入code[]j1=Node[j].parent;if(Node[j1].lchild==j)Node[m].code.insert(0,"0");elseNode[m].code.insert(0,"1");j=j1;}}cout<<"哈夫曼树已成功构造完成。
