第三章 导数与微分习题答案
经济管理类微积分龚德恩第二版参考答案 第三章导数与微分

(2) 已知 y = f (3)
a + x
2
x
4 2
,则 y ′ =
f ( θn ) =
(5) 设 y =f ( x ) =x 在点 (1,1 ) 处的切线与 x 轴的交点为 ( θn ,0 ) , 则 nlim
n
1 (4) 曲线 y = 2 在点 ( - 1,1) 的切线方程为 x ;
d ( arcsin x ) = d ( arccos x )
16.求下列各数的近似值 : (1) 2 解
1. 001
(3) sin 29° ;
; (2) ln1. 002; (4)
3
76 .
(2 ln 2) Δ x. (1) 令 f ( x ) = 2 ,d f =
x x
取 x0 = 1,Δ x- 0. 001,则 2
1. 00 1 1 1
≈ f (1) + df | x 0 =1 , Δ x =0 . 0 01 = 2+ 0. 002 × ln2≈2. 001386( ln2≈0. 6931) . ln (1. 002) ≈ f(1) + df
边际收益为
于是 ,边际利润为
18.已知某产品的需求函数和总成本函数分别为 : 其中 x 为销售量 ,P 为价格 . 解 利润函数为
1 10 . L′ ( x) = [ R ( x) - C( x) ] ′ = R′ ( x) - C′ ( x) = 2 - (x + 2) x p= 1000 - 2 x ,C ( x ) = 5000 + 20 x
2 2
∴y ′ ( x) = lim Δ x 0
→
= (x + Δ x) - x + 3Δ x= (2 x + 3+ Δ x) Δ x Δ y =lim (2 x + 3+ Δ x) = 2x + 3. Δ x Δx → 0
第三章 导数与微分 习题及答案

第三章 导数与微分同步练习 一、填空 1、若[]1cos 1)0()(lim=--→xf x f x x ,则)0(f '= 。
2、设)100()3)(2)(1()(----=x x x x x x f ,则)0(f '= 。
3、若)(x e f y -=,且x x x f ln )(=',则1=x dxdy = 。
4、若)()(x f x f =-,且3)1(=-'f ,则)1(f '= 。
5、设某商品的需求函数是Q=10-0.2p ,则当价格p=10时,降价10%,需求量将 。
6、设某商品的需求函数为:Q=100-2p ,则当Q=50时,其边际收益为 。
7、已知x x y ln =,则)10(y = 。
8、已知2arcsin )(),2323(x x f x x f y ='+-=,则:0=x dxdy = 。
9、设1111ln22++-+=x x y ,则y '= 。
10、设方程y y x =确定y 是x 的函数,则dy = 。
11、已知()xke x f =',其中k 为常数,求()x f 的反函数的二阶导数=22dyxd 。
二、选择1、设f 可微,则=---→1)1()2(lim1x f x f x ( )A 、)1(-'-x fB 、)1(-'fC 、)1(f '-D 、)2(f ' 2、若2)(0-='x f ,则=--→)()2(lim000x f x x f xx ( )A 、41 B 、41- C 、1 D 、-1 3、设⎪⎩⎪⎨⎧=≠=0001arctan )(x x xx x f ,则)(x f 在0=x 处( )A 、不连续B 、极限不存在 C、连续且可导 D、连续但不可导 4、下列函数在[]1,1-上可微的有( ) A、x x y sin 32+= B、x x y sin =C、21x x y +=D、x x y cos += 5、设)(x f 为不恒等于零的奇函数,且)0(f '存在,则函数xx f x g )()(=( ) A、在0=x 处极限不存在 B、有跳跃间断点0=x C、在0=x 处右极限不存在 D、有可去间断点0=x6、设函数)(),(21x y x y 的弹性分别为)0(,≠b b a ,则函数)()(21x y x y y =的弹性为( ) A、b a - B、b aC、2112y by ay - D、以上都不对 7、已知)(x f e y =,则y ''=( )A、)(x f e B、)]()([)(x f x f e x f ''+' C、)()(x f e x f '' D、)}()]({[2)(x f x f e x f ''+'8、设函数⎩⎨⎧≤+>+=11)ln()(2x bx x x a x f 在1=x 处可导。
《高等数学一》第三章 导数与微 试题模拟课后习题汇总(含答案解析)

第三章导数与微分[单选题]1、设函数,则高阶导数=()A、12!B、11!C、10!D、0【从题库收藏夹删除】【正确答案】 D【您的答案】您未答题【答案解析】本题考察高阶导数计算.因为多项式的最高次幂为11,故=0.[单选题]2、f(x)=4x-x3在点(-1,-3)处的切线方程为( )A、y=x-2B、y=x+2C、y=-x+2D、y=-2x+1【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】f(x)=4x-x3, f(-1)=-4+1=-3,故(-1,-3)在所给的曲线上. 又f ' (x)=4-3x2故f ' (-1)=4-3=1∴过(-1,-3)的切线方程为y=(x+1)-3=x-2.[单选题]3、y=cos3x-cos3x的导数为( )A、3(sin3x-sinxcos2x)B、3(sin3x+sinxcos2x)C、3(sinx-sinxcos2x)D、3(sin3x-sin3xcos2x)【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】 y’=(cos3x)' -(cos3x) '=3cos2x(-sinx)-(-sin3x)×3=3(sin3x-sinxcos2x)[单选题]4、设y=x n+e-x,则y(n)(0)=()A、n!+(-1)nB、n!C、n!+(-1)n-1D、n!-1【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】y(n)(x)=n!+(-1)n e-x,从而y(n)(0)=n!+(-1)n[单选题]5、设函数f(x)=arctanx,求=( )A、-2B、1C、3D、0【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】[单选题]6、设y=lnx,则y(n)=()A、(-1)n n!x-nB、(-1)n(n-1)!x-2nC、(-1)n-1(n-1)!x-nD、(-1)n-1n!x-n+1【从题库收藏夹删除】【正确答案】C【您的答案】您未答题【答案解析】y′=x-1,y′′=-1!x-2, y′′′=2!x-3,…. y(n)= (-1)n-1(n-1)!x-n[单选题]7、已知函数,则f(x)在点x=0处()A、连续但导数不存在B、间断C、导数f ’(0)=-1D、导数f ’(0)=1【从题库收藏夹删除】【正确答案】B【您的答案】您未答题【答案解析】所以,f(x)在点x=0处间断,答案为B.[单选题]8、y=(2x2-x+1)2的导数为( )A、2(2x2-x+1)(4x-1)B、(2x2-x+1)(4x-1)C、(2x2-x+1)(4x+1)D、(2x2+x+1)(4x-1)【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】y’=2(2x2-x+1)(2x2-x+1)’=2(2x2-x+1)(4x-1)[单选题]9、设函数f(x)在x0点可微是f(x)在该点可导的( )A、充分必要条件B、充分条件C、必要条件D、无关条件【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】设函数f(x)在x0点可导是f(x)在该点可微的充要条件,对于一元函数,两者是等价的。
第三章 导数与微分习题

习 题 三1.根据导数的定义求下列函数的导数:(1)221x y -= (2)21x y = (3)32x y =2.给定函数f (x )=ax 2+bx +c ,其中a 、b 、c 为常量,求:)(x f ',)0(f ',)21(f ',)2(a b f -' 3.一物体的运动方程为s =t 3+10,求该物体在t =3时的瞬时速度。
4.求在抛物线y =x 2上点x =3处的切线方程。
5.自变量x 取哪些值时,抛物线y =x 2与y =x 3的切线平行?6.函数⎪⎩⎪⎨⎧≤-<≤+=x x x x x f 113101)(2在点x =1处是否可导?为什么?7.讨论函数y =x|x|在点x =0处的可导性。
8.用导数定义求⎩⎨⎧≥+<=0)1ln(1)(x s x xx f 在点x =0处的导数。
9.设⎩⎨⎧<<--+≤<-+=101101)1ln()(x xx x x x f 讨论f (x )在x =0处的连续性与可导性。
10.函数⎪⎩⎪⎨⎧=+≠=0)1ln(1sin )(12x s x x x f x 在点x =0处是否继续?是否可导?11.讨论⎪⎪⎩⎪⎪⎨⎧<≤<+≤<+≤=x xx x x x x x f 2212101201)(2在x =0,x =1,x =2处的连续性与可导性。
12.求下列各函数的导数(其中a ,b 为常量):(1)532+-=x x y (2)b a x y +=(3)3412+-=xx y (4)2222x x y += (5)x x y 31-= (6))12(2-=x x y(7))11)(1(-+=x x y (8)x x y 2)1(+=(9)ba b ax y ++= (10)))((b x a x y --=(10))1)(1(a b bx ax y ++=13.求下列各函数的导数(其中a ,b ,c ,d ,n 为常量):(1))3)(2)(1(+++=x x x y(2)x x y ln =(3)x x y n ln = (4)x y alog = (5)11-+=x x y (6)215xx y += (7)x x x y --=223 (8)n cx b a y += (9)x x y ln 1ln 1+-= (10)2211xx x x y +--+= 14.求下列各函数的导数:(1)x x x y cos sin += (2)xx y cos 1-=(3)x x x y tan tan -= (4)xx y cos 1sin 5+= (5)x x x x y sin sin += (6)x x x y ln sin ⋅= 15.求曲线x y sin =在点x =π处的切线方程。
第三章导数及其应用含详细答案
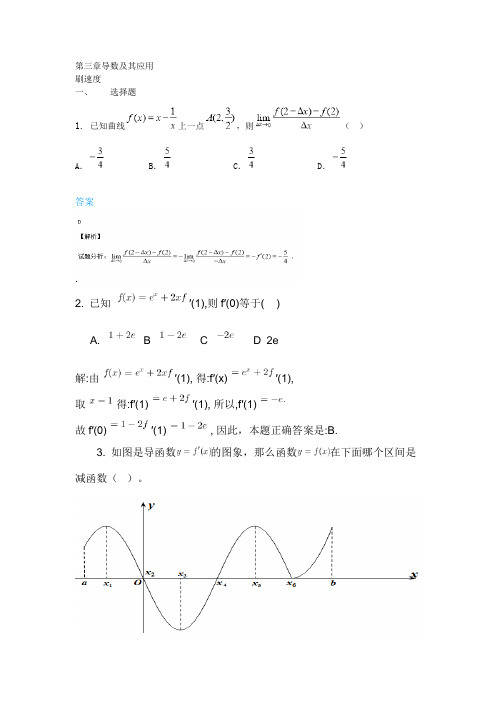
第三章导数及其应用刷速度一、选择题1. 已知曲线上一点,则()A.B.C.D.答案.2. 已知′(1),则f′(0)等于( )A. B C D 2e解:由′(1),得:f′(x)′(1),取得:f′(1)′(1),所以,f′(1)故f′(0)′(1), 因此,本题正确答案是:B.3. 如图是导函数的图象,那么函数在下面哪个区间是减函数()。
A: B: C: D:答案详解B解析:本题主要考查函数的单调性。
当函数为减函数时,函数的导数小于零,根据图象,在区间内导函数小于零,即为减区间。
故本题正确答案为B。
4. 函数,的最大值为( )A. B. 1 C. D.答案详解C解:令得或当时,或;当时,当时;当时,;当时,所以函数的最大值为所以C选项是正确的解析:求出函数的导函数,令导数为0求出根,判断根左右两边导函数的符号,求出函数的极值及端点值,在其中选出最大值.5. 已知曲线的一条切线的斜率为,则切点的横坐标为( )A. 3 B 2 C 1 D答案详解A解析:函数的定义域为,函数的导数为,由,得,解得或(舍去),选A.6. 函数有极值的充要条件是A、a≥1或a≤0B、a>1或a<0C、a≥1或a<0D、0<a<1答案B解析【分析】将函数f(x)有极值转化成f′(x)有两不等的根,再利用判别式进行判定即可.【解答】函数有极值则f′(x)=ax2+2ax+1=0有两不等的根当a=0时,无解当a≠0时,Δ>0.即4a2-4a>0解得a>1或a<0,故选B.7. 若在上是减函数,则的取值范围是()。
A: B: C: D:答案详解D解析:本题主要考查导数的应用。
由题意可知,在上恒成立,即在上恒成立,令,因为,所以。
要使,即需要小于等于其最小值,所以。
8.9.函数有三个相异的零点,则a的取值范围是( )A. B C D答案C解:函数,,,,,,, ,,函数在单调递减,单调递增,,使得函数有三个零点,必须:,计算得出.所以C选项是正确的.10. 已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为________.答案2解析切点在切线上也在曲线上得到切点坐标满足两方程;又曲线切点处的导数值是切线斜率得第三个方程.三个方程联立即可求出a的值.解答:设切点P(x 0,y 0),则y 0=x 0+1,y 0=ln(x 0+a),又∵切线方程y=x+1的斜率为1,即,∴x 0+a=1,∴y 0=0,x 0=-1,∴a=2.故答案为:211.12,设是定义在R上的函数,其导函数为f′(x),若′(x) , ,则不等式(其中e为自然对数的底数)的解集为( )A. B C D解:设,则g′(x)′(x)′(x),′(x),, ′(x)′(x),是R上的增函数, 又,的解集为,即不等式的解集为所以B选项是正确的.二、填空题13.、曲线在点处的切线方程是。
高中数学导数与微分练习题及参考答案2023

高中数学导数与微分练习题及参考答案2023一、选择题1.设y=(x-2)^2, 则y的导数为A. 2(x-2)B. (x-2)^2C. 2(x-2)^2D. 1/(x-2)2.已知函数f(x)=2x^3+x^2-4x, 则f'(2) =A. 2B. 20C. -8D. 283. 设f(x)=3x^(1/3)+2x^(-1/3), 则f'(x)=A. (6/x)^(1/3)B. (9/x^(2/3))C. (1/x^(4/3))D. 3(x^2/3)-2(x^-4/3)4. 若y=log_2(x^2+1), 则y''=A. [2(x^2+1)]/[ln2(x^2+1)^3]B. [2(x^2-1)]/[ln2(x^2+1)^3]C. [2(x^2+1)]/[ln2(x^2+1)^2(x^2-1)]D. [2(x^2-1)]/[ln2(x^2+1)^2(x^2+1)]5. 已知f(x)=5^x-3x, 则f'(log_53)=A. 2ln5-3/ln5B. 2ln5+3/ln5C. 2ln5-1/ln5D. 2ln5+1/ln5二、计算题1. 求函数y=4x^3-6x^2+2x的导数。
2. 已知函数f(x)=e^x/(x^2-4), 求f'(x)。
3. 已知y=sinx/x, 求y'(0)。
4. 若f(x)=x^3-3x^2+2, 求f(x)在x=2处的切线方程。
5. 求函数y=xlnx的导函数。
6. 求函数y=ln(x^2+1)的导函数。
7. 求直线y=2x-5与函数y=x^2-x+2的交点坐标。
8. 已知f(x)=xlnx, 求f''(x)。
三、应用题1. 筒形的长为20cm,半径为5cm,求其外表面积变化率和体积变化率,当半径增加0.05cm时,长增加0.1cm。
2. 一枚铜币的半径为3cm,厚度为0.2cm,求其体积在半径扩大到4cm时的变化率。
第三章导数及其应用参考答案

数的单调递减区间为(0,1].
7.答案 D
解析 依题意得,f′(x)=aex+cos x≥0,
即
a≥-coesx x对
x∈
-π,0 2
恒成立,
设
g(x)=-coesx x,x∈
-π,0 2
,
x+π
g′(x)= 2sin 4 ,令 g′(x)=0,则 x=-π,
ex
4
-π,-π 当 x∈ 2 4 时,g′(x)<0;
2 13.解 (1)∵f(x)=4ln x-mx2+1,
∴f′(x)=4-2mx, x
∴f′(1)=4-2m,
∵函数 f(x)在(1,f(1))处的切线与直线 2x-y-1=0 平行,∴f′(1)=4-2m=2,
∴m=1.
(2)∵对于任意 x∈[1,e],f(x)≤0 恒成立,
∴4ln x-mx2+1≤0,在 x∈[1,e]上恒成立,
由 f′(x)<0,得 x>-1, a
0,-1
-1,+∞
函数 f(x)在
a 上单调递增,在 a
上单调递减.
(2)①当 a=0 时,函数 f(x)在(0,1]内有 1 个零点 x0=1;
0, 1
1 ,+∞
②当 a>0 时,由(1)知函数 f(x)在 2a 上单调递增,在 2a
上单调递减.
若 1 ≥1,即 0<a≤1时,f(x)在(0,1]上单调递增,由于当 x→0 时,f(x)→-∞且 f(1)=-a2-a<0
e4
(e4 ,e)
g′(x)
+
0
-
g(x)
极大值
1
∴函数
g(x)在区间[1,e]上的最大值
高等数学习题详解-第3章 导数与微分.

习题3-11.设某产品的总成本C是产量q的函数:C=q2+1,求(1) 从q=100到q=102时,自变量的改变量∆q;(2) 从q=100到q=102时,函数的改变量∆C;(3) 从q=100到q=102时,函数的平均变化率;(4) 总成本在q=100处的变化率.解:(1) ∆q=102-100=2,(2) ∆C=C(102)-C(100)=(1022+1)-(1002+1)=404(3) 函数的平均变化率为∆CC(q0+∆q)-C(q0)404∆q=∆q=2=202.(4) 总成本在q=100处的变化率为C(q)-C(100)21002qlim→100q-100=qlimq-→100q-100=qlim→100(q+100)=2002.设f(x)=f'(4). 解f'(4)=limf(x)-f(4)x→4x-4=limx→4x-4=lim1x→4=23.根据函数导数定义,证明(cosx)'=-sinx. 证根据函数导数定义及“和差化积”公式,得h(cosx)'=limcos(x+h)-cosxhsin=-sinx. h→0h=-hlim→0sin(x+2)⋅h24.已知f'(a)=k,求下列极限: (1) limf(a-x)-f(a)x→0x; (2) limf(a+x)-f(a-x)x x→0解 (1) limf(a-x)-f(a)x=-limf(a-x)-f(a)-x=-f'(a)=-k;x→0x→0(2) limf(a+x)-f(a-x)x→0x=limf(a+x)-f(a)+f(a)-f(a-x)x→0x=limf(a+x)-f(a)f(a-x)-f(a)x+limx→0x→0-x=f'(a)+f'(a)=2k5.已知f(0)=0.f'(0)=1,计算极限limf(2x)x→0x.解 limf(2x)f(2x)-f(0)x=2limx→0x→02x=2f'(0)=26.求下列函数的导数:(1) y=x5;(2) y=- 1 -(3) y=e-x; (5) y=lgx;(4) y=2xex; (6) y=sin 34x-π4解(1) (x5)'=5x4;314;(2) '=(x4)'=(3) (e-x)'=e-xlne-1=-e-x;1xln10(4) (2xex)'=[(2e)x]'=(2e)xln(2e)=2xex(ln2+1); (5) (lgx)'= (6) (sin π4;)'=0⎧sinx,⎩x,7.问函数f(x)=⎨x<0x≥0在x=0处是否可导?如可导,求其导数.解考察x=0处的左、右导数f-'(0)=lim-h→0f(0+h)-f(0)f+'(0)=lim+h→0hf(0+h)-f(0)h=lim-h→0sinhhhh=1,=lim+h→0=1,所以,函数在x=0处的可导,且f'(0)=1. 8.讨论函数⎧-x,x≤0⎪f(x)=⎨2x,0<x<1⎪2⎩x+1,x≥1在点x=0和x=1处的连续性与可导性.解 (1)考察x=0处的左、右导数f-'(0)=lim-h→0f(0+h)-f(0)hf(0+h)-f(0)h=lim-h→0-hh2hh=-1, =2,f+'(0)=lim+h→0=lim+h→0所以,函数在x=0处不可导;又limf(x)=limf(x)=0=f(0),所以,函数在x=0处连续. x→0-x→0+(2) 考察x=1处的左、右导数f-'(1)=lim-x→1f(x)-f(1)x-1x-1=lim-x→12x-2x-1=2,f+'(1)=lim+x→1f(x)-f(1)=lim+x→1(x+1)-2x-1=2,所以,函数在x=1处的可导,且f'(1)=2.9.求等边双曲线y=线方程.- 2 -1x在点⎛1⎫,2⎪处的切线的斜率, 并写出在该点处的切线方程和法⎝2⎭解由导数的几何意义,得切线斜率为'1⎛1⎫k=y'x=3= ⎝x⎪⎭x=1/2=-x2x=1/2=-4. 所求切线方程为y-2=-4 ⎛x-1⎫⎝2⎪, 即⎭4x+y-4=0. 法线方程为y-2=1⎛4 x-1⎫⎪, 即⎝2⎭2x-8y+15=0.10.求曲线y=lnx在点(e,1)处的切线与y轴的交点. 解曲线y=lnx在点(e,1)处的切线斜率为k=y'=⎛1x=1 ⎫⎪=1⎝x⎭x=ee故切线方程为y-1=1e(x-e).上式中,令x=0,得y=0.所以,曲线y=lnx在点(e,1)处的切线与y轴的交点为(0,0).习题3-21.求下列函数的导数:(1) y=x2+3x-sinx;(2) y=x(3) s=t+ln2; (4) y=xcosx⋅lnx x(5) y=x+1x-1; (6) y=ex2+1解 (1) y'=2x+3-cosx; (2) y'=(x3)'+2(x-52)'-(x-3)'=3x2+5x-72-3x-4;(3) s'='sint+t)'+0=t;(4) y'=x'cosx⋅lnx+x(cosx)'⋅lnx+xcosx(lnx)'=cosx⋅lnx-xsinx⋅lnx+cosx (5) y'=(x+1)'(x-1)-(x+1)(x-1)'- (x-1)2=2; (x-1)2x(6) y'=eex)'(x2+1)-(x2+1)'exx2+1=((x2+1)2ex(x2+1)-2xex2ex=(x2+1)2=(x-1)(x2+1)2 .2.求下列函数在给定点处的导数:(1) y=xarccosx,求y';x=12(2) ρ=θtanθ+secθ,求dρdθ;θ=π4- 3 -(3) f(x)=lnf'(0).解 (1) y'=x'arccosx+x(arccosx)'=arccosx-1y'=arccos1πx=122-3- (2) dρ2dθ=tanθ+θsecθ+secθtanθdρdθπ=1+ππθ=44⋅2+1=2 (3) f(x)=3x-122ln(e3x+1),f'(x)=332-2(e3x+1)故f'(0)f'(0)=32-32(1+1)=33.曲线y=x3-x+2上哪一点的切线与直线2x-y-1=0平行?解 y'=3x2-1,令y'=2,即3x2-1=2,得x=1或x=-1,代入原曲线方程都有:y=2,故所求点为:(1,2)或(-1,2).4.求下列函数的导数:(1) y=lnsinx; (2) y=(x3-1)10;(3) y=(x+cos2x)3;(4) y=ln(5) y=sin2x⋅sinx2; (6) y=tan[ln(1+x2)] ; x(7) y=2sin1x ; (8)y=elnx;(9)y=ln(x+; (10)y=xa2-x22+a22arcsinxa(a>0)解(1) y'=1sinx⋅(sinx)'=cosxsinx=cotx;(2) y'=10(x3-1)9(x3-1)'=30x2(x3-1)9;(3) y'=3(x+cos2x)2(x+cos2x)'=3(x+cos2x)2(1+2cosx⋅(-sinx))=3(x+cos2x)2(1-sin2x);(4) y=ln=1ln(x-2)-1ln(x2+1)32y'=13(x-2)-1122x2+1(x+1)'=13(x-2)-xx2+1;(5) y'=2sinxcosx⋅sinx2+sin2x⋅cosx2⋅2x=sin2x⋅sinx2+2xsin2x⋅cosx2;- 4 -(6) y'=sec2[ln(1+x2)]⋅[ln(1+x2)]'12x=sec2[ln(1+x2)]⋅2221+x2(1+x)'=1+x2sec[ln(1+x)] ;1(7) y'=2sin11sinxln2⋅(sin1sin xx)'=2ln2⋅cos1x(1 x)'=-2xln2x2 cos1x; xx(8)y'=elnx(x xxx'lnx-x(lnx)' xlnx)' =elnln22eln;x=lnx-1lnx 22 (9)y'= x+'=+'=+(10)y'= 22+2=2+5.已知f(u)可导,求下列函数的的导数:(1) y=f(cscx); (2) y=f(tanx)+tan[f(x)].解 (1) y'=f'(cscx)⋅(cscx)'=-f'(cscx)⋅cscx⋅cotx (2) y'=f'(tanx)⋅(tanx)'+sec2[f(x)]⋅f'(x) =sec2x⋅f'(tanx)+sec2[f(x)]⋅f'(x).习题3-31.求下列由方程所确定的隐函数y=y(x)的导数dydx:(1) x4-y4=4-4xy; (2); ysinx+cos(x-y)=0;(3) ex-ey-sinxy=0;(4) arctanyx=ln.解 (1)方程两边同时对自变量x求导,得4x3-4y3dydx=-4y-4xdydx, (y3-x)dy3dx=x+y,故dydx=x3整理得 +yy3-x;(2) ycosx+sinx⋅dydydx-sin(x-y)⋅(1-dx)=0整理求得dy-y)-ycosxdx=sin(xsin(x-y)+sinx(3) ex-eydydydx-cosxy(y+xdx)=0求得dyxdx=e-ycosxyey+xcosxy- 5 -(4) 1.xy'-y111+(y2x2=2x2+y2(2x+2yy') x)整理求得 xy'-yx+yy'x2+y2=x2+y2故 dyydx=x+x-y.2.求曲线x3+3xy+y3=5在点(1,1)处的切线方程和法线方程. 解方程两边同时对自变量x求导,得3x2+3y+3xy'+3y2y'=0解得 dy+x2dx=-y2, y+x在点(1,1)处,y'(1,1)=-1,于是,在点(1,1)处的切线方程为y-1=-1(x-1),即x+y-2=0,法线方程为 y-1=1(x-1)即y=x.3.用对数求导法求下列各函数的导数dydx:(1) y=xsinx(x>0); (2) y=xa+ax+xx;(3) y= (4) (sinx)y=(cosy)x. 解 (1)等式两边取对数lny=sinx⋅lnx两边对x求导得1yy'=cosx⋅lnx+sinx⋅1x,故 dydx=xsixn⎛ cosx⋅lnx+sinx⋅1⎫⎝x⎪.⎭(2) y'=axa-1+axlna+(xx)'=axa-1+axlna+xx(x⋅lnx+1) (3) y=12[ln(x-1)+ln(x-2)-ln(x-3)-ln(x-4)] 11⎛1111yy'=2 +-2-x-3-⎫⎝x-1xx-4⎪⎭得y'=11⎫+-1-1x-1x-2x-3x-4⎪.⎭(4) ylnsinx=xlncosyy'lnsinx+ycotx=lncosy-xtany⋅y' dydx=lncosy-ycotxxtany+lnsinx4.求下列参数方程所确定的函数的导数dy dx:- 6 -⎧x=t-t2(1) ⎨; (2) ⎧⎨x=acos3θ⎩y=1-t2⎩y=asin3θ. 解 (1) dyy'(t)-2tdx=x'(t)=1-2t (2) dyy'(θ)asin2θ⋅cosθdx=x'(θ)=33acos2θ⋅(-sinθ)=-tanθ5.求椭圆⎨⎧x=6cost⎩y=4sint在t=π4相应点处的切线方程.解 dy(4sint)'dx=y'(t)4cost2x'(t)==-6sint=-3cott.(6cost)'t=π4时,切线斜率为dyπdxt=π=-243,x(4)=y(π4)=.故所求切线方程为y-=-23(x- .习题3-41.求函数y=x2当x由1改变到1.005的微分. 解因为dy=y'dx=2xdx, 由题设条件知 x=1,dx=∆x=1.005-1=0.005 故所求微分为 dy=2⨯1⨯0.00=50 .2.求函数y=sin2x在x=0处的微分. 解所求微分为dy=(sin2x)'x=0dx=2cos2xx=0dx=2dx3.求下列各微分dy:(1) y=e3xcosx; (2) y=sin2xx2;(3) y=ln(1+e-x2);(4) y=arctan(5) exy=3x+y2; (6) xy2+x2y=1. 解 (1) dy=cosxd(e3x)+e3xd(cosx)=cosx⋅3e3xdx-e3x⋅sinxdx=e3x(3cosx-sinx)dx;22xdx2(2) dy=xdsin2x-sin2x2cos2xdx-2xsin2xx4=x4dx=2(xcos2x-sin2x)x3dx; -x2(3) dy=1(1+e-x2)=-2xe1+-x2d1+e-x2dx; (4)dy==12) (1+x- 7 -=;(5)方程两边对求微分exy(xdy+ydx)=3dx+2ydy.整理得 (xexy-2y)dy=(3-yexy)dx 解得 dy=3-yexy; xexy-2ydx(6) 方程两边对求微分y2dx+2xydy+2xydx+x2dy=0.整理得 (2xy+x2)dy=-(y2+2xy)dx 解得 dy=-2xy+y2x2+2xydx4.计算下列各数的近似值: (1) e0.03;(2) 解(1) e0.03≈1+0.03=1.03;(2)===≈2(1-15⋅116)=1.975.5.在下列等式的括号中填入适当的函数, 使等式成立.(1) d()=3dx; (2) d()=2xdx;(3) d()=sinωt dt;(4) d(cosx2)=()d. 解(1) 3x+c;(2) x2+c; (3) -1ωcosωt;(4) d(cosx2)=-2xsinx2dxd=即dx=,x故d(cosx2)=-4x2d.习题3-51.求下列函数的二阶导数:(1) y=x3+8x-cosx; (2) y=(1+x2)arctanx;(3) y=xex2; (4) y=xx.解(1) y'=3x2+8+sinx,y''=6x+cosx;(2) y'=2xarctanx+1,y''=2arctanx+2x1+x2;(3) y'=ex2+2x2ex2,y''=2xex2+4xex2+4x2ex2=2xex2(3+2x2);(4) lny=xlnx,1yy'=lnx+1,y'=xx(lnx+1)y''=(xx)'(lnx+1)+xx(lnx+1)'=xx(1+lnx)2+xx-12. 验证函数y=C2x-3x1e+C2e(其中C1,C2为任意常数)满足方程- 8 -y''+y'-6y=0.证:y'=2C1e2x-3C2e-3x,y''=4C1e2x+9C2e-3x(4C1e2x+9C2e-3x)+(2C1e-3C2e2x-3x)-6(C1e2x+C2e-3x)=0.3.设函数y=f(x)二阶可导,求下列函数的二阶导数: (1) y=f(sinx); (2) y=x2f(lnx). 解 (1)求导数dydx22dydx=f'(sinx)⋅(sinx)'=cosx⋅f'(sinx),于是=(cosx)'⋅f'(sinx)+cosx⋅f''(sinx)⋅(sinx)'=cos2x⋅f''(sinx)-sinx⋅f'(sinx) (2) dydx22dydx=2xf(lnx)+xf'(lnx)=2f(lnx)+2f'(lnx)+f'(lnx)+f''(lnx)=2f(lnx)+3f'(lnx)+f''(lnx).dydx224.对下列方程所确定的函数y=y(x)求(1) ey+xy=e2;(2) ln解 (1)方程两边对x求导:yx=arctan.ey'+y+xy'=0y得 y'=-因此求得dydx22ye+xy.=-y'(e+x)-y(e⋅y'+1)(e+x)-yyyyyy2-yy(e+x)-y(e⋅(e+x)y2yy2y+1)=-=2xy+2ye-ye(e+x)y3;(2) 方程两边对x求导1x+y22(x+yy')=11+yx22xy'-yx2得 y'=因此求得dydx22x+yx-y.=(1+y')(x-y)-(x+y)(1-y')(x-y)2(x+y)(x-y)3222=- 9 -5.对下列参数方程所确定的函数y=y(x)求d2y: dx2 (1) ⎧⎪x=t2-2t⎨⎧x=a(t-sint).⎪⎩y=t3-3t(t≠1); (2) ⎨⎩y=a(1-cost)解(1) dy)t2-33dx=y'(tx'(t)=32t-2=2(t+1).321)'故 dy(t+3; dx2=2t-2=4(t-1)(2) dy'(t)a(1-cost)'dx=yx'(t)==sint1-cost.a(t-sint)'(sint2)'故 dycostdx2=1-a(1-cost)cost(1-cost)-sint⋅sint2=(1-cost)a(1-cost)-1a(1-cost)2(t≠2nπ,n∈Z).6.求下列函数的n阶导数:(1) y=sin2x; (2) y=ln(x+1); (3) y=1(4) x2; -1y=x(x+1)(x+2) (x+n). 解(1) (sin2x)(n)=(1-cos2xn)2)((1-cos2x)'=-12x)=-122⋅2(-sin2⋅2cos⎛π 2x+⎫⎝2⎪,⎭(1+cos2x2)''=-12⋅22⎡-sin⎛π⎫⎤1⎫⎢2⎛ππ⎣ 2x+⎝2⎪⎭⎥=-⋅2cos⎦2 2x++⎝22⎪,⎭(sin2x)(n)=(1+cos2x(n)nπ2)=-2n-1cos(2x+2);(2) [ln(x+1)]'=1x+1[ln(x+1)]''=-1(x+1)2 ,[ln(x+1)](3)=2(x+1)3[ln(x+1)](n)=(-1)n-1(n-1)!(x+1)n; (3) y=11x2-1=12(x-1-1x+1), n故y(n)=(-1)n!⎡11⎤2⎢⎣(x-1)n+1-(x+1)n+1⎥;⎦(4) y=x(x+1)(x+2) (x+n)=xn+1+(1+2+ +n)xn+ - 10 -y(n)=(n+1)!x+n(n+1)2n!=(x+n2)(n+1)!复习题3(A)1.已知f'(x0)=k(k为常数),则 (1) lim=;∆x1(2) limn[f(x0+)-f(x0)]=n→∞n∆x→0f(x0+2∆x)-f(x0)(3) limf(x0+h)-f(x0-2h)hf(x0+2∆x)-f(x0)∆xh→0= .1.解 (1)2k; (2) k; (3) 3k. (1) lim ∆x→0=2limf(x0+2∆x)-f(x0)2∆x∆x→0=2k;(2) limn[f(x0+n→∞1nf(x0+)-f(x0)]=limn→∞1)-f(x0)n=k; 1(3) lim=limf(x0+h)-f(x0-2h)h→0hf(x0+h)-f(x0)h=limnf(x0+h)-f(x0)+f(x0)-f(x0-2h)h-2hh→0h→0+2limh→0f(x0-2h)-f(x0)=3k.2.函数y=f(x)在点x0处的左导数f-'(x0)和右导数f+'(x0)都存在,是f(x)在x0可导的( )A. 充分必要条件;B. 充分但非必要条件;C. 必要但非充分条件;D. 既非充分又非必要条件. 2 .答C. f(x)在x0可导的充分必要条件是f-'(x0)和f+'(x0)都必须存在且相等;反之,f-'(x0)和f+'(x0)都存在,不能保证f(x)在x0可导.3.函数f(x)=sinx在x=0处 ( A. 可导; C. 不连续;)B. 连续但不可导; D. 极限不存在.3.答B. 函数f(x)=sinx在x=0连续;但f-'(0)=-1≠f+'(0)=1,故f(x)=x在x=0不可导.4.设f(x)对定义域中的任意x均满足f(x+1)=mf(x),且f'(0)=n则必有 ( )A. f'(1)不存在;B. f'(1)=m;C. f'(1)=n; 4.答D. f'(1)=limh→0D. f'(1)=mn.hf(1+h)-f(1)=mlimf(h)-f(0)hh=mf'(0)=mnh→0=limmf(h)-mf(0)h→05.解答下列各题: (1)设y=ln2,求y';- 11 -(2) 设y=xa+ax+xx+aa(a>0,a≠1),求dydx;(3)设y=x2⋅f(e2x),f(u)可导,求dy;(4) y=,求dy;dx(5) 求曲线xy-sin(x+y)=0在点(π,0)的切线与法线方程;(6) 已知函数y=y(x)由方程⎧⎨x=acos3tdyd2y⎩y=asin3t 确定,求dx,dx2;(7) 设f'(sinx)=cos2x+cscx,求f''(x);(8) 设y=x3,求x+1y(n)(n≥3).25.解(1)y'='=2x2x⋅cot(2) y'=axa-1+axlna+(xx)' 由对数求导法,可求得(xx)'=xx(1+lnx) 故y'=axa-1+axlna+xx(1+lnx);(3) dy=2xdx⋅f(e2x)+x2⋅f'(e2x)de2x=2xf(e2x)dx+x2⋅f'(e2x)⋅2e2xdx =2x[f(e2x)+xe2x⋅f'(e2x)]dx;(4)取对数 lny=1⎡2⎢xlnb+b(lna-lnx)+a(lnx-lnb)⎤⎣a⎥⎦两边求导 11⎛bbayy'=2 ln-+⎫⎝axx⎪⎭故y'=1⎛ba-b2 ln+⎫⎝ax⎪⎭(5) 两边求导y+xy'-cos(x+y)(1+y')=0 得y'=cos(x+y)-y,故1x-cos(x+y)y'(π,0)=-π+1 因此切线方程为 y=-1π+1(x-π),法线方程为y=(π+1)(x-π); (6) dy)3asin2t⋅costdx=y'(tx'(t)=3acos2t⋅(-sint)=-tant d2y(-tant)'-sec2tsec4tdx2=3acos2t⋅(-sint)=3acos2t⋅(-sint)=3asint;(7) 由f'(sinx)=cos2x+cscx=1-2sin2x+1sinx 知f'(x)=1-2x2+1x故f''(x)=-4x-1x2;- 12 -(8) y=y(n)x3x+1n+1=x-1+1x+13=x-x+1+21x+1=(-1)⋅n!n(x+1)(n≥3).⎧ax+b,x<16.设函数f(x)=⎨2 在x=1处可导,求a,b的值.x≥1⎩x,6.解:因可导必连续,所以lim-(ax+b)=lim+x=1,得a+b=1x→1x→12考察x=1处的左、右导数f-'(1)=lim-x→1f(x)-f(1)x-1f(x)-f(1)x-1=lim-x→1ax+b-1x-1=lim-x→1ax-ax-1=af+'(1)=lim+x→1=lim+x→1x-1x-12=2,所以,得到a=2,b=-1.7. 设函数g(x)在x=a点连续, 且f(x)=(x-a)g(x), 证明f(x)在x=a的可导,并求出f'(a).7.证:因g(x)在x=a点连续,故limg(x)=g(a),x→a又limf(x)-f(a)x-ax-a故f(x)在x=a的可导,f'(a)=g(a) x→ax→a=lim(x-a)g(x)-0=limg(x)=g(a)x→a8.验证函数y=C11+C2e其中C1,C2为任意常数)满足方程4xy''+2y'-y=0.8.证:因y'=y''=-C1-C2e, (C1C1-C2e+14x+C2e故4xy''+2y'-y=4x⎢- ⎣+2C1(4C1e2x⎡C1-C2e+14x(C1+C2e⎤⎥⎦-C2e⎤⎥-C1⎦(+C2e=02x+9C2e-3x)+(2C1e-3C2e2x-3x)-6(C1e+C2e-3x)=0.(B)1. 设函数f(x)在x=0连续,下列命题错误的是( ) A. 若limB. 若lim f(x)xf(x)xx→0存在,则f(0)=0;存在,则f'(0)存在;x→0C. 若limf(2x)+f(x)xf(x)-f(-x)xx→0存在,则f(0)=0;存在,则f'(0)存在.D. 若limx→01.答:D.- 13 -A.正确,因为limf(0)=x→0f(x)xx→0存在,则limfx()=,0又f(x)在x=0连续,所以x→0limfx();= 0f(x)B.正确,因为若limC.正确,因若limx→0x→0xf(2x)+f(x)xx→0存在,则f'(0)=limx→0f(x)-f(0)x=limf(x)x存在;x→0存在,x→0x→0则lim[f(2x)+f(x)]=limf(2x)+limf(x)=2f(0)=0,故f(0)=0; D.错,如f(x)=x, lim2. 若f(t)=limt(1+x→∞f(x)-f(-x)xx→02tx=0,但f'(0)不存在.1x),则f'(t)= .1x)2tx2. (1+2t)e2t,f(t)=limt(1+x→∞=te,所以f'(t)=(te)'=(1+2t)e.f(1)-f(13x-)x=1,则曲线y=f(x)2t2t2t3.设周期函数f(x)在(-∞,∞)周期为3,且lim在点(4,f(4))的切线斜率为 . 3. -3,f'(4)=lim=limf(x+4)-f(4)x=-3limx→0x→0x→0=limf(x+1)-f(1)x=-3,x→0=-limf(1)-f(x+1)xx→0=f(1)-f(1-t)-tf(1)-f(1-x)x→04. 已知f(x)=3x(x-1)(x-2) (x-10)(x+1)(x+2) (x+10)f(x)-f(1),求f'(1).(x-1)(x-2) (x-10)4. 解:f'(1)=limx-11-1⋅(-2) (-9)=- =lim=x→1(x+1)(x+2) (x+10) 110 2⋅3 9⋅10⋅11 x-1(x-2) (x-10)x→1=lim(x+1)(x+2) (x+10)x→15.设f'(a)存在,求limxf(a)-af(x)x-axf(a)-af(x)xf(a)-af(a)+af(a)-af(x)=lim5. 解:limx→ax→ax-ax-af(x)-f(a)=f(a)-alim=f(a)-af'(a)x→ax-ax→a.6.设f(x)=max{x6.解:f(x)=max{x,在区间(0,2)内求f'(x).0<x≤1, =1<x<2⎪⎩x,f(x)-f(1)x-1考察x=1处的左、右导数f-'(1)=lim-x→1=lim-x→1x-1=lim-x→1=12,- 14 -f+'(1)=lim+x→1f(x)-f(1)x-1=lim+x→1x-1x-1=1,所以,函数在x=1处不可导.故所求导数为:⎧⎪0<x<1' f(x)=⎨1<x<2⎪⎩1,7. 设函数g(x)在x=x0点连续, 且f(x)=x-ag(x), 讨论f(x)在x=x0的可导性. 7. 解:f'(x0)=limf(x)-f(x0)x-x0x→x0x→x0=limx-x0g(x)x-x0x→x0(1)若g(x0)≠0,则g(x0)limx-x0x-x0不存在,此时f(x)在x=x0不可导=0,此时f(x)在x=x0可导.(2)若g(x0)=0,则 f'(x0)=limx-x0g(x)x-x0x→x08. 验证下列命题:(1) 若定义在(-∞,∞)内以周期为T的周期函数f(x)可微,则f'(x)也是以周期为T的周期函数.(2) 若函数f(x)在(-a,a)内是可微奇(偶)函数,则f'(x)(-a,a)内必为偶(奇)函数. 8. 证: (1)因f(x+T)=f(x),又f'(x)=limf(x+h)-f(x)h→0f'(x+T)=limhf(x+T+h)-f(x+T)h,因此h→0=limf(x+h)-f(x)hh→0=f'(x)(2) 若函数f(x)在(-a,a)内是可微奇函数,则有f'(-x)=lim=limf(-x+h)-f(-x)hh→0=lim-f(x-h)+f(x)hh→0f(x-h)-f(x)-hh→0=f'(x),即证得:若函数f(x)在(-a,a)内是可微奇函数,则f'(x)(-a,a)内必为偶函数. 同理可证得:若函数f(x)在(-a,a)内是可微偶函数,则f'(x)(-a,a)内必为奇函数.9. 设函数f(x)可微,且f(x+y)=f(x)+f(y)-2xy,f'(0)=3,求f(x). 9. 解:由f(x+y)=f(x)+f(y)-2xy,令x=y=0,则f(0)=f(0)+f(0),得f(0)=0f'(x)=lim=limf(y)yf(x+y)-f(x)yy→0=limf(x)+f(y)-2xy-f(x)yy→0y→0-2x=f'(0)-2x=3-2x22因此f(x)=3x-x+C(C为任意常数),又f(0)=0则C=0,故f(x)=3x-x 10. 设在(-∞,∞)内函数f(x)有定义, 且f(0)=0,f'(0)=C(C≠0),又g(x)=esinx+x2co, sx对任意x,y有关系式f(x+y)=f(x)g(y)+f(y)g(x)成立,证明f'(x)=C⋅g(x)10. 证:f'(x)=limf(x+y)-f(x)yy→0=limf(x)g(y)+f(y)g(x)-f(x)yy→0- 15 -=f(x)limg(y)-1yyy→0+g(x)limf(y)yf(y)-f(0)y y→0=f(x)limg(y)-g(0)y→0+g(x)limy→0=f(x)g'(0)+g(x)f'(0) 又 g'(x)=exsin2x+exsin2x-sinx,得g'(0)=0 故f'(x)=C⋅g(x).- 16 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 导数与微分习题答案练习题3.11. 根据导数定义,求下列函数的导数: (1)12+=x y ,求1='x y 。
解:111|x x x y =→→'===(2)()ln f x x =,求()f x '。
解:()()100ln ln 1limlim ln 1xx x x x x x f x x x x∆∆→∆→∆+-∆⎛⎫'==+=⎪∆⎝⎭。
2. 求抛物线22y x =在点()2,8-处的切线方程和法线方程。
解:在()2,8-处的切线斜率为2|8x y =-'=-,法线斜率为18, 在()2,8-处的切线方程为88y x =--;法线方程为13384y x =+。
3. a 为何值时,2y ax =与ln y x =相切?解:设2y ax =与ln y x =在0x 相切,则有0020012ln ax x ax x⎧=⎪⎨⎪=⎩,解得 12a e =。
4. 试求出曲线1y x x=-与x 轴交点处的切线方程。
解:曲线1y x x=-与x 轴的交点为()1,0,()1,0-;切线斜率为1|2x y =±'=, 切线方程为()21y x =±。
5. 讨论()ln 1,10()01x x f x x +-<≤⎧⎪=<<在0x =处的连续性和可导性。
解:由于()0lim ln 10x x -→+=,0lim 0x +→=,(0)0f =,则()f x 在0x =处连续。
又()0ln 1(0)lim 1x x f x--→+'==,0(0)lim 1x f ++→'==,(0)(0)1f f -+''==, 所以 ()f x 在0x =处可导且'(0)1f =。
6. 讨论21,021,01()2,12,2x x x f x x x x x ≤⎧⎪+<≤⎪=⎨+<≤⎪⎪>⎩ 分别在0x =,1x =,2x =处的连续性与可导性,并求出()f x '。
解:在0x =处,0lim 11x -→=,()0lim 211x x +→+=,()01f =,故()f x 在0x =处连续。
又011(0)lim 00x f x --→-'==-,0211(0)lim 20x x f x ++→+-'==-,故()f x 在0x =处不可导。
在1x =处,()1lim 213x x -→+=,()21lim 23x x +→+=,()13f =,故()f x 在1x =处连续。
又()12131lim 21x x f x --→+-'==-,()21231lim 21x x f x ++→+-'==-,故()f x 在1x =处可导。
在2x =处,()22lim 26x x -→+=,2lim 2x x +→=,则()f x 在2x =处不连续,从而()f x 在2x =处不可导。
且 ()0,02,012,121,2x x f x x x x <⎧⎪<≤⎪'=⎨<<⎪⎪>⎩ 。
练习题3.21. 求下列函数的导数(其中,a b 为常量):(1)101010lg 10xy x x =+++: 9110ln1010ln10x y x x '=++(2)(2)a b y u+=:()212a b y a b u+-'=+(3)3333x y x =+:249y x x'=- (4)3y =:153322225122y x x x x --'⎛⎫'=-=-- ⎪⎝⎭(5)2()(21)f t t t =-:2()62f t t t '=-(6)y =718878y x x -'⎛⎫'== ⎪⎝⎭2. 求下列函数在指定点的导数:(1)已知()ln 2cos 7f x x x x =+-,求2f π⎛⎫'⎪⎝⎭,()f π'。
解:1()2sin 7f x x x '=--,292f ππ⎛⎫'=- ⎪⎝⎭,1()7f ππ'=-。
(2)已知1()sin x x x ϕ=+,求2πϕ⎛⎫'- ⎪⎝⎭,2πϕ⎛⎫' ⎪⎝⎭。
解:21()cos x x x ϕ'=-+,2422ππϕϕπ⎛⎫⎛⎫''-==- ⎪ ⎪⎝⎭⎝⎭。
练习题3.31. 求下列函数的导数:(1)2(23y x =+223326296x xa x x y +--'==(2)(log a y x =+:1y ⎛'== ⎝ (3)y =:y ''==(4)22sin sin xy x =:()22222sin 2sin 2cos sin sin x x x x x y x -'= (5)ln ln ln y x =:()11ln ln ln ln ln ln ln y x x x x x''=⋅=⋅ (6)ln tan 2x y =:21111tan sec csc 222sin tan tan 22x x y x x x x '⎛⎫'=⋅=⋅⋅== ⎪⎝⎭(7)21siny x x =:22111112sin cos 2sin cos y x x x x x x x x'=-⋅=- (8)2arcsin 2x y ⎛⎫= ⎪⎝⎭:arcsin 2x y '=(9)y =21ln x y '+'==(10)2sin()()ax bx c g x e++=:()()2sin()2()cos 2axbx c g x eax bx c ax b ++'=⋅++⋅+(11)y =1111111222y x y y y ⎡⎤⎡⎤⎡⎤'''=⋅+=⋅++=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(12)()23sin cosy xx ⎡⎤=+⎣⎦:()()()233322cos cos ()cos sin 31y x x x x x x x '⎡⎤=-+⋅+⋅+⋅+⎣⎦2. 若函数()2()f x x a ϕ=,且()()1ln f x f x a'=⋅,求()x ϕ'。
解:()()()()()222()()()1ln 2ln 22ln f x fx f x x aa f x f x a a f x a f x aϕ''=⋅⋅=⋅⋅=⋅。
3. 证明:(1)可导的偶函数的导数是奇函数。
证明:设()f x 为偶函数且可导,则有()()f x f x =-,两边对x 求导,有()()()()1f x f x f x '''=-⋅-=--,即 ()()f x f x ''-=-,得证。
(2)可导的奇函数的导数是偶函数。
证明:设()f x 为奇函数且可导,则有()()f x f x -=-,两边对x 求导,有()()()1f x f x ''-⋅-=-,即 ()()f x f x ''-=,得证。
(3)可导的周期函数的导数是具有相同周期的周期函数。
证明:设()f x 为可导周期函数,周期为T ,则有()()f x T f x +=,两边再对x 求导, 得到()()f x T f x ''+=,得证。
4. 设()f x 在0x =处连续,且()limx f x x→=A (A 为常数),证明:()f x 在0x =处可导。
证明:由于()f x 在0x =处连续,则()()0lim 0x f x f →=,又因为()0limx f x x→=A ,极限存在,则必有()0lim 0x f x →=,即()00f =,从而()()()000limlim 0x x f x f f x x x→→-==A -,即()f x 在0x =处可导。
5. 求下列隐函数的导数:(1)3330x axy y -+=:()223330x a y xy y y ''-++=,22ay x y y ax-'=-(2)ln ln 0x y y x +=:ln ln 0y y y x y x y x''+⋅++=,2'2ln ln y xy y y x xy x --=+6. 利用对数求导法求下列函数的导数:(1)2y =)1ln 2y x y''=,ln 22122x y y x x +⎫'=+=⎪⎭(2)()()cos sin sin 0xy x x =>:()1cos ln sin y x x y''=⋅, ()()cos 1'22cos sin ln sin cos sin sin ln sin cos sin x x y y x x x x x x x x -⎛⎫=-⋅+=-⋅+ ⎪⎝⎭(3)y x =()()111ln ln 1ln 122y x x x y '⎡⎤'=+--+⎢⎥⎣⎦;()()1112121y y x x x ⎡⎤'=--⎢⎥-+⎣⎦ (4)21x y x=- ()()()112ln ln 1ln 3ln 32y x x x x y '⎡⎤'=--+--+⎢⎥⎣⎦()21111233y y x x x x ⎡⎤'=+--⎢⎥--+⎣⎦7. 求下列函数的高阶导数: (1)()2ln 1y x =-,求y ''。
解:221xy x '=--,22222(1)x y x --''=-。
(2)()2y f x b =+,求y ''。
解:()22y f x b x ''=+⋅,()()()()2222222242y xf x b x f x b x f x b f x b ''''''''=+⋅++=+++。
(3)arcsin y x =,求y ''。
解:y '=,y ''=(4)22arctan1xy x=-,求y ''。
解()()()2222222222222112224211214111x x x x y x x x x x x x '--+⎛⎫'=⋅=⋅= ⎪-+⎝⎭⎛⎫-+-+ ⎪-⎝⎭ ()241xy x ''=-+。
