江苏省南通市海门市包场高中届高三数学上学期9月调研试卷(含解析)【含答案】
高三上学期9月联考数学试题及答案

高三上学期9月联考数学试题一、单项选择题:本大题共8小题,每小题5 分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合A =x x 2-x -2≤0 ,B =x y =x -1 ,则A ∪B =()A.1,2B.-1,+∞C.-1,1D.1,+∞2.已知角θ的终边经过点P 32,-12,则角θ可以为()A.5π6B.2π3C.11π6D.5π33.已知A ,B 为两个随机事件,P A ,P B >0,则“A ,B 相互独立”是“P A B =P A B”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.衡量曲线弯曲程度的重要指标是曲率,曲线的曲率定义如下:若f x 是f x 的导函数,f x 是f x 的导函数,则曲线y =f x 在点x ,f x 处的曲率K =fx1+fx 232.已知f x =ln x -cos x -1 ,则曲线y =f x 在点1,f 1 处的曲率为()A.0B.24C.22D.25.已知函数f x =2sin ωx +φ ω>0,0<φ<π2 的部分图象如图,f x 1 =f x 2 =-32,则cos π6x 2-x 1 =()A.-34B.-74C.34D.746.已知(mx +1)n n ∈N *,m ∈R 的展开式只有第5项的二项式系数最大,设(mx +1)n =a 0+a 1x +a 2x 2+⋯+a n x n ,若a 1=8,则a 2+a 3+⋯+a n =()A.63B.64C.247D.2557.已知tan α,tan β是方程ax 2+bx +c =0a ≠0 的两根,有以下四个命题:甲:tan α+β =-12;乙:tan αtan β=7:3;丙:sin α+β cos α-β =54;丁:tan αtan βtan α+β -tan α+β =5:3.如果其中只有一个假命题,则该命题是()A.甲B.乙C.丙D.丁8.已知函数f x =ax ln x -x 2+3-a x +1a ∈R ,若f x 存在两个极值点x 1,x 2x 1<x 2 ,当x 2x 1取得最小值时,实数a 的值为()A.0B.1C.2D.3二、多项选择题:本大题共4个小题,每小题5分,共20分。
2022届江苏省南通市高三上学期9月第一次教学质量监测数学试题(word版含答案)

3.某亲子栏目中,节目组给6位小朋友布置一项搜寻空投食物的任务.已知:①食物投掷点有远、近两处;②由于小朋友甲年纪尚小,所以要么不参与该项任务,要么参与搜寻近处投掷点的食物,但不参与时另需1位小朋友在大本营陪同;③所有参与搜寻任务的小朋友被均匀分成两组,一组去远处,一组去近处.那么不同的搜寻方案有()
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知集合 ,则 ()
A. B. 或
C. D. 或
【答案】B
2.已知复数 ,则 在复平面内对应的点所在的象限为()
A.第一象限B.第二象限C.第三象限D.第四象限
C.若 D.若 ,则 与平行
【答案】BD
11.若二项式 展开式中二项式系数之和为 ,展开式的各项系数之和为 ,各项系数的绝对值之和为 ,则下列结论正确的是()
A.
B.存在 ,使得
C. 的最小值为2
D.
【答案】AB
12.“阿基米德多面体”也称为半正多面体(semi-regularsolid),是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图所示,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形、六个面为正方形的一种半正多面体.已知 ,则关于如图半正多面体的下列说法中,正确的有()
A.该半正多面体的体积为
B.该半正多面体过 三点的截面面积为
C.该半正多面体外接球的表面积为
D.该半正多面体的顶点数 、面数 、棱数 满足关系式
【答案】ACD
三、填空题:本题共4小题,每小题5分,共20分
13.已知 ,则实数 的取值分别为______.
2021届江苏省海门中学高三上学期9月学情调研化学试卷
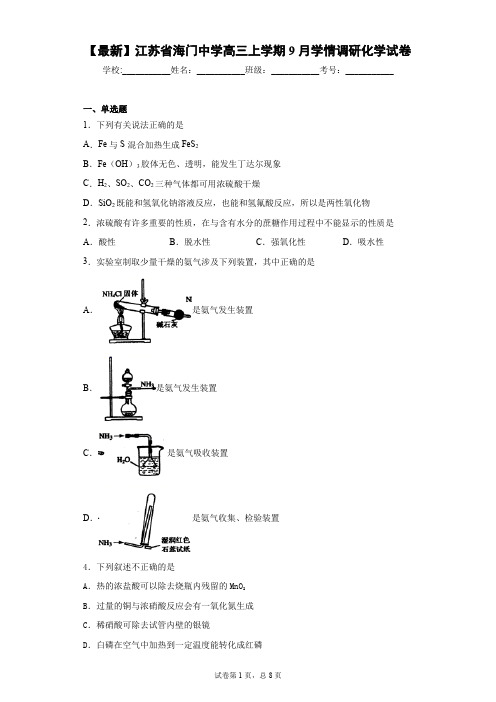
【最新】江苏省海门中学高三上学期9月学情调研化学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列有关说法正确的是A.Fe与S混合加热生成FeS2B.Fe(OH)3胶体无色、透明,能发生丁达尔现象C.H2、SO2、CO2三种气体都可用浓硫酸干燥D.SiO2既能和氢氧化钠溶液反应,也能和氢氟酸反应,所以是两性氧化物2.浓硫酸有许多重要的性质,在与含有水分的蔗糖作用过程中不能显示的性质是A.酸性B.脱水性C.强氧化性D.吸水性3.实验室制取少量干燥的氨气涉及下列装置,其中正确的是A.是氨气发生装置B.是氨气发生装置C.是氨气吸收装置D.是氨气收集、检验装置4.下列叙述不正确的是A.热的浓盐酸可以除去烧瓶内残留的MnO2B.过量的铜与浓硝酸反应会有一氧化氮生成C.稀硝酸可除去试管内壁的银镜D.白磷在空气中加热到一定温度能转化成红磷5.下列关于物质或离子检验的叙述正确的是A.在溶液中加KSCN,溶液显红色,证明原溶液中有Fe3+,无Fe2+B.气体通过无水硫酸铜,粉末变蓝,证明原气体中含有水蒸气C.灼烧白色粉末,火焰成黄色,证明原粉末中有Na+,无K+D.将气体通入澄清石灰水,溶液变浑浊,证明原气体是CO26.下列溶液中通入SO2一定不会产生沉淀的沉淀的是A.Ba(OH)2 B.Ba(NO3)2 C.Na2S D.BaCl27.下列叙述正确的是A.Fe分别与氯气和稀盐酸反应所得氯化物相同B.Al、Fe、Cu三者的单质放置在空气中均只生成氧化物C.Al、Fe、Cu三者对应的氧化物均为碱性氧化物D.C、P、S、Cl的最高价氧化物对应水化物的酸性逐渐增强8.下列各选项中,不能利用置换反应通过Y得到W的一组化合物是A.A B.B C.C D.D 9.高铁酸钾(K2FeO4)是一种新型的自来水处理剂,它的性质和作用是A.有强氧化性,可消毒杀菌,还原产物能吸附水中杂质B.有强还原性,可消毒杀菌,氧化产物能吸附水中杂质C.有强氧化性,能吸附水中杂质,还原产物能消毒杀菌D.有强还原性,能吸附水中杂质,氧化产物能消毒杀菌10.NaCl是一种化工原料,可以制备一系列物质。
江苏海门中学2025届高三上学期第一次调研考试数学试题+答案

2024/2025学年度高三第一次调研测试数学2025.09一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“ x ∀∈N ,20x >”的否定为( ) A . x ∀∈N ,20x ≤ B . x ∃∈N ,20x ≤ C . x ∃∈N ,20x >D . x ∀∈N ,20x <2.已知集合{}||2,A x x x =<∈Z ,(){}2ln 3B x y x x ==−,则A B = ( ) A .{}02x x <<B .{}23x x −<<C .{1}D .{0,1,2}3.已知点(3,4)P −是角α终边上一点,则cos2α=( ) A .725B .725−C .2425D .2425−4.已知函数1,12()1,12xa x f x x x+≤ = > 在R 上单调递减,则实数a 的取值范围为( ) A .0a < B .12a >−C .102a −<< D .102a ≤<5.已知函数()f x 部分图象如图所示,则其解析式可能为( )A .()2()e e x x f x x −=− B .()2()e e x x f x x −=+ C .()()e e x x f x x −=−D .()()e e x x f x x −=+6.过点(3,1)作曲线ln(1)y x =−的切线,则这样的切线共有( ) A .0条B .1条C .2条D .3条7.锐角α、β满足sin cos()sin βαβα=+,若1tan 2α=,则cos()αβ+=( )A .12BCD. 8.若函数2()sin 20)f x x x ωωω=−+>在0,2π上只有一个零点,则ω的取值范围为( ) A .14,33B .14,33C .17,66D .17,66二、选择题:本题共3小题,每小题6分,共18分。
2024-2025学年江苏省南通市高三(上)调研数学试卷(9月份)(含答案)

2024-2025学年江苏省南通市高三(上)调研数学试卷(9月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A,B,若A={−1,1},A∪B={−1,0,1},则一定有( )A. A⊆BB. B⊆AC. A∩B=⌀D. 0∈B2.已知命题p:∀x∈R,|x+1|>1,命题q:∃x>0,x3=x,则( )A. p和q都是真命题B. ¬p和q都是真命题C. p和¬q都是真命题D. ¬p和¬q都是真命题3.函数f(x)=(e x+e−x)sinx−2x在区间[−2,2]的大致图象为( )A. B. C. D.4.设α是空间中的一个平面,l,m,n是三条不同的直线,则( )A. 若m⊂α,n⊂α,l⊥m,l⊥n,则l⊥αB. 若l//m,m//n,l⊥α,则n⊥αC. 若l//m,m⊥α,n⊥α,则l⊥nD. 若m⊂α,n⊥α,l⊥n,则l//m5.在正三棱台ABC−A1B1C1中,AB=4,A1B1=2,A1A与平面ABC所成角为π4,则该三棱台的体积为( )A. 523B. 283C. 143D. 736.设a=2π,b=log2π,c=π,则( )A. c<b<aB. b>c>aC. a>c>bD. a>b>c7.若函数f(x)={log2(x+1),−1<x≤3x+ax,x>3,在(−1,+∞)上单调递增,则a的取值范围是( )A. [−3,9]B. [−3,+∞)C. [0,9]D. (−∞,9]8.设函数f(x)=(x2+ax+b)lnx,若f(x)≥0,则a的最小值为( )A. −2B. −1C. 2D. 1二、多选题:本题共3小题,共18分。
在每小题给出的选项中,有多项符合题目要求。
9.下列函数中最小值为4的是( )A. y=lnx+4lnxB. y=2x+22−xC. y=4|sinx|+1|sinx|D. y=x2+5x2+110.定义在R上的偶函数f(x),满足f(x+2)−f(x)=f(1),则( )A. f(1)=0B. f(1−x)+f(1+x)=0C. f(1+2x)=f(1−2x)D. ∑20i=1f(i)=1011.在正方体ABCD−A1B1C1D1中,M,N分别为AC,A1B的中点,则( )A. MN//平面ADD1A1B. MN⊥AC1C. 直线MN与平面AA1C1C所成角为π4D. 平面MND1经过棱A1B1的三等分点三、填空题:本题共3小题,每小题5分,共15分。
江苏省南通市2025届高三上学期九月份调研测试数学试题及参考答案

江苏省南通市2025届高三上学期九月份调研测试数学试题及参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}11,-=A ,{}101,,-=B A ,则()A.BA ⊆ B.AB ⊆ C.ϕ=B A D.B ∈02.已知命题11,>+∈∀x R x p :;命题x x x q =>∃3,0:,则()A.p 和q 都是真命题B.p ⌝和q 都是真命题C.p 和q ⌝都是真命题D.p ⌝和q ⌝都是真命题3.函数()()x x ee xf xx2sin -+=-在区间[]2,2-的大致图象为()4.设α是空间中的一个平面,n m l ,,是三条不同的直线,则下列说法正确的是()A.若n l n m ⊥⊥⊂,,αα,则m l ∥B.若m l ∥,n m ∥,α⊥l ,则α⊥nC.若m l ∥,α⊥m ,α⊥n ,则n l ⊥D.若n l m l n m ⊥⊥⊂⊂,,,αα,则α⊥l 5.在正三棱台111C B A ABC -中,2411==B A AB ,,A A 1与平面ABC 所成角为4π,则该三棱台的体积为()A.352 B.328 C.314 D.376.设π2=a ,π2log =b ,π=c ,则()A.ab c << B.ac b >> C.bc a >> D.cb a >>7.若函数()()⎪⎩⎪⎨⎧>+<<-+=3,31,1log 2x x ax x x x f ,在()∞+-,1上单调递增,则a 的取值范围是()A.[]93,- B.[)∞+-,3 C.[]9,0 D.(]9,∞-8.设函数()()x b ax x x f ln 2++=,若()0≥x f ,则a 的最小值为()A.2- B.1- C.2D.1二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,由多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列函数中最小值为4的是()A.xx y ln 4ln += B.xxy -+=222C.xx y sin 1sin 4+= D.1522++=x x y 10.定义在R 上的偶函数()x f ,满足()()()12f x f x f =-+,则()A.()01=f B.()()011=++-x f x f C.()()x f x f 2121-=+ D.()10201=∑=i i f 11.在正方体1111D C B A ABCD -中,N M ,分别为B A AC 1,的中点,则()A.∥MN 平面11A ADD B.1AC MN ⊥C.直线MN 与平面C C AA 11所成角为4πD.平面1MND 经过棱11B A 的三等分点三、填空题:本题共3小题,每小题5分,共15分.12.“0>xy ”是“y x y x +=+”的.(在“充分不必要条件”,“必要不充分条件”,“充要条件”,“既不充分又不必要条件”中选择一个填空)13.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的侧面积为.14.已知ba323+=,则b a -2的最小值为.四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,在直三棱柱111C B A ABC -中,F E D ,,分别为B B BC AB 1,,的中点.(1)证明:∥11C A 平面DE B 1;(2)若1=AB ,AC AB ⊥,F A D B 11⊥,求点E 到平面11FC A 的距离.16.(本小题满分15分)已知函数()xxx f +-=11log 2.(1)判断并证明()x f 的奇偶性;(2)若对任意⎥⎦⎤⎢⎣⎡-∈31,31x ,[]2,2-∈t ,不等式()62-+≥at t x f 恒成立,求实数a 的取值范围.17.(本小题满分15分)如图,四边形ABCD 为菱形,⊥PB 平面ABCD .(1)证明:平面⊥P AC 平面PBD ;(2)若PC P A ⊥,二面角C BP A --的大小为120°,求PC 与BD 所成角的余弦值.18.(本小题满分17分)设函数()cx bx ae x f x++=2.(1)若1=a ,1-==c b ,求证:()x f 有零点;(2)若0=a ,1-=b ,是否存在正整数n m ,,使得不等式()n c x f m ≤-≤的解集为[]n m ,,若存在,求n m ,;若不存在,说明理由.(3)若0≠b ,非空集合(){}()(){}00=∈==∈x f f R x x f R x ,求c a +的取值范围.19.(本小题满分17分)已知有限集{}()N n n a a a A n ∈≥=,2,,,21 ,若n n a a a a a a 2121=+++,则称A 为“完全集”.(1)判断结合{}222,1221+---,,是否为“完全集”,并说明理由;(2)若集合{}b a ,为“完全集”,且b a ,均大于0,证明:b a ,中至少有一个大于2;(3)若A 为“完全集”,且*N A ⊆,求A .参考答案一、单选题1.D 解析:∵{}11,-=A ,{}101,,-=B A ,∴B ∈0.2.B解析:命题p :0=x 时,11=+x ,假命题;命题q :0=x 或1或1-,真命题,则p ⌝和q 都是真命题.3.C解析:()x f 为奇函数,图象关于原点对称,排除AB,2π=x 时,0222>-⎪⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-ππππe e f ,排除D,故选C.4.B解析:αα⊥⊂n m ,,则n m ⊥,又n l ⊥,m 与l 可能相交,A 错.m l ∥,n m ∥,则n l ∥,α⊥l ,则α⊥n ,B 正确.5.C解析:延长111CC BB AA ,,交于S 点,1AA 与平面ABC 所成角为SAO ∠,∴SO AO =,而3344233232=⋅⋅==AD AO ,3321=OO ,34234421=⨯⨯⨯=∆ABC S ,3232221=⨯⨯⨯=∆ABC S ,()3143323233431=⨯++⨯=V .6.C解析:22>=πa ,()2,1log 2∈=πb ,()2,1∈=πc ,a 最大.设()x x x f ln =,则()2ln 1xxx f -=',令()0='x f ,解得e x =,∴()x f 在()e ,0上单调递增,在()+∞,e 上单调递减,∵e <<2π,∴()()2f f <π,即22ln ln <ππ,即22ln 2ln <ππ,∴2ln ln <ππ∴ππ<2ln ln ,即ππ<2log ,即c b <,∴b c a >>.7.A解析:∵()x f 在()∞+,3上单调递增,∴()012≥-='x ax f 在()∞+,3上恒成立,∴9≤a ,∵()x f 在()∞+-,1上单调递增,∴()3313log 2a+≤+,∴3-≥a ,综上,a 的取值范围是[]93,-.8.B解析:∵()0≥x f 恒成立,则1是02=++b ax x 的根,即01=++b a ,∴ab --=1则()()()()x a x x x b ax x x f ln 11ln 2++-=++=,∵01≥++a x ,∴01≥+a ,即1-≥a ,∴a 的最小值为1-.二、选择题9.BCD解析:选项A,()1,0∈x 时,0ln 4ln <+=xx y ,A 错误;选项B,4222222=≥+=-xxy ,当且仅当x x -=222,即1=x 时“=”成立.B 正确;选项C,242sin 1sin 4=≥+=x x y ,当且仅当xx sin 1sin 4=,即21sin ±=x 时“=”成立,C 正确;选项D,4421411412222=≥+++=+++=x x x x y ,当且仅当14122+=+x x ,即32=x 时“=”成立.D 正确.10.AC解析:当1-=x 时,()()()111f f f =---,∴()()011==-f f ,A 正确;∴()()02=-+x f x f ,即()()x f x f -=+2,即()x f 关于1=x 对称,则()()x f x f +=-11,∴B 错,C 对;()()x f x f =+2,则()x f 的周期为2,无法判断()0f 的值,()10201=∑=i i f 的值无法判断,故D 错.11.ABD解析:∵M 分别为AC 的中点,∴M 也是BD 中点,又N 分别为B A 1的中点,∴MN 为D BA 1∆的中位线,则D A MN 1∥,又⊂D A 1平面11A ADD ,⊄MN 平面11A ADD ,∴∥MN 平面11A ADD ,故A 正确;如图建系,设正方体的边长为1,则()()11000,11,,,,C A ,()()0001011,,,,,D A∴()1111,,-=AC ,()1011--=,,D A ,∴011=⋅AC D A ,即11AC D A ⊥,∴1AC MN ⊥,B 正确;平面C C AA 11的垂线为BD ,而D A 1与BD 所成角为3π,∴直线MN 与平面C C AA 11所成角为6π,C 错误;()10021,2110,21,211,,,,,D N M ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛,则⎪⎭⎫ ⎝⎛=210,21,MN ,⎪⎭⎫⎝⎛-=21,21,11N D ,设平面1MND 的法向量为()c b a n ,,= ,则⎪⎪⎩⎪⎪⎨⎧=-+=⋅=+=⋅02121021211c b a N D n c a MN n,不妨设1=a ,则1,3-=-=c b ,∴()1,3,1--=n,11B A 靠近1A 的三等分点⎪⎭⎫ ⎝⎛1311,,P ,则⎪⎭⎫⎝⎛=0,3111,P D ,∴01=⋅n P D ,∈P 平面1MND ,D 正确.三、填空题12.充分不必要解析:∵0>xy ,∴y x ,同号,∴y x y x +=+,∴是充分条件,由y x y x +=+,则0≥xy ,∴是不必要条件,∴“0>xy ”是“y x y x +=+”的充分不必要条件.13.π3解析:球的直径为2,半径为1,设圆柱底面圆半径为r ,∴1412=+r ,∴23=r ,∴ππ312=⋅=r S 侧.14.8log 3解析:方法一:()ba 32log 3+=,∴()()b b b a bb-+⋅=-+=-3ln 32ln 232log 223,令()()x x f x-+⋅=32ln 3ln 2,则()23233232321323ln 33ln 2+-=+--⋅=-+⋅⋅='xx xx x x x x f ,令()0='x f ,解得2log 3=x ,∴()x f 在()2log 3,∞-上单调递减,在()∞+,2log 3上单调递增,∴()()8log 2log 4ln 3ln 22log 333=-⋅=≥f x f .方法二:由bba322323⋅≥+=可得:b a3832⋅≥,可得832≥-ba ,∴8log 23≥-b a ,当且仅当2log 3=b ,4log 3=a 时“=”成立.∴b a -2的最小值为8log 3.四、解答题15.解:(1)证明:∵E D ,分别为BC AB ,的中点,∴AC DE ∥.又∵11C A AC ∥,∴DE C A ∥11,∵⊄11C A 平面DE B 1,⊂DE 平面DE B 1,∴∥11C A 平面DE B 1.(2)法一:设O D B F A =11 ,∵F A D B 11⊥,∴︒=∠+∠9021,又∵︒=∠+∠9032,∴31∠=∠,又∵︒=∠=∠90111BD B F B A ,∴BD B F B A 111~∆∆,设m BF F B ==1,∴2121mm =,∴21=m ,∵∥DE 平面11FC A ,∴点D 到平面11FC A 的距离即为点E 到平面11FC A 的距离,由AB AC ⊥,A A AC 1⊥,A A A AB =1 ,∴⊥AC 平面AB A 1,∴DO AC ⊥,即11C A DO ⊥,又∵F A DO 1⊥,∴⊥DO 平面11FC A ,且254111=+=DB ,5525211==OB ,∴1053=OD ,即点E 到平面11FC A 的距离为1053.法二:建立如图所示空间直角坐标系,设m BF =,∴()()()⎪⎭⎫ ⎝⎛0,0212,0,1,0,12,0,011,,,,D m B m F m A ,∴()m F A m D B -=⎪⎭⎫⎝⎛--=,0,12,0,2111,,∴0221211=+-=⋅m F A D B ,解得21=m .设n AC =,∴()()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛0,2,21,1,021011,0,011n E n C F A ,,,,,,∴⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=21,,1210111n FC F A ,,,,设平面11FC A 的一个法向量()z y x n ,,=,∴⎪⎪⎩⎪⎪⎨⎧=++-=-021021z ny x z x ,∴()2,0,1=n ,⎪⎭⎫ ⎝⎛-=1,2,211n E A ,∴点E 到平面11FC A的距离1053523===d .16.解:(1)由对数函数的定义可得011>+-xx,即()()011<+-x x ,∴11<<-x ,∴函数()x f 的定义域为()1,1-,关于原点对称,∵()()01log 11log 11log 222==+-+-+=+-xxx x x f x f ,∴()()x f x f -=-,∴()x f 为奇函数.(2)()()⎪⎭⎫ ⎝⎛++-=+++-=x x x x f 121log 121log 22,由复合函数的单调性可知,()x f 在⎦⎤⎢⎣⎡-31,31上单调递减,由题意知()()max 2min 6-+≥at t x f ,∴()1316max2-=⎪⎭⎫⎝⎛≤-+f at t.法一:由162-≤-+at t 在[]2,2-∈t 上恒成立,可得052≤-+at t 恒成立,令()52-+=at t t g ,只需()()⎩⎨⎧≤-+=≤--=-0524205242a g a g ,解得2121≤≤-a ,即a 的取值范围为⎥⎦⎤⎢⎣⎡-2121,.法二:当0=t 时,16-≤-显然成立;当[)0,2-∈t 时,25t at -≤,即215max-=⎪⎭⎫⎝⎛-≥t t a ;当(]2,0∈t 时,25t at -≤,即215min =⎪⎭⎫⎝⎛-≤t t a ;∴2121≤≤-a ,即a 的取值范围为⎦⎤⎢⎣⎡-2121,.17.解:(1)证明:∵四边形ABCD 为菱形,∴BD AC ⊥,又∵⊥PB 平面ABCD ,∴AC PB ⊥,又B PB BD = ,∴⊥AC 平面PBD ,又∵⊂AC 平面P AC ,∴平面⊥P AC 平面PBD .(2)∵⊥PB 平面ABCD ,∴AB PB ⊥,BC PB ⊥,∴ABC ∠即为二面角C BP A --的平面角,即︒=∠120ABC ,建立如图所示空间直角坐标系,设m PB BC AB ===,2,由222AC PC P A =+,∴124422=+++m m ,解得2=m ,∴()()()()0,31000002200,,,,,,,,,,D B C P ,∴()()0,31202,,,,=-=BD PC ,设PC 与BD 所成角为θ,∴66262cos =⨯==θ.∴PC 与BD 所成角的余弦值为66.18.解:(1)当1=a ,1-==c b 时,()x x e x f x --=2,∵()0222<-=--e f ,()ef 11=-,且()x f 在R 上连续,由零点存在定理知,()x f 在()12--,上存在零点.(2)当0=a ,1-=b 时,()cx x x f +-=2,不等式()n c x f m ≤-≤的解集为[]n m ,,由图知m c cx x =-+-2的两根为n m ,,且442--≥c c n ,即02=++-c m cx x 的两根为n m ,,∴⎩⎨⎧+==+cm mn c n m ,∴mn n m =+2,即121=+n m ,∴2,1>>n m ,∴()()222=---n n m ,即()()221=--n m ,由n m <知⎩⎨⎧=-=-2211n m ,解得⎩⎨⎧==42n m ,此时6=c ,且满足442--≥c c n ,∴存在4,2==n m 符合题意.(3)由题意知()0=x f 的根均为()()0=x f f 的根,设0x 为()0=x f 的一个根,即()00=x f ,∴()()00=x f f ,∴()00=f ,∴0=a ,∴()()c bx x cx bx x f +=+=2,∴()()()()()()[]()()c bcx x b x f c x bf x f x cf x bfx f f ++=+=+=222,令()c bcx x b x g ++=22,当0=c 时,()0=x f 的两根b c x x -==21,0,而()00≠g ,022≠=+-=⎪⎭⎫ ⎝⎛-c c c c b c g ,∴必有()x g 中04222<-=∆c b c b ,∴40<<c ,综上40<≤c .∴[)4,0∈=+c c a ,即c a +的取值范围为[)4,0.19.解:(1)∵()()()2222212212221221=+⨯-⨯-⨯-=++-+--,∴{}222,1221+---,,为“完全集”.(2)∵集合{}b a ,为“完全集”,∴ab b a =+,0,>b a ,∴ab b a ab 2≥+=,∴4≥ab ,∵b a ≠,∴4>ab .假设2,0≤<b a ,则40≤<ab ,这与4>ab 矛盾,故b a ,中至少有一个大于2.(3)若2=n ,设{}b a A ,=,∵A 为完全集,∴ab b a =+,且*,N b a ∈,b a ≠,由()()111=---b b a ,∴()()111=--b a ,∴⎩⎨⎧=-=-1111b a ,解得2==b a ,这与b a ≠矛盾,舍去.若3=n ,设{}c b a A ,,=,∵A 为完全集,∴abc c b a =++,且*,N c b a ∈,,c b a ≠≠,不妨设c b a <<,∴c abc 3<,∴3<ab ,故2,1==b a ,∴c c 23=+,∴3=c ,∴{}3,2,1=A 符合.若4≥n ,设{}n a a a A ,,,21 =,不妨设n a a a <<< 21,∵A 为完全集,,∴n n n na a a a a a a <=+++ 2121,∴n a a a n <-121 ,①另一方面()()!1121121-=-⋅≥-n n a a a n ,下证:()n n >-!1,4≥n ,∵4≥n 时,()()()022421!12>≥+-=---≥--n n n n n n n ,∴()n n >-!1,这与①矛盾,舍去.综上,{}3,2,1=A .。
江苏省南通市海门市包场高中高三数学上学期9月调研试

江苏省南通市海门市包场高中2015 届高三上学期9月调研数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.(5分)已知集合A={﹣1,3,2m﹣1},B={3,m2},且A∩B=B,那么实数m=.2.(5分)函数f(x)=+lg(x﹣1)的定义域是.3.(5分)“若x2+x﹣6≥0,则x>2”的否命题是.4.(5分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为.5.(5分)命题“∀x∈R,x2﹣4bx+3b>0”是假命题,则b的取值范围为.6.(5分)已知函数f(x)=x|x﹣4|,x∈[0,m],其中m∈R且m>0,若函数f(x)的值域为[0,4],则m的取值范围为.7.(5分)已知f(x)=x2﹣2x+3,g(x)=kx﹣1,则“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的条件.(填“充分不必要、必要而不充分、充要、既不充分也不必要”之一)8.(5分)设函数f(x)=在区间(a,a+2)上单调递增,则a的取值范围为.9.(5分)在平面直角坐标系xOy中,直线y=x+b是曲线y=alnx的切线,则当a>0时,实数b的最小值是.10.(5分)设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)﹣e x]=e+1,则f(ln2)的值为.11.(5分)已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a>),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于.12.(5分)已知函数f(x)=,若∀x∈R,f(x)≤ax+2(a∈R),则a的最大值为.13.(5分)已知函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax(a>0)恰有三个零点,则实数a的取值范围为.14.(5分)已知a>0,函数f(x)=在区间[0,4]上的最大值为,则a的值为.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(14分)设全集U=R,f(x)=x2+3x+2,g(x)=x2+(m+1)x+m,m∈R.(1)设集合A={x|f(x)=0},B={x|g(x)=0}.若(∁U A)∩B=Φ,求m的值.(2)设集合P={y|y=f(x)},Q={m|g(x)在区间[﹣1,+∞)上是增函数},求P∩Q.16.(14分)设函数f(x)=2x+.(1)若f(x)=,求x的值;(2)若关于x的方程f(2x)+af(x)+4=0在x∈(0,+∞)上有解,求实数a的取值范围.17.(14分)已知函数f(x)=ax﹣lnx,g(x)=e ax+3x,其中a∈R.(Ⅰ)求f(x)的极值;(Ⅱ)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.18.(16分)某地发生某种自然灾害,使当地的自来水受到了污染.某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中f(x)=,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的取值范围.19.(16分)设a∈R,函数f(x)=x3﹣(2a+1)x2+(a2+a)x.(1)若函数g(x)=(x≠0)为奇函数,求a的值;(2)若函数f(x)在x=2处取得极小值,求a的值;(3)若a>﹣1,试求x∈[0,1]时,函数f(x)的最大值.20.(16分)已知函数f(x)=(x2﹣3x+3)e x,x∈[﹣2,a],a>﹣2,其中e是自然对数的底数.(1)若a<1,求函数y=f(x)的单调区间;(2)求证:f(a)>;(3)对于定义域为D的函数y=g(x),如果存在区间[m,n]⊆D,使得x∈[m,n]时,y=g(x)的值域是[m,n],则称[m,n]是该函数y=g(x)的“保值区间”.设h(x)=f(x)+(x﹣2)e x,x∈(1,+∞),问函数y=h(x)是否存在“保值区间”?若存在,请求出一个“保值区间”;若不存在,请说明理由.江苏省南通市海门市包场高中2015届高三上学期9月调研数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.(5分)已知集合A={﹣1,3,2m﹣1},B={3,m2},且A∩B=B,那么实数m=1.考点:交集及其运算.专题:计算题.分析:根据题目给出的集合A与B,结合两个集合的关系得到m2=2m﹣1,求解后验证A满足集合中元素的互异性,则m可求.解答:解:由A∩B=B,得B⊆A.又A={﹣1,3,2m﹣1},B={3,m2},∴m2=2m﹣1,解得m=1.此时集合A有意义.故答案为1.点评:本题考查了交集及其运算,考查了集合之间的关系,考查了集合中元素的特性,是基础题.2.(5分)函数f(x)=+lg(x﹣1)的定义域是(1,2).考点:函数的定义域及其求法.专题:函数的性质及应用.分析:根据偶次根式及对数函数的性质得不等式组,解出即可.解答:解:由题意得:,解得:1<x<2,故答案为:(1,2)点评:本题考查了偶次根式及对数函数的性质,求函数的定义域,是一道基础题.3.(5分)“若x2+x﹣6≥0,则x>2”的否命题是若x2+x﹣6<0,则x≤2.考点:四种命题.专题:证明题.分析:命题“若p,则q”的否命题是“若¬p,则¬q”.据此可得出答案.解答:解:根据命题“若p,则q”的否命题是“若¬p,则¬q”.所以命题“若x2+x﹣6≥0,则x>2”的否命题是“若x2+x﹣6<0,则x≤2”.故答案为“若x2+x﹣6<0,则x≤2”.点评:掌握四种命题间的关系是解决问题的关键.4.(5分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为2ln2﹣2.考点:利用导数研究函数的极值.专题:导数的综合应用.分析:先求导数,当x=1时,即可得到f′(1),再令导数大于0或小于0,解出x的范围,即得到函数的单调区间,进而可得函数的极大值.解答:解:由于函数f(x)=2f′(1)lnx﹣x,则f′(x)=2f′(1)×﹣1(x>0),f′(1)=2f′(1)﹣1,故f′(1)=1,得到f′(x)=2×﹣1=,令f′(x)>0,解得:x<2,令f′(x)<0,解得:x>2,则函数在(0,2)上为增函数,在(2,+∞)上为减函数,故f(x)的极大值为f(2)=2ln2﹣2故答案为:2ln2﹣2点评:本题考查了利用导数研究函数的极值,属于基础题.5.(5分)命题“∀x∈R,x2﹣4bx+3b>0”是假命题,则b的取值范围为b≤0或.考点:全称命题.专题:简易逻辑.分析:令f(x)=x2﹣4bx+3b,利用“∀x∈R,x2﹣4bx+3b>0”是假命题⇔△=16b2﹣12b≥0,解出即可.解答:解:∵命题“∀x∈R,x2﹣4bx+3b>0”是假命题.令f(x)=x2﹣4bx+3b,则必有“∀x∈R,x2﹣4bx+3b>0”是假命题⇔△=16b2﹣12b≥0,解得b≤0或.故答案为:b≤0或.点评:熟练掌握一元二次不等式的解集与判别式△的关系、“三个二次”的关系是解题的关键.6.(5分)已知函数f(x)=x|x﹣4|,x∈[0,m],其中m∈R且m>0,若函数f(x)的值域为[0,4],则m的取值范围为[2,2+2].考点:函数的值域.专题:函数的性质及应用.分析:去绝对值,f(x)=,画出该函数的图象,根据图象即可得到m 的取值范围.解答:解:f(x)=,图象如下:令x2﹣4x=4,x≥4,解得x=;∴由图象可知m的取值范围为.故答案为:[2,2+2].点评:考查含绝对值函数的处理办法,分段函数,以及二次函数图象.7.(5分)已知f(x)=x2﹣2x+3,g(x)=kx﹣1,则“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.(填“充分不必要、必要而不充分、充要、既不充分也不必要”之一)考点:必要条件、充分条件与充要条件的判断.专题:规律型.分析:根据不等式的解法,利用充分条件和必要条件的定义进行判断.解答:解:∵f(x)=x2﹣2x+3,g(x)=kx﹣1,∴要使f(x)≥g(x)在R上恒成立,则x2﹣2x+3≥kx﹣1,即x2﹣(2+k)x+4≥0恒成立,∴△=(2+k)2﹣4×4≤0,‘即(2+k)2≤16,∴﹣4≤2+k≤4,即﹣6≤k≤2,∴“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.故答案为:充分不必要.点评:本题主要考查充分条件和必要条件的定义,利用函数恒成立是解决本题的关键.8.(5分)设函数f(x)=在区间(a,a+2)上单调递增,则a的取值范围为[0,e﹣2].考点:利用导数研究函数的单调性;函数单调性的性质.专题:导数的综合应用.分析:求出函数的导数,利用函数单调性的和导数之间的关系即可得到结论.解答:解:∵f(x)=的定义域为(0,+∞),∴f′(x)=,由f′(x)=>0,解得0<x<e,即函数的递增区间为(0,e),若函数f(x)在区间(a,a+2)上单调递增,则,即0≤a≤e﹣2,故答案为:[0,e﹣2]点评:本题主要考查函数单调性和导致的关系,求出函数的单调区间是解决本题的关键.9.(5分)在平面直角坐标系xOy中,直线y=x+b是曲线y=alnx的切线,则当a>0时,实数b的最小值是﹣1.考点:利用导数研究曲线上某点切线方程.专题:计算题;导数的概念及应用.分析:设出曲线上的一个切点为(x,y),利用导数的几何意义求切线的坐标,可得b=alna ﹣a,再求导,求最值即可.解答:解:设出曲线上的一个切点为(x,y),由y=alnx,得y′=,∵直线y=x+b是曲线y=alnx的切线,∴y′==1,∴x=a,∴切点为(a,alna),代入y=x+b,可得b=alna﹣a,∴b′=lna=0,可得a=1,∴函数b=alna﹣a在(0,1)上单调递减,在(1,+∞)上单调递增,∴a=1时,b取得最小值﹣1.故答案为:﹣1.点评:本题主要考查导数的几何意义的应用,利用导数的运算求出切线斜率,根据切线斜率和导数之间的关系建立方程进行求解是解决本题的关键,考查学生的运算能力.10.(5分)设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)﹣e x]=e+1,则f(ln2)的值为3.考点:函数单调性的性质.专题:函数的性质及应用.分析:利用换元法将函数转化为f(t)=e+1,根据函数的对应关系求出t的值,即可求出函数f(x)的表达式,即可得到结论.解答:解:设t=f(x)﹣e x,则f(x)=e x+t,则条件等价为f(t)=e+1,令x=t,则f(t)=e t+t=e+1,∵函数f(x)为单调递增函数,∴函数为一对一函数,解得t=1,∴f(x)=e x+1,即f(ln2)=e ln2+1=2+1=3,故答案为:3点评:本题主要考查函数值的计算,利用换元法求出函数的解析式是解决本题的关键.11.(5分)已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a>),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于1.考点:奇偶性与单调性的综合.专题:综合题;函数的性质及应用.分析:根据函数的奇偶性,确定f(x)在(0,2)上的最大值为﹣1,求导函数,确定函数的单调性,求出最值,即可求得a的值.解答:解:∵f(x)是奇函数,x∈(﹣2,0)时,f(x)的最小值为1,∴f(x)在(0,2)上的最大值为﹣1,当x∈(0,2)时,f′(x)=﹣a,令f′(x)=0得x=,又a>,∴0<<2,令f′(x)>0,则x<,∴f(x)在(0,)上递增;令f′(x)<0,则x>,∴f(x)在(,2)上递减,∴f(x)max=f()=ln﹣a•=﹣1,∴ln=0,得a=1.故答案为:1.点评:本题考查函数单调性与奇偶性的结合,考查导数知识的运用,考查学生的计算能力,属于中档题.12.(5分)已知函数f(x)=,若∀x∈R,f(x)≤ax+2(a∈R),则a的最大值为2﹣2.考点:分段函数的应用.专题:计算题;数形结合;函数的性质及应用.分析:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),将直线绕着点(0,2)旋转时,当直线与y=﹣x2﹣2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,联立直线方程和抛物线方程,消去y,运用判别式为0,通过图象观察,舍去负值.解答:解:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),将直线绕着点(0,2)旋转时,当直线与y=﹣x2﹣2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,联立直线y=ax+2和y=﹣x2﹣2x,消去y得,x2+(a+2)x+2=0,由判别式为0,即有(a+2)2﹣8=0解得a=﹣2+2或﹣2﹣2由图象可知a=﹣2﹣2不成立,舍去.故答案为:2﹣2.点评:本题考查分段函数的图象和运用,考查数形结合的思想方法,以及直线与抛物线相切的条件,考查运算能力,属于中档题.13.(5分)已知函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax(a>0)恰有三个零点,则实数a的取值范围为[,).考点:函数零点的判定定理.专题:函数的性质及应用.分析:先求出x时f(x)的解析式,再研究f(x)﹣ax=0在区间[,3]上的零点个数,即此时y=f(x)与y=ax交点的个数,注意数形结合.解答:解:设x∈[,1],则∈[1,3]又因为:函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,所以f(x)=2=2,x∈[,1]所以f(x)=,g(x)=f(x)﹣ax(a>0)恰有三个零点,即在[,3]内f(x)的图象与y=ax有三个交点,如图所示:当直线y=ax介于直线l1(过原点和(3,ln3)的直线)和直线l2(当x∈[1,3]时y=lnx的过原点的切线)易知,设y=lnx过原点的切线切点为(a,lna),则y′=,所以切线斜率为,所以切线为y﹣lna=,又因为过原点,所以lna=1,所以a=e∈[1,3]故,故实数a的范围是故答案为:点评:本题的解题思路充分体现了转化思想以及数形结合的思想,即把根的问题转化为函数零点问题,再进一步转化为两个函数图象交点的问题,做出图象直观的判断,再进行计算.本题难度较大.14.(5分)已知a>0,函数f(x)=在区间[0,4]上的最大值为,则a的值为.考点:函数的最值及其几何意义.专题:综合题;函数的性质及应用.分析:利用绝对值的几何意义,分类讨论,结合导数确定函数的单调性,从而可得函数f (x)=在区间[0,4]上的最大值,利用条件,即可求出a的值.解答:解:记f(x)在区间[0,4]上的最大值为g(a),当0≤x≤a时,f(x)=;当x>a时,f(x)=∴当0≤x≤a时,f′(x)=<0,f(x)在(0,a)上单调递减;当x>a时,f′(x)=>0,f(x)在(a,+∞)上单调递增.①若a≥4,则f(x)在(0,4)上单调递减,g(a)=f(0)=,不符合;②若0<a<4,则f(x)在(0,a)上单调递减,在(a,4)上单调递增∴g(a)=max{f(0),f(4)}∵f(0)﹣f(4)=∴当0<a≤1时,g(a)=f(4)=;当1<a<4时,g(a)=f(0)=,∴=,∴a=.故答案为:.点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,正确分类是关键.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(14分)设全集U=R,f(x)=x2+3x+2,g(x)=x2+(m+1)x+m,m∈R.(1)设集合A={x|f(x)=0},B={x|g(x)=0}.若(∁U A)∩B=Φ,求m的值.(2)设集合P={y|y=f(x)},Q={m|g(x)在区间[﹣1,+∞)上是增函数},求P∩Q.考点:交、并、补集的混合运算.专题:集合.分析:(1)解方程可得集合A={x|f(x)=0}={﹣1,﹣2},B={x|g(x)=0}.﹣1∈B,﹣m∈B,由(∁U A)∩B=∅,可得m∈A,进而可得答案.(2)根据二次函数的图象和性质,可得集合P=[﹣,+∞),Q=[1,+∞),代入集合交集定义,可得答案.解答:解:(1)∵集合A={x|f(x)=0}={﹣1,﹣2},B={x|g(x)=0}.∴﹣1∈B,﹣m∈B,若(∁U A)∩B=∅,则m∈A,即m=1或m=2,(2)∵集合P={y|y=f(x)}=[﹣,+∞),Q={m|g(x)在区间[﹣1,+∞)上是增函数}={m|}=[1,+∞),∴P∩Q=[1,+∞).点评:本题考查的知识点是集合的交,并,补集混合运算,难度不大,属于基础题.16.(14分)设函数f(x)=2x+.(1)若f(x)=,求x的值;(2)若关于x的方程f(2x)+af(x)+4=0在x∈(0,+∞)上有解,求实数a的取值范围.考点:函数的值域.专题:函数的性质及应用.分析:(1)x<0时,f(x)=2•2x<2,所以讲f(x)=带入f(x)=求x即可;(2)带入f(x)=,求出f(2x),从而得到,解出a=,这便求出了a的取值范围.解答:解:(1)f(x)=;∵x<0时,2•2x<2;∴只能,解得x=1,或﹣1(舍去);即x的值为1;(2);∴=;∴a的取值范围是(﹣∞,﹣2].点评:考查含绝对值函数,分段函数,已知函数值求自变量值,基本不等式:.17.(14分)已知函数f(x)=ax﹣lnx,g(x)=e ax+3x,其中a∈R.(Ⅰ)求f(x)的极值;(Ⅱ)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.考点:函数在某点取得极值的条件;利用导数研究函数的单调性.专题:计算题;导数的综合应用.分析:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=,对a分a≤0与a>0讨论,通过f′(x)的符号可判断f(x)在相应区间上的单调性,从而可求得f(x)的极值;(Ⅱ)可求得g′(x)=ae ax+3,对a分a>0,a=0与a<0讨论,通过f′(x)的符号可判断f(x)在相应区间上的单调性,可求得a的取值范围.解答:解:(Ⅰ)f(x)的定义域为(0,+∞),且f′(x)=a﹣=.①当a≤0时,f'(x)<0,故f(x)在(0,+∞)上单调递减.从而f(x)没有极大值,也没有极小值.②当a>0时,令f′(x)=0,得x=.f(x)和f′(x)的情况如下:x (0,)(,+∞)f′(x)﹣0 +f(x)↘↗故f(x)的单调减区间为(0,);单调增区间为(,+∞).从而f(x)的极小值为f()=1+lna;没有极大值.(Ⅱ)解:g(x)的定义域为R,且g′(x)=ae ax+3.③当a>0时,显然g′(x)>0,从而g(x)在R上单调递增.由(Ⅰ)得,此时f(x)在(,+∞)上单调递增,符合题意.④当a=0时,g(x)在R上单调递增,f(x)在(0,+∞)上单调递减,不合题意.⑤当a<0时,令g′(x)=0,得x0=ln(﹣).g(x)和g′(x)的情况如下表:x (﹣∞,x0) x0(x0,+∞)g′(x)﹣0 +g(x)↘↗当﹣3≤a<0时,x0≤0,此时g(x)在(x0,+∞)上单调递增,由于f(x)在(0,+∞)上单调递减,不合题意.当a<﹣3时,x0>0,此时g(x)在(﹣∞,x0)上单调递减,由于f(x)在(0,+∞)上单调递减,符合题意.综上,a的取值范围是(﹣∞,﹣3)∪(0,+∞).点评:本题考查函数在某点取得极值的条件,考查利用导数研究函数的单调性,突出考查分类讨论思想与方程思想,属于难题.18.(16分)某地发生某种自然灾害,使当地的自来水受到了污染.某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中f(x)=,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的取值范围.考点:函数模型的选择与应用.专题:函数的性质及应用.分析:(1)由题设:投放的药剂质量为m=4,自来水达到有效净化等价于4f(x)≥6,利用分段函数,建立不等式,即可求得结论;(2)由题意,∀x∈(0,7],6≤mf(x)≤18,m>0,由函数y是分段函数,故分段建立不等式组,从而解出m的值.解答:解:(1)由题设:投放的药剂质量为m=4,自来水达到有效净化等价于4f(x)≥6…(2分)∴f(x)≥,∴或…(4分)∴0<x≤6,亦即:如果投放的药剂质量为m=4,自来水达到有效净化一共可持续6天;…(8分)(2)由题设:∀x∈(0,7],6≤mf(x)≤18,m>0,…(10分)∵f(x)=,∴∀x∈(0,4],6≤mlog2(x+4)≤18,且∀x∈(4,7],6≤≤18,…(12分)∴且,…(14分)∴5≤m≤6,亦即:投放的药剂质量m的取值范围为[5,6].…(16分)点评:本题考查了分段函数模型的灵活应用,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.19.(16分)设a∈R,函数f(x)=x3﹣(2a+1)x2+(a2+a)x.(1)若函数g(x)=(x≠0)为奇函数,求a的值;(2)若函数f(x)在x=2处取得极小值,求a的值;(3)若a>﹣1,试求x∈[0,1]时,函数f(x)的最大值.考点:利用导数求闭区间上函数的最值;函数奇偶性的性质;函数在某点取得极值的条件.专题:导数的综合应用.分析:(1)求导函数,确定函数g(x)的解析式,利用函数为奇函数,即可求a的值;(2)确定函数f(x)的单调性,可求函数的极小值,利用函数在x=2处取得极小值,可求a 的值;(3)若a>﹣1,对a解析分类讨论,确定函数在x∈[0,1]上的单调性,即可求出函数f(x)的最大值.解答:解:(1)由题意,f′(x)=x2﹣(2a+1)x+(a2+a),…(1分)∴g(x)==x+﹣(2a+1)x(x≠0),∵函数g(x)=(x≠0)为奇函数,∴g(﹣x)+g(x)=0,即2a+1=0,∴a=﹣;…(4分)(2)f′(x)=(x﹣a)[x﹣(a+1)]…(5分)x (﹣∞,a)(a,a+1)(a+1,+∞)f′(x)+ ﹣+∴f(x)在x=a+1处取得极小值,在x=1处取得极大值,…(7分)由题设a+1=2,∴a=1;…(8分)(3)由(2)知:①a≥1时,f(x)在[0,1]上是增函数,∴[f(x)]max=f(1)=;…(10分)②a=0时,f(x)在[0,1]上是减函数,∴[f(x)]max=f(0)=0;…(11分)③0<a<1时,f(x)在[0,a]上是增函数,f(x)在[a,1]上是减函数,∴[f(x)]max=f(a)=;…(13分)④﹣1<a<0时,f(x)在[0,a+1]上是减函数,f(x)在[a+1,1]上是增函数,∵f(1)﹣f(0)=,∴﹣1<a<﹣时,f(1)>f(0,∴[f(x)]max=f(1)=;﹣≤a<0时,f(1)≤f(0),∴[f(x)]max=f(0)=0;…(15分)综上,[f(x)]max=.…(16分)点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.20.(16分)已知函数f(x)=(x2﹣3x+3)e x,x∈[﹣2,a],a>﹣2,其中e是自然对数的底数.(1)若a<1,求函数y=f(x)的单调区间;(2)求证:f(a)>;(3)对于定义域为D的函数y=g(x),如果存在区间[m,n]⊆D,使得x∈[m,n]时,y=g(x)的值域是[m,n],则称[m,n]是该函数y=g(x)的“保值区间”.设h(x)=f(x)+(x﹣2)e x,x∈(1,+∞),问函数y=h(x)是否存在“保值区间”?若存在,请求出一个“保值区间”;若不存在,请说明理由.考点:利用导数研究函数的单调性;函数的定义域及其求法;函数的值域.专题:综合题;新定义;导数的综合应用.分析:(1)求导数,分类讨论,利用导数的正负,即可求函数y=f(x)的单调区间;(2)由题意求证f(t)>13e﹣2,可解出函数f(x)在区间[﹣2,+∞)上的最小值,由此最小值与13e﹣2作比较即可证明此不等式;(3)函数y=h(x)存在“保值区间”[m.n]等价于,等价于关于x的方程h(x)=x在(1,+∞)有两个不相等的实数根.解答:(1)解:f(x)=(x2﹣3x+3)e x,f'(x)=(x2﹣x)e x=x(x﹣1)e x,x∈[﹣2,a],a>﹣2x (﹣∞,0)(0,1)(1,+∞)f′(x)+ ﹣+…(2分)由表知道:①﹣2<a≤0时,x∈(﹣2,a)时,f′(x)>0,∴函数y=f(x)的单调增区间为(﹣2,a);…(3分)②0<a<1时,x∈(﹣2,0)时,f′(x)>0,x∈(0,a)时,f′(x)<0,∴函数y=f(x)的单调增区间为(﹣2,0),单调减区间为(0,a);…(4分)(2)证明:f(a)=(a2﹣3a+3)e a,f′(a)=a(a﹣1)e a,a>﹣2,a (﹣2,0)(0,1)(1,+∞)f′(a)+ ﹣+从而函数f(x)在区间[﹣2,+∞)上有唯一的极小值f(1)=e …(6分)但f(﹣2)=13e﹣2<e,故函数f(x)在区间[﹣2,+∞)上的最小值为f(﹣2)=13e﹣2,…(8分)因为t>﹣2,所以f(t)>f(﹣2)=13e﹣2…(8分)(3)解:h(x)=f(x)+(x﹣2)e x=(x2﹣2x+1)e x,x∈(1,+∞),h′(x)=(x2﹣1)e x,∴x∈(1,+∞)时,h′(x)>0,∴y=h(x)在(1,+∞)上是增函数,…(9分)函数y=h(x)存在“保值区间”[m.n]等价于等价于关于x的方程h(x)=x在(1,+∞)有两个不相等的实数根,…(11分)令H(x)=h(x)﹣x,则H′(x)=(x2﹣1)e x﹣1,H″(x)=(x2+2x﹣1)e x,∵x∈(1,+∞),∴H″(x)>0,∴H′(x)在(1,+∞)上是增函数,∵H′(1)=﹣1<0,H′(2)>0,且y=H′(x)在[1,2]图象不间断,∴∃x0∈(1,2)使得H′(x0)=0,…(13分)∴函数y=H(x)在(1,x0)上是减函数,在(x0,+∞)上是增函数,∵H′(1)=﹣1<,∴x∈(1,x0],H(x)<0,∴函数y=H(x)在(1,+∞)至多有一个零点,即关于x的方程h(x)=x在(1,+∞)至多有一个实数根,…(15分)∴函数y=h(x)是不存在“保值区间”.…(16分)点评:本题考查导数在最值问题中的运用,利用导数研究单调性,再利用单调性求最值,这是导数的重要运用.。
2021年9月江苏省南通市名校2022届高三上学期9月质量检测数学试卷及答案

2021年9月江苏省南通市名校2022届高三上学期9月质量检测数学试卷★祝考试顺利★ (含答案)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填写在答题卡相应位置上.1.已知函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π)的图象如图所示,则( )A .ω=2,φ=π B.ω=2,φ=π2 C .ω=12,φ=π4 D .ω=12,φ=-3π42.若a ,b ,c 满足2a =3,b =log 25,c =log 32,则( )A .c <a <bB .b <c <aC .a <b <cD .c <b <a 3.若函数f (x )=⎩⎪⎨⎪⎧(3a -1)x +4a ,x <1-ax ,x ≥1是R 上的减函数,则a 的取值范围为( )A .[18,13)B .(0,13)C .[18,+∞) D.(-∞,18]∪[13,+∞)4.下列函数中,最小值为4的是( )A .y =x +4xB .y =sin x +4sin x (0<x <π)C .y =e x +4e -xD .y =x 2+1+2x 2+15.已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=x 2-4x ,则不等式f (x +2)<5的解集为( )A.(-3,7) B.(-4,5) C.(-7,3) D.(-2,6)6.函数f(x)=x(2x+2-x)2+cos x的部分图像大致为()A.B.C.D.7.设a>0,b>0,且2a+b=1,则1a+2aa+b()A.有最小值为4 B.有最小值为22+1 C.有最小值为143D.无最小值8.已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于12的个数的最大值是()A.0 B.1 C.2 D.3二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知f(x)是定义域为R的函数,满足f(x+1)=f(x-3),f(1+x)=f(3-x),当0≤x≤2时,f(x)=x2-x,则下列说法正确的是()A.f(x)的最小正周期为4B.f(x)的图像关于直线x=2对称C.当0≤x≤4时,函数f(x)的最大值为2D.当6≤x≤8时,函数f(x)的最小值为-1 210.已知函数f (x )=cos(2x -π3)则( ) A .函数y =f (x )的图象可以由y =cos2x 的图象向左平移5π6得到;B .函数y =f (x )的图象关于点P (5π12,0)对称; C .函数y =f (x )的图象关于直线x =7π12对称;D .函数y =f (x )在(2π3,π)上单调递增 11.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F ,G 分别为BC ,CC 1,BB 1的中点,则( )A .直线DD 1与直线AF 垂直B .直线A 1G 与平面AEF 平行C .点C 与点G 到平面AEF 的距离相等D .平面截正方体所得的截面面积为9812.已知ln x 1-x 1-y 1+2=0,x 2+2y 2-2ln2-6=0,记M =(x 1-x 2)2+(y 1-y 2)2,则( ) A .M 的最小值为165 B .当M 最小时,x 2=145C .M 的最小值为45D .当M 最小时,x 2=125三、填空题:本题共4小题,每小题5分,共20分. 13.已知tan α=2,则cos(2α+π2)=______________. 14.设函数f (x )是定义在R 上的奇函数,且f (x )=⎩⎨⎧log 2(x +1),x ≥0g (x ),x <0,则g [f (-7)]的值为______________.15.已知四棱锥P -ABCD 的顶点都在球O 的球面上,底面ABCD 是边长为2的正方形,且PA ⊥面ABCD ,若四棱锥的体积为163,则该球的体积为______________.16.已知函数f (x )=⎩⎨⎧2x ,x ≤ax 2,x >a ,①若a =1,则不等式f (x )≤1的解集为______________;若存在实数b ,使函数g (x )=f (x )-b 有两个零点,则实数a 的取值范围是___________________________.四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.17. 已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P (-35,-45).(1)求sin(α+π)的值; (2)若角β满足sin(α+β)=513,求cos β的值. 18. 已知函数f (x )=ax 3-x +b (a ≠0),若函数f (x )在点(1,f (1))处的切线方程是2x -y +3=0.(1)求函数f (x )的解析式; (2)求f (x )的单调区间.19.在①f (x )+f (-x )=0,②f (x )-f (-x )=0,③f (-2)=-f (2)这三个条件中选择一个,补充在下面问题中,并给出解答. 已知函数f (x )=log 2(x 2+a +x )(a ∈R )满足______________.(1)求a 的值;(2)若函数g (x )=2f (-x )+1-x 2+1,证明:g (x 2-x )≤54.20.已知函数f (x )=3sin x cos x +sin 2x -12.(1)求f (x )的最小正周期及其对称轴方程;(2)设函数g (x )=f (ωx 2+π6),其中常数ω>0,ω>0.(i)若函数g (x )在区间[-π9,π9]上是增函数,求ω的最大值.(ii)当ω=4时,函数y =g (x )-4λf (x ),f (x )在[π12,π3]上的最大值为32,求实数λ的值. 21.如图1,在边长为4的菱形ABCD 中,∠BAD =60°,DE ⊥AB 于点E ,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1D ⊥DC ,如图2.(1)求证:A 1E ⊥平面BCDE ; (2)求二面角E -A 1B -C 的余弦值.22.已知函数f (x )=x 2-2x ln x ,g (x )=x +a x-(ln x )2,其中a ∈R ,x 0是g (x )的一个极值点,且g (x 0)=2.(1)讨论函数f (x )的单调性; (2)求实数x 0和a 的值:(3)证明k =1n14k 2-1>12ln(2n+1)(n ∈N *).2021年9月江苏省南通市名校2022届高三上学期9月质量检测数学参考答案一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填写在答题卡相应位置上. 1.【答案】D【解析】由图像可知:函数周期27422T ππππω⎛⎫==--= ⎪⎝⎭,解得12ω=. 故14sin 2y x ϕ⎛⎫=+ ⎪⎝⎭.由于函数经过5,42π⎛⎫ ⎪⎝⎭,故有142sin x ϕ⎛⎫+ ⎪⎝⎭,即52,42k k Z ππϕπ+=+∈.又因为||ϕπ≤,所以34ϕπ=-.故选:D . 2.【答案】A【解析】由于23a =.所以2log 3a =,根据对数函数的单调性可知:a b <. 又由于2223log 3log 21,log 3log 31a c =>==<=.所以c a <. 综上所述,有c a b <<. 故选:A . 3.【答案】A【解析】由于函数()f x 是R 上的减函数,所以有3100a a -<⎧⎨-<⎩,解得103a <<又因为314a x a ax -+<-,解得18a ≥.综上所述,1183a ≤<.故选:A . 4.【答案】C【解析】对于A :当0x <时,40y x x=+<.故A 项不符合题意.对于B :当0x π<<时,0sin 1x <≤,所以4sin 5sin y x x=+≥,故B 项不符合题意. 对于C :由于0x e >,所以根据基本不等式可以得出44x x y e e -=+≥,当且仅当2x e =时取得最小值4,故C 项不符合题意.对于D0>,所以根据基本不等式可以得出y =≥当且仅当21x =±时取得最小值故D 项不符合题意.综上所述,A 正确. 故选:A . 5.【答案】C【解析】当0x <时,0x -≥,则有22()()4()4f x x x x x -=--⨯-=+,由于()f x 为偶函数,故224,0()4,0x x x f x x x x ⎧-≥=⎨+<⎩进行分类讨论如下:①20x +≥,即2x ≥-时,2(2)5(2)4(2)5f x x x +<↔+-+<,解得33x -<<,则此时23x -≤<. ②20x +<,即2x <-时,2(2)5(2)4(2)5f x x x +<⇒+++<,解得33x -<<,则此时72x -<<-.综上所述,不等式(2)5f x +<的解集为(7,3)-. 故选:C . 6.【答案】C【解析】首先研究函数的奇偶性:函数()f x 定义域为R()()()2222()()2cos()2cos()x x x x x x f x f x x x ---⨯+⨯+-==-=-+-+-,所以()f x 为奇函数.故可以排除A 、B 项;然后尝试代入特殊点进行判断,由于()22()02cos()x f x πππ-⨯+=>+-.故排除D 项,C 项正确.故选:C . 7.【答案】B【解析】∵0,0,21a b a b >>+=∴1120,02b a a =-><<121212(1)212[(1)](12)11a a a a a a a b a a a a a a a --+⎛⎫+=+=+=+⨯+-- ⎪++---⎝⎭12211a aa a-=-≥-当且仅当1a =-时等号成立. 故选:B . 8.【答案】C【解析】由于,,αβγ是互不相同的锐角,所以sin cos ,sin cos ,sin cos αββγγα均为正数,根据基本不等式有222222sin cos sin cos ,sin cos 2sin cos sin cos ,sin cos 2sin cos sin cos ,sin cos 2αβαβαβγββγβγαγγαγα⎧+≤=⎪⎪+⎪≤=⎨⎪⎪+≤=⎪⎩当且仅当时等号成立当且仅当时等号成立当且仅当时等号成立,将这个不等式相加,得到3sin cos sin cos sin cos 2αββγγα++≤,所以sin cos ,sin cos ,sin cos αββγγα三个值不能均大于12,故排除D 项; 代入特殊值进行计算.取,,463πππαβγ===,则1sin cos 2αβ==>,11sin cos 22βγ==<,1sin cos 2γα==>,所以C 项正确. 故选:C .二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分. 9.【答案】ABC【解析】对于A :由(1)(3)f x f x +=-,可得()[(1)1][(1)3](4)f x f x f x f x =-+=--=-,所以()f x 的最小正周期为4,故A 项正确. 对于B :由(1)(3)f x f x +=-,可得(1(1))(3(1))f x f x ++=-+,即(2)(2)f x f x +=-,所以函数()f x 关于直线2x =对称,故B 项正确.对于C :由于函数()f x 关于直线2x =对称,所以可以仅研究02x ≤≤时,函数()f x 的最大值.因为当02x ≤≤时,2()f x x x =-,所以函数的最大值为(2)2f =,故C 项正确.对于D :由于函数()f x 的最小正周期为4,所以68x ≤≤时,函数()f x 的性质与02x ≤≤时,函数()f x 的最小值.因为当02x ≤≤时,2()f x x x =-,所以函数的最小值为1124f ⎛⎫=- ⎪⎝⎭,故D 项错误. 故选:ABC . 10.【答案】ABD【解析】对于A :cos2y x =的图象向左平移56π, 得到55cos 2cos2cos 2633y x x x πππ⎡⎤⎛⎫⎛⎫=+=+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦对于B :根据余弦函数的对称中心,可得2,32x k k Z πππ-=+∈,即5,122k x k Z ππ=+∈, 所以当0k =时,函数y 的图象关于点5,012P π⎛⎫⎪⎝⎭对称,故A 项正确;对于C :根据余弦函数的对称直线,可得2,3x k k Z ππ-=∈,即62k x ππ=+,所以不存在k 使得712x π=,故C 项错误; 对于D :根据余弦函数的单调递增区间,可得2(2),3x k k Z πππ-∈-+∈,即函数的单调增区间为,,36k k k Z ππππ⎛⎫++∈ ⎪⎝⎭,所以当1k =,函数的单调增区间为27,36ππ⎛⎫ ⎪⎝⎭,所以函数y 在2,3ππ⎛⎫⎪⎝⎭上单调递增,故D 项正确; 故选:ABD . 11.【答案】BC【解析】对于A :取1DD 中点H ,则AH 为AF 在平面1111A B C D 上的射 ∵AH 与1DD 不垂直∴直线1DD 与直线AF 不垂直,故A 错;对于B :取11B C 中点I ,连接1A I 、GI ,如下图所示.所以在正方体1111ABCD A B C D -中,1//,//A I AE IG EF . ∵1A I平面AEF ,AE ⊆平面AEF∴1//A I 平面AEF ,同理可证//IG 平面AEF ∵1A IIG I =∴平面1//AGI 平面AEF 又∵1AG ⊂平面1A GI ∴1//AG 平面AEF 故A 正确.对于C :利用反证法.假设C 项成立,则平面AEF 将CG 平分,CG 的中点在平面AEF 内.由于CG 与EF 交点M ,但M 不是CG 中点,所以假设不成立,故C 项错误.对D :连接11,AD D F .在正方体1111ABCD A B C D -中,1//AD EF ,所以平面AEF 截正方体所得的四边形1AEFD 为等腰梯形.梯形的对角线32d ===.所以根据等腰梯形面积计算公式,求得面积13392228S =⨯⨯=.故D 项正确. 12.【答案】AB【解析】根据条件可以将()()221212M x x y y =-+-的最小值转化为直线ln 2y x x =-+上的点11(,)A x y 到直线22ln 260x y +--=上的点22(,)B x y 的距离的最小值的平方,当直线ln 2y x x =-+上的点A 的切线平行于B 点所在的直线时,两点距离最小,即M 可取得最小值.对于函数ln 2y x x =-+,11y X '=-;对于函数122ln 260ln 232x y y x +--=⇔=-++,斜率为12-,所以令1112x -=-,解得2x =,切点为(2,ln 2);则该点到直线22ln 260x y +--=的距离为d =所以M 的最小值为2d ==.故A 正确,C 错误; 当M 最小时,可得,2222ln 220x y +--=①,()()222242ln 25x y -+-=② 为方便计算,将B 、D 项的2x 的值代入式①,分别求出2y 的值,将求得的值代入式②的左端,检查式子是否成立,故B 正确,D 错误; 故选:AB .三、填空题:本题共4小题,每小题5分,共20分.13.【答案】45-【解析】∵tan 2α=∴2222sin cos 2tan 224cos 2sin 22sin cos 1tan 145παααααα---⨯⎛⎫+=-====- ⎪+++⎝⎭14.【答案】2-【解析】由于()f x 是定义在R 上的奇函数,所以(7)(7)log2(71)3f f -=-=-+=-,故[(7)](3)(3)(3)log2(31)2g f g f f -=-=-=-=-+=-故答案为2-15.【答案】【解析】将四棱锥P ABCD -扩展为长方体,则长方体的对角线的长是外接球的直径. ∵四棱锥的体积为163,底面ABCD 是边长为2的正方形,且PA ⊥面ABCD ∴2116233PA ⨯⨯=,解得4PA =∴222(2)2R =+,解得R =∴外接球的体积343V π=⨯=故答案为:16.【答案】①(,0]-∞;②(,2)(4,)-∞+∞【解析】①当1a =,22,1(),1x x f x x x ⎧≤=⎨>⎩,所以()121,1x f x x ≤⇔≤≤或21,1x x ≤>,解得0x ≤,故()f x 解集为(,0]-∞故答案为:(,0]-∞②2,24,4a a a <≤≤>的情况下函数2,x y x a =≤与2()y x x a =>的函数图象如下:函数()()g x f x b =-可看作()f x 向上或向下移动||b 个单位长度.所以由图可知:当(,2)(4,)a ∈-∞+∞时,b R ∃∈,使得()()g x f x b =-有两个零点;故答案为:(,2)(4,)-∞+∞四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.17.【答案】(1)45;(2)1665或5665- 【解析】(1)由题可得:4sin 5α=-,所以4sin()sin 5απα+=-=(2)由题可得:3cos 5α=-.∵5sin()13αβ+=∴12cos()13αβ+=±∵cos cos[()]cos()cos sin()sin a βαβααβαβα=+-=+++ ∴16cos 65β=或56cos 65β=- 18.【答案】(1)3()5f x x x =-+;(2)()f x 的单调递减区间为33⎛- ⎝⎭,单调递增区间为,33⎛⎫-∞-⋃+∞ ⎪⎝⎦⎣⎭【解析】(1)由3()f x ax x b =-+,得到2()31f x ax ='-,由题可得:(1)312f a ='-=,解得1a =. 将1x =代入230x y -+=,得到(1)5f =, 所以(1)115f b =-+=,解得5b =. 所以3()5f x x x =-+(2)由(1)知:2()31f x x =-',令()0f x '=,则3x =或3-将()f x '绘制图象如下图:由图像可知:当33x -<<时,()0f x '<;当x ≤或3x ≥,()0f x '>.所以()f x 的单调递减区间为33⎛- ⎝⎭,单调递增区间为3,,33⎛⎡⎫-∞-+∞ ⎪⎢⎝⎦⎣⎭. 19.【答案】选择①1:(1)1a =(2)证明见解析: 不能选择②:选择③:(1)1a =(2)证明见解析: 【解析】选择①:(1)由于()()0f x f x +-=,所以))22log log 0x x +=.即)2log 0x x ⎡⎤=⎢⎥⎣⎦,解得1a =;由(1)知:))22()log ,()log f x x f x x =+-=.所以)2log ()()212111xf xg x x x -=+-=+-=+=-+故()()222215511244g x x x x x x x ⎛⎫-=--+=-++=--+≤ ⎪⎝⎭选择②:(1)由于()()0f x f x--=,所以)) 22log log0x x+=,即x x=,解得0,0x a=≥,无法求出具体a的值,故不能选择②.选择③:(1)由于(2)(2)f f-=-,所以22log2)log2)=-+,即2)1=,所以1a=;(2)由(1)知:))22()log,()logf x x f x x=+-=.所以)2log()()212111xf xg x x x-=+-=+-=+=-+故()()222215511244g x x x x x x x⎛⎫-=--+=-++=--+≤⎪⎝⎭20.【答案】(1)最小正周期222Tπππω===;对称轴方程为,32kx k Zππ=+∈;(2)(ⅰ)3ω≤;(ⅱ)12λ=-【解析】(1)函数21()cos sin2f x x x x=+-,化简得到1()2cos2sin2226f x x x xπ⎛⎫=-=-⎪⎝⎭,所以()f x的最小正周期222Tπππω===;根据正弦函数的对称轴,可得到2,62x k k Zπππ-=+∈,即对称轴方程为,32kx k Zππ=+∈(2)(ⅰ)()sin2sin262666x xg x f xωπωπππω⎡⎤⎛⎫⎛⎫⎛⎫=+=+-=+⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,当,99xππ⎡⎤∈-⎢⎥⎣⎦时,,69696xπππππωωω⎡⎤+∈-++⎢⎥⎣⎦因为()g x在,99ππ⎡⎤-⎢⎥⎣⎦为增函数,且0ω>,则2,9622,962k k Zk k Zπππωππππωπ⎧-+≥-+∈⎪⎪⎨⎛⎤⎪+≤+∈⎥⎪⎝⎦⎩,化简得到618318kkωω≤-⎧⎨≥+⎩因为0ω>,所以1163k-<<,但,k Z∈,所以0k=,从而得到3ω≤,故ω的最大值为3.()4()sin44sin266y g x f x x xππλλ⎛⎫⎛⎫=-=+--⎪ ⎪⎝⎭⎝⎭cos 44sin 236x x ππλ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭(ⅱ)当4ω=时,212sin 24sin 266x x ππλ⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭222sin 2126x πλλ⎡⎤⎛⎫=--+++ ⎪⎢⎥⎝⎭⎣⎦因为,123x ππ⎡⎤∈⎢⎥⎣⎦,所以20,,sin 2[0,1]626x x πππ⎡⎤⎛⎫-∈-∈ ⎪⎢⎥⎣⎦⎝⎭当[1,0]λ∈-时,若y 取得最大值,则有23122λ+=,解得12λ=-. 当(0,)λ∈+∞时,则在sin 206x π⎛⎫-= ⎪⎝⎭时,y 可以取得最大值1,与题目不符,故舍去.当(,1)λ∈-∞-时,则在sin 216x π⎛⎫-= ⎪⎝⎭时,y 可以取得最大值,则有2232[1]122λλ-+++=,解得58λ=-,矛盾,故舍去.所以满足题意的λ为12-.21.【答案】(1)证明见解析:(2)【解析】(1)∵DE BE ⊥,//BE BC ∴DE DC ⊥ 又∵11,A D DC A D DE D ⊥=∴DC ⊥平面1A DE ∴1DC A E ⊥ ∵1A E DE ⊥,DEDE D =∴1A E ⊥平面BCDE(2)∵1A E ⊥平面,BCDE DE BE ⊥∴以E 为原点,1,,EB ED EA 所在直线分别为x 轴,y 轴,z 轴,建立直角坐标系,如下图所示.由题可知DE =,则1(0,0,2),(2,0,0),A B C D ,所以1(2,0,2),BA BC =-= 设平面1A BC 的法向量(,,)n x y z =,则有10,10BA n BA n ⋅=⋅=,得22020x z x -+=⎧⎪⎨+=⎪⎩,令1y =,则(3,1,n =-又∵显然,(0,1,0)m =为平面1A BE 的法向量 ∴7cos(,)||||7m n m n m n ⨯==⋅由图可知,二面角1E A B C --为钝角,所以二面角1E A B C --的余弦值为-22.【答案】(1)()f x 在(0,)+∞上单调递增;(2)01x =,1a =;(3)证明见解析 【解析】(1)由2()2ln ,(0,)f x x x x x =-∈+∞,可得2()22ln 2,()2f x x x f x x=--='-''. 令()0f x ''=,即220-=,解得1x =.当1x=时,()0,(),(),()f x f x f x f x =''''关系如下表: 所以()f x 在(0,)+∞上单调递增.(2)由2()(ln ),(0,)a g x x x x x =+-∈+∞,可得22ln ()1a x xg x x x-'=-. ∵0x 是()g x 的一个极值点,且()02g x = ∴()0002002ln 10a x x g x x x =--='①,()()20000ln 2a g x x x x =+-=② 联立①②消去a ,得()20002ln 2ln 20x x x ---=③.令()2000()2ln 2ln 2h t x x x =---,则2(ln 1)()x x h t x-'-=.由(1)知:ln 10x x --≥,故2(ln 1)()0x x h t x--'=≥,即()h t '在(0,)+∞上单调递增.所以①③的解唯一.又因为(1)0h =,所以由③可得01x =,将其代入①,可得1a =.(3)由(1)知2()2ln f x x x x =-在在(0,)+∞上单调递增,故当(1,)x ∈+∞时,()(1)1f x f >=,所以222ln ()1()10a x x f x g x x x x-=--=>',即()g x 在(1,)+∞上单调递增,故(1,)x ∈+∞时,()(1)2g x g >=,即222(ln )2(ln )a x x x x +->⇒>.0,ln 0x ->>,ln x >. 令21,21k x k N k +=∈-,21ln ln(21)ln(21)21k k k k +>⇒>+---.对不等式两边进行求和,得到11ln(21)2nk n =>+,原命题得证.2021年9月江苏省南通市名校2022届高三上学期9月质量检测数学试卷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省南通市海门市包场高中2015 届高三上学期9月调研数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.(5分)已知集合A={﹣1,3,2m﹣1},B={3,m2},且A∩B=B,那么实数m=.2.(5分)函数f(x)=+lg(x﹣1)的定义域是.3.(5分)“若x2+x﹣6≥0,则x>2”的否命题是.4.(5分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为.5.(5分)命题“∀x∈R,x2﹣4bx+3b>0”是假命题,则b的取值范围为.6.(5分)已知函数f(x)=x|x﹣4|,x∈[0,m],其中m∈R且m>0,若函数f(x)的值域为[0,4],则m的取值范围为.7.(5分)已知f(x)=x2﹣2x+3,g(x)=kx﹣1,则“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的条件.(填“充分不必要、必要而不充分、充要、既不充分也不必要”之一)8.(5分)设函数f(x)=在区间(a,a+2)上单调递增,则a的取值范围为.9.(5分)在平面直角坐标系xOy中,直线y=x+b是曲线y=alnx的切线,则当a>0时,实数b的最小值是.10.(5分)设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)﹣e x]=e+1,则f(ln2)的值为.11.(5分)已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a>),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于.12.(5分)已知函数f(x)=,若∀x∈R,f(x)≤ax+2(a∈R),则a的最大值为.13.(5分)已知函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax(a>0)恰有三个零点,则实数a的取值范围为.14.(5分)已知a>0,函数f(x)=在区间[0,4]上的最大值为,则a的值为.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(14分)设全集U=R,f(x)=x2+3x+2,g(x)=x2+(m+1)x+m,m∈R.(1)设集合A={x|f(x)=0},B={x|g(x)=0}.若(∁U A)∩B=Φ,求m的值.(2)设集合P={y|y=f(x)},Q={m|g(x)在区间[﹣1,+∞)上是增函数},求P∩Q.16.(14分)设函数f(x)=2x+.(1)若f(x)=,求x的值;(2)若关于x的方程f(2x)+af(x)+4=0在x∈(0,+∞)上有解,求实数a的取值范围.17.(14分)已知函数f(x)=ax﹣lnx,g(x)=e ax+3x,其中a∈R.(Ⅰ)求f(x)的极值;(Ⅱ)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.18.(16分)某地发生某种自然灾害,使当地的自来水受到了污染.某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中f(x)=,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的取值范围.19.(16分)设a∈R,函数f(x)=x3﹣(2a+1)x2+(a2+a)x.(1)若函数g(x)=(x≠0)为奇函数,求a的值;(2)若函数f(x)在x=2处取得极小值,求a的值;(3)若a>﹣1,试求x∈[0,1]时,函数f(x)的最大值.20.(16分)已知函数f(x)=(x2﹣3x+3)e x,x∈[﹣2,a],a>﹣2,其中e是自然对数的底数.(1)若a<1,求函数y=f(x)的单调区间;(2)求证:f(a)>;(3)对于定义域为D的函数y=g(x),如果存在区间[m,n]⊆D,使得x∈[m,n]时,y=g(x)的值域是[m,n],则称[m,n]是该函数y=g(x)的“保值区间”.设h(x)=f(x)+(x﹣2)e x,x∈(1,+∞),问函数y=h(x)是否存在“保值区间”?若存在,请求出一个“保值区间”;若不存在,请说明理由.江苏省南通市海门市包场高中2015届高三上学期9月调研数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.(5分)已知集合A={﹣1,3,2m﹣1},B={3,m2},且A∩B=B,那么实数m=1.考点:交集及其运算.专题:计算题.分析:根据题目给出的集合A与B,结合两个集合的关系得到m2=2m﹣1,求解后验证A满足集合中元素的互异性,则m可求.解答:解:由A∩B=B,得B⊆A.又A={﹣1,3,2m﹣1},B={3,m2},∴m2=2m﹣1,解得m=1.此时集合A有意义.故答案为1.点评:本题考查了交集及其运算,考查了集合之间的关系,考查了集合中元素的特性,是基础题.2.(5分)函数f(x)=+lg(x﹣1)的定义域是(1,2).考点:函数的定义域及其求法.专题:函数的性质及应用.分析:根据偶次根式及对数函数的性质得不等式组,解出即可.解答:解:由题意得:,解得:1<x<2,故答案为:(1,2)点评:本题考查了偶次根式及对数函数的性质,求函数的定义域,是一道基础题.3.(5分)“若x2+x﹣6≥0,则x>2”的否命题是若x2+x﹣6<0,则x≤2.考点:四种命题.专题:证明题.分析:命题“若p,则q”的否命题是“若¬p,则¬q”.据此可得出答案.解答:解:根据命题“若p,则q”的否命题是“若¬p,则¬q”.所以命题“若x2+x﹣6≥0,则x>2”的否命题是“若x2+x﹣6<0,则x≤2”.故答案为“若x2+x﹣6<0,则x≤2”.点评:掌握四种命题间的关系是解决问题的关键.4.(5分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为2ln2﹣2.考点:利用导数研究函数的极值.专题:导数的综合应用.分析:先求导数,当x=1时,即可得到f′(1),再令导数大于0或小于0,解出x的范围,即得到函数的单调区间,进而可得函数的极大值.解答:解:由于函数f(x)=2f′(1)lnx﹣x,则f′(x)=2f′(1)×﹣1(x>0),f′(1)=2f′(1)﹣1,故f′(1)=1,得到f′(x)=2×﹣1=,令f′(x)>0,解得:x<2,令f′(x)<0,解得:x>2,则函数在(0,2)上为增函数,在(2,+∞)上为减函数,故f(x)的极大值为f(2)=2ln2﹣2故答案为:2ln2﹣2点评:本题考查了利用导数研究函数的极值,属于基础题.5.(5分)命题“∀x∈R,x2﹣4bx+3b>0”是假命题,则b的取值范围为b≤0或.考点:全称命题.专题:简易逻辑.分析:令f(x)=x2﹣4bx+3b,利用“∀x∈R,x2﹣4bx+3b>0”是假命题⇔△=16b2﹣12b≥0,解出即可.解答:解:∵命题“∀x∈R,x2﹣4bx+3b>0”是假命题.令f(x)=x2﹣4bx+3b,则必有“∀x∈R,x2﹣4bx+3b>0”是假命题⇔△=16b2﹣12b≥0,解得b≤0或.故答案为:b≤0或.点评:熟练掌握一元二次不等式的解集与判别式△的关系、“三个二次”的关系是解题的关键.6.(5分)已知函数f(x)=x|x﹣4|,x∈[0,m],其中m∈R且m>0,若函数f(x)的值域为[0,4],则m的取值范围为[2,2+2].考点:函数的值域.专题:函数的性质及应用.分析:去绝对值,f(x)=,画出该函数的图象,根据图象即可得到m 的取值范围.解答:解:f(x)=,图象如下:令x2﹣4x=4,x≥4,解得x=;∴由图象可知m的取值范围为.故答案为:[2,2+2].点评:考查含绝对值函数的处理办法,分段函数,以及二次函数图象.7.(5分)已知f(x)=x2﹣2x+3,g(x)=kx﹣1,则“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.(填“充分不必要、必要而不充分、充要、既不充分也不必要”之一)考点:必要条件、充分条件与充要条件的判断.专题:规律型.分析:根据不等式的解法,利用充分条件和必要条件的定义进行判断.解答:解:∵f(x)=x2﹣2x+3,g(x)=kx﹣1,∴要使f(x)≥g(x)在R上恒成立,则x2﹣2x+3≥kx﹣1,即x2﹣(2+k)x+4≥0恒成立,∴△=(2+k)2﹣4×4≤0,‘即(2+k)2≤16,∴﹣4≤2+k≤4,即﹣6≤k≤2,∴“(|k|≤2)”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.故答案为:充分不必要.点评:本题主要考查充分条件和必要条件的定义,利用函数恒成立是解决本题的关键.8.(5分)设函数f(x)=在区间(a,a+2)上单调递增,则a的取值范围为[0,e﹣2].考点:利用导数研究函数的单调性;函数单调性的性质.专题:导数的综合应用.分析:求出函数的导数,利用函数单调性的和导数之间的关系即可得到结论.解答:解:∵f(x)=的定义域为(0,+∞),∴f′(x)=,由f′(x)=>0,解得0<x<e,即函数的递增区间为(0,e),若函数f(x)在区间(a,a+2)上单调递增,则,即0≤a≤e﹣2,故答案为:[0,e﹣2]点评:本题主要考查函数单调性和导致的关系,求出函数的单调区间是解决本题的关键.9.(5分)在平面直角坐标系xOy中,直线y=x+b是曲线y=alnx的切线,则当a>0时,实数b的最小值是﹣1.考点:利用导数研究曲线上某点切线方程.专题:计算题;导数的概念及应用.分析:设出曲线上的一个切点为(x,y),利用导数的几何意义求切线的坐标,可得b=alna ﹣a,再求导,求最值即可.解答:解:设出曲线上的一个切点为(x,y),由y=alnx,得y′=,∵直线y=x+b是曲线y=alnx的切线,∴y′==1,∴x=a,∴切点为(a,alna),代入y=x+b,可得b=alna﹣a,∴b′=lna=0,可得a=1,∴函数b=alna﹣a在(0,1)上单调递减,在(1,+∞)上单调递增,∴a=1时,b取得最小值﹣1.故答案为:﹣1.点评:本题主要考查导数的几何意义的应用,利用导数的运算求出切线斜率,根据切线斜率和导数之间的关系建立方程进行求解是解决本题的关键,考查学生的运算能力.10.(5分)设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)﹣e x]=e+1,则f(ln2)的值为3.考点:函数单调性的性质.专题:函数的性质及应用.分析:利用换元法将函数转化为f(t)=e+1,根据函数的对应关系求出t的值,即可求出函数f(x)的表达式,即可得到结论.解答:解:设t=f(x)﹣e x,则f(x)=e x+t,则条件等价为f(t)=e+1,令x=t,则f(t)=e t+t=e+1,∵函数f(x)为单调递增函数,∴函数为一对一函数,解得t=1,∴f(x)=e x+1,即f(ln2)=e ln2+1=2+1=3,故答案为:3点评:本题主要考查函数值的计算,利用换元法求出函数的解析式是解决本题的关键.11.(5分)已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a>),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于1.考点:奇偶性与单调性的综合.专题:综合题;函数的性质及应用.分析:根据函数的奇偶性,确定f(x)在(0,2)上的最大值为﹣1,求导函数,确定函数的单调性,求出最值,即可求得a的值.解答:解:∵f(x)是奇函数,x∈(﹣2,0)时,f(x)的最小值为1,∴f(x)在(0,2)上的最大值为﹣1,当x∈(0,2)时,f′(x)=﹣a,令f′(x)=0得x=,又a>,∴0<<2,令f′(x)>0,则x<,∴f(x)在(0,)上递增;令f′(x)<0,则x>,∴f(x)在(,2)上递减,∴f(x)max=f()=ln﹣a•=﹣1,∴ln=0,得a=1.故答案为:1.点评:本题考查函数单调性与奇偶性的结合,考查导数知识的运用,考查学生的计算能力,属于中档题.12.(5分)已知函数f(x)=,若∀x∈R,f(x)≤ax+2(a∈R),则a的最大值为2﹣2.考点:分段函数的应用.专题:计算题;数形结合;函数的性质及应用.分析:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),将直线绕着点(0,2)旋转时,当直线与y=﹣x2﹣2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,联立直线方程和抛物线方程,消去y,运用判别式为0,通过图象观察,舍去负值.解答:解:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),将直线绕着点(0,2)旋转时,当直线与y=﹣x2﹣2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,联立直线y=ax+2和y=﹣x2﹣2x,消去y得,x2+(a+2)x+2=0,由判别式为0,即有(a+2)2﹣8=0解得a=﹣2+2或﹣2﹣2由图象可知a=﹣2﹣2不成立,舍去.故答案为:2﹣2.点评:本题考查分段函数的图象和运用,考查数形结合的思想方法,以及直线与抛物线相切的条件,考查运算能力,属于中档题.13.(5分)已知函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax(a>0)恰有三个零点,则实数a的取值范围为[,).考点:函数零点的判定定理.专题:函数的性质及应用.分析:先求出x时f(x)的解析式,再研究f(x)﹣ax=0在区间[,3]上的零点个数,即此时y=f(x)与y=ax交点的个数,注意数形结合.解答:解:设x∈[,1],则∈[1,3]又因为:函数f(x)满足f(x)=2f(),当x∈[1,3]时,f(x)=lnx,所以f(x)=2=2,x∈[,1]所以f(x)=,g(x)=f(x)﹣ax(a>0)恰有三个零点,即在[,3]内f(x)的图象与y=ax有三个交点,如图所示:当直线y=ax介于直线l1(过原点和(3,ln3)的直线)和直线l2(当x∈[1,3]时y=lnx的过原点的切线)易知,设y=lnx过原点的切线切点为(a,lna),则y′=,所以切线斜率为,所以切线为y﹣lna=,又因为过原点,所以lna=1,所以a=e∈[1,3]故,故实数a的范围是故答案为:点评:本题的解题思路充分体现了转化思想以及数形结合的思想,即把根的问题转化为函数零点问题,再进一步转化为两个函数图象交点的问题,做出图象直观的判断,再进行计算.本题难度较大.14.(5分)已知a>0,函数f(x)=在区间[0,4]上的最大值为,则a的值为.考点:函数的最值及其几何意义.专题:综合题;函数的性质及应用.分析:利用绝对值的几何意义,分类讨论,结合导数确定函数的单调性,从而可得函数f (x)=在区间[0,4]上的最大值,利用条件,即可求出a的值.解答:解:记f(x)在区间[0,4]上的最大值为g(a),当0≤x≤a时,f(x)=;当x>a时,f(x)=∴当0≤x≤a时,f′(x)=<0,f(x)在(0,a)上单调递减;当x>a时,f′(x)=>0,f(x)在(a,+∞)上单调递增.①若a≥4,则f(x)在(0,4)上单调递减,g(a)=f(0)=,不符合;②若0<a<4,则f(x)在(0,a)上单调递减,在(a,4)上单调递增∴g(a)=max{f(0),f(4)}∵f(0)﹣f(4)=∴当0<a≤1时,g(a)=f(4)=;当1<a<4时,g(a)=f(0)=,∴=,∴a=.故答案为:.点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,正确分类是关键.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(14分)设全集U=R,f(x)=x2+3x+2,g(x)=x2+(m+1)x+m,m∈R.(1)设集合A={x|f(x)=0},B={x|g(x)=0}.若(∁U A)∩B=Φ,求m的值.(2)设集合P={y|y=f(x)},Q={m|g(x)在区间[﹣1,+∞)上是增函数},求P∩Q.考点:交、并、补集的混合运算.专题:集合.分析:(1)解方程可得集合A={x|f(x)=0}={﹣1,﹣2},B={x|g(x)=0}.﹣1∈B,﹣m∈B,由(∁U A)∩B=∅,可得m∈A,进而可得答案.(2)根据二次函数的图象和性质,可得集合P=[﹣,+∞),Q=[1,+∞),代入集合交集定义,可得答案.解答:解:(1)∵集合A={x|f(x)=0}={﹣1,﹣2},B={x|g(x)=0}.∴﹣1∈B,﹣m∈B,若(∁U A)∩B=∅,则m∈A,即m=1或m=2,(2)∵集合P={y|y=f(x)}=[﹣,+∞),Q={m|g(x)在区间[﹣1,+∞)上是增函数}={m|}=[1,+∞),∴P∩Q=[1,+∞).点评:本题考查的知识点是集合的交,并,补集混合运算,难度不大,属于基础题.16.(14分)设函数f(x)=2x+.(1)若f(x)=,求x的值;(2)若关于x的方程f(2x)+af(x)+4=0在x∈(0,+∞)上有解,求实数a的取值范围.考点:函数的值域.专题:函数的性质及应用.分析:(1)x<0时,f(x)=2•2x<2,所以讲f(x)=带入f(x)=求x即可;(2)带入f(x)=,求出f(2x),从而得到,解出a=,这便求出了a的取值范围.解答:解:(1)f(x)=;∵x<0时,2•2x<2;∴只能,解得x=1,或﹣1(舍去);即x的值为1;(2);∴=;∴a的取值范围是(﹣∞,﹣2].点评:考查含绝对值函数,分段函数,已知函数值求自变量值,基本不等式:.17.(14分)已知函数f(x)=ax﹣lnx,g(x)=e ax+3x,其中a∈R.(Ⅰ)求f(x)的极值;(Ⅱ)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.考点:函数在某点取得极值的条件;利用导数研究函数的单调性.专题:计算题;导数的综合应用.分析:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=,对a分a≤0与a>0讨论,通过f′(x)的符号可判断f(x)在相应区间上的单调性,从而可求得f(x)的极值;(Ⅱ)可求得g′(x)=ae ax+3,对a分a>0,a=0与a<0讨论,通过f′(x)的符号可判断f(x)在相应区间上的单调性,可求得a的取值范围.解答:解:(Ⅰ)f(x)的定义域为(0,+∞),且f′(x)=a﹣=.①当a≤0时,f'(x)<0,故f(x)在(0,+∞)上单调递减.从而f(x)没有极大值,也没有极小值.②当a>0时,令f′(x)=0,得x=.f(x)和f′(x)的情况如下:x (0,)(,+∞)f′(x)﹣0 +f(x)↘↗故f(x)的单调减区间为(0,);单调增区间为(,+∞).从而f(x)的极小值为f()=1+lna;没有极大值.(Ⅱ)解:g(x)的定义域为R,且g′(x)=ae ax+3.③当a>0时,显然g′(x)>0,从而g(x)在R上单调递增.由(Ⅰ)得,此时f(x)在(,+∞)上单调递增,符合题意.④当a=0时,g(x)在R上单调递增,f(x)在(0,+∞)上单调递减,不合题意.⑤当a<0时,令g′(x)=0,得x0=ln(﹣).g(x)和g′(x)的情况如下表:x (﹣∞,x0) x0(x0,+∞)g′(x)﹣0 +g(x)↘↗当﹣3≤a<0时,x0≤0,此时g(x)在(x0,+∞)上单调递增,由于f(x)在(0,+∞)上单调递减,不合题意.当a<﹣3时,x0>0,此时g(x)在(﹣∞,x0)上单调递减,由于f(x)在(0,+∞)上单调递减,符合题意.综上,a的取值范围是(﹣∞,﹣3)∪(0,+∞).点评:本题考查函数在某点取得极值的条件,考查利用导数研究函数的单调性,突出考查分类讨论思想与方程思想,属于难题.18.(16分)某地发生某种自然灾害,使当地的自来水受到了污染.某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中f(x)=,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的取值范围.考点:函数模型的选择与应用.专题:函数的性质及应用.分析:(1)由题设:投放的药剂质量为m=4,自来水达到有效净化等价于4f(x)≥6,利用分段函数,建立不等式,即可求得结论;(2)由题意,∀x∈(0,7],6≤mf(x)≤18,m>0,由函数y是分段函数,故分段建立不等式组,从而解出m的值.解答:解:(1)由题设:投放的药剂质量为m=4,自来水达到有效净化等价于4f(x)≥6…(2分)∴f(x)≥,∴或…(4分)∴0<x≤6,亦即:如果投放的药剂质量为m=4,自来水达到有效净化一共可持续6天;…(8分)(2)由题设:∀x∈(0,7],6≤mf(x)≤18,m>0,…(10分)∵f(x)=,∴∀x∈(0,4],6≤mlog2(x+4)≤18,且∀x∈(4,7],6≤≤18,…(12分)∴且,…(14分)∴5≤m≤6,亦即:投放的药剂质量m的取值范围为[5,6].…(16分)点评:本题考查了分段函数模型的灵活应用,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.19.(16分)设a∈R,函数f(x)=x3﹣(2a+1)x2+(a2+a)x.(1)若函数g(x)=(x≠0)为奇函数,求a的值;(2)若函数f(x)在x=2处取得极小值,求a的值;(3)若a>﹣1,试求x∈[0,1]时,函数f(x)的最大值.考点:利用导数求闭区间上函数的最值;函数奇偶性的性质;函数在某点取得极值的条件.专题:导数的综合应用.分析:(1)求导函数,确定函数g(x)的解析式,利用函数为奇函数,即可求a的值;(2)确定函数f(x)的单调性,可求函数的极小值,利用函数在x=2处取得极小值,可求a 的值;(3)若a>﹣1,对a解析分类讨论,确定函数在x∈[0,1]上的单调性,即可求出函数f(x)的最大值.解答:解:(1)由题意,f′(x)=x2﹣(2a+1)x+(a2+a),…(1分)∴g(x)==x+﹣(2a+1)x(x≠0),∵函数g(x)=(x≠0)为奇函数,∴g(﹣x)+g(x)=0,即2a+1=0,∴a=﹣;…(4分)(2)f′(x)=(x﹣a)[x﹣(a+1)]…(5分)x (﹣∞,a)(a,a+1)(a+1,+∞)f′(x)+ ﹣+∴f(x)在x=a+1处取得极小值,在x=1处取得极大值,…(7分)由题设a+1=2,∴a=1;…(8分)(3)由(2)知:①a≥1时,f(x)在[0,1]上是增函数,∴[f(x)]max=f(1)=;…(10分)②a=0时,f(x)在[0,1]上是减函数,∴[f(x)]max=f(0)=0;…(11分)③0<a<1时,f(x)在[0,a]上是增函数,f(x)在[a,1]上是减函数,∴[f(x)]max=f(a)=;…(13分)④﹣1<a<0时,f(x)在[0,a+1]上是减函数,f(x)在[a+1,1]上是增函数,∵f(1)﹣f(0)=,∴﹣1<a<﹣时,f(1)>f(0,∴[f(x)]max=f(1)=;﹣≤a<0时,f(1)≤f(0),∴[f(x)]max=f(0)=0;…(15分)综上,[f(x)]max=.…(16分)点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.20.(16分)已知函数f(x)=(x2﹣3x+3)e x,x∈[﹣2,a],a>﹣2,其中e是自然对数的底数.(1)若a<1,求函数y=f(x)的单调区间;(2)求证:f(a)>;(3)对于定义域为D的函数y=g(x),如果存在区间[m,n]⊆D,使得x∈[m,n]时,y=g(x)的值域是[m,n],则称[m,n]是该函数y=g(x)的“保值区间”.设h(x)=f(x)+(x﹣2)e x,x∈(1,+∞),问函数y=h(x)是否存在“保值区间”?若存在,请求出一个“保值区间”;若不存在,请说明理由.考点:利用导数研究函数的单调性;函数的定义域及其求法;函数的值域.专题:综合题;新定义;导数的综合应用.分析:(1)求导数,分类讨论,利用导数的正负,即可求函数y=f(x)的单调区间;(2)由题意求证f(t)>13e﹣2,可解出函数f(x)在区间[﹣2,+∞)上的最小值,由此最小值与13e﹣2作比较即可证明此不等式;(3)函数y=h(x)存在“保值区间”[m.n]等价于,等价于关于x的方程h(x)=x在(1,+∞)有两个不相等的实数根.解答:(1)解:f(x)=(x2﹣3x+3)e x,f'(x)=(x2﹣x)e x=x(x﹣1)e x,x∈[﹣2,a],a>﹣2x (﹣∞,0)(0,1)(1,+∞)f′(x)+ ﹣+…(2分)由表知道:①﹣2<a≤0时,x∈(﹣2,a)时,f′(x)>0,∴函数y=f(x)的单调增区间为(﹣2,a);…(3分)②0<a<1时,x∈(﹣2,0)时,f′(x)>0,x∈(0,a)时,f′(x)<0,∴函数y=f(x)的单调增区间为(﹣2,0),单调减区间为(0,a);…(4分)(2)证明:f(a)=(a2﹣3a+3)e a,f′(a)=a(a﹣1)e a,a>﹣2,a (﹣2,0)(0,1)(1,+∞)f′(a)+ ﹣+从而函数f(x)在区间[﹣2,+∞)上有唯一的极小值f(1)=e …(6分)但f(﹣2)=13e﹣2<e,故函数f(x)在区间[﹣2,+∞)上的最小值为f(﹣2)=13e﹣2,…(8分)因为t>﹣2,所以f(t)>f(﹣2)=13e﹣2…(8分)(3)解:h(x)=f(x)+(x﹣2)e x=(x2﹣2x+1)e x,x∈(1,+∞),h′(x)=(x2﹣1)e x,∴x∈(1,+∞)时,h′(x)>0,∴y=h(x)在(1,+∞)上是增函数,…(9分)函数y=h(x)存在“保值区间”[m.n]等价于等价于关于x的方程h(x)=x在(1,+∞)有两个不相等的实数根,…(11分)令H(x)=h(x)﹣x,则H′(x)=(x2﹣1)e x﹣1,H″(x)=(x2+2x﹣1)e x,∵x∈(1,+∞),∴H″(x)>0,∴H′(x)在(1,+∞)上是增函数,∵H′(1)=﹣1<0,H′(2)>0,且y=H′(x)在[1,2]图象不间断,∴∃x0∈(1,2)使得H′(x0)=0,…(13分)∴函数y=H(x)在(1,x0)上是减函数,在(x0,+∞)上是增函数,∵H′(1)=﹣1<,∴x∈(1,x0],H(x)<0,∴函数y=H(x)在(1,+∞)至多有一个零点,即关于x的方程h(x)=x在(1,+∞)至多有一个实数根,…(15分)∴函数y=h(x)是不存在“保值区间”.…(16分)点评:本题考查导数在最值问题中的运用,利用导数研究单调性,再利用单调性求最值,这是导数的重要运用.。
