第24讲 圆的有关性质(含答案点拨)
人教版九年级数学第24章 圆的有关性质 知识点精讲精练(含答案)

第二十四章 圆的有关性质知识点思维导图能力培养:符号意识、几何直观、推理能力、运算能力 【实战篇】知识点一:圆的有关概念 1. 圆的定义(1)描述性定义:如图,在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆. 其固定的端点O 叫做圆心,线段OA 叫做半径.(2)集合性定义:圆可以看成是所有到定点(圆心)的距离等于定长(半径)的点的集合. 2. 圆的表示方法:以点O 为圆心的圆,记作⊙O ,读作“圆O ”. 3. 圆具有的特性(1)圆上各点到定点(圆心O )的距离都等于定长(半径r ); (2)到定点的距离等于定长的点都在同一个圆上.注意:(1)确定一个圆取决于两个因素:圆心和半径. 圆心确定圆的位置,半径确定圆的大小.(2)同一个圆中的所有半径都相等,所以圆上任意两点和圆心(三点不共线)构成的三角A形都是等腰三角形.4. 圆的有关概念【例1】如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心、CB长为半径的圆恰好经过AB的中点D,则AC的长为______________.【例1】【解析】同一个圆中的所有半径都相等,所以在圆中“连半径”是常用的辅助线,本题先连接CD,根据直角三角形斜边上的中线的性质得出CD=5,所以半径BC=CD=5,又由已知AB=10,利用勾股定理得出AC==【答案】 【巩固】1. 如图,AB 是⊙O 的直径,点C 在圆上,∠ABC =65°,那么∠OCA 的度数是( ) A. 25°B. 35°C. 15°D. 20°2. 如图,在⊙O 中,下列说法不正确的是( ) A. AB 是⊙O 的直径B. 有5条弦C. AD 和BD 都是劣弧,ABD 是优弧D. CO 是圆O 的半径【巩固答案】 1. A 2.B知识点二:垂直于弦的直径CB DAABBA1. 圆的轴对称性圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴. 2. 垂径定理垂直于弦的直径平分弦,并且平分弦所对的两条弧. 符号语言:∵如图,CD 是直径,CD ⊥AB 于点M ,∴AM =BM ,AC =BC ,AD =BD .3. 垂径定理的推论平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 符号语言:∵如图,CD 是直径,AM =BM (AB 不是直径),∴CD ⊥AB ,AC =BC ,AD =BD .【例2】如图,AB ,BC 是⊙O 的两条弦,AO ⊥BC ,垂足为D ,若⊙O 的半径为5,BC =8,则AB 的长为( ) A. 8B. 10C.34D. 54【例2】【解析】连接OB ,根据垂径定理求出BD =12BC =4,已知半径OB =5,在Rt △OBD中,由勾股定理求出OD3,所以AD =8,在Rt △ABD 中,再由勾股定理求出AB.【答案】D 【巩固】1. 下列说法不正确的是( )A. 圆既是轴对称图形又是中心对称图形B. 圆有无数条对称轴C. 圆的每一条直径都是它的对称轴D. 圆的对称中心是它的圆心2. 如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,OC =5 cm ,CD =8 cm ,则AE 的长为( ) A. 8 cmB. 5 cmC. 3 cmD. 2 cm【巩固答案】 1. C 2. A知识点三:弧、弦、圆心角 1. 圆的旋转对称性圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合. 因此,圆也是中心对称图形,圆心就是它的对称中心. 2. 圆心角的定义顶点在圆心的角叫做圆心角.如图:∠AOB 是AB 所对的圆心角,AB 是∠AOB 所对的弧. 注意:一条弧所对的圆心角只有一个. 3. 弧、弦、圆心角之间的关系A【例3】如图,点A ,B ,C ,D 在⊙O 上,且AB =CD . 求证:AC =BD .【例3】【解析】根据圆心角、弧、弦的关系,由AB =CD 得到AB =CD ,进而AB +BC =CD +BC ,即AC =BD ,所以AC =BD . 【答案】证明:∵AB =CD ∴AB =CD ,∴AB+BC =CD +BC , 即AC =BD , ∴AC =BD . 【巩固】1. 如图,在⊙O 中,∠AOB =∠COD ,那么AC 和BD 的大小关系是( )A. AC >BDB. AC <BDC. AC =BDD. 无法确定D2. 如图,C 是⊙O 上的点,CD ⊥OA 于点D ,CE ⊥OB 于点E ,且CD =CE ,则AC 与BC 的关系是( )A. AC =BCB. AC >BCC. AC <BCD. 不能确定【巩固答案】 1. C 2. A知识点四:圆周角 1. 圆周角的定义顶点在圆上,并且两边都与圆相交的角叫做圆周角.注意:(1)圆周角必须具备两个条件:①顶点在圆上;②两边都与圆相交. (2)同一条弧所对的圆周角有无数个. 2. 圆周角和圆心角的区别和联系3. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.如图,∠ACB =21∠AOB .4. 圆周角定理的推论推论1 同弧或等弧所对的圆周角相等.推论2 (1)半圆(或直径)所对的圆周角是直角; (2)90°的圆周角所对的弦是直径. 5. “五量关系”定理在同圆或等圆中,如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.【例4】如图,AB 为⊙O 的直径,C 、D 为⊙O 上两点,∠BCD =40°,则∠ABD 的大小为( ) A. 60°B. 50°C. 40°D. 20°【例4】【解析】本题考查的是圆周角定理的两个推论,根据题意先连接AD ,根据圆周角定理的推论可知,∠A =∠BCD =40°,又由AB 为⊙O 的直径知∠ADB =90°,所以∠ABD =90°-∠A =50°. 故选B.【答案】B 【巩固】1. 如图,点A ,B ,C 在⊙O 上,若∠OAB =54°,则∠C 的度数为( ) A. 54°B. 46°C. 36°D. 27°BAAB2. 如图,点A,B,C,D在⊙O上,BC=CD,∠CAD=30°,∠ACD=50°,则∠ADB =___________.【巩固答案】1.C2.70°知识点五:圆内接多边形1.圆内接多边形的定义如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.2.圆内接四边形的性质圆内接四边形的对角互补.注意:每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.拓展:圆内接四边形的每一个外角都等于它的内对角.【例5】如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD =130°,则∠DCE的度数为()A. 45°B. 50°C. 65°D. 75°【例5】【解析】根据圆周角定理求出∠A =12∠BOD =65°,再根据圆内接四边形的性质得出∠BCD =180°-∠A =115°,则∠DCE =180°-∠BCD =65°. 故选C. 【答案】C 【巩固】1. 如图,在⊙O 中,∠AOB =120°,P 为劣弧AB 上的一点,则∠APB 的度数是_____________.2. 如图,四边形ABCD 为⊙O 的内接四边形,已知∠C =∠D. 问AB 与CD 有怎样的位置关系,请说明理由.【巩固答案】 1. 120° 2. 解:AB ∥CDB理由如下:∵四边形ABCD为⊙O的内接四边形,∴∠A+∠C=180°,∵∠C=∠D,∴∠A+∠D=180°,∴AB∥CD.。
九年级数学上册第二十四章圆24.1圆的有关性质24.1.1圆ppt作业课件新版新人教版

14.(练习3变式)如图,已知BD,CE是△ABC的高,试说明:B,C,D, E四点在同一个圆上.
解:取 BC 的中点 F,连接 DF,EF.∵BD,CE 是△ABC 的高,∴△ BCD 和△BCE 都是直角三角形,∴DF,EF 分别为 Rt△BCD 和 Rt△BCE 斜边上的中线,∴DF=EF=BF=CF=12 BC,∴E,B,C,D 四点在以
第11题图
12.如图,矩形PAOB的顶点P在弧MN上,且不与M,N重合.顶点A,B
分别在线段OM,ON上.当P点在弧MN上移动时,PA2+PB2的值( C )
A.逐渐变大 B.逐渐变小
C.不变
D.不能确定
第12题图
13.(随州中考)如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则 ∠B=_____6_0__度.
解:连接 OA,∵∠POM=45°,四边形 ABCD 为正方形,∴AB=BC =CD=OC,设 AB=x,则 OB=2x,又 OA=5,在 Rt△ABO 中,由勾股定 理有 x2+(2x)2=52,∴x= 5 (取正值),即 AB 的长为 5
第7题图
8.(新县月考)若圆的半径为3,则圆中的弦AB长度的取值范围是 ___0_<__A__B_≤_6_.
9.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于 点E,F,∠B=∠C,求证:CE=BF.
解:易证△BOE≌△COF(ASA),∴OF=OE,∴CO+OE=BO+ OF,即CE=BF
第二十四章 圆
24.1.1 圆
知识点1:圆的定义 1.平面内已知点P,以点P为圆心,3 cm为半径作圆,这样的圆可以作( )
A
A.1个 B.2个 C.3个 D.无数个
第24章 圆章节知识点及习题及答案

第二十四章圆章节知识点思维导图:一、圆的有关性质(一)与圆有关的概念1、定义:在一个平面内线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
2、弦:连接圆上任意两点的线段叫做弦,经过圆心的弦,叫做直径。
3、弧:圆上任意两点间的部分(曲线)叫做圆弧,简称弧。
能够互相重合的弧叫等弧。
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆,大于半圆的弧叫优弧;小于半圆的弧叫劣弧,由弦及其所对的弧组成的圆形叫弓形。
4、圆心角:我们把顶点在圆心的角叫做圆心角。
5、圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
注意:在圆中,同一条弦所对的圆周角有无数个。
6、弦心距:从圆心到弦的距离叫弦心距。
7、同心圆、等圆:圆心相同,半径不相等的两个圆叫同心圆;能够重合的两个圆叫等圆。
8、点的轨迹:1)圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;2)垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3)角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4)到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5)到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
(二)圆的性质1、对称性:圆是轴对称图形,任何一条直径所在直线都是它的对称轴;圆也是以圆点为对称中心的中心对称图形。
2、性质:①垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧;推论1 :平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个,就可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧。
推论2:圆两条平行弦所夹的弧相等。
②圆心角定理(圆心角、弧、弦、弦心距之间的关系):在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦心距相等;圆心角的度数与它所对的度数相等。
数学中考一轮复习学案 第24节 圆的有关概念与性质(含解析)

第四章图形的性质第24节圆的有关概念与性质■知识点一:圆的有关概念(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点为圆心,定长为半径.(2)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧称为优弧,小于半圆的弧称为劣弧.(3)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.(4)相关概念:同心圆、弓形、等圆、等弧.(5)圆心角:顶点在圆心的角叫做圆心角.(6)圆周角:顶点在圆上,并且两边和圆相交的角是圆周角.(7)确定圆的条件:过已知一点可作无数个圆,过已知两点可作无数个圆,过不在同一条直线上的三点可作一个圆.(8)圆的对称性:圆是轴对称图形,其对称轴是直径所在的直线;圆是中对称图形,对称中心为圆心,并且圆具有旋转不变性.■知识点二:垂径定理及推论:①垂直于弦的直径平分弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,③弦的垂直平分线经过圆心,并且平分弦所对的两条弧.④平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.⑤圆的两条平行弦所夹的弧相等.■知识点三:圆心角、弧、弦的关系(1)定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.(3)正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.(4)在具体应用上述定理解决问题时,可根据需要,选择其有关部分.■知识点四:圆周角定理及推论①圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等.推论2:直径所对的网周角是直角;90°的圆周角所对的弦是直径.推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.②圆内接四边形的任意一组对角互补.■考点1.圆的有关概念◇典例:(2017年黑龙江大庆)如图,点M,N在半圆的直径AB上,点P,Q在上,四边形MNPQ 为正方形.若半圆的半径为,则正方形的边长为.【考点】正方形的性质;勾股定理;圆的认识.【分析】连接OP,设正方形的边长为a,则ON=,PN=a,再由勾股定理求出a的值即可.解:连接OP,设正方形的边长为a,则ON=,PN=a,在Rt△OPN中,ON2+PN2=OP2,即()2+a2=()2,解得a=2.故答案为:2.【点评】本题考查的是正方形的性质,勾股定理;圆的认识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.◆变式训练(2017•宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 __________■考点2.垂径定理及其推论◇典例:(2018年黑龙江省龙东、七台河、佳木斯、鸡西、伊春、鹤岗、双鸭山)如图,AB为⊙O 的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为.【考点】垂径定理,勾股定理【分析】连接OC,由垂径定理知,点E是CD的中点,AE=CD,在直角△OCE中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.解:连接OC,∵AB为⊙O的直径,AB⊥CD,∴CE=DE=CD=×6=3,设⊙O的半径为xcm,则OC=xcm,OE=OB﹣BE=x﹣1,在Rt△OCE中,OC2=OE2+CE2,∴x2=32+(x﹣1)2,解得:x=5,∴⊙O的半径为5,故答案为:5.【点评】本题利用了垂径定理和勾股定理求解,熟练掌握并应用定理是解题的关键.◆变式训练1.(2018年山东省烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C 三点的圆的圆心坐标为.2.(2018年浙江省绍兴市)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)■考点3. 圆心角、弧、弦的关系◇典例(2017•牡丹江)如图,在⊙O中,=,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.【考点】圆心角、弧、弦的关系;垂径定理.【分析】连接OC,先根据=得出∠AOC=∠BOC,再由已知条件根据AAS定理得出△COD ≌△COE,由此可得出结论.证明:连接OC,∵=,∴∠AOC=∠BOC.∵CD⊥OA于D,CE⊥OB于E,∴∠CDO=∠CEO=90°在△COD与△COE中,∵,∴△COD≌△COE(AAS),∴OD=OE,∵AO=BO,∴AD=BE.【点评】本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.◆变式训练(2017•宜昌)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A.AB=AD B.BC=CD C. D.∠BCA=∠DCA■考点4. 圆周角定理及其推论◇典例:1.(2018 年广西梧州市)如图,已知在⊙O 中,半径 OA=2,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO=__________度.【考点】圆周角定理,勾股定理的逆定理,等腰三角形的性质【分析】根据勾股定理的逆定理可以判断△AOB 的形状,由圆周角定理可以求得∠BOD 的度数,再根据三角形的外角和不相邻的内角的关系,即可求得∠AOC的度数.解:∵OA=2,OB=2,AB=2,∴OA 2+OB2=AB2,OA=OB,∴△AOB 是等腰直角三角形,∠AOB=90°,∴∠OBA=45°,∵∠BAD=18°,∴∠BOD=36°,∴∠ACO=∠OBA+∠BOD=45°+36°=81°,故答案为:81.【点评】本题考查圆周角定理、勾股定理的逆定理、等腰三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.◆变式训练1.(2018年四川省南充)如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B 的度数是()A.58° B.60° C.64° D.68°2.(2017•锦州)如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为()A.55°B.50°C.45°D.40°一、选择题1.(2018年广西柳州市)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为()A.84°B.60°C.36°D.24°2.(2018年内蒙古赤峰市)如图,AB是⊙O的直线,C是⊙O上一点(A.B除外),∠AOD=130°,则∠C的度数是()A.50°B.60°C.25°D.30°3.(2018年浙江省衢州市)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是()A.75°B.70°C.65°D.35°4.(2018年湖北省襄阳)如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.4 B.2C. D.25.(2018年四川省甘孜州)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD二、填空题6.(2018年广东省)同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是.7.(2018年青海省)如图,A.B、C是错误!未找到引用源。
人教版九年级数学上册第24章24.1圆的有关性质考点与题型归纳

人教版九年级数学上册第二十四章圆24.1 圆的有关性质一:考点归纳考点一、圆在一个平面内,一条线段O A绕它的一个端点O旋转一周,另一个端点A所形成的图形叫作圆. 圆心:固定的端点叫作圆心.半径:线段OA的长度叫作这个圆的半径.(1)圆的表示方法:以点O为圆心的圆,记作“ ⊙O ”,读作“圆O”. 同圆的第二定义:所有到定点的距离等于定长的点组成的图形叫作圆.考点二、垂直于弦的直径(1)圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,圆有无数条对称轴.(2)垂直于弦的直径平分弦,并且平分弦所对的弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.考点三、弧、弦、圆心角(1)顶点在圆心的角叫做圆心角 .(2)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(3)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等. 在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.考点四、圆周角(1)圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角. 特征:①角的顶点在圆上;②角的两边都与圆相交.(2)同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.(3)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(5)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.圆内接四边形的对角互补.二:【题型归纳】【题型一】圆1.下列说法正确的是()①弦是圆上两点间的部分;②直径是弦;③经过圆心的每一条直线都是圆的对称轴;A.0个B.1个C.2个D.3个2.下列说法:①直径是弦;②长度相等的两条弧是等弧;③半圆是弧,但弧不一定是半圆;④圆的对称轴是直径;⑤外心在三角形的一条边上的三角形是直角三角形,正确的命题有()A.1个B.2个C.3个D.4个【题型二】垂直于弦的直径3.如图,DC是⊙O的直径,弦AB⊥CD于点F,连接BC,BD,则错误结论为()A.OF=CF B.AF=BF C.AD BDD.∠DBC=90°4.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5º,AB=2,则半径OB等()A .1B .22C .2D .2【题型三】弧、弦、圆心角5.给出下列命题:①弦是直径;②圆上两点间的距离叫弧;③长度相等的两段弧是等弧;④圆心角的度数与它所对的弧的度数相等;⑤圆是轴对称图形,不是中心对称图形;⑥直径是弦.其中正确的个数为( )A .1B .2C .3D .46.如图,AB 为O 的直径,点D 是弧AC 的中点,过点D 作DE AB ⊥于点E ,延长DE 交O 于点F ,若12AC =,3AE =,则O 的直径长为( )A .10B .13C .15D .16.7.O 是四边形ABCD 的外接圆,AC 平分BAD ∠,则正确结论是( )A .AB AD = B .BC CD = C .AB BD = D .ACB ACD ∠=∠【题型四】圆周角8.如图,O 是ABC 的外接圆,CD 是O 的直径,35B ∠=︒,则ACD ∠的度数是( )A .45︒B .50︒C .55︒D .60︒9.如图,AB 为⊙O 的直径,CD 为⊙O 的弦,∠ACD=40°,则∠BAD 的大小为()A .60ºB .30ºC .45ºD .50º三:基础巩固和培优一、单选题1.如图,点A 、B 、C 在⊙O 上,CO 的延长线交AB 于点D ,∠A =50°,∠B =30°,∠ACD 的度数为( )A .10°B .15°C .20°D .30°2.如图,在5×5的正方形网格中,一条圆弧经过A ,B ,C 三点,那么这条弧所在圆的半径是( )A .2B .5C .22D .33.如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB 宽为4m ,水面最深地方的高度为1m ,则该输水管的半径为( )A .2mB .2.5mC .4mD .5m4.如图,在⊙O 中,半径OC 垂直弦AB 于D ,点E 在⊙O 上,∠E =22.5º,AB =2,则半径OB 等( )A .1B .22C .2D .25.下列说法中,正确的是( )A .直径所对的弧是半圆B .相等的圆周角所对的弦相等C .两个半圆是等弧D .一条弧所对的圆心角等于它对的圆周角的一半6.如图,已知抛物线()()31916y x x =---与x 轴交于,A B 两点,对称轴与抛物线交于点C ,与x 轴交于点D ,C 的半径为2,G 为C 上一动点,P 为AG 的中点,则DP 的最大值为( )A .412B .23C .72D .57.如图,AB 是O 的直径,弦CD 交AB 于点P ,4AP =,8BP =,45APC ∠=︒,则CD 的长为( )A .34B .62C .234D .128.已知,AB 为圆O 的一条弦,∠AOB=80°,则弦AB 所对的圆周角的度数为( )A .40︒B .140︒C .70︒D .40︒或140︒9.下列说法:①直径是弦;②长度相等的两条弧是等弧;③半圆是弧,但弧不一定是半圆;④圆的对称轴是直径;⑤外心在三角形的一条边上的三角形是直角三角形,正确的命题有 ( )A .1个B .2个C .3个D .4个10.如图,已知100BOC ∠=︒,则A ∠的度数为( )A .50︒B .80︒C .100︒D .130︒二、填空题 11.圆弧形蔬菜大棚的剖面如图,已知AB =16m ,半径OA =10m ,OC ⊥AB ,则中柱CD 的高度为_________m .12.若圆的半径为6cm ,圆中一条弦长为3cm ,则此弦中点到此弦所对弧的中点的距离为_______cm.13.如图,在⊙O中,CA DB,∠1=30°,则∠2=_________°.14.如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则CD=______.15.如图,△ABC的三个顶点都在⊙O上,∠ACB=40°,则∠OAB=______.三、解答题16.如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.(1)求OA的长度;(2)求CE的长度.17.如图,已知,AB是O的直径,弦CD⊥AB于点E,∠ACD=30°,AE=3cm,求BD的长度.18.如图,D 是O 弦BC 的中点,A 是BC 上一点,OA 与BC 交于点E ,已知8AO =,12BC =. (1)求线段OD 的长.(2)当2EO BE =时,求ED ,EO 的长.19.已知P 是O 上一点,过点P 作不过圆心的弦PQ ,在劣弧PQ 和优弧PQ 上分别有动点A B 、 (不与P ,Q 重合),连接AP 、BP 若=APQ BPQ ∠∠.(1)如图1,当=45APQ ∠︒,=1AP ,=22BP O 的半径;(2)如图2,选接AB ,交PQ 于点M ,点N 在线段PM 上(不与P M 、重合),连接ON OP 、,若+2=90NOP OPN ∠∠︒,探究直线AB 与ON 的位置关系,并证明.20.如图,90BCD ∠=︒,BC DC =,直线PQ 经过点D .设PDC α∠=(45135α︒<<︒),BA PQ ⊥于点A ,将射线CA 绕点C 按逆时针方向旋转90︒,与直线PQ 交于点E .(1)判断:ABC ∠________PDC ∠(填“>”或“=”或“<”);(2)猜想ACE △的形状,并说明理由;(3)若ABC的外心在其内部(不含边界),直接写出 的取值范围.参考答案题型归纳【解析】:1【详解】①弦是连接圆上两点间线段,故不正确;②直径是最长的弦,故正确;③经过圆心的每一条直线都是圆的对称轴,故正确;故选C.2.【详解】解:①直径是弦,是真命题;②在同圆与等圆中,长度相等的两条弧是等弧,原命题是假命题;③半圆是弧,但弧不一定是半圆,是真命题;④圆的对称轴是直径所在的直线,原命题是假命题;⑤外心在三角形的一条边上的三角形是直角三角形,是真命题;故选:C.【解析】3.【详解】解:∵DC是⊙O直径,弦AB⊥CD于点F,∴AF=BF,AD BD,∠DBC=90°,∴B、C、D正确;∵点F不一定是OC的中点,∴A错误.故选:A.4.【详解】解:∵半径OC⊥弦AB于点D,∴=AC BC,∴∠E=12∠BOC=22.5°,∴∠BOD=45°,∴△ODB是等腰直角三角形,∵AB=2,10∴DB=OD=1,则半径OB.故选:D.【解析】:5【详解】解:①弦不一定是直径,原命题是假命题;②圆上任意两点间的部分叫弧,原命题是假命题;③在同圆或等圆中,长度相等的两段弧是等弧,原命题是假命题;④圆心角的度数与它所对的弧的度数相等,是真命题;⑤圆是轴对称图形,也是中心对称图形,原命题是假命题;⑥直径是弦,是真命题.故选:B.6【详解】解:连接OD交AC于点G,∵AB⊥DF,∴AD AF=,DE=EF.又点D是弧AC的中点,∴AD CD AF==,OD⊥AC,∴AC DF=,∴AC=DF=12,∴DE=6.设O的半径为r,∴OE=AO-AE=r-3,在Rt△ODE中,根据勾股定理得,OE2+DE2=OD2,∴(r-3)2+62=r2,解得r=152.∴O的直径为15.故选:C.7.【详解】解:ACB ∠与ACD ∠的大小关系不确定,AB ∴与AD 不一定相等,故选项A 错误; AC 平分BAD ∠,BAC DAC ∴∠=∠,BC CD ∴=,故选项B 正确;ACB ∠与ACD ∠的大小关系不确定,∴AB 与AD 不一定相等,选项C 错误;∵BCA ∠与DCA ∠的大小关系不确定,选项D 错误;故选B .8.【详解】解:连接AD ,∵CD 是圆的直径,∴∠DAC=90°,∵∠B=∠D=35°,∴∠ACD=90°-∠D=90°-35°=55°,故选C .9.【详解】连结BD ,∵同弧所对的圆周角相等,∴∠B=∠C=40º,∵AB 为直径,∴∠ADB=90º,∴∠DAB+∠B=90º,∴∠DAB=90º-40º=50º.故选择:D.二:基础巩固和培优1.C【详解】解:∵∠A=50°,∴∠BOC=2∠A=100°,∵∠B=30°,∠BOC=∠B+∠BDC,∴∠BDC=∠BOC-∠B=100°-30°=70°,∴∠ACD=70°-50°=20°;故选:C.2.B【详解】解:如图线段AB的垂直平分线和线段BC的垂直平分线的交点M,即点M为圆心,22+125故选:B.3.B【详解】过点O作OD⊥AB于点D,连接OA,设OA=x,则OD=x-1,在Rt△AOD中, x2=(x-1)2+22,解得x=2.5m.故选B.4.D【详解】解:∵半径OC⊥弦AB于点D,∴=AC BC,∴∠E=12∠BOC=22.5°,∴∠BOD=45°,∴△ODB是等腰直角三角形,∵AB=2,∴DB=OD=1,则半径OB2211=2.故选:D.5.A【详解】解:A、直径所对的弧是半圆,正确,符合题意;B、同圆或等圆中,相等的圆周角所对的弦相等,故原命题错误,不符合题意;C、半径相等的两个半圆是等弧,故原命题错误,不符合题意;D、同圆或等圆中,一条弧所对的圆心角等于它对的圆周角的一半,故原命题错误,不符合题意,故选:A.6.C【详解】如图,连接BG,由题意可得:A(1,0),B(9,0),D是AB的中点,∴AB=8,∴BD=4, 3y=(1)(9)16x x ---=23(5)316x --+, ∴C(5,3),∴CD=3,由D 、P 分别是AB 、AG 的中点可得:DP 是ABG 的中位线, ∴DP=12BG ,要求DP 的最大值,即要求BG 的最大值,当G 、C 、B 三点共线时,BG 最大,BC=22345+=,BG=5+2=7,DP=12BG=72.故选:C .7.C【详解】解:∵4AP =,8BP =,∴AB=12,AO=6,∴PO=2,作OM ⊥CD ,连接OC ,∵45DPB APC ∠=∠=︒,∴∠AOM=45°,△MOP 为等腰直角三角形,∴222MO OP ,在Rt △OCM 中根据勾股定理22226(2)34CMCO OM , ∴2234CD CM .故选:C .8.D【详解】解:如图,弦AB 所对的圆周角为C D ∠∠,,80AOB ∠=︒,40D ∴∠=︒,四边形ADBC 为O 的内接四边形,180C D ∴∠+∠=︒,=140C ∴∠︒.故选D .9.C【详解】解:①直径是弦,是真命题;②在同圆与等圆中,长度相等的两条弧是等弧,原命题是假命题; ③半圆是弧,但弧不一定是半圆,是真命题;④圆的对称轴是直径所在的直线,原命题是假命题;⑤外心在三角形的一条边上的三角形是直角三角形,是真命题; 故选:C .10.A【详解】解:∵100BOC ∠=︒,∴A ∠=1250BOC ∠=︒,故选A .11.4【详解】解:∵CD 垂直平分AB ,∴AD =8.∴OD =22108-=6m ,∴CD =OC−OD =10−6=4(m ).故答案是:412.3或9【详解】在⊙O 中,弦AB=63cm ,半径6R =;过圆心O 作直径MN ,且MN ⊥AB 于点C ,连接OB ;则AC=BC=12AB=33,OB=6, 由勾股定理得:()22226333OB BC -=-=,∴CM=6+3=9,CN=6-3=3;∵MN ⊥AB ,且MN 为⊙O 的直径,∴点M 、N 分别为AMB 、ANB 的中点, ∴AB 弦中点到弦所对应的弧的中点的距离分别为3或9. 故答案为:3或9.13.30【详解】解:CA DB =,BC BC =,∴AB CD =,∴∠1=∠2,∠1=30°,∴∠2=30°;故答案为30.14.2【详解】∵OD ⊥AB ,OD 过圆心O , ∴162AD BD AB ===,由勾股定理可得:8OD ===, ∴1082CD CO OD =-=-=; 故答案是2.15.50°【详解】解:根据圆周角定理得:∠AOB=2∠ACB ,∵∠ACB=40°,∴∠AOB=2×40°=80°,∵OA=OB ,∴∠OAB=∠OBA ,∴∠OAB+∠OBA+∠AOB=180°, ∴∠OAB=50°.故答案为: 50°.16.(1)5;(2)【详解】解:(1)∵在⊙O 中,OD ⊥弦AB , ∴AC =BC =12AB =4,设OA 为x ,则OD =OA =x ,∵CD =2,∴OC=x﹣2在Rt△ACO中,AC2+OC2=AO2∴42+(x﹣2)2=x2,解得x=5,∴OA=5;(2)连接BE,∵OA=OE,AC=BC,∴OC∥BE且OC=12 BE,∴∠EBA=∠OCA=90°,∵OC=OD﹣CD=5﹣2=3,∴BE=6,在Rt△ECB中,BC2+EB2=EC2∴42+62=EC2,∴CE=213.17.63BD cm=【详解】连接OC、OD,AB是⊙O的直径,弦CD⊥AB,∴CE=DE,∠AEC=∠DEB=90°,AC AD=,∴30ACD ∠=︒,∴260COA DOA ACD ∠=∠=∠=︒, OC =OA ,∴AOC △是等边三角形,∴AE =EO =3cm ,∴AO =DO =OB =6cm ,∴BE =9cm ,DE =22226333OD OE -=-=cm , ∴BD =22229(33)63BE DE +=+=cm . ∴DB 的长为63cm .18.(1)线段OD 的长为27;(2)ED 2=,EO=42【详解】解:(1)连接OB .∵OD 过圆心,且D 是弦BC 中点, ∴OD ⊥BC ,BD=12BC , 在Rt △BOD 中,OD 2+BD 2=BO 2. ∵BO=AO=8,BD=6.∴22228627BO BD --= (2)在Rt △EOD 中,OD 2+ED 2=EO 2. 设BE=x ,则2x ,DE=6x -, (())222762x x +-=, 整理得:212640x x +-=,解得:12416x x ==-,(舍去).∴BE=4,ED=642-=,EO=42.19.(1) ☉O 的半径是32;(2)A B ∥ON ,证明见解析 【详解】解:(1)连接AB ,在☉o 中,o APQ BPQ 45∠=∠=,o APB APQ BPQ 90∴∠=∠+∠=AB ∴是☉0的直径.Rt APB ∴∆在中,22AB AP BP =+AB=3∴∴☉0的半径是32(2)AB//ON证明:连接OA , OB , OQ ,在☉0中, AQ AQ =, BQ BQ =,Q 2APQ,B0Q 2BPO AO ∴∠=∠∠=∠.又APQ BPQ ∠=∠,AOQ BOQ ∴∠=∠.在AOB ∆中,OA OB =, AOQ BOQ ∠=∠,OC AB ∴⊥,即o OCA 90∠=连接OQ ,交AB 于点C在☉0中,OP OQ =OPN OQP.∴∠=∠延长PO 交☉0于点R ,则有2OPN QOR ∠=∠o NOP 2OPN 90∴∠+∠=,又:o NOP NOQ QOR 180∠+∠+∠=,NOQ 90O ∴∠=NOQ OCA 180O ∴∠+∠= .AB//ON ∴20.(1)=;(2)ACE △是等腰直角三角形;理由见解析;(3)4590α︒<<︒.【详解】解:(1) 90AB AD DCB ⊥∠=︒,,3609090180CDA ABC ∴∠+∠=︒-︒-︒=︒,180CDA CDE ∠+∠=︒,.EDC ABC ∴∠=∠故答案为:=.(2)ACE △是等腰直角三角形.理由如下:由旋转可得:90ACE BCD ∠=∠=︒,90ECD DCA DCA BCA ∴∠+∠=︒=∠+∠,ECD BCA ∴∠=∠,在ECD 与ACB △中,ECD BCA CD CBEDC ABC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ECD ACB ASA ∴≌EC AC ∴=,又90ACE ∠=︒ACE ∴是等腰直角三角形.(3)当∠ABC=α=90°时, ABC 的外心在其斜边上,∠ABC=α>90°时,ABC 的外心在其外部,由PDC ∠>45EAC ∠=︒,PDC DCA EAC ∠=∠+∠<135︒, ∴ 45°<α<135°,故:4590α︒<<︒.。
人教版初中九年级数学上册第二十四章《圆》知识点(含答案解析)
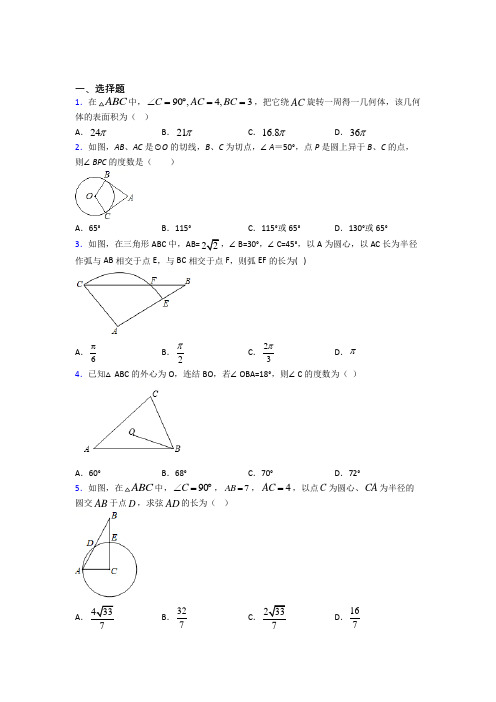
一、选择题1.在ABC 中,90,4,3C AC BC ∠=︒==,把它绕AC 旋转一周得一几何体,该几何体的表面积为( )A .24πB .21πC .16.8πD .36π 2.如图,AB 、AC 是⊙O 的切线,B 、C 为切点,∠A =50°,点P 是圆上异于B 、C 的点,则∠BPC 的度数是( )A .65°B .115°C .115°或65°D .130°或65° 3.如图,在三角形ABC 中,AB=22,∠B=30°,∠C=45°,以A 为圆心,以AC 长为半径作弧与AB 相交于点E ,与BC 相交于点F ,则弧EF 的长为( )A .6πB .2πC .23πD .π4.已知△ABC 的外心为O ,连结BO ,若∠OBA=18°,则∠C 的度数为( )A .60°B .68°C .70°D .72°5.如图,在ABC 中,90C ∠=︒,7AB =,4AC =,以点C 为圆心、CA 为半径的圆交AB 于点D ,求弦AD 的长为( )A 433B .327C .337D .1676.如图,正方形ABCD 内接于O ,直径//MN AD ,则阴影部分的面积占圆面积的( )A .12B .16C .13D .147.若圆锥的底面半径为5cm ,侧面积为265cm π,则该圆锥的高是( ) A .13cm B .12cm C .11cm D .10cm 8.如图,ABC 的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将ABC 绕点B 顺时针旋转到A B C '''的位置,且点A '、C '仍落在格点上,则线段AB 扫过的图形的面积是( )平方单位(结果保留)A .254πB .134πC .132πD .136π 9.如图,在⊙O 中,AB 是直径,弦AC=5,∠BAC=∠D .则AB 的长为( )A .5B .10C .52D .10210.如图,AB 是⊙O 的直径,C ,D 是⊙O 上的点,28CDB ∠=︒,过点C 作⊙O 的切线交AB 的延长线于点E ,则E ∠等于( )A .28︒B .34︒C .44︒D .56︒ 11.如图,⊙O 的半径为1,点 O 到直线 a 的距离为2,点 P 是直线a 上的一个动点,PA 切⊙O 于点 A ,则 PA 的最小值是( )A .1B .3C .2D .5 12.如图,ABC 的顶点A 是O 上的一个动点,90ACB ∠=︒,30BAC ∠=︒,边AC ,AB 分别交O 于点E ,D ,分别过点E ,D 作O 的切线交于点F ,且点F 恰好在边BC 上,连接OC ,若O 的半径为6,则OC 的最大值为( )A .393+B .2103+C .353+D .53 13.如图,点M 是矩形ABCD 的边BC 、CD 上的点,过点B 作BN ⊥AM 于点P ,交矩形ABCD 的边于点N ,连接DP ,若AB=6,AD=4,则DP 的长的最小值为( )A .2B .121313C .4D .514.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A.112.5°B.120°C.135°D.150°15.在△ABC中,∠ACB为锐角,分别以AB,AC为直径作半圆,过点B,A,C作弧BAC,如图所示.若AB=4,AC=2,图中两个新月形面积分别为S1,S2,两个弓形面积分别为S3,S4,S1-S2=14π,则S3-S4的值是( )A.294πB.234πC.114πD.54π二、填空题16.如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=________°.17.如图,四边形ABCD是O的内接四边形,对角线AC,BD交于点E,且AC BD AB==,若70AEB∠=︒,则AOB∠等于______︒.18.已知半径为5的圆O中,弦AB=8,则以AB为底边的等腰三角形腰长为___________.19.如图,PA,PB分别与O相切于A、B两点,点C为劣弧AB上任意一点,过点C的切线分别交AP,BP于D,E两点.若8AP=,则PDE△的周长为______.20.如图,O 的半径为6,AB 、CD 是互相垂直的两条直径,点P 是O 上任意一点,过点P 作PM AB ⊥于M ,PN CD ⊥于N ,点Q 是MN 的中点,当点P 沿着圆周从点D 逆时针方向运动到点C 的过程中,当∠QCN 度数取最大值时,线段CQ 的长为______.21.如图,已知正方形ABCD 的边长为2,点M 和N 分别从B 、C 同时出发,以相同的速度沿BC 、CD 方向向终点C 和D 运动.连接AM ,BN 交于点P ,则PC 长的最小值为____________.22.如图,直线AB 、CD 相交于点,30O AOC ∠=︒,半径为1cm 的⊙P 的圆心在直线AB 上,且与点O 的距离为8cm ,如果⊙P 以2cm/s 的速度,由A 向B 的方向运动,那么_________秒后⊙P 与直线CD 相切.23.在矩形ABCD 中,43AB =6BC =,若点P 是矩形ABCD 上一动点,要使得60APB ∠=︒,则AP 的长为__________.24.小明用一张扇形纸片做一个圆锥的侧面,已知该扇形的半径是10cm ,弧长是12πcm 2,那么这个圆锥的高是________cm .参考答案25.如图,在⊙O 中,弦AC 、BD 相交于点E ,且AB BC CD ==,若∠BEC=130°,则∠ACD 的度数为_____26.如图,已知空间站A 与星球B 距离为a ,信号飞船C 在星球B 附近沿圆形轨道行驶,B ,C 之间的距离为b .数据S 表示飞船C 与空间站A 的实时距离,那么S 的最小值________.三、解答题27.如图,AB 是O 的弦,CD 是O 的直径,CD AB ⊥,垂足为E .1CE =,3ED =.(1)求O 的半径.(2)求AB 的长.28.如图,在Rt △ABC 中,∠C =90°,以BC 为直径的圆O 交AB 于点D ,切线DE 交AC 于点E .(1)求证:∠A =∠ADE ;(2)若AD =8,DE =5,求BC 的长.29.如图,一条公路的转弯处是一段圆弧CD ,点O 是CD 的圆心,E 为 CD 上一点,OE ⊥CD ,垂足为F .已知CD=300m ,EF=50m ,求这段弯路的半径.30.如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧MN 的长度.。
人教版九年级数学上第24章圆24.1圆的有关性质弧、弦、圆心角讲义

合作探究探究点1 圆的定义情景激疑在准备好的一张纸上以点〇为圆心、3 cm为半径画一个圆,观察画图过程.由此你会得出什么结论?知识讲解定义1:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的圆形叫做圆.其固定的端点O叫做圆心,线段OA叫倣半径.以O点为圆心的圆,记作O,读作“圆O〞.定义2:圆心为O、半径为r的圆可以看成是所有到定点O的间隔等于定长r的点的集合.注意〔1)圆心确定圆的位置,半径确定圆的大小.(2) 确定一个圆首先确定圆心,再确定半径,二者缺一不可.(3) 定点是圆心,定长是半径.(4) “圆〞指的是“圆周〞,而不是“圆平面〞.典例剖析例1 以下说法错误的有 ( )(1) 经过P点的圆有无数个;(2) 以P点为圆心的圆有无数个;(3) 半径为3cm且经过P点的圆有无数个。
(4) 以P点为圆心、3cm为半径的圆有无数个.A. 1个B. 2个C. 3个D. 4个解析确定一个圆必须满足两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,故(1)(2)正确,(3)虽然半径,但P点不是圆心,实际上也只是一个条件,能作无数个圆,故(3)正确;(4)满足两个条件,只能作一个圆,所以(4)错误.综上所述,错误的说法有1个,应选A答案 A错因分析导致此题错误的主要原因是对于确定一个圆的两个要素(圆心和半径)理解不够准确。
类题打破1 以O点为圆心画圆,可以画______ 个圆;以4 cm为半径画圆.可以面_____个圆.答案无数无数点拨确定圆的条件:一是圆心,二是半径.探究点2 与圆有关的概念知识讲解连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径。
圆上任意两点间的局部AB.读作“圆弧AB〞或“弧AB〞,圆的任意一条直径的两个端点把图分成两条弧,每一条弧都叫做半圆。
注意 (1)弦和弧是有区别的,弦是线段,而弧是曲线。
(2)直径是圆中最长的弦,而弦不都是直径。
第24讲 圆的基本性 含答案

第24讲圆的基本性质1. (16,河北)如图所示的为4×4的网格图,A,B,C,D,O均在格点上,点O是( )第1题图第2题图第3题图例1题图A. △ACD的外心B. △ABC的外心C. △ACD的内心D. △ABC的内心2. (15,河北)如图,AC,BE是⊙O的直径,弦AD与BE相交于点F.下列三角形中,外心不是点O的是( )A. △ABEB. △ACFC. △ABDD. △ADE3. (12,河北)如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( )A. AE>BEB. »AD=»BCC. ∠D=12∠AEC D. △ADE∽△CBE圆的有关概念例1 (2019,扬州邗江区一模)如图,⊙O的直径BA的延长线与弦DC的延长线相交于点E,且CE=OB.已知∠DOB =72°,则∠E的度数为( )A. 36° B. 30° C. 18° D. 24°训练1题图训练2题图训练3题图例3题图针对训练1如图所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2 cm.若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是( )A. 1 cmB. 2 cmC. 4 cmD. πcm针对训练2 (2019,海口模拟)如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )A. 70° B. 60° C. 50° D. 40°确定圆的条件例2 (2019,北京)在平面内,给定不在同一条直线上的点A,B,C,如图所示,点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.(1)求证:AD=CD;(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.例2题图针对训练3 (10,河北)如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )A. 点P B. 点Q C. 点R D. 点M针对训练4 (2019,绥化)半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB 于点D.若△OBD是直角三角形,则弦BC的长为().圆的基本性质例3 (19,沈阳)如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD.若⊙O的半径是13,BD=24,则sin∠ACD的值是( )A. 1213 B.125 C.512 D.513针对训练5 (2019,绵阳)如图,AB 是⊙O 的直径,C 为»BD的中点,CF 为⊙O 的弦,且CF ⊥AB ,垂足为E ,连接BD 交CF 于点G ,连接CD ,AD ,BF .(1)求证:△BFG ≌△CDG ;(2)若AD =BE =2,求BF 的长.训练5题图垂径定理及其应用 例4 (2019,梧州)如图,在半径为13的⊙O 中,弦AB 与CD 相交于点E ,∠DEB=75°,AB =6,AE =1,则CD 的长是( )A. 2 6 B. 210 C. 211 D. 4 3例4题图训练6题图针对训练6 (19,黄冈)如图,一条公路的转弯处是一段圆弧(»AB ),点O 是这段弧所在圆的圆心,AB =40 m ,C 是»AB 的中点,D 是AB 的中点,且CD =10 m ,则这段弯路所在圆的半径为( )A. 25 m B. 24 m C. 30 m D. 60 m1. (2019,广元)如图,AB ,AC 分别是⊙O 的直径和弦,OD ⊥AC于点D ,连接BD ,BC ,且AB =10,AC =8,则BD 的长为( )A. 2 5 B. 4 C. 213 D. 4.81题图2题图3题图4题图5题图2. (2019,吉林)如图,在⊙O 中,»AB 所对的圆周角∠ACB =50°.若P 为»AB 上一点,∠AOP =55°,则∠POB 的度数为( )A. 30° B. 45° C. 55° D. 60°3. (2019,白银)如图,点A ,B ,S 在圆上,若弦AB 的长度等于圆半径的2倍,则∠ASB 的度数是( )A. 22.5°B. 30°C. 45°D. 60°4. (19镇江如图,四边形ABCD 是半圆的内接四边形,AB 是直径,»»DC CB =.若∠C =110°,则∠ABC 的度数为( )A. 55°B. 60°C. 65°D. 70°5. (2019,贵港)如图,AD 是⊙O 的直径,»»AB CD =.若∠AOB =40°,则圆周角∠BPC 的度数是( ) A. 40° B. 50° C. 60° D. 70°6. (2019,聊城)如图,BC 是半圆O 的直径,D ,E 是»BC上两点,连接BD ,CE 并延长相交于点A ,连接OD ,OE .如果∠A =70°,那么∠DOE 的度数为( )A. 35° B. 38° C. 40° D. 42°7. (2019,安顺)如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 的值为( )A. 13 B. 2 2 C. 223 D. 248. (2019,天水)如图,四边形ABCD 是菱形,⊙O 经过点A ,C ,D ,与BC 相交于点E ,连接AC ,AE .若∠D =80°,则∠EAC的度数为( )A. 20° B. 25° C. 30° D. 35°第6题图第7题图第8题图第9题图9. (2019,通辽)如图,等边三角形ABC内接于⊙O.若⊙O的半径为2,则图中阴影部分的面积等于( )A. π3 B.2π3 C.4π3 D. 2π10. (19,菏泽)如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( ) A. OC∥BD B. AD⊥OC C. △CEF≌△BED D. AF=FD11. (2019,陕西)如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB相交于点C,连接OF.若∠AOF=40°,则∠F的度数是( )A. 20° B. 35° C. 40° D. 55°第10题图第11题图第12题图第13题图12. (2019,赤峰)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,D是⊙O上一点,∠ADC=30°,则∠BOC的度数为( )A. 30° B. 40° C. 50° D. 60°.13. (2019,宁夏)如图,AB是⊙O的弦,OC⊥AB,垂足为C,将劣弧»AB沿弦AB折叠交于OC的中点D.若AB=210,则⊙O的半径为().14. (2019,盐城)如图,点A,B,C,D,E在⊙O上,且»AB所对的圆心角为50°,则∠E+∠C=°.第14题图第15题图第16题图第17题图15. (2019,安徽)如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D.若⊙O的半径为2,则CD的长为().16. (2019,广元)如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是().17. (2019,嘉兴)如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为().18. (2019,包头)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=23,弦BM平分∠ABC交AC于点D,连接MA,MC.(1)求⊙O的半径;(2)求证:AB+BC=BM.(1)解:如答图①,连接OA,OC,过点O作OH⊥AC于点H.第18题图19. (2019,荆门)如图,已知锐角三角形ABC的外接圆圆心为O,半径为R. (1)求证:ACsin B=2R;(2)若在△ABC 中,∠A =45°,∠B =60°,AC =3,求BC 的长及sin C 的值.第19题图1. (2019,湘潭)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=12(弦×矢+矢2).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC ⊥弦AB 时,OC 平分AB )可以求解.现已知弦AB =8 m ,半径等于5 m 的弧田,按照上述公式计算出弧田面积为 m 2.第1题图第2题图2. (2019,潍坊)如图,在平面直角坐标系xOy 中,一组同心圆的圆心为坐标原点O ,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线l 0,l 1,l 2,l 3,…都与x 轴垂直,相邻两直线的间距为1,其中l 0与y 轴重合.若半径为2的圆与l 1在第一象限内交于点P 1,半径为3的圆与l 2在第一象限内交于点P 2……半径为n +1的圆与l n 在第一象限内交于点P n ,则点P n 的坐标为 .(n 为正整数)3. (2019,福建)如图,四边形ABCD 内接于⊙O ,AB =AC ,BD ⊥AC ,垂足为E ,点F 在BD 的延长线上,且DF =DC ,连接AF ,CF .(1)求证:∠BAC =2∠DAC ;(2)若AF =10,BC =45,求tan ∠BAD 的值.第3题图4. (2019,温州)如图,在△ABC 中,∠BAC =90°,点E 在BC 边上,且CA =CE ,过A ,C ,E 三点的⊙O 交AB 于另一点F ,作直径AD ,连接DE 并延长交AB 于点G ,连接CD ,CF .(1)求证:四边形DCFG 是平行四边形; (2)当BE =4,CD =38AB 时,求⊙O 的直径. 第4题图第24讲圆的基本性质1. (16,河北)如图所示的为4×4的网格图,A,B,C,D,O均在格点上,点O是(B)第1题图第2题图第3题图A. △ACD的外心B. △ABC的外心C. △ACD的内心D. △ABC的内心【解析】由网格图,知点O是边AC,BC的垂直平分线的交点.根据三角形外心的定义,知点O是△ABC的外心.2. (15,河北)如图,AC,BE是⊙O的直径,弦AD与BE相交于点F.下列三角形中,外心不是点O的是(B)A. △ABEB. △ACFC. △ABDD. △ADE【解析】只有△ACF的三个顶点不都在⊙O上,故外心不是点O的是△ACF.3. (12,河北)如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是(D)A. AE>BEB. »AD=»BCC. ∠D=12∠AEC D. △ADE∽△CBE 【解析】∵CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,∴AE=BE,»».AC BC=∴选项A,B错误.∵∠AEC不是圆心角,∴∠D≠12∠AEC. ∴选项C错误.∵∠AED=∠CEB=90°,∠DAE=∠BCE,∴△ADE∽△CBE.∴选项D正确.圆的有关概念例1 (2019,扬州邗江区一模)如图,⊙O的直径BA的延长线与弦DC的延长线相交于点E,且CE=OB.已知∠DOB =72°,则∠E的度数为(D)A. 36° B. 30° C. 18° D. 24°【解析】如答图,连接CO.可知CE=OB=CO,得∠E =∠1.由∠2是△EOC的外角,得∠2=∠E+∠1=2∠E.由OC=OD,得∠D=∠2=2∠E.由∠3是△ODE的外角,得∠3=∠E+∠D=∠E+2∠E=3∠E.由∠3=72°,得3∠E=72°.解得∠E=24°.1题图1答图训练1题图训练2题图针对训练1如图所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2 cm.若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是(C)A. 1 cmB. 2 cmC. 4 cmD. πcm 【解析】∵AB=2 cm,∴圆的直径是4 cm.针对训练2 (2019,海口模拟)如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为(D)A. 70° B. 60° C. 50° D. 40°【解析】∵AD∥OC,∴∠AOC=∠DAO=70°.又∵OD=OA,∴∠ADO=∠DAO=70°.∴∠AOD=180-70°-70°=40°.确定圆的条件例2 (2019,北京)在平面内,给定不在同一条直线上的点A,B,C,如图所示,点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.(1)求证:AD=CD;(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.(1)证明:如答图.∵到点O的距离等于a的所有点组成图形G,∴图形G为△ABC的外接圆⊙O.∵BD平分∠ABC,∴∠ABD=∠CBD.∴»»AD CD=.∴AD=CD. (2)解:如答图,连接OD.∵AD=CM,AD=CD,∴CD=CM.∵DF⊥BC,∴BC垂直平分DM.易得BC为直径.∵OB=OD,∴∠OBD=∠ODB=∠ABD.∴OD∥AB.∵DE ⊥AB ,∴OD ⊥DE .∴DE 为⊙O 的切线.∴直线DE 与图形G 的公共点个数为1.2题图 例2答图训练3题图 训练3答图针对训练3 (10,河北)如图,在5×5的正方形网格中,一条圆弧经过A ,B ,C 三点,那么这条圆弧所在圆的圆心是(B )A. 点P B. 点Q C. 点R D. 点M【解析】 如答图,连接BC ,作AB 和BC 的垂直平分线,它们相交于点Q ,则点Q 即为圆心.针对训练4 (2019,绥化)半径为5的⊙O 是锐角三角形ABC 的外接圆,AB =AC ,连接OB ,OC ,延长CO 交弦AB 于点D .若△OBD 是直角三角形,则弦BC 的长为( 53或5 2 ). 【解析】 如答图①,当∠ODB =90°时,CD ⊥AB ,∴AD =BD.∴AC =BC.∵AB =AC ,∴△ABC 是等边三角形.∴∠DBO =30°.∵OB =5,∴BD =32OB =532.∴BC =AB =2BD =5 3.如答图②,当∠DOB =90°时,∠BOC =90°.∴△BOC 是等腰直角三角形.∴BC =2OB =5 2.综上所述,若△OBD 是直角三角形,则弦BC 的长为53或5 2.训练4答图例3图训练5图训练5答图圆的基本性质 例3 (19,沈阳)如图,AB 是⊙O 的直径,点C 和点D 是⊙O 上位于直径AB 两侧的点,连接AC ,AD ,BD ,CD .若⊙O 的半径是13,BD =24,则sin ∠ACD 的值是(D )A. 1213 B. 125 C. 512 D. 513【解析】 ∵AB 是直径,∴∠ADB =90°.∵⊙O 的半径是13,∴AB =2×13=26.在Rt △ABD 中,由勾股定理得AD =10,∴sin B =AD AB =1026=513.∵∠ACD =∠B ,∴sin ∠ACD =sin B =513. 针对训练5 (2019,绵阳)如图,AB 是⊙O 的直径,C 为»BD的中点,CF 为⊙O 的弦,且CF ⊥AB ,垂足为E ,连接BD 交CF 于点G ,连接CD ,AD ,BF .(1)求证:△BFG ≌△CDG ;(2)若AD =BE =2,求BF 的长.(1)证明:∵C 是»BD的中点,∴»»CD BC =.∵AB 是⊙O 的直径,且CF ⊥AB ,∴»»BC BF =.∴»»CD BF =.∴CD =BF . 在△BFG 和△CDG 中,⎩⎪⎨⎪⎧∠F =∠CDG ,∠FGB =∠DGC ,BF =CD ,∴△BFG ≌△CDG (AAS).(2)解:如答图,连接OC ,交BD 于点H ,连接OD ,BC .∵C 是»BD的中点,∴DC =BC .∵OD =OB ,∴OC 垂直平分BD .∴OC ⊥BD .∴DH =BH .∵OA =OB ,∴OH =12AD =1.∵OC =OB ,∠COE =∠BOH ,∠OEC =∠OHB =90°,∴△COE ≌△BOH (AAS).∴OE =OH =1.∴OB =OE +BE =1+2=3.∴OC =3.∵CF ⊥AB ,∴CE =EF .在Rt △OEC 中,CE =OC 2-OE 2=32-12=22,∴EF =2 2.在Rt △BEF 中,BF =BE 2+EF 2=22+()222=2 3.垂径定理及其应用 例4 (19梧州)如图,在半径为13的⊙O 中,弦AB 与CD 相交于点E ,∠DEB =75°,AB =6,AE =1,则CD 的长是(C )A. 2 6 B. 210 C. 211 D. 43 【解析】 如答图,过点O 作OF ⊥CD于点F ,OG ⊥AB 于点G ,连接OB ,OD ,OE ,则DF =CF ,AG =BG =12AB =3.∴EG =AG -AE =2.在Rt △BOG 中,OG =OB 2-BG 2=13-9=2,∴EG =OG .∴△EOG 是等腰直角三角形.∴∠OEG =45°,OE =2OG =2 2.∵∠DEB =75°,∴∠OEF =30°.∴OF =12OE = 2.在Rt △ODF 中,DF =OD 2-OF 2=13-2=11,∴CD =2DF =211. 例4题图例4答图训练6题图训练6答图针对训练6 (19黄冈)如图,一条公路的转弯处是一段圆弧(»AB ),点O 是这段弧所在圆的圆心,AB =40 m ,C 是»AB 的中点,D 是AB 的中点,且CD =10 m ,则这段弯路所在圆的半径为(A ) A. 25 m B. 24 m C. 30 m D. 60 m【解析】 如答图,连接OD.由题意可知点O ,D ,C 共线,且OC ⊥AB ,AD =DB =12AB =20 m .在Rt △AOD 中,OA 2=OD 2+AD 2.设这段弯路所在圆的半径为r ,得r 2=(r -10)2+202.解得r =25(m ).∴这段弯路所在圆的半径为25 m .1. (2019,广元)如图,AB ,AC 分别是⊙O 的直径和弦,OD ⊥AC 于点D ,连接BD ,BC ,且AB =10,AC =8,则BD 的长为(C )A. 2 5 B. 4 C. 213 D. 4.8【解析】 ∵AB 为直径,∴∠ACB =90°.∴BC =AB 2-AC 2=102-82=6.∵OD ⊥AC ,∴CD =AD =12AC =4.在Rt △CBD 中,BD =42+62=213. 第1题图第2题图第3题图第3题答图2. (2019,吉林)如图,在⊙O 中,»AB 所对的圆周角∠ACB =50°.若P 为»AB 上一点,∠AOP =55°,则∠POB 的度数为(B )A. 30° B. 45° C. 55° D. 60°【解析】 ∵∠ACB =50°,∴∠AOB =2∠ACB =100°.∵∠AOP =55°,∴∠POB =45°.3. (19白银)如图,点A ,B ,S 在圆上,若弦AB 的长度等于圆半径的2倍,则∠ASB 的度数是(C )A. 22.5°B. 30°C. 45°D. 60° 【解析】 如答图设圆心为O ,连接OA ,OB.∵弦AB 的长度等于圆半径的2倍,即AB =2OA ,∴OA 2+OB 2=AB 2.∴△OAB 为等腰直角三角形,即∠AOB =90°.∴∠ASB =12∠AOB =45°. 4. (19镇江如图,四边形ABCD 是半圆的内接四边形,AB 是直径,»»DCCB =.若∠C =110°,则∠ABC 的度数为(A )第4题图第4题答图第5题图A. 55°B. 60°C. 65°D. 70° 【解析】 如答图,连接AC.∵四边形ABCD 是半圆的内接四边形,∴∠DAB =180°-∠BCD =70°.∵»»DCCB =,∴∠CAB =12∠DAB =35°.∵AB 是直径,∴∠ACB =90°.∴∠ABC =90°-∠CAB =55°. 5. (2019,贵港)如图,AD 是⊙O 的直径,»»AB CD =.若∠AOB =40°,则圆周角∠BPC 的度数是(B )A. 40°B. 50°C. 60°D. 70° 【解析】 ∵»»AB CD =,∠AOB =40°,∴∠COD =∠AOB =40°.∵∠AOB +∠BOC +∠COD =180°,∴∠BOC =100°.∴∠BPC =12∠BOC =50°. 6. (2019,聊城)如图,BC 是半圆O 的直径,D ,E 是»BC上两点,连接BD ,CE 并延长相交于点A ,连接OD ,OE .如果∠A =70°,那么∠DOE 的度数为(C )A. 35° B. 38° C. 40° D. 42°【解析】 如答图,连接CD.∵BC 是半圆O 的直径,∴∠BDC =90°.∴∠ACD =90°-∠A =20°.∴∠DOE =2∠ACD =40°第6题图第6题答图第7题图第7题答图7. (2019,安顺)如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 的值为(D )A. 13 B. 2 2 C. 223 D. 24【解析】 如答图,设⊙A 与x 轴负半轴相交于点D ,连接CD.∵∠COD =90°,∴CD 是直径.在Rt △OCD 中,CD =6,OC =2,∴OD =CD 2-OC 2=4 2.∴tan ∠CDO =OC OD =24.由圆周角定理得∠OBC =∠CDO ,则tan ∠OBC =24. 8. (2019,天水)如图,四边形ABCD 是菱形,⊙O 经过点A ,C ,D ,与BC 相交于点E ,连接AC ,AE .若∠D =80°,则∠EAC 的度数为(C )A. 20° B. 25° C. 30° D. 35°第8题图第9题图第9题答图第10题图【解析】 ∵四边形ABCD 是菱形,∠D =80°,∴∠ACB =12∠DCB =12(180°-∠D)=50°.∵四边形AECD 是圆内接四边形,∴∠AEC =180°-∠D =100°.∴∠EAC =180°-∠AEC -∠ACB =180°-100°-50°=30°.9. (2019,通辽)如图,等边三角形ABC 内接于⊙O .若⊙O 的半径为2,则图中阴影部分的面积等于(C )A. π3B. 2π3C. 4π3D. 2π 【解析】 如答图,连接OC.∵△ABC 为等边三角形,∴∠AOC =120°,S △AOB =S △AOC .∴阴影部分的面积=S 扇形AOC =120·π×22360=4π3. 10. (2019,菏泽)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是(C )A. OC ∥BDB. AD ⊥OCC. △CEF ≌△BEDD. AF =FD【解析】 ∵AB 是⊙O 的直径,BC 平分∠ABD ,∴∠ADB =90°,∠OBC =∠DBC.∴AD ⊥BD.∵OB =OC ,∴∠OCB =∠OBC.∴∠DBC =∠OCB.∴OC ∥BD ,选项A 成立.∴AD ⊥OC ,选项B 成立.∵OA =OB ,OC ∥BD ,∴AF =FD ,选项D 成立.∵△CEF 和△BED 中,没有相等的边,∴△CEF 与△BED 不全等,选项C 不成立.11. (2019,陕西)如图,AB 是⊙O 的直径,EF ,EB 是⊙O 的弦,且EF =EB ,EF 与AB 相交于点C ,连接OF .若∠AOF =40°,则∠F 的度数是(B )A. 20° B. 35° C. 40° D. 55°第11题图第11题答图第12题图【解析】 如答图,连接FB.∵∠AOF =40°,∴∠FOB =180°-40°=140°.∴∠FEB =12∠FOB =70°.∵EF =EB ,∴∠EFB =∠EBF =55°.∵FO =BO ,∴∠OFB =∠OBF =20°.∴∠EFO =∠EFB -∠OFB =35°.12. (2019,赤峰)如图,AB 是⊙O 的弦,OC ⊥AB 交⊙O 于点C ,D 是⊙O 上一点,∠ADC =30°,则∠BOC 的度数为(D )A. 30° B. 40° C. 50° D. 60° 【解析】 ∵∠ADC =30°,∴∠AOC =2∠ADC =60°.∵AB 是⊙O 的弦,OC ⊥AB 交⊙O 于点C ,∴»»AC BC =.∴∠AOC =∠BOC =60°. 13. (2019,宁夏)如图,AB 是⊙O 的弦,OC ⊥AB ,垂足为C ,将劣弧»AB 沿弦AB 折叠交于OC 的中点D .若AB =210,则⊙O 的半径为( 3 2 ).第13题图第13题答图第14题图第14题答图【解析】 如答图,连接OA.设⊙O 的半径为x.∵将劣弧»AB 沿弦AB 折叠交于OC 的中点D ,∴OC =23x.∵OC ⊥AB ,∴AC =12AB =10.∵OA 2-OC 2=AC 2,∴x 2-⎝⎛⎭⎫23x 2=10.解得x =3 2.∴⊙O 的半径为3 2. 14. (2019,盐城)如图,点A ,B ,C ,D ,E 在⊙O 上,且»AB 所对的圆心角为50°,则∠E +∠C = 155 °. 【解析】 如答图,连接EA.∵»AB 所对的圆心角为50°,∴∠BEA =25°.∵四边形DCAE 为⊙O 的内接四边形,∴∠DEA +∠C =180°.∴∠DEB +∠C =180°-25°=155°.15. (2019,安徽)如图,△ABC 内接于⊙O ,∠CAB =30°,∠CBA =45°,CD ⊥AB 于点D .若⊙O 的半径为2,则CD 的长为( 2 ).【解析】 如答图,连接CO 并延长交⊙O 于点E ,连接BE ,则∠E =∠A =30°,∠EBC =90°.∵⊙O 的半径为2,∴CE =4.∴BC =12CE =2.∵CD ⊥AB ,∠CBA =45°,∴CD =22BC = 2. 第15题图第15题答图第16题图第16题答图16. (2019,广元)如图,△ABC 是⊙O 的内接三角形,且AB 是⊙O 的直径,P 为⊙O 上的动点,且∠BPC =60°,⊙O 的半径为6,则点P 到AC 距离的最大值是( 6+3 3 ).解析】 如答图,过点O 作OM ⊥AC 于点M ,延长MO 交⊙O 于点P ,则此时点P 到AC 的距离最大,且点P 到AC 距离的最大值=PM.∵OM ⊥AC ,∠A =∠BPC =60°,⊙O 的半径为6,∴OP =OA =6.∴OM =32OA =32×6=3 3.∴PM =OP +OM =6+3 3.∴点P 到AC 距离的最大值是6+3 3.17. (2019,嘉兴)如图,在⊙O 中,弦AB =1,点C 在AB 上移动,连接OC ,过点C 作CD ⊥OC 交⊙O 于点D ,则CD 的最大值为( 12).【解析】 如答图,连接OD.设⊙O 的半径为r.∵CD ⊥OC ,∴∠DCO =90°.∴CD =OD 2-OC 2=r 2-OC 2.∴当OC 的值最小时,CD 的值最大.∴当OC ⊥AB 时,OC 最小,此时OC =r 2-⎝⎛⎭⎫12AB 2.∴CD 的最大值为r 2-⎝⎛⎭⎫r 2-14AB 2=12AB =12×1=12.第17题图第17题答图三、 解答题 18. (2019,包头)如图,在⊙O 中,B 是⊙O 上的一点,∠ABC =120°,弦AC =23,弦BM 平分∠ABC 交AC 于点D ,连接MA ,MC .(1)求⊙O 的半径;(2)求证:AB +BC =BM . (1)解:如答图①,连接OA ,OC ,过点O 作OH ⊥AC 于点H .第18题图第18题答图∴AH =HC =12AC .∵OA =OC ,∴∠AOH =∠COH =12∠AOC .∵∠ABC =120°∴∠AMC =180°-∠ABC =60°.∴∠AOC =2∠AMC =120°.∴∠AOH =12∠AOC =60°.∵AC =23,∴AH =12AC = 3. 在Rt △AOH 中,sin ∠AOH =AH OA ,∴OA =AH sin 60°=2.∴⊙O 的半径为2. (2)证明:如答图②,在BM 上截取BE =BC ,连接CE .∵∠ABC =120°,BM 平分∠ABC ,∴∠ABM =∠CBM =12∠ABC =60°.∵BE =BC ,∴△EBC 是等边三角形.∴∠BEC =60°,BC =EC .∴∠MEC =120°.∴∠ABC =∠MEC .∵∠BAC =∠BMC ,∴△ACB ≌△MCE (AAS).∴AB =ME .∵ME +EB =BM ,∴AB +BC =BM .19. (2019,荆门)如图,已知锐角三角形ABC 的外接圆圆心为O ,半径为R . (1)求证:AC sin B=2R ; (2)若在△ABC 中,∠A =45°,∠B =60°,AC =3,求BC 的长及sin C 的值.第19题图第19题答图第1题图(1)证明:如答图①,连接AO 并延长交⊙O 于点D ,连接CD ,则∠DCA =90°,∠B =∠ADC .在Rt △ACD 中,sin ∠ADC =AC AD =AC 2R , ∴sin B =AC 2R .∴AC sin B=2R . (2)解:由(1)同理可得AC sin B =AB sin C =BC sin A =2R . ∵AC =3,∠B =60°,∴2R =3sin 60°=2.∴BC =2R ·sin A =2sin 45°= 2.如答图②,过点C 作CE ⊥AB 于点E .在Rt △BCE 中,BE =BC ·cos B =2cos 60°=22.在Rt △ACE 中,AE =AC ·cos A =3cos 45°=62.∴AB =AE +BE =6+22.∵AB sin ∠ACB=2R ,∴sin ∠ACB =AB 2R =6+24.1. (2019,湘潭)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=12(弦×矢+矢2).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC ⊥弦AB 时,OC 平分AB )可以求解.现已知弦AB=8 m ,半径等于5 m 的弧田,按照上述公式计算出弧田面积为 10 m 2. 【解析】 ∵AB =8,OC ⊥AB ,∴AD =4.∴OD =OA 2-AD 2=3.∴OC -OD =2.∴弧田面积=12×(8×2+22)=10(m 2). 2. (2019,潍坊)如图,在平面直角坐标系xOy 中,一组同心圆的圆心为坐标原点O ,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线l 0,l 1,l 2,l 3,…都与x 轴垂直,相邻两直线的间距为1,其中l 0与y 轴重合.若半径为2的圆与l 1在第一象限内交于点P 1,半径为3的圆与l 2在第一象限内交于点P 2……半径为n +1的圆与l n 在第一象限内交于点P n ,则点P n 的坐标为 (n ,2n +1) .(n 为正整数)【解析】 如答图,连接OP 1,OP 2,OP 3,l 1,l 2,l 3与x 轴分别交于点A 1,A 2,A 3.在Rt △OA 1P 1中,OA 1=1,OP 1=2,∴A 1P 1=OP 21-OA 21=22-12= 3.同理A 2P 2=32-22=5,A 3P 3=42-32=7.∴点P 1的坐标为(1,3),点P 2的坐标为(2,5),点P 3的坐标为(3,7).按照此规律可得点P n 的坐标是(n ,()n +12-n 2),即(n ,2n +1).3. (2019,福建)如图,四边形ABCD 内接于⊙O ,AB =AC ,BD ⊥AC ,垂足为E ,点F 在BD 的延长线上,且DF =DC ,连接AF ,CF .(1)求证:∠BAC =2∠DAC ;(2)若AF =10,BC =45,求tan ∠BAD 的值.2题图2题答图3题图3题答图(1)证明:∵AB =AC ,∴»»AB AC =,∠ABC =∠ACB .∴∠ABC =∠ADB ,∠ABC =12(180°-∠BAC )=90°-12∠BAC .∵BD ⊥AC ,∴∠ADB =90°-∠DAC .∴12∠BAC =∠DAC .∴∠BAC =2∠DAC . (2)解:∵DF =DC ,∴∠DFC =∠DCF .∴∠BDC =2∠DFC .∴∠BFC =12∠BDC =12∠BAC =∠DAC =∠FBC . ∴CB =CF =4 5.又∵BD ⊥AC ,∴AC 是线段BF 的垂直平分线.∴AB =AF =10.∴AC =10. 设AE =x ,则CE =10-x .由AB 2-AE 2=BC 2-CE 2,得100-x 2=80-(10-x )2.解得x =6.∴AE =6,CE =4.∴BE =EF =8.设DE =y ,则CD =DF =8-y .在Rt △CDE 中,CD 2=DE 2+CE 2,即(8-y )2=y 2+42.解得y =3,即DE =3.∴BD =BE +DE =8+3=11.如答图,过点D 作DH ⊥AB ,垂足为H .∵12AB ·DH =12BD ·AE ,∴DH =BD ·AE AB =11×610=335.在Rt △BDH 中,BH =BD 2-DH 2=445.∴AH =AB -BH =10-445=65.∴tan ∠BAD =DH AH =33565=112. 4. (2019,温州)如图,在△ABC 中,∠BAC =90°,点E 在BC 边上,且CA =CE ,过A ,C ,E 三点的⊙O 交AB 于另一点F ,作直径AD ,连接DE 并延长交AB 于点G ,连接CD ,CF .(1)求证:四边形DCFG 是平行四边形; (2)当BE =4,CD =38AB 时,求⊙O 的直径. 第4题图第4题答图(1)证明:如答图,连接AE .∵∠BAC =90°,∴CF 是⊙O 的直径.∵AC =EC ,∴CF ⊥AE .∵AD 是⊙O 的直径,∴∠AED =90°.∴GD ⊥AE .∴CF ∥DG .∵AD 是⊙O 的直径,∴∠ACD =90°.∴∠ACD +∠BAC =180°.∴AB ∥CD .∴四边形DCFG 是平行四边形. (2)解:由CD =38AB ,设CD =3x ,则AB =8x .由(1)知四边形DCFG 是平行四边形,∴CD =FG =3x .∵∠AOF =∠COD ,∴AF =CD =3x .∴BG =8x -3x -3x =2x .∵GE ∥CF ,∴BE EC =BG GF =23.∵BE =4,∴CE=6.∴AC=CE=6,BC=6+4=10.在Rt△ABC中,AB=102-62=8=8x.∴x=1.在Rt△ACF中,AF=3,AC=6,∴CF=32+62=3 5.∴⊙O的直径为3 5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七单元圆第24讲圆的有关性质纲要求命题趋势1.理解圆的有关概念和性质,了解圆心角、弧、弦之间的关系.2.了解圆心角与圆周角及其所对弧的关系,掌握垂径定理及推论.中考主要考查圆的有关概念和性质,与垂径定理有关的计算,与圆有关的角的性质及其应用.题型以选择题、填空题为主.知识梳理一、圆的有关概念及其对称性1.圆的定义(1)圆是平面内到一定点的距离等于定长的所有点组成的图形.这个定点叫做________,定长叫做________;(2)平面内一个动点绕一个定点旋转一周所形成的图形叫做圆,定点叫做圆心,定点与动点的连线段叫做半径.2.圆的有关概念(1)连接圆上任意两点的________叫做弦;(2)圆上任意两点间的________叫做圆弧,简称弧.(3)________相等的两个圆是等圆.(4)在同圆或等圆中,能够互相________的弧叫做等弧.3.圆的对称性(1)圆的轴对称性:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;(2)圆的中心对称性:圆是以圆心为对称中心的中心对称图形;(3)圆是旋转对称图形:圆绕圆心旋转任意角度,都能和原来的图形重合.这就是圆的旋转不变性.二、垂径定理及推论1.垂径定理垂直于弦的直径________这条弦,并且________弦所对的两条弧.2.推论1(1)平分弦(________)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过________,并且平分弦所对的________弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.3.推论2圆的两条平行弦所夹的弧________.4.(1)过圆心;(2)平分弦(不是直径);(3)垂直于弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧.若一条直线具备这五项中任意两项,则必具备另外三项.三、圆心角、弧、弦之间的关系1.定理在同圆或等圆中,相等的圆心角所对的弧________,所对的弦________.2.推论同圆或等圆中:(1)两个圆心角相等;(2)两条弧相等;(3)两条弦相等.三项中有一项成立,则其余对应的两项也成立.四、圆心角与圆周角1.定义顶点在________上的角叫做圆心角;顶点在________上,角的两边和圆都________的角叫做圆周角.2.性质(1)圆心角的度数等于它所对的______的度数.(2)一条弧所对的圆周角的度数等于它所对________的度数的一半.(3)同弧或等弧所对的圆周角________,同圆或等圆中相等的圆周角所对的弧________.(4)半圆(或直径)所对的圆周角是______,90°的圆周角所对的弦是________.五、圆内接四边形的性质圆内接四边形的对角互补.自主测试1.如图,⊙O的弦AB垂直平分半径OC,若AB=6,则⊙O的半径为()A. 2 B.2 2C.22D.622.如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为()5.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M,N两点,若点M的坐标是(-4,-2),则弦MN的长为__________.(第5题图)【例1】在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为()A .6分米B .8分米C .10分米D .12分米分析:如图,油面AB 上升1分米得到油面CD ,依题意得AB =6,CD =8,过O 点作AB 的垂线,垂足为E ,交CD 于F 点,连接OA ,OC ,由垂径定理,得AE =12AB =3,CF =12CD =4,设OE =x ,则OF =x -1,在Rt △OAE 中,OA 2=AE 2+OE 2,在Rt △OCF 中,OC 2=CF 2+OF 2,由OA =OC ,列方程求x 即可求得半径OA ,得出直径MN .解析:如图,依题意得AB =6,CD =8,过O 点作AB 的垂线,垂足为E ,交CD 于F 点,连接OA ,OC ,由垂径定理,得AE =12AB =3,CF =12CD =4,设OE =x ,则OF =x -1, 在Rt △OAE 中,OA 2=AE 2+OE 2, 在Rt △OCF 中,OC 2=CF 2+OF 2,∵OA =OC ,∴32+x 2=42+(x -1)2,解得x =4,∴半径OA =32+42=5,∴直径MN =2OA =10(分米).故选C.答案:C方法总结 有关弦长、弦心距与半径的计算,常作垂直于弦的直径,利用垂径定理和解直角三角形来达到求解的目的.触类旁通1 如图所示,若⊙O 的半径为13 cm ,点P 是弦AB 上一动点,且到圆心的最短距离为5 cm ,则弦AB 的长为__________ cm.考点二、圆心(周)角、弧、弦之间的关系【例2】如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD .(1)求证:DB 平分∠ADC ;(2)若BE =3,ED =6,求AB 的长. 解:(1)证明:∵AB =BC , ∴AB BC =.∴∠ADB =∠BDC , ∴DB 平分∠ADC .(2)由(1)知AB BC =,∴∠BAE =∠ADB .∵∠ABE =∠ABD ,∴△ABE ∽△DBA .∴AB BE =BDAB .∵BE =3,ED =6,∴BD =9.∴AB 2=BE ·BD =3×9=27.∴AB =3 3.方法总结 圆心角、弧、弦之间的关系定理,提供了从圆心角到弧到弦的转化方式,为我们证明角相等、线段相等和弧相等提供了新思路,解题时要根据具体条件灵活选择应用. 触类旁通2 如图,AB 是⊙O 的直径,C ,D 两点在⊙O 上,若∠C =40°,则∠ABD 的度数为( )A .40°B .50°C .80°D .90°考点三、圆周角定理及推论【例3】如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°,则∠BCD =( )A .116°B .32°C .58°D .64°解析:根据圆周角定理求得,∠AOD =2∠ABD =116°(同弧所对的圆周角是所对的圆心角的一半),∠BOD =2∠BCD (同弧所对的圆周角是所对的圆心角的一半);根据平角是180°知∠BOD =180°-∠AOD .还有一种解法,即利用直径所对的圆周角等于90°,可得∠ADB =90°,则∠DAB=90°-∠ABD=32°,∵∠DAB=∠DCB,∴∠DCB=32°.答案:B方法总结求圆中角的度数时,通常要利用圆周角与圆心角或圆心角与弧之间的关系.触类旁通3 如图,点A,B,C,D都在⊙O上,CD的度数等于84°,CA是∠OCD 的平分线,则∠ABD+∠CAO=__________.A.CM=DM B.CD DBC.∠ACD=∠ADC D.OM=MD3.(2012浙江湖州)如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是()(第3题图)A.45°B.85°C.90°D.95°4.(2012浙江衢州)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10 mm,测得钢珠顶端离零件表面的距离为8 mm,如图所示,则这个小圆孔的宽口AB的长度为__________ mm.7.(2012湖南长沙)如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC =60°.(1)求证:△ABC是等边三角形;(2)求圆心O到BC的距离OD.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为()A .5B .4C .3D .22.如图,直径为10的⊙A 经过点C (0,5)和点O (0,0),B 是y 轴右侧⊙A 优弧上一点,则∠OBC 的余弦值为( )A .12B .34C .32D .453.一条排水管的截面如图所示.已知排水管的截面圆半径OB =10,截面圆圆心O 到水面的距离OC 是6,则水面宽AB 是( )A .16B .10C .8D .64.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA ,OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE =8个单位,OF =6个单位,则圆的直径为( )(第4题图)A .12个单位B .10个单位C .4个单位D .15个单位5.已知如图,在圆内接四边形ABCD 中,∠B =30°,则∠D =__________.(第5题图)6.如图,过A,C,D三点的圆的圆心为E,过B,F,E三点的圆的圆心为D,如果∠A=63°,那么∠DBE=__________.(第6题图)7.如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,DC=3,AB=42,则⊙O的直径等于________.(第7题图)8.如图,在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于点E.求证:(1)△ABD为等腰三角形;(2)AC·AF=DF·FE.参考答案导学必备知识自主测试1.A2.D3.60°4.90°5.3如图,过点A作AB⊥MN,连接AM,设MB 为x ,则AM =AO =4-x . 在Rt △AMB 中, ∵AM 2=MB 2+AB 2, ∴(4-x )2=x 2+22,解得x =32.∴MN =2MB =3. 探究考点方法触类旁通1.24 连接OA ,当OP ⊥AB 时,OP 最短,此时OP =5 cm ,且AB =2AP .在Rt △AOP 中,AP =OA 2-OP 2=132-52=12,所以AB =24 cm.触类旁通2.B 由题意,得∠A =∠C =40°,由直径所对的圆周角是直角,得∠ADB =90°,根据直角三角形两锐角互余或三角形内角和定理得∠A +∠ABD =90°,从而得∠ABD =50°.触类旁通3.48° 因为CD 的度数等于84°,所以∠COD =84°.因为OC =OD ,所以∠OCD =48°.因为CA 是∠OCD 的平分线,所以∠ACD =∠ACO =24°,因为OA =OC ,所以∠OAC =∠ACO =24°,因为∠ABD =∠ACD =24°,所以∠ABD +∠CAO =48°. 品鉴经典考题1.A ∵OA ⊥OB ,∴∠AOB =90°,∴∠ACB =45°.故选A. 2.D ∵AB 是⊙O 的直径,弦CD ⊥AB ,垂足为M , ∴M 为CD 的中点,即CM =DM ,选项A 成立; B 为CD 的中点,即CB =DB ,选项B 成立; 在△ACM 和△ADM 中,∵AM =AM ,∠AMC =∠AMD =90°,CM =DM , ∴△ACM ≌△ADM (SAS), ∴∠ACD =∠ADC ,选项C 成立;而OM 与MD 不一定相等,选项D 不成立. 故选D.3.B ∵AC 是⊙O 的直径,∴∠ABC =90°.∵∠ABC 的平分线BD 交⊙O 于点D ,∴∠ABD =45°.∵∠C =50°,∴∠D =50°,∴∠BAD 的度数是180°-45°-50°=85°.4.8 如图所示,在⊙O 中,连接OA ,过点O 作OD ⊥AB 于点D ,则AB =2AD .∵钢珠的直径是10 mm ,∴钢珠的半径是5 mm.∵钢珠顶端离零件表面的距离为8 mm ,∴OD =3 mm.在Rt △AOD 中,∵AD =OA 2-OD 2=52-32=4(mm).∴AB =2AD =2×4=8(mm).故答案为8.5.2 ∵AB 是⊙O 的弦,OC ⊥AB 于C ,AB =23,∴BC =12AB = 3.∵OC =1, ∴在Rt △OBC 中,OB =OC 2+BC 2=12+(3)2=2.故答案为2.6.150 因为∠AOC =60°,则它所对的弧度为60°,所以∠ABC 所对的弧度为300°.因为∠ABC 是圆周角,所以∠ABC =150°.7.(1)证明:在△ABC 中,∵∠BAC =∠APC =60°,∠APC =∠ABC ,∴∠ABC =60°,∴∠ACB =180°-∠BAC -∠ABC =180°-60°-60°=60°,∴△ABC 是等边三角形.(2)解:如图,连接OB ,则OB =8,∠OBD =30°.又∵OD ⊥BC 于D ,∴OD =12OB =4. 研习预测试题1.C 2.C 3.A 4.B5.150° 6.18° 7.52 连接AO 并延长交圆于点E ,连接BE .(如图)∵AE 为⊙O 的直径,∴∠ABE =90°.∴∠ABE =∠ADC .又∵∠AEB =∠ACD ,∴△ABE ∽△ADC .∴AB AD =AE AC.∵在Rt △ADC 中,AC =5,DC =3, ∴AD =4.∴AE =5 2.8.证明:(1)由圆的性质知∠MCD =∠DAB ,∠DCA =∠DBA ,而∠MCD =∠DCA , ∴∠DBA =∠DAB ,故△ABD 为等腰三角形.(2)∵∠DBA =∠DAB ,∴AD BD =.又∵BC =AF ,∴BC AF =,∠CDB =∠FDA ,∴CD DF =,∴CD =DF .由“圆的内接四边形外角等于它的内对角”知,∠AFE =∠DBA =∠DCA ,①∠F AE =∠BDE .∴∠CDA =∠CDB +∠BDA =∠FDA +∠BDA =∠BDE =∠F AE ,②由①②得△CDA ∽△F AE .∴AC FE =CD AF, ∴AC ·AF =CD ·FE .而CD =DF ,∴AC ·AF =DF ·FE .。
