2007年浙江省高中数学竞赛(A)卷
2007年高考.浙江卷.理科数学试题及解答

2007年普通高等学校招生全国统一考试(浙江卷)数学(理工类)第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)“1x >”是“2x x >”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分不必要条件 D.既不充分也不必要条件 (2)若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =则( )A .126ωϕπ==,B .123ωϕπ==, C .26ωϕπ==, D .23ωϕπ==,(3)直线210x y -+=关于直线1x =对称的直线方程是( )A.210x y +-= B.210x y +-= C.230x y +-= D.230x y +-=(4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是( ) A.3 B.4 C.5 D.6(5)已知随机变量ξ服从正态分布2(2)N σ,,(4)0.84P ξ=≤,则(0)P ξ=≤( )A .0.16B .0.32C .0.68D ,0.84(6)若P 两条异面直线l m ,外的任意一点,则( ) A.过点P 有且仅有一条直线与l m ,都平行 B.过点P 有且仅有一条直线与l m ,都垂直 C.过点P 有且仅有一条直线与l m ,都相交 D.过点P 有且仅有一条直线与l m ,都异面(7)若非零向量,a b 满足+=a b b ,则( )A.2>2+a a b B.22<+a a b C.2>+2b a bD. 22<+b a b(8)设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )A .B .C .D .(9)已知双曲线22221(00)x ya ba b-=>>,的左、右焦点分别为1F,2F,P是准线上一点,且12PF PF⊥,124PF PF ab=,则双曲线的离心率是()C.2D.3(10)设21()1x xf xx x⎧⎪=⎨<⎪⎩,≥,,,()g x是二次函数,若(())f g x的值域是[)0+,∞,则()g x的值域是()A.(][)11--+∞,,∞B.(][)10--+∞,,∞C.[)0+,∞D.[)1+,∞第II卷(共100分)二、填空题:本大题共7小题,每小题4分,共28分.(11)已知复数11iz=-,121iz z=+,则复数2z=.(12)已知1sin cos5θθ+=,且324θππ≤≤,则cos2θ的值是.(13)不等式211x x--<的解集是.(14)某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是(用数字作答).(15)随机变量ξ的分布列如下:其中a b c,,成等差数列,若3Eξ=,则Dξ的值是.(16)已知点O在二面角ABαβ--的棱上,点P在α内,且45POB∠=.若对于β内异于O的任意一点Q,都有45POQ∠≥,则二面角ABαβ--的大小是.(17)设m为实数,若{}22250()30()25x yx y x x y x ymx y⎧⎫-+⎧⎪⎪⎪-⊆+⎨⎨⎬⎪⎪⎪+⎩⎩⎭≥,≥,≤≥,则m的取值范围是.三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤.(18)(本题14分)已知ABC△1,且sin sinA B C+=.(I)求边AB的长;(II)若ABC△的面积为1sin6C,求角C的度数.(19)(本题14分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点. (I )求证:CM EM ⊥;(II )求CM 与平面CDE 所成的角.(20)(本题14分)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S .(I )求在0k =,01b <<的条件下,S 的最大值; (II )当2AB =,1S =时,求直线AB 的方程.(21)(本题15分)已知数列{}n a 中的相邻两项212k k a a -,是关于x 的方程2(32)320k kx k x k -++=的两个根,且212(123)k k a a k -=≤,,,. (I )求1a ,2a ,3a ,7a ; (II )求数列{}n a 的前2n 项和2n S ;(Ⅲ)记sin 1()32sin nf n n ⎛⎫=+⎪⎝⎭, (2)(3)(4)(1)123456212(1)(1)(1)(1)f f f f n n n n T a a a a a a a a +-----=++++…, 求证:15()624n T n ∈*N ≤≤.(22)(本题15分)设3()3x f x =,对任意实数t ,记232()3t g x t x t =-.(I )求函数()()t y f x g x =-的单调区间; (II )求证:(ⅰ)当0x >时,()f x g ()()t f x g x ≥对任意正实数t 成立;(ⅱ)有且仅有一个正实数0x ,使得00()()x t g x g x ≥对任意正实数t 成立.ED C M A(第19题) B2007年普通高等学校招生全国统一考试(浙江卷)数学(理工类)答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分. (1)A (2)D (3)D (4)B (5)A (6)B (7)C (8)D (9)B (10)C二、填空题:本题考查基本知识和基本运算.每小题4分,满分28分. (11)1 (12)725- (13){}02x x << (14)266(15)59(16)90(17)403m ≤≤三、解答题(18)解:(I)由题意及正弦定理,得1AB BC AC ++=,BC AC +=, 两式相减,得1AB =.(II )由ABC △的面积11sin sin 26BC AC C C =,得13BC AC =, 由余弦定理,得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--==, 所以60C =.(19)本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分. 方法一:(I )证明:因为AC BC =,M 是AB 的中点, 所以CM AB ⊥. 又EA ⊥平面ABC , 所以CM EM ⊥.(II )解:过点M 作MH ⊥平面CDE ,垂足是H ,连结CH 交延长交ED 于点F ,连结MF ,MD . FCM ∠是直线CM 和平面CDE 所成的角. 因为MH ⊥平面CDE ,所以MH ED ⊥,又因为CM ⊥平面EDM , 所以CM ED ⊥,则ED ⊥平面CMF ,因此ED MF ⊥. 设EA a =,2BD BC AC a ===, 在直角梯形ABDE 中,AB =,M 是AB 的中点,所以3DE a =,EM =,MD =, 得EMD △是直角三角形,其中90EMD =∠, 所以2EM MDMF a DE==.在Rt CMF △中,tan 1MFFCM MC==∠, 所以45FCM =∠,E DC MAE H故CM 与平面CDE 所成的角是45. 方法二:如图,以点C 为坐标原点,以CA ,CB 分别为x 轴和y 轴,过点C 作与平面ABC 垂直的直线为z 轴,建立直角坐标系C xyz -,设EA a =,则(2)A a 00,,,(020)B a ,,,(20)E a a ,,.(022)D a a ,,,(0)M a a ,,.(I )证明:因为()EM a a a =--,,,(0)CM a a =,,, 所以0EM CM =, 故EM CM ⊥.(II )解:设向量001y z (),,n =与平面CDE 垂直,则CE ⊥n ,CD ⊥n , 即0CE =n ,0CD =n .因为(20)CE a a =,,,(022)CD a a =,,, 所以02y =,02x =-, 即(122)=-,,n ,2cos 2CM CM CM ==,n n n, 直线CM 与平面CDE 所成的角θ是n 与CM所以45θ=,因此直线CM 与平面CDE 所成的角是45. (20)本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分14分.(Ⅰ)解:设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,,由2214x b +=,解得12x =±, 所以1212S b x x =-221b b =-2211b b +-=≤.当且仅当b =S 取到最大值1.(Ⅱ)解:由2214y kx b x y =+⎧⎪⎨+=⎪⎩,,得22212104k x kbx b ⎛⎫+++-= ⎪⎝⎭,2241k b ∆=-+,11||||AB x x =-222424k b k -==+. ②设O 到AB 的距离为d ,则21||Sd AB ==,x又因为d =,所以221b k =+,代入②式并整理,得42104k k -+=,解得212k =,232b =,代入①式检验,0∆>,故直线AB 的方程是y x =或y x =y x =+,或y x =-21.本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分15分.(I )解:方程2(32)320k kx k x k -++=的两个根为13x k =,22k x =,当1k =时,1232x x ==,, 所以12a =;当2k =时,16x =,24x =, 所以34a =;当3k =时,19x =,28x =, 所以58a =时;当4k =时,112x =,216x =, 所以712a =.(II )解:2122n n S a a a =+++2(363)(222)n n =+++++++2133222n n n ++=+-.(III )证明:(1)123456212111(1)f n n n nT a a a a a a a a +--=+-++, 所以112116T a a ==, 2123411524T a a a a =+=.当3n ≥时,(1)3456212111(1)6f n n n nT a a a a a a +--=+-++, 345621211116n n a a a a a a -⎛⎫+-++⎪⎝⎭≥2311111662622n ⎛⎫+-++ ⎪⎝⎭≥ 1116626n =+>,同时,(1)5678212511(1)24f n n n nT a a a a a a +--=--++5612212511124n n a a a a a a -⎛⎫-+++ ⎪⎝⎭≤31511112492922n ⎛⎫-+++ ⎪⎝⎭≤ 515249224n =-<. 综上,当n ∈N*时,15624n T ≤≤.22.本题主要考查函数的基本性质,导数的应用及不等式的证明等基础知识,以及综合运用所学知识分析和解决问题的能力.满分15分.(I )解:316433x y x =-+. 由240y x '=-=,得 2x =±.因为当(2)x ∈-∞-,时,y '>0, 当(22)x ∈-,时,0y '<, 当(2)x ∈+∞,时,0y '>,故所求函数的单调递增区间是(2)-∞-,,(2)+∞,, 单调递减区间是(22)-,.(II )证明:(i )方法一:令2332()()()(0)33t x h x f x g x t x t x =-=-+>,则 223()h x x t '=-,当0t >时,由()0h x '=,得13x t =,当13()x x ∈+∞,时,()0h x '>, 所以()h x 在(0)+∞,内的最小值是13()0h t =. 故当0x >时,()()t f x g x ≥对任意正实数t 成立. 方法二:对任意固定的0x >,令232()()(0)3t h t g x t x t t ==->,则 11332()()3h t t x t -'=-,由()0h t '=,得3t x =.当30t x <<时,()0h t '>.当3t x >时,()0h t '<,所以当3t x =时,()h t 取得最大值331()3h x x =. 因此当0x >时,()()f x g x ≥对任意正实数t 成立.(ii )方法一:8(2)(2)3t f g ==. 由(i )得,(2)(2)t t g g ≥对任意正实数t 成立. 即存在正实数02x =,使得(2)(2)x t g g ≥对任意正实数t 成立. 下面证明0x 的唯一性: 当02x ≠,00x >,8t =时,300()3x f x =,0016()43x g x x =-,由(i )得,30016433x x >-, 再取30t x =,得30300()3x x g x =,所以303000016()4()33x x x g x x g x =-<=, 即02x ≠时,不满足00()()x t g x g x ≥对任意0t >都成立.故有且仅有一个正实数02x =,使得00()0()x t g x g x ≥对任意正实数t 成立. 方法二:对任意00x >,0016()43x g x x =-, 因为0()t g x 关于t 的最大值是3013x ,所以要使00()()x t g x g x ≥对任意正实数成立的充分必要条件是:300161433x x -≥, 即200(2)(4)0x x -+≤, ①又因为00x >,不等式①成立的充分必要条件是02x =, 所以有且仅有一个正实数02x =,使得00()()x t g x g x ≥对任意正实数t 成立.。
2007年温州市摇篮杯高一数学竞赛试题及答案

2007年温州市摇篮杯高一数学竞赛试题及答案2007年浙江省温州市摇篮杯高一数学竞赛试题(2007年4月15日)1、已知集合{}|1,A x x x R =≠∈,A B R =U ,则集合B 不可能...是( )A 、{}|1,x x x R >-∈B 、{}|1,x x x R <-∈C 、{}|1,x x x R ≠-∈D 、{}0,1 2、已知sin36a ︒=,则sin108︒等于( )A 、3aB 、334a a - C 、334a a + D 、221a --3、已知c b a ,,均为正数,且都不等于1,若实数z y x ,,满足0111,=++==zy x c b a z y x ,则abc 的值等于( )A 、1B 、2C 、3D 、44、将正整数中所有被7整除的数删去,剩下的数依照从小到大的顺序排成一个数列{}na ,则100a 等于( ) A 、114 B 、115C 、116D 、1175、今有一组实验数据如下:x 0 1 2 3 4 y15312最能近似地表达这些数据规律的函数模型是( )A 、xy b a =•B 、21y bxax =++C 、2()y x x a b=-+D 、sin()y A x B ωϕ=++6、已知函数()2f x x bx c=++,若方程()f x x =无实根,则( )A 、对一切实数x ,不等式()f f x x >⎡⎤⎣⎦都成立B 、对一切实数x ,不等式()f f x x <⎡⎤⎣⎦都成立C 、存在实数b 和c ,使得不等式()f f x x <⎡⎤⎣⎦对一切实数x 都成立D 、不存在实数b 和c ,使得不等式()f f x x >⎡⎤⎣⎦对一切实数x 都成立7、某流程如右图所示,现输入如下四个函数,则可以输出的函数是 ( )A 、2()f x x =B 、()1sin f x x =+C 、()ln 26f x x x =+-D 、2()lg(1)f x x x =+8、已知点O 是ABC∆所在平面内的一点,3260OA OB OC +-=u u u r u u u r u u u r r且::5:4:3AB BC CA =,下列结论错误..的是 ()A 、点O 在ABC ∆外;B 、::6:3:2AOBBOC COA SS S ∆∆∆=C 、点O 到,,AB BC CA 距离的比是72:45:40D 、,,,O A B C 四点共圆;二、填空题:本大题共6小题,每小题8分,共48分。
2007年浙江省高中数学竞赛A卷(附参考答案)

2007年浙江省高中数学竞赛A卷(附参考答案)一、选择题1.如果,则使的的取值范围为()A.B.C.D.解:显然,且。
要使。
当时,,即;当时,,此时无解。
由此可得,使的的取值范围为。
应选B。
2.已知集合,,则=()A. B. R C.D.解:没有实数可以使上述不等式成立。
故。
从而有。
应选C。
3.以为六条棱长的四面体个数为()A. 2B. 3C.4D. 6解:以这些边为三角形仅有四种:,,,。
固定四面体的一面作为底面:当底面的三边为时,另外三边的取法只有一种情况,即;当底面的三边为时,另外三边的取法有两种情形,即,。
其余情形得到的四面体均在上述情形中。
由此可知,四面体个数有3个。
应选B。
4.从1至169的自然数中任意取出3个数构成以整数为公比的递增等比数列的取法有()种。
A. 89B. 90C.91D. 92解:若取出的3个数构成递增等比数列,则有。
由此有。
当固定时,使三个数为整数的的个数记作。
由,知应是的整数部分。
,,,,,,,,.因此,取法共有。
应选C5.若在复平面上三个点构成以A为直角顶点的等腰直角三角形,其中,则△ABC的面积为()A. B. C.1 D.解:依题意,,。
△ABC的面积为。
应选A。
6.2007重的末二位数字是()A. 01B. 07C.43D. 49解:记k重。
题目要求的末二位数。
其中M为正整数。
由此可得的末二位数与的末二位数字相同。
首先来观察的末二位数字的变化规律。
2 3 4 5 6 7 8 9的末二位数字49 43 01 07 49 43 01 07的末二位数字的变化是以4为周期的规律循环出现。
(为奇整数)(为正整数)因此,与的末二位数字相同,为43。
应选C。
二、填空题7.设为的单调递增数列,且满足,则。
解:(由题意可知取正号。
)因此,公差为2的等差数列,即。
从而可得。
答案为。
8.设为方程的根(),则。
解:由题意,。
由此可得,,以及。
答案为:。
9.设均为非负实数,则的最小值为。
2007年全国高中数学联合竞赛试题及解答.

2007年全国高中数学联合竞赛一试一、填空题:本大题共6个小题,每小题6分,共36分。
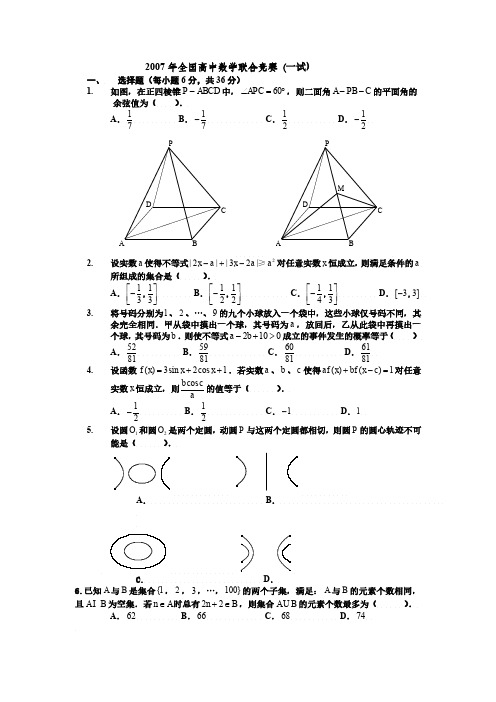
2007*1、如图,在正四棱锥ABCD P -中,060=∠APC ,则二面角C PB A --的平面角的余弦值为A.71 B.71- C.21 D.21-◆答案:B★解析:如图,在侧面PAB 内,作AM ⊥PB ,垂足为M 。
连结CM 、AC ,则∠AMC 为二面角A−PB−C 的平面角。
不妨设AB =2,则22==AC PA ,斜高为7,故2272⋅=⨯AM ,由此得27==AM CM 。
在△AMC 中,由余弦定理得712cos 222-=⋅⋅-+=∠CM AM AC CM AM AMC 。
2007*2、设实数a 使得不等式2232a a x a x ≥-+-对任意实数x 恒成立,则满足条件的a 所组成的集合是A.⎥⎦⎤⎢⎣⎡-31,31 B.⎥⎦⎤⎢⎣⎡-21,21 C.⎥⎦⎤⎢⎣⎡-31,41 D.[]3,3-◆答案:A★解析:令a x 32=,则有31||≤a ,排除B 、D 。
由对称性排除C ,从而只有A 正确。
一般地,对R k ∈,令ka x 21=,则原不等式为2|||34|||23|1|||a k a k a ≥-⋅+-⋅,由此易知原不等式等价于|34|23|1|||-+-≤k k a ,对任意的R k ∈成立。
由于⎪⎪⎪⎩⎪⎪⎪⎨⎧<-<≤-≥-=-+-125334121134325|34|23|1|k k k k k k k k ,所以31|}34|23|1{|min R =-+-∈k k k ,从而上述不等式等价于31||≤a 。
2007*3、将号码分别为9,,2,1 的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同。
甲从袋中摸出一个球,其号码为a ,放回后,乙从袋中再摸出一个球,其号码为b 。
则使不等式0102>+-b a 成立的事件发生的概率等于A.8152 B.8159 C.8160 D.8161◆答案:D ★解析:甲、乙二人每人摸出一个小球都有9种不同的结果,故基本事件总数为8192=个。
2007年全国高中数学联赛试题及答案
2007年全国高中数学联合竞赛 (一试)一、 选择题(每小题6分,共36分) 1. 如图,在正四棱锥P ABCD -中,60APC ∠=︒,则二面角A PB C --的平面角的余弦值为( ).A .17B .17-C .12D .12-2.设实数a 使得不等式2|2||32|x a x a a -+-≥对任意实数x 恒成立,则满足条件的a 所组成的集合是( ).A .1133,⎡⎤-⎢⎥⎣⎦B .1122,⎡⎤-⎢⎥⎣⎦C .1143,⎡⎤-⎢⎥⎣⎦D .[]33,-3.将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,其号码为a ,放回后,乙从此袋中再摸出一个球,其号码为b .则使不等式2100a b -+>成立的事件发生的概率等于( )A .5281B .5981C .6081D .61814.设函数()3sin 2cos 1f x x x =++.若实数a 、b 、c 使得()()1af x bf x c +-=对任意实数x 恒成立,则cos b ca的值等于( ).A .12-B .12C .1-D .15.设圆1O 和圆2O 是两个定圆,动圆P 与这两个定圆都相切,则圆P 的圆心轨迹不可能是( ).A .B .C. D .6.已知A 与B 是集合{1,2,3,…,100}的两个子集,满足:A 与B 的元素个数相同,且A B I 为空集.若n A ∈时总有22n B +∈,则集合A B U 的元素个数最多为( ).A . 62B .66C .68D .74A B CDPMPDCBA二.填空题(每小题9分,共54分) 7. 在平面直角坐标系内,有四个定点(30),A -,(11),B -,(03),C ,(13),D -及一个动点P ,则||||||||PA PB PC PD +++的最小值为__________.8.在ABC ∆和AEF ∆中,B 是EF 的中点,1AB EF ==,6BC =,CA =,若2AB AE AC AF ⋅+⋅=,则EF 与BC 的夹角的余弦值等于___________.9. 已知正方体1111ABCD A B C D -的棱长为1,以顶点A则球面与正方体的表面相交所得到的曲线的长等于___________.10.已知等差数列{}n a 的公差d 不为0,等比数列{}n b 的公比q 是小于1的正有理数.若1a d =,21b d =,且222123123a a ab b b ++++是正整数,则q 等于__________.11.已知函数15()()44f x x =≤≤,则()f x 的最小值为__________. 12.将2个a 和2个b 共4个字母填在如图所示的16个小方格内,每个小方格内至多填1个字母,若使相同字母既不同行也不同列,则不同的填法共有__________种(用数字作答).二、 解答题(本题每小题20分,共计60分)13. 设11(1)nn k a k n k ==+-∑,求证:当正整数2n ≥时,1n n a a +<.P F DC BA14.已知过点(0,1)的直线l 与曲线C :1(0)y x x x=+>交于两个不同点M 和N .求曲线C 在点M 、N 处切线的交点轨迹.15.设函数()f x 对所有的实数x 都满足(2π)()f x f x +=,求证:存在4个函数()i f x ()1234,,,i =满足:⑴ 对1234,,,i =,()i f x 是偶函数,且对任意的实数x ,有(π)()i i f x f x +=; ⑵ 对任意的实数x ,有1234()()()cos ()sin ()sin 2f x f x f x x f x x f x x =+++.2007年全国高中数学联合竞赛 (二试)一、(本题满分50分) 如图,在锐角ABC ∆中,AB AC <,AD 是边BC 上的高,P 是线段AD 内一点.过P 作PE AC ⊥,垂足为E ,作PF AB ⊥,垂足为F .1O 、2O 分别是BDF ∆、CDE ∆的外心.求证:1O 、2O 、E 、F 四点共圆的充要条件为P 是ABC ∆的垂心.二.(本题满分50分) 如图,在78⨯的长方形棋盘的每个小方格的中心点各放一个棋子.如果两个棋子所在的小方格共边或共顶点,那么称这两个棋子相连.现从这56个棋子中取出一些,使得棋盘上剩下的棋子,没有五个在一条直线(横、竖、斜方向)上依次相连.问最少取出多少个棋子才可能满足要求?并说明理由.三 (本题满分50分) 设集合{}12345,,,,P =,对任意k P ∈和正整数m ,记(),f m k =∑=⎥⎦⎤⎢⎣⎡++5111i i k m ,其中[]a 表示不大于a 的最大整数.求证:对任意正整数n ,存在k P ∈和正整数m ,使得(),f m k n =.1234567876543211254311109876543211234567876543212007年全国高中数学联合竞赛 (一试)一选择题(每小题6分,共36分)1如图,在正四棱锥P ABCD -中,60APC ∠=︒,则二面角A PB C --的平面角的 余弦值为( )A .17B .17-C .12D .12-A B CDPMPDCBA【解答】B如图,在侧面PAB 内,作AM PB ⊥,垂足为M .连接CM 、AC ,则AMC ∠为二面角A PB C --的平面角.不妨设2AB =,则PA AC ==,故222AM =⋅,由此得CM AM ==.在A M C ∆中,由余弦定理得2221cos 27AM CM AC AMC AM CM +-∠==-⋅⋅. 2.设实数a 使得不等式2|2||32|x a x a a -+-≥对任意实数x 恒成立,则满足条件的a 所组成的集合是( ).A .1133,⎡⎤-⎢⎥⎣⎦B .1122,⎡⎤-⎢⎥⎣⎦C .1143,⎡⎤-⎢⎥⎣⎦ D .[]33,-【解答】A .令23x a =,则有1||3a ≤,排除B 、D .由对称性排除C ,从而只有A 正确.一般地,对k ∈R ,令12x ka =,则原不等式为234|||1|||||23a k a k a ⋅-+⋅-≥,由此易知原不等式等价于34|||1|23a k k -+-≤,对任意的k ∈R 成立.由于543,233414|1|1,1232353,12k k k k k k k k ⎧-⎪⎪⎪-+-=-<⎨⎪⎪-<⎪⎩≥≤,所以R 341min |1|233k k k ∈⎧⎫-+-=⎨⎬⎩⎭,从而上述不等式等价于1||3a ≤.3将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,其号码为a ,放回后,乙从此袋中再摸出一个球,其号码为b .则使不等式2100a b -+>成立的事件发生的概率等于( )A .5281B .5981C .6081D .6181【解答】D甲、乙二人每人摸出一个小球都有9种不同的结果,故基本事件总数为2981=个.由不等式2100a b -+>得210b a <+,于是,当1b =、2、3、4、5时,每种情形a 可取1、2、…、9中每一个值,使不等式成立,则共有9545⨯=种;当6b =时,a 可取3、4、…、9中每一个值,有7种;当7b =时,a 可取5、6、7、8、9中每一个值,有5种;当8b =时,a 可取7、8、9中每一个值,有3种;当9b =时,a 只能取9,有1种.于是,所求事件的概率为457531618181++++=.4.设函数()3sin 2cos 1f x x x =++.若实数a 、b 、c 使得()()1af x bf x c +-=对任意实数x 恒成立,则cos b ca 的值等于( )A .12-B .12 C .1- D .1【解答】C .令πc =,则对任意的x ∈R ,都有()()1f x f x c +-=,于是取12a b ==,πc =,则对任意的x ∈R ,()()1af x bf x c +-=,由此得cos 1b ca=-.一般地,由题设可得())1f x x ϕ++,())1f x c x c ϕ-+-+,其中02πϕ<<且2tan 3ϕ=,于是()()1af x bf x c +-=可化为sin()sin()1x x c a b ϕϕ++-++=,即sin()sin()cos sin cos()(1)0x x c c x a b ϕϕϕ+++++-=,所以cos )sin()sin cos()(1)0a b c x c x a b ϕϕ+++++-=.由已知条件,上式对任意x ∈R 恒成立,故必有cos 0(1)sin 0(2)10(3)a b c b c a b +=⎧⎪=⎨⎪+-=⎩, 若0b =,则由⑴知0a =,显然不满足⑶式,故0b ≠.所以,由⑵知sin 0c =,故2ππc k =+或2πc k =()k ∈Z .当2πc k =时,cos 1c =,则⑴、⑶两式矛盾.故2ππc k =+()k ∈Z ,cos 1c =-.由⑴、⑶知12a b ==,所以cos 1b ca =-.5.设圆1O 和圆2O 是两个定圆,动圆P 与这两个定圆都相切,则圆P 的圆心轨迹不可能是( ).A .B .C. D .【解析】A .设圆1O 和圆2O 的半径分别是1r 、2r ,122O O c =,则一般地,圆P 的圆心轨迹是焦点为1O 、2O ,且离心率分别是122c r r +和122||cr r -的圆锥曲线(当12r r =时,12O O的中垂线是轨迹的一部份,当0c =时,轨迹是两个同心圆).当12r r =且122r r c +<时,圆P 的圆心轨迹如选项B ;当1202c r r <<-时,圆P 的圆心轨迹如选项C ;当12r r ≠且122r r c +<时,圆P 的圆心轨迹如选项D .由于选项A 中的椭圆和双曲线的焦点不重合,因此圆P 的圆心轨迹不可能是选项A .6.已知A 与B 是集合{1,2,3,…,100}的两个子集,满足:A 与B 的元素个数相同,且A B 为空集.若n A ∈时总有22n B +∈,则集合A B U 的元素个数最多为( ). A .62 B .66 C .68 D .74 【解析】B .先证66A B U ≤,只须证33A ≤,为此只须证若A 是{1,2,…,49}的任一个34元子集,则必存在n A ∈,使得22n B +∈.证明如下:将{1,2,…,49}分成如下33个集合:{1,4},{3,8},{5,12},…,{23,48}共12个;{2,6},{10,22},{14,30},{18,38}共4个;{25},{27},{29},…,{49}共13个;{26},{34},{42},{46}共4个.由于A 是{1,2,…,49}的34元子集,从而由抽屉原理可知上述34个集合中至少有一个2元集合中的数均属于A ,即存在n A ∈,使得22n B +∈.如取A ={1,3,5,…,23,2,10,14,18,25,27,29,…,49,26,34,42,46},{22},B n n A =+∈,则A 、B 满足题设且66A B U ≤.三. 填空题(每小题9分,共54分)7.在平面直角坐标系内,有四个定点(30),A -,(11),B -,(03),C ,(13),D -及一个动点 P ,则||||||||PA PB PC PD +++的最小值为__________.【解析】 如图,设AC 与BD 交于F 点,则 ||||||||||PA PC AC FA FC +=+≥, ||||||||||PB PD BD FB FD +=+≥. 因此,当动点P 与F 点重合时,||||||||PA PB PC PD +++取到最小值||||AC BD +=8.在ABC ∆和AEF ∆中,B 是EF 的中点,1AB EF ==,6BC =,CA =若2AB AE AC AF ⋅+⋅=,则EF 与BC 的夹角的余弦值等于___________.【解析】∵2AB AE AC AF ⋅+⋅=u u u r u u u r u u u r u u u r,∴()()2AB AB BE AC AB BF ⋅++⋅+=u u u r u u u r u u u r u u u r u u u r u u u r,即22AB AB BE AC AB AC BF +⋅+⋅+⋅=u u u r u u u r u u u r u u u r u u u r u u u r u u u r .∵21AB =u u u r,11AC AB ⋅==-u u u r u u u r ,BE BF =-u u u r u u u r , ∴1()12BF AC AB +⋅--=u u u r u u u r u u u r ,即2BF BC ⋅=.设EF u u u r 与BC u u ur 的夹角为θ,则有||||cos 2BF BC θ⋅⋅=u u u r u u u r ,即3cos 2θ=,所以2cos 3θ=.9.已知正方体1111ABCD A B C D -的棱长为1,以顶点A面与正方体的表面相交所得到的曲线的长等于___________.【解析】如图,球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A 所在的三个面上,即面11AA BB 、面ABCD 和面11AA D D 上;另一类在不过顶点A 的三个面上,即面11BB C C 、面11CC D D 和面1111A B C D 上.在面11AA B B 上,交线为弧EF 且在过球心A 的大圆上,因为AE ,11AA =,则1π6A AE ∠=.同理π6BAF ∠=,所以π6EAF ∠=,故弧EF PFD CBAπ6,而这样的弧共有三条.在面11BB C C上,交线为弧FG且在距球心为1的平面与球面相交所得的小圆上,此时,小圆的圆心为Bπ2 FBG∠=,所以弧FG的长为π2=.这样的弧也有三条.于是,所得的曲线长为3π3966⨯+⨯=.10.已知等差数列{}n a的公差d不为0,等比数列{}n b的公比q是小于1的正有理数.若1a d=,21b d=,且222123123a a ab b b++++是正整数,则q等于__________.【解析】12.因为22222212311122123111()(2)141a a a a a d a db b b b b q b q q q++++++==++++++,故由已知条件知道:21q q++为14m,其中m为正整数.令2141q qm++=,则1122q=-+=-+由于q是小于1的正有理数,所以1413m<<,即513m≤≤且5634mm-是某个有理数的平方,由此可知12q=.11.已知函数15()()44f x x=≤≤,则()f x的最小值为__________..实际上πs i nπ215()()44xf x x⎛⎫-+⎪=≤≤,设π15()π()444g x x x⎛⎫=-⎪⎝⎭≤≤,则()0g x≥,()g x在13,44⎡⎤⎢⎥⎣⎦上是增函数,在35,44⎡⎤⎢⎥⎣⎦上是减函数,且()y g x=的图像关于直线34x=对称,则对任意113,44x⎡⎤∈⎢⎥⎣⎦,存在235,44x⎡⎤∈⎢⎥⎣⎦,使21()()g x g x=.11A1于是12()()f x f x ===,而()f x 在35,44⎡⎤⎢⎥⎣⎦上是减函数,所以5()45f x f ⎛⎫= ⎪⎝⎭≥,即()f x 在15,44⎡⎤⎢⎥⎣⎦上的最小值是5.12.将2个a 和2个b 共4个字母填在如图所示的16个小方格内,每个小方格内至多填1个字母,若使相同字母既不同行也不同列,则不同的填法共有__________种(用数字作答).【解答】 3960.使2个a 既不同行也不同列的填法有2244C A 72=种,同样,使2个b 既不同行也不同列的填法也有2244C A 72=种,故由乘法原理,这样的填法共有272种,其中不符合要求的有两种情况:2个a 所在的方格内都填有b 的情况有72种;2个a 所在的方格内仅有1个方格内填有b 的情况有12169C A 种.所以,符合题设条件的填法共有2121697272C A 3960--=种.四. 解答题(本题每小题20分,共计60分) 13.设11(1)nn k a k n k ==+-∑,求证:当正整数2n ≥时,1n n a a +<.【解析】由于1111(1)11k n k n k n k ⎛⎫=+ ⎪+-++-⎝⎭,因此1211n n k a n k ==+∑,于是,对任意的正整数2n ≥,有111111111()212n n n n k k a a n k n k++==-=-++∑∑111111111012(1)(2)(1)(2)n n k k n n k n n n n k ==⎛⎫⎛⎫=--=-> ⎪ ⎪++++++⎝⎭⎝⎭∑∑,即1n n a a +<. 14.已知过点(0,1)的直线l 与曲线C :1(0)y x x x=+>交于两个不同点M 和N .求曲线C在点M 、N 处切线的交点轨迹.【解析】设点M 、N 的坐标分别为1(x ,1)y 和2(x ,2)y ,曲线C 在点M 、N 处的切线分别为1l 、2l ,其交点P 的坐标为(P x ,)P y .若直线l 的斜率为k ,则l 的方程为1y kx =+. 由方程组11y x x y kx ⎧=+⎪⎨⎪=+⎩,消去y ,得11x kx x +=+,即2(1)10k x x -+-=.由题意知,该方程在(0,)+∞上有两个相异的实根1x 、2x ,故1k ≠,且 14(1)0k ∆=+-> ……①,12101x x k +=>- ……②,12101x x k=>- ……③,由此解得314k <<.对1y x x=+求导,得211y'x =-,则1211|1x x y'x ==-,2221|1x x y'x ==-,于是直线1l 的方程为112111()y y x x x ⎛⎫-=-- ⎪⎝⎭,即11211111()y x x x x x ⎛⎫⎛⎫-+=-- ⎪ ⎪⎝⎭⎝⎭,化简后得到直线1l 的方程为211121y x x x ⎛⎫=-+ ⎪⎝⎭……④.同理可求得直线2l 的方程为222121y x x x ⎛⎫=-+ ⎪⎝⎭……⑤.④-⑤得22211211220p x x x x x ⎛⎫-+-= ⎪⎝⎭,因为12x x ≠,故有12122p x x x x x =+ ……⑥.将②③两式代入⑥式得2P x =.④-⑤得222212*********p p y x x x x x ⎡⎤⎛⎫⎛⎫=-+++⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦……⑦,其中121212111x xx x x x ++==,2222121212122222221212121212()211212(1)21x x x x x x x x k k x x x x x x x x x x ⎛⎫++-++===-=--=- ⎪⎝⎭, 代入⑦式得2(32)2p P y k x =-+,而2P x =,得42P y k =-.又由314k <<得522p y <<,即点P 的轨迹为(2,2),(2,2.5)两点间的线段(不含端点).15.设函数()f x 对所有的实数x 都满足(2π)()f x f x +=,求证:存在4个函数()i f x ()1234,,,i =满足:⑴ 对1234,,,i =,()i f x 是偶函数,且对任意的实数x ,有(π)()i i f x f x +=; ⑵ 对任意的实数x ,有1234()()()cos ()sin ()sin 2f x f x f x x f x x f x x =+++.【解析】记()()()2f x f x g x +-=,()()()2f x f x h x --=,则()()()f x g x h x =+,且()g x 是偶函数,()h x 是奇函数, 对任意的x ∈R ,(2π)()g x g x +=,(2π)()h x h x +=.令1()(π)()2g x g x f x ++=,2()(π)ππ2cos 2()ππ2g x g x x k x f x x k -+⎧≠+⎪⎪=⎨⎪=+⎪⎩,3()(π)π()2sin 0πh x h x x k f x xx k -+⎧≠⎪=⎨⎪=⎩,4()(π)π2sin 22()π02h x h x k x x f x k x ++⎧≠⎪⎪=⎨⎪=⎪⎩,其中k 为任意整数.容易验证()i f x ,1234,,,i =是偶函数,且对任意的x ∈R ,(π)()i i f x f x +=,1234,,,i =.下证对任意的x ∈R ,有12()()cos ()f x f x x g x +=.当ππ2x k ≠+时,显然成立;当ππ2x k =+时,因为121()(π)()()cos ()2g x g x f x f x x f x +++==,而3π3πππ(π)ππ2(1)π(π)π()2222g x g k g k k g k g k g x ⎛⎫⎡⎤⎛⎫+=+=+-+=--=+= ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭, 故对任意的x ∈R ,12()()cos ()f x f x x g x +=.下证对任意的x ∈R ,有34()sin ()sin 2()f x x f x x h x +=.当π2k x ≠时,显然成立; 当πx k =时,()(π)(π2π)(π)(π)h x h k h k k h k h k ==-=-=-,所以()(π)0h x h k ==, 而此时34()sin ()sin 20f x x f x x +=,故34()sin ()sin 2()f x x f x x h x +=;当ππ2x k =+时,3π3πππ(π)(π)π2(1)πππ()2222h x h k h k k h k h k h x ⎛⎫⎛⎫⎛⎫+=+=+-+=--=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故3()(π)()sin ()2h x h x f x x h x -+==,又4()sin 20f x x =,从而有34()sin ()sin 2()f x x f x x h x +=.于是,对任意的x ∈R ,有34()sin ()sin 2()f x x f x x h x +=. 综上所述,结论得证.2007年全国高中数学联合竞赛 (二试)一(本题满分50分) 如图,在锐角ABC ∆中,AB AC <,AD 是边BC 上的高,P 是线段AD 内一点.过P 作PE AC ⊥,垂足为E ,作PF AB ⊥,垂足为F .1O 、2O 分别是BDF ∆、CDE ∆的外心.求证:1O 、2O 、E 、F 四点共圆的充要条件为P 是ABC ∆的垂心.【解答】 连接BP 、CP 、12O O 2、2EO 2、EF 、1FO 1.∵PD BC ⊥,PF AB ⊥,∴B 、D 、P 、F 四点共圆,且BP 为该圆的直径. 又∵1O 是BDF ∆的外心,∴1O 1在BP 上且是BP 的中点.同理可证C 、D 、P 、E 四点共圆,且2O 是CP 的中点.综合以上知12O O BC ∥,所以21PO O PCB ∠=∠.∵AF AB AP AD AE AC ⋅=⋅=⋅,∴B 、C 、E 、F 四点共圆. 充分性:设P 是ABC ∆的垂心,由于PE AC ⊥,PF AB ⊥,所以B 、1O 、P 、E 四点共线,C 、2O 、P 、F 四点共线,211FO O FCB FEB FEO ∠=∠=∠=∠ 1,故1O 、2O 、E 、F 四点共圆. 必要性:设1O 、2O 、E 、F 四点共圆,则121180O O E EFO ∠+∠=︒. 由于21PO O PCB ACB ACP ∠=∠=∠-∠,又∵O 2是直角CEP ∆的斜边中点,也就是CEP ∆的外心,∴22PO E ACP ∠=∠. ∵2O 是直角BFP ∆的斜边中点,也就是BFP ∆的外心,从而119090FPO BFO ABP ∠=︒-∠=︒-∠.∵B 、C 、E 、F 四点共圆,∴AFE ACB ∠=∠,90PFE ACB ∠=︒-∠.于是,由121180O O E EFO ∠+∠=︒得()2(90)(90)180ACB ACP ACP ABP ACB ∠-∠+∠+︒-∠+︒-∠=︒,即A B ∠=∠. 又∵AB AC <,AD BC ⊥,故BD CD <.设B '是点B 关于直线AD 的对称点,则B '在线段DC 上且B D BD '=. 连接AB '、PB '.由对称性,有AB P ABP '∠=∠,从而AB P ACP '∠=∠, ∴A 、P 、B '、C 四点共圆.由此可知90PB B CAP ACB '∠=∠=︒-∠.∵PBC PB B '∠=∠,∴(90)90PBC ACB ACB ACB ∠+∠=︒-∠+∠=︒,故直线BP 和AC 垂直.由题设P 在边BC 的高上,所以P 是ABC ∆的垂心.二、 (本题满分50分) 如图,在78⨯的长方形棋盘的每个小方格的中心点各放一个棋子.如果两个棋子所在的小方格共边或共顶点,那么称这两个棋子相连.现从这56个棋子中取出一些,使得棋盘上剩下的棋子,没有五个在一条直线(横、竖、斜方向)上依次相连.问最少取出多少个棋子才可能满足要求?并说明理由.123456787654321125431110987654321123456787654321【解答】 最少要取出11个棋子,才可能满足要求.其原因如下:如果一个方格在第i 行第j 列,则记这个方格为(i ,)j .第一步证明若任取10个棋子,则余下的棋子必有一个五子连珠,即五个棋子在一条直线(横、竖、斜方向)上依次相连.用反证法.假设可取出10个棋子,使余下的棋子没有一个五子连珠. 如图,在每一行的前五格中必须各取出一个棋子,后三列的前五格中也必须各取出一个棋子.这样,10个被取出的棋子不会分布在右下角的阴影部分. 同理,由对称性,也不会分布在其他角上的阴影部分.第1、2行必在每行取出一个,且只能分布在(14),、(15),、(24),、(25),这些方格.同理(64),、(65),、(74),、(75),这些方格上至少要取出2个棋子.在第1、2、3列,每列至少要取出一个棋子,分布在(31),、(32),、(33),、(41),、(42),、(43),、(51),、(52),、(53),所在区域,同理(36),、(37),、(38),、(46),、(47),、(48),、(56),、(57),、(58),所在区域内至少取出3个棋子.这样,在这些区域内至少已取出了10个棋子.因此,在中心阴影区域内不能取出棋子.由于①、②、③、④这4个棋子至多被取出2个,从而,从斜的方向看必有五子连珠了.矛盾.第二步构造一种取法,共取走11个棋子,余下的棋子没有五子连珠. 如图,只要取出有标号位置的棋子,则余下的棋子不可能五子连珠.综上所述,最少要取走11个棋子,才可能使得余下的棋子没有五子连珠.三、 (本题满分50分) 设集合{}12345,,,,P =,对任意k P ∈和正整数m ,记(),f m k =∑=⎥⎦⎤⎢⎣⎡++5111i i k m ,其中[]a 表示不大于a 的最大整数. 求证:对任意正整数n ,存在k P ∈和正整数m ,使得(),f m k n =. 【解答】 定义集合{}*,A k P =∈∈N ,其中*N 为正整数集.由于对任意k 、i P ∈且k i ≠,11++i k 是无理数, 则对任意的1k 、2k P ∈和正整数1m 、2m,m m =当且仅当12m m =,12k k =.由于A 是一个无穷集,现将A 中的元素按从小到大的顺序排成一个无穷数列.对于任意的正整数n ,设此数列中第n项为 下面确定n 与m 、k的关系.若m ≤,则1m ≤由1m 是正整数可知,对12345,,,,i =,满足这个条件的1m的个数为⎡⎢⎣.从而n =∑=⎥⎦⎤⎢⎣⎡++5111i i k m (),f m k =.因此对任意*n ∈N ,存在*m ∈N ,k P ∈,使得(),f m k n =.。
2007年浙江省数学分析竞赛试题及答案

2007浙江省第六届数学分析竞赛试题一.计算题 1. 求951x dx x +⎰.解:原式()55215x d x =+⎰()232211553t dt t t C ⎛⎫=-=-+ ⎪⎝⎭⎰. 2. 求()()1120112limsin xxx x x x→+-+.解:令()()11xf x x =+,则原式()()002lim limsin x x f x f x xx x→→-=()()()0lim 22x f x f x →''=-()()()()()()00002lim lim 2lim 2lim 2x x x x f x f x f x f x f x f x →→→→''=-()()()()002lim 2lim 2x x f x f x e e f x f x →→''=-()()limx f x e f x →'=-()()2001ln 11lim lim 1x x x x x e x x →→-++=-+()0ln 1lim22x x ee x →-+=-=.3. 求p 的值,使()()220070bx p ax p edx ++=⎰.解:情形一,当a b =时,p 的值可以任意取;情形二,当a b ≠时,做变换t x p =+,则 原式左边22007b pt a pt e dt ++=⎰,因为被积函数是奇函数,故当()a p b p +=-+时,即2a b p +=-时,有()()220070b x p a x p e dx ++=⎰. 4. 设(),x ∀∈-∞+∞,()0f x ''≥,且()201x f x e-≤≤-,求()f x 的表达式.解:(1)由()2011x f x e-≤≤-<,知()f x 有界;(2)下证()0f x '=,(),x ∀∈-∞+∞.假若存在()0,x ∈-∞+∞,使得()00f x '≠,则()()()()()()2000012f x f x f x x x f x x ξ'''=+-+- ()()()000f x f x x x '≥+-,若()00f x '>,则()()()()000f x f x f x x x '≥+-→+∞,()x →+∞,这与()f x 有界矛盾;若()00f x '<,则()()()()000f x f x f x x x '≥+-→+∞,()x →-∞,这与()f x 有界矛盾,因此()00f x '=,(),x ∀∈-∞+∞,()f x C =,(),x ∀∈-∞+∞;(3)由()00010f e ≤≤-=,知()00f =,因此()0f x =,(),x ∀∈-∞+∞.5. 计算()2Sxy dS +⎰⎰,其中S 为柱面224x y +=,()01z ≤≤.解:方法一 因圆柱面224xy +=,()01z ≤≤的参数方程为2c o s 2s i nx uy u z v =⎧⎪=⎨⎪=⎩, 故2dSEG F dudv =-,其中2224u u u E x y z =++=,0u v u v u v F x x y y z z =++=,2221v v v G x y z =++=, 于是()()122224cos 2sin Sxy dS dv u u du π+=+⎰⎰⎰⎰()2224cos 2sin u u du π=+⎰20cos21882u du ππ-==⎰.方法二 注意到对称性()22SSx y dS x dS +=⎰⎰⎰⎰()2212Sx y dS =+⎰⎰()1144221822S dS ππ==⋅⋅⋅⋅=⎰⎰. 二.设1211211212345632313nu n n n=+-++-+++--- , 111123n v n n n=+++++ ,求(1)1010u v ,(2)lim n n u →∞.解:(1)因为111111232n u n n ⎛⎫=+++-+++ ⎪⎝⎭,111111232n v n n ⎛⎫=+++-+++ ⎪⎝⎭, 故n n u v =,因此10101u v =, (2)方法一 2111lim lim lim 1n n n n n n k u v k n n→∞→∞→∞===+∑()22001ln 1ln31dx x x ==+=⎡⎤⎣⎦+⎰.方法二 利用111ln 2n n c nε+++=++ ,其中lim 0n n ε→∞=,()()3lim lim ln3ln n n n n n u n c n c εε→∞→∞⎡⎤=++-++⎣⎦()3lim ln3n n n εε→∞=+- ln3=.三.有一个边长为4π的正方形纸(如图),C 、D 分别为AA '、BB '的中点,E 为DB '的中点.现将纸卷成圆柱形,使A 与A '重合,B 与B '重合,并将圆柱垂直放在xoy 平面上,且B 与原点O 重合,D 落在y 轴正向上.求:(1)通过C ,E 两点的直线绕z 轴旋转所得的旋转面方程; (2)此旋转面、xoy 平面和过A 点垂直于z 轴的平面所围成的立体体积. 解:()0,0,0B ,()0,4,4C π,()0,4,0D ,()2,2,0E ,通过()0,4,4Cπ和()2,2,0E 两点的直线l 方程为22224x y z π--==-,即22z x π=-,22zy π=+, (1)通过C ,E 两点的直线l 绕z 轴旋转所得的旋转面方程为22222222z z x y ππ⎛⎫⎛⎫+=-++ ⎪ ⎪⎝⎭⎝⎭,即222282z x y π+=+; (2)此旋转曲面()222228z x y π=+-,xoy 平面0z=和过A 点垂直于z 轴的平面4z π=所围成的立体体积为22224082z x y V dxdydz dzdxdy ππΩ+≤+==⎰⎰⎰⎰⎰⎰242082z dz πππ⎛⎫=+ ⎪⎝⎭⎰432086z z πππ⎛⎫=+⎪⎝⎭ 222321283233πππ=+=.四.求函数()2222,,x yz f x y z x y z+=++,在(){}222,,:14D x y z x y z =≤++≤上的最大值和最小值.解:解法一 令cos x ρϕ=,cos sin y ρθϕ=,sin sin zρθϕ=,则()222221,,1sin 21sin 2x yz f x y z x y z θϕ+⎛⎫==+- ⎪++⎝⎭, 其中[]0,ϕπ∈,[],θππ∈-,因()311sin 21222g θθ-≤=-≤-,且32-,12-分别是()1sin 212g θθ=-的最小值和最大值, 故()2222,,x yz f x y z x y z +=++在D 上的最小值和最大值为别为31122⎛⎫+-=- ⎪⎝⎭,101+=.解法二 由()()22221122y z yz y z -+≤≤+, 得()()22222222213112222x y z x x yz x y z x -+++≤+≤+++, ()222222212x y z x yz x y z -++≤+≤++, ()1,,12f x y z -≤≤, 且等号能达到,(),0,01f x =,()10,,2f y y -=-,故()2222,,x yz f x y z x y z +=++在D 上的最小值和最大值为别为12-,1. 五.求11limnk n k n n knC →∞=+-∑. 解:记11n n kk n n kx nC =+-=∑, ()()()22212!3!4!10112n x n n n n n n n n≤=+++++---()212!12n n n n ≤+-+()441n n n=-<, 故11lim0nk n k n n knC →∞=+-=∑. 六.证明:24cos 21x x x ≤-++,20,4x π⎡⎤∈⎢⎥⎣⎦.证明:只要证()224cos 21x x x +≤+,20,4x π⎡⎤∈⎢⎥⎣⎦.该不等式等价于222cos 2cos 21x x x +≤,20,4x π⎡⎤∈⎢⎥⎣⎦,即222cos 2sin 2x x x ≤,20,4x π⎡⎤∈⎢⎥⎣⎦,令2tx =,则只要证 sin cos tt t≤,0,2t π⎡⎫∈⎪⎢⎣⎭, 为此,作()sin ,cos t f t t t =-0,2t π⎡⎫∈⎪⎢⎣⎭则()31cos cos 12t t f t +'=-,0,2t π⎡⎫∈⎪⎢⎣⎭因此()31cos cos 12t t f t +'=-311cos 110cos cos t tt≥⋅-=-≥,0,2t π⎡⎫∈⎪⎢⎣⎭ 于是当02t π≤<时,()()sin 00cos tf t t f t=-≥=.结论得证.。
通知

林炜
镇海中学
A组
绍兴
111
姚元
诸暨中学
A组
宁波
150
虞华艇
镇海中学
A组
绍兴
112
刘于绰
诸暨中学
A组
宁波
151
陈培文
镇海中学
A组
绍兴
113
张家怡
诸暨中学
A组
宁波
152
杨根茂
象山中学
A组
杭州
114
杨嘉胤
杭州二中
A组
宁波
153
杨起帆
镇海中学
A组
嘉兴
115
陆范菲
嘉善高级中学
A组
绍兴
154
徐远
新昌中学
A组
郦润华
诸暨中学
A组
宁波
94
井永乐
效实
A组
温州
133
叶立早
温州中学
A组
宁波
95
叶荔
余姚中学
A组
湖州
134
郑欣
湖州中学
A组
宁波
96
马潇辉
慈溪中学
A组
金华
135
陈赞迪
兰溪一中
A组
宁波
97
丁雪成
慈溪中学
A组
台州
136
杨羲
路桥中学
A组
宁波
98
陈超丰
慈溪中学
A组
嘉兴
137
皮学锋
嘉兴一中
A组
宁波
99
陈硕冰
镇海中学
杭州二中
A组
金华
65
华佳驹
东阳中学
2007年高考浙江卷(理科数学)

2007年普通高等学校招生全国统一考试理科数学(浙江卷)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.“1x >”是“2x x >”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件2.若函数()2sin()f x x ωϕ=+,x R ∈(其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =A .12ω=,6ϕπ= B .12ω=,3ϕπ=C .2ω=,6ϕπ=D .2ω=,3ϕπ=3.直线210x y -+=关于直线1x =对称的直线方程是 A .210x y +-= B .230x y +-= C .230x y +-= D .210x y +-=4.要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是A .3B .4C .5D .6 5.已知随机变量ξ服从正态分布2(2,)N σ,(4)0.84P ξ≤=,则(0)P ξ≤= A .0.16 B .0.32 C .0.68 D.0.84 6.若P 两条异面直线l ,m 外的任意一点,则 A .过点P 有且仅有一条直线与l ,m 都平行 B .过点P 有且仅有一条直线与l ,m 都垂直 C .过点P 有且仅有一条直线与l ,m 都相交 D .过点P 有且仅有一条直线与l ,m 都异面 7.若非零向量a ,b 满足a b b +=,则A .2a a b >2+B .2a a b <2+C .2b a b >+2 D.2b a b <+28. 设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能的是9.已知双曲线22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,P 是准线上一点,且12PF PF ⊥,124PF PF ab ⋅=,则双曲线的离心率是 ABC .2D .310.设21()1x x f x xx ⎧≥⎪=⎨<⎪⎩,()g x 是二次函数,若(())f g x 的值域是[0)+∞,,则()g x 的值域是A .(1][1)-∞-+∞,3B .(1][0)-∞-+∞,C .[0)+∞,D .[1)+∞, 二、填空题:本大题共7小题,每小题4分,共28分. 11.已知复数11z i =-,121z z i ⋅=+,则复数2z = .12.已知1sin cos 5θθ+=,且324ππθ≤≤,则cos2θ的值是 .13.不等式211x x --<的解集是 .14.某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答). 15.随机变量ξ的分布列如下:其中a ,b ,c 成等差数列,若3E ξ=,则D ξ的值是.16.已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=.若对于β内异于O 的任意一点Q ,都有45POQ ∠≥,则二面角AB αβ--的大小是 .17.设m 为实数,若{}22250()30()250x y x y x x y x y mx y ⎧⎫-+≥⎧⎪⎪⎪-≥⊆+≤⎨⎨⎬⎪⎪⎪+≥⎩⎩⎭,,,则m 的取值范围是 .三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤.18.(本小题满分14分)已知ABC ∆1,且sin sin A B C +=. (Ⅰ)求边AB 的长;(Ⅱ)若ABC ∆的面积为1sin 6C ,求角C 的度数.19.(本小题满分14分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且AC =BC 2BD AE ==,M 是AB 的中点. (Ⅰ)求证:CM EM ⊥;(Ⅱ)求CM 与平面CDE 所成的角.20.(本小题满分14分)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S .(Ⅰ)求在0k =,01b <<的条件下,S(Ⅱ)当2AB =,1S =时,求直线ABABCDEM21.(本小题满分15分)已知数列{}n a 中的相邻两项21k a -,2k a 是关于x 的方程2(32)320k k x k x k -++⋅=的两个根,且212k k a a -≤(123k =,,,). (Ⅰ)求1a ,3a ,5a ,7a ; (Ⅱ)求数列{}n a 的前2n 项和2n S ;(Ⅲ)记sin 1()(3)2sin n f n n =+,(2)(3)(4)(1)123456212(1)(1)(1)(1)f f f f n n n nT a a a a a a a a +-----=++++…, 求证:15()624n T n N ≤≤∈*.22.(本小题满分15分)设3()3x f x =,对任意实数t ,记232()3t g x t x t =-.(Ⅰ)求函数8()()y f x g x =-的单调区间;(Ⅱ)求证:①当0x >时,()()t f x g x ≥对任意正实数t 成立; ②有且仅有一个正实数0x ,使得800()()t g x g x ≥对任意正实数t 成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年浙江省高中数学竞赛A卷(附参考答案)
一、选择题
1.如果,则使的的取值范围为()
A. B. C. D.
解:显然,且。
要使。
当时,,即;当时,,此时无解。
由此可得,使的的取值范围为。
应选B。
2.已知集合,
,则=()
A. B. R C. D.
解:
没有实数可以使上述不等式成立。
故。
从而有。
应选C。
3.以为六条棱长的四面体个数为()
A. 2
B. 3
C.4
D. 6
解:以这些边为三角形仅有四种:,,,。
固定四面体的一面作为底面:
当底面的三边为时,另外三边的取法只有一种情况,即;
当底面的三边为时,另外三边的取法有两种情形,即,。
其余情形得到的四面体均在上述情形中。
由此可知,四面体个数有3个。
应选B。
4.从1至169的自然数中任意取出3个数构成以整数为公比的递增等比数列的取法有()种。
A. 89
B. 90
C.91
D. 92
解:若取出的3个数构成递增等比数列,则有。
由
此有。
当固定时,使三个数为整数的的个数记作。
由
,知应是的整数部分。
,,
,,,,,
,.
因此,取法共有。
应选C
5.若在复平面上三个点构成以A为直角顶点的等腰直角三角形,其中,则△ABC的面积为()
A. B. C.1 D.
解:依题意,,。
△ABC的面积为。
应选A。
6.2007重的末二位数字是()
A. 01
B. 07
C.43
D. 49
解:记k重。
题目要求的末二位数。
其中M为正整数。
由此可得的末二位数与的末二位数字相同。
首先来观察的末二位数字的变化规律。
的末二位
的末二位数字的变化是以4为周期的规律循环出现。
(为奇整数)
(为正整数)
因此,与的末二位数字相同,为43。
应选C。
二、填空题
7.设为的单调递增数列,且满足,则。
解:
(由题意可知取正号。
)
因此,公差为2的等差数列,即。
从而可得。
答案为。
8.设为方程的根(),则。
解:由题意,。
由此可得
,,以及。
答案为:。
9.设均为非负实数,则
的最小值为。
解:在直角坐标系中,作点,,,
,。
则
I=
=+++(应用三角不等式)
+++=2007。
如果取,即,那么I取到最小值2007。
答案为2007。
10.设是定义在R上的奇函数,且满足;又当时,
,则=。
解:依题意,,即是以4为周期的周期函数。
因为当时,,且为奇函数,所以当时,。
此时有。
可得。
又因为是以4为周期的周期函数,
所以也有,()。
答案为()。
11.设,则不超过的最大整数为。
解:
,
,
,
,
不超过的最大整数为。
答案为。
12.整数,且,则整数组为。
解:方程两边同乘以8,得。
因为,所以要使左边为奇数,只有,即。
则。
要使左边为奇数,只有,即。
从而有,即。
故有。
答案为。
三、解答题
13.已知抛物线和点。
过点任作直线,交抛物
线于B,C两点。
(1)求△ABC的重心轨迹方程,并表示成形式;
(2)若数列,,满足。
试证:。
解:(1)设过的直线方程为。
又设,
,联立方程组,
消去,得。
从而有,
,。
…………5分设△ABC的重心坐标为,则
消去k,即得。
…………10分
(2)因为,,所以
,
上式右边等号成立当且仅当。
假设,则
,…………15分
上式右边等号成立当且仅当。
由此得到()。
从而有。
…………20分
14.设正实数及非负实数满足条件
求的最小值,并论证之。
解:根据,有…………5分
…………10分
()
…………15分
上式取等号当且仅当。
…………20分
15.设,为子集。
若,且存在,,
,则称为“好集”。
求最大的,使含的任意33元子集为好集。
解:令,。
显然对任意,不存在,使得成立。
故P是非好集。
因此。
…………5分
下面证明:包含21的任意一个33元子集A一定为好集。
设。
若1,3,7,42,63中之一为集合A的元素,显然为好集。
…………10分
现考虑1,3,7,42,63都不属于集合A。
构造集合
,,,,
,,,,
,,,,,
,。
…………15分
由上可见,每个集合中两个元素都是倍数关系。
考虑最不利的情况,
即,也即中16个元素全部选作A的元素,A中剩下16个元素必须从
这15个集合中选取16个元素。
根据抽屉原理,至少有一个集合有两个元素被选,即集合A中至少有两个元素存在倍数关系。
综上所述,包含21的任意一个33元子集A一定为好集,即的最大值为21。
……20分。
