六杆机构运动分析
六杆压延机构结构参数对滑块运动的影响分析

一
2 滑 块 位 移 、 速 度 和 加 速 度 计 算 及 曲 线 绘 制 0 一3 0 。 6 。每 间隔 1 。的滑块位移 、 速度 和加 速度值 , 输 出 从 MA L B程 序 TA 结果分析 可知 , 在其他 参数确定的情况下 , 随曲柄半径值增加
速度值也较快 地增 大 , 数值列表 中可直接检查 出位移 、 从 速度
果 和曲线 ,设计者可分析 、比较各参数 对滑块运功 的影 响规
卢y ,——分别 为 z f与铅垂方 向所夹之锐角 ; :3 、
: ,
l——分别为 f 与水平方 向所夹 之锐 角。 f , 4 、
11 滑块位移公式 .
若 以距下 止点位置的距 离算起 , 滑块位移 s为
律。 为设计工作提供更直观 、 可靠 的决策依据 。 在此基础上 , 也
d
一
2 — — r 一
一
;
s l[L = s tl(r) 图形标注 t = ‘ I ’ ie t ;% r ;t s 1
ed n
1
一
lsn / : o l i ̄+ 4 cs
一
一 ] —
不 同曲柄 半径 的速度 曲线 如图 3所示。如果要显示各点 位移 、 速度和加 速度值 , 可在上述 程序 后面补充如下语 句 : M= 【h;va ds M 。这样 ,计算机在绘制 曲线之后立 即显示 p i;;; i s ] p( )
《 装备制造技术) os 2o 年第 1 期 2
六杆压 延机构 结构 参数对 滑块运 动的影响分析
陈 晨 , 鹤辉 , 双 翼 黄 梁
( 广西工学院机械工程系 , 西 柳州 5 50 ) 广 406
摘要 : 绍了利 用 MA L B强大的数值计算功能和数据 可视化 功能 介 TA 分析 六杆压延机工作机构各结 构参数对 滑块运 动规 律的影响。 关键词 : 压力杌 : 六杆机 构; 结构分析 ; T A MA L B应 用
机械原理课程设计六杆机构运动与动力分析

机械原理课程设计六杆机构运动与动⼒分析⽬录第⼀部分:六杆机构运动与动⼒分析⼀.机构分析分析类题⽬ 3 1分析题⽬ 32.分析内容 3 ⼆.分析过程 4 1机构的结构分析 42.平⾯连杆机构运动分析和动态静⼒分析 53机构的运动分析8 4机构的动态静⼒分析18 三.参考⽂献21第⼆部分:齿轮传动设计⼀、设计题⽬22⼆、全部原始数据22三、设计⽅法及原理221传动的类型及选择22 2变位因数的选择22四、设计及计算过程241.选取两轮齿数242传动⽐要求24 3变位因数选择244.计算⼏何尺⼨25 五.齿轮参数列表26 六.计算结果分析说明28 七.参考⽂献28第三部分:体会⼼得29⼀.机构分析类题⽬3(⽅案三)1.分析题⽬对如图1所⽰六杆机构进⾏运动与动⼒分析。
各构件长度、构件3、4绕质⼼的转动惯量如表1所⽰,构件1的转动惯量忽略不计。
构件1、3、4、5的质量G1、G3、G4、G5,作⽤在构件5上的阻⼒P⼯作、P空程,不均匀系数δ的已知数值如表2所⽰。
构件3、4的质⼼位置在杆长中点处。
2.分析内容(1)对机构进⾏结构分析;(2)绘制滑块F的运动线图(即位移、速度和加速度线图);(3)绘制构件3⾓速度和⾓加速度线图(即⾓位移、⾓速度和⾓加速度线图);(4)各运动副中的反⼒;(5)加在原动件1上的平衡⼒矩;(6)确定安装在轴A上的飞轮转动惯量。
图1 六杆机构⼆.分析过程:通过CAD制图软件制作的六杆机构运动简图:图2 六杆机构CAD所做的图是严格按照题所给数据进⾏绘制的。
并机构运动简图中活动构件的序号从1开始标注,机架的构件序号为0。
每个运动副处标注⼀个字母,该字母既表⽰运动副,也表⽰运动副所在位置的点,在同⼀点处有多个运动副,如复合铰链处或某点处既有转动副⼜有移动副时,仍只⽤⼀个字母标注。
见附图2所⽰。
1.机构的结构分析如附图1所⽰,建⽴直⾓坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
机械原理课程设计六杆机构运动分析

机械原理课程设计说明书题目六杆机构运动分析学院工程机械学院专业机械设计制造及其自动化班级机制三班设计者秦湖指导老师陈世斌2014年1月15日目录一、题目说明∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 21、题目要求∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 32、原理图∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 33、原始数据∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 3二、结构分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 4三、运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 51、D点运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 82、构件3运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙93、构件4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙94、点S4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10四、结论∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10五、心得体会∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10六、参考文献∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11一、题目说明1、题目要求此次机械原理课程设计是连杆机构综合,通过对其分析,选择合适的机构的尺寸大小,并进行下列操作:⑴对机构进行结构分析;⑵绘制滑块D的运动线图(即位移、速度和加速度线图);⑶绘制构件3和4的运动线图(即角位移、角速度和角加速度线图);⑷绘制S4点的运动轨迹。
基于UGCAE的平面六杆机构的运动分析

基于UG/CAE的平面六杆机构的运动分析1、题目说明如上图所示平面六杆机构,试用计算机完成其运动分析。
已知其尺寸参数如下表所示:题目要求:两人一组计算出原动件从0到360时(计算点数37)所要求的各运动变量的大小,并绘出运动曲线图及轨迹曲线。
注:为了使计算的结果更好的拟合运动的实际情况,同时考虑到UG在运动仿真分析计算方面的快速性,我们决定在绘制曲线时将计算点由37点增加到600点。
数据输出到Excel表格时计算点取100点。
建模及其分析方法附后!2、建模及其运动分析软件介绍:UG NX是集CAD\CAE\CAM于一体的三维参数化软件,也是当今世界最先进的设计软件,它广泛应用于航空航天、汽车制造、机械电子等工程领域。
还有在系统创新、工业设计造型、无约束设计、装配设计、钣金设计、工程图设计等方面的功能。
运动仿真是UG/CAE(Computer Aided Engineering)模块中的主要部分,它能对任何二维或三维机构进行复杂的运动学分析、动力分析和设计仿真。
通过UG/Modeling的功能建立一个三维实体模型,利用UG/Motion的功能给三维实体模型的各个部件赋予一定的运动学特性,再在各个部件之间设立一定的连接关系既可建立一个运动仿真模型。
UG/Motion的功能可以对运动机构进行大量的装配分析工作、运动合理性分析工作,诸如干涉检查、轨迹包络等,得到大量运动机构的运动参数。
通过对这个运动仿真模型进行运动学或动力学运动分析就可以验证该运动机构设计的合理性,并且可以利用图形输出各个部件的位移、坐标、加速度、速度和力的变化情况,对运动机构进行优化。
我们通过学习UG,通过建立平面六杆机构模型,通过UG/CAE模块对平面连杆的运动进行分析。
3.六连杆机构的三维造型连杆L1连杆L2连杆L3连杆L5连杆L6六杆机构装配示意图机构装配后运动演示见附件—平面六杆运动演示.avi (本报告相同目录下)3. 运动分析数据计算结果在附件的Excel表格中。
基于ADAMS的六连杆机构的运动学分析论文

基于ADAMS的六连杆机构的运动学分析论文摘要:六连杆机构是一种常见的机械结构,广泛应用于机械工程领域。
本文以ADAMS软件为工具,对六连杆机构的运动学进行了分析。
通过建立六连杆机构的模型,并设置合理的运动学约束条件,可以准确地描述机构的运动规律。
通过对模型进行求解和仿真,可以得到机构各连杆的位移、速度和加速度等关键参数。
通过分析这些参数的变化规律,可以深入理解六连杆机构的运动特性,并为机构的设计和优化提供理论依据。
本文通过对六连杆机构的运动学分析,验证了ADAMS软件在机构分析中的有效性和准确性,对于提高机构设计的效率和可靠性具有重要意义。
关键词:ADAMS;六连杆机构;运动学分析;模型建立;仿真1.引言六连杆机构是一种典型的机械运动结构,具有广泛的应用前景。
在机械工程领域,六连杆机构被广泛应用于发动机、变速器、悬挂系统等装置中。
在这些应用中,准确地分析六连杆机构的运动学特性对于机构设计和优化具有重要意义。
2.模型建立在ADAMS软件中建立六连杆机构的模型是进行运动学分析的第一步。
模型需要包括六个连杆和几个关节。
通过设置适当的约束条件,模拟机构的运动。
通过添加质点和其他物理特性,可以更准确地描述机构的运动。
3.运动学约束条件为了准确地描述六连杆机构的运动,需要设置合理的运动学约束条件。
这些约束条件可以包括连杆的长度、角度、运动范围等。
通过调整这些约束条件,可以模拟机构在不同工况下的运动。
4.求解和仿真通过对六连杆机构模型进行求解和仿真,可以得到机构的位移、速度和加速度等关键参数。
这些参数的变化规律可以直观地反映六连杆机构的运动特性。
通过研究这些特性,可以发现机构的局限性和改进方向。
5.结果分析基于ADAMS软件的运动学分析可以得到六连杆机构的运动规律。
通过分析仿真结果,可以得出结论如下:(1)六连杆机构的运动较为复杂,各连杆之间的相互作用会导致运动规律的改变;(2)约束条件的变化会对机构的运动产生较大的影响;(3)仿真结果和理论计算结果吻合较好,验证了ADAMS软件在机构分析中的准确性和有效性。
六连杆铰链机构的运动仿真分析
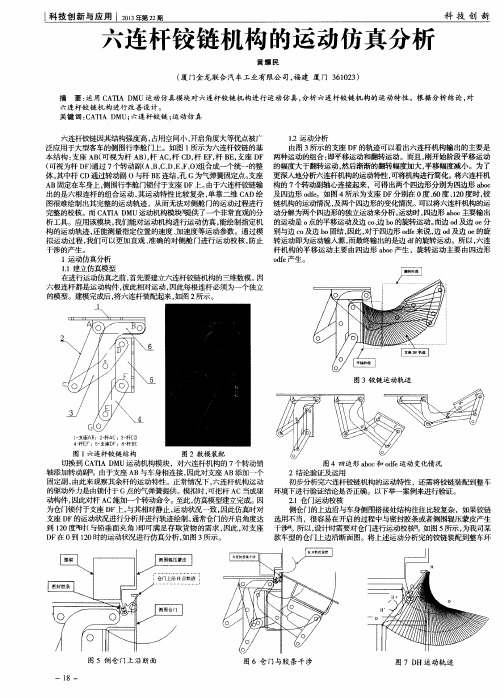
图 3铰 链 运 动 轨 迹
卜 支座A B:2 - 杆A C ;3 - ; q { : C D 4 ~ 杆[ F 5 一 支座D F 6 - 杆B E
图1 六连杆铰 链结构
图 2数模装 配 图 4 四边形 a b o c 和o d f e 运 动 变化情 况 2结论验证 及运用 初 步分析完六连 杆铰链机构 的运动 斗 寺 J 性,还需 将铰链 装配到 整车 环境 下进 行验 证结论 是否正确 。以下举一案例来 进行验证 。 2 . 1仓 门运动校核 侧仓 门的上边沿 与车身侧 围搭 接处结 构往往 比较 复杂 ,如果 铰链 选用不 当 ,很容 易在开启 的过程 中与密封 胶条或者 侧 围辊 压蒙皮 产生 干涉日 。 所以, 设计 时需要对仓 门进行运动校 核目 。如图 5 所示 , 为 我司某 款车 型的仓 门上 边沿断 面图 。将上 述运动 分析完 的铰链装 配到整 车环
体。 其中杆 C D通过转动副 O与杆 B E连结 , 孑 L G为气弹簧固定点。 支座 A B固定在车身上, 侧围行李舱门锁付于支座 D F 上。 由于六连杆铰链输 出的是 六根 连杆 的组合运 动 , 其 运动 特性 比较 复杂 , 单靠 二维 C A D绘 图很难绘制出其完整的运动轨迹 , 从而无法对侧舱门的运动过程进行 完整的校核 。而 C A T I A D M U运动机构模块 了—个 非常直观 的分 析工具 。应 用该模 块 , 我们 能对运 动机构进行 运动仿 真 , 能绘制 指定 机 构的运 动轨迹 , 还 能测量指 定位置 的速度 、 加 速度等运 动参数 。通过 模 拟运 动过程 , 我们 可 以更 加直观 、 准确 的对 侧舱 门进 行运 动校 核 , 防止
链机构的运动 隋况, 及两个四边形的变化情况。可以将六连杆机构 的运 动分 解为两个 四边形 的独立 运动来分析 。 运动时 , 四边形 a b o c 主要输 出 的运动是 O 点的平移运 动及边 C O 、 边b o的旋 转运 动。 而边 0 d 及边 O e 分 别 与边 C O 及边 b o 固结 , 因此 , 对于 四边 形 o d f e 来说, 边o d 及边 o e 的旋 转 运动 即为运动输入源 , 而 最终 输 出的是 边 d f 的旋 转运动 。所 以, 六连 杆机构的平移运动主要由四边形 a b o c 产生 ,旋转运动主要 由四边形
基于MATLAB与SolidWorks的平面六杆机构运动分析及仿真
表3平面六杆机构中预设的部分构件初始参数
3.2平面六杆机构motion运动分析
本部分介绍了利用SolidWorks中的motion插件
进行运动仿真分析以输出平面六杆机构中构件5的
运动图像。首先,利用SolidWorks中的motion功能,将
电机加装在杆*上,设定电机转速恒定为10 r=d・s>#
,X motion 分析中,对构件 5 进行运动分析
终端
发
至
,
回 入库
旧管
系统,
资 的用 ,
本:
Research and Design "0 Fixed Network Terminal Inventory Management
U*#=)-
bang bing
(Chongbo Information Technology Researph Institute Ko・HLtd・,Nanjing Jiangs. 211500)
,
输出平面六杆机构中构件 5 的位移、速度、加速度运
动图像⑷(构件5运动图像如图4所示)。
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>1
Ie
>FG
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>2滑块I方
-速度
@
50 100 150 200 250 300 350 400
角度JM
图!平面六杆机构构件4的运动图像
' (" " 789:;<FG*H
铰链六杆机构的运动分析
铰链六杆机构的运动分析1.题目:铰链六杆机构的运动分析如图所示,已知铰链六杆机构各构件的尺寸为:AB=100mm,BC=370mm, CD=150mm,DE=150mm,EF=250mm,a=120mm,b=360mm,c=90mm,=45°及原动件1以转速n=1000npm逆时针转动,计算杆2,3,4及滑块5的角位移,角速度,角加速度及位移,速度和加速度,并绘制出运动线图。
2.数学模型(1)位置分析由图知:,即:由几何关系:(2)速度分析对(1)中式子关于时间t求导得:对应矩阵:(3)加速度分析对(2)中式子关于时间t求导,得:对应矩阵:+=3、程序设计主程序文件%1.输入已知数据clear;l1=100;l2=370;lcd=150;lde=150;l4=250;;a=120;b=360;c=90;n=1000;du=180/pi;hd=pi/180;omega1=2*pi*n/60;alpha1=0;%2.调用子函数计算机构位移、速度、加速度、角位移、角速度、角加速度for n1=1:361theta1=(n1-1)*hd;[theta,omega,OMEGA,alpha,ALPHA,s5(n1),v5(n1),a5(n1)]=crank_rock er(theta1,omega1,alpha1,l1,l2,lcd,lde,l4,a,b,c);theta2(n1)=theta(2);theta3(n1)=theta(3);theta4(n1)=theta(4);omega2(n1)=omega(1);omega3(n1)=omega(2);omega4(n1)=OMEGA(1);alpha2(n1)=alpha(1);alpha3(n1)=alpha(2);alpha4(n1)=ALPHA(1);end%3.角位移、角速度、角加速度和滑块的位移、速度、加速度输出figure(1);n1=1:361;subplot(2,3,1); %绘角位移线图plot(n1,theta2*du,n1,theta3*du,n1,theta4*du);title('角位移线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;text(200,150,'\theta_2')text(100,100,'\theta_3')text(200,300,'\theta_4')subplot(2,3,2); %绘角速度线图plot(n1,omega2,n1,omega3,n1,omega4);title('角速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')grid on;hold on;text(200,-50,'\omega_2')text(200,75,'\omega_3')text(200,0,'\omega_4')subplot(2,3,3); %绘角加速度线图plot(n1,alpha2,n1,alpha3,n1,alpha4);title('角加速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')grid on;hold on;text(200,-2*10^4,'\alpha_2')text(200,-10*10^4,'\alpha_3')text(200,5*10^4,'\alpha_4')subplot(2,3,4); %绘滑块位移线图plot(n1,s5);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ')ylabel('滑块位移/mm')grid on;hold on;text(150,300,'s_5')subplot(2,3,5); %绘滑块速度线图plot(n1,v5);title('滑块速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;text(200,-0.5*10^4,'v_5')subplot(2,3,6) %绘滑块加速度图plot(n1,a5);title('滑块加速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;text(200,10*10^6,'a_5')%4.机构图形输出figure(2);x(1)=0;y(1)=0;x(2)=l1*cos(45*hd);y(2)=l1*sin(45*hd);x(3)=x(2)+l2*cos(theta2(45));y(3)=y(2)+l2*sin(theta2(45));x(4)=-a;y(4)=b;x(5)=2*x(4)-x(3);y(5)=2*y(4)-y(3);x(6)=x(5)+l4*cos(theta4(45));y(6)=b+c;x(7)=x(6)+40;y(7)=y(6)+20;x(8)=x(6)+40;y(8)=y(6)-20;x(9)=x(6)-40;x(10)=x(6)-40;y(10)=y(6)+20;x(11)=x(6)+40;y(11)=y(6)+20;i=1:6;plot(x(i),y(i));grid on;hold on;i=7:11;plot(x(i),y(i));plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(3),y(3),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(6),y(6),'o');title('曲柄滑块机构');grid on;hold on;xlabel('mm')ylabel('mm')axis([-400 500 -100 600]);%5.曲柄滑块机构运动仿真figure(3)m=moviein(20);j=0;for n1=1:5:360j=j+1;clf;x(1)=0;y(1)=0;x(2)=l1*cos(n1*hd);y(2)=l1*sin(n1*hd);x(3)=x(2)+l2*cos(theta2(n1)); y(3)=y(2)+l2*sin(theta2(n1)); x(4)=-a;y(4)=b;x(5)=2*x(4)-x(3);y(5)=2*y(4)-y(3);x(6)=x(5)+l4*cos(theta4(45)); y(6)=b+c;x(7)=x(6)+40;y(7)=y(6)+20;x(8)=x(6)+40;y(8)=y(6)-20;y(9)=y(6)-20;x(10)=x(6)-40;y(10)=y(6)+20;x(11)=x(6)+40;y(11)=y(6)+20;i=1:6;plot(x(i),y(i));grid on;hold on;i=7:11;plot(x(i),y(i));plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(3),y(3),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(6),y(6),'o');axis([-400 500 -100 600]);title('曲柄滑块机构仿真');xlabel('mm');ylabel('mm');m(j)=getframe;endmovie(m);子程序文件function[theta,omega,OMEGA,alpha,ALPHA,s5,v5,a5]=crank_rocker(theta1, omega1,alpha1,l1,l2,lcd,lde,l4,a,b,c)%1.计算从动件的角位移和滑块5的位移L1=sqrt((a+l1*cos(theta1))*(a+l1*cos(theta1))+(b-l1*sin(theta1))*(b-l 1*sin(theta1)));beta1=acos((L1*L1+l2*l2-lcd*lcd)/(2*L1*l2));beta2=atan((a+l1*cos(theta1))/(b-l1*sin(theta1)));theta2=pi/2+beta1+beta2;theta3=atan(-b/(a-(-l2*cos(theta2)-l1*cos(theta1))));theta4=asin((c-lde*sin(theta3))/l4);theta=[theta1;theta2;theta3;theta4];s5=l4*cos(theta4)+lde*cos(theta3);%2.计算从动件的角速度和滑块5的线速度A=[-l2*sin(theta2),-lcd*sin(theta3);-l2*cos(theta2),-lcd*cos(theta3)] ;B=[l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);omega3=omega(2);C=[l4*sin(theta4),1;-l4*cos(theta4),0];D=[-lde*sin(theta3);lde*cos(theta3)];OMEGA=C\(omega3*D);omega4=OMEGA(1);v5=OMEGA(2);%3.计算从动件的角加速度和滑块5的加速度A=[-l2*sin(theta2),lcd*sin(theta3);l2*cos(theta2),lcd*cos(theta3)];At=[omega2*l2*cos(theta2),omega3*lcd*cos(theta3); omega2*l2*sin(theta2),omega3*lcd*sin(theta3)]; B=[omega1*l1*cos(theta1);omega1*l1*sin(theta1)];alpha=A\(At*omega+omega1*B);alpha2=alpha(1);alpha3=alpha(2);C=[l4*sin(theta4),1;-l4*cos(theta4),0];D=[-lde*sin(theta3),-omega3*lde*cos(theta3);lde*cos(theta3),-omega3*lde*sin(theta3)];Ct=[omega4*l4*cos(theta4),0;omega4*l4*sin(theta4),0];Dt=[alpha3;omega3];ALPHA=C\(D*Dt-Ct*OMEGA);alpha4=ALPHA(1);a5=ALPHA(2);4、计算结果下图为六杆机构的运动线图:。
毕业设计(论文)-牛头刨床六杆机构运动分析
毕业设计(论文)-牛头刨床六杆机构运动分析河南理工大学本科毕业设计,论文,摘要在工程技术领域,经常会遇到一些需要反复操作,重复性很高的工作,如果能有一个供反复操作且操作简单的专用工具,图形用户界面就是最好的选择。
如在本设计中对于牛头刨床平面六杆机构来说,为了保证结构参数与运动参数不同的牛头刨床的运动特性,即刨刀在切削过程中接近于等速运动从而保证加工质量和延长刀具寿命,以及刀具的急回性能从而提高生产率,这样的问题如果能够通过设计一个模型平台,之后只需改变参量就可以解决预期的问题,这将大大的提高设计效率。
设计本设计中正是通过建立牛头刨床六杆机构的数学模型,然后用MATLAB程序出一个友好的人机交互的图形界面,并将数学模型参数化,使用户只需改变牛头刨床的参数就可以方便的实现运动分析和运动仿真,用户可以形象直观地观察到牛头刨床的运动轨迹、速度变化及加速度变化规律。
关键词:牛头刨床六杆机构 MATLAB 运动仿真程序开发1河南理工大学本科毕业设计,论文,AbstractIn the engineering area, often repeatedly encountered some operational needs, repetitive highly, and if the operation can be repeated for a simple operation and dedicated tool graphical user interface is the best choice. As in the planer graphic design for six pole bodies, and campaigns to ensure the structural parameters of different parameters planer movement characteristics, planning tool inthe process of cutting close to equal campaign to ensure processing quality and extended life cutlery and cutlery rush back to the performance enhancing productivity, If such issues can be adopted to design a model platform parameter can be changed only after the expected settlement, which will greatly enhance the efficiency of the design. It is through the establishment of this design planer six pole bodies mathematical model, and then use MATLAB to devise procedures of a friendly aircraft in the world graphics interface, and mathematical models of the parameters, so that users only need to change the parameters planer can facilitate the realization of movement analysis and sports simulation, Users can visual image observed in planer movement trajectories, speed changes and acceleration changes.Keywords:Planer 6 pole bodies MATLAB Campaign simulation Procedure development.2河南理工大学本科毕业设计,论文,目录1 绪论 (4)2牛头刨床六杆机构运动分析程序设计2.1 MATLAB介绍 (5)2.2 MATLAB的特点 (6)2.3 用MATLAB处理工程问题优缺点................................7 3牛头刨床运动分析的模型3.1 基本概念与原理 (9)3.2 牛头刨床六杆机构的数学模型 .................................9 4图形用户界面GUI4.1界面设计的原则 (13)4.2 功能要求 (16)4.3界面结构设计 (17)4.4 程序框图的设计 .............................................19 5运动仿真程序界面设计与编程实现5.1 句柄图形体系 (21)5.1.1 图形对象、对象句柄和句柄图形树结构 (22)5.1.2 对象属性 (23)5.1.3 对象句柄的获取方法 (23)5.1.4 对象句柄的获取和设置 (25)5.2 主界面参数含义 (27)5.3 界面制作步骤 (27)6总结 (49)7致谢 (50)8参考书目 (51)9附录程序源代码 (52)3河南理工大学本科毕业设计,论文,1 绪论1.1本课题的意义机构运动分析是不考虑引起机构运动的外力的影响,而仅从几何角度出发,根据已知的原动件的运动规律(通常假设为匀速运动),确定机构其它构件上各点的位移、速度、加速度,或构件的角位移、角速度、角加速度等运动参数。
平面六杆机构运动分析
平面六杆机构运动分析平面六杆机构的结构由六个连杆组成,其中包括三个固定连杆和三个可动连杆。
固定连杆通常被称为定态杆,可动连杆则被称为转动杆。
根据转动杆的数量和连杆相互连接的方式,平面六杆机构可以分为多种类型,如四杆机构、多杆机构等。
在运动分析中,首先需要确定平面六杆机构的运动副,即确定机构中的可动部分和约束部分。
在平面六杆机构中,三个固定连杆固定在轴上,不发生相对运动,因此构成了三个约束副。
而另外三个可动连杆可以沿着其中一方向进行平移或转动,从而实现不同的运动形式。
平面六杆机构的运动是通过连杆相互连接而实现的。
连杆之间的连接点称为铰链,铰链的位置确定了连杆之间的运动关系。
根据铰链的位置不同,连杆之间可以形成不同的树状结构,如三杆树状结构、四杆树状结构等。
通过这些连杆和铰链的组合,平面六杆机构可以实现复杂的运动路径和运动轨迹。
在几何分析中,可以利用连杆的长度和连接点位置来确定连杆的运动范围和运动路径。
通过使用向量和矩阵的运算,可以推导出连杆的运动方程和运动状态方程。
这些方程可以用来描述连杆的位移、速度和加速度,并进一步分析机构的运动性能和稳定性。
在力学分析中,可以应用牛顿定律和动力学原理来分析连杆之间的力学关系和力学性能。
通过建立连杆之间的功率传递和力矩平衡方程,可以计算出机构的输入功率和输出功率,并进一步分析机构的能量转换和运动效率。
平面六杆机构的运动分析在工程设计中具有广泛的应用。
它可以用来实现复杂的运动路径和运动轨迹,广泛应用于各种机械设备和机器人的设计中。
例如,在运动控制领域,平面六杆机构可以用来控制机械臂的运动轨迹和末端位置,实现精确的定位和操作。
在工业自动化领域,平面六杆机构可以用来控制机器人的运动路径和运动速度,实现灵活的操作和自动化生产。
总而言之,平面六杆机构是一种重要的机械结构,它可以实现复杂的运动功能和运动轨迹。
通过几何分析和力学分析,可以对平面六杆机构的运动进行详细的分析和研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理课程设计
六杆机构运动分析
学院:工程机械
专业:机械设计制造及其自动化
班级:25041004
设计者:王东升于新宇
2013年 1月8日一、分析题目
如图1所示六杆机构,对其进行运动和动力分析。
已知数据如表1所示。
r1=r3=L2=110mm ,L4=600mm ,L AD=39mm ,n1=40r/min ,L CS4=220mm.
图1 六杆机构
二、分析内容
(1)进行机构的结构分析;
如2图所示,建立直角坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
A、C、B、D、E处运动副为低副(6个转动副,1个移动副),共7个,即P l=7。
则机构的自由度为:F=3n-2P l=3Χ5-2Χ7=1。
图2(a)图2(b) 图2(c)
如图2,拆出基本杆组,(a)为原动件,(b)、(c)为二级杆组,该机构是由机架0、原动件1和2个Ⅱ级杆组组成,故该机构是Ⅱ级机构。
(2)绘制滑块E的运行线图;
利用JYCAE软件求解。
1、将题设所给的原始数据(机构的活动构件数、转动副数、移动副数、己知长度值总数
和机构的自由度)分别输入JYCAE软件中,如图3:
图3—1
图3—2
图3—3
图3—4
2、机构的运动分析
输入完所有的原始数据以后,开始运动分析。
求E点的运动线图,要选取基本单元5,但是利用基本单元5的条件是已知C点的运动状态,所以先利用基本单元1、2求得C点的运动状态,然后求的E点运动线图。
如图4。
图4—1 解得B点运动参数
图4—2 解得C点运动参数
图4—3 解得E点运动参数共选取3个基本单元,如图4—4,然后运算。
图4—4
运算后,E点运动参数如表1,运动线图如图5。
表1 点E的x、y方向的运动参数
图5 点E运动线图
(3)绘制构件3和4的运动线图;
由(2)可知各点运动参数,继续上述程序求解。
如下图:求构件3运动线图是,选取基本单元6中的摆动倒杆(1),如图6—1,运算后,运动参数如表2,运动线图如图6—2。
图6—1
表2 构件3的运动参数
图6—2
求构件4运动线图时,选取基本单元6中的摆动倒杆(1),如图6—3,运算后,运动参数
如表3,运动线图如图6—2。
表3 构件4的运动参数
图6—4
(4)绘制点S4的轨迹线图。
选取基本杆组1求点S4运动轨迹,不妨设θ的起始角度为0,如图7—1;
图7—1
运算后坐标值表4,运动轨迹如图7—2:
图7—2。
