美妙的幻方
美妙的幻方

类型 的幻方也各具风彩 , 深受人们 的喜爱.
4
1 5
1 4
1
图 7
图 8
大约 l 世纪 ,我 国的纵横 图传 到欧洲 , 5 引 起了当地人们 的极大兴趣 ,成千上万 的人沉醉 于幻方 之 中. 国 画家丢勒 (47 12 ) 德 12- 5 8 就是 其 中的一位. 他找到 了一个 四阶幻方 , 如图 8 并 ,
图 1 2
4 1 9 1 2 6 4 2
3 6 2 2 7 4 5
我 国数学家张潮 (6 年~ 在他 的“ 15 ) 算法补
图” 介绍 了许多非常别 致的幻 方 , 中, 优美 的“ 龟
图9
6 7 一¨ 一 l 1 2 0 4 —3 —5 2 —8 l 9
●
据说 , 大约公元前 20 年 , 0 0 位于 陕西的洛 数学家杨辉给 出了一种 T々 々{ 如、 、 , 简便 的方法 : 图 3 将 | ^ , It , . . 河 常常泛滥 成灾 。 威胁着 两岸人们 的生产与生 活. , 于是 大禹 E夜奔波忙碌 , t 三过家门而不入 ,
文聚六 图” 是其 中的一种 . 图 1. 1 就 如 1 图 1中,
有 2 个数 。 4 每块龟文六边形上的数字和为 7 . 5 在幻方 中。最为稀有 的幻方莫过于六角幻
5 — 1
8 — 2 O 9 3 —4
方, 如图 1. 2它的 l 条 直线上 的数字 和都 为 1 5 9 的 2 , 3. 倍 即 8它是 由一位名 叫阿 当斯 的人 , 经 过 四十多年 的不懈 努力 才创作 出来 的. 它的完
9 2 1+ = 4更为奇妙的是 把这个 幻方边上的 限于篇幅 , + +58 3. 这里就不作介绍 了. 行或列移到另一边上去 ,所得到 的正方形排列 除了上面提及的一类正方形幻方外 ,其它 仍是一个幻方 .
关于幻方的收获与感悟

关于幻方的收获与感悟嘿,朋友们!咱今天来聊聊幻方这个奇妙的玩意儿。
你们知道吗,幻方就像是一个隐藏着无数秘密的神秘盒子。
刚开始接触它的时候,我就跟那刘姥姥进大观园似的,充满了好奇和惊叹。
你瞧啊,那一个个数字在方格里排列得整整齐齐,就像是训练有素的士兵在站队。
可别小看这些数字,它们之间有着千丝万缕的联系,稍有变动,整个幻方的感觉就全变了。
这多像我们的生活呀,一个小小的改变可能就会引发一系列的连锁反应。
研究幻方的时候,有时候我感觉自己就像个侦探,在努力寻找着那些隐藏的线索和规律。
每当我发现一个新的规律,那兴奋劲儿,就跟找到了宝藏似的!这难道不有趣吗?而且,幻方还特别锻炼人的耐心和思维能力。
你得静下心来,一点点地去琢磨,去尝试。
有时候可能会遇到困难,怎么都找不到答案,但咱可不能轻易放弃啊!就像爬山一样,虽然过程累,但当你爬到山顶,看到那美丽的风景时,一切都值了。
幻方还让我明白了一个道理,那就是细节决定成败。
一个数字放错了位置,可能整个幻方就不成立了。
这多像我们做事啊,一点小马虎都可能导致大问题。
我们得像对待幻方一样,认真对待每一件事,注意每一个细节。
我还记得有一次,我花了好长时间研究一个幻方,可就是解不出来。
我都有点灰心丧气了,心想这也太难了吧!但后来我静下心来,重新仔细地观察,终于发现了一个之前忽略的小细节,结果一下子就解开了。
哇,那感觉,真的是无法用言语来形容!这不就跟我们生活中遇到困难一样吗?只要不放弃,总会找到解决办法的。
幻方啊,它不仅仅是一堆数字,它更是一个能让我们不断探索、不断成长的神奇世界。
它让我们学会思考,学会坚持,学会在看似不可能中找到可能。
所以啊,朋友们,别错过幻方这个好东西。
去尝试一下,去感受一下它带给你的收获和感悟。
相信我,你一定会爱上它的!它会像一个好朋友一样,一直陪伴着你,给你带来无尽的乐趣和启发。
难道不是吗?。
奇妙的16宫幻方
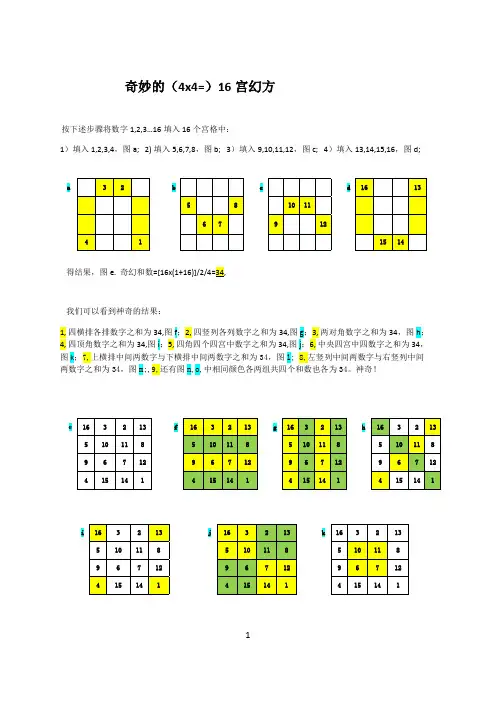
1奇妙的(4x4=)16宫幻方按下述步骤将数字1,2,3…16填入16个宫格中:1)填入1,2,3,4,图a; 2) 填入5,6,7,8,图b; 3)填入9,10,11,12,图c; 4)填入13,14,15,16,图d;a 3 2 bcd 16 13 5 810 116 7 9 12411514得结果,图e. 奇幻和数=[16x(1+16)]/2/4=34,我们可以看到神奇的结果:1, 四横排各排数字之和为34,图f ;2, 四竖列各列数字之和为34,图g ;3, 两对角数字之和为34,图h ; 4, 四顶角数字之和为34,图i ;5, 四角四个四宫中数字之和为34,图j ;6, 中央四宫中四数字之和为34, 图k ;7,上横排中间两数字与下横排中间两数字之和为34,图l; 8,左竖列中间两数字与右竖列中间 两数字之和为34,图m;,9,还有图n,o,中相同颜色各两组共四个和数也各为34。
神奇!e 16 3 2 13fg h510 11 89 6 7 12 4 15 14 1i 16 3 2 13 j k 5 10 11 8 9 6 7 12 4 15 14 12l 16 3 2 13 m 16 3 2 13 5 10 11 8 5 10 11 89 6 7 12 9 6 7 12 4 15 14 1 4 15 14 1n16 3 2 13 o 16 3 2 13 5 10 11 8 5 10 11 8 9 6 7 12 9 6 7 12 4 15 14 1 4 15 14 1再介绍6x6=36和8x8=64两个偶阶幻方(1)36宫相同和数为(2)64宫相同和数为3此幻方中,可看到从1开始,也是按马步进行,但不像奇数幻方(见《九宫格解法》一文)中按顺序有规律前行。
而且两个对角线上的和也都不是下面再介绍两个幻方(1) 所谓的生日 幻方,下图:幻方中,各排、列和对角四数之和都为22。
现在把你的年龄减去22后分别与黄色宫格中的数字相加再填入。
幻方原理及方法

幻方原理及方法
1. 你知道幻方原理多奇妙吗?就像变魔术一样!就拿三阶幻方来说,每行、每列以及对角线上的数字之和都相等。
比如说常见的九宫格,1、2、3、4、5、6、7、8、9 填入九宫格中,经过巧妙排列,就能实现神奇的相等和哦,是不是很有趣?
2. 要想了解幻方方法,那可得好好琢磨一番呢!好比搭积木,要一块一块恰到好处地放。
比如试着将奇数阶幻方用“罗伯法”来填,一步步地,按照规则,嘿,一个完美的幻方就出现啦!难道你不想试试吗?
3. 幻方原理其实并不难理解呀!就如同解开一个复杂的谜题。
想想看,把一些数字摆来摆去,就能找到那神奇的规律。
比如四阶幻方,通过特定的算法和步骤,哇,最终的成果会让你惊叹不已呢,难道不是吗?
4. 幻方方法可是有很多窍门的哟!好像寻找宝藏的钥匙。
比如说五阶幻方,运用特定的策略,一点点地推进,嘿嘿,就能得到让人惊喜的结果啦!这多让人兴奋呀!
5. 幻方原理真的超级神奇的呢!可以类比成音乐的旋律,有节奏有规律。
比如六阶幻方,尝试着去感受那数字的排列,就如同聆听美妙的音乐,太赞了吧!
6. 想要掌握幻方方法,就得像探险家一样勇敢尝试哦!好比在未知的领域探索。
像七阶幻方,大胆地去实践,不断调整,哇塞,那成功后的满足感简直爆棚啦!总之,幻方就是这么神奇又有趣!。
幻方的口诀顺口溜

幻方的口诀顺口溜
1. 幻方真奇妙,口诀要记牢,一居上行正中央,这个例子很明了,就像找到了宝藏的钥匙哟!比如3×3 的幻方,数字1 不就放在最上面一行的正中央嘛!
2. 依次斜填切莫忘,哎呀呀,可别小看它呀!就像走迷宫有了方向一样。
你看那个 4 不就斜着填下去嘛!
3. 上出框时往下填,这多有意思呀,就好比球弹到了地上又弹起来。
像 7 超出框了,不就往下填嘛!
4. 右出框时往左填,嘿,是不是很好玩呀,如同汽车拐弯换了个道儿。
数字 9 不就这样填嘛!
5. 排重便在下格填,哇塞,这感觉就像纠错一样呢!要是碰到重复的数字,不就往下一格填嘛,就像避开障碍。
6. 右上排重一个样,可不是嘛,就像遇到同样的困难有同样的解决办法。
比如右上有数字了,也得这样处理呀!
7. 幻方口诀真好用,绝对让你大不同,你想想,用了口诀解幻方多轻松呀!
8. 记住口诀不慌张,仿佛有了定海神针呀!不管遇到啥样的幻方都不怕啦!
9. 轻松玩转幻方界,哎呀呀,那感觉就像武林高手称霸江湖一样呢!
10. 幻方口诀顺口溜,大家一定要记熟,真的超级有用处哟!就像拥有了神奇的魔法棒!
我的观点结论:幻方的口诀顺口溜真的太重要啦,能让我们快速掌握幻方的技巧,大家一定要好好记住呀!。
美丽的变形幻方

美丽的变形幻方作者:小五来源:《数学大王·中高年级》2014年第08期幻方是一种将数字安排在正方形格子中,使每行、列和对角线上的数字和都相等的方法。
在传统幻方里,用来组合的元素是数字。
是不是还有别的形式的三阶幻方呢?来见识一下吧!这是一个三阶几何幻方,由中间的9个不规则方块组成。
这些不规则方块所含的小方格数分别是2、6、8、10、12、14、16、18、22,每行、每列和两条对角线上的方格总数都是36。
更特别的是,每行、每列和两条对角线上的3个不规则方块组合起来,都能拼出一个6×6的正方形。
如果有人开发出这样的幻方积木玩具,我相信一定深受同学们喜爱。
竟然会喜欢这么伤脑筋的玩具,难道同学们都是自虐狂吗?这个更酷!每行、每列和两条对角线上的小方块总数都是15,并且,每行、每列和两条对角线上的3个大方块都可以拼成一个正三角形!五颜六色的,像水果糖,看起来好有食欲呀!贝卡你这个吃货,你说你还有救吗?我还有救的,你们要相信我!哎呀,下面这个幻方……算了,让我当个永恒的吃货吧,你们甭救我了!这个可以说是三重幻方了:幻方中不规则方块里所包含的数字恰好是1~15这15个自然数,并且,每行、每列和两条对角线上的3个方块都正好能拼成一个中间带有空洞的正方形,而这些4×4的正方形本身又构成了幻方(空洞代表0)。
我已晕死,有事烧香!别晕!还有呢!下面是一个四阶几何幻方。
幻方由16条白条组成,它们大致排成了4×4的形状。
组成幻方的16条白条本身已经拼成了4个小正方形,同时,每行、每列和两条对角线上的4条白条也都能拼成正方形。
(有气无力)乔乔,我真的只是一个纯粹的吃货而已,你千万不要对我寄予厚望。
这个幻方……它是幻方吗?难道不是什么中国风图案吗?算了,我懒得浪费精力跟你说!我找《数学大王》的铁杆粉丝聊一聊。
嗨……你们别走呀!嗨,你们等等我,请带我一起走呀!右边是一个不是幻方的“几何幻方”。
神奇的幻方小课题研究报告
神奇的幻方小课题研究报告神奇的幻方小课题研究报告【导语】幻方,是指一个矩阵中的每一行、每一列和每一条对角线上的数字之和都相等的特殊矩阵。
它以其独特的数学性质和趣味性,吸引了众多数学爱好者的关注。
本文将深入探讨幻方的原理、发展以及应用,帮助读者全面了解这一神奇的数学现象。
【概述】幻方最早可以追溯到中国古代的《周髀算经》中,其中详细介绍了3阶幻方的构造方法。
随后,幻方的研究逐渐发展起来,并在各个国家和时期都有所贡献。
幻方独特的数学性质使其成为数学和逻辑的重要研究对象,同时也被广泛应用于密码学、游戏以及图像处理等领域。
【主体】一、幻方的基本原理幻方的基本原理是通过排列数字,使得矩阵中的每一行、每一列和每一条对角线上的数字之和都相等。
在初步了解幻方之后,我们可以通过以下步骤来构造一个简单的3阶幻方:1. 将数字1放在矩阵中间的行、最左侧的列。
2. 将数字2放在数字1的上方。
3. 将数字3放在数字2的右上方。
4. 依次类推,将数字4至9依次放入矩阵中,直至填满整个矩阵。
二、幻方的发展历程幻方最早出现在中国古代,《周髀算经》中记载了3阶幻方的构造方法。
在随后的历史中,欧洲的数学家也开始对幻方进行研究,如德国数学家Euler以及瑞士数学家Lagrange等。
在18世纪,Lagrange提出了一个重要的定理——拉格朗日定理,即任何一个正整数都可以表示为4个平方数之和。
而这一定理与幻方之间的联系被后来的数学家进一步研究和发展。
三、幻方的应用领域1. 密码学:幻方可用于密码学中的加密和解密过程,通过将明文和密文映射到一个幻方上,实现信息的保密性。
2. 游戏:幻方被广泛用于各类数字游戏中,如数独、魔方等。
通过排列和填充数字,玩家需要根据幻方的规则来达到游戏目标。
3. 图像处理:幻方可以用于图像生成和编码,通过将图像的像素值与幻方矩阵的数字对应,实现图像的压缩和解压缩。
【总结与回顾】通过本文的探讨,我们对幻方的原理、发展和应用有了更深入的理解。
美妙的幻方
美妙的幻方据传说,大约公元前2000年前的时候,位于陕西的洛河常常泛滥成灾,威胁着两岸人们的生活与生产。
于是,大禹日夜奔忙,三过家门而不入,带领人们开沟挖渠,疏通河道,驯服了河水,感动了上天。
事后,一只神龟从河中跃出,驮着一张图献给大禹。
图上有九个数字。
大禹因此得到上天赐给的九种治理天下的方法。
这张图,就是闻名于世的洛书,见图1。
洛书中每个小圆圈都代表一个l。
所以把它写成现在的形式就是图2。
图 1图 2图2是由三行三列九个数字组成的正方形排列,它的每一行、每一列、每条对角线上的三个数字的和都是同一个常数15。
这种美妙的正方形排列,在我国历史上,曾叫做“九宫图”,亦叫做纵横图。
后来,人们称它为“幻方”。
因为图2是由三行三列组成的,所以它被称为三阶幻方。
现已确认,洛书是世界上最古老的幻方。
三阶幻方是怎样构造出来的呢?我国宋朝数学家杨辉给出了一种简便的方法:如图3,将1至9九个数字斜着排列,然后把上下两个数字1和9对调,左右两个数字7和3对换,得到图4。
再将图4中的上下左右四个数字9,1,3,7分别写进与它相邻的空格中,就得到前述的图2。
图 3图 4不仅如此,杨辉对幻方还进行了较系统的研究,他是世界上第一位把幻方当作数学问题来研究的数学家。
他构造出多种幻方,其中之一就是图5。
它是由十六个数字组成的一种正方排列,其中每行每列、每条对角线上的数字和都是34。
图5 图 6图5是怎样构造出来的呢?数学家杨辉为此给出了一种十分简单的方法,它与三阶幻方的构造有所不同。
如图6,先将1至16的十六个数字按顺序排列在四行四列的方格中,然后把两条对角上、关于正方形中心对称的四对数,6和11,1和16,7和10,4和13分别对换,就得到图5。
在四阶幻方中,一个颇为著名的幻方是印度太苏神庙石碑上的幻方,如图7,它刻于十一世纪。
这个幻方中,不但每行每列每条对角线上的数字和为34,而且有20组某两行两列交叉点上的四个数字,它们的和也都为34,例如9+2+15+8=34。
妙趣横生的三阶幻方
妙趣横生的三阶幻方肖乐农(湖南新化县教师进修学校 417600)相传在4000多年前的夏禹治水的时候,黄河支流洛水(既现在陕西境内的洛河)里浮出一只大乌龟,龟背上刻有一个奇特的图(如图1),后来的人把它叫做“洛书”。
图1 图2现在大家已经知道,这实际上是一个三阶幻方(如图2)。
它的一个被人们津津乐道的有趣性质是:九宫格中的横、竖、对角线上三个数的和都等于15。
然而,这个古老问题的内涵远远不只于此,下面让我们作一点稍为深入的探索吧。
一、制作关于三阶幻方,我国古代有“四二为肩,八六为足,左三右七,戴九履一,五居中央”的记载。
然而,这只是记录了三阶幻方中的数字和排列方法。
它们是怎样得出来的呢?却无史籍可考。
十七世纪,法国数学家巴谢发明了一种三阶幻方的简捷制作方法:首先作一个如图3的图形,再把1到9的数字按斜线方向排出,最后把四方突出的一格中的数,转放到所在的行或列的与它不相邻空格中,就得到了一个三阶幻方(如图4)。
这个幻方与图2所示的幻方是一致的。
图3 图4这种制作方法,读者只要仔细想一想,其道理是不言自明的。
并且,这种制作法可以推广到奇数阶幻方。
二、探奇有人说,三阶幻方是一个“神来之图”。
确是如此!它之神,之奇,远远不只是“横、竖、对角线上三个数的和都等于15”,还有更加神奇的呢!1、被中心数“5”隔开的横、竖、对角的两个数拼合成四个二位数,这四个数的和,正好等于各数数位颠倒后所成的四个数的和。
我们把这样的等式叫做“回文等式”(以下均以图2为例):91+37+28+64=46+82+73+19(=220); 把这个等式中各加数都平方,等式仍然成立:912+372+282+642=462+822+732+192(=14530)。
2、以“5”为中心的四个三位数构成回文等式:951+357+258+654=456+852+753+159(=2220); 把这个等式中各加数都平方,等式仍然成立:9512+3572+2582+6542=4562+8522+7532+1592(=1526130)。
趣味数学-幻方PPT优秀课件
1、幻方的定义(三阶8+5幻+2=方15 )
49 2
35 7
8 16
49 2 35 7 +8 +1 +6 15 15 15
4+9+2=15 3+5+7=15 8+1+6=15
4+5+6=15
每行、每列、对角线上的三个数的和都相等的方格,叫 “幻方”。这个相等的和叫三阶幻方的幻和。
练习1 它们是幻方么?你怎样来判别?
20 2 6 7 15 8 4 3 15
15 8 1 6 15 3 5 7 15
9 1 5 15
4 9 2 15
19 11 15 11 不是
15 15 15 15 是
每行每列斜着的三个数的和是否都相等,来判断是不姐背上的有些图案看不清了,你能帮它 找出来吗?
92
4 3
4、探究改变幻方的规律: 共有8种:
4 92 357 816
83
59 72
618 7 53 2 94
27 6 951 438
8 16 357 492
6 72 159 834
2 94 753 618
4 38 753 276
将幻方围绕中心,向右旋转90度一次、二次、三次
向右旋转90度一次、二次、三次后将幻方上下对换。
百子回归碑是一幅 十阶幻方,中央四 数连读 “1999 · 12 · 20 ”, 标示澳门回归日。
百子回归碑是一部 百年澳门简史,可 查阅四百年来澳门 沧桑巨变的重大历 史事件以及有关史 地、人文资料等。
中间两列上部(系十九
世纪):“ 1887 ” 年《中葡条约》正式 签署,从此成为葡人 上百年(距今 100 余 13 年)“永久管理澳 门”的法律依据。又 如中间两列下部(系 二十世纪):“ 49 ” 年中华人民公和国成 立,从此中国人民站 起来了;“ 97 ”年香 港回归祖国。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
美妙的幻方中图分类号:论文编号:10006ZY1021226摘要在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵行及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方“。
我国古代称为“河图”、“洛书”,又叫“纵横图”。
本文对幻方的由来及组成进行了简单的介绍和说明。
并对幻方的几种常见的构造方法进行了说明。
关键词:幻方,洛书,纵横图,九宫图目录第一章幻方的历史4第二章幻方的构造7第三章幻方构造的实现93.1 一般方法103.1.1 N为基数时103.1.2 N为4的倍数时103.1.3 N为其他偶数时103.2 其他方法153.2.1 Merzirac法生成奇阶幻方153.2.2 loubere法生成奇阶幻方163.2.3 horse法生成奇阶幻方 163.2.4 Hire法生成偶阶幻方 163.2.5 Strachey法生成单偶幻方 183.2.6 Spring法生成以偶幻方 183.2.7 YinMagic构造偶阶幻方 193.2.8 魔鬼幻方 193.2.9 罗伯法20第四章总结20第一章幻方的历史据传说,大约公元前2000年前的时候,位于陕西的洛河常常泛滥成灾,威胁着两岸人们的生活与生产。
于是,大禹日夜奔忙,三过家门而不入,带领人们开沟挖渠,疏通河道,驯服了河水,感动了上天。
事后,一只神龟从河中跃出,驮着一张图献给大禹。
图上有九个数字。
大禹因此得到上天赐给的九种治理天下的方法。
这张图,就是闻名于世的洛书,见图1。
洛书中每个小圆圈都代表一个l。
所以把它写成现在的形式就是图2。
图 1图 2图2是由三行三列九个数字组成的正方形排列,它的每一行、每一列、每条对角线上的三个数字的和都是同一个常数15。
这种美妙的正方形排列,在我国历史上,曾叫做“九宫图”,亦叫做纵横图。
后来,人们称它为“幻方”。
因为图2是由三行三列组成的,所以它被称为三阶幻方。
现已确认,洛书是世界上最古老的幻方。
所谓纵横图,它是由1到n^2,这n^2个自然数按照一珲的规律排列成N行、N列的一个方阵。
它具有一种厅妙的性质,在各种几何形状的表上排列适当的数字,如果对这些数字进行简单的逻辑运算时,不论采取哪一条路线,最后得到的和或积都是完全相同的。
大约两千多年前西汉时代,流传夏禹治水时,黄河中跃出一匹神马,马背上驮着一幅图,人称「河图」;又洛水河中浮出一只神龟,龟背上有一张象征吉祥的图案称为「洛书」.他们发现,这个图案每一列,每一行及对角线,加起来的数字和都是一样的,这就是我们现在所称的幻方.也有人认为"洛书"是外星人遗物;而"河图"则是描述了宇宙生物(包括外星人)的基因排序规则,幻方是外星人向地球人的自我介绍.另外前几年在上海浦东陆家嘴地区挖出了一块元朝时代伊斯兰教信徒所挂的玉挂,玉挂的正面写着:「万物非主,惟有真宰,默罕默德,为其使者」,而玉挂的另一面就是一个四阶幻方.关于幻方的起源,我国有“河图”和“洛书”之说。
相传在远古时期,伏羲氏取得天下,把国家治理得井井有条,感动了上天,于是黄河中跃出一匹龙马,背上驮着一张图,作为礼物献给他,这就是“河图”,也是最早的幻方。
伏羲氏凭借着“河图”而演绎出了八卦,后来大禹治洪水时,洛水中浮出一只大乌龟,它的背上有图有字,人们称之为“洛书”。
“洛书”所画的图中共有黑、白圆圈45个。
把这些连在一起的小圆和数目表示出来,得到九个。
这九个数就可以组成一个纵横图,人们把由九个数3行3列的幻方称为3阶幻方,除此之外,还有4阶、5阶...后来,人们经过研究,得出计算任意阶数幻方的各行、各列、各条对角线上所有数的和的公式为:S=n(n ^2+1) /2其中n为幻方的阶数,所求的数为S.幻方最早记载于我国公元前500年的春秋时期《大戴礼》中,这说明我国人民早在2500年前就已经知道了幻方的排列规律。
而在国外,公元130年,希腊人塞翁才第一次提起幻方。
我国不仅拥用幻方的发明权,而且是对幻方进行深入研究的国家。
公元13世纪的数学家杨辉已经编制出3-10阶幻方,记载在他1275年写的《续古摘厅算法》一书中。
在欧洲,直到574年,德国著名画家丢勒才绘制出了完整的四阶幻方。
而在国外,十二世纪的阿拉伯文献也有六阶幻方的记载,我国的考古学家们曾经在西安发现了阿拉伯文献上的五块六阶幻方,除了这些以外,历史上最早的四阶幻方是在印度发现的,那是一个完全幻方(后面会提到),而且比中国的杨辉还要早了两百多年,印度人认为那是天神的手笔.1956年西安出土一铁片板上所刻的六阶幻方(古阿拉伯数字)十三世纪,东罗马帝国才对幻方产生兴趣,但却没有什么成果.直到十五世纪,住在君士坦丁堡的魔索普拉才把我国的纵横图传给了欧洲人,欧洲人认为幻方可以镇压妖魔,所以把它作为护身符,也把它叫作「Magic Square」.欧洲最早的幻方是在德国一位名画家Albrecht Dure的画里的第二章幻方的构造三阶幻方是怎样构造出来的呢?我国宋朝数学家杨辉给出了一种简便的方法:如图3,将1至9九个数字斜着排列,然后把上下两个数字1和9对调,左右两个数字7和3对换,得到图4。
再将图4中的上下左右四个数字9,1,3,7分别写进与它相邻的空格中,就得到前述的图2。
图 3图 4不仅如此,杨辉对幻方还进行了较系统的研究,他是世界上第一位把幻方当作数学问题来研究的数学家。
他构造出多种幻方,其中之一就是图5。
它是由十六个数字组成的一种正方排列,其中每行每列、每条对角线上的数字和都是34。
图5 图6图5是怎样构造出来的呢?数学家杨辉为此给出了一种十分简单的方法,它与三阶幻方的构造有所不同。
如图6,先将1至16的十六个数字按顺序排列在四行四列的方格中,然后把两条对角上、关于正方形中心对称的四对数,6和11,1和16,7和10,4和13分别对换,就得到图5。
在四阶幻方中,一个颇为著名的幻方是印度太苏神庙石碑上的幻方,如图7,它刻于十一世纪。
这个幻方中,不但每行每列每条对角线上的数字和为34,而且有20组某两行两列交叉点上的四个数字,它们的和也都为34,例如 9+2+15+8=34。
更为奇妙的是把这个幻方边上的行或列移到另一边上去,所得到的正方形排列仍是一个幻方。
图 7 图 8大约十五世纪,我国的纵横图传到欧洲,引起了人们的普遍兴趣,成千上万的人沉醉于幻方之中。
德国画家丢勒(1427—1528)就是其中的一位。
他找到了一个四阶幻方,如图8,并把它反映在他的著名版画《忧郁症》中。
它也许是欧洲最早的幻方。
有趣的是,丢勒在这一幻方中把版画创作的年代1514也放了进去。
他可能正是从这两个数出发,通过不断的试验而找出了其余的数字。
图9 图10图9是一个五阶幻方,其中隐藏着一条绝妙的性质:幻方中的每个数字减去中心位置数字 12后,得到一个这样的幻方(如图10),它的中心对称或轴对称上的两个数字互为相反数,并且中间位置上的九个数字也构成一个幻方。
更值得一提的是,图 10中隐含了如何由三阶幻方出发构造五阶幻方,又进而由五阶幻方构造出七阶幻方,等等行之有效的方法,限于篇幅,这里就不作介绍了。
除了上面提及的一类方形幻方外,其它类型的幻方也各具风彩,深受人们的喜爱。
图 11 图 12我国数学家张潮(165~?年)在他的“算法补图”中,介绍了多种非常别致的幻方,优美的“龟文聚六图”就是其中之一,如图11。
图11中,有二十四个数,每块龟文六边形上的数字和为75。
在幻方中,最为稀有的幻方莫过于六角幻方,如图12。
它的十五条直线上的数字和都为19的2倍38。
它是由一位名叫阿当斯的人,经过四十多年的不懈努力才搞出来的。
它的完美形式令人赞叹不已,他的锲而不舍的精神更感人至深。
第三章幻方构造的实现最简单的幻方就是平面幻方,还有立体幻方、高次幻方等。
对于立体幻方、高次幻方目前世界上很多数学家仍在研究,现在只讨论平面幻方。
对平面幻方的构造,分为三种情况:N为奇数、N为4的倍数、N为其它偶数(4n+2的形式)3.1一般方法3.1.1N 为奇数时最简单(1) 将1放在第一行中间一列;(2) 从2开始直到n×n止各数依次按下列规则存放:按45°方向行走,如向右上每一个数存放的行比前一个数的行数减1,列数加1(3) 如果行列范围超出矩阵范围,则回绕。
例如1在第1行,则2应放在最下一行,列数同样加1;(4) 如果按上面规则确定的位置上已有数,或上一个数是第1行第n列时,则把下一个数放在上一个数的下面。
3.1.2 N为4的倍数时采用对称元素交换法。
首先把数1到n×n按从上至下,从左到右顺序填入矩阵然后将方阵的所有4×4子方阵中的两对角线上位置的数关于方阵中心作对称交换,即a(i,j)与a(n-1-i,n-1-j)交换,所有其它位置上的数不变。
(或者将对角线不变,其它位置对称交换也可)3.1.3 N 为其它偶数时当n为非4倍数的偶数(即4n+2形)时:首先把大方阵分解为4个奇数(2m+1阶)子方阵。
按上述奇数阶幻方给分解的4个子方阵对应赋值上左子阵最小(i),下右子阵次小(i+v),下左子阵最大(i+3v),上右子阵次大(i+2v) 即4个子方阵对应元素相差v,其中v=n*n/4 四个子矩阵由小到大排列方式为① ③ ④ ②然后作相应的元素交换:a(i,j)与a(i+u,j)在同一列做对应交换(j<t或j>n-t+2), a(t-1,0)与a(t+u-1,0);a(t-1,t-1)与a(t+u-1,t-1)两对元素交换其中u=n/2,t=(n+2)/4 上述交换使每行每列与两对角线上元素之和相等。
C语言实现#include"stdio.h"#include"math.h"int a[256][256];int sum;int check();void ins(int n);main(){inti,j,n,k,t,p,x;scanf("%d",&n);sum=(n*n+1)*n/2;if(n%2==1)//奇数幻方{ins(n);k=n;}if(n%4==2)//单偶数幻方{k=n/2;ins(k);for(i=0;i<k;i++)for(j=0;j<k;j++){a[j+k]=a[j]+2*k*k;a[i+k][j]=a[j]+3*k*k;a[i+k][j+k]=a[j]+k*k;}t=(n-2)/4;for(i=0;i<k;i++)for(j=0;j<k;j++){if((j<t)&&(i<t)){p=a[j];a[j]=a[i+k][j];a[i+k][j]=p;}if((j<t)&&(i>k-t-1)){p=a[j];a[j]=a[i+k][j];a[i+k][j]=p;}if((i>=t&&i<=k-t-1)&&(j>=t&&j<t*2)) {p=a[j];a[j]=a[i+k][j];a[i+k][j]=p;}if(j>1&&j<=t){p=a[j+k];a[j+k]=a[i+k][j+k];a[i+k][j+k]=p; }}}if(n%4==0)//双偶数幻方{x=1;for(i=0;i<n;i++)for(j=0;j<n;j++)a[j]=x++;for(i=0;i<n;i++)for(j=0;j<n;j++){if(i%4==0&&abs(i-j)%4==0)for(k=0;k<4;k++)a[i+k][j+k]=n*n-a[i+k][j+k]+1; else if(i%4==3&&(i+j)%4==3) for(k=0;k<4;k++)a[i-k][j+k]=n*n-a[i-k][j+k]+1;}}if(check(n)==1){for(i=0;i<n;i++){for(j=0;j<n;j++)printf("%5d",a[j]);printf("\n");}return ;}}int check(int n)//检验是否是幻方{int i,j,sum1=0,sum2;for(i=0;i<n;i++){for(j=0;j<n;j++)sum1+=a[j];if(sum1!=sum) return 0;sum1=0;}for(i=0;i<n;i++){for(j=0;j<n;j++)sum1+=a[j];if(sum1!=sum) return 0;sum1=0;}for(sum1=0,sum2=0,i=0,j=0;i<n;i++,j++) {sum1+=a[j];sum2+=a[n-j-1];}if(sum1!=sum) return 0;if(sum2!=sum) return 0;else return 1;}void ins(int n)//单偶数幻方的输入{ intx,y,m;x=0;y=n/2;for(m=1;m<=n*n;m++){a[x][y]=m;if (m%n!=0){x--;y++;if(x<0) x=x+n;if(y==n) y=n-y;}else{x++;if(x==n) x=x-n;}}}3.2 其他方法奇阶幻方当n为奇数时,我们称幻方为奇阶幻方。
