12-5轴对称类全等问题(1).题库教师版
全等、轴对称小题复习

全等、轴对称小题复习题型一:判断全等1.不能说明两个三角形全等的条件是( )A.三边对应相等B.两边及其夹角对应相等C.两角及其夹边对应相等D.有一角和一边对应相等的两个直角三角形全等2.不能说明两个三角形全等的条件是( )A.三条边对应相等B.两边及其夹角对应相等C.两角及其中一角的对边对应相等D.两条边和一条边所对的角对应相等3. 如图,点E在△ABC的外部,点D在BC边上,DE交AC于点,若1=2=3,AC =AE,请写出一对全等三角形.题型二:看图找出正确结论的个数1.如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB、AC的距离相等;③AD⊥BC且BD=CD;④∠BDE=∠CDF.其中正确的个数是()A.1个B.2个C.3个D.4个(第1题图)(第2题图)2.如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC的中点.其中正确结论的个数有()A.4个B.3个C.2个D.1个3.如图所示,从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是()A.4个B.3个C.2个D.1个4.如图:在不等边△ABC中,PM⊥AB,垂足为M,PN⊥AC,垂足为N,且PM=PN,Q 在AC上,PQ=QA,下列结论:①AN=AM,②QP∥AM,③△BMP≌△QNP,其中正确的是()A.①②③B.①②C.②③D.①(第4题图)(第5题图)5.如图,在△ABC中,BC=AC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,垂足为E.则结论:①AD=BF;②CF=CD;③AC+CD=AB;④BE=CF;⑤BF=2BE 其中正确结论的个数是()A.1 B.2 C.3 D.4题型三:补一个条件能证出全等的选择题1.如图,EA∥DF,AE=DF,要使△AEC≌△DFB,只要()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC(第1题图)(第2题图)2.如图,已知DA=CB,要使△ABD≌△BAC,只要添加一个条件是,依据.(只要填一个你认为适合的条件,不添加其它的字母和辅助线)3.如图,已知AB=AC,则只要添加条件,就可以使△ABD≌△ACE.(第3题图)(第4题图)4.如图,点F、C在线段BE上,且∠1=∠2,BF=EC,若要使△ABC≌△DEF,则还须补充一个条件.(只要填一个)题型四:与角平分线线有关的填空选择题1. 如图,在△ABC中,∠C=90,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是.2.如图,在△ABC中,∠C=90,AD是∠BAC的平分线交BC于D,已知AB=10cm,CD=3cm,则△ABD的面积是.3. 如图,已知点P是∠BAC的平分线上的一点,PM⊥AB与点M,PN⊥AC于点N,下列结论①PM=PN②AM-AN=0③△APM与△APN的面积相等④∠PAN+∠APN=90°,其中正确的是.4. 如图,△ABC中,∠C=90,AC=BC,AD是∠CAB交BC于D,DE⊥AB于点E,若AB=6cm则△BDE的周长是.5. 如图所示,在△ABC中,P,Q•分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S。
第十三章轴对称验收卷-八年级上册考点专训(解析版)(人教版)

第十三章轴对称验收卷一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)1.下列防疫标志中,是轴对称图形的是()A.B.C.D.【答案】D【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,据此判断即可.【详解】解:A.不是轴对称图形,故本选项不合题意;B.不是轴对称图形,故本选项不合题意;C.不是轴对称图形,故本选项不合题意;D.是轴对称图形,故本选项符合题意;故选:D.【点睛】本题主要考查了轴对称图形,熟记定义是解答本题的关键.是将长方形纸片ABCD沿BD折叠得到的,图中(包括实线、虚线在内)共有全等三2.如图所示,BDC角形()对A.2B.3C.4D.5【答案】C【分析】从最简单的开始找,因为图形对折,所以首先△CDB≌△C′DB,由于四边形是长方形所以,△ABD≌△CD B.进而可得另有2对,分别为:△ABE≌△C′DE,△ABD≌△C′DB,如此答案可得.【详解】解:∵△BDC′是将长方形纸片ABCD沿BD折叠得到的,∴C′D=CD,BC′=BC,∵BD=BD,∴△CDB≌△C′DB(SSS),同理可证明:△ABE≌△C′DE,△ABD≌△C′DB,△ABD≌△CDB三对全等.所以,共有4对全等三角形.故选:C.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SS A、HL.注意:AA A、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要由易到难,循序渐进.3.如图,已知钝角ABC,依下列步骤尺规作图,并保留了作图痕迹.步骤1:以C为圆心,CA长为半径画弧①;步骤2:以B为圆心,BA长为半径画弧②,交弧①于点D;步骤3:连接AD,交BC的延长线于点H.则下列说法不正确的是()A.AH是ABC中BC边上的高B.AH DHC .AC 平分BAD∠D .作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上【答案】C【分析】根据线段的垂直平分线的判定解决问题即可.【详解】解:如图,连接CD ,BD ,由作图步骤可知,AC DC =,AB DB =,由①两点确定一条直线,②到线段两端点距离相等的点在线段的垂直平分线上,可知BH 为AD 的垂直平分线,即AD BH ⊥,AH DH =,故选C .【点睛】本题考查作图-基本作图,线段的垂直平分线的判定等知识,解题的关键是判定图示所做为垂直平分线.4.如图,ABC 中,AD BC ⊥,AD 平分BAC ∠,以下结论:①线段AD 是线段BC 的垂直平分线②ABC 是等腰三角形;③ABD ACD S S = ;④D 为BC 的中点.其中正确的有()A .1个B .2个C .3个D .4个【答案】D【分析】根据已知条件证明出△ADB ≌△ADC ,由全等得到AB =AC ,BD =CD ,最后得出结论.【详解】解:∵AD BC ⊥,AD 平分BAC ∠,∴∠ADB =∠ADC =90°,∠BAD =∠CAD ,在△ADB 和△ADC 中,BAD CAD AD AD ADB ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADB ≌△ADC (ASA )∴AB =AC ,BD =CD ,ABD ACDS S = ∵AD BC ⊥,D 为BC 的中点,∴线段AD 是线段BC 的垂直平分线,∴①②③④说法正确,故选:D .【点睛】本题主要考查了等腰三角形的判定与线段垂直平分线的定义,证明出三角形全等是解本题的关键.5.如图,点P 是AOB ∠内的一点,PC OA ⊥于点C ,PD OB ⊥于点D ,连接OP ,CD .若PC PD =,则下列结论不一定...成立的是()A .AOP BOP∠=∠B .OPC OPD ∠=∠C .PO 垂直平分CD D .PD CD=【答案】D【分析】根据角平线的判定定理可判断A ,证明Rt COP Rt DOP ≌,可判断B ,根据Rt COP Rt DOP ≌,可得OC =OD ,进而可判断C ,根据等边三角形的定义,可判断D .【详解】解:∵点P 是AOB ∠内的一点,PC OA ⊥于点C ,PD OB ⊥于点D ,PC PD =,∴OP 是∠AOB 的平分线,即AOP BOP ∠=∠,故A 成立,不符合题意;∵OP =OP ,AOP BOP ∠=∠,∴Rt COP Rt DOP ≌(HL ),∴OPC OPD ∠=∠,故B 成立,不符合题意;∵Rt COP Rt DOP ≌,∴OC =OD ,又∵PC PD =,∴PO 垂直平分CD ,故C 成立,不符合题意;∵PCD 不一定是等边三角形,∴PD CD =不一定成立,故D 符合题意.故选D .【点睛】本题主要考查角平分线的判定,垂直平分线的判定,全等三角形的判定和性质以及等边三角形的定义,掌握上述定理和定义是解题的关键.6.如图,在△ABC 中,∠C =60°,AD 是BC 边上的高,点E 为AD 的中点,连接BE 并延长交AC 于点F .若∠AFB =90°,EF =2,则BF 长为()A.4B.6C.8D.10【答案】D【分析】根据三角形内角和定理求出∠DAC=30°和∠EBD=30°,根据含30°角的直角三角形的性质得出AE=2EF,BE=2DE,代入求出即可.【详解】∵在△ABC中,∠C=60°,AD是BC边上的高,∴∠DAC=180°﹣∠C﹣∠ADC=180°﹣60°﹣90°=30°,∵∠AFB=90°,EF=2,∴AE=2EF=4,∵点E为AD的中点,∴DE=AE=4,∵∠C=60°,∠BFC=180°﹣90°=90°,∴∠EBD=30°,∴BE=2DE=8,∴BF=BE+EF=8+2=10,故选:D.【点睛】本题主要考查了三角形的内角和定理、含30︒角的直角三角形的性质,熟练掌握相关知识是解题的关键.7.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=2,则CE的长为()A.B.4C.D.2【答案】B【分析】先根据线段垂直平分线的性质得出BE =CE ,故可得出∠B =∠DCE ,再由直角三角形的性质即可得出结论.【详解】解:∵在△ABC 中,∠B =30°,BC 的垂直平分线交AB 于E ,ED =2,∴BE =CE ,∴∠B =∠DCE =30°,在Rt △CDE 中,∵∠DCE =30°,ED =2,∴CE =2DE =4.故选:B .【点睛】本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.8.如图,在ABC 中,AC BC =,D 、E 、F 分别是各边延长线的点,131DAC ∠=︒,则ECF ∠的度数为()A .49︒B .88︒C .98︒D .131︒【答案】C【分析】根据邻补角的定义求出49BAC ∠=︒,根据等边对等角得到49ABC BAC ∠=∠=︒,再根据三角形外角的性质即可求解.【详解】解:∵131DAC ∠=︒,∴49BAC ∠=︒,∵AC BC =,∴49ABC BAC ∠=∠=︒,∴98ECF ∠=︒,故选:C .【点睛】本题考查邻补角的定义、等边对等角、三角形外角的性质等内容,掌握上述性质定理是解题的关键.9.如图,在ABC 中,90ACB ∠=︒,30CAD ∠=︒,AC BC AD ==,则CBD ∠的度数为()A .12°B .13°C .14°D .15°【答案】D【分析】可过C 作CE ⊥AD 于E ,过D 作DE ⊥BC 于F ,依据题意可得∠FCD =∠ECD ,进而得到△CED ≌△CFD ,得到CF =BF ,再利用等腰三角形的判定可得出结论.【详解】解:如图,过C 作CE ⊥AD 于E ,过D 作DF ⊥BC 于F.∵∠CAD =30°,∴∠ACE =60°,且CE =12AC ,∵AC =AD ,∠CAD =30°,∴∠ACD =75°,∴∠FCD =90°-∠ACD =15°,∠ECD =∠ACD -∠ACE =15°,在△CED 和△CFD 中,CED CFD ECD FCD CD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CED ≌△CFD (AAS ),∴CF =CE =12AC =12BC ,∴CF =BF ,∵DF ⊥BC ,∴BD =CD ,∴∠DCB =∠CBD =15°,故选:D .【点睛】本题主要考查了全等三角形的判定和性质,等腰三角形的判定和性质,能够熟练运用其性质进行解题是关键.10.如图,在锐角三角形ABC 中,BC BA >,按以下步骤作图:①以点B 为圆心,BA 长为半径作圆弧,交AC 于点D ;②分别以点A 、D 为圆心,大于12AD 长为半径作圆弧,计两弧交于点E ;③作射线BE ,交AC 于点P ,若60A ∠=︒,则ABP ∠的大小为()A .20︒B .25︒C .30°D .35︒【答案】C【分析】根据作图步骤可知BP ⊥AC ,根据直角三角形两锐角互余的性质即可得答案.【详解】由作图步骤可知:BP ⊥AC ,∴∠BPA =90°,∵60A ∠=︒,∴ABP∠=90°-∠A=30°,故选:C.【点睛】本题考查尺规作图——作垂线,熟练掌握各基本作图的步骤是解题关键.△都是等边三角形,连接AD,BE,OC:下列11.如图,A,B,E三点在同一直线上,ABC,CDE结论中正确的是()①△ACD≌△BCE;②△CPQ是等边三角形;∠;③OC平分AOE④△BPO≌△EDO.A.①②B.①②③C.①②④D.①②③④【答案】B【分析】利用等边三角形的性质,三角形的全等,逐一判断即可.【详解】∵△ABC,△CDE都是等边三角形,∴CA=CB,CD=CE,∠ACB=∠ECD=60°,∴∠ACB+∠PCQ=∠ECD+∠PCQ,∠PCD=60°,∴∠ACD=∠BCE,∴△ACD≌△BCE,∴①的说法是正确的;∵△ACD≌△BCE,∴∠PDC=∠QEC,∵∠PCD=∠QCE=60°,CD=CE,∴△PCD≌△QCE,∴△CPQ 是等边三角形;∴②的说法是正确的;∵△PCD ≌△QCE ,∴PD =QE ,PCD QCE S S =△△,过点C 作CG ⊥PD ,垂足为G ,CH ⊥QE ,垂足为H ,∴1122PD CG QE CE ∙=∙,∴CG =CH ,∴OC 平分AOE ∠,∴③的说法是正确的;无法证明△BPO ≌△EDO .∴④的说法是错误的;故答案为①②③,故选B .【点睛】本题考查了等边三角形的性质与判定,三角形的全等与性质,角平分线的性质定理,熟练掌握等边三角形的性质,灵活进行三角形全等的判定,活用角的平分线性质定理的逆定理是解题的关键.12.如图,等腰ABC 的底边BC 长为4cm ,面积为216cm ,腰AC 的垂直平分线EF 交AC 于点E ,交AB 于点F ,D 为BC 的中点,M 为直线EF 上的动点.则CDM V 周长的最小值为()A .6cmB .8cmC .9cmD .10cm【分析】连接AD ,AM ,由于△ABC 是等腰三角形,点D 是BC 边的中点,故AD ⊥BC ,再根据三角形的面积公式求出AD 的长,再根据EF 是线段AC 的垂直平分线可知,点A 关于直线EF 的对称点为点C ,MA =MC ,推出MC +DM =MA +DM ≥AD ,故AD 的长为BM +MD 的最小值,由此即可得出结论.【详解】解:连接AD ,MA .∵△ABC 是等腰三角形,点D 是BC 边的中点,∴AD ⊥BC ,∴S △ABC =12BC •AD =12×4×AD =16,解得AD =8cm ,∵EF 是线段AC 的垂直平分线,∴MA =MC ,∴MC +DM =MA +DM ≥AD ,∴AD 的长为CM +MD 的最小值,∴△CDM 的周长最短=(CM +MD )+CD =AD +12BC =8+12×4=10(cm ).故选:D .【点睛】本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质和垂直平分线的性质是解答此题的关键.13.等边三角形ABC 所在平面内有一点P ,且点P 不与点A ,B ,C 重合,使得PAB △,PBC ,PCA V 都是等腰三角形,这样的点P 共有()A .1个B .4个C .7个D .10个【答案】D【分析】当点P 在三角形的内部时,点P 到△ABC 的三个顶点的距离相等,则点P 是三角形的外心,当点P 在三角形的外部时,只要每条边的垂直平分线上的点到三角形的各个顶点连接而成的三角形是等腰三角形即可.【详解】如图所示:当点P 在三角形的内部时,点P 到△ABC 的三个顶点的距离相等,则点P 是三角形的外心,分别以三角形各顶点为圆心,边长为半径,与各边的垂直平分线的交点就是满足要求的点,每条垂直平分线上有3个交点,再加上三角形的外心,一共有10个点.故选D .【点睛】本题主要考查等腰三角形的定义,掌握中垂线的性质与等边三角形的性质,是解题的关键.14.如图,过边长为3的等边ABC 的边AB 上一点P ,作PE AC ⊥于E ,Q 为BC 延长线上一点,当PA CQ=时,连接PQ 交边AC 于点D ,则DE 的长为()A .13B .12C .32D .2【答案】C【分析】过P 作//PF BC 交AC 于F ,得出等边三角形APF ,推出AP PF QC ==,根据等腰三角形性质求出EF AE =,证PFD QCD ∆≅∆,推出FD CD =,推出12DE AC =即可.【详解】解:过P 作//PF BC 交AC 于F ,//PF BC ,ABC ∆是等边三角形,PFD QCD ∴∠=∠,60APF B ∠=∠=︒,60AFP ACB ∠=∠=︒,60A ∠=︒,APF ∴∆是等边三角形,AP PF AF ∴==,PE AC ⊥ ,AE EF ∴=,AP PF = ,AP CQ =,PF CQ ∴=,在PFD ∆和QCD ∆中PFD QCD PDF CDQ PF CQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD QCD ∴∆≅∆,FD CD ∴=,AE EF = ,EF FD AE CD ∴+=+,12AE CD DE AC ∴+==,3AC = ,32DE ∴=,故选:C.【点睛】本题综合考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰三角形的性质,平行线的性质等知识点的应用,能综合运用性质进行推理是解此题的关键,通过做此题培养了学生分析问题和解决问题的能力,题型较好,难度适中.二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)15.若点A (a ,4)和点B (-1,b +5)关于y 轴对称,则点a -b =_______________【答案】2【分析】根据关于y对称,则横坐标互为相反数,纵坐标不变,从而确定对称点的坐标,从而求得,a b的值,再代入代数式求解即可【详解】点A(a,4)和点B(-1,b+5)关于y轴对称∴(1) 45 ab=--⎧⎨=+⎩解得:11 ab=⎧⎨=-⎩2a b∴-=故答案为:2【点睛】本题考查了平面直角坐标系的定义,关于坐标对称,代数式求值,理解关于y轴对称的点的坐标关系是解题的关键.16.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=130°,则∠B +∠C=___°.【答案】115【分析】先根据∠1+∠2=130°得出∠AMN+∠DNM的度数,再由四边形内角和定理即可得出结论.【详解】解:∵∠1+∠2=130°,∴∠AMN+∠DNM=3601302︒-︒=115°.∵∠A+∠D+(∠AMN+∠DNM)=360°,∠A+∠D+(∠B+∠C)=360°,∴∠B+∠C=∠AMN+∠DNM=115°.故答案为:115.【点睛】本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.17.如图.在Rt ABC △中,90C ∠=︒,AF EF =.若72CFE ∠=︒,则B ∠=______.【答案】54°【分析】首先根据等腰三角形的性质得出∠A =∠AEF ,再根据三角形的外角和定理得出∠A +∠AEF =∠CFE ,求出∠A 的度数,最后根据三角形的内角和定理求出∠B 的度数即可.【详解】∵AF =EF ,∴∠A =∠AEF ,∵∠A +∠AEF =∠CFE=72°,∴∠A =36°,∵∠C =90°,∠A +∠B +∠C =180°,∴∠B =180°-∠A -∠C =54°.故答案为:54°.【点睛】本题考查了三角形的外角和定理,等腰三角形的性质,掌握相关定理和性质是解题的关键.18.如图,已知等边△AOC 的边长为1,作OD ⊥AC 于点D ,在x 轴上取点C 1,使CC 1=DC ,以CC 1为边作等边△A 1CC 1;作CD 1⊥A 1C 1于点D 1,在x 轴上取点C 2,使C 1C 2=D 1C 1,以C 1C 2为边作等边△A 2C 1C 2;作C 1D 2⊥A 2C 2于点D 2,在x 轴上取点C 3,使C 2C 3=D 2C 2,以C 2C 3为边作等边△A 3C 2C 3;…,且点A ,A 1,A 2,A 3,…都在第一象限,如此下去,则等边△A 2021C 2020C 2021的边A 2021C 2021中点D 2021横坐标为_________.【答案】20242023252-【分析】根据等边三角形的性质分别求出C 1C 2,C 2C 3,C 3C 4,…,C 2020C 2021的边长,即刻求出OC 2021边长,进而求出点C 2021、点A 2021的横坐标,即可求出点D 2021横坐标.即可解决问题.【详解】解:∵等边△AOC 的边长为1,作OD ⊥AC 于点D ,∴OC =1,C 1C 2=CD =12OC =12∴OC ,CC 1,C 1C 2,C 2C 3,…,C 2020C 2021的长分别为232021*********⋯,,,,,OC 2021=OC +CC 1+C 1C 2+C 2C 3,…+C 2020C 2021=202223202120211111211=22222-++++⋯+,∴点C 2021的横坐标为20222021212-,∴等边△A 2021C 2020C 2021顶点A 2021的横坐标为20222023202120212022211123=2222---⨯,∴等边△A 2021C 2020C 2021的边A 2021C 2021中点D 2021横坐标为2023202220242022202120232321125=2222⎛⎫---+⨯ ⎪⎝⎭.故答案为:20242023252-.【点睛】本题为坐标规律题,考查了点的坐标和等边三角形的性质,有理数的运算等知识,综合性强,难度大,熟知等边三角形性质,准确找出A n 点的横坐标变化规律并熟练运算是解题的关键.三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)19.已知:如图,∠CAE 是ABC 的外角,AD ∥BC 且∠1=∠2,求证:AB =AC .【答案】见解析【分析】先由平行线的性质得∠1=∠B,∠2=∠C,再由角平分线定义得∠1=∠2,则∠B=∠C,然后由等角对等边即可得出结论.【详解】解:∵AD∥BC,∴∠1=∠B,∠2=∠C,∵∠1=∠2,∴∠B=∠C,∴AB=AC.【点睛】本题考查了等腰三角形的判定、平行线的性质以及角平分线定义等知识;熟练掌握等腰三角形的判定和平行线的性质是解题的关键.20.下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.(1)如图①,整个图形是轴对称图形,画出它的对称轴;(2)如图②,将某一个方格涂上阴影,使整个图形有两条对称轴;(3)如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)直接利用轴对称图形的性质得出答案;(2)直接利用轴对称图形的性质得出答案;(3)直接利用轴对称图形的性质得出答案.【详解】解:(1)如图①所示:(2)如图②所示:(3)如图③所示:【点睛】此题主要考查了利用轴对称设计图案,解题的关键是:正确掌握轴对称图形的性质.21.如图,在Rt ABC 中,=90C ∠︒.(1)请用尺规作图:作A ∠的平分线AD ,AD 交BC 于点D ;(保留作图痕迹,不要求写作法)(2)若点D 恰好在线段AB 的垂直平分线上,求BAC ∠的度数.【答案】(1)见解析;(2)60°【分析】(1)以点A 为圆心,以任意长为半径画弧交AC ,AB 于两点,分别以这两点为圆心,以大于这两点距离的一半长为半径画弧,连结点A 与这两弧交点交BC 于点D .(2)根据线段垂直平分线的性质可得DA DB =,结合角平分线的性质可得B DAB DAC ∠=∠=∠,根据直角三角形的性质即可求出BAC ∠的度数.【详解】解:(1)如答题20图,AD 即为所求.(2)∵点D 恰好在线段AB 的垂直平分线上,∴DA DB =;∴B DAB DAC ∠=∠=∠.∵90B DAB DAC ∠+∠+∠=︒,∴30.B DAB DAC ∠=∠=∠=︒∴60BAC ∠=︒.【点睛】本题主要考查了基本作图,角平分线的性质,线段垂直平分线的性质,直角三角形的性质.正确掌握线段垂直平分线的性质是解题的关键.22.如图,在平面直角坐标系中,△ABC 的顶点坐标分别是A (0,0),B (5,1),C (2,4).(1)在平面直角坐标系中描出点A ,B ,C ,并作出△ABC 关于y 轴对称的△A 1B 1C 1;(2)如果将△ABC 向下平移3个单位长度,再向左平移4个单位长度,得到△A 2B 2C 2,直接写出2A ,B 2,C 2的坐标,(3)求△A 2B 2C 2的面积;【答案】(1)见解析;(2)222(4,3),(1,2),(2,1)A B C ----;(3)9【分析】(1)根据A 、B 、C 三点坐标描出各点即可;依据轴对称的性质,作出对称点,顺次连接各点即可得出△A 1B 1C 1;(2)依据平移性质,可得到△A 2B 2C 2,进而可得到2A ,B 2,C 2的坐标;(3)依据网格特点,利用割补法和三角形面积公式求解即可.【详解】(1)如图所示;(2)作出△A 2B 2C 2,如图所示,则222(4,3),(1,2),(2,1)A B C ----;(3)由图象可知,△A 2B 2C 2的面积111542433519222S =⨯-⨯⨯-⨯⨯-⨯⨯=.【点睛】本题考查坐标与图形变换-轴对称、坐标与图形变换-平移、三角形的面积公式,作图时找到图形的关键点是解答的关键.23.如图1,三角形ABC 中,64A ∠=︒,90B ∠=︒,26C ∠=︒.点D 是AC 边上的定点,点E 在BC 边上运动,沿DE 折叠三角形CDE ,点C 落在点G 处.(1)如图2,若//DE AB ,求ADG ∠的度数.(2)如图3,若//EG AB ,求ADG ∠的度数.(3)当三角形DEG 的三边与三角形ABC 的三边有一组边平行时,直接写出其他所有情况下ADG ∠的度数.【答案】(1)52°;(2)142°;(3)116°或26°或38°或64°【分析】(1)根据折叠的性质得到∠CDE =∠A =∠GDE =64°,即可求出∠ADG ;(2)根据GE ∥AB ,得到∠BEG =90°,算出∠BFD ,利用四边形内角和即可求出∠ADG ;(3)找出其他所有情况,画出图形,利用平行线的性质求解即可.【详解】解:(1)由折叠可知:∠C =∠DGE =26°,∠CDE =∠GDE ,∵DE ∥AB ,AB ⊥BC ,∴DE ⊥BC ,则G 在BC 上,∴∠CDE =∠A =∠GDE =64°,∴∠ADG =180°-64°×2=52°;(2)由折叠可知:∠C =∠DGE =26°,∠CDE =∠GDE ,∠DEC =∠DEG ,∵GE ∥AB ,∴∠B =∠CEG =∠BEG =90°,∴∠EFG =90°-26°=64°,∵∠A =64°,∠B =90°,∴∠ADG=360°-64°-90°-64°=142°;(3)如图,DG∥AB,则∠ADG=180°-∠A=116°;如图,DG∥BC,∠ADG=∠C=26°;如图,EG∥AC,∠ADG=∠G=∠C=26°;如图,EG∥AB,∴∠A=∠CFE=64°,∠B=∠CEG=90°,由折叠可知:∠DEG=∠DEC=45°,∴∠CDE=180°-45°-26°=109°=∠EDG,∴∠EDF=180°-109°=71°,∴∠ADG=109°-71°=38°;如图,DG∥AB,∴∠ADG=∠A=64°;综上:其他所有情况下∠ADG的度数为116°或26°或38°或64°.【点睛】本题考查了平行线的性质,折叠问题,解题的难点在于找出所有符合题意的情况,得到角的关系.24.(1)如图1,在△ABC中,∠ABC,∠ACB的平分线交于点O,过点O作EF∥BC分别交AB,AC于点E,F.直接写出线段EF与BE,CF之间的数量关系:.(2)如图2,若△ABC外角平分线BO和CO交于点O,过点O作OE∥BC分别交边AB和AC的延长线于点E和F.线段EF与BE,CF之间的数量关系是否依然成立?若成立,请说明理由;若不成立,请写出它们之间的数量关系.(3)如图3,若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于点O,过O点作OE∥BC交AB 于点E,交AC于点F.则EF与BE,CF之间的数量关系又如何?说明你的理由.【答案】(1)EF=BE+CF;(2)成立,理由见解析;(3)EF=BE-CF,理由见解析(1)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系;(2)根据角平分线性质和平行线性质和平行线的性质即可推出;(3)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系.【详解】解:(1)EF=BE+CF;理由如下:∵BO平分∠ABC,CO平分∠ACB,∴∠EBO=∠OBC,∠FCO=∠OCB,∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,∴∠EBO=∠EOB,∠FOC=∠FCO,∴BE=OE,CF=OF,∴△BEO和△CFO是等腰三角形即图中等腰三角形有△BEO,△CFO;EF与BE、CF之间的关系是EF=BE+CF,(2)结论依然成立.理由:∵BO平分∠CBE∴∠CBO=∠EBO∵EF∥BC∴∠CBO=∠EOB∴∠EBO=∠EOB∴BE=OE同理可证:CF=OF∵EF=OE+OF∴EF=BE+CF(3)EF=BE-CF∵BO平分∠ABC∴∠ABO=∠CBO∵EF∥BC∴∠EOB=∠CBO∴∠ABO=∠EOB∴BE=OE同理可证:CF=OF∵EF=OE-OF∴EF=BE-CF【点睛】本题考查了角平分线的性质,平行线的性质,等腰三角形的判定等知识点,掌握三者的性质是解题的关键25.如图,△ABC中,∠ABC=60°,分别以AB,AC为边向三角形外作等边△ABD和等边△ACE,解答下列各题,并要求标注推导理由:(1)如图1,求证:AD∥BC;(2)如图2,连接CD、BE,求证:DC=BE;(3)如图3,若∠ACB=90°,连接DE,交AB于点F,求证:DF=EF.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)根据同旁内角互补,两直线平行证明即可;(2)由等边三角形的性质得∠DAB=∠EAC=60°,AD=AB,AE=AC,运用SAS证明△ADC≌△ABE即可得到结论;(3)作DG//AE,证明DGB ACB∆≅∆得DG=AC,再根据AAS证明DGF EAF∆≅∆即可得到.【详解】解:(1)证明:∵△ABD 是等边三角形(已知)∴∠ADB =∠ABD =60°(等边三角形每个内角都相等,都等于60°)∵∠ABC =60°(已知)∴∠ABD +∠ABC =120°∴∠ADB +∠DBC =180°∴AD //BC (同旁内角互补,两直线平行)(2)∵△ABD ,△ACE 是等边三角形(已知)∴∠DAB =∠EAC =60°(等边三角形每个内角都相等,都等于60°)AD =AB ,AC =AE (等边三角形,三条边相等)∴∠DAB +∠BAC =∠EAC +∠CAB (等式的性质)∴∠BAC =∠EAD∴△ADC ≌△ABE (SAS )∴DC =BE (全等三角形对应边相等)(3)如图,作DG //AE ,交AB 于点G,∵∠ABC =60°,∠ACB =90°(已知)∴∠BAC =30°(直角三角形两锐角互余)∴90FAE EAC CAB ︒∠=∠+∠=∴∠DGA =∠FAE =90°(两直线平行,内错角相等)∴∠DGB =90°(补角的定义)在△DBG 和△ABC 中AB DB DBG ABC DGB ACB =⎧⎪∠=∠⎨⎪∠=∠⎩∴△DBG ≌△ABC (AAS)∴DG=AC∵△AEC是等边三角形(已知)∴AE=CE(等边三角形的性质)∴DG=AE(等量代换)∵∠DFG=∠EFA(对顶角相等)又∠DGF=∠EAF(已证)∴△DGF≌△EAF(AAS)∴DF=EF(全等三角形对应边相等).【点睛】此题主要考查了全等三角形的判定与性质,平行线的性质,以及等边三角形的性质,熟练掌握等边三角形和全等三角形的性质和判定是关键.26.如图,在等边△ABC中,点D,E分别是AC,AB上的动点,且AE=CD,BD交CE于点P.(1)如图1,求证:∠BPC=120°;(2)点M是边BC的中点,连接PA,PM,延长BP到点F,使PF=PC,连接CF,①如图2,若点A,P,M三点共线,则AP与PM的数量关系是.②如图3,若点A,P,M三点不共线,问①中的结论还成立吗?若成立,请给出证明,若不成立,说明理由.【答案】(1)见解析;(2)①AP=2PM;②成立,证明见解析【分析】(1)由“SAS”可证△AEC≌△CDB,得到∠ACE=∠CBD,根据三角形的内角和定理计算,得出结论;(2)①由等边三角形的性质和已知条件得出∠BAC=∠ABC=∠ACB=60°,AM⊥BC,∠BAP=∠CAP=1 2∠BAC=30°,得出PB=PC,由等腰三角形的性质得出∠PBC=∠PCB=30°,得出PC=2PM,证出∠ACP=60°﹣30°=30°=∠CAP ,得出AP =PC ,即可得出AP =2PM ;②延长PM =MH ,连接CH ,由“SAS ”可证△ACF ≌△BCP ,可得AF =BP ,∠AFC =∠BPC =120°,由“SAS ”可证△CM H ≌△BMP ,可得CH =BP =AF ,∠H CM =∠PBM ,由“SAS ”可证△AFP ≌△HCP ,可得AP =PN =2PM .【详解】(1)证明:∵△ABC 为等边三角形,∴AB =AC =BC ,∠A =∠ABC =∠ACB =60°,在△AEC 和△CDB 中,AE CD A BCD AC CB =⎧⎪∠=∠⎨⎪=⎩,∴△AEC ≌△CDB (SAS ),∴∠ACE =∠CBD ,∵∠BPC +∠DBC +∠BCP =180°,∴∠BPC +∠ACE +∠BCP =180°,∴∠BPC =180°﹣60°=120°;(2)①解:AP =2PM ,理由如下:∵△ABC 为等边三角形,点M 是边BC 的中点,∴AM ⊥BC ,∠BAM =∠CAM =30°,∵AM ⊥BC ,点M 是边BC 的中点,∴PB =PC ,∵∠BPC =120°,∴∠PBC =∠PCB =30°,∴PC =2PM ,∠ACP =30°,∴∠PAC =∠PCA ,∴PA =PC ,∴AP =2PM ,故答案为:AP =2PM ;②解:①中的结论成立,理由如下:延长PM 至H ,是MH =PM ,连接AF 、CH ,∵∠BPC =120°,∴∠CPF =60°,∵PF =PC ,∴△PCF 为等边三角形,∴CF =PF =PC ,∠PCF =∠PFC =60°,∵△ABC 为等边三角形,∴BC =AC ,∠ACB =60°=∠PCF ,∴∠BCP =∠ACF ,在△BCP 和△ACF 中,BC AC BCP ACF CP CF =⎧⎪∠=∠⎨⎪=⎩,∴△BCP ≌△ACF (SAS ),∴AF =BP ,∠AFC =∠BPC =120°,∴∠AFP =60°,在△CM H 和△BMP 中,CM BM CMH BMP HM PM =⎧⎪∠=∠⎨⎪=⎩,∴△CM H ≌△BMP (SAS ),∴CH =BP =AF ,∠MCH =∠MBP ,∴CH ∥BP ,∴∠HCP +∠BPC =180°,∴∠HCP =60°=∠AFP ,在△AFP 和△HCP 中,CH AF HCP AFP CP PF =⎧⎪∠=∠⎨⎪=⎩,∴△AFP ≌△HCP (SAS ),∴AP=PH=2PM.【点睛】本题考查了三角形全等的判定和性质、等边三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.。
【中考数学】《轴对称及其应用》专项练习题5套含答案

专题线段的垂直平分线的应用类型1线段的垂直平分线的性质在求线段长中的应用1.如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为F,G,已知△ADE的周长为12 cm,则BC=12_cm.2.如图,AB比AC长3 cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14 cm,求AB和AC的长.解:∵△ACD的周长是14 cm,∴AD+DC+AC=14 cm.又∵DE是BC的垂直平分线,∴BD=DC.∴AD+DC=AD+BD=AB.∴AB+AC=14 cm.∵AB比AC长3 cm,∴AB-AC=3 cm.∴AB=8.5 cm,AC=5.5 cm.3.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.证明:(1)∵AD∥BC,∴∠ADE=∠FCE.∵E是CD的中点,∴DE=CE.又∵∠AED=∠FEC,∴△ADE≌△FCE(ASA).∴FC=AD.(2)∵△ADE≌△FCE,∴AE=EF,AD=CF.又∵BE⊥AE,∴BE是线段AF的垂直平分线.∴AB=BF=BC+CF.∵AD=CF,∴AB=BC+AD.类型2线段垂直平分线的性质在实际问题中的应用4.如图,某城市规划局为了方便居民的生活,计划在三个住宅小区A,B,C之间修建一个购物中心,试问:该购物中心应建于何处,才能使得它到三个小区的距离相等?解:连接AB,BC,分别作AB,BC的垂直平分线DE,GF,两直线交于点M,则点M就是所要确定的购物中心的位置,如图.类型3线段的垂直平分线的性质在判定两线段位置关系中的应用5.如图,OE,OF分别是△ABC中AB,AC边的中垂线(即垂直平分线),∠OBC,∠OCB的平分线相交于点I,试判定OI与BC的位置关系,并给出证明.解:OI ⊥BC.证明:连接AO ,延长OI 交BC 于点M. ∵OE ,OF 分别为AB ,AC 的中垂线, ∴OA =OB ,OA =OC.∴OB =OC.又∵BI ,CI 分别为∠OBC ,∠OCB 的平分线, ∴点I 必在∠BOC 的平分线上. ∴∠BOI =∠COI. 在△BOM 和△COM 中,⎩⎨⎧OB =OC ,∠BOM =∠COM ,OM =OM ,∴△BOM ≌△COM(SAS ). ∴∠BMO =∠CMO.又∵∠BMO +∠CMO =180°. ∴∠BMO =∠CMO =90°. ∴OI ⊥BC.专题轴对称变换的应用类型1轴对称图形的展开与折叠1.(绥化中考)把一张正方形纸片如图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后的图形是(C)类型2翻折式的轴对称变换2.(娄底中考)将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为13.3.(潜江中考)如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,求∠CDE的度数.解:∵在Rt△ABC中,∠ACB=90°,∠A=26°,∴∠B=64°.∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,且∠ACB=90°,∴∠BCD=∠ECD=45°,∠CED=∠B=64°.∴∠CDE=180°-∠ECD-∠CED=71°.4.(枣庄中考改编)如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C 落在直线AD上的C′处,P为直线AD上的一点,求线段BP的最短长度.解:过点B 作BM ⊥AD 于点M ,由题意可知△ABC ≌△ABC′, ∴S △ABC =S △ABC′=6.∵S △ABC ′=12AC′·BM =6,AC ′=AC =3,∴BM =4.根据垂线段最短可知BM ≤BP ,∴BP ≥4. ∴BP 的最短长度为4.类型3 轴对称变换与坐标5.已知点M(2a -b ,5+a),N(2b -1,-a +b).(1)若点M ,N 关于x 轴对称,求a 、b 的值; (2)若点M ,N 关于y 轴对称,求(4a +b)2 017的值. 解:(1)∵M ,N 关于x 轴对称,∴⎩⎪⎨⎪⎧2a -b =2b -1,5+a -a +b =0. 解得⎩⎪⎨⎪⎧a =-8,b =-5.(2)∵M ,N 关于y 轴对称,∴⎩⎪⎨⎪⎧2a -b +2b -1=0,5+a =-a +b. 解得⎩⎪⎨⎪⎧a =-1,b =3.∴(4a +b)2 017=-1.6.如图所示,在平面直角坐标系xOy 中,A(-1,5),B(-1,0),C(-4,3),直线m 为横坐标都为2的点组成的一条直线.(1)作出△ABC关于直线m对称的△A1B1C1;(2)直接写出A1,B1,C1的坐标;(3)求出△A1B1C1的面积.解:(1)如图所示.(2)A1(5,5),B1(5,0),C1(8,3).(3)△A1B1C1的面积为7.5.专题 与等腰三角形的性质与判定相关的证明类型1 证明线段或角的数量关系1.如图,△ABC 中,AB =AC ,D 是BC 的中点,E ,F 分别是AB ,AC 上的点,且AE =AF ,求证:DE =DF.证明:连接AD.∵AB =AC ,D 是BC 的中点, ∴∠EAD =∠FAD. 在△AED 和△AFD 中,⎩⎨⎧AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△AED ≌△AFD(SAS ). ∴DE =DF.2.已知,如图,△ABC 中,AB =AC ,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 和BE 交于H ,且BE =AE.求证:AH =2BD.证明:∵AD ⊥BC ,BE ⊥AC , ∴∠BEC =∠ADB =90°. ∴∠EBC =∠EAH. ∵BE =AE , ∴△AHE ≌△BCE. ∴AH =BC.∵AB =AC ,AD ⊥BC , ∴BC =2BD. ∴AH =2BD.3.如图,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 的中点,AE ⊥BD 于F ,交BC 于E ,求证:∠ADB =∠CDE.证明:过点C 作CG ⊥AC 交AE 的延长线于G ,则CG ∥AB ,∴∠BAF =∠G. 又∵AF ⊥BD ,AC ⊥CG ,∴∠BAF +∠ABF =90°,∠CAG +∠G =90°. ∴∠ABF =∠CAG. 在△ABD 和△CAG 中,⎩⎨⎧∠ABF =∠CAG ,AB =AC ,∠BAD =∠ACG =90°,∴△ABD ≌△CAG(ASA ). ∴AD =CG ,∠ADB =∠G. 又∵D 为AC 中点,∴AD =CD. ∴CD =CG.∵AB =AC ,∴∠ABC =∠ACB. 又∵AB ∥CG ,∴∠ABC =∠GCE. ∴∠ACB =∠GCE. ∴△CDE ≌△CGE(SAS ). ∴∠CDE =∠G. ∴∠ADB =∠CDE.4.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.证明:延长CB至E,使BE=BA,则∠BAE=∠E.又∵∠ABC=2∠C=2∠E,∴∠E=∠C.∴AE=AC.∵AD平分∠BAC,∴∠BAD=∠DAC.∵∠BAE=∠E,∠E=∠C,∴∠BAE=∠C.又∵∠EAD=∠BAE+∠BAD,∠EDA=∠C+∠DAC,∴∠EAD=∠EDA.∴AE=DE.∴AC=DE=BE+BD=AB+BD.类型2证明线段的位置关系5.如图,点C是线段AB上任意一点(点C与点A,B不重合),分别以AC,BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N,连接MN.求证:(1)△ACM≌△DCN;(2)MN∥AB.证明:(1)∵△ACD和△BCE都是等边三角形,∴AC=DC,BC=EC,∠ACD=∠BCE=60°.∵∠ACD+∠DCE+∠ECB=180°,∴∠DCE =60°.∴∠ACE =∠DCB =120°. 在△ACE 和△DCB 中,⎩⎨⎧AC =DC ,∠ACE =∠DCB ,CE =CB ,∴△ACE ≌△DCB(SAS ). ∴∠EAC =∠BDC. 在△ACM 和△DCN 中,⎩⎨⎧∠MAC =∠NDC ,AC =DC ,∠ACM =∠DCN =60°,∴△ACM ≌△DCN(ASA ). (2)由(1)知△ACM ≌△DCN , ∴CM =CN.又∵∠MCN =60°,∴△CNM 为等边三角形,∠NMC =60°. ∴∠NMC =∠ACM =60°. ∴MN ∥AB.6.如图,在△ABC 中,AB =AC ,点D ,E ,F 分别在边BC ,AB ,AC 上,且BD =CF ,BE =CD ,G 是EF 的中点,求证:DG ⊥EF.证明:连接ED ,FD.∵AB =AC , ∴∠B =∠C.在△BDE 和△CFD 中,⎩⎨⎧BD =CF ,∠B =∠C ,BE =CD ,∴△BDE ≌△CFD(SAS ). ∴DE =DF.又∵G 是EF 的中点, ∴DG ⊥EF.类型3 判断三角形的形状7.已知:如图,OA 平分∠BAC ,∠1=∠2.求证:△ABC 是等腰三角形.证明:过点O 作OD ⊥AB 于D ,OE ⊥AC 于E ,则△BOD 和△COE 都是直角三角形. ∵OA 平分∠BAC ,OD ⊥AB ,OE ⊥AC , ∴OD =OE. ∵∠1=∠2, ∴OB =OC.∴Rt △BOD ≌Rt △COE(HL ). ∴∠ABO =∠ACO. ∴∠ABC =∠ACB. ∴AB =AC.∴△ABC 是等腰三角形.8.已知△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点.(1)如图1,E ,F 分别是AB ,AC 上的点,且BE =AF ,试判断△DEF 的形状,并说明理由; (2)如图2,若E ,F 分别为AB ,CA 的延长线上的点,仍有BE =AF.请判断△DEF 是否仍具有(1)中的形状,并说明理由.解:(1)△DEF为等腰直角三角形.理由:连接AD,易证△BDE≌△ADF,∴DE=DF,∠BDE=∠ADF.又∵∠BAC=90°,AB=AC,D为BC的中点,∴AD⊥BC.∴∠ADB=90°.∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠ADB=90°. ∴△DEF为等腰直角三角形.(2)是,理由略.专题运用分类讨论求解等腰三角形相关的多解问题类型1针对腰长和底边长进行分类方法归纳:在解答已知等腰三角形边长的问题时,当题目中的条件没有指明已知的这条边是腰长还是底边长时,就要分类讨论,按腰和底边两种情况分类.若涉及边的长度,应运用三角形的三边关系进行辨别取舍.1.(武汉中考)平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是(A)A.5 B.6 C.7 D.82.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有(B)A.7个B.6个C.5个D.4个3.若实数x,y满足|x-5|+y-10=0,则以x,y的值为边长的等腰三角形的周长为25.类型2针对顶角和底角进行分类方法归纳:对于等腰三角形,只要已知它的一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,就要分两种情况来讨论.在分类时要注意:三角形的内角和等于180°;等腰三角形中至少有两个角相等.4.等腰三角形有一个角为52°,它的一条腰上的高与底边的夹角为多少度?解:①若已知的这个角为顶角,则底角的度数为(180°-52°)÷2=64°,故一腰上的高与底边的夹角为26°;②若已知的这个角为底角,则一腰上的高与底边的夹角为38°. 故所求的一腰上的高与底边的夹角为26°或38°.5.如果等腰三角形中的一个角是另一个角度数的一半,求该等腰三角形各内角的度数.解:设∠A ,∠B ,∠C 是该等腰三角形的三个内角,且∠A =12∠B.设∠A =x °,则∠B =2x °.①若∠B 是顶角,则∠A ,∠C 是底角,于是有∠C =∠A =x °. ∵∠A +∠B +∠C =180°,∴x +2x +x =180. 解得x =45,故∠A =∠C =45°,∠B =90°; ②若∠B 是底角,∵∠A ≠∠B , ∴∠A 是顶角,∠C =∠B =2x °.∵∠A +∠B +∠C =180°,∴x +2x +2x =180. 解得x =36,故∠A =36°,∠B =∠C =72°.综上所述,等腰三角形的各内角分别为45°、45°、90°或36°、72°、72°.类型3 针对锐角、直角和钝角三角形进行分类方法归纳:根据等腰三角形顶角的大小可以将其分为锐角、直角或钝角三角形.不同的三角形其高、中线、垂直平分线的交点位置均不同,比如锐角三角形腰上的高的交点在这个三角形的内部;直角三角形腰上的高的交点为两直角边的交点;钝角三角形腰上的高的交点在这个三角形的外部,因此在解答时需要分类讨论.6.已知△ABC 中,AB =AC ,AB 的垂直平分线与AC 所在的直线相交成50°的角,求底角的度数.解:由题意可判断该三角形不可能是直角三角形,可能是锐角三角形或钝角三角形,故分两种情况讨论:①如图1,垂直平分线DE 与腰AC 相交,且∠AED =50°,则∠A =40°,所以∠B =∠C =70°;②如图2,垂直平分线DE 与腰AC 的反向延长线相交,且∠AED =50°,则∠EAD =40°,∠BAC =140°,所以∠B =∠C =20°.综上可知,等腰三角形的底角为70°或20°.7.一个等腰三角形一边上的高等于另一边的一半,则等腰三角形底角的度数是多少?解:设∠A 为顶角,则∠ABC 、∠ACB 为底角. (1)若∠A 为锐角,如图1,作BD ⊥AC 于点D , 根据题意有BD =12AB ,∠BDA =90°,∴∠A =30°,∠ABC =∠ACB =75°;(2)若∠A 为直角,根据题意“等腰三角形一边上的高等于另一边的一半”,这种情况无解; (3)若∠A 为钝角,有三种情况:①如图2,作AD ⊥BC 于点D , 根据题意有AD =12AB ,∠ADB =90°,∴∠ABC =∠ACB =30°;②如图3,作BD ⊥CA 的延长线于点D , 根据题意有BD =12BC ,∠ADB =90°,∴∠ABC =∠ACB =30°;③如图4,作BD ⊥CA 的延长线于点D , 根据题意有BD =12AB ,∠ADB =90°,∴∠BAD =30°,∠ABC =∠ACB =15°.综上所述,等腰三角形底角的度数是75°、30°或15°.8.AC 为等腰△ABD 的腰BD 上的高,且∠CAB =60°.求这个三角形各内角的度数.解:①如图1,高AC 在△ABD 的内部, 因为∠CAB =60°,∠ACB =90°, 所以∠B =30°.因为BA =BD ,所以∠BAD =∠D =75°; ②如图2,高AC 在△ABD 的外部, 因为∠CAB =60°,∠ACB =90°, 所以∠ABC =30°. 所以∠ABD =150°.因为BA =BD ,所以∠BAD =∠D =15°; ③如图3,高AC 在△ABD 的外部, 因为∠CAB =60°,∠ACB =90°, 所以∠B =30°.因为DA=DB,所以∠BAD=∠B=30°.所以∠ADB=120°.综上所述,这个三角形各内角的度数分别为30°,75°,75°或150°,15°,15°或120°,30°,30°.复习轴对称01基础题知识点1轴对称与轴对称图形1.(赤峰中考)下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是①②③④(填序号).2.图中有阴影的三角形与哪些三角形成轴对称?整个图形是轴对称图形吗?它共有几条对称轴?解:1和3,是,两条.知识点2线段的垂直平分线3.(遂宁中考)如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7 cm,则BC的长为(C)A.1 cmB.2 cmC.3 cmD.4 cm知识点3画轴对称图形4.请作出图中四边形ABCD关于直线a的轴对称图形,要求:不写作法,但必须保留作图痕迹.解:如图所示:四边形A′B′C′D′即为所求.知识点4等腰三角形5.(荆门中考改编)如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知BD=4,则BC的长为(C)A.5B.6C.8D.106.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的平分线,则图中的等腰三角形有(A)A.5个B.4个C.3个D.2个知识点5等边三角形7.如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为(D) A.15°B.30°C.45°D.60°8.(义乌中考)由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是18cm.知识点6含30°角的直角三角形的性质9.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=3.10.如图,△ABC是等边三角形,AD∥BC,CD⊥AD,若AD=2 cm,则△ABC的周长为12cm.知识点7最短路径问题11.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是(B)A.3B.4C.5D.602中档题12.如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为(A)A.15°B.17.5°C.20°D.22.5°13.(雅安中考)如图所示,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,若DE=2,则EC=8.14.如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).(1)在图中作出△ABC关于y轴对称的△A1B1C1;(2)△A1B1C1的面积为4.5.解:如图所示:△A1B1C1即为所求.15.如图所示,MP和NQ分别垂直平分AB和AC.(1)若△APQ的周长为12,求BC的长;(2)∠BAC=105°,求∠PAQ的度数.解:(1)∵MP和NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ.∴△APQ的周长为AP+PQ+AQ=BP+PQ+CQ=BC.∵△APQ的周长为12,∴BC =12.(2)∵AP =BP ,AQ =CQ ,∴∠B =∠BAP ,∠C =∠CAQ.∵∠BAC =105°,∴∠BAP +∠CAQ =∠B +∠C =180°-∠BAC =180°-105°=75°.∴∠PAQ =∠BAC -(∠BAP +∠CAQ)=105°-75°=30°.03 综合题16.如图,在等边△ABC 中,点E 为边AB 上任意一点,点D 在边CB 的延长线上,且ED =EC.(1)当点E 为AB 的中点时(如图1),则有AE =DB(填“>”“<”或“=”);(2)猜想AE 与DB 的数量关系,并证明你的猜想.解:当点E 为AB 上任意一点时,AE 与DB 的大小关系不会改变.理由如下:过E 作EF ∥BC 交AC 于F ,∵△ABC 是等边三角形,∴∠ABC =∠ACB =∠A =60°,AB =AC =BC.∴∠AEF =∠ABC =60°,∠AFE =∠ACB =60°,即∠AEF =∠AFE =∠A =60°.∴△AEF 是等边三角形.∴AE =EF =AF.∵∠ABC =∠ACB =∠AFE =60°,∴∠DBE =∠EFC =120°,∠D +∠BED =∠FCE +∠ECD =60°.∵DE =EC ,∴∠D =∠ECD.∴∠BED =∠ECF.在△DEB 和△ECF 中,⎩⎨⎧∠DEB =∠ECF ,∠DBE =∠EFC ,DE =EC ,∴△DEB ≌△ECF(AAS ).∴BD =EF =AE ,即AE =BD.。
第13章 轴对称 几何综合题专题练习题(教师版)

人教版八年级数学上册第十三章 轴对称 几何综合题专题练习题专题(1) 等腰三角形的性质与全等三角形综合1.如图,点D ,E 在△ABC 的边BC 上,AB =AC ,BD =CE .求证:AD =AE .证明:∵AB =AC , ∴∠B =∠C .在△ABD 和△ACE 中, ⎩⎪⎨⎪⎧AB =AC ,∠B =∠C ,BD =CE ,∴△ABD ≌△ACE (SAS ). ∴AD =AE .2.如图,在等腰△ABC 中,AB =AC ,CD ,BE 是两腰上的中线,求证:CD =BE .证明:∵CD ,BE 是两腰上的中线, ∴AD =AE .在△ADC 和△AEB 中, ⎩⎪⎨⎪⎧AD =AE ,∠A =∠A ,AC =AB ,∴△ADC ≌△AEB (SAS ). ∴CD =BE .3.如图,在△ABC 中,AB =AC ,AD ⊥BC ,垂足为D ,E ,F 分别是AB ,AC 的延长线上的点,且BE =CF .求证:DE =DF .证明:∵AB =AC ,AD ⊥BC , ∴∠DAE =∠DAF . 又∵BE =CF , ∴AB +BE =AC +CF . 即AE =AF .在△ADE 和△ADF 中,⎩⎪⎨⎪⎧AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△ADE ≌△ADF (SAS ). ∴DE =DF .4.已知:如图,△ABC 是等腰三角形,AB =AC ,且∠ABO =∠ACO .求证: (1)∠1=∠2; (2)OA ⊥BC .证明:(1)∵AB =AC , ∴∠ABC =∠ACB .∵∠ABO =∠ACO ,∴∠1=∠2. (2)∵∠1=∠2, ∴OB =OC .在△ABO 和△ACO 中,⎩⎪⎨⎪⎧AB =AC ,∠ABO =∠ACO ,OB =OC ,∴△ABO ≌△ACO (SAS ). ∴∠BAO =∠CAO . ∴AO 平分∠BAC . ∵△ABC 是等腰三角形, ∴OA ⊥BC .5.如图,在△ABC 中,AB =AC ,D ,E ,F 分别为边BC ,AB ,AC 上的点,且BE =CD ,CF =BD .(1)试说明:△BDE 与△CFD 全等的理由; (2)若∠A =40°,求∠EDF 的度数.解:(1)∵AB =AC ,∴∠B =∠C . 在△BDE 和△CFD 中,⎩⎪⎨⎪⎧BE =CD ,∠B =∠C ,BD =CF ,∴△BDE ≌△CFD (SAS ).(2)∵∠A =40°,∴∠B =∠C =70°. ∵△BDE ≌△CFD , ∴∠BED =∠CDF . ∵∠EDC =∠B +∠BED , ∴∠EDF =∠B =70°.6.如图,在△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,EF =BE . (1)△AEF 与△CEB 全等吗?请说明理由; (2)说明AF =2BD 的理由.解:(1)全等. 理由:∵AD ⊥BC , ∴∠B +∠BAD =90°. ∵CE ⊥AB ,∴∠B +∠BCE =90°,∠AEF =∠BEC =90°. ∴∠EAF =∠ECB ,∠AEF =∠BEC . 又∵BE =EF ,∴△AEF ≌△CEB (AAS ).(2)∵△AEF ≌△CEB ,∴AF =BC . ∵AB =AC ,AD ⊥BC , ∴BC =2BD . ∴AF =2CD .7.已知,如图,在△ABC 中,∠B =∠C ,D 是BC 上一点,点E ,F 分别在AB ,AC 上,BD =CF ,CD =BE ,G 为EF 的中点,问: (1)△BDE 与△CFD 全等吗?请说明理由; (2)判断DG 与EF 的位置关系,并说明理由.解:(1)△BDE 与△CFD 全等, 理由:∵AB =AC ,∴∠B =∠C . 在△BDE 和△CFD 中, ⎩⎪⎨⎪⎧BE =CD ,∠B =∠C ,BD =CF ,∴△BDE ≌△CFD (SAS ). (2)DG ⊥EF .理由: ∵△BDE ≌△CFD , ∴DE =DF .∵G 是EF 的中点, ∴DG ⊥EF .8.在等腰△OAB 和等腰△OCD 中,OA =OB ,OC =OD ,连接AC ,BD 交于点M . (1)如图1,若∠AOB =∠COD =40°: ①AC 与BD 的数量关系为AC =BD ; ②∠AMB 的度数为40°.(2)如图2,若∠AOB =∠COD =90°:①判断AC 与BD 之间存在怎样的数量关系?并说明理由; ②求∠AMB 的度数.解:(2)①AC =BD ,理由如下: ∵∠AOB =∠COD =90°,∴∠AOB +∠AOD =∠COD +∠AOD . ∴∠BOD =∠AOC ,在△BOD 和△AOC 中,⎩⎪⎨⎪⎧OB =OA ,∠BOD =∠AOC ,OD =OC ,∴△BOD ≌△AOC (SAS ). ∴BD =AC .②设OA ,BD 相交于点E .∵△BOD≌△AOC,∴∠OBD=∠OAC.又∵∠AEM=∠BEO,∴∠AMB=∠AOB=90°.专题(2)角的平分线与线段的垂直平分线1.如图,已知在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.求证:∠BAF=∠ACF.证明:∵AD是∠BAC的平分线,∴∠BAD=∠DAC.∵FE是AD的垂直平分线,∴F A=FD.∴∠F AD=∠FDA.∵∠BAF=∠F AD+∠BAD,∠ACF=∠FDA+∠DAC,∴∠BAF=∠ACF.2.如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线.求证:点D在线段AB的垂直平分线上.证明:作DE ⊥AB 于点E ,则∠AED =90°. ∵∠C =90°, ∴∠AED =∠C .∵AD 为∠BAC 的平分线, ∴∠EAD =∠CAD . 在△AED 和△ACD 中, ⎩⎪⎨⎪⎧∠AED =∠C ,∠EAD =∠CAD ,AD =AD ,∴△AED ≌△ACD (AAS ).∴AE =AC . ∵AB =2AC ,∴AB =2AE .∴BE =AE . 又∵DE ⊥AB ,∴DE 是线段AB 的垂直平分线, 即点D 在线段AB 的垂直平分线上.3.如图,在△ABC 中,∠A =60°,点D 是BC 边的中点,DE ⊥BC ,∠ABC 的平分线BF 交DE 于△ABC 内一点P ,连接PC . (1)若∠ACP =24°,求∠ABP 的度数;(2)若∠ACP =m °,∠ABP =n °,请直接写出m ,n 满足的关系式m +3n =120.解:∵点D是BC边的中点,DE⊥BC,∴PB=PC.∴∠PBC=∠PCB.∵BP平分∠ABC,∴∠PBC=∠ABP.∴∠PBC=∠PCB=∠ABP.∵∠A=60°,∠ACP=24°,∴∠PBC+∠PCB+∠ABP=180°-60°-24°.∴3∠ABP=96°.∴∠ABP=32°.4.如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P,PD⊥AB于点D,PE⊥AC于点E.求证:BD=CE.证明:连接BP,CP.∵点P在BC的垂直平分线上,∴BP=CP.∵AP是∠DAC的平分线,PD ⊥AB ,PE ⊥AC , ∴DP =EP .在Rt △BDP 和Rt △CEP 中,⎩⎪⎨⎪⎧BP =CP ,DP =EP , ∴Rt △BDP ≌Rt △CEP (HL ). ∴BD =CE .专题(3) 特殊三角形中常见辅助线的作法1.如图,在△ABC 中,AB =AC ,AE ⊥BE 于点E ,且BE =12BC .若∠EAB =20°,则∠BAC =40°.2.如图,在△ABC 中,AB =AC ,∠BAC =120°,AC 的垂直平分线交BC 于点D ,交AC 于点E ,DE =2,则BC 的长为12.3.如图,四边形ABCD 中,AD =4,BC =1,∠A =30°,∠B =90°,∠ADC =120°,则CD =2.4.如图,∠AOE =∠BOE =15°,EF ∥OB ,EC ⊥OB 于点C .若EC =1,则OF =2.5.如图,在△ABC 中,AC =2AB ,AD 平分∠BAC 交BC 于点D ,E 是AD 上一点,且EA =EC ,求证:EB ⊥AB .证明:作EF ⊥AC 于点F .∵EA =EC ,∴AF =FC =12AC . ∵AC =2AB ,∴AF =AB .∵AD 平分∠BAC ,∴∠BAD =∠CAD .在△ABE 和△AFE 中,⎩⎪⎨⎪⎧AB =AF ,∠BAE =∠FAE ,AE =AE ,∴△ABE ≌△AFE (SAS ).∴∠ABE =∠AFE =90°.∴EB ⊥AB .6.如图,在Rt △ABC 中,AC =BC ,∠ACB =90°,点O 为AB 的中点,OE ⊥OF 分别交AC ,BC 于点E ,F .求证:OE =OF .证明:连接OC .∵AC =BC ,∠ACB =90°,点O 为AB 的中点,∴∠B =∠ACO =∠BCO =45°,CO ⊥AB .∴OC =OB ,∠COB =90°.又∵∠EOF =90°,∴∠EOC =∠FOB .在△EOC 和△FOB 中,⎩⎪⎨⎪⎧∠EOC =∠FOB ,OC =OB ,∠OCE =∠OBF ,∴△EOC ≌△FOB (ASA ).∴OE =OF .7.如图,在△ABC 中,AB =AC ,∠BAC =120°,D 为BC 的中点,DE ⊥AC 于点E ,AE =2,求CE 的长.解:连接AD .∵AB =AC ,∠BAC =120°,D 为BC 的中点,∴∠DAC =12∠BAC =60°,∠ADC =90°. ∵DE ⊥AC ,∴∠ADE =90°-60°=30°.∴AD =2AE =4.又∵∠C =90°-∠DAC =30°,∴AC =2AD =8.∴CE =AC -AE =8-2=6.8.如图,在△ABC 中,BD 是AC 边上的中线,BD ⊥BC 于点B ,∠ABD =30°,求证:AB =2BC .证明:作AM ⊥BD ,交BD 延长线于点M . ∵在Rt △ABM 中,∠ABD =30°,∴AB =2AM .∵BD 为AC 边上的中线,∴AD =CD .∵DB ⊥BC ,AM ⊥BD ,∴∠DBC =∠M =90°.在△BCD 和△MAD 中,⎩⎪⎨⎪⎧∠DBC =∠M ,∠BDC =∠MDA ,CD =AD ,∴△BCD ≌△MAD (AAS ).∴BC =AM .∴AB =2BC .。
全等和轴对称解答答案

全等和轴对称解答练习答案和解析【答案】1.(1)证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE,∵在△ABF和△DCE中,,∴△ABF≌△DCE(AAS);(2)∵△ABF≌△DCE,∴ AFB=DEC,∴OE=OF.2.解:(1)过C作CM⊥x轴于M点,如图1,∵CM⊥OA,AC⊥AB,∴ MAC+OAB=90°, OAB+OBA=90°则 MAC=OBA°在△MAC和△OBA中则△MAC≌△OBA(AAS)则CM=OA=2,MA=OB=4,则点C的坐标为(-6,-2);(2)过D作DQ⊥OP于Q点,如图2,则OP-DE=PQ,APO+QPD=90°APO+OAP=90°,则 QPD=OAP,°在△AOP和△PDQ中则△AOP≌△PDQ(AAS)∴OP-DE=PQ=OA=2;(3)结论②是正确的,m+n=-4,如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,则FS=FT=2, FHS=HFT=FGT,°在△FSH和△FTG中则△FSH≌△FTG(AAS)则GT=HS,又∵G(0,m),H(n,0),点F坐标为(-2,-2),∴OT═OS=2,OG=|m|=-m,OH=n,∴GT=OG-OT=-m-2,HS=OH+OS=n+2,则-2-m=n+2,则m+n=-4.3.证明:∵ 1=2,∴ 1+COD=2+COD,即 AOD=COB,在△AOD和△COB中,,∴△AOD≌△COB(AAS),∴AD=CB.4.解:(1)证明:∵PQ⊥AP,∴ ABP=90°∴ APB+QPC=90°,∵AB⊥BC于点B,∴ A+APB=90°,∴ A=QPC;(2)当P运动到离C处距离为2时,PA=PQ,证明:当PC=2时,PC=AB,在△ABP与△PCQ中,∵,∴△ABP≌△PCQ(ASA),∴PA=PQ;同理,BP=7时,PC=2也符合,所以,点P运动到与点C距离为2时,PA=PQ.5.证明:∵AB∥CD,∴ DCE=B,在△ABC和△ECD中,∴△ABC≌△ECD(SAS).6.解:(1)在R t△ABE和R t△CBF中,∴R t△ABE≌R t△CBF(HL),∴BE=BF;(2)∵ ABC=90°,AB=CB,∴ BAC=BCA=45°,又∵ CAE=60°,∴ BAE=15°,由(1)R t△ABE≌R t△CBF,∴ BAE=BCF=15°,∴ ACF=BCA-BCF=45°-15°=30°.7.△ACD≌△EBD;1<x<48.解:∵BD平分 ABC, A=90°,DE⊥BC,∴DE=AD=6cm,∴△BDC的面积=×BC×DE=×15×6=45cm2.9.解:在△ABE和△ACD中,,∴△ABE≌△ACD(ASA),∴AE=AD,∵AC=AB,∴AC-AE=AB-AD,即BD=EC,在△BOD和△COE中,,∴△BOD≌△COE(AAS),∴OB=OC.10.证明:(1)∵ ACB=90°,AC=BC,CG平分 ACB,∴ CAF=CBA=45°, BCG=ACG=45°,∴ BCG=CAF=45°∵ CBG=ACF,AC=BC∴△BCG≌△CAF,∴AF=CG;(2)连接AG,如图1所示:在△ACG与△BCG中,,∴△ACG≌△BCG,∴AG=BG,∴ GBA=GAB,∵AD⊥AB∴ D=90°-GBA=90°-GAB=GAD,∴AG=DG.∵由(1)BG=CF,∴DG=CF;(3)如图2,延长CG交AB于H,∵CG平分 ACB,AC=BC,∴CH⊥AB,CH平分AB,∵AD⊥AB,∴ D=EGC,在△ADE与△CGE中,,∴△ADE≌△CGE(AAS),∴DE=GE,即DG=2DE,∵AD∥CG,CH平分AB,∴DG=BG,∵△AFC≌△CBG,∴CF=BG,∴CF=2DE.11.证明:∵ BAE=BCE=90°,∴ B+AEC=180°,而 DEC+AEC=180°,∴ B=DEC,在△ABC和△DEC中,,∴△ABC≌△DEC(SAS).12.证明:∵ DAB=EAC,∴ DAB+BAC=EAC+BAC,即 DAC=AEB,在△ACD与△ABE中,,∴△ACD≌△ABE,∴ D=E,在△ADM与△AEN中,,∴△ADM≌△AEN,∴AM=AN.13.解:(1)如图1,过E作EF⊥AC于F,∵ B=90°,AE平分BAC,∴EF=BE,∵E是BD的中点,∴BE=DE,∴EF=DE,∵ D=90°,∴CE平分 ACD;(2)如图2,过E作EF⊥AC于F,∵AM∥CN,BD⊥AM,∴BD⊥CD,∵AE平分 BAC,∴BE=EF,在R t△AEF与R t△ABE中,,∴R t△AEF≌R t△ABE,同理CF=CD,∵AC=AF+CF,∴AC=AB+CD;(3)成立,如图3,在AC上截取AF=AB,∵AE平分 BAC,∴ BAE=FAE,在△ABE与△AFE中,,∴△ABE≌△AFE,∴ AFE=ABE,∵AM∥CN,∴ ABE+CDE=180°,∵ AFE+EFC=180°,∴ CFE=CDE,∵CE平分 ACD,∴ FCE=DCE,在△CEF与△CDE中,,∴△CEF≌△CDE,∴CF=CD,∵AC=AF+CF,∴AC=AB+CD.14.解:设 A=x,则∵AD=DE,∴ AED=A=x;∵DE=BE,∴ EDB=EBD=x;又∵BD=BC,∴ C=BDC=A+EBD=1.5x;∵AB=AC,∴ ABC=C=1.5x;在△ABC中, A+ABC+ACB=4x=180°,∴ A=x=45°.故答案为:45°.15.解:∵DE=EA,∴ ADE=A,∴ BED=A+ADE=2A,∵BD=DE,∴ BED=EBD=2A,∴ BDC=A+EBD=3A,∵BC=BD,∴ BDC=C,∵AB=AC,∴ ABC=C=3A,在△ABC中, A+ABC+C=A+3A+3A=180°,解得 A=°.16.解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,所以,AC•BD=AB•PF+AC•PE,∵AB=AC,∴BD=PE+PF;(2)连接AP,则S△ABC=S△ABP-S△ACP,所以,AB•CD=AB•PF-AC•PE,∵AB=AC,∴CD=PF-PE.17.15°;20°; BAD=2EDC(或 EDC=BAD);6cm18.=;280°;300°;60°; BDA+CEA=2 A19.解:如图所示.【解析】1.(1)利用等式的性质可以证得BF=CE,则依据AAS即可证得三角形全等;(2)依据全等三角形的性质,即可证得 AFB=DEC,然后依据等角对等边从而证得.本题考查了全等三角形的判定与性质,以及等腰三角形的判定定理:等角对等边,正确证明两个三角形全等是关键.2.(1)要求点C的坐标,则求C的横坐标与纵坐标,因为AC=AB,则作CM⊥x轴,即求CM 和AM的值,容易得△MAC≌△OBA,根据已知即可求得C点的值;(2)求OP-DE的值则将其放在同一直线上,过D作DQ⊥OP于Q点,即是求PQ的值,由图易求得△AOP≌△PDQ(AAS),即可求得PQ的长;(3)利用(2)的结论,可知m+n为定长是正确的,过F分别作x轴和y轴的垂线,类似(2),即可求得m+n的值.本题考查了三角形全等的判定和性质;熟记三角形全等的求法,尤其是R t△,数形结合是重要的解题方法,同学们一定要学会应用.3.证出 AOD=COB,由AAS证明△AOD≌△COB,得出对应边相等即可.本题考查了全等三角形的判定与性质、等式的性质;证明三角形全等是解决问题的关键.4.(1)根据直角三角形的两内角互余以及 A+APB=90°,根据同角的余角相等,即可证得;(2)P运动到离C处距离为2时,PA=PQ,此时易证△ABP≌△PCQ,即可证得.本题考查了全等三角形的判定与性质以及余角的性质:同角的余角相等,正确证明A=QPC是关键.5.利用平行线的性质可得 DCE=B,再利用SAS判定△ABC≌△ECD即可.本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.6.(1)利用HL定理得出R t△ABE≌R t△CBF即可得出答案;(2)利用三角形内角和定理以及等腰三角形的性质得出即可.此题主要考查了全等三角形的判定与性质以及三角形内角和定理等知识,根据已知得出R t△ABE≌R t△CBF是解题关键.7. (1)证明:在△ADC与△EDB中,,∴△ADC≌△EDB;故答案为:△ADC≌△EDB;(2)解:如图2,延长EP至点Q,使PQ=PE,连接FQ,在△PDE与△PQF中,,∴△PEP≌△QFP,∴FQ=DE=3,在△EFQ中,EF-FQ<QE<EF+FQ,即5-3<2x<5+3,∴x的取值范围是1<x<4;故答案为:1<x<4;(3)证明:如图3,延长AD到M,使MD=AD,连接BM,∴AM=2AD,∵AD是△ABC的中线,∴BD=CD,在△BMD与△CAD中,,∴△BMD≌△CAD,∴BM=CA, M=CAD,∴ BAC=BAM+CAD=BAM+M,∵ ACB=Q+CAQ,AB=BC,∵ ACQ=180°-( Q+CAQ), MBA=180°-( BAM+M),∴ ACQ=MBA,∵QC=BC,∴QC=AB,在△ACQ与△MBA中,,∴△ACQ≌△MBA,∴AQ=AM=2AD.(1)根据全等三角形的判定即可得到结论;(2)延长EP至点Q,使PQ=PE,连接FQ,根据全等三角形的性质得到FQ=DE=3,根据三角形的三边关系即可得到结论;(3)延长AD到M,使MD=AD,连接BM,于是得到AM=2AD由已知条件得到BD=CD,根据全等三角形的性质得到BM=CA, M=CAD,于是得到BAC=BAM+CAD=BAM+M,推出△ACQ≌△MBA,根据全等三角形的性质即可得到结论.本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.8.根据角平分线的性质得到DE=AD=6cm,根据三角形的面积公式计算即可.本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.9.易证△ABE≌△ACD,可得AE=AD,再根据AB=AC,可得BD=EC,即可证明△BOD≌△COE,即可解题.本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BOD≌△COE是解题的关键.10.(1)要证AF=CG,只需证明△AFC≌△CBG即可;(2)连接AG,证明△ACG≌△BCG,得出AG=BG,再证出 D=GAD,得出AG=DG,从而证出DG=CF;(3)延长CG交AB于H,则CH⊥AB,H平分AB,继而证得CH∥AD,得出DG=BG和△ADE 与△CGE全等,从而证得CF=2DE.本题考查了三角形全等的判定和性质、等腰三角形的性质、平行线的判定及性质,三角形全等是解本题的关键.11.先根据四边形的内角和定理得到 B+AEC=180°,而 DEC+AEC=180°,则B=DEC,然后根据“SAS”可得到△ABC≌△DEC.本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.12.可先证明△ACD与△ABE全等,得出 D=E,进而证得△ADM≌△AEN,结论可得.本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.13.(1)过点E作EF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;(2)如图2,过E作EF⊥AC于F,根据平行线的性质得到BD⊥CD,由角平分线的性质得到BE=EF,证得R t△AEF≌R t△ABE,根据全等三角形到现在得到AF=AB,同理CF=CD,等量代换得到结论;(3)成立,如图3,在AC上截取AF=AB,根据角平分线的定义得到 BAE=FAE,推出△ABE≌△AFE,根据全等三角形的性质得到 AFE=ABE,根据角平行线的性质得到ABE+CDE=180°,求得 CFE=CDE,证得△CEF≌△CDE,根据全等三角形的性质即可得到结论.本题考查了全等三角形的判定和性质,角平分线的性质,角平分线的定义,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.14.题中给出了多组相等的边,而让求角的度数,这实际上就是由边相等关系转化为角相等关系的题,可以利用方程来解决.本题主要考查了等腰三角形的性质,这类题一般把底角和顶角的数量关系转化为方程来求解.15.根据等边对等角可得 ADE=A,再根据三角形的一个外角等于与它不相邻的两个内角的和可得 BED=A+ADE=2A,根据等边对等角可得 BED=EBD,再利用三角形的一个外角等于与它不相邻的两个内角的和可得 BDC=A+EBD=3A,再次利用等边对等角可得 BDC=C, ABC=C,然后利用三角形的内角和等于180°列出方程求解即可.本题考查了三角形的内角和定理,等边对等角和三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.16.(1)连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解;(2)连接AP,根据S△ABC=S△ABP-S△ACP列式整理即可得解.本题考查了等腰三角形的性质,利用三角形的面积列出等式是解题的关键.17. 解:(1)∵在△ABC中,AB=AC,AD是BC上的高,∴ BAD=CAD,∵ BAD=30°,∴ BAD=CAD=30°,∵AD=AE,∴ ADE=AED=75°,∴ EDC=15°.(2)∵在△ABC中,AB=AC,AD是BC上的高,∴ BAD=CAD,∵ BAD=40°,∴ BAD=CAD=40°,∵AD=AE,∴ ADE=AED=70°,∴ EDC=20°.(3) BAD=2EDC(或 EDC=BAD)(4)∵ BAD=30°,AD是BC上的高,BD=3cm,∴AB=AC=6cm.故答案为:15°,20°, BAD=2EDC(或 EDC=BAD);6cm.(1)等腰三角形三线合一,所以 DAE=30°,又因为AD=AE,所以 ADE=AED=75°,所以 EDC=15°.(2)同理,易证 ADE=70°,所以 EDC=20°.(3)通过(1)(2)题的结论可知, BAD=2EDC(或 EDC=BAD).(4)根据含30°角的直角三角形所对的直角边是斜边的一半可得AB的长,进一步得到AC 的长.本题考查了等腰三角形三线合一这一性质,即等腰三角形底边上中线、高线以及顶角的平分线三线合一.得到角之间的关系是正确解答本题的关键.18. 解:(1)根据三角形内角是180°可知: 1+2=180°-A, B+C=180°- A ∴ 1+2=B+ C(2)∵ 1+2+BDE+CED=B+C+BDE+CED=360°∴ 1+2=B+ C当 A=40°时, B+C+1+2=140×2=280°(3)如果 A=30°,则x+y=360°-( B+C+1+2)=360°-300°=60°所以 BDA+CEA与 A的关系为: BDA+CEA=2 A根据三角形内角是180度可得出, 1+2=B+C,从而求出当 A=40°时,B+C+1+2=140×2=280°,有以上计算可归纳出一般规律:BDA+CEA=2A.本题考查图形的翻折变换和三角形,四边形内角和定理,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.19.作点P关于直线OA的对称点P′,作点Q关于直线OB的对称点B′,连接P′B′分别交OA,OB于点M、N,则点MN即为所求.本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.。
三角形全等和轴对称试题

三角形全等和轴对称竞赛试题一、选择题(每小题3分共39分)1.下列平面图形中,不是轴对称图形的是()2.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有()A.1个B.2个C.3个D.4个3. △ABC中, AC=5, 中线AD=7, 则AB边的取值范围是()A. 1<AB<29B. 4<AB<24C. 5<AB<19D. 9<AB<194. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC 交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,则斜边AB的长为()A.8 cm B.10 cm C.12 cm D.20 cm5.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是()A.20° B.25° C.30° D.45°6.如图,ΔABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD,BE交于F,则∠AFB=()度A、126B、120C、116D、1107. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于D,DE=4cm,AD=6 cm,则BE的长是( )A.2cm B.1.5 cm C.1 cm D.3 cm8.如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC =54°,则∠E=()A.25°B.27°C.30°D.45°9. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO 等于()A.1︰1︰1 B.1︰2︰3 C.2︰3︰4 D.3︰4︰5BOC A 7题图8题图9题图10.如图:AB=AC=BD,则∠1和∠2的关系是( )A. ∠1=2∠2B. 2∠1+∠2=180°C. ∠1+3∠2=180°D. 3∠1-∠2=180° 11下列各式中,正确的是 ( )A .BC .y x y x y x y x -+=--+-D .y x yx y x y x +-=-+-12.三角形内有一点到三角形三个顶点的距离相等,则这点一定是三角形( )A.三条中线的交点B. 三条垂直平分线的交点C.三条高的交点D.三条角平分线的交点 13若分式6522+--x x x 的值为0,则x 的值为( )A 2B -2C 2或-2D 2或3二 填空题(每题3分 共12分) 14下列四个分式(1) 21227b a (2)22()a b b a-- (3)22x y x y ++ (4)22x y x y--中是最简分式的为15在平面直角坐标系xOy 中,已知A(2,-2),在y 轴确定点P ,使△AOP 为等腰三角形,则符合条件的点有 个16如图,△ABC 中,∠C =90°,AD 平分∠BAC ,AB =5,CD =2,则△ABD 的面积是______;yx yx y x y x +-=--+-yx yx y x y x ---=-+-17 ΔABC 是等腰三角形,分别以ΔABC 的腰为边,向外做等边三角形ΔADB 和等边ΔACE 。
初中数学轴对称全等综合练习(含答案)
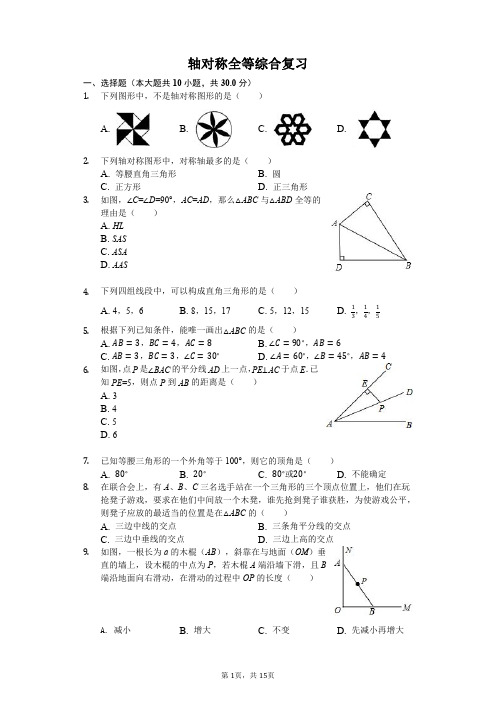
2 . 如图,一张长方形 ABCD 纸片中,∠A=∠B=∠C=∠D=90°, AD=BC=8,AB=CD=6.现将这张纸片折叠,使点 A 与点 C 重合,折痕交 AD 于点 E,交 BC 于点 F. 求:(1)AE 的长; (2)折痕 EF 的长.
27. 如图 1,△ABC 中,CD⊥AB 于 D,且 BD:AD:CD=2:3:4, (1)试说明△ABC 是等腰三角形; (2)已知 S△ABC=40cm2,如图 2,动点 M 从点 B 出发以每秒 1cm 的速度沿线段 BA 向点 A 运动,同时动点 N 从点 A 出发以相同速度沿线段 AC 向点 C 运动,当其中 一点到达终点时整个运动都停止.设点 M 运动的时间为 t(秒), ①若△DMN 的边与 BC 平行,求 t 的值; ②若点 E 是边 AC 的中点,问在点 M 运动的过程中,△MDE 能否成为等腰三角形? 若能,求出 t 的值;若不能,请说明理由.
第 页,共 15页
夹一边可确定三角形的形状,否则三角形则并不是唯一存在,可能有多种情况存在. 本题考查了全等三角形的判定方法,只有符合全等判定方法的条件画出的三角形才都是 一样的,也就是说是唯一的.本问题界定的是唯一三角形,要注意要求. 6.【答案】C 【解析】 解:如图,过点 P 作 PF⊥AB 于 F, ∵AD 是∠BAC 的平分线,PE⊥AC, ∴PF=PE=5, 即点 P 到 AB 的距离是 5. 故选:C. 过点 P 作 PF⊥AB 于 F,根据角平分线上的点到角的两边距离相 等可得 PF=PE. 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键. 7.【答案】C 【解析】 解:①若 100°是顶角的外角,则顶角=180°-100°=80°; ②若 100°是底角的外角,则底角=180°-100°=80°,那么顶角=180°-2×80°=20°. 故选:C. 此外角可能是顶角的外角,也可能是底角的外角,需要分情况考虑,再结合三角形的内 角和为 180°,可求出顶角的度数. 当外角不确定是底角的外角还是顶角的外角时,需分两种情况考虑,再根据三角形内角 和 180°、三角形外角的性质求解. 8.【答案】C 【解析】 解:∵三角形的三条垂直平分线的交点到三角形各顶点的距离相等, ∴凳子应放在△ABC 的三条垂直平分线的交点最适当. 故选:C. 为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段 两端的距离相等可知,要放在三边中垂线的交点上. 本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一 种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键. 9.【答案】C 【解析】 解:∵AO⊥BO,点 P 是 AB 的中点,
1215轴对称类全等问题(4)讲义学生版

与角平分线相关的问题角平分线的两个性质:⑴角平分线上的点到角的两边的距离相等; ⑵到角的两边距离相等的点在角的平分线上.它们具有互逆性.角平分线是天然的、涉及对称的模型,一般情况下,有下列三种作辅助线的方式: 1. 由角平分线上的一点向角的两边作垂线,2. 过角平分线上的一点作角平分线的垂线,从而形成等腰三角形, 3. OA OB =,这种对称的图形应用得也较为普遍,AB OPPOB A ABOP【例1】 已知点M 是四边形ABCD 的BC 边的中点,且120AMD ∠=︒,证明:12AB BC CD AD ++≥.AB CDM【巩固】设M 是凸四边形ABCD 的边BC 的中点,135AMD ∠=︒,求证:2AB CD AD +≥. M DCB A【例2】 如图所示,已知在ABC ∆中,6AB =,3AC =,120BAC ∠=︒,BAC ∠的平分线交BC 于D ,求AD例题精讲之长.CBAD【巩固】如图所示,在ABC ∆中,AD 是BAC ∠的平分线,M 是BC 的中点,M E AD ⊥且交AC 的延长线于E ,12CE CD =,求证2ACB B ∠=∠.EMDCBA【例3】 如图所示,在ABC ∆中,AB AC =,AD 是BC 边上的高,点P 在ABD ∆内部,求证:APB APC ∠>∠.P DCBA【巩固】在ABC ∆中,AB AC =,60120A ︒<∠<︒,P 为ABC ∆内部一点,PC AC =,120PCA A ∠=︒-∠,求CBP ∠的度数.PCBA【例4】 如图所示,在ABC ∆中,A ∠的平分线交BC 于点D ,已知2BD DC AD ⋅=,且45ADB ∠=︒,求ABC∆的各个内角.AB CD【巩固】如图所示,P 为ABC ∆边BC 上的一点,且2PC PB =,已知45ABC ∠=︒,60APC ∠=︒,试求ACB ∠的度数.CP B A【例5】 如图所示,在四边形ABCD 中,30AB =,48AD =,14BC =,40CD =,90ABD BDC ∠+∠=︒,求四边形ABCD 的面积.48401430AB CD【例6】 如图所示,在ABC ∆中,2ACB ABC ∠=∠,P 为三角形内一点,AP AC =,PB PC =,求证:3BAC BAP ∠=∠.PCBA【例7】 如图所示,在四边形ABCD 中,BC CD =,60BCA ACD ∠-∠=︒,求证:AD CD AB +≥.DCB A【例8】 在等腰ABC ∆中,AB AC =,顶角20A ∠=︒,在边AB 上取点D ,使AD BC =,求BDC ∠.DCB A【巩固】如图所示,在ABC ∆中,AC BC =,20C ∠=︒,又M 在AC 上,N 在BC 上,且满足50BAN ∠=︒,60ABM ∠=︒,求NMB ∠.NMCBA【例9】 如图所示,在四边形ABCD 中,12DAC ∠=︒,36CAB ∠=︒,48ABD ∠=︒,24DBC ∠=︒,求ACD∠的度数.DCBA【例10】 在正ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.DECBA【例11】 在ABC ∆内取一点M ,使得M BA ∠=30︒,10MAB ∠=︒.设80ACB ∠=︒,AC BC =,求AMC ∠.MCBA【例12】 如图所示,在ABC ∆中,44BAC BCA ∠=∠=︒,M 为ABC ∆内一点,使得30MCA ∠=︒,16MAC ∠=︒,求BMC ∠的度数.MCAB1.如图所示,在四边形ABCD中,AB CD∥,AC BD⊥,求证:(1) AD BC AB CD+≥+;(2) AD BC AB CD⋅≥⋅.D CBA2.在凸四边形ABCD中,105ADB ABC∠=∠=︒,75CBD∠=︒.如果15AB CD==厘米,求四边形ABCD的面积.A B CD3.在四边形ABCD中,已知AB AC=,60ABD∠=︒,76ADB∠=︒,28BDC∠=︒,求DBC∠的度数.CDBA课后作业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与角平分线相关的问题角平分线的两个性质:⑴角平分线上的点到角的两边的距离相等; ⑵到角的两边距离相等的点在角的平分线上. 它们具有互逆性.角平分线是天然的、涉及对称的模型,一般情况下,有下列三种作辅助线的方式: 1. 由角平分线上的一点向角的两边作垂线,2. 过角平分线上的一点作角平分线的垂线,从而形成等腰三角形, 3. OA OB =,这种对称的图形应用得也较为普遍,AB OPPOB A A BOP【例1】 已知:如图,AD BC =,AC BD =,求证:C D ∠=∠.ODCBA【考点】轴对称型全等问题 【难度】2星 【题型】解答【关键词】2008年,宜宾市,中考 【解析】略【答案】连结AB在ADB ∆与BCA ∆中 AD BC AB BA BD AC =⎧⎪=⎨⎪=⎩∴ADB BCA ∆∆≌ ∴ D C ∠=∠ODCBA轴对称类全等问题【例2】 如图,已知AC BD =,AD AC ⊥,BC BD ⊥,求证:AD BC =.DC BA【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】连结CD在Rt ADC ∆和Rt BCD ∆中 AC BDDC CD =⎧⎨=⎩∴Rt Rt ADC BCD ∆∆≌ ∴AD BC =ABC D【例3】 已知:如图,B 、E 、F 、C 四点在同一条直线上,AB DC =,BE CF =,B C ∠=∠.求证:OA OD =.F E ODCB A【考点】轴对称类全等问题【难度】1星 【题型】解答【关键词】2008 年,哈尔滨,中考【解析】∵BE CF =,∴BE EF EF CF +=+,∴BF CE =在ABF ∆与DCE ∆中 AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩ ∴ABF DCF ∆∆≌ ∴AF DE =,AFB DEC ∠=∠ ∴OF OE = ∴AF OF DE OE -=- ∴OA OD =【答案】【例4】 如图所示,已知AD AE =,DF EF =.求证:AB AC =.A BC DEF【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】连接AF ,根据SSS 易得ADF ∆≌AEF ∆,进而得C B ∠=∠根据AAS 易得ABE ∆≌ACD ∆,进而得AB AC =.【例5】 在ABC ∆中,D 为BC 边上的点,已知BAD CAD ∠=∠,BD CD =,求证:AB AC =.D CBA【考点】轴对称类全等问题 【难度】1星 【题型】解答 【关键词】 【解析】略【答案】延长AD 到E ,使ED AD =,连结BE ,ED CBA在ADC ∆和EDB ∆中 AD ED ADC EDB DC DB =⎧⎪∠=∠⎨⎪=⎩∴ADC EDB ∆∆≌∴AC EB =,CAD BED ∠=∠ 又∵BAD CAD ∠=∠ ∴BAD BED ∠=∠ ∴AB EB = ∴AB AC =.【例6】 已知ABC ∆中,AB AC =,BE 、CD 分别是ABC ∠及ACB ∠平分线.求证:CD BE =.ED CB【考点】轴对称类全等问题 【难度】1星 【题型】解答 【关键词】 【解析】略【答案】∵AB AC =∴ABC ACB ∠=∠∵CD 平分ACB ∠,∴12DCB ACB ∠=∠.同理12EBC ABC ∠=∠.在DCB ∆与EBC ∆中,ABC ACB ∠=∠,DCB EBC ∠=∠,BC CB = ∴DCB EBC ∆∆≌,∴CD BE =.点评:其实就是等腰三角形底角平分线相等.【例7】 已知,如图,AB AC =,CE AB ⊥,BF AC ⊥,求证:BF CE =.F E CBA【考点】轴对称类全等问题 【难度】1星 【题型】解答 【关键词】 【解析】略【答案】在BCE ∆和CBF ∆BEC CFB CBE BCF BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BCE CBF ∆∆≌,BF CE =. 另一方法:面积法.1122ABC S AB CE AC BF ∆=⋅=⋅,∵AB AC =,∴BF CE =.等腰三角形两腰上的高相等.【例8】 如图,在ABC ∆中,60B ∠=︒,AD 、CE 分别平分BAC ∠、BCA ∠,且AD 与CE 的交点为F .求证:FE FD =.FBEDC【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】在AC 上截取AG AE =,连结FG ,AEF AGF ∆∆≌,AFE AFG ∠=∠,FE FG =,可推出60CFG CFD ∠=︒=∠, 进而证明CFG CFD ∆∆≌,有FA=FD ,进而得FE FD =.【例9】 如图,已知E 是AC 上的一点,又12∠=∠,34∠=∠.求证:ED EB =.E DC B A4321【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略 【答案】∵12∠=∠,34∠=∠,AC AC =∴ACD ACB ∆∆≌ ∴AB AD = ∴12∠=∠,AE AE = ∴AED AEB ∆∆≌ ∴ED EB =【例10】 如图所示,OP 是AOC ∠和BOD ∠的平分线,OA OC =,OB OD =.求证:AB CD =.PDBOCA【考点】轴对称类全等问题 【难度】2星 【题型】解答【关键词】2006年,北京,中考 【解析】略【答案】∵OP 是AOC ∠和BOD ∠的角平分线∴AOP COP ∠=∠,BOP DOP ∠=∠ ∴AOB COD ∠=∠ 在AOB ∆和COD ∆中 OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩∴AOB COD ∆∆≌(SAS),∴AB CD =.【例11】 已知ABC ∆中,AB AC =,GE 过A 且GE BC ∥,B ∠的平分线与AC 和GE 分别交于D ,E ,C∠的平分线与AB 和GE 分别交于F ,G .求证DE FG =.GFEDCBA【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】先证ABE AGC ∆∆≌,得到GC BE =;再证BFC BDC ∆∆≌,得到FC BD =; 得到DE FG =.【例12】 如图所示, 已知AB DC =,AE DF =,CE BF =,证明:AF DE =.F E DC BA【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】∵CE FB =, ∴CE EF FB EF +=+, 即CF BE =.在AEB ∆和DFC ∆中, CF BE DC AB DF AE =⎧⎪=⎨⎪=⎩,∴AEB ∆≌DFC ∆(SSS )∴AEF DFE ∠=∠,在AEF ∆和DFE ∆中,AE DF AEF DFE EF FE =⎧⎪∠=∠⎨⎪=⎩∴AEF ∆≌DFE ∆(SAS ),∴AF DE =.【例13】 如图所示:AB AC =,AD AE =,CD 、BE 相交于点O .求证:OA 平分DAE ∠.ABCDEO【考点】轴对称类全等问题 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】利用SAS 证得ABE ∆≌ACD ∆,∴E D ∠=∠,根据已知可得BD CE =,利用AAS 证得BOD ∆≌COE ∆, ∴OD OE =,利用SAS 证得AOD ∆≌AOE ∆, ∴OAD OAE ∠=∠,∴OA 平分DAE ∠.【例14】 如图所示,C 是AB 的中点,CD CE =,DCA ECB ∠=∠,求证DAE EBD ∠=∠.EDC BA【考点】轴对称类全等 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】因为DCA ECB ∠=∠,所以DCA DCE ECB DCE ∠+∠=∠+∠,即ACE BCD ∠=∠.在ACE ∆和BCD ∆中,由于AC BC =,ACE BCD ∠=∠,CD CE =, 则ACE BCD ∆∆≌,从而EAC DBC ∠=∠,AE BD =.又在ABD ∆和BAE ∆中,注意到AB 公用,则ABD BAE ∆∆≌, 从而DAB EBA ∠=∠,所以DAB EAC EBA DBC ∠-∠=∠-∠, 故DAE EBD ∠=∠.【例15】 如图,在△ABC 中,90BAC ∠=︒,BD 平分ABC ∠交AC 于D ,AE BC ⊥于E 交BD 于G ,FG ∥AC 交BC 于F ,连接DF .求证:DF BC ⊥GFEDCBA【考点】轴对称类全等问题 【难度】3星 【题型】解答【关键词】2000年,南昌市,中考 【解析】略【答案】先证△AGB ≌△FGB ,再证△FDB ≌△ADB【例16】 如图,ABC ∆中,AB BC =,90ABC ∠=︒,D 是AC 上一点,且CD CB AB ==,DE AC ⊥交AB 于E 点.求证:AD DE EB ==.CB DEA【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】解法一:如图,连结CE .∵ED AC ⊥,∴90EDC EDA ∠=∠=︒.∵90B ∠=︒,∴EDC B ∠=∠.在CDE ∆与CBE ∆中,CD CB =,CE 公共,EDC B ∠=∠, ∵AB BC =,45A ∠=︒.∵45AED ∠=︒,A AED ∠=∠. ∴AD DE =.∴AD DE EB ==. 解法二:连结DB . ∵CD CB =,∴CBD CDB ∠=∠.∵ED AC ⊥,90CDE ∠=︒. ∵90ABC ∠=︒, ∴CDE ABC ∠=∠. ∴EBD EDB ∠=∠, ∴DE EB =.∵AB AC =,∴45A ∠=︒. ∵90ADE ∠=︒, ∴45AED ∠=︒. ∴AD DE EB ==.CB DEA【例17】 如图,ABC ∆中,AB AC =,D 、E 分别是AB 、AC 的中点,DG BC ⊥于G ,EH BC ⊥于H .求证:DG EH =.HG ED CBA【考点】轴对称类全等 【难度】2星 【题型】解答 【关键词】 【解析】略【答案】∵D 、E 分别是AB 、AC 的中点又∵AB AC =,∴DB EC =. ∵AB AC =,∴B C ∠=∠. ∵DG BC ⊥,EH BC ⊥ ∴90DGB EHC ∠=∠=︒. 在DGB ∆和EHC ∆中 DGB EHC B CDB EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DGB EHC ∆∆≌,∴DG EH =.【例18】 在凸五边形中,B E ∠=∠,C D ∠=∠,BC DE =,M 为CD 中点.求证:AM CD ⊥.M EDC B A【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】延长AB ,AE ,交直线CD 于F ,G .∵ABC AED ∠=∠. ∴FBC GED ∠=∠.∵BCM EDM ∠=∠. ∴BCF EDG ∠=∠. ∴在BCF ∆与EDG ∆中 FBC GED BC EDBCF EDG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴(ASA)BCF EDG ∆∆≌ ∴F G ∠=∠.FC GD =. ∴AG AF = ∵CM MD = ∴FM MG =∴在AM F ∆与AMG ∆中 AM AM FM MG AF AG =⎧⎪=⎨⎪=⎩∴()SSS AMF AMG ∆∆≌ ∴180902AMF AMG ︒∠=∠==︒ ∴AM CD ⊥G F M EDC B A【例19】 如图,AB AE =,ABC AED ∠=∠,BC ED =,点F 是CD 的中点.求证:AF CD ⊥.F EDC BA【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】连结AC 、AD .ABC F DE∵AB AE =,ABC AED ∠=∠,BC ED = ∴ABC AED ∆∆≌,∴AC AD =又∵F 为CD 的中点,∴AF BE ⊥.【例20】 如图,在等腰ABC ∆中,AB AC =,D 是BC 的中点,过A 作AE DE ⊥,AF DF ⊥,且A E A F =.求证:EDB FDC ∠=∠.DFECBA【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】连结AD ,则AD BC ⊥.∵AE AF =,AD AD =,∴Rt Rt AED AFD ∆∆≌ ∴AD E AD F ∠=∠,∴EDB FDC ∠=∠.DBCFAE【例21】 如图,AB AC =,D 、E 分别是AB 、AC 的中点,AM CD ⊥于M ,AN BE ⊥于N .求证:AM AN =.E D NM CBA【考点】轴对称类全等问题【难度】2星 【题型】解答 【关键词】 【解析】略【答案】∵AB AC =,∴ABC ACB ∠=∠.∵D 、E 是AB 、AC 的中点,∴DB EC =,AD AE =.在DBC ∆与ECB ∆中,BC CB =,DBC ECB ∠=∠,DB EC =, ∴DBC ECB ∆∆≌.∴BDC CEB ∠=∠ ∵ADM BDC ∠=∠,AEN CEB ∠=∠,∴ADM AEN ∠=∠.在AM D ∆与ANE ∆中,90M N ∠=∠=︒AD AE =,ADM AEN ∠=∠,∴AMD ANE ∆∆≌,∴AM AN =. 证法二:∵AB AC =,∵D 、E 是AB 、AC 的中点, ∴AD AE =.在DAC ∆与EAB ∆中,AB AC =,AE AD =,A A ∠=∠,∴DAC EAB ∆∆≌,∴ACD ABE ∠=∠.AM CD ⊥于M ,AN BE ⊥于N . ∴90M N ∠=∠=︒,在AMC ∆与ANB ∆中,AC AB =,ACM ABN ∠=∠,M N ∠=∠, ∴AMC ANB ∆∆≌,∴AM AN =. 证法三:∵AB AC =,∵D 、E 是AB 、AC 的中点,∴12ADC ABC S S ∆∆=,12AEB ABC S S ∆∆=及AD AE =,∴ADC AEB S S ∆∆=,在ADC ∆与AEB ∆中,AD AE =,AC AB =,A A ∠=∠,∴ADC AEB ∆∆≌,∴CD BE =.∴1122CD AM BE AN ⋅=⋅,∴AM AN =.【例22】 在凸五边形中,B E ∠=∠,C D ∠=∠,BC DE =,M 为CD 中点.求证:AM CD ⊥.M EDC B A【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】延长AB ,AE ,交直线CD 于F ,G .∵ABC AED ∠=∠. ∴FBC GED ∠=∠. ∵BCM EDM ∠=∠. ∴BCF EDG ∠=∠. ∴在BCF ∆与EDG ∆中 FBC GED BC EDBCF EDG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴(ASA)BCF EDG ∆∆≌ ∴F G ∠=∠.FC GD =. ∴AG AF = ∵CM MD = ∴FM MG =∴在AM F ∆与AMG ∆中 AM AM FM MG AF AG =⎧⎪=⎨⎪=⎩∴()SSS AMF AMG ∆∆≌ ∴180902AMF AMG ︒∠=∠==︒ ∴AM CD ⊥G F M EDC B A【例23】 如图,在四边形ABCD 中,AD BC A ∠∥,的平分线AE 交DC 于E .求证:当BE 是B ∠的平分线时,有AD BC AB +=.EDCBA【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】在AB 上截取AF ,使AF AD =,连接EF ,则可得ADE AFE ∆∆≌,于是ADE AFE ∠=∠.由AD BC ∥,知180ADE C ∠+∠=︒, 而180EFB AFE ∠+∠=︒, 从而EFB C ∠=∠注意到BE 平分B BE ∠,公用,于是,由角边角公理的推论,知EFB ECB ∆∆≌, 从而BF BC =.故AD BC AF BF AB +=+=.FEDCBA【例24】如图,在ABC∆中,BE、CD分别是ABC∠、ACB∠的角平分线,且BD CE BC+=,则A∠的度数为.EDCBA【考点】轴对称类全等问题【难度】4星【题型】填空【关键词】【解析】略【答案】60︒.【例25】如图所示,在ABC∆中,100A∠=︒,40ABC∠=︒,BD是ABC∠的平分线,延长BD至E,使DE AD=.求证:BC AB CE=+EDCA【考点】轴对称类全等问题【难度】4星【题型】解答【关键词】【解析】略【答案】在BC上取一点F,使得BF BA=FE DCA 易证得ADB FDB∆∆≌∴DF AD=,又∵DA DE=∴DF DE=∵100A∠=︒,AB AC=∴40ABC∠=︒∵BD平分ABC∠,∴20ABD∠=︒∴60ADB FDB∠=∠=︒∵60CDE ADB∠=∠=︒∴60FDC EDC∠=∠=︒∴DCF DCE∆∆≌∴FC EC=∴BC BF FC AB CE=+=+【例26】 已知ABC ∆中,60A ∠=︒,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.OED CBA【考点】轴对称类全等问题 【难度】4星 【题型】解答【关键词】2006年,北京,中考 【解析】BE CD BC +=理由是:在BC 上截取BF BE =,连结OF 利用SAS 证得BEO ∆≌BFO ∆ ∴12∠=∠ ∵60A ∠=︒∴1901202BOC A ∠=︒+∠=︒∴120DOE ∠=︒∴180A DOE ∠+∠=︒ ∴180AEO ADO ∠+∠=︒ ∴13180∠+∠=︒ ∵24180∠+∠=︒ ∴12∠=∠ ∴34∠=∠利用AAS 证得CDO ∆≌CFO ∆ ∴CD CF =∴BC BF CF BE CD =+=+4321F O DE C BA【例27】 如图(1)所示,OP 是MON ∠的平行线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题: (1)如图(2),在ABC ∆中,ACB ∠是直角,60B ∠=︒,AD 、CE 分别是BAC ∠、BCA ∠的平分线,AD 、CE 相交于点F . 请你判断并写出FE 与FD 之间的数量关系. (2)如图(3),在ABC ∆中,如果ACB ∠不是直角,而(1)中的其他条件均不变,请问,你在(1)中得到的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(1)PNMO(2)FED CBA(3)FEDCBA【考点】轴对称类全等问题 【难度】4星 【题型】解答【关键词】06北京课改第23题 【解析】略 【答案】(1)FE FD =.证明:在AC 上取点M ,使得AM AE =,连接FM .易证AEF AM F ∆∆≌,故EF FM =. 可证MCF DCF ∆∆≌,故FD FM EF ==.MFED CBA(2)在AC 上取点M ,使得AM AE =,连接FM .M FEDCBA∵BAD CAD ∠=∠,AF AF =,AE AM = ∴AEF AM F ∆∆≌ ∴EF FM =,AFE AFM ∠=∠∵BAD CAD ∠=∠,BCE ACE ∠=∠,60B ∠=︒ ∴120AFC ∠=︒,60AFE ∠=︒ ∴60MFC DFC ∠=︒=∠∵BCE ACE ∠=∠,CF CF = ∴MFC DFC ∆∆≌ ∴DF FM EF ==【例28】 如图,I 是ABC △的内心,且CA AI BC +=.若80BAC ∠=︒,求ABC ∠和AIB ∠的大小.ABCI【考点】轴对称类全等问题 【难度】4星 【题型】解答【关键词】第19届“希望杯”,初二试题【解析】略【答案】因为有内心,故可以用角平分线构造全等三角形,从而使问题容易解决.如图,在BC 上取点D ,使CD AC =,连接DI . 因为CA AI BC +=, 所以BD AI =.在ACI △和DCI △中,AC DC =,ACI DCI ∠=∠,CI CI =. 所以ACI DCI △≌△. 于是AI D I =. 所以DI BD =. 因为80BAC ∠=︒,所以40CAI ∠=︒,40CDI ∠=︒. 又CDI ∠是等腰BDI △的外角,所以20DBI DIB CDI ∠=∠=∠=︒,40ABC ∠=︒. 在AIB △中,40BAI ∠=︒,20ABI ∠=︒, 所以()1802040120AIB ∠=︒-︒+︒=︒.20︒40︒40︒ID CBA【例29】 在ABC ∆中,AB AC >,AD 是BAC ∠的平分线.P 是AD 上任意一点.求证:AB AC PB PC ->-.CD B PA【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】在AB 上截取AE AC =,连结EP ,根据SAS 证得AEP ∆≌ACP ∆,ECD B PA∴PE PC =,AE AC =又BEP ∆中,BE PB PE >-,BE AB AC =-,∴AB AC PB PC ->-【例30】 在四边形ABCD 中,AD BC ∥,A ∠的平分线AE 交DC 于E .求证:当BE 是B ∠的角平分线时,有AD BC AB +=.【考点】轴对称类全等问题 【难度】3星 【题型】解答 【关键词】 【解析】略【答案】在AB 上截取AF ,使AF AD =,连EF ,则可得ADE AFE ∆∆≌. ∴ADE AFE ∠=∠. ∵AD BC ∥,知 180ADE C ∠+∠=︒. ∵180EFB AFE ∠+∠=︒. ∴EFB C ∠=∠.注意到BE 平分B ∠,BE 公用, ∴EFB ECB ∆∆≌,∴BF BC =. ∴AD BC AF BF AB +=+=.【例31】 如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.D CB A【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】解法1:如图所示,延长AB 至E 使BE BD =,连接ED 、EC .ED CB A由AC AB BD =+知AE AC =,而60BAC ∠=,则AEC ∆为等边三角形.注意到EAD CAD ∠=∠,AD AD =,AE AC =, 故AED ACD ∆∆≌.从而有DE DC =,DEC DCE ∠=∠,故2BED BDE DCE DEC DEC ∠=∠=∠+∠=∠.所以20DEC DCE ∠=∠=︒,602080ABC BEC BCE ∠=∠+∠=︒+︒=︒.ED CB解法2:在AC 上取点E ,使得AE AB =,则由题意可知CE BD =.在ABD ∆和AED ∆中,AB AE =,BAD EAD ∠=∠,AD AD =, 则ABD AED ∆∆≌,从而BD DE =, 进而有DE CE =,ECD EDC ∠=∠, AED ECD EDC ∠=∠+∠=2ECD ∠. 注意到ABD AED ∠=∠,则:1318012022ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=︒-∠=︒,故80ABC ∠=.【点评】由已知条件可以想到将折线ABD “拉直”成AE ,利用角平分线AD 可以构造全等三角形.同样地,将AC 拆分成两段,之后再利用三角形全等亦可,此思路也是十分自然的. 需要说明的是,无论采取哪种方法,都体现出关于角平分线“对称”的思想.上述方法我们分别称之为“补短法”和“截长法”,它们是证明等量关系时优先考虑的方法.【例32】 如图,在ABC ∆中,2B C ∠=∠,BAC ∠的平分线AD 交BC 与D .求证:AB BD AC +=.DC B A【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】方法一:在AC 上取一点E ,使得AB AE =EDC B A连结DE .在ABD ∆和AED ∆中AB AE =,BAD EAD ∠=∠ AD AD =∴ABD AED ∆∆≌∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠EDC C ∠=∠,ED EC =∴AB BD AC +=. 方法二:在AB 的延长线上取一点EBCDE使得AC AE =,连结DE .在AED ∆和ACD ∆中,AE AC = EAD CAD ∠=∠,AD AD = ∴AED ACD ∆∆≌,∴C E ∠=∠又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠∴E BDE ∠=∠∴BE BD =,∴AB BD AC +=. 方法三:延长DB 到点E 使得AB BE =,连结AE 则有EAB E ∠=∠2ABC E EAB E ∠=∠+∠=∠又∵2ABC C ∠=∠,∴AE AC =又∵EAD EAB BAD E DAC ∠=∠+∠=∠+∠ C DAC ADE =∠+∠=∠∴AE DE =,∴AB BD EB BD ED AE AC +=+===ABCDEEDCB A FM方法四:如图,作BF 平分ABC ∠交AD 、AC 于E 、F 点 延长BF 到M ,使FM FA =,连结AM ∴ABF FBC ∠=∠∵2ABC C ∠=∠,∴FBC C ∠=∠.∴FB FC = ∵AF FM =,∴M FAM ∠=∠∵AFE FBC C ∠=∠+∠,又AFE M FAM ∠=∠+∠ 即22AFE M C ∠=∠=∠.∴C M ∠=∠∴M ABM DBF C ∠=∠=∠=∠.∴AB AM = ∵ADB C DAC ∠=∠+∠ 且D EB EBA BAE ∠=∠+∠∵BAD DAC ∠=∠,∴ADB DEB ∠=∠.∴BD BE = 同理MA ME =∵AF FM =,FB FC =,∴AC BM =.∴AC AB BD =+【例33】 在ABC ∆中,AD 平分BAC ∠,AB BD AC +=.求:B C ∠∠的值.CD B A【考点】轴对称类全等问题 【难度】4星【关键词】2001年,河南省,中考 【解析】略【答案】在AC 上截取AE AB =,连结DE根据SAS 证得ABD ∆≌AED ∆,∴AED B EDC C ∠=∠=∠+∠,DE BD =, 结合已知可得ED EC =,∴EDC C ∠=∠,∴2B C ∠=∠,:2:1B C ∠∠=ECD B A【例34】 如图,在ABC ∆中,AB BD AC +=,BAC ∠的平分线AD 交BC 与D .求证:2B C ∠=∠.DC B A【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】在AC 上取一点E ,使得AB AE =,连结DE .EDC B A在ABD ∆和AED ∆中,AB AE =,BAD EAD ∠=∠, AD AD =.∴ABD AED ∆∆≌,∴BD ED =,B AED ∠=∠又∵AB BD AC +=,∴EC BD ED == 2AED EDC C C B ∠=∠+∠=∠=∠. 其他方法参考例题.【例35】 如图,ABC ∆中,AB AC =,108A ∠=︒,BD 平分ABC ∠交AC 于D 点.求证:BC AC CD =+.AB CD【考点】轴对称类全等问题【关键词】 【解析】略【答案】方法一:在BC 上截取E 点使BE BA =,连结DE .E DCB A∵BD 平分ABC ∠,∴ABD EBD ∠=∠. 在ABD ∆与EBD ∆中∵AB EB =,ABD EBD ∠=∠,BD BD = ∴ABD EBD ∆∆≌,∴A DEB ∠=∠∵108A ∠=︒, ∴108DEB ∠=∠︒∴72DEC ∠=︒. 又∵361854ADB ∠=︒+︒=︒ ∴72CDE ∠=︒ ∴CDE DEC ∠=∠ ∴CD CE =∵BC BE EC =+,∴BC AC CD =+方法二:如图,延长CA 到F ,使CF CB =,连结BF .DCBAF∵AB AC =,且108BAC ∠=︒, ∴36ABC C ∠=∠=︒. ∵CB CF =, ∴F FBC ∠=∠.∴FAB C ABC ∠=∠+∠. ∴72FAB ∠=︒.∵12ADB C ABC ∠=∠+∠,∴54ADB ∠=︒.又∵54FBD ∠=︒ ∴BF AB AC FD ===.∴AF CD =.∴BC AC CD =+.【例36】 如图,ABC ∆中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,那么C ∠的大小是__________. D CB A【考点】轴对称类全等问题【难度】4星 【题型】填空 【关键词】“希望杯”培训题【解析】在AB 上取点E ,使得AE AC =,连接DE .ED CB A∵AE AC =,BAD CAD ∠=∠,AD AD =, ∴ACD AED ∆∆≌∴C AED ∠=∠,CD CE =∵AB AC CD =+,AE AC =,∴CD BE DE == ∴40EBD EDB ∠=∠=︒,80C AED ∠=∠=︒【答案】80︒【例37】 如图,在ABC ∆中,90BAC ∠=︒,2B C ∠=∠,D 点在BC 上,AD 平分BAC ∠,若1AB =,则BD的长为____________.D CB A【考点】轴对称类全等问题 【难度】4星 【题型】填空 【关键词】【解析】在BC 上截取AE AB =,连接DE .ED CB A∵AE AB =,BAD CAD ∠=∠,AD AD = ∴ABD AED ∆∆≌∴BD DE =,ABD AED ∠=∠,AB AE =∵90BAC ∠=︒,2B C ∠=∠ ∴60B ∠=︒,30C ∠=︒∴30DEC C ∠=︒=∠ ∴DE CE =∴1BD AC AB =-=【例38】 已知等腰ABC ∆,100A ∠=︒,ABC ∠的平分线交AC 于D ,则BD AD BC +=.DCB A【难度】4星 【题型】解答 【关键词】 【解析】略【答案】解法一:如图,在BC 上截取BE BD =,连接DE ,过D 作DF BC ∥,交AB 于F ,于是32∠=∠,ADF ECD ∠=∠.BAF EDC321又∵12∠=∠,∴13∠=∠,故DF BF =.显然FBCD 是等腰梯形. ∴BF DC =,DF DC =.∵()111218010020222ABC ∠=∠=⨯︒-︒=︒,()11802802BED BDE ∠=∠=︒-∠=︒,∴180100DEC BED ∠=︒-∠=︒,∴100FAD DEC ∠=∠=︒,∴AFD EDC ∆∆≌,AD EC =. 又∵BE BD =,∴BC BD EC BD AD =+=+. 解法二:如图,延长BD 到E ,使DE AD =,在BC 上截取BF BA =.BADC21FE43∵12∠=∠,BD 为公共边,∴BAD BFD ∆≌,AD FD =,ADB FDB ∠=∠.∵()111118010020222ABC ∠=∠=⨯︒-︒=︒,∴()()18011801002060ADB A ∠=︒-∠+∠=︒-︒+︒=︒.∴60FDB ∠=︒,故60FDC ∠=︒,60EDC ∠=︒.∵DF DE =,∴DFC DEC ∆∆≌.∴E DFC ∠=∠,34∠=∠. ∵2206080DFC FDB ∠=∠+∠=︒+︒=︒, ∴80E ∠=︒.∵440∠=︒,∴340∠=︒,故3480ECB ∠=∠+∠=︒. ∴ECB E ∠=∠,故BC BE =.∵BE BD DE =+,∴BC BD AD =+. 解法三:如图,延长BD 到E ,使BE BC =.延长BA 到F ,使BF BC =.连接CE 、EF 、DF .BADC21FE∵12∠=∠,BD 公共, ∴BDC BDF ∆∆≌.∴BDC BDF ∠=∠,BCD BFD ∠=∠.又∵120100120BDC BAC ∠=∠+∠=︒+︒=︒,40BCD ∠=︒, ∴40BFD ∠=︒.∵BE BF =,120∠=︒. ∴80BEF BFE ∠=∠=︒, ∴804040DFE ∠=︒-︒=︒.而180********FAD BAD ∠=︒-∠=︒-︒=︒. ∴FAD DEF ∠=∠.又FD 公共,∴FAD FED ∆∆≌.∴ED AD =. ∴BC BE BD AD ==+【例39】 已知:在ABC ∆中,AB CD BD =-,AD BC ⊥,求证: 2B C ∠=∠.D CBA【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】方法一:在DC 上取一点E ,使BD DE =,如图1,图1E AB CD在ABD ∆和AED ∆中,AD BC ⊥,BD ED =,AD AD =. ∴ABD AED ∆∆≌.∴AB AE =,B AED ∠=∠. 又∵AE AB CD BD CD DE EC ==-=-=∴C EAC ∠=∠,∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠.方法二:延长DB 到点E ,使BE AB =,如图2,图2EAB CD∴E EAB ∠=∠.∵AB CD BD =-,∴ED CD =.在AED ∆和ACD ∆中,AD BC ⊥,ED CD =,AD AD =. ∴AED ACD ∆∆≌.∴E C ∠=∠. ∴2B C ∠=∠.【例40】 如图所示,在ABC △中,AD BC ⊥于点D ,2B C ∠=∠.求证:AB BD CD +=.C D BA【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】由已知AD BC ⊥,2B C ∠=∠知如果我们在CD 上截取DE DB =,连接AE ,就可以构造出两个等腰三角形ABE △和AEC △.如图,在CD 上截取DE DB =,连接AE . 因为AD BC ⊥,DE DB =,所以AE AB =,于是B AEB ∠=∠,又因为AEB C CAE ∠=∠+∠,2B C ∠=∠, 所以CAE C ∠=∠, 于是AE EC =,故AB BD AE ED EC ED CD +=+=+=.ABD E C【例41】 如图,ABC ∆中,120BAC ∠=︒,AD BC ⊥于D ,且AB BD CD +=,则C ∠的大小是( )A .20︒B .25︒C .30︒D .大于30︒AB CD【考点】轴对称类全等问题 【难度】3星 【题型】选择 【关键词】【解析】如图,在DC 上取DE DB =,连接AE ,易得Rt Rt ABD AED ∆∆≌.AB AE CE ==,2AEB C ∠=∠,所以22(902)120BAC EAD C C C ∠=∠+∠=︒-∠+∠=︒,得20C ∠=︒.EAB CD【答案】A【例42】 (1)已知:如图1,Rt ABC ∆中,90ACB AC BC ∠=︒=,,点D E 、在斜边AB 上,且45DCE ∠=︒.求证:线段DE AD EB 、、总能构成一个直角三角形;(2)已知:如图2,等边三角形ABC 中,点D E 、在边AB 上,且30DCE ∠=︒,请你找出一个条件,使线段DE AD EB 、、能构成一个等腰三角形,并求出此时等腰三角形顶角的度数; (3)在⑴的条件下,如果10AB =,求BD AE ⋅的值.图2图1E CBA ECBA【考点】旋转类全等问题;轴对称类全等问题;相似三角形 【难度】4星 【题型】解答【关键词】几何综合题,2009年,朝阳,一模 【解析】略 【答案】(1)如图1,∵90ACB AC BC ∠=︒=,,∴45A B ∠=∠=︒.以CE 为一边作ECF ECB ∠=∠,在CF 上截取CF CB =, 则CF CB AC ==,连接DF EF 、,则CFE CBE ∆∆≌,∴145FE BE B =∠=∠=︒,. ∵45DCE ECF DCF ∠=∠+∠=︒,∴45DCA ECB ∠+∠=︒, ∴DCF DCA ∠=∠,∴DCF DCA ∆∆≌,∴245A DF AD ∠=∠=︒=,,∴2190DFE ∠=∠+∠=︒, ∴DFE ∆是直角三角形. 又AD DF =,EB EF =,∴线段DE AD EB 、、总能构成一个直角三角形.(2)当AD BE =时,线段DE AD EB 、、能构成一个等腰三角形.如图2,与⑴类似,以CE 为一边,作ECF ECB ∠=∠,在CF 上截取CF CB =,可得CFE CBE DCF DCA ∆∆∆∆,≌≌. ∴AD DF EF BE ==,,∴12120DFE A B ∠=∠+∠=∠+∠=︒. 若使DFE ∆为等腰三角形,只需DF EF =,即AD BE =.∴当AD BE =时,线段DE AD EB 、、能构成一个等腰三角形, 且顶角DFE ∠为120︒.(3)如图1,∵ACE ACD DCE CDB ACD A ∠=∠+∠∠=∠+∠,, 又45DCE A ∠=∠=︒,∴ACE CDB ∠=∠.又A B ∠=∠,∴ACE BDC ∆∆∽,∴AE ACBC BD=,∴BD AE AC BC ⋅=⋅, ∵Rt ACB ∆中,由222210AC BC AB +==,得2250AC BC ==,∴250BD AE AC BC AC ⋅=⋅==.21FABCD E图112A BCD E图2【例43】 如图,已知60ABD ACD ∠=∠=︒,且1902ADB BDC ∠=︒-∠.求证:ABC ∆是等腰三角形.DBA【考点】轴对称类全等问题 【难度】4星 【题型】解答 【关键词】 【解析】略【答案】延长BD 到E ,使得DE CD =,连接AE .∵1902ADB BDC ∠=︒-∠,∴2180ADB BDC ∠+∠=︒,即180ADC ADB ∠+∠=︒.∵180ADE ADB ∠+∠=︒,∴ADC ADE ∠=∠, ∵CD DE AD AD ==,,∴()SAS ADC ADE ∆∆≌,∴60ACD E ∠=∠=︒,AC AE =,∵60ABD ACD ∠=∠=︒,∴ABD E ∠=∠,∴AB AE =,∴AB AC =,∴ABC ∆是等腰三角形.ED BA【例44】 在ABC ∆中,AB AC =,CG BA ⊥交BA 的延长线于点G .一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F ,一条直角边与AC 边在一条直线上,另一条直角边恰好经过点B . (1)在图1中请你通过观察、测量BF 与CG 的长度,猜想并写出BF 与CG 满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC 方向平移到图2所示的位置时,一条直角边仍与AC 边在同一直线上,另一条直角边交BC 边于点D ,过点D 作DE BA ⊥于点E .此时请你通过观察、测量DE 、DF 与CG 的长度,猜想并写出DE DF +与CG 之间满足的数量关系,然后证明你的猜想;(3)当三角尺在⑵的基础上沿AC 方向继续平移到图3所示的位置(点F 在线段AC 上,且点F 与点C 不重合)时,⑵中的猜想是否仍然成立?(不用说明理由)【考点】轴对称类全等问题 【难度】4星 【题型】解答【关键词】几何综合题,2007年,河北省,中考 【解析】略 【答案】(1)BF CG =;在ABF ∆和ACG ∆中,∵90F G FAB GAC AB AC ∠=∠=︒∠=∠=,,, ∴(AAS)ABF ACG ∆∆≌, ∴BF CG =.(2)DE DF CG +=;过点D 作DH CG ⊥于点H (如图4).∵DE BA ⊥于点E ,90G DH CG ∠=︒⊥,,∴四边形EDHG 为矩形,∴DE HG DH BG =,∥,∴GBC HDC ∠=∠,∵AB AC =,∴FCD GBC HDC ∠=∠=∠,又∵90F DHC CD DC ∠=∠=︒=,, ∴(AAS)FDC HCD ∆∆≌,∴DF CH =.∴GH CH DE DF CG +=+=,即DE DF CG +=. (3)仍然成立.(注:本题还可以利用面积来进行证明,比如⑵中连结AD )【例45】 如图,在Rt ABC ∆中,,,D E F 分别为AB 、AC 、BC 中点,H 为斜边AB 的高的垂足,G 是DH的中点.设O 为AB 上的任一点,求证:EOF ∠的最大的角便是EGF ∠.B【考点】轴对称类全等问题 【难度】 【题型】 【关键词】 【解析】分析 设EG 交OF 于M .注意到在OEM ∆与FGM ∆中,OME FMG ∠=∠,故欲证EOF EGF ∠∠≤,只需证OEM GFM ∠∠≥,利用对称性,可将GFM ∠与OEM ∠统一到一个三角形中便于比较.图3图解连接CH,则HF为Rt CHB∆斜边BC上的中线,故12HF BC FB==.D、E分别为AB、AC的中点,故DE BC∥且12DE BC=,所以DE HF=.ADE ABC FHB∠=∠=∠,从而EDG FHG∠=∠,故EDG FHG∆∆≌.于是有EG GF=,EGD FGH∠=∠.延长EG至N,使GN EG=,连接HN.由于NGH EGD FGH∠=∠=∠,GN EG GF==,GH GH=,故FGH NGH∆∆≌.从而FH HN=.结合GF GN=知GH为线段FN的垂直平分线.设O为AB上任一异于G的点,则OF ON=,且易知ON OF OE=>(若O在G的左边,OF OE>,O在G的右边,则OE OF>).从而OFG ONG OEG OEM∠=∠∠=∠≤,在OEM∆与MGF∆中,EMO∠与FMG∠为对顶角,于是有:EOF EOM MGF EGF∠=∠∠=∠≤(等号当且仅当点O与点G重合时取到).这就证明了EOF∠取最大角时便是EGF∠.说明本题为1993年浙江省全国初中数学联赛选拔赛试题.解法中巧妙地将结论”转化”,然后利用对称性将中间结论统一于同一个三角形中,又一次”转化”.转换、转化、化归是解决数学问题的常用的基本的数学思想方法.。
