复数 三角函数 圆锥曲线
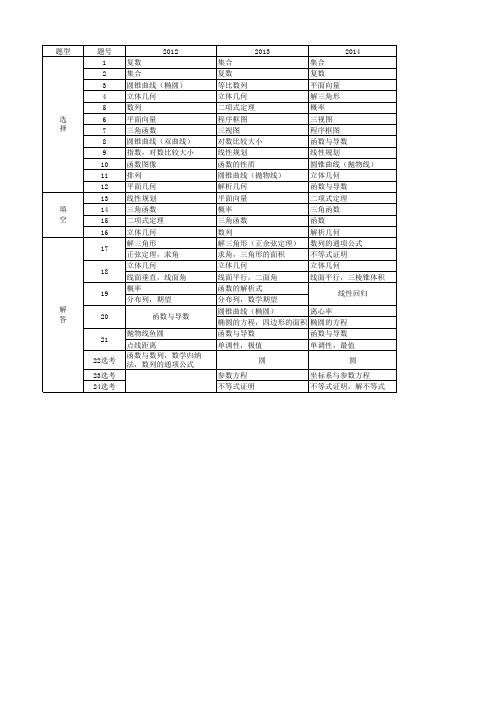
全国2卷2012—2014年高考数学知识点统计
选 择
填 空
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2012 复数 集合 圆锥曲线(椭圆) 立体几何 数列 平面向量 三角函数 圆锥曲线(双曲线) 指数,对数比较大小 函数图像 排列 平面几何 线性规划 三角函数 二项式定理 立体几何 解三角形 正弦定理,求角 立体几何 线面垂直,线面角 概率 分布列,期望 函数与导数 抛物线鱼圆 点线距离 函数与数4 集合 复数 平面向量 解三角形 概率 三视图 程序框图 函数与导数 线性规划 圆锥曲线(抛物线) 立体几何 函数与导数 二项式定理 三角函数 函数 解析几何 数列的通项公式 不等式证明 立体几何 线面平行,三棱锥体积 线性回归 离心率 椭圆的方程 函数与导数 单调性,最值 圆 坐标系与参数方程 不等式证明,解不等式
解 答
20 21 22选考 23选考 24选考
2013 集合 复数 等比数列 立体几何 二项式定理 程序框图 三视图 对数比较大小 线性规划 函数的性质 圆锥曲线(抛物线) 解析几何 平面向量 概率 三角函数 数列 解三角形(正余弦定理) 求角,三角形的面积 立体几何 线面平行,二面角 函数的解析式 分布列,数学期望 圆锥曲线(椭圆) 椭圆的方程,四边形的面 积 函数与导数 单调性,极值 圆 参数方程 不等式证明
(完整版)近三年高考数学分值分布

5
向量的分解
5
立体几何,三视图,距离
5
抛物线,向量
5
函数,零点
5
数学文化,统计概率
5
双曲线,弦长
5
立体几何
5
线性规划
5
数列
5
排列组合
5
函数最值
5
解三角形
12
立体几何
12
椭圆,直线方程
12
统计概率期望
12
函数与导数,单调性
12
参数与极坐标普通方程, 交点
10
立体几何分值:22分
三角函数分值:一大12 数列分值:两小15分 概率统计:一大三小27分
2018年高 考数学 题序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
20
21
22
总结:
高考动态:删掉程序框 图,删掉积分,删掉二 选一,弱化逻辑关联 词,加入三视图,弱化 线性规划,弱化排列组 合,
内容
分值
复数的模
5
不等式,补集
5
统计
5
数列
5
函数的切线与奇偶性
圆锥曲线:一大两小22分 向量:一小5分
2017年高 考数学 题序 内容
1 不等式,集合 2 概率 3 复数 4 数列 5 函数的奇偶性,单调性 6 二项式定理 7 三视图,面积 8 程序框图,数列 9 三角函数平移 10 抛物线 11 比较大小 12 数列 13 向量的模 14 线性规划 15 双曲线离心率 16 立体几何,最值 17 解三角形 18 立体几何 19 统计,正态分布
12
18 立体几何
12
19 抛物线与直线
三角函数公式表

三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosα tan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——————1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin———·cos———2 2α+βα-βsinα-sinβ=2cos———·sin———2 2α+βα-βcosα+cosβ=2cos———·cos———2 2α+βα-βcosα-cosβ=-2sin———·sin———2 2 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式集合、函数集合简单逻辑任一x∈A x∈B,记作A BA B,B A A=BA B={x|x∈A,且x∈B}A B={x|x∈A,或x∈B}c ard(A B)=card(A)+card(B)-card(A B)(1)命题原命题若p则q逆命题若q则p否命题若 p则 q逆否命题若 q,则 p(2)四种命题的关系(3)A B,A是B成立的充分条件B A,A是B成立的必要条件A B,A是B成立的充要条件函数的性质指数和对数(1)定义域、值域、对应法则(2)单调性对于任意x1,x2∈D若x1<x2 f(x1)<f(x2),称f(x)在D上是增函数若x1<x2 f(x1)>f(x2),称f(x)在D上是减函数(3)奇偶性对于函数f(x)的定义域内的任一x,若f(-x)=f(x),称f (x)是偶函数若f(-x)=-f(x),称f(x)是奇函数(4)周期性对于函数f(x)的定义域内的任一x,若存在常数T,使得f(x+T)=f(x),则称f(x)是周期函数(1)分数指数幂正分数指数幂的意义是负分数指数幂的意义是(2)对数的性质和运算法则loga(MN)=logaM+logaNlogaMn=nlogaM(n∈R)指数函数对数函数(1)y=ax(a>0,a≠1)叫指数函数(2)x∈R,y>0图象经过(0,1)a>1时,x>0,y>1;x<0,0<y<10<a<1时,x>0,0<y<1;x<0,y>1a> 1时,y=ax是增函数0<a<1时,y=ax是减函数(1)y=logax(a>0,a≠1)叫对数函数(2)x>0,y∈R图象经过(1,0)a>1时,x>1,y>0;0<x<1,y<00<a<1时,x>1,y<0;0<x<1,y>0a>1时,y=logax是增函数0<a<1时,y=logax是减函数指数方程和对数方程基本型logaf(x)=b f(x)=ab(a>0,a≠1)同底型logaf(x)=logag(x) f(x)=g(x)>0(a>0,a≠1)换元型 f(ax)=0或f (logax)=0数列数列的基本概念等差数列(1)数列的通项公式an=f(n)(2)数列的递推公式(3)数列的通项公式与前n项和的关系an+1-an=dan=a1+(n-1)da,A,b成等差 2A=a+bm+n=k+l am+an=ak+al等比数列常用求和公式an=a1qn_1a,G,b成等比 G2=abm+n=k+l aman=akal不等式不等式的基本性质重要不等式a>b b<aa>b,b>c a>ca>b a+c>b+ca+b>c a>c-ba>b,c>d a+c>b+da>b,c>0 ac>bca>b,c<0 ac<bca>b>0,c>d>0 ac<bda>b>0 dn>bn(n∈Z,n>1)a>b>0 >(n∈Z,n>1)(a-b)2≥0a,b∈R a2+b2≥2ab|a|-|b|≤|a±b|≤|a|+|b|证明不等式的基本方法比较法(1)要证明不等式a>b(或a<b),只需证明a-b>0(或a-b<0=即可(2)若b>0,要证a>b,只需证明,要证a<b,只需证明综合法综合法就是从已知或已证明过的不等式出发,根据不等式的性质推导出欲证的不等式(由因导果)的方法。
圆锥曲线的参数方程 课件

已知圆 O1:x2+(y-2)2=1 上一点 P 与双曲线 x2 -y2=1 上一点 Q,求 P、Q 两点距离的最小值.
【分析】 圆具有对称性,可转化为用参数法求 Q 到圆心的 距离的最小值.
【解】 设 Q(sec θ,tan θ), 易知 O1(0,2), 则|O1Q|2=sec2θ+(tan θ-2)2 =(tan2θ+1)+(tan2θ-4tan θ+4) =2tan2θ-4tan θ+5=2(tan θ-1)2+3. 当 tan θ=1,即 θ=4π时,|O1Q|2 取最小值 3, 此时有|O1Q|min= 3. ∴|PQ|min= 3-1.
圆锥曲线的参数方程
1.椭圆的参数方程 普通方程 ax22+by22= 1(a>b>0)
ay22+bx22= 1(a>b>0)
参数方程 x=acos φ, y=bsin φ (φ
为参数) x=bcos φ, y=asin φ (φ
为参数)
问题探究:椭圆的参数方程xy==abcsions
φ, φ
中的参数 φ 与圆的
双
曲线ax22
-
y2 b2
=
1(a>0
,b>0)的参数
方程为
x=asec y=btan
φ, φ.
(φ
为参数)
3.抛物线的参数方程 普通方程
参数方程
y2=2px(p>0)
x=2pt2, y=2pt
(t 为参数)
y2=-2px(p>0)
x=-2pt2, y=2pt
(t 为参数)
x2=2py(p>0)
x=2pt, y=2pt2
示同一个椭圆.同样对于双曲线、抛物线也可以用其他形式的参
高中数学三角函数公式大全

第一部分 集合1.理解集合中元素的意义.....是解决集合问题的关键:元素是函数关系中自变量的取值?还是因变量的取值?还是曲线上的点?… ; 2.数形结合....是解集合问题的常用方法:解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解决; 3.(1)含n 个元素的集合的子集数为2n ,真子集数为2n -1;非空真子集的数为2n -2;(2);B B A A B A B A =⇔=⇔⊆ 注意:讨论的时候不要遗忘了φ=A 的情况。
4.φ是任何集合的子集,是任何非空集合的真子集。
第二部分 函数与导数1.映射:注意 ①第一个集合中的元素必须有象;②一对一,或多对一。
2.函数值域的求法:①分析法 ;②配方法 ;③判别式法 ;④利用函数单调性 ;⑤换元法 ;⑥利用均值不等式2222b a b a ab +≤+≤; ⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等);⑧利用函数有界性(xa 、x sin 、x cos 等);⑨导数法 3.复合函数的有关问题 (1)复合函数定义域求法:① 若f(x)的定义域为[a ,b ],则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b 解出② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x ∈[a,b]时,求g(x)的值域。
(2)复合函数单调性的判定:①首先将原函数)]([x g f y =分解为基本函数:内函数)(x g u =与外函数)(u f y =;②分别研究内、外函数在各自定义域内的单调性;③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性。
4.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论。
5.函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件....; ⑵)(x f 是奇函数⇔f(-x)=-f(x);)(x f 是偶函数⇔f(-x)= f(x) ⑶奇函数)(x f 在原点有定义,则0)0(=f ;⑷在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性;⑸若所给函数的解析式较为复杂,应先等价变形,再判断其奇偶性; 6.函数的单调性 ⑴单调性的定义:①)(x f 在区间M 上是增函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x <;②)(x f 在区间M 上是减函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x >;⑵单调性的判定① 定义法:一般要将式子)()(21x f x f -化为几个因式作积或作商的形式,以利于判断符号; ②导数法(见导数部分);③复合函数法;④图像法。
高中数学三角函数公式大全

第一部分 集合1.理解集合中元素的意义.....是解决集合问题的关键:元素是函数关系中自变量的取值?还是因变量的取值?还是曲线上的点?… ; 2.数形结合....是解集合问题的常用方法:解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解决; 3.〔1〕含n 个元素的集合的子集数为2n ,真子集数为2n -1;非空真子集的数为2n -2;〔2〕;B B A A B A B A =⇔=⇔⊆ 注意:讨论的时候不要遗忘了φ=A 的情况。
4.φ是任何集合的子集,是任何非空集合的真子集。
第二部分 函数与导数1.映射:注意 ①第一个集合中的元素必须有象;②一对一,或多对一。
2.函数值域的求法:①分析法 ;②配方法 ;③判别式法 ;④利用函数单调性 ;⑤换元法 ;⑥利用均值不等式2222b a b a ab +≤+≤; ⑦利用数形结合或几何意义〔斜率、距离、绝对值的意义等〕;⑧利用函数有界性〔xa 、x sin 、x cos 等〕;⑨导数法 3.复合函数的有关问题 〔1〕复合函数定义域求法:① 假设f(x)的定义域为[a ,b ],则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b 解出② 假设f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x ∈[a,b]时,求g(x)的值域。
〔2〕复合函数单调性的判定:①首先将原函数)]([x g f y =分解为基本函数:内函数)(x g u =与外函数)(u f y =;②分别研究内、外函数在各自定义域内的单调性;③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性。
4.分段函数:值域〔最值〕、单调性、图象等问题,先分段解决,再下结论。
5.函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件....; ⑵)(x f 是奇函数⇔f(-x)=-f(x);)(x f 是偶函数⇔f(-x)= f(x) ⑶奇函数)(x f 在原点有定义,则0)0(=f ;⑷在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性;⑸假设所给函数的解析式较为复杂,应先等价变形,再判断其奇偶性; 6.函数的单调性 ⑴单调性的定义:①)(x f 在区间M 上是增函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x <;②)(x f 在区间M 上是减函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x >;⑵单调性的判定① 定义法:一般要将式子)()(21x f x f -化为几个因式作积或作商的形式,以利于判断符号; ②导数法〔见导数部分〕;③复合函数法;④图像法。
圆锥曲线的参数方程全解

将y=
b
a x代入①,解得点A的横坐标为
a
①
xA = a2(sec tan).
解: 同理可得,点B的横坐标为xB = a2(sec tan).
设AOx=,则tan b . 所以MAOB的面积为
a
S MAOB =|OA||OB|sin2 =
xA
cos
xB
cos
sin2
过点A作圆C1的切线AA '与x轴交于点A ' ,
过圆C2与x轴的交点B作圆C2的切线BB'与直线OA交于点B'. 过点A ' ,B'分别作y轴,x轴的平行线A' M,B' M交于点M.
双曲线的参数方程
y
设M (x, y) 则A' (x, 0), B'(b, y).
a
B'
A
•M
点A在圆C1上 A(acos,asin).
又OA AA',OA AA'=0
o B A' x
b
AA' =(x-acos,-asin )
a cos(x a cos) (a sin)2 0 解得:x a
又 点B'在角的终边上,记 由三角函数定义有:tan y .
co1sy消saxbe去22cta参n数by22得:x1
2
2
说明:⑴ 这里参数 叫做双曲线的离心角与直线OM
的倾斜角不同. ⑵ 双曲线的参数方程可以由方程
x2 a2
y2 b2
1
与三角
恒等式sec2 1 tan2 相比较而得到,所以双曲
线的参数方程的实质是三角代换.
圆锥曲线的参数方程 课件

规律技巧 利用双曲线的参数方程,可以求目标函数的最 值,这是常见题型的解题方法,一定要熟练掌握.
点M所对应的圆的半径OA(或OB)的旋转角,不是OM的旋转角,
而圆的参数方程中的θ是半径OM的旋转角,椭圆参数方程中的φ称
为点M的离心角.
思考探究2
抛物线y2=2px(p>0)的参数方程
x=2pt2, y=2pt
(t为
参数)中参数t的几何意义是什么?
提示 由抛物线参数方程的推导过程可知,参数t表示抛物线
【例2】
已知A、B分别是椭圆
x2 36
+
y2 9
=1的右顶点和上顶
点,动点C在该椭圆上运动,求△ABC的重心G的轨迹的普通方
程.
【解】 如图所示:
由动点C在该椭圆上运动,故可设C的坐标为(6cosθ,3sinθ), 点G的坐标为(x,y),由题意可知A(6,0),B(0,3),由三角形重心坐 标公式可知:
(φ为参数).通常规定参数φ的取值范围为
[0,2π).
(2)双曲线ay22-bx22=1的参数方程为xy= =batsaencφφ, (φ为参数).
(3)另三种情况抛物线的参数方程如下:
普通方程
参数方程
y2=-2px(p>0)
x=-2pt2, y=2pt
(t为参数)
x2=2py(p>0)
x=2pt, y=2pt2
上除顶点外的任意一点与原点连线的斜率的倒数.
名师点拨 1.圆、椭圆、双曲线的参数方程
圆、椭圆、双曲线的参数方程如下表:
点所在的 x2+y2=r2
曲线
ax22+by22=1
ax22-by22=1
参数方程
x=rcosθ, y=rsinθ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
a 2.定义运算 c
A. 3 i
b 1 1 ad bc ,则符合条件 4 2i 的复数 z 为( d z zi
B. 1 3i
2
)
C. 3 i
D. 1 3i )
3.在复数集 C 内分解因式 2 x 4 x 5 ,则分解为( A. ( x 1 3i)( x 1 3i) C. 2( x 1 i)( x 1 i)
命题,棱长为 a 的正四面体内任一点到四个面的距离之和为( ) D.
4 A. a 3
6 B. a 3
5 C. a 4
BB
1, 6.复平面内点 A,B,C 对应的复数分别为 i ,4 2i ,由 A B C D 按逆时针顺序
作平行四边形 ABCD ,则 BD 等于( A. 5 B. 13 ) C. 15 D. 17
y x 上,则 mn 的值等于(
A. 0 B. 1 C. 10
)
1 D. 10
DBB
4.用反证法证明某命题时,对其结论: “自然数 a,b,c 中恰有一个偶数”正确的反设为 ( ) A. a,b,c 都是奇数 B. a,b,c 都是偶数 C. a,b,c 中至少有两个偶数 D. a,b,c 中至少有两个偶数或都是奇数 5.若关于 x 的方程 x2 (1 2i) x (3m 1)i 0 有实根,则纯虚数 m 等于( )
2 b2 x2 y 2 y 2 y0 b2 2 2 ,即 k AP kBP 2 . 故椭圆 2 2 1(a b 0) 中过中心的一条弦 2 a a b x x0 a
k 的两个端点 A,B,P 为异于 A,B 的椭圆上的任意一点,则有 k AP BP
b2 2 . a
*
)
7.把数列 2n 1 (n N ) 依次按第一个括号一个数,第二个括号两个数,第三个括号三
7) 1113) 个数,第四个括号四个数,第五个括号一个数,„循环,分别为: (3) , (5, , (9,, ,
(1517 19 21) , (23) , (25, , (29,, , (35, , , ,„,则第 104 个括号内各 ,,, 31 33) 37 39 41) 27)
A. 9(n 1) n 10n 9 C. 9n (n 1) 10n 1
)
B. 9(n 1) n 10n 9 D. 9(n 1) (n 1) 10n 10
3 5.平面几何中,有边长为 a 的正三角形内任一点到三边距离之和为定值 a ,类比上述 2
x2 y 2 kAC kBC 1.你能用类比的方法得出椭圆 2 2 1(a b 0) 中有什么样的结论? a b
x2 y 2 2 2 a 2 b 2 1, x 2 x0 y 2 y0 0, 由于 A,B,P 三点在椭圆上, 2 两式相减,有 2 a2 b2 x0 y0 1. a 2 b2
1.下面几种推理是合情推理的是( ) ①由圆的性质类比得出球的有关性质; ②由直角三角形、等腰三角形、等边三角形内角和是 180°,归纳出所有三角形的内角和都 是 180 ;
360 ,五边形内角和是 540 ,由此得出凸多边形内角和是 (n 2) . 180 ③四边形内角和是
A.①② B.①③ C.②③ D.①②③
B. ( 2x 2 3i)( 2x 2 3i) D. 2( x 1 i)( x 1 i)
AB
4 . 观 察 按 下 列 顺 序 排 列 的 等 式 : 9 0 1 1 , 9 1 2 11 , 9 2 3 21 ,
9 3 4 31,„,猜想第 n(nN* ) 个等式应为(
n2 11.答案: f (2 ) 2 12.答案: 2
2
1.复数 z i 的虚部为(
1 i
5
测试三
)
A. 16 i B. 32 i C. 32 D. 32 2.下列①②③可组成一个“三段论” ,则“小前提”是( ) ①只有船准时起航,才能准时到达目的港; ②这艘船是准时到达目的港的; ③这艘船是准时起航的. A.① B.② C.②和③ D.③ 3.已知复数 z lg m (lg n )i ,其中 i 是虚数单位.若复数 z 在复平面内对应的点在直线
2 2
.
9 在 △ ABC 中,若 C 90 ,则 cos A cos B 1 .在立体几何中,给出四面体类似性 质的猜想.
3 8 答案: sin 10 cos 40 sin10 sin 40 4
2 2
2 2 a b a b 2 2 9 解:如图, ,在 Rt△ ABC 中, cos A cos B 1. 2 c c c 2 2
测 1.演绎推理是( ) A.特殊到一般的推理
C.一般到特殊的推理
B.特殊到特殊的推理 D.一般到一般的推理
试 A. m 1 或 m 2 一3.设 S (n) 1
2 1 C. m 2
2. m R ,复数 (2m2 3m 2) (m2 3m 2)i 表示纯虚数的充要条件是( B. m 2 D. m 2 或 m 1
8.用数学归纳法证明“ 5 2 能被 3 整除”的第二步中,当 n k 1 时,为了使用假设的
n n
结论,应将 5 2 变形为( A. (5 2 ) 4 5 2
k k k k
k 1
k 1
) B. 5(5 2 ) 3 2
k k k
CB
C. (5 2)(5 2 )
)
x y 5.在平面直角坐标系内,方程 1 表示在 x 轴、 y 轴上的截距分别为 a,b 的直线, a b
拓展到空间,在 x 轴、 y 轴、 z 轴上的截距分别为 a,b,c(abc 0) 的平面方程为(
)
x y z A. 1 a b c xy yz zx C. 1 ab bc ca
P(0) 0 ,则下列结论中错误的是(
A. P(3) 3 C. P(2007) P(2006)
) B. P(5) 1 D. P(2003) P(2006)
D
(1 i) 3(1 i) 9.已知复数 z ,若 z 2 az b 1 i(a,b R) ,求 a b 的值. 2i
1 A. i 12
1 B. 12
1 C. i 12
1 D. 12
π π 6. “三角 函数是 周期函 数, y tan x , x , 是三角函 数,所 以 y tan x , 2 2 π π .在以上演绎推理中,下列说法正确的是( x , 是周期函数” 2 2
于是, 把结论类比到四面体, 我们猜想: 在四面体 P ABC 中 (如图 2) 若三个侧面 PAB , ,
PBC , PCA 两 两 互 相 垂 直 , 且 分 别 与 底 面 所 成 的 角 为 ,, , 则
c o 2s c 2 os
2 c o . s
1
测 试 二
解:设 A( x0,y0 ) 为椭圆上的任意一点,则 A 关于中心的对称点 B 的坐标为 B( x0, y0 ) , 点 P( x,y ) 为椭圆上异于 A,B 两点的任意一点,则 k AP BP k
2 y y0 y y0 y 2 y0 . 2 2 x x0 x x0 x x0
k k
D. 2(5 2 ) 3 5
k k
k
9..若复数 z A. 2
a 3i (a R ) 是纯虚数,则 a 的值等于( ) 1 2i B. 4 C. 6 D. 6
2 2
11 观察给出的下列各式:
a 10.若 a,bR ,且 (a i) (1 b i) 3 2i ,则 的值等于 b
2
2i 3 3i 3 i 解: z 1 i , 2i 2i
(1 i)2 a(1 i) b 1 i ,
(a b) (2 2i) 1 i , a b 1
10.在圆 x2 y 2 r 2(பைடு நூலகம்r 0) 中, AB 为直径 , C 为圆上 异于 A,B 的任 意一 点, 则有
x y z B. 1 ab bc ca
D. ax by cz 1
DA
a bi R ,则( 6.设 a,b,c,d R 且 c, d 不全为零,若 cdi A. bc ad 0 B. bc ad 0 C. bc ad 0 D. bc ad 0
.
(1) tan10 tan 20 tan 20 tan 60 tan 60 tan10 1 ; (2) tan5 tan15 tan15 tan 70 tan 70 tan5 1 .
由以上两式成立,你能得到一个什么样的推广? π π 若 , 且 ,, 都 不 等 于 kπ (k Z) , 则 有 2 2
1 1 1 3 5 * 11.f (n) 1 (n N ) , 计算得 f (2) ,f (4) 2 ,f (8) ,f (16) 3 , 2 3 n 2 2 7 . f (32) .由此推测,当 n 2 时,有 2 a i 12.已知 z ,其中 a 0 ,i 为虚数单位.复数 z( z i) 的虚部减去它的实部所得 1 i 3 的差为 ,则 a 2
)
1 1 1 1 2 (n N* ) ,当 n 2 时, S (2) ( n n 1 n 2 n 3 n 1 1 1 A. B. 2 2 3 1 1 1 1 1 1 1 C. D. 2 3 4 2 3 4 5
