2020年土木工程高起本高等数学期末考试答案
高等数学期末试题(含答案)

高等数学期末试题(含答案) 高等数学检测试题一。
选择题(每题4分,共20分)1.计算 $\int_{-1}^1 xdx$,答案为(B)2.2.已知 $2x^2y=2$,求$\lim\limits_{(x,y)\to(0,0)}\frac{x^4+y^2}{x^2y}$,答案为(D)不存在。
3.计算 $\int \frac{1}{1-x}dx$,答案为(D)$-2(x+\ln|1-x|)+C$。
4.设 $f(x)$ 的导数在 $x=a$ 处连续,且 $\lim\limits_{x\to a}\frac{f'(x)}{x-a}=2$,则 $x=a$ 是 $f(x)$ 的(A)极小值点。
5.已知 $F(x)$ 的一阶导数 $F'(x)$ 在 $\mathbb{R}$ 上连续,且 $F(0)=0$,则 $\frac{d}{dx}\int_0^x F'(t)dt$ 的值为(D)$-F(x)-xF'(x)$。
二。
填空:(每题4分,共20分)1.$\iint\limits_D dxdy=1$,若 $D$ 是平面区域 $\{(x,y)|-1\leq x\leq 1,1\leq y\leq e\}$,则 $\iint\limits_D y^2x^2dxdy$ 的值为(未完成)。
2.$\lim\limits_{x\to\infty}\frac{\left(\cos\frac{\pi}{n}\right)^2+\left(\cos\frac{2\pi}{n}\right)^2+\cdots+\left(\cos\frac{(n-1)\pi}{n}\right)^2}{n\pi}$ 的值为(未完成)。
3.设由方程 $xyz=e$ 确定的隐函数为 $z=z(x,y)$,则$\frac{\partial z}{\partial x}\bigg|_{(1,1)}$ 的值为(未完成)。
4.设 $D=\{(x,y)|x^2+y^2\leq a^2\}$,若$\iint\limits_D\sqrt{a^2-x^2-y^2}dxdy=\pi$,则 $D$ 的面积为(未完成)。
2020年土木工程高起本画法几何与工程制图期末考试答案
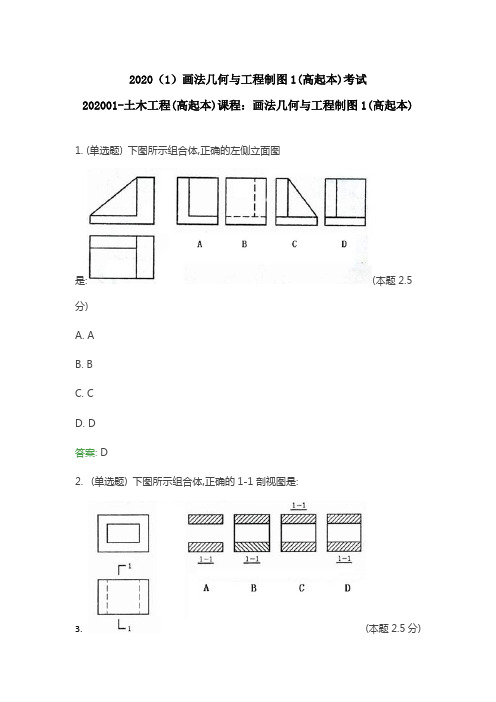
2020(1)画法几何与工程制图1(高起本)考试202001-土木工程(高起本)课程:画法几何与工程制图1(高起本) 1. (单选题) 下图所示组合体,正确的左侧立面图是:(本题2.5分)A. AB. BC. CD. D答案: D2. (单选题) 下图所示组合体,正确的1-1剖视图是:3.(本题2.5分)A. AB. BC. CD. D答案: B3. (单选题) 下图所示组合体,正确的1-1断面图是:(本题2.5分)A. AB. BC. CD. D答案: A4. (单选题) 下图中已知组合体正面图和侧面图,正确的平面图是:(本题2.5分)A. AB. BC. CD. D答案: D5. (单选题) 下图为截切后正圆柱的三面投影,正确的H面投影是:(本题2.0分)A. AB. BC. CD. D答案: C6. (单选题) 下图所示圆锥被正垂面P所截,其截交线的形状是:(本题2.0分)A. 三角形B. 椭圆与直线C. 双曲线与直线D. 抛物线与直线答案: B7. (单选题) 下图所示三棱柱与半球相贯,相贯线的空间形状是:(本题2.0分)A. 圆曲线、椭圆与椭圆的组合B. 空间曲线C. 圆曲线、圆曲线与圆曲线的组合D. 椭圆、椭圆与椭圆的组合答案: C8. (单选题) 在下图中已知形体的三面投影图,则与其吻合的轴测图是:(本题2.0分)A. AB. BC. CD. D答案: D9. (单选题) 下图所示六棱锥被正垂面P所截,其截交线的形状是:(本题2.0分)A. 三角形B. 五边形C. 六边形D. 七边形答案: D10. (单选题) 下图所示正垂面圆O的水平投影是:(本题2.0分)A. 直线B. 椭圆C. 圆D. 双曲线答案: B11. (单选题) 下图所示的曲面是:(本题2.0分)A. 柱面B. 锥面C. 回转面D. 螺旋面答案: D12. (单选题) 下图所示AB直线与三角形CDE平面的相对几何关系是:(本题2.0分)A. AB在三角形CDE内B. AB与三角形CDE相交不垂直C. AB与三角形CDE垂直D. AB与三角形CDE平行答案: D13. (单选题) 下图所示A、D两点是:(本题2.0分)A. V面投影重影点B. H面投影重影点C. W面投影重影点D. 非投影重影点答案: C14. (单选题) 下图所示五棱柱表面上一点K,其正确的侧面投影是:(本题2.0分)A. AB. BC. CD. D答案: B15. (单选题) 下图所示AB直线是:(本题2.0分)A. 水平线B. 正平线C. 侧平线D. 一般倾斜直线答案: D16. (单选题) 在下面的投影图中,反映线段实长的投影是:(本题2.0分)A. a'b'B. b'c'C. acD. 无答案: A17. (单选题) 下图所示AB、CD两直线的相对几何关系是:(本题2.0分)A. 平行B. 相交C. 相交垂直D. 交错答案: B18. (单选题) 下图所示AB、CD两直线的相对几何关系是:(本题2.0分)A. 平行B. 相交垂直C. 相交不垂直D. 交错答案: D19. (单选题) 下图所示ABCDE平面的类型是:(本题2.0分)A. 正垂面B. 铅垂面C. 侧垂面D. 一般倾斜平面答案: B20. (单选题) 下图所示K点在球面上的位置是:(本题2.0分)A. 球面的左下前部B. 球面的右下前部C. 球面的左上前部D. 球面的左上后部答案: D21. (单选题) 轴测投影是根据什么原理投射得到的:(本题2.0分)A. 平行投影B. 中心投影C. 正投影D. 斜投影答案: A22. (单选题) 下图所示正平面P与三角形平面ABC的交线是:(本题2.0分)A. 正平线B. 水平线C. 铅垂线D. 一般倾斜直线答案: A23. (单选题) 下图所示P、Q两平面的相对几何关系是:(本题2.0分)A. 平行B. 垂直C. 相交D. 不确定答案: B24. (单选题) 下图为球面被两个正垂面切割,其切口的空间形状是:(本题2.0分)A. 椭圆曲线与椭圆曲线的组合B. 椭圆曲线与双曲线的组合C. 圆曲线与圆曲线的组合D. 矩形与椭圆曲线的组合答案: C25. (多选题) 关于投影法及视图,下列说法正确的是( )。
土木工程施工期末考试试卷带答案

8皮数杆是木质标志杆,皮数杆上标明(D)
A柱的平面位置B窗的平面位置C圈梁的平面位置D过梁的标高
9砌块砌体的砂浆中的砂宜采用(A)
A中砂B粗砂C细砂D粗细砂
10后张法灌浆施工中优先灌注(B)
A下层孔道B上层孔道C中间孔道D左右孔道
三、简答题( 每题5分,共20分)
A混凝土的浇筑一次完成,不允许留施工缝
B混凝土的浇筑二次完成,不允许留施工缝
C混凝土的浇筑一次完成,允许留施工缝
D混凝土的浇筑二次完成,允许留施工缝
5下列土中不适宜作为填土的土料是(A)。
A冻土B粘性土C石子D砂子
6预制桩打桩施工中,垂直度偏差不得超过(A)
A0.5%B1%C1.5% D2%
7泥浆护壁成孔灌注桩的混凝土浇筑方法是(D)
N=8
H=Na^2=(Σa^2(H(i1)+H(i2)+H(i4))/4)
则H0=(Σ(H(i1)+H(i2)+H(i3)+H(i4))/4N=(ΣH1+2ΣH2+3ΣH3+4H4)/4N
因为土的可松性,在调整:Hn=H0±Lx*I
3三顺一丁
三皮顺砖与一皮丁砖相间,顺砖与顺砖上下皮,垂直灰缝相互错开1/2砖,长顺砖与丁砖上下皮,垂直灰缝相互错开1/4砖长
4卷材防水屋面
只采用高分化购物卷材,柔性防水材料贴成一整片,防水屋面覆盖层
二、单项选择题(每题3分,共30分)
1正铲挖土机的工作特点是(C)。
A后退向下,强制切土B后退向上,强制切土
C前进向上,强制切土D后退向上,被动切土
2根据《建筑装饰装修工程质量验收规范》,一般抹灰工程阴阳角方正的检验方法是用(C)检测。
高数本科期末试题及答案

高数本科期末试题及答案一、选择题(每题5分,共20分)1. 设函数f(x)=x^2-2x+1,下列说法正确的是:A. 函数在(-∞,1)上单调递减B. 函数在(1,+∞)上单调递增C. 函数在(-∞,1)和(1,+∞)上单调递增D. 函数在(-∞,1)和(1,+∞)上单调递减答案:B2. 曲线y=x^3-3x^2+4x在点(1,2)处的切线斜率为:A. 2B. 4C. 6D. 8答案:A3. 以下哪个选项是函数y=e^x的原函数:A. x*e^xB. x^2*e^xC. x*e^x + 1D. e^x + x答案:C4. 极限lim(x→0) (sin x)/x的值为:A. 0B. 1C. 2D. ∞答案:B二、填空题(每题5分,共20分)1. 设f(x)=x^3-6x^2+11x-6,f'(x)=______。
答案:3x^2-12x+112. 曲线y=x^2+2x-3在点(-1,0)处的法线方程为______。
答案:x-y+1=03. 函数y=ln(x)的不定积分为______。
答案:x*ln(x)-x+C4. 级数1+1/2+1/4+1/8+...的和为______。
答案:2三、解答题(每题15分,共30分)1. 求函数f(x)=x^3-3x^2+2x+1在区间[0,2]上的最大值和最小值。
答案:首先求导数f'(x)=3x^2-6x+2。
令f'(x)=0,解得x=1或x=2/3。
检验得在x=1处函数取极小值,为f(1)=-1;在x=2/3处函数取极大值,为f(2/3)=19/27。
在区间端点处,f(0)=1,f(2)=3,故最大值为3,最小值为-1。
2. 计算定积分∫(0到1) (2x+1)dx。
答案:首先求原函数F(x)=x^2+x。
代入积分限得F(1)-F(0)=1^2+1-(0^2+0)=2。
因此,定积分的值为2。
四、证明题(每题15分,共15分)1. 证明函数f(x)=x^3在(-∞,+∞)上是单调递增的。
2020-2021学年高等数学期末考试题(含答案)

2020-2021学年高等数学期末考试(含答案)一、填空题 (本大题分6小题, 每小题3分, 共18分)1. 已知f (x ) =x-11, 则f [f (x )] = .2. 设f (1+Δx ) - f (1) = 2Δx + (Δx )2, 则)1(f '= .3. f (x ) = x + cos x 的单调递增区间为 .4. 不定积分⎰=+xdx x 22tan )tan 1( . 5.⎰-=++113)1cos 3(dx x x x .6. 点M (-1, 2, 3)关于坐标面x o y 的对称点为 . 二、单项选择题 (本大题分6小题, 每小题3分, 共18分)1. 设函数f (x ) =⎪⎩⎪⎨⎧≥+<0,,0,2sin x x a x x x 在x = 0处连续, 则常数a =( )A . 0;B . 1;C . 2;D . 3. 2. 已知一个函数的导数为x y 2=', 且x = 1时y = 2, 则这个函数是( )A . 12+=x y ;B . 23212+=x y ; C . C x y +=2;D . y = x + 1. 3. 下列函数中在[-1, 1]上满足拉格朗日中值定理条件的是( )A . ||x y =;B . )1ln(2x y +=;C . )1ln(x y +=;D . x y 1=. 4. 设f (x ) =⎰x tdt 0sin , 则f (f (2π))等于( )A . -1;B . 1;C . -cos1;D . 1-cos1.5. 下列反常积分收敛的是( )A . ⎰∞+e dx xx ln ;B . ⎰∞+e xx dxln ;C .⎰∞+ex x dx2)(ln ;D . ⎰∞+e x x dx ln .6. 同时垂直于向量a = (2, 1, 1)和b = (0, 1, 1)的单位向量是( )A . )21,21,0(; B . )21,21,0(-;C . )31,31,31(-; D . )31,31,31(.三、计算题 (本大题分5小题, 每小题8分, 共40分)1. 求极限: ⎪⎭⎫⎝⎛-+∞→x x x arctan 2lim π.2. 求曲线922=-xy y 在点(0, 3)处的切线方程和法线方程.3. 设函数f (x )的一个原函数为xxsin , 求⎰'.)(dx x f x4. 计算I =⎰++70311x dx.5. 计算I =⎰-1.|)12(|dx x x四、应用题(本大题分2小题, 每小题9分, 共18分)1. 已知函数f (x ) =dt t kt t x )2sin (1⎰-在x =6π处有极值, 求常数k 的值, 并讨论是极大值还是极小值.2. 求曲线y = e x , y = e -x 和直线x = 1所围成平面图形的面积A 以及其绕x 轴旋转而成的旋转体的体积V x .五、证明题(本大题6分) 证明: 当x > 0时, 有ln(1+x ) >xx+1.一、填空题 (本大题分6小题, 每小题3分, 共18分)1. x 11-;2. 2;3. (-∞, +∞);4.C x +3tan 31; 5. 2;6. (-1, 2, -3).二、单项选择题 (本大题分6小题, 每小题3分, 共18分) 1. C ; 2.A ; 3. B ; 4.D ; 5. C ; 6. B .三、计算下列各题 (本大题分5小题, 每小题8分, 共40分)1. 解: ⎪⎭⎫ ⎝⎛-+∞→x x x arctan 2lim π=x x x 1arctan 2lim -+∞→π (2分) =22111lim xx x -+-+∞→ (2分)=221lim x x x ++∞→ (2分)=1. (2分) 2. 解: 0222='--'⋅y x y y y , (2分)xy yy -=', (1分)10='=x y . (1分) 因此,所求切线方程为y - x = 3; (2分) 法线方程为y + x = 3. (2分)3. 解: 因为2sin cos )(xxx x x f -=, (2分)所以, ⎰'dx x f x )(=⎰)(x xdf (2分) = ⎰-dx x f x xf )()((2分) =2sin cos xx x x x -⋅C x x +-sin (1分) =C x x x +-sin 2cos .(1分) 4. 解: 设t x =+31, (1分)则13-=t x , dt t dx 23=. 当x = 0时, t =1; 当x = 7时, t = 2. (1分)因此⎰++70311x dx =⎰+21213tdtt =(1分)⎰++-2121113tdtt =⎰++-21)111(3dt tt (2分) =))1ln(21(32121212t t t ++- (2分)=)2ln 3ln 123(3-+-=23ln 23+. (1分)5. 解: ⎰-10|)12(|dx x x =⎰-210)21(dx x x +⎰-121)12(dx x x (4分)=210221032132x x+-121212132132x x -+(2分)=81211213281121+--++-=41. (2分) 四、应用题(本大题分2小题, 每小题9分, 共18分)1. 解: )(x f '=x k x 2sin 2-, (2分)若f (x )在x =6π处有极值, 则0)6(='πf , (2分)即得k = 1. (1分)又)(x f ''=221sin 2cos 2x x x x +-, (2分)从而0)6(>''πf ,(1分)所以f (6π)为f (x )的极小值. (1分) 2. 画图, (1分)所求面积为⎰--=10)(dx e e A x x (2分)=110x xe e -+=21-+-e e . (2分)所求体积为V x =⎰--1022)(dx eexxπ(2分)=)2121(10212x xe e -+π=)2(2122-+-e e π.(2分)五、证明题(本大题6分)证明: 设x x x x f -++=)1ln()1()(, (1分)则)1ln()(x x f +=', (1分)当x > 0时, 有0)(>'x f , (1分)即f (x )在[0, +∞)上单调增加, (1分)所以, 当x > 0时, 有f (x ) > f (0) = 0, (1分)因此, 当x > 0时, 有ln(1+x ) >xx+1.(1分)。
吉大2019-2020学年第二学期期末考试《土木工程制图》大作业参考答案

我国的非标准劳动关系是在市场经济快速发展,就业形式日益严峻的大背景下产生并发展 起来的,更多的是缓解就业压力的产物。由于国有企业改革,我国的城镇失业率一直居高不下, 而传统的僵化的固定就业模式刚性太大,不利于缓解就业压力。非标准劳动关系对于降低用人 单位的用工成本、方便劳动者自由选择劳动时间、缓解就业压力、扩大就业机会等作用越来越 突出,正成为就业的重要渠道,使劳动关系呈现出多元化、复杂化格局。非标准劳动关系突破 了标准劳动关系的内涵,对原有的劳动关系法律调整机制提出了新的挑战。随着非标准劳动关 系的不断发展,我国传统的标准劳动关系法律调整体系已经越来越不适应非标准劳动关系调整 的需求。非标准劳动关系对传统法律的挑战主要体现在以下几方面:
法权利。但是,目前我国法律对于社会保险制度的规范,都是按照标准就业的特点设计运作的, 包括计费年限、缴费办法和待遇标准等。这种模式的社会保障制度以就业的稳定性和缴费的连 续性为基础,而这种制度不完全适合非标准劳动关系就业的特点。比如社会保险的转移由于各 地社会保险的缴费标准、待遇标准等不同,操作起来比较困难。
吉林大学网络教育学院
2019-2020 学年第二学期期末考试《土木工程制图》大作业
作业要求:大作业要求学生手写完成,提供手写文档的清晰扫描图片,并将图片添加到 word 文档内,最终 wod 文档上传平台,不允许学生提交其他格式文件(如 JPG,RAR 等非 word 文档格式),如有雷同、抄袭 成绩按不及格处理。
1.法律适用和劳动主体方面 我国现行的劳动法律主要以标准劳动关系为主,很多非标准劳动关系被排斥在基本法律调 整的范围之外。 此外,我国《劳动法》主要覆盖的是传统行业的劳动者,范围狭窄。非标准 劳动关系就业人员中有些是在《劳动法》或者《劳动合同法》调整范围之内,如劳动者派遣关 系中的劳动者等,但还有很多人被排斥在这两部法律的调整之外,如家政人员等。我国非标准 劳动关系调整的现状要求劳动主体适用范围必须扩大。 2.劳动关系的建立ห้องสมุดไป่ตู้面 根据《劳动法》的规定,只有用人单位与劳动者之间才能建立劳动关系。用人单位可以是 企业也可以是个体经营者,但不能是个人。但是在非标准劳动关系领域,用人的一方有可能是 个人、家庭和自营经济实体等。不属于《劳动法》规定的用人单位,因此这种法律关系不受劳 动法的调整。因此,很长时间以来,非标准劳动关系就业人员与用人方之间仅被视为具有平等 主体之间的民事权利义务关系。发生民事权益问题,按民事诉讼的程序处理。实际上,无论是 标准劳动关系就业还是非标准劳动关系就业,都是具有劳动能力的公民从事为国家和社会承认 的社会工作,并以此获得用以维持本人及家庭生活的劳动报酬或者经营收入。因此,将非标准 劳动关系放在劳动关系调整之外不符合非标准劳动关系的本质特征,也容易导致非标准劳动关 系就业人员丧失本该享有的劳动权利。 3.劳动关系和雇佣关系的处理 劳动关系中对劳动者的保护比较全面,它包括了劳动过程中的各项权利,除法定的劳动标 准外,还包括无过错责任的工伤保护原则和接触劳动关系的补偿原则等。而雇佣关系中的劳动 者的权利仅受私法的调整,按照平等主体之间的民事权利义务关系来处理,如出现劳动中的人 身伤害,只能根据过错程度来分担责任。但实际上,雇佣关系跟劳动关系在本质上是相同的, 因为两种关系中间的劳动者都不拥有生产资料且劳动的目的都是生产过程和获得劳动报酬,而 且雇佣关系和劳动关系一样,具有从属性,雇员接受雇主的指挥、管理和监督,雇主为雇员提 供合理的劳动条件和安全保障。因此,如果直接用雇佣关系的原则来调整一些非标准劳动关系 不符合我国劳动者权益保护这一劳动法宗旨。 4.社会保障方面 在我国,社会保障是实现社会保护的核心所在,非标准劳动关系的社会保障问题是一项宪
2020年国家开放大学电大《土木工程力学》期末考试题及答案

A b c d e f g h i j k l m n o p q r s t u v w x y z B5.不能作为建筑结构使用的是(D )D几何可变体系B64、不考虑杆件的轴向变形,竖向杆件的EI=常数。
图示体系的振动自由度为()A1C16、超静定结构产生内力的原因有()D以上三种原因(荷载温度、支座、制造)C17、超静定结构在荷载作用下产生的内力与刚度()A相对值有关C18、超静定结构在支座移动作用下产生的内力与刚度()C绝对值有关C84.超静定结构的超静定次数等于结构中(B )B.多余约束的数目D28、对称结构作用正对称荷载时,对称轴穿过的截面()D既有轴力又有弯矩D29、对称结构在反对称荷载作用下,内力图中()A 剪力图正对称D30、对称结构在反对称荷载作用下,内力图中()B 弯矩图反对称D31、对称结构在正对称荷载作用下,内力图中()C 剪力图反对称F68、反映结构动力特性的重要物理参数是()B自振频率G61、根据影响线的定义,图示悬臂梁A截面的剪力影响线在B点的纵坐标为()C1G75.根据影响线的定义,图示悬臂梁A截面的剪力影响线在B点的纵坐标为( A )A. 1 B.-4 C. 4 D.-1A4mB1PF左上右下剪力为正,左顺右逆弯矩为正。
G T 1C 0G1.根据影响线的定义,图示悬臂梁A截面的弯矩(下侧受拉为正)影响线在B点的纵坐标为( B )。
A.0 B.-4m C.4m D.-1mH49、汇交于一刚结点的各杆端弯矩分配系数之和等于()A1H57、绘制影响线采用的是()D单位移动荷载H 9.荷载作用下产生桁架位移的主要原因是(A )A 轴向变形H66、忽略直杆轴向变形的影响,图示体系有振动自由度为()C4J1、静定结构产生位移的原因有()D以上四种原因(荷载温度、支座、制造)J 3.静定结构产生内力的原因有()。
荷载作用J2、静定结构由于温度变化、制造误差或支座位移,()C不发生变形,但产生位移J6.静定结构由于支座位移,()。
2021年工程大学土木工程专业《高等数学A1》 期末考试试卷及答案

2021年工程大学土木工程专业 《高等数学A1》 期末考试试卷(闭卷)专业: 姓名: 学号:一、填空题(本大题共10个空,每空3分,共30分)1. 函数y =的定义域为.2. 设函数sin ,0()4,0kxx f x x x x ⎧<⎪=⎨⎪+≥⎩在0x =处连续,则k = .3. 曲线y =1,2)处的法线方程为 .4. 函数221y x x =-+在区间[1,3]-上满足拉格朗日中值定理的ξ= .5. 332235lim 351x x x x x →∞-+=+- .6. 21()x d tdt dx =⎰ .7. 曲线131y x =+的凹区间为 . 8. 若2()xf x dx x eC -=+⎰,则()f x = .9. 3331cos xdx x ππ-+⎰= .10.221dx x+∞⎰= .二、选择题(本大题共5小题,每题3分,共15分)11. 当0x →时,下列无穷小量中,与21x e-等价的无穷小量为( )A. 2x B. 2sin x x C. 23x D. 23x12. 函数()f x 在0x 可导是()f x 在0x 连续的( )条件 A. 充要条件 B. 充分条件 C. 必要条件 D. 无关条件 13. 设sin y x x =,则dy =( )A .(1cos )x dx -B . cos xdxC .(sin cos )x x x dx +D .(sin cos )x x dx +14. 设0()f x '存在,则下列4个极限中等于0()f x '的是( )A.000()()lim x f x x f x x ∆→-∆-∆ B.000()()lim h f x f x h h →--C.000()()limx x f x f x x x →-- D.000()()lim h f x h f x h h→+--15. 由抛物线2y x =与22y x =-所围成的图形绕x 轴旋转所得旋转体的体积为( ) A. 1221[(2)]V x x dx -=--⎰B. 1221[(2)]V x x dx -=--⎰C. 1142211(2)V x dx x dx ππ--=--⎰⎰D. 1122411(2)V x dx x dx ππ--=--⎰⎰装订线《高等数学A1》第 1页(共6页)《高等数学A1》第 2页(共6页)三、计算题(本大题共9小题,每小题5分,共45分)16. 30sin lim x x xx→- 17. 0lim ln x x x +→18. 120lim(13)xx x →+19. (ln x x dx ⎰20.21. 22ππ-⎰22. 求由方程x yxy e+=所确定的隐函数的导数dy dx.23. 求函数32395y x x x =--+的极值.24. 求由参数方程2ln(1)arctan x t y t t⎧=+⎨=-⎩确定的函数的导数dydx .装订线《高等数学A1》第 3页(共6页)《高等数学A1》第 4页(共6页)四、应用题(本大题共2小题,每题5分,共10分)25. 求由曲线sin y x =、cos y x =与直线0x =、2x π=所围成的图形的面积(作图).26. 证明:当1x >时,xe e x >⋅.装订线《高等数学A1》第 5页(共6页)《高等数学A1》第 6页(共6页)《高等数学A1》 期末考试试卷答案及评分标准一、填空题(本大题共10个空,每空3分,共30分)1.(0,2)2.43.2y x =4.15.236.32x7.(,0]-∞ 8.(2)xxe x -- 9.0 10.12二、选择题(本大题共5小题,每题3分,共15分)11.A 12.B 13.C 14.B 15.D三、计算题(本大题共9小题,每小题5分,共45分)16. 30sin limx x xx→- 20cos 1lim 3x x x →-= 2分0sin lim 6x xx→-=4分16=-5分17. 0lim ln x x x +→0ln lim 1x xx+→= 2分lim()x x +→=- 4分 0=5分 18.令3,,0,03tx t x x t ==→→1分120lim(13)xx x →+320lim(1)tt t →=+3分3121lim (1)tt t →⎡⎤=+⎢⎥⎣⎦4分32e =5分19.解:(ln x x dx ⎰ln x xdx =+⎰⎰1分22111ln (1)222x x xdx x =---⎰3分32422111ln (1)243x x x x C =---+5分20.解:令2tan ,,sec 22x t t dx t dt ππ=-<<=1分2sec sec tdt t =⎰2分 dt =⎰3分 t C =+4分arctan x C =+5分21.解:22ππ-⎰2=1分2xdx =2分2(cos )x =-3分32204[cos ]3x π=-4分=435分 22.解:方程两边对x 求导得1分 (1)x yy xy e y +''+=+3分解得x y x ydy e ydx x e++-=-5分23.解:23693(1)(3)y x x x x '=--=+- 令0y '=,得1,3x x =-=2分(,1)x ∈-∞-时,0y '>,(1,3)x ∈-时,0y '< (,1)x ∈-∞-时,0y '>3分 函数在1x =-取得极大值, 在3x =取得极小值4分 (1)10,(3)22f f -==-5分24.解:2211121dy t t dxt -+=+3分2t=5分四、应用题(本大题共2小题,每题5分,共10分)25.解:如图1分4(cos sin )S x x dx π=-⎰24(sin cos )x x dx ππ+-⎰3分4204[sin cos ][cos sin ]t t x πππ=++--4分2=-5分 26.证明:令 ()xf x e e x =-⋅1分 ()xf x e e '=-2分 当1x >时,()0f x '>,()f x 在[1,)+∞单调递增3分 又(1)0f =,所以1x >时,()0f x >4分 即当1x >时,xe e x >⋅5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学上高起本期末考试
202001-土木工程(高起本)课程:高等数学上册(高起本)
1. (单选题) 设函数,则其间断点的个数是()。
(本题4.0分)
A. 0
B. 1
C. 2
D. 3
答案: C
2. (单选题) (). (本题4.0分)
A.
B.
C.
D.
答案: C
3. (单选
题) (本题4.0分)
A.
B.
C.
D.
答案: A
4. (单选题) (). (本题4.0分)
A.
B. 1
C.
D.
答案: D
5. (单选题) (本题4.0分)
A. 0
B. 1
C.
D. 不存在
答案: B
6. (单选题) 下列各对函数相同的是()(本题4.0分)
A.
B.
C.
D.
答案: A
7. (单选题) 不定积分()(本题4.0分)
A.
B.
C.
D.
答案: C
8. (单选题) 函数的图形关于()。
(本题4.0分)
A. x轴(直线y=0)对称
B. y轴(直线 x=0)对称
C. 直线 y=x 对称
D. 原点对称
答案: B
9. (单选题) (). (本题4.0分)
A. 高阶无穷小
B. 等价无穷小
C. 低阶无穷小
D. 同阶但非等价无穷小
答案: D
10. (单选题) 不定积分()(本题4.0分)
A.
B.
C.
D.
答案: B
11. (单选题) (本题4.0分)
A. 0
B. 1
C. 2
D. 3
答案: B
12. (单选题) (本题4.0分)
A.
B.
C.
D.
答案: B
13. (单选题) (本题4.0分)
A.
B.
C.
D.
答案: D
14. (单选题) (本题4.0分)
A.
B.
C.
答案: B
15. (单选题) (本题4.0分)
A.
B.
C.
D.
答案: A
16. (判断题) (本题3.0分)
A. 正确
B. 错误
答案: A
17. (判断题) (本题3.0分)
A. 2
B. 1
18. (判断题) (本题3.0分)
A.
B.
答案: A
19. (判断题) (本题3.0分)
A. 正确
B. 错误
答案: A
20. (判断
题)
(本题3.0分)
A. 正确
B. 错误
答案: A
21. (判断
题) (本题3.0分)
A. 正确
B. 错误
答案: B
22. (判断题) (本题3.0分)
A. true
B. false
答案: B
23. (判断题) (本题3.0分)
A. 正确
B. 错误
答案: A
24. (判断题) (本题3.0分)
A. 正确
B. 错误
答案: A
25. (判断题) (本题
3.0分)
A. 正确
B. 错误
答案: B
26. (问答题) (本题10.0分)
答案:。
