数学课本习题整理(完整版 )
高等数学教材习题全解

高等数学教材习题全解一、选择题1. 已知函数f(x) = 2x^3 - 3x^2 - 36x + 4,那么f(-2)的值为多少?答:将x替换为-2,计算得到f(-2) = 2(-2)^3 - 3(-2)^2 - 36(-2) + 4 = 64 + 12 + 72 + 4 = 152。
2. 已知函数y = e^2x,那么y'(x)的值为多少?答:对y = e^2x求导,得到y'(x) = 2e^2x。
3. 已知函数f(x) = ln(x^2 - 1),那么f'(x)的值为多少?答:对f(x) = ln(x^2 - 1)求导,得到f'(x) = 2x / (x^2 - 1)。
二、填空题1. 若f(x) = x^2 + bx + c 是一个完全平方三项式,那么b和c的取值分别是多少?答:对于完全平方三项式,b的取值为2ac,c的取值为a^2,其中a、b、c为常数。
所以b = 2ac,c = a^2。
2. 若y = 3x^2 + k 在点(2, -5)处的切线与y轴垂直,那么k的值为多少?答:求导得到y' = 6x,切线的斜率为6,因为与y轴垂直,所以斜率为0。
代入点(2, -5)得到6 * 2 + k = 0,解方程得到k = -12。
三、计算题1. 计算∫(0 to π/2) sin^2 x dx。
答:∫sin^2 x dx = ∫(1/2 - 1/2cos2x) dx = 1/2x - 1/4sin2x + C。
将上限和下限代入得到1/2(π/2) - 1/4sin(2(π/2)) = π/4。
2. 计算∫√(1 + x^3) dx。
答:将√(1 + x^3)展开得到√(1 + x^3) = (1 + x^3)^(1/2) = (√(x^3 + 1))/(x + 1)。
所以∫√(1 + x^3) dx = ∫(√(x^3 + 1))/(x + 1) dx。
采用换元法,令u = x^3 + 1,那么du = 3x^2 dx,将原式变换得到(1/3)∫(√u)/(x + 1) du。
高等数学教材题目及答案

高等数学教材题目及答案一、导数与微分1. 求函数f(x) = 3x^2 - 2x + 1在x = 2处的导数。
答案:f'(2) = 12 - 4 = 8。
2. 求函数f(x) = ln(x^2 + 1)的导数。
答案:f'(x) = 2x / (x^2 + 1)。
3. 已知函数f(x) = e^x,求其微分。
答案:df = f'(x)dx = e^xdx。
二、积分与不定积分1. 求函数f(x) = 2x的不定积分。
答案:∫f(x)dx = ∫2xdx = x^2 + C (C为常数)。
2. 求函数f(x) = sin(x)的不定积分。
答案:∫f(x)dx = -cos(x) + C (C为常数)。
3. 计算定积分∫[0, 2π] sin(x)dx的值。
答案:∫[0, 2π] sin(x)dx = -cos(x)∣[0, 2π] = -cos(2π) - (-cos(0)) = -1 - (-1) = 0。
三、级数与收敛性1. 判断级数∑(n=1, ∞) (1/n)的收敛性。
答案:根据调和级数的性质,该级数发散。
2. 判断级数∑(n=1, ∞) (1/2^n)的收敛性。
答案:根据等比级数的性质,该级数收敛于1。
3. 判断级数∑(n=1, ∞) (1/n^2)的收敛性。
答案:根据比较判别法,与p级数(p>1)收敛性相同,因此该级数收敛。
四、多元函数与偏导数1. 求函数f(x, y) = x^2 + y^2的偏导数∂f/∂x。
答案:∂f/∂x = 2x。
2. 求函数f(x, y) = x^3y^2的偏导数∂f/∂y。
答案:∂f/∂y = 2x^3y。
3. 已知函数f(x, y) = x^2y,求其全微分df。
答案:df = ∂f/∂x dx + ∂f/∂y dy = 2xydx + x^2dy。
五、重积分1. 计算二重积分∬D (x^2 + y^2) dxdy,其中D为单位圆盘。
数学课本习题整理(完整版 )

(4)P (-3,-8) L1:2y-7=0
2.已知三角形ABC三个顶点坐标分别为A(2,1)B(5,3)C(-1,5)求三角形ABC,BC边上的高h.
3.已知三角形ABC三个顶点坐标分别为A(1,1)B(9,3)C(2,5)求角BAC的角平分线所在的直线方程。
例4求经过A(1,0) B(3,0) C(2,2)三点的圆的方程.
例5求过点M(2,2 )且与圆 + =4相切的直线的方程.
练习12.2(2)
1.判断下列方程是否表示圆,并说明理由.
(1) + -2x -4y + 6 = 0
(2) + -2x -4y = 0
(3) + -2x -4y + 5 = 0
3.已知直线l:y=ax+2和A(1,4)B(3,1)两点。当l与线段AB相交时,求实数a的取值范围。
4.直线l经过点P(-2,1)且点A(-1,-2)到l的距离等于1,求直线l方程。
12.1曲线和方程
例1已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线ℓ的方程是2x-y-2=0。
例3已知三角形ABC三个顶点坐标分别为A(1,3) B(3,1)C(-1,0),求△ABC面积。
例4已知直线l:y=kx+1与两点A(-1.5)B(4,-2)若直线l与线段AB相交,求k取值范围.
11.4(2)
1.求两条平行线x+y-1=0与2x+2y+1=0得距离
2.已知直线x-y+3平行且距离等于2的直线的方程。
例2造船时,在船体放样中,要画出甲板圆弧线.由于这条圆弧线的半径很大,无法在钢板上用圆规画出,因此需要先求出这条圆弧线的方程,再用描点法画出圆弧线.已知圆弧AB的半径r=29米,圆弧AB所对的弦长l=12米,以米为单位,建立适当的坐标系,并求圆弧AB的方程(答案中的数据精确到0.001米)
人教版五年级数学下册课本习题大全完整版

人教版五年级数学下册课本习题大全完整版1、求2和5的公倍数,即为10,再求10的倍数中能被3整除的最小数,即30.2、妈妈购买的花的总价为3x + 5y + 10z = 50,找回的钱为13元,所以方程为3x + 5y + 10z + 13 = 50,解得x = 3.y = 1.z = 2.找回的钱对了。
3、22人分成3人一组,至少再来2人才能正好分完。
56个桃子,无法3个3个的装完,最后剩余1个。
无法2个2个的装完,最后剩余2个。
可以5个5个的装完,正好装完。
4、纸巾盒的前面和上面是长方形,和它形状相同的面分别是后面和下面;右面是正方形,和它形状相同的面也是正方形。
前面和后面的面积均为24cm x 9cm = 216平方厘米;左面和右面的面积均为12cm x 9cm = 108平方厘米;上面和下面的面积均为24cm x 12cm = 288平方厘米。
5、俱乐部四周的周长为2 x (90m + 55m) = 290m,至少需要290m的彩灯。
6、柜台四周需要装上4条角铁,长分别为40cm。
40cm。
80cm。
80cm,总长为240cm,即需要2.4米的角铁。
7、一个大正方体有6个面,每个面都由小正方体组成,所以至少需要6个小正方体。
体积为1cm x 1cm x 1cm x 6 = 6立方厘米。
8、微波炉包装箱的长、宽、高分别为a、b、c,需要的硬纸板面积为2ab + 2bc + 2ac,至少需要2(a+b+c)平方米的硬纸板。
9、简易衣柜的表面积为2(ab + ac + bc),至少需要2 x (1.2 x 1.8 + 1.2 x 0.6 + 1.8 x 0.6) = 7.92平方米的布。
10、正方体礼品盒的表面积为6a²,至少需要6 x 0.25 = 1.5平方分米的包装纸。
11、玻璃鱼缸的表面积为6a²,制作这个鱼缸需要6 x 0.09 = 0.54平方米的玻璃。
13、邮箱的表面积为2ab + 2bc + 2ac,至少需要2 x (0.5 x 0.4 + 0.5 x 0.78 + 0.4 x 0.78) = 0.764平方米的铁皮。
新版人教版八年级数学上册全册习题集

新版人教版八年级数学上册全册习题集目录1. 第一章:整数2. 第二章:有理数3. 第三章:代数式4. 第四章:图形的认识5. 第五章:图形的性质6. 第六章:相交线与平行线7. 第七章:三角形8. 第八章:全等三角形9. 第九章:五边形与多边形10. 第十章:集合第一章:整数本章介绍整数的概念、整数之间的大小比较、整数的加减法运算以及整数的乘法运算。
通过题练,加深对整数概念的理解,并掌握整数的运算方法和技巧。
第二章:有理数本章介绍有理数的概念、有理数之间的大小比较、有理数的加减法运算以及有理数的乘除法运算。
通过题练,巩固对有理数概念的掌握,提高有理数运算的能力。
第三章:代数式本章介绍代数式的概念、代数式的计算与化简、代数式的值、代数式的应用等内容。
通过题练,培养代数思维能力,掌握代数式的运算技巧。
第四章:图形的认识本章介绍图形的基本概念和常见图形的性质。
通过题练,加深对图形认识的理解,掌握图形的命名、计算面积和周长的方法。
第五章:图形的性质本章介绍圆和与圆有关的性质,以及相似图形的性质。
通过题练,加深对圆和相似图形性质的理解,提高解决相关问题的能力。
第六章:相交线与平行线本章介绍平行线和相交线的性质,以及平行线与相交线间夹角和对应角的关系。
通过题练,掌握平行线和相交线的性质,提高几何问题的解决能力。
第七章:三角形本章介绍三角形的定义、分类和性质,以及三角形的角平分线和垂线的性质。
通过题练,加深对三角形性质的理解,提高解决相关问题的能力。
第八章:全等三角形本章介绍全等三角形的概念和性质,以及全等三角形的判定方法。
通过题练,掌握全等三角形的判定和应用,提高解决相关问题的能力。
第九章:五边形与多边形本章介绍五边形和多边形的定义、分类和性质,以及多边形的内角和外角的关系。
通过题练,加深对五边形和多边形性质的理解,提高解决相关问题的能力。
第十章:集合本章介绍集合及其表示方法、集合的运算和集合的应用。
通过题练,培养集合思维能力,巩固对集合概念的掌握。
(完整版)新人教版五年级数学下册数学课本习题(一)
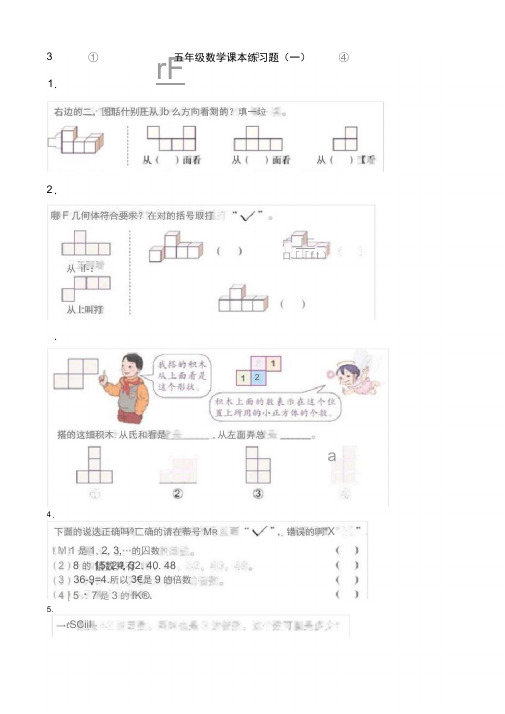
1匚从从【曲h23 3 2arF FI①④4搭的这细积木.从氏和看是_________ ,从左面弄总五年级数学课本练习题(一)下面的说迭正确吗?匸确的请在蒂号M R ,错误的啊“Xt SCiil-42的右边的二,图聒什别圧从lb 么方向看刘的?填一垃哪F 几何体符合要求?在对的括号取打t M 1是1, 2, 3,…的囚数 2 8 的15. 24, 32. 40. 48 3 36-9=4.所以3€是9的倍数 4 [ 5・7是3的fK®.5.广 『匚 - 口「「f t )从I:叫打从 if-:iftifi两个数位上的数•样■并且聚5的倍敖「I 比是Z 的借数.乂it 5的倍数lit 巫2的储数,又地$99倍敢的J»小的二位数8.在口则•个敎依便毎个数都雄3的借数□ 了 4口2 口“ 65口100. 98, 96.94 * …* 8+ 6 * 4 * 2这艸数叩F hi 个数都址—_的 倍数.第15个数& _________ .9.F 面的说法对吗?说说你的腥由■ I '个位llid 3” 6. 9的数”郁肚3的倍数 ■ 2「个位I :楚1, 3. 5+ 7. 9的数祁肚奋数(丄)在全部笙数里,不是奇数就是偶SU按耍求7. 「它还是2⑴□□(2 3 5 口小□□□这样数数「数出束旳数都址 _______ 的陪数.笫25个数是_「「各有此种填法 佗口1(L )既AV 2 fil 5的倍数.乂丛3的催数的堆小阿位数见( );2既是2的倍数.乂浪3的倍数的M 小二位救虽( ).皿大二位数韭()*个Q 理*高分别>j20cm. 30 cm. 40皿的小纸徘,在所有的棱上 辂上T ■胶带*至少錨蟹筋氏的胶带?14.卜面的说法1E 确吗?说说你的理由。
-I )所有的奇数都JS 质数 '2)所有的偶数都是合散< 3) A 1. 2. 3. 4. 5.…申.除广质数订外都浪舍数(4)两个质数的和是偶数11. 从Fasia 张数字卡片中取出二账.按要求细成匚位数偶数 _______________________________2的借数 ____________ 3的借数 ____________ 吁的倍散 ___________________________既处2的倍数・兀是3的借数 _________13.将下面备数分别堆人指宦的圈吧27 37 41 5861 73 83 95 1114334757628799 M舍数WVLflftf 1L1JCJ/ \\ C \16. 17.30卜学生咚分成屮.乙两队、如果屮駅人敦为奇数’乙队人m 数还 是個数?如果甲队人数为偶数呢?18.水夷部费做2.2 m. 40 cm, A 80 <m的玻璃柜會 现fl 浚fl 植令备边都安VM.这个僵仔至少需婪爹少来的ffitt?20.中队爻员把、个梭氏46 cm 附正方休抵 箱的齐【砒I ;贴匕红瑕.将它作为给希Si 小学雰知的“愛心?T .(i )他们至少備赛爹少平方佩米的紆纸? f 2 I 如果只在樓匕粘贴胶带纵* &|<4.5 m 的胶带ift 够用吗?19.为迎按瓦一国际臂功界.1: 人叔叔娶程匸人倶乐部的四 尚装上彩灯(地面的例边不 装)已知匸人俱乐部氏gom. 电55 m ,岛22 m.匸人叔報 至少需要多氏的彩訂线?你知道它们并是匕少已?* //n21.下图垦用边长15的小止方体拼成的长方体 朴面的图形哪一个是这个22.折样总.■些图形能!8咸左«(的疋方体?覆插号中画H xZ*23.胚託家咚绪一个长0・75审・覽Q5m.咼 的简抽衣柜换布罩(麵右图•没有底面) 至少需姿 用帝莎少平方米?24.光华街口呢了一个新的氏方休铁皮邮綺* K50 cm, it 40cm.關78cm.做这个邮箱住少需要多少F 方厘米的扶皮?氏方tf25.一个玻璃他tec 的形状崔正方体. 槻氏3 dm 制作这个鱼SI 时至 少需罄玻璃罗少乎方分来? ( I : 面没有靳)26.•个正方体礼品盒.楼任12血 如果实际用纸是表向枳的 包装腔个礼A 占盒至少要用多少平 方分来的包装纸?2 M{)个3 cm I )个27.tK 方体的Wf F 盒,Lt 10 cm,宽6 cm . ft 12 <rn 加枭国看它貼- M 曲标纸(1:卞面不妙)・这嵌商林纸的曲积至少爹少平方ft (米?33.28.”个正方体礼品29.-卜新建30.牛新建的游冰池氏50 m,长是 宽的2倍.深2.5 m .现在要在 游沐池的四周和底帼贴t*砖. 一共雷要骷多少平方米的瓷砖?31.学校妥粉刷新找电巳知教窃的 | < 448 m 、电上 6 m. fij Ji 3 m * 知除门拚的面积ft 11.4如 果每平方米需腔崔4尤涂14« 粉刷这个教室镒要花费皴列削32.0 06町 区供術临台v iii 3 氏丹f 木“ ir 而成的它的前晴两面涂上黄色 讪播.比他磔阳来的画诲红色沽 淺 涂黄油沬 和红油涤 的 幽书i 各 址名少--Wife 方体木料.K5m.蹴旅药的面积是0』6肺区脱木 料(iM lab'll 适肖的体枳单位35、耳一臥4 = 4x3" 8 二“8 x2 =36、迢筑丁地建挖-tL<50 m ・宽30d 深50 cm 的快方体土城, 丿咚37、 38、蚂妈送给仍仍的K 方体生H 贲搓K 2dm,宽 2 dm 、0.6 dm 奶仍 把它甲肉分底4块氏方休形状的小 attE,想•想她址怎样分的,毎亍 人分到芬大的一块货構丁urim BOO 根方木•毎根力: 木槌栽面的囲槪迢24民址J 3m 这些木料寸:扯岁4方?: 1 H■ .d40、哽砌-道K 15 m. )f X 24 cm. ft 3 m 的 砖Ifi 如橡皮的体积约 址-to ______踣碟机的休枳约 是22 _________集裝箱的体枳约 址 40 --挖出苏少方的t?39、M 梭R 30 cm 的止Ji 体冰决. 它的体枳址多少立方蛆贰?果毎立方米用砖吕25块,-典熒用砖多少快?45、一・■' ■ ■ ■ ■■■■■■■■ ■ ■ ■ ■■■■■ ■ ■■ m ■ ■ ■ ■ ■■,■■■■ ■,■■■■ ■■ ■,■ m ■■■■■■■■ ■■■■■■■ ■ ■ ■ ■■■■!■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ r B ■ ■' ■ ■个艮方体包髅紀 从嵬面量拴2肌m,宽2仏叫体积11-76dm* 爸爸想用它包装-件长25cm.:&16cm h 岛48 cm 的玻璃器 IHL 址再可以装得下?43、学校运来76丹的沙衣铺H -个j£5m 俺38dm 的沙坑£可以他多厚Y44、亠个民方体的尤盖贰族箱.尺是6巾,宽£60小叽A Ji 1.5 m.这个木 濮简再地血枳仃多丈?而发用雪少邓方来附玻碣,它腐体枳址多少?3.5 dm J = ____ 700 din J =40、六一KiftU iKL 全市的小宰厂 维代衣用撓圧3 cm 的疋力体 刼料拼締积木生广场中央裕 遅了一面长 6",(f5 2.7 ni . 旱6 m 的熨运心愿墙这亦 墙一戻用『多少块积木?rn 30.25 ni'= ____ um ]41、花园小区为履民新安装了 50 个休息的覺子,建面的长■寬、A 分别!丄 100 on > 45 Cm 、4.5 tm ・陡腿的氏*宽、高分 別是 45 cm . 5 cm , 35 uni 这些凳子典用混凝上参少方?42、1.02 nf 960 dnf - 6270 cnr =36000 cm '= din j 8.63 in =dtm23 dm = cm f ■>某薄曲趙士为解决岛上诜木缺乏「可KfL和当地届民共同幡建了Mi 22 m. H 10 m. 1.8 m的淡水暮水泄一这个摘水池皿名可醤水圣少45、50、ft-Bits 上垃上介适的容枳单位一糠果木约 桶色拉油50 ______ 豹 5 ___________-1L=ml.4800 mi -L82m500 mL =L 35dm 3=mL 2,4 L= mL8.04 dm - L =inL78& rnl.=cm' sd m47、48、珊刪柑的休积是名少!•丸稠旷泉贰梧当T1500 mL 的矿泉水a 0 IB I,1500 it神a yit 人城尺tftii 池魏液约返测舱的容机为6—__100 ............49、爸爸在•个底面■个长方体倉塘尺8口宽4百真探2帕这个做堆的磔积大约是多步叨用血线上的点衣示下面各分数1 ■ *ti r| |)壬 7 7o ---------- ---------- ---------- ---------- L*125 3 3 60 i~上丽条直线中・每条直线上的最小刻度用分数衷示分別赴爹少?它们分 别是嚟些分数的分数弧位?把2快梭抚为的正方侔木堆折成•伊尺庁侏 迖牛氏方体的体积、 占咐枳分别是衣少?期来址用3块止加*折的怡形呢?52、切祇筑比也订做「25 皿灯讪坨圾 M (如片图)堆圾Hi 外恻需塑貼h ■ 层外怖面如果外怖(8毎平方米180元. 这些垃圾桶的外饰面一如要花參少栈?53、54、55、9 cm —dm(>30 cm 二 ------ d m 53 mL 二—-L 1 33dm J =——in 123「克工一吨79 dm = --------- J m H3秒=;;分56 cm a = -------- dm a4甘公顷=y —|平方千*57、小期用15分种走r 1 km H .平拘毎分钟走几分之扎F 来10. fi (1)班获冇1 了編书茁作品冬加宁松的甘达 ttW,其中4幅作品从金咬255幅齧禅作品中 脱裁而岀井轶奖f 1 ' 1)班获奖作骷占全班參春作品的几分之几? (2)1£( 1)班寥梯作骷占全校奪赛作殆的儿分之儿?12, ift 空(1 >弄有(}个月.护)牛月(2)-年叩・大片的月份占H ,小月的月粉占{(,一个龜期中•休也H 是工作H 的一;2.把F 面轴假分数化成帶分数或幣数43 69 30 158 21 50 25 7 9 12 20 15«■ 4 1*写曲分母是了的所有具分敎识)写出井子是7的所有假fr »两小曲中的单位”广号那走什强?' ?「2. 下而的说法对叫?为什么? 5 (1 )我吃了 1个西瓜的萼。
高中教材练习题及讲解答案数学
高中教材练习题及讲解答案数学### 高中数学练习题及讲解答案#### 一、基础练习题1. 题目一:求函数 \( f(x) = 3x^2 - 2x + 1 \) 在 \( x = 2 \) 时的导数值。
2. 题目二:解不等式 \( |x - 3| < 5 \) 并表示解集。
3. 题目三:已知 \( a \) 和 \( b \) 是正数,求证\( \frac{1}{a} + \frac{1}{b} \geq 4 \)。
#### 二、中等难度练习题4. 题目四:计算定积分 \( \int_{1}^{2} (4x - 3) \, dx \)。
5. 题目五:给定圆 \( x^2 + y^2 = 9 \),求圆上点到直线 \( 2x - y + 6 = 0 \) 的最短距离。
6. 题目六:证明等差数列的前 \( n \) 项和公式 \( S_n =\frac{n(a_1 + a_n)}{2} \)。
#### 三、高难度练习题7. 题目七:已知 \( \sin(x) + \cos(x) = \frac{1}{2} \),求\( x \) 的值。
8. 题目八:求函数 \( y = x^3 - 3x^2 + 2 \) 的极值点。
9. 题目九:解方程组:\[\begin{cases}x^2 + y^2 = 4 \\x + y = 2\end{cases}\]#### 四、讲解与答案1. 解答一:首先求导 \( f'(x) = 6x - 2 \),代入 \( x = 2 \)得 \( f'(2) = 10 \)。
2. 解答二:解不等式得 \( -5 < x - 3 < 5 \),即 \( -2 < x < 8 \)。
3. 解答三:利用调和平均数的性质,\( \frac{1}{a} + \frac{1}{b} \geq 2 \times \frac{2ab}{ab} = 4 \)。
数学一年级上册课本习题及答案
数学一年级上册课本习题及答案数学是基础学科之一,对于一年级的学生来说,掌握基本的数学概念和运算是非常重要的。
以下是一些适合一年级上册数学课本的习题和答案,供学生练习和参考。
# 习题1:认识数字题目:请从1数到10。
答案: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10。
# 习题2:加法基础题目:计算下列各题的和。
1. 2 + 32. 5 + 4答案:1. 52. 9# 习题3:减法基础题目:计算下列各题的差。
1. 8 - 22. 10 - 5答案:1. 62. 5# 习题4:认识形状题目:请指出下列图形中哪些是正方形,哪些是圆形。
- 图形A:正方形- 图形B:圆形- 图形C:正方形答案:- 图形A:正方形- 图形B:圆形- 图形C:正方形# 习题5:比较大小题目:比较下列数字的大小。
1. 7 和 92. 4 和 6答案:1. 9 大于 72. 6 大于 4# 习题6:认识钟表题目:看图回答问题,时针指向2,分针指向12,是几点?答案: 2点整。
# 习题7:简单的乘法题目:计算下列乘法。
1. 3 × 22. 4 × 1答案:1. 62. 4# 习题8:简单的除法题目:计算下列除法。
1. 6 ÷ 22. 8 ÷ 1答案:1. 32. 8# 习题9:认识分数题目:将一个苹果平均分给两个小朋友,每个小朋友得到这个苹果的几分之几?答案:每个小朋友得到这个苹果的1/2。
# 习题10:应用题题目:如果小明有5个苹果,他给了小红2个,小明现在还有几个苹果?答案:小明现在有3个苹果。
希望这些习题能够帮助一年级的学生巩固他们在数学课上学到的知识。
练习是提高数学能力的关键,因此,鼓励学生多做练习,理解数学概念和运算规则是非常重要的。
人教版版高中数学必修1全册课后习题及答案整理汇总
人教版高中数学必修1课后习题答案第一章 集合与函数概念1.1集合1.1.1集合的含义与表示练习(第5页)1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A ;中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.(2)1-∉A2{|}{0,1}A x x x ===. (3)3∉B 2{|60}{3,2}B x x x =+-==-.(4)8∈C ,9.1∉C 9.1N ∉.2.解:(1)因为方程290x -=的实数根为123,3x x =-=,所以由方程290x -=的所有实数根组成的集合为{3,3}-;(2)因为小于8的素数为2,3,5,7,所以由小于8的所有素数组成的集合为{2,3,5,7}; (3)由326y x y x =+⎧⎨=-+⎩,得14x y =⎧⎨=⎩,即一次函数3y x =+与26y x =-+的图象的交点为(1,4),所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)};(4)由453x -<,得2x <, 所以不等式453x -<的解集为{|2}x x <.1.1.2集合间的基本关系练习(第7页)1.解:按子集元素个数来分类,不取任何元素,得∅;取一个元素,得{},{},{}a b c ;取两个元素,得{,},{,},{,}a b a c b c ;取三个元素,得{,,}a b c ,即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅.2.(1){,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素;(2)20{|0}x x ∈= 2{|0}{0}x x ==;(3)2{|10}x R x ∅=∈+= 方程210x +=无实数根,2{|10}x R x ∈+==∅;(4){0,1}N (或{0,1}N ⊆) {0,1}是自然数集合N 的子集,也是真子集;(5){0}2{|}x x x = (或2{0}{|}x x x ⊆=) 2{|}{0,1}x x x ==;(6)2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==.3.解:(1)因为{|8}{1,2,4,8}B x x ==是的约数,所以AB ;(2)当2k z =时,36k z =;当21k z =+时,363k z =+,即B 是A 的真子集,B A ; (3)因为4与10的最小公倍数是20,所以A B =.1.1.3集合的基本运算练习(第11页)1.解:{3,5,6,8}{4,5,7,8}{5,8}A B == ,{3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}A B == .2.解:方程2450x x --=的两根为121,5x x =-=,方程210x -=的两根为121,1x x =-=,得{1,5},{1,1}A B =-=-, 即{1},{1,1,5}A B A B =-=- .3.解:{|}A B x x = 是等腰直角三角形,{|}A B x x = 是等腰三角形或直角三角形.4.解:显然{2,4,6}U B =ð,{1,3,6,7}U A =ð,则(){2,4}U A B = ð,()(){6}U U A B = ðð.1.1集合习题1.1 (第11页) A 组1.(1)237Q ∈ 237是有理数; (2)23N ∈ 239=是个自然数;(3)Q π∉π是个无理数,不是有理数; (4R 是实数;(5Z3=是个整数; (6)2N ∈ 25=是个自然数.2.(1)5A ∈;(2)7A ∉; (3)10A -∈. 当2k =时,315k -=;当3k =-时,3110k -=-;3.解:(1)大于1且小于6的整数为2,3,4,5,即{2,3,4,5}为所求;(2)方程(1)(2)0x x -+=的两个实根为122,1x x =-=,即{2,1}-为所求;(3)由不等式3213x -<-≤,得12x -<≤,且x Z ∈,即{0,1,2}为所求.4.解:(1)显然有20x ≥,得244x -≥-,即4y ≥-,得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-;(2)显然有0x ≠,得反比例函数2y x=的自变量的值组成的集合为{|0}x x ≠;(3)由不等式342x x ≥-,得45x ≥,即不等式342x x ≥-的解集为4{|}5x x ≥.5.(1)4B -∉; 3A -∉; {2}B ; B A ; 2333x x x -<⇒>-,即{|3},{|2}A x x B x x =>-=≥;(2)1A ∈; {1}-A ; ∅A ; {1,1}-=A ; 2{|10}{1,1}A x x =-==-;(3){|}x x 是菱形{|}x x 是平行四边形; 菱形一定是平行四边形,是特殊的平行四边形,但是平行四边形不一定是菱形;{|}x x 是等边三角形{|}x x 是等腰三角形.等边三角形一定是等腰三角形,但是等腰三角形不一定是等边三角形.6.解:3782x x -≥-,即3x ≥,得{|24},{|3}A x x B x x =≤<=≥,则{|2}A B x x =≥ ,{|34}A B x x =≤< .7.解:{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数,则{1,2,3}A B = ,{3,4,5,6}A C = ,而{1,2,3,4,5,6}B C = ,{3}B C = ,则(){1,2,3,4,5,6}A B C = ,(){1,2,3,4,5,6,7,8}A B C = .8.解:用集合的语言说明这项规定:每个参加上述的同学最多只能参加两项,即为()A B C =∅ .(1){|}A B x x = 是参加一百米跑或参加二百米跑的同学; (2){|}A C x x = 是既参加一百米跑又参加四百米跑的同学.9.解:同时满足菱形和矩形特征的是正方形,即{|}B C x x = 是正方形,平行四边形按照邻边是否相等可以分为两类,而邻边相等的平行四边形就是菱形,即{|}A B x x =是邻边不相等的平行四边形ð, {|}S A x x =是梯形ð.10.解:{|210}A B x x =<< ,{|37}A B x x =≤< ,{|3,7}R A x x x =<≥或ð,{|2,10}R B x x x =≤≥或ð,得(){|2,10}R A B x x x =≤≥ 或ð,(){|3,7}R A B x x x =<≥ 或ð,(){|23,710}R A B x x x =<<≤< 或ð, (){|2,3710}R A B x x x x =≤≤<≥ 或或ð.B 组1.4 集合B 满足A B A = ,则B A ⊆,即集合B 是集合A 的子集,得4个子集.2.解:集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合, 即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,点(1,1)D 显然在直线y x =上,得D C .3.解:显然有集合{|(4)(1)0}{1,4}B x x x =--==,当3a =时,集合{3}A =,则{1,3,4},A B A B ==∅ ;当1a =时,集合{1,3}A =,则{1,3,4},{1}A B A B == ;当4a =时,集合{3,4}A =,则{1,3,4},{4}A B A B == ; 当1a ≠,且3a ≠,且4a ≠时,集合{3,}A a =,则{1,3,4,},A B a A B ==∅ .4.解:显然{0,1,2,3,4,5,6,7,8,9,10}U =,由U A B = ,得U B A ⊆ð,即()U U A B B = ðð,而(){1,3,5,7}U A B = ð,得{1,3,5,7}U B =ð,而()U U B B =ðð,即{0,2,4,6,8.9,10}B =.第一章 集合与函数概念1.2函数及其表示1.2.1函数的概念练习(第19页)1.解:(1)要使原式有意义,则470x +≠,即74x ≠-, 得该函数的定义域为7{|}4x x ≠-;(2)要使原式有意义,则1030x x -≥⎧⎨+≥⎩,即31x -≤≤, 得该函数的定义域为{|31}x x -≤≤.2.解:(1)由2()32f x x x =+,得2(2)322218f =⨯+⨯=,同理得2(2)3(2)2(2)8f -=⨯-+⨯-=,则(2)(2)18826f f +-=+=,即(2)18,(2)8,(2)(2)26f f f f =-=+-=;(2)由2()32f x x x =+,得22()3232f a a a a a =⨯+⨯=+, 同理得22()3()2()32f a a a a a -=⨯-+⨯-=-,则222()()(32)(32)6f a f a a a a a a +-=++-=,即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=.3.解:(1)不相等,因为定义域不同,时间0t >;(2)不相等,因为定义域不同,0()(0)g x x x =≠.1.2.2函数的表示法练习(第23页)1,y ==,且050x <<,即(050)y x =<<.2.解:图象(A )对应事件(2),在途中遇到一次交通堵塞表示离开家的距离不发生变化;图象(B )对应事件(3),刚刚开始缓缓行进,后来为了赶时间开始加速;图象(D )对应事件(1),返回家里的时刻,离开家的距离又为零; 图象(C )我出发后,以为要迟到,赶时间开始加速,后来心情轻松,缓缓行进.3.解:2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩,图象如下所示.4.解:因为sin 60= ,所以与A 中元素60 相对应的B;因为sin 45=B 相对应的A 中元素是45 .1.2函数及其表示习题1.2(第23页)1.解:(1)要使原式有意义,则40x -≠,即4x ≠,得该函数的定义域为{|4}x x ≠;(2)x R ∈,()f x =都有意义, 即该函数的定义域为R ;(3)要使原式有意义,则2320x x -+≠,即1x ≠且2x ≠,得该函数的定义域为{|12}x x x ≠≠且;(4)要使原式有意义,则4010x x -≥⎧⎨-≠⎩,即4x ≤且1x ≠, 得该函数的定义域为{|41}x x x ≤≠且.2.解:(1)()1f x x =-的定义域为R ,而2()1x g x x=-的定义域为{|0}x x ≠,即两函数的定义域不同,得函数()f x 与()g x 不相等;(2)2()f x x =的定义域为R ,而4()g x =的定义域为{|0}x x ≥,即两函数的定义域不同,得函数()f x 与()g x 不相等;(32x =,即这两函数的定义域相同,切对应法则相同,得函数()f x 与()g x 相等.3.解:(1)定义域是(,)-∞+∞;-∞+∞,值域是(,)(2)定义域是(,0)(0,);-∞+∞,值域是(,0)(0,)-∞+∞(3)定义域是(,)-∞+∞;-∞+∞,值域是(,)(4)定义域是(,)-∞+∞,值域是[2,)-+∞.4.解:因为2()352f x x x =-+,所以2(3(5(28f =⨯-⨯+=+即(8f =+同理,22()3()5()2352f a a a a a -=⨯--⨯-+=++,即2()352f a a a -=++;22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++,即2(3)31314f a a a +=++;22()(3)352(3)3516f a f a a f a a +=-++=-+, 即2()(3)3516f a f a a +=-+.5.解:(1)当3x =时,325(3)14363f +==-≠-,即点(3,14)不在()f x 的图象上;(2)当4x =时,42(4)346f +==--,即当4x =时,求()f x 的值为3-;(3)2()26x f x x +==-,得22(6)x x +=-, 即14x =.6.解:由(1)0,(3)0f f ==,得1,3是方程20x bx c ++=的两个实数根,即13,13b c +=-⨯=,得4,3b c =-=,即2()43f x x x =-+,得2(1)(1)4(1)38f -=--⨯-+=,即(1)f -的值为8.7.图象如下:8.解:由矩形的面积为10,即10xy =,得10(0)y x x =>,10(0)x y y=>,由对角线为d ,即d =,得(0)d x =>,由周长为l ,即22l x y =+,得202(0)l x x x =+>, 另外2()l x y =+,而22210,xy d x y ==+,得(0)l d ===>,即(0)l d =>.9.解:依题意,有2(2d x vt π=,即24v x t d π=, 显然0x h ≤≤,即240v t h d π≤≤,得204h d t vπ≤≤, 得函数的定义域为2[0,]4h d v π和值域为[0,]h .10.解:从A 到B 的映射共有8个.分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩.B组1.解:(1)函数()r f p =的定义域是[5,0][2,6)- ;(2)函数()r f p =的值域是[0,)+∞; (3)当5r >,或02r ≤<时,只有唯一的p 值与之对应.2.解:图象如下,(1)点(,0)x 和点(5,)y 不能在图象上;(2)省略.3.解:3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4.解:(1,步行的路程为12x -,得125x t -=+,(012)x ≤≤,即125x t -=,(012)x ≤≤.(2)当4x =时,12483()55t h -=+=≈.第一章 集合与函数概念1.3函数的基本性质1.3.1单调性与最大(小)值练习(第32页)1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.解:图象如下[8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间.3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数.4.证明:设12,x x R ∈,且12x x <,因为121221()()2()2()0f x f x x x x x -=--=->,即12()()f x f x >, 所以函数()21f x x =-+在R 上是减函数.5.最小值.1.3.2单调性与最大(小)值练习(第36页)1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=,所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-,所以函数3()2f x x x =-为奇函数;(3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞ ,因为对定义域内每一个x 都有22()11()()x x f x f x x x-++-==-=--,所以函数21()x f x x+=为奇函数;(4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=,所以函数2()1f x x =+为偶函数.2.解:()f x 是偶函数,其图象是关于y 轴对称的;()g x 是奇函数,其图象是关于原点对称的.习题1.3A 组1.解:(1)函数在5(,2-∞上递减;函数在5[,)2+∞上递增; (2)函数在(,0)-∞上递增;函数在[0,)+∞上递减.2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-,由12120,0x x x x +<-<,得12()()0f x f x ->, 即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=,由12120,0x x x x >-<,得12()()0f x f x -<, 即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数.3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数; 当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数,令()f x mx b =+,设12x x <,而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <, 得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >,得一次函数y mx b =+在(,)-∞+∞上是减函数.4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.解:对于函数21622100050x y x =-+-, 当162405012()50x =-=⨯-时,max 307050y =(元),即每辆车的月租金为4050元时,租赁公司最大月收益为307050元.6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-, 所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数, 函数()g x 的单调区间为[2,4],且函数()g x 在[2,4]上为增函数;(2)当1x =时,min ()1f x =-,因为函数()g x 在[2,4]上为增函数, 所以2min ()(2)2220g x g ==-⨯=.2.解:由矩形的宽为x m ,得矩形的长为3032x m -,设矩形的面积为S , 则23033(10)22x x x S x --==-,当5x =时,2max 37.5S m =, 即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是237.5m .3.判断()f x 在(,0)-∞上是增函数,证明如下:设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-, 又因为函数()f x 是偶函数,得12()()f x f x <,所以()f x 在(,0)-∞上是增函数.复习参考题A 组1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-;(2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320x x -+=的解为121,2x x ==,即集合{1,2}C =.2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等,即{|}P PA PB =表示的点组成线段AB 的垂直平分线; (2){|3}P PO cm =表示的点组成以定点O 为圆心,半径为3cm 的圆.3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线,集合{|}P PA PC =表示的点组成线段AC 的垂直平分线, 得{|}{|}P PA PB P PA PC == 的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点,即ABC ∆的外心.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==,当0a =时,集合B =∅,满足B A ⊆,即0a =; 当0a ≠时,集合1{}B a =,而B A ⊆,则11a =-,或11a=,得1a =-,或1a =, 综上得:实数a 的值为1,0-,或1.5.解:集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭ ,即{(0,0)}A B = ; 集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭,即A C =∅ ; 集合3039(,)|{(,2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭ ; 则39()(){(0,0),(,)}55A B B C =- .6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥,得函数的定义域为[2,)+∞;(2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠, 得函数的定义域为[4,5)(5,)+∞ .7.解:(1)因为1()1x f x x-=+, 所以1()1a f a a -=+,得12()1111a f a a a-+=+=++, 即2()11f a a+=+; (2)因为1()1x f x x-=+, 所以1(1)(1)112a a f a a a -++==-+++,即(1)2a f a a +=-+.8.证明:(1)因为221()1x f x x +=-, 所以22221()1()()1()1x x f x f x x x +-+-===---,即()()f x f x -=; (2)因为221()1x f x x +=-, 所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-.9.解:该二次函数的对称轴为8k x =, 函数2()48f x x kx =--在[5,20]上具有单调性,则208k ≥,或58k ≤,得160k ≥,或40k ≤,即实数k 的取值范围为160k ≥,或40k ≤.10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数;(2)函数2y x -=的图象关于y 轴对称;(3)函数2y x -=在(0,)+∞上是减函数; (4)函数2y x -=在(,0)-∞上是增函数.B 组1.解:设同时参加田径和球类比赛的有x 人,则158143328x ++---=,得3x =,只参加游泳一项比赛的有15339--=(人), 即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人.2.解:因为集合A ≠∅,且20x ≥,所以0a ≥.3.解:由(){1,3}U A B = ð,得{2,4,5,6,7,8,9}A B = ,集合A B 里除去()U A B ð,得集合B , 所以集合{5,6,7,8,9}B =.4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=;当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=; (1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩.5.证明:(1)因为()f x ax b =+,得121212(()222x x x x a f a b x x b ++=+=++,121212()()()222f x f x ax b ax b a x x b ++++==++, 所以1212()()(22x x f x f x f ++=; (2)因为2()g x x ax b =++,得22121212121()(2)(242x x x x g x x x x a b ++=++++,22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()(22x x x x a b +=+++,因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤,即222212121211(2)()42x x x x x x ++≤+,所以1212()()(22x x g x g x g ++≤.6.解:(1)函数()f x 在[,]b a --上也是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >,所以函数()f x 在[,]b a --上也是减函数; (2)函数()g x 在[,]b a --上是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-, 又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >,所以函数()g x 在[,]b a --上是减函数.7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩ 由该人一月份应交纳此项税款为26.78元,得25004000x <≤,25(2500)10%26.78x +-⨯=,得2517.8x =,所以该人当月的工资、薪金所得是2517.8元.新课程标准数学必修1第二章课后习题解答第二章 基本初等函数(I )2.1指数函数练习(P54)1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32,(2)43)(b a +=(a +b )43,(3)32n)-(m =(m -n )32,(4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=[(76)2]23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121+=2×3=6;(3)a 21a 41a 81-=a 814121-+=a 85;(4)2x 31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-.练习(P58)1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为{x |x ≥2};(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是{x ∣x ≠0}.3.y =2x (x ∈N *)习题2.1 A 组(P59)1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解:(1)623ba ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1.(2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m ∙∙∙=4165413121mm m m m ∙∙=4165413121+++mm=m 0=1.点评:遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行.3.解:对于(1),可先按底数5,再按键,再按12,最后按,即可求得它的值.答案:1.710 0;对于(2),先按底数8.31,再按键,再按12,最后按即可. 答案:2.881 0;对于(3)这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案:4.728 8;对于(4)这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案:8.825 0.4.解:(1)a 31a 43a 127=a1274331++=a 35;(2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462r ts -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts =6393652----rt s =36964125s r r ;(6)(-2x 41y 31-)(3x 21-y 32)(-4x 41y 32)=[-2×3×(-4)]x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y21-;(8)4x 41 (-3x 41y 31-)÷(-6x21-y32-)=3231214141643-++-⨯-y x =2xy 31.点评:进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.(1)要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R .(2)要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R .(3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R .(4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评:求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解:设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ).点评:根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值;因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值;因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值;因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5.(4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值;因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n .(2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1,所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n .(3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1,所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n .(4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1,所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n .点评:利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002.答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰,因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的.B 组1. 当0<a <1时,a 2x -7>a 4x -12⇒x -7<4x -1⇒x >-3;当a >1时,a 2x -7>a 4x -1⇒2x -7>4x -1⇒x <-3.综上,当0<a <1时,不等式的解集是{x |x >-3};当a >1时,不等式的解集是{x |x <-3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用.解:(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35.点评:整体代入和平方差,完全平方公式的灵活运用是解题的突破口.3.解:已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ),2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2,3期后的本利和为y 3=a (1+r )3,…x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1000×1.02255≈1118.答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元.4.解:(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-.(2)因为y 1>y 2,所以a 3x +1>a -2x .所以当a >1时,3x +1>-2x .所以x >51-.当0<a <1时,3x +1<-2x .所以x <51-.2.2对数函数练习(P64)1.(1)2log 83=; (2)2log 325=; (3)21log 12=-; (4)2711log 33=-2.(1)239=;(2)35125=;(3)2124-=; (4)41381-=3.(1)设5log 25x =,则25255x ==,所以2x =;(2)设21log 16x =,则412216x -==,所以4x =-;(3)设lg1000x =,则310100010x ==,所以3x =;(4)设lg 0.001x =,则3100.00110x -==,所以3x =-;4.(1)1; (2)0; (3)2; (4)2; (5)3; (6)5.练习(P68)1.(1)lg()lg lg lg xyz x y z =++;(2)222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z =-=++=++;(3)3311lg()lg lg lg lg 3lg lg 22xy x y z x y z =-=+-=+-;(4)2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z =-=-+=--.2.(1)223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=;(2)22lg1002lg1002lg104lg104====;(3)5lg 0.00001lg105lg105-==-=-; (4)11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg 5lg 2lg101+==;(3)555511log 3log log (3log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-.4.(1)1; (2)1; (3)54练习(P73)1.函数3log y x =及13log y x =的图象如右图所示.相同点:图象都在y 轴的右侧,都过点(1,0)不同点:3log y x =的图象是上升的,13log y x =的图象是下降的关系:3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞; (2)(0,1)(1,)+∞ ;(3)1(,3-∞; (4)[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组(P74)1. (1)3log 1x =; (2)41log 6x =; (3)4log 2x =; (4)2log 0.5x= (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x =(4)173x =(5) 100.3x = (6) x e =3. (1)0;(2) 2;(3) 2-;(4)2;(5) 14-; (6) 2.4. (1)lg 6lg 2lg 3a b =+=+;(2) 3lg 42lg 22log 4lg 3lg 3ab===;(3) 2lg122lg 2lg 3lg 3log 1222lg 2lg 2lg 2ba+===+=+; (4)3lg lg 3lg 22b a=-=-5. (1)x ab =; (2) mx n=;(3) 3n x m=;(4)x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番,则(10.073)4x += 解得 1.073log 420x =≈. 答:设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4.8. (1)m n <;(2) m n <;(3) m n >;(4)m n >.9. 若火箭的最大速度12000v =,那么62000ln 112000ln(161402MM M M e m m m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答:当燃料质量约为火箭质量的402倍时,火箭的最大速度可达12km/s.10. (1)当底数全大于1时,在1x =的右侧,底数越大的图象越在下方.所以,①对应函数lg y x =,②对应函数5log y x =,③对应函数2log y x =.(2)略. (3)与原函数关于x 轴对称.11. (1)235lg 25lg 4lg 92lg 52lg 22lg 3log 25log 4log 98lg 2lg 3lg 5lg 2lg 3lg 5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯=12. (1)令2700O =,则312700log 2100v =,解得 1.5v =. 答:鲑鱼的游速为1.5米/秒.(2)令0v =,则31log 02100O=,解得100O =. 答:一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得:143,43x x -==,于是11044333x x -+=+=2. ①当1a >时,3log 14a <恒成立;②当01a <<时,由3log 1log 4a a a <=,得34a <,所以304a <<.综上所述:实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时,112110lg 12010L -==;(2)当1210I -= W/m 2时,121121010lg 010L --==答:常人听觉的声强级范围为0120dB .4. (1)由10x +>,10x ->得11x -<<,∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知:函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()log (1)log (1)()()a a f x g x x x f x g x -+-=-++=+∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =,0.3log y x =; (2)3x y =,0.1x y =.习题2.3 A 组(P79)1.函数y =21x是幂函数.2.解析:设幂函数的解析式为f (x )=x α,因为点(2,2)在图象上,所以2=2α.所以α=21,即幂函数的解析式为f (x )=x 21,x ≥0.3.(1)因为流量速率v 与管道半径r 的四次方成正比,所以v =k ·r 4;(2)把r =3,v =400代入v =k ·r 4中,得k =43400=81400,即v =81400r 4;(3)把r =5代入v =81400r 4,得v =81400×54≈3 086(cm 3/s ),即r =5 cm 时,该气体的流量速率为3 086 cm 3/s .第二章 复习参考题A 组(P82)1.(1)11; (2)87; (3)10001; (4)259.2.(1)原式=))(()()(212121212212122121b a b a b a b a -+++-=ba b b a a b b a a -++++-2121212122=b a b a -+)(2;(2)原式=))(()(1121----+-a a a a a a =aa a a 11+-=1122+-a a .3.(1)因为lg 2=a ,lg 3=b ,log 125=12lg 5lg =32lg 210lg2∙=3lg 2lg 22lg 1+-,所以log 125=b a a +-21.(2)因为2log 3a =,3log 7b=37147log 27log 56log 27⨯=⨯=2log 112log 377++=7log 2log 11)7log 2(log 33333÷++÷=b ab a ÷++÷111)1(3=13++ab ab .4.(1)(-∞,21)∪(21,+∞);(2)[0,+∞).5.(32,1)∪(1,+∞);(2)(-∞,2);(3)(-∞,1)∪(1,+∞).6.(1)因为log 67>log 66=1,所以log 67>1.又因为log 76<log 77=1,所以log 76<1.所以log 67>log 76.(2)因为log 3π>log 33=1,所以log 3π>1.又因为log 20.8<0,所以log 3π>log 20.8.7.证明:(1)因为f (x )=3x ,所以f (x )·f (y )=3x ×3y =3x +y .又因为f (x +y )=3x +y ,所以f (x )·f (y )=f (x +y ).(2)因为f (x )=3x ,所以f (x )÷f (y )=3x ÷3y =3x -y .又因为f (x -y )=3x -y ,所以f (x )÷f (y )=f (x -y ).8.证明:因为f (x )=lgxx+-11,a 、b ∈(-1,1),所以f (a )+f (b )=lgb b a a +-++-11lg 11=lg )1)(1()1)(1(b a b a ++--,f (ab b a ++1)=lg (ab b a ab ba +++++-1111)=lg b a ab b a ab +++--+11=lg )1)(1()1)(1(b a b a ++--.所以f (a )+f (b )=f (abba ++1).9.(1)设保鲜时间y 关于储藏温度x 的函数解析式为y =k ·a x (a >0,且a ≠1).因为点(0,192)、(22,42)在函数图象上,所以022192,42,k a k a ⎧=⋅⎪⎨=⋅⎪⎩解得⎪⎩⎪⎨⎧≈==.93.0327,19222a k 所以y =192×0.93x ,即所求函数解析式为y =192×0.93x .(2)当x =30 ℃时,y ≈22(小时);当x =16 ℃时,y ≈60(小时),即温度在30 ℃和16 ℃的保鲜时间约为22小时和60小时.(3)图象如图:图2-210.解析:设所求幂函数的解析式为f (x )=x α,因为f (x )的图象过点(2,22),所以22=2α,即221-=2α.所以α=21-.所以f (x )=x 21-(x >0).图略,f (x )为非奇非偶函数;同时它在(0,+∞)上是减函数.B 组1.A2.因为2a =5b =10,所以a =log 210,b =log 510,所以a 1+b 1=10log 12+10log 15=lg 2+lg 5=lg 10=1.3.(1)f (x )=a 122+-x 在x ∈(-∞,+∞)上是增函数.证明:任取x 1,x 2∈(-∞,+∞),且x 1<x 2.f (x 1)-f (x 2)=a 122+-x -a +1222+x =1222+x -1221+x =)12)(12()22(21221++-x x x x .因为x 1,x 2∈(-∞,+∞),所以.012.01212>+>+x x 又因为x 1<x 2,所以2122x x <即2122x x <<0.所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).所以函数f (x )=a 122+-x 在(-∞,+∞)上是增函数.(2)假设存在实数a 使f (x )为奇函数,则f (-x )+f (x )=0,即a 121+--x +a 122+-x =0⇒a =121+-x +121+x =122+x +121+x =1,即存在实数a =1使f (x )=121+--x 为奇函数.4.证明:(1)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以[g (x )]2-[f (x )]2=[g (x )+f (x )][g (x )-f (x )]=22)(22(xx x x x x x x e e e e e e e e -----++++=e x ·e -x =e x -x =e 0=1,即原式得证.(2)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以f (2x )=222x x e e -+,2f (x )·g (x )=2·2x x e e --·2x x e e -+=222xx e e --.所以f (2x )=2f (x )·g (x ).(3)因为f (x )=2x x e e --,g (x )=2x x e e -+,所以g (2x )=222xx e e -+,[g (x )]2+[f (x )]2=(2xx e e -+)2+(2xx e e --)2=4222222x x x x e e e e --+-+++=222xx e e -+.所以g (2x )=[f (x )]2+[g (x )]2.5.由题意可知,θ1=62,θ0=15,当t =1时,θ=52,于是52=15+(62-15)e -k ,解得k ≈0.24,那么θ=15+47e -0.24t . 所以,当θ=42时,t ≈2.3;当θ=32时,t ≈4.2.答:开始冷却2.3和4.2小时后,物体的温度分别为42 ℃和32 ℃.物体不会冷却到12 ℃.6.(1)由P=P 0e -k t 可知,当t =0时,P=P 0;当t =5时,P=(1-10%)P 0.于是有(1-10%)P 0=P 0e -5k ,解得k =51-ln 0.9,那么P=P 0e t )9.0ln 51(.所以,当t =10时,P=P 0e 9.01051n I ⨯⨯=P 0e ln 0.81=81%P 0.答:10小时后还剩81%的污染物.(2)当P=50%P 0时,有50%P 0=P 0e t )9.0ln 51(,解得t =9.0ln 515.0ln ≈33.答:污染减少50%需要花大约33h .(3)其图象大致如下:图2-3新课程标准数学必修1第三章课后习题解答第三章 函数的应用3.1函数与方程练习(P88)1.(1)令f (x )=-x 2+3x +5,作出函数f (x )的图象(图3-1-2-7(1)),它与x 轴有两个交点,所以方程-x 2+3x +5=0有两个不相等的实数根.(2)2x (x -2)=-3可化为2x 2-4x +3=0,令f (x )=2x 2-4x +3,作出函数f (x )的图象(图3-1-2-7(2)),它与x 轴没有交点,所以方程2x (x -2)=-3无实数根.(3)x2=4x-4可化为x2-4x+4=0,令f(x)=x2-4x+4,作出函数f(x)的图象(图3-1-2-7(3)),它与x轴只有一个交点(相切),所以方程x2=4x-4有两个相等的实数根.(4)5x2+2x=3x2+5可化为2x2+2x-5=0,令f(x)=2x2+2x-5,作出函数f(x)的图象(图3-1-2-7(4)),它与x轴有两个交点,所以方程5x2+2x=3x2+5有两个不相等的实数根.图3-1-2-72.(1)作出函数图象(图3-1-2-8(1)),因为f(1)=1>0,f(1.5)=-2.875<0,所以f(x)=-x3-3x+5在区间(1,1.5)上有一个零点.又因为f(x)是(-∞,+∞)上的减函数,所以f(x)=-x3-3x+5在区间(1,1.5)上有且只有一个零点.(2)作出函数图象(图3-1-2-8(2)),因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x-2)-3在区间(3,4)上有一个零点.又因为f(x)=2x·ln(x-2)-3在(2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点.(3)作出函数图象(图3-1-2-8(3)),因为f(0)<0,f(1)>0,所以f(x)=e x-1+4x-4在区间(0,1)上有一个零点.又因为f(x)=e x-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点.(4)作出函数图象(图3-1-2-8(4)),因为f(-4)<0,f(-3)>0,f(-2)<0,f(2)<0,f(3)>0,所以f(x)=3(x+2)(x-3)(x+4)+x在(-4,-3),(-3,-2),(2,3)上各有一个零点.图3-1-2-8练习(P91)1.由题设可知f(0)=-1.4<0,f(1)=1.6>0,于是f(0)·f(1)<0,所以函数f(x)在区间(0,1)内有一个零点x0.下面用二分法求函数f(x)=x3+1.1x2+0.9x-1.4在区间(0,1)内的零点.取区间(0,1)的中点x1=0.5,用计算器可算得f(0.5)=-0.55.因为f(0.5)·f(1)<0,所以x0∈(0.5,1).再取区间(0.5,1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32.因为f(0.5)·f(0.75)<0,所以x0∈(0.5,0.75).同理,可得x0∈(0.625,0.75),x0∈(0.625,0.687 5),x0∈(0.656 25,0.687 5).由于|0.687 5-0.656 25|=0.031 25<0.1,所以原方程的近似解可取为0.656 25.2.原方程可化为x+lgx-3=0,令f(x)=x+lgx-3,用计算器可算得f(2)≈-0.70,f(3)≈0.48.于是f(2)·f(3)<0,所以这个方程在区间(2,3)内有一个解x0.下面用二分法求方程x=3-lgx在区间(2,3)的近似解.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)≈-0.10.因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.562 5,2.625),x0∈(2.562 5,2.593 75),x0∈(2.578 125,2.593 75),x0∈(2.585 937 5,2.59 375).由于|2.585 937 5-2.593 75|=0.007 812 5<0.01,所以原方程的近似解可取为2.593 75.习题3.1 A组(P92)1.A,C 点评:需了解二分法求函数的近似零点的条件.2.由x,f(x)的对应值表可得f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,又根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.”可知函数f(x)分别在区间(2,3),(3,4),(4,5)内有零点.3.原方程即(x+1)(x-2)(x-3)-1=0,令f(x)=(x+1)(x-2)(x-3)-1,可算得f(-1)=-1,f(0)=5.于是f(-1)·f(0)<0,所以这个方程在区间(-1,0)内有一个解.下面用二分法求方程(x+1)(x-2)(x-3)=1在区间(-1,0)内的近似解.取区间(-1,0)的中点x1=-0.5,用计算器可算得f(-0.5)=3.375.因为f(-1)·f(-0.5)<0,所以x0∈(-1,-0.5).再取(-1,-0.5)的中点x2=-0.75,用计算器可算得f(-0.75)≈1.58.因为f(-1)·f(-0.75)<0,所以x0∈(-1,-0.75).同理,可得x0∈(-1,-0.875),x0∈(-0.937 5,-0.875).由于|(-0.875)-(-0.937 5)|=0.062 5<0.1,所以原方程的近似解可取为-0.937 5.4.原方程即0.8x-1-lnx=0,令f(x)=0.8x-1-lnx,f(0)没有意义,用计算器算得f(0.5)≈0.59,f(1)=-0.2.于是f(0.5)·f(1)<0,所以这个方程在区间(0.5,1)内有一个解.下面用二分法求方程0.8x-1=lnx在区间(0,1)内的近似解.取区间(0.5,1)的中点x1=0.75,用计算器可算得f(0.75)≈0.13.因为f(0.75)·f(1)<0,所以x0∈(0.75,1).再取(0.75,1)的中点x2=0.875,用计算器可算得f(0.875)≈-0.04.因为f(0.875)·f(0.75)<0,所以x0∈(0.75,0.875).同理,可得x0∈(0.812 5,0.875),x0∈(0.812 5,0.843 75).由于|0.812 5-0.843 75|=0.031 25<0.1,所以原方程的近似解可取为0.843 75.5.由题设有f(2)≈-0.31<0,f(3)≈0.43>0,于是f(2)·f(3)<0,所以函数f(x)在区间(2,3)内有一个零点.。
人教版五年级数学下册课本习题大全完整版
人教版五年级数学下册课本习题大全HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】1、即是2和5的倍数,有是3的倍数的最小三位数是多少?2、3、妈妈去花店买花,玫瑰花每枝3元,郁金香每枝5元马蹄莲每枝10元,妈妈付出50元,找回13元,找回的钱对吗?4、现在有22人,3个人分成一组,至少再来几人才能正好分完有56个桃子。
3个3个的装能正好装完吗2个2个的装能正好装完吗5个5个的装能正好装完吗4、一个纸巾盒的长是24cm,宽是12cm,高是9cm,纸巾盒的前面是什么形状和它形状相同的面是哪个纸巾盒的右面是什么形状和它形状相同的面是哪个纸巾盒的上面是什么形状和它形状相同的面是哪个分别说说每个面的面积。
5为迎接五一劳动节,工人叔叔要在工人俱乐部的四周装上彩灯(地面四周不装),俱乐部的长90米,宽55米,高20米,至少需要多长的彩灯?6小卖部要做一个长,宽40cm,高80cm的玻璃柜台,现要在柜台各边装上角铁,这个柜台需要多少米角铁。
7、用棱长1cm的小正方体摆成一个大正方体,至少需要几个小正方体体积是多少8、做一个微波炉包装箱,长,宽,高,至少需要多少平方米的硬纸板?9、亮亮家要给一个长,宽,高的简易衣柜换布罩,至少需要用多少布?10、一个正方体礼品盒,棱长,包装这个礼品盒至少需要多少平方分米的包装纸?11、一个玻璃鱼缸的形状是正方形(无盖),棱长3dm,制作这个鱼缸需要多少平方米玻璃?13、光华街口装了新铁皮邮箱,长50cm,宽40cm,高78cm,做这个邮箱至少要多少铁皮?14、中队委员把一个棱长46cm的纸箱各面贴上红纸作“爱心箱”,至少需要多少红纸15、一个饼干盒长10cm,宽6cm,高12cm,围着四周贴商标纸(上下不贴),商标纸多大16、加工一批洗衣机机套(没底),长59、5m,宽,高80m,做1000个需要多少布?17、一个游泳池长50m,是宽的2倍,深,要在四周和底面贴瓷砖,需要多少瓷砖?18、37页第9题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1已知A(4,6)、B(-3,-1)、C(4,-5)三点,求经过点A且与BC平行的直线ℓ的点方向式方程。
例2求经过点A(-3,1)和点B(4,-2)的直线ℓ的点方向式方程。
练习11.1(1)
1.已知直线ℓ的方程是5x−12y+13=0,判断点A(-17,-6)、B(2,-2)是否在直线ℓ上。
⑷P(3,0),n=(1,0)。
2.已知△ABC的三个顶点为A(1,6)、B(-1,-2)、C(6,3)。
⑴求AB边上的高CF所在直线的方程;
⑵求AC边的垂直平分线的方程。
例5已知A(1,2)、B(4,1)、C(3,6)三点,点M为AC的中点,求直线BM的方程。
例6已知在△ABC中,∠BAC=90°,点B、C的坐标分别为(4,2)、(2,8),向量d=(3,2),且d与AC边平行,求△ABC的两条直角边所在直线的方程。
2.是否存在实数k,使直线l1:(k-3)x+(4-k)y+1=0与直线l2:2(k-3)x-2y+(2-k)=0平行?若存在,求k的值;若不存在,请说明理由。
3.已知四边形ABCD的四个顶点的坐标分别为A(-1,2)、B(3,4)、C(3,2)、D(1,1)。求证:四边形ABCD是梯形。
11.4点到直线的距离
4.已知直线l1:mx+3y+m+3=0,直线l2:x+(m-2)y+2=0。求当m为何值时,直线l1与l2分别有如下位置关系:
(1)相交;(2)平行;(3)重合。
例3已知两条直线的方程分别是l1:3x+y+2=0,l2:2x-y-3=0,求两条直线的夹角α。
例4已知直线l经过点P(-2, ),且与直线l0:x- y+2=0的夹角为 ,求直线l的方程。
例2(1)已知点A(1,0)、B(0,1),线段AB的方程是不是x+y-1=0?为什么?
(2)到两坐标轴距离相等的点的轨迹C的方程是不是x-y=0?为什么?
例3已知两定点P1(-1,0)和P2(3,0),求到点P1和P2的距离的平方和是16的点的轨迹方程。
例4动点M与距离为4的两个定点A、B满足(向量)MA·MB=5,建立适当的坐标系,并求动点M的轨迹方程。
2.求过点P且与向量d平行的直线ℓ的点方向式方程。
⑴P(3,-5),d=(3,4)
⑵P(0,3),d=(3,-4)
3.求经过A、B两点的直线ℓ的点方向式方程
⑴.A(-3,-2),B(3,-7)
⑵.A(0,3),B(2,4)
例3已知点A(-1,2)和点B(3,4),求线段AB的垂直平分线ℓ的点法向式方程。
2.求过点A(3,2) B(1,1) C(2,-1)三点的圆地方程.
3.讨论 + + ax + 2y + 2 = 0所表示的曲线.
4.求当a为何值时,直线l:x+y-a=0与圆 + = 2分别有下列位置关系:
(1)相交(2)相离(3)相切
例6已知直线l:x+2y=0 ,圆 + - 6x - 2y - 15 = 0,求直线l被圆C所截得的线段的长.
练习11.1(3)
1.已知A(x1,y1)和B(x2,y2)是直线ℓ上的两点,若x2-x1≠0,y2-y1≠0,求直线ℓ的法向量。
2.已知△ABC的三个顶点为A(1,2)、B(4,1)、C(3,6),求BC边上的中线AM和高AH所在直线的方程。
11.2直线的倾斜角和斜率
例1已知直线l上的两点A,B ,求直线l的斜率k及倾斜角α:
练习11.3(2)
1.求下列各组直线的夹角 。
(1)l1:y=3x-1,l2:3y+x-4=0;
(2)l1:y-x+1=0,l2:y=4;
(3)l1:x+y+1=0,l2:x=2。
2.已知直线l1:ax+y-1=0,直线l2:x-ay+2=0,其中a R且a 0,求直线l1与l2的夹角。
3.已知直线ℓ经过原点,且与直线y= x+1的夹角为30 ,求直线ℓ的方程。
例1求点P(2,3)到直线5x+12y-3=0的距离.
例2(1)求证两条平行线L1:ax+by+c1=0L2:ax+by+c2=0的距离
(2)求平行线2x-7y+8=0和2x-7y-6=0之间的距离
练习11.4(1)
1.求P到直线的距离
(1)P(-2,3)L1:8x+15y-3=0
(2)P(-2,3)L1:2x+4=0
2.求下列方程所表示的直线的斜率.
(1).(x+2)/2=3(y-1)
(2).3(x-3)-4(y+1)=0
3.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)P(2,3) Q(6,5)
(2) A(-3,5) B(4,-2)
4.已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),且a,b均不为0,求直线l的方程。
例5已知定点A(4,0)和曲线方程x²+y²=1上的动点B,求线段AB的中点P的轨迹方程。
例6已知曲线C的方程是x²+y²=9,当b为何值时,直线ℓ:2x-y+b=0与曲线C有两个不同的交点?一个交点?没有交点?
12.2圆的方程
例1求以C(-1,2)为圆心,且和直线L:2x-3y-5=0相切的圆的方程.
12.3椭圆的标准方程
例1求焦点在x轴上,焦距为2
,且过点( , )的椭圆的标准方程。
例2已知定点F1(-4,0)、F2(4,0)和动点M(x,y),求满足|MF1|+|MF2|=2a(a>0)的动点M的轨迹及其方程。
例3已知椭圆的两个焦点都在坐标轴上,且关于原点对称,焦距为6,该椭圆经过点(0,4),求它的标准方程。
练习12.2(1)
1.(1)求以点C(3,4)为圆心,且过点M(1,-3)的圆的方程.
(2)已知P(3,4) Q(-5,6)两点,求以PQ为直径的圆的方程.
2.求经过点(-3,4)且与圆x2+ y2=25相切的直线方程.
3.求以点(1,2)为圆心,且与直线4x+3y-35=0相切的圆的方程.
4.圆拱桥的一孔圆拱如图所示,该圆拱的跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一个支柱支撑,求支柱A2B2的长度(精确到0.01米).
(1)A(1,2) B(3,4)
(2)A(0,3) B(2, )
例2已知直线l的倾斜角为α(0≤α<π,α≠π/2),且通过点N(Xo,Yo),求直线l的方程.
练习11.2(1)
1.已知直线l与向量d平行,求直线l的斜率与倾斜角.
(1)向量d=(2,- )
(2)向量d=(-4,-3)
(3)向量d=(-2,0)
(2)P(-8,-5) lo:4x+5y-9=0
2.求过点P且垂直于直线lo的直线的一般式方程.
(1)P(-3,24) lo:3x+y-3=0
(2)P(-4,-1) lo:x-3=0
3.已知方程ax+by+c=0表示的直线分别满足下列条件,求系数a,b,c的一组值。
(1)经过原点和P(3,4)
(2)经过P1(0,3)和P2(4,0)
3.已知直线l:y=ax+2和A(1,4)B(3,1)两点。当l与线段AB相交时,求实数a的取值范围。
4.直线l经过点P(-2,1)且点A(-1,-2)到l的距离等于1,求直线l方程。
12.1曲线和方程
例1已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线ℓ的方程是2x-y-2=0。
2.讨论下列各组直线的位置关系。
(1)l1:( -1)x+y+3=0,l2:2x+( +1)y+1=0;
(2)l1: x-y+1=0,l2:(a2+1)x-2a=0,a R。
3.已知直线l1:2x+by-1=0,直线l2:3x-5y+c=0。求当b、c为何值时,直线l1与l2分别有如下位置关系:
(1)相交;(2)平行;(3)重合。
例6.求下列方程所表示的直线的斜率.
(1)
(2) 3(x-1)-5(y-2)=0
例7.已知A(3,2),B(-4,1),C(0,-1)三点,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
练习11.2(3)
1.求过点P且平行于直线lo的直线的一般式方程.
(1)P(4,12) lo:3x-y+1=0
例4已知直线l经过点P(1,2),且垂直于直线lo:x-3y-5=0,求直线l的方程.
例5已知直线l:2x+3y-6=0,求直线l的点法向式方程和点方向式方程.
练习11.2(2)
1.如果过点P(-2,m),Q(m,4)两点的直线的斜率为1,那么m的值是( )
A. 1 B. 4
C. 1 or 3 D. 1 or 4
4.求经过点A(1,0)且与直线x-y+3=0成30 角的直线的方程。
例5是否存在实数k,使直线l1:3x-(k+2)y+6=0与直线l2:kx+(2k-3)y+2=0平行?若存在,求k的值;若不存在,请说明理由。
练习11.3(3)
1.已知平行四边形ABCD中,一组对边AB、CD所在直线的方程分别为ax+4y=a+2,x+ay=a,求实数a的值。
11.3两条直线的位置关系
例1判断பைடு நூலகம்列各组直线的位置关系,如果相交,那么求出交点坐标:
(1)l1:3x+4y-12=0,l2:7x-12y-1=0;
