高等数学-中值定理证明
高等数学 第5章 第二节 定积分的性质 中值定理
（2）记 f ( x) e x2 x , x 0,2 , 则 f ( x) e x2 x 2x 1 ,
令 f ( x) 0, 得唯一驻点 x 1 ,
2
又
f
(
1
)
e
1 4
,
f (0) 1, f (2) e 2 ,
2
1
所以 m e 4 , M e 2
1
e 4 2 0
y gx
推论1 若 f x gx, x a, b,
y
则
b
a
f xdx
b
a
g
x
dx
a b.
推论 2
b
a
f
xdx
b
a
f xdx
(a b).
性质6 (估值不等式)
y f x
O xa
xbx
设 M max f x, m min f x, 则
x[ a ,b ]
x[ a ,b ]
mb
a
b
a
f
xdx
加性
c
b
c
a f ( x)dx a f ( x)dx b f ( x)dx
b
a
f ( x)dx
c
a
c
f ( x)dx b
f ( x)dx
c
a
b
f ( x)dx c
f ( x)dx
1
性质4
b
b
1dx dx b a
a
a
性质5
若 f x 0, x a,b,
则
b
a
f
xdx
0
a b.
M b
a
a b.
如
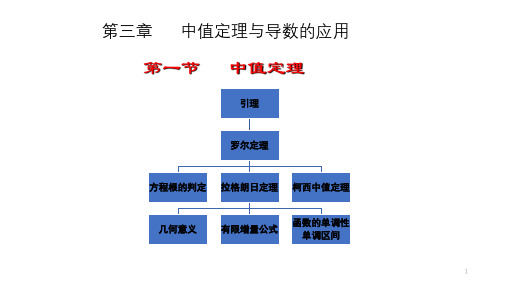
高等数学 第3章 第一节 中值定理
（函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数， 且当
x
6
ln sin x 定义域内的一部分；
,
5
6
时，cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件，且：
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理，至少存在一点 ∈（a，b） ，
即：
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程， 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时， x ln1 x x
1 x
证 设f x ln1 x, 显然，函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于： f f b f a
ba
或： f f b f a 0
ba
AB的方程为：
高等数学6讲中值定理
第六讲 中值定理一、罗尔(Rolle)定理1、引理(费马引理) 设函数()f x 在点0x 的某邻域0()U x 内有定义,若()f x 在点0x 可导,且0()x U x ∀∈有0()()f x f x ≤ (或0()()f x f x ≥).则0()0f x '=.2、定理(罗尔定理) 若函数()f x 满足:(1)在闭区间[,]a b 上连续; (2)在开区间(,)a b 内可导; (3)()()=f a f b , 则至少存在一点(,)∈a b ξ,使()0'=f ξ3、几何意义：例1 验证函数3()3=-f x x x在[内至少存在一点ξ,使得()0'=f ξ,并求出ξ的具体位置例 2 设,,a b c 是任意实数,证明32432ax bx cx a b c ++=++在(0,1)内至少有一个实根.二、拉格朗日(Lagrange)中值定理1、定理(拉格朗日中值定理) 如果函数()f x 满足：(1)在闭区间[,]a b 上连续； (2)在开区间(,)a b 内可导,则至少存在一点(,)∈a b ξ,使得： ()()()-'=-f b f a f b a ξ. 2、几何意义：例3 证明不等式ln --<<b a b b a b a a (0)<<a b . 3. 两个重要推论推论 1 如果函数()f x 在区间(,)a b 内可导,则()f x 在(,)a b 内恒等于常数的充要条件是()0'≡f x .推论2 如果函数()f x 、()g x 在区间(,)a b 内可导,且对任意的(,)∈x a b 有()()''=f x g x ,则在区间(,)a b 内()f x 与()g x 只差一个常数C ,即()()=+f x g x C例4 试证明恒等式:arctan arctan ()2x x e e x π-+=-∞<<+∞课堂练习1. 利用微分中值定理证明下列不等式: (1)sin sin b a b a -≤-;(2)1(0)x x x e xe x <-<>.2. 证明恒等式: arcsin arccos (11)2x x x π+=-≤≤.3. 设()f x 在[0,1]上连续,在(0,1)内可导,且(1)0f =,证明存在一点(0,1)ξ∈,使 ()()0f f ξξξ'+=.。
高等数学- 中值定理
2
( x (0,1) ) .
拉四、格设朗a日 b(La0g，ranng1e，)中证值明定理主要用来证明不等式
nb n1 (a b) a n bn na n1 (a b) .
例五5、证明下列不等式：
1、 arctana arctanb a b ； 2、当x 1时，e x ex .
两个重要结论: (1) 如果函数 f ( x) 在区间 I 上的导数恒为零, 那末 f (x) 在区间 I 上是一个常数. 即x (a,b),若有 f ( x) 0 f ( x) C
(2) x (a,b),若有 f ( x) g( x) f (x) g(x) C
例3 验证 f (x) arctan x 在[0,1] 上满足 Lagrange中值定理的条件 .
则在 (a,b) 内至少存在一点 ，使 f() =0 .
例1 验证 f (x) x2 2x 3在区间[1,3]上满足 Rolle定理.
几何解释:
y
连续光滑曲线 y f (x)
C
在点 A、B处纵坐标相
等,则弧 AB 上至少有一
点C ,在该点处的切线是
水平的.
o a 1
y f (x)
2 b x
(1) f C[a,b] D(a,b) 且 f (a) f (b)
(a,b) , 使 f ( ) 0 ;
(2) f C[a,b] D(a,b)
(a,b)，使 f (b) f (a) f ( );
ba
f ( x) 在 x0, x1 之间满足罗尔定理的条件,
至少存在一个 (在 x0, x1 之间),使得 f () 0. 但 f ( x) 5( x4 1) 0, ( x (0,1)) 矛盾, x0为唯一实根.
高等数学常见中值定理证明及应用
中值定理首先我们来看看几大定理：1、 介值定理：设函数f(x)在闭区间[a,b]上连续，且在该区间的端点取不同的函数值f(a)=A及f(b)=B ，那么对于A 与B 之间的任意一个数C ，在开区间(a,b)内至少有一点ξ使得f(ξ)=C(a<ξ<b).Ps:c 是介于A 、B 之间的，结论中的ξ取开区间。
介值定理的推论：设函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M ，最小值m,若m ≤C ≤M,则必存在ξ∈[a,b], 使得f(ξ)=C 。
（闭区间上的连续函数必取得介于最大值M 与最小值m 之间的任何值。
此条推论运用较多）Ps ：当题目中提到某个函数f(x),或者是它的几阶导函数在某个闭区间上连续，那么该函数或者其几阶导函数必可以在该闭区间上取最大值和最小值，那么就对于在最大值和最小值之间的任何一个值，必存在一个变量使得该值等于变量处函数值。
2、 零点定理：设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号，即f(a).f(b)<0,那么在开区间内至少存在一点ξ使得f(ξ)=0.Ps:注意条件是闭区间连续，端点函数值异号，结论是开区间存在点使函数值为0.3、 罗尔定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、在区间端点处函数值相等，即f(a)=f(b).那么在(a,b)内至少有一点ξ(<a ξ<b),使得f`(x)=0;4、 拉格朗日中值定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导;那么在(a,b)内至少有一点ξ(<a ξ<b),使得 f(b)-f(a)=f`(ξ).(b-a).5、 柯西中值定理：如果函数f(x)及g(x)满足（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、对任一x(a<x<b),g`(x)≠0,那么在(a,b)内至少存在一点ξ,使得)`()`()()()()(ξξg f a g b g a f b f =--Ps ：对于罗尔定理、拉格朗日中值定理、柯西中值定理结论都是开开区间内取值。
高数大一上知识点总结中值定理
高数大一上知识点总结中值定理高等数学（一）知识点总结：中值定理在大一上学期的高等数学课程中，我们学习了许多重要的数学知识和定理，其中之一就是中值定理。
中值定理是微积分中的重要定理之一，它在分析函数的性质以及解决实际问题中扮演着重要的角色。
本文将对中值定理进行总结和讨论。
一、中值定理概述中值定理是微积分的基本定理之一，它包括三个重要的定理：拉格朗日中值定理、柯西中值定理和罗尔中值定理。
这些定理都是以其创立者的名字命名的，它们在解决函数连续性和导数性质相关问题时非常有用。
二、拉格朗日中值定理拉格朗日中值定理是中值定理中最常见和基础的一个。
它得出的结论是：如果一个函数在闭区间[a, b]上连续，并且在开区间(a, b)上可导，那么在(a, b)上至少存在一个点c，使得函数的导数等于函数在区间[a, b]上的平均变化率。
换句话说，存在c∈(a, b)，使得f'(c)=(f(b)-f(a))/(b-a)。
三、柯西中值定理柯西中值定理是在拉格朗日中值定理的基础上进行拓展得到的。
柯西中值定理的条件为：设函数f(x)和g(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且g'(x)≠0。
那么在(a, b)上至少存在一点c，使得(f(b)-f(a))/(g(b)-g(a)) = f'(c)/g'(c)。
柯西中值定理的重要性在于它将一个函数的导数和在另一个函数上的值联系在一起。
这个定理可以用于证明其他重要的数学定理，如罗尔定理和拉格朗日定理的推广形式。
四、罗尔中值定理罗尔中值定理是中值定理中的一个特例，它的前提条件是函数在闭区间[a, b]上连续，在开区间(a, b)上可导，并且满足f(a)=f(b)。
那么在(a, b)上至少存在一个点c，使得f'(c)=0。
罗尔中值定理的直观理解是：如果一个函数在两个端点处取相同的值，那么在函数曲线上至少存在一个点处的切线斜率为零。
高等数学第一节中值定理、罗比塔法则
例 2 lim e x - e-x - 2 x x0 x - sin x
lim e x e-x - 2 x0 1 - cos x
(0) 0
lim e x - e-x lim e x e-x 2
x0 sin x
x0 cos x
注
在反复使用法则时，要时刻注意检查是否为
未定式，若不是未定式，不可使用法则。
- arctan x
例3
求 lim 2 x
1
.
(0) 0
x
解
原式
lim
x
-
1 -
1
x 1 x2
2
x2
lim x1
x2
1.
例4 求 lim ln cot x . x0 ln x
()
1 (-x
x0
1
lim - x0 sin x cosx
（3）本节定理给出的是求未定式的一种方法。当定理 条件满足时，所求的极限当然存在(或为)，但定理条件 不满足时，所求极限却不一定不存在。
3.其它类型的不定式
(1)"0 "型
1
例6
lim
x0
x ln x
ln x
lim
x0
1
x
lim
x0
-
x 1
x2
- lim x x0
0
1. 0型不定式
0
定理2(洛必达法则1) 设函数 f (x)、j(x) 在点
x0 的左右近旁有定义，若有
（1） lim f ( x) = lim j( x) = 0;
x → x0
x → x0
高数中值定理
高数中值定理，语句通顺顺畅中值定理是高等数学中的一个重要定理，它指的是一个多项式的极值点（最大值点或最小值点）必须是位于它的表达式和它的一阶导数之间的根点（即零点）。
它建立在极值定理的基础上，是几何分析学的一项重要基础理论。
中值定理的主要应用在几何分析学中，即，如果一个函数f(x)在一段区间上经过最大值点，或者在另一段区间上经过最小值点，那么这两个区间之间，必然存在一个极点，它是函数f(x)和它的一阶导数f'(x)的零点，也就是说，当函数f(x)的值等于f'(x)的值时，函数f(x)在此点取到最大值，或者最小值。
中值定理的原理可以用一个例子简单地表述，假设有一个函数f(x)，它满足条件f(x) >= 0和f'(x) = 0这样的关系，那么说明函数f(x)在点x处取到最大值，这就是中值定理的基本原理。
因此，中值定理为几何学研究者提供了参数估计、函数研究、函数优化和曲线研究等等实用的技术手段，其中，最基本的应用有两个。
一是采用中值定理的思路，可以轻松地求出一个下限，数学上叫最小值；二是采用中值定理的思路，可以求出一个上限，数学上叫最大值。
中值定理的对象也比较广泛，其函数不仅可以是二元函数（一般情况下，指多项式函数），也可以是n元函数（一般情况下，指函数组）。
不管哪种函数，在经过极值点后，它们都可以使用中值定理去验证它们是否达到极值点。
此外，中值定理也可以用于数学研究中求解积分。
例如，当估算函数f(x)在（a,b）内的最小值时，可以使用中值定理求解积分。
总之，中值定理是一个非常有用的定理，它不仅可以用于几何分析，而且可以应用于数学的普遍性研究。
学习和使用中值定理，非常有必要，能使我们更加深入地理解几何学和数学，并有效解决实际问题。
高等数学——积分中值定理
⾼等数学——积分中值定理本⽂始发于个⼈公众号：TechFlow，原创不易，求个关注今天是⾼等数学专题的第12篇，我们继续来看定积分。
之前在讲微分求导内容的时候，介绍过⼀系列微分中值定理的推导。
既然有微分中值定理，那么⾃然也有积分中值定理，我们下⾯就来看看积分中值定理的定义。
极值定理极值定理也叫最⼤最⼩值定理，它的含义⾮常直观：如果函数f(x)在区间[a,b]上连续的函数，必然存在最⼤值和最⼩值，并且取到最⼤值和最⼩值⾄少⼀次。
这是⼀个⾮常有名的定理，定理的内容很直观，也不难理解。
但是证明它不太容易，是由区间套定理与B-M定理等多个定理推导得到的，这段证明过程⽐较复杂，由于篇幅和⽔平的限制，本⽂当中只能跳过这部分，感兴趣的同学可以⾃⾏了解。
我们假设m和M分别是区间[a, b]上函数f(x)的最⼩值和最⼤值，那么根据极值定理，可以得到以下式⼦成⽴：这个式⼦光看可能会觉得有些复杂，但是我们把图画出来之后⾮常简单：上图当中灰⾊阴影部分就是定积分的结果，蓝⾊的矩形⾯积是m(b-a)，⼤的矩形⾯积是M(b-a)。
通过⼏何⾯积的关系我们可以很容易证明结论。
数学证明也很简单，由于m和M分别是最⼩值和最⼤值，所以我们可以得到。
我们把常数也看成是函数，进⾏积分，于是可以得到：两边积分的结果就是矩形⾯积，于是我们就得到了证明。
积分中值定理极值定理⾮常简单，但是是很多定理的基础，⽐如我们的积分中值定理就和它密切相关。
我们对上⾯的式⼦做⼀个简单的变形，由于b-a是常数并且⼤于0，所以我们在这个不等式两边同时除以b-a，可以得到：我们把这个式⼦看成⼀个整体，它的值位于函数在区间的最⼤值和最⼩值之间。
根据连续函数的介值定理，我们⼀定可以在[a, b]上找到⼀点，使得f(x)在这点的取值与这个数值相等，也就是说：上⾯这个式⼦就是积分中值定理了，这⾥有两点要注意，我们先来说简单的⼀点，就是我们⽤到了连续函数介值定理。
所以限定了这必须是⼀个连续函数，否则的话，可能刚好函数在点处没有定义。
高等数学-中值定理
即
因为
故
3.1 中值定理·第3章 10
思考与练习
1. 填空题
1) 函数 条件, 则中值 2) 设 在区间 [1, 2] 上满足拉格朗日定理
3 15 4 . _____
方程
有 3 个根 , 它们分别在区间 (1, 2) , (2 , 3) , (3 , 4) 上.
3.1 中值定理·第3章 11
3.1 中值定理·第3章 2
一、罗尔( Rolle )定理
费马(fermat)引理
且 证: 设 则
存在
(或 )
y
o
x0
x
0 0
证毕
3.1 中值定理·第3章 3
罗尔（ Rolle ）定理
满足: (1) 在区间 [a , b] 上连续 (2) 在区间 (a , b) 内可导 (3) f ( a ) = f ( b )
3.1 中值定理·第3章 6
有且仅有一个小于1 的 例1. 证明方程 正实根 . 证: 1) 存在性 . 5 设 f ( x) x 5 x 1, 则 f ( x) 在 [0 , 1 ] 连续 , 且 由介值定理知存在 x0 (0 ,1) , 使
f ( x0 ) 0, 即方程有小于 1 的正根
3.1 中值定理·第3章 8
f (b) f (a ) ( ) x ( x) f ( x)
b a
例2. 证明等式 证: 设
由推论可知 令x=0,得
(常数)
又
故所证等式在定义域
上成立.
经验: 欲证 x I 时 f ( x) C0 , 只需证在 I 上 f ( x) 0,
y
y f ( x)
(完整版)高等数学中值定理的题型与解题方法
高等数学中值定理的题型与解题方法高数中值定理包含：1.罗尔中值定理(rolle); 2.拉格朗日中值定理(lagrange); 3.柯西中值定理(cauchy); 还有经常用到的泰勒展开式(taylor), 其中(,)a b ξ∈，一定是开区间.全国考研的学生都害怕中值定理，看到题目的求解过程看得懂，但是自己不会做，这里往往是在构造函数不会处理，这里给总结一下中值定理所涵盖的题型，保证拿到题目就会做。
题型一：证明：()0nf ξ=基本思路，首先考虑的就是罗尔定理(rolle)，还要考虑极值的问题。
例1. ()[,]f x C a b ∈在(,)a b 可导，()()0f a f b >>，()()02a bf a f +<， 证明：存在(,)a b ξ∈，使得'()0f ξ=.分析：由()()0f a f b >>，()()02a bf a f +<，容易想到零点定理。
证明：()()02a b f a f +<，∴存在1(,)2a bx a +∈，使得1()0f x =，又()()0f a f b >>，∴(),()f a f b 同号，∴()()02a bf b f +<，∴存在2(,)2a bx b +∈，使得2()0f x =，∴12()()0f x f x ==，所以根据罗尔中值定理：存在(,)a b ξ∈，使得'()0f ξ=.例2. ()[0,3]f x C ∈在(0,3)内可导，(0)(1)(2)3f f f ++=，(3)1f =， 证明：存在(0,3)ξ∈，使得'()0f ξ= 证明：（1）()[0,3]f x C ∈，∴()f x 在[0,3]使得上有最大值和最小值,M m ，∴根据介值性定理(0)(1)(2)3f f f m M ++≤≤，即1m M ≤≤∴存在[0,3]c ∈，使得()1f c =，（2）()(3)1f c f ==，所以根据罗尔中值定理：存在(,3)(0,3)c ξ∈⊂，使得'()0f ξ=.例3. ()f x 在(0,3)三阶可导，[0,1]x ∈，(1)0f =，3()()F x x f x = 证明：存在(0,1)ξ∈，使得'''()0F ξ= 证明：（1）(0)(1)0F F ==，∴存在1(0,1)ξ∈，使得1'()0F ξ=，（2）23'()3()'()F x x f x x f x =+，所以1'(0)'()0F F ξ==，∴存在21(0,)ξξ∈，使得2''()0F ξ=，（3）223''()6()3'()3'()''()F x xf x x f x x f x x f x =+++，所以2''(0)''()0F F ξ==，∴存在2(0,)(0,1)ξξ∈⊂，使得'''()0F ξ=，例3. ()[0,1]f x C ∈在(0,1)内可导，[0,1]x ∈，(0)1f =，11()22f =，(1)2f = 证明：存在(0,1)ξ∈，使得'()0f ξ= 证明：(0)1f =，11()22f =，(1)2f =∴存在(0,1)ξ∈，使得()f m ξ=，又()f x 在(0,1)内可导，∴存在(0,1)ξ∈，使得'()0f ξ=题型二：证明：含ξ，无其它字母 基本思路，有三种方法： （1）还原法。
高等数学 第四章 第1节 中值定理(中央财经大学)
极值的定义若内有定义在设 , )(U )( 0x x f , )(Uˆ )()(00x x x f x f ∈≤, )( )( 0的极大值为则称x f x f , )(Uˆ )()(00x x x f x f ∈≥, )( )( 0的极小值为则称x f x f .0为函数的极大点x .0为函数的极小点x定理)(是特殊情况C x f ≡证二. 罗尔中值定理设;]) ,([)( )1(b a C x f ∈;) ,( )( )2(内可导在b a x f ,)()( )3(b f a f =则至少存在一点.0)( , ) ,(=′∈ξξf b a 使得定理实际上, 切线与弦线AB 平行.实际上, 切线与弦线AB 平行.]) ,([)( b a C x f ∈∵上取到它的最大值、必在 ] ,[ )( b a x f ∴最小值至少各一次.)(min , )(max ],[] ,[x f m x f M b a x b a x ∈∈==令mM = )1(若],[ )( b a x M x f m ∈∀≤≤∵],[ )( b a x m x f ∈=∴.0)( , ) ,( =′∈∀ξξf b a 均有故证)( )2(m M M m ≠<即若]) ,([)( b a C x f ∈∵上取到它的最大值、必在 ] ,[ )( b a x f ∴最小值至少各一次., )()( b f a f =又 . )( m M b x a x x f 和处分别取到和不能同时在故==使得即至少存在一点 ,) ,( b a ∈ξ.)( )(m f M f ==ξξ或由费马定理可知：.) ,( 0)(b a f ∈=′ξξ证又, )( 是四次多项式x f ∵, )( 是三次多项式x f ′∴.0)(至多有三个实根=′x f 综上所述,,0)(仅有三个实根=′x f .) ,( ), ,( ), ,(中分别在d c c b b a分析在证则由证证定理切线与弦线 AB 平行 切线与弦线 AB 平行)()()()( a x a b a f b f a f y AB −−−+=的方程：弦如何利用罗尔定理来证明？如何利用罗尔定理来证明？证推论 1推论 2推论 3用来证明一些重要的不等式用来证明一些重要的不等式推论 4用来判断函数的单调性用来判断函数的单调性证证证 )()( C e x f x x ==ϕ证证证例10)].0()1([2)(),1,0(:,)1,0(,]1,0[)(f f f x f −=′∈ξξξ使至少存在一点证明内可导在上连续在设函数证结论可变形为ξξ2)(01)0()1(f f f ′=−−.)()(2ξ=′′=x x x f ,)(2x x g =设,]1,0[)(),(条件上满足柯西中值定理的在则x g x f 有内至少存在一点在,)1,0(ξ∴ξξ2)(01)0()1(f f f ′=−−)].0()1([2)(f f f −=′ξξ即Rolle 定理Lagrange中值定理Cauchy中值定理xxg=)()()(bfaf=罗尔定理、拉格朗日中值定理及柯西中值定理之间的关系；。
高等数学常见中值定理证明及应用
中值定理首先我们来看看几大定理：1、 介值定理：设函数f(x)在闭区间[a,b]上连续，且在该区间的端点取不同的函数值f(a)=A及f(b)=B ，那么对于A 与B 之间的任意一个数C ，在开区间(a,b)内至少有一点ξ使得f(ξ)=C(a<ξ<b).Ps:c 是介于A 、B 之间的，结论中的ξ取开区间。
介值定理的推论：设函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M ，最小值m,若m ≤C ≤M,则必存在ξ∈[a,b], 使得f(ξ)=C 。
（闭区间上的连续函数必取得介于最大值M 与最小值m 之间的任何值。
此条推论运用较多）Ps ：当题目中提到某个函数f(x),或者是它的几阶导函数在某个闭区间上连续，那么该函数或者其几阶导函数必可以在该闭区间上取最大值和最小值，那么就对于在最大值和最小值之间的任何一个值，必存在一个变量使得该值等于变量处函数值。
2、 零点定理：设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号，即f(a).f(b)<0,那么在开区间内至少存在一点ξ使得f(ξ)=0.Ps:注意条件是闭区间连续，端点函数值异号，结论是开区间存在点使函数值为0.3、 罗尔定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、在区间端点处函数值相等，即f(a)=f(b).那么在(a,b)内至少有一点ξ(<a ξ<b),使得f`(x)=0;4、 拉格朗日中值定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导;那么在(a,b)内至少有一点ξ(<a ξ<b),使得 f(b)-f(a)=f`(ξ).(b-a).5、 柯西中值定理：如果函数f(x)及g(x)满足（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、对任一x(a<x<b),g`(x)≠0,那么在(a,b)内至少存在一点ξ,使得)`()`()()()()(ξξg f a g b g a f b f =--Ps ：对于罗尔定理、拉格朗日中值定理、柯西中值定理结论都是开开区间内取值。
高等数学拉格朗日中值定理
高等数学拉格朗日中值定理高等数学拉格朗日中值定理是微积分中的一项重要定理，它被广泛应用于求解函数的极值、证明函数的性质以及推导其他数学定理等方面。
拉格朗日中值定理是法国数学家约瑟夫·路易斯·拉格朗日于18世纪提出的，它建立在导数的基础上，描述了函数在某个区间内的平均变化率与其导数在该区间内某点的值之间的关系。
拉格朗日中值定理的表述如下：若函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，那么在(a, b)内至少存在一个点c，使得f(b) - f(a) = f'(c)(b - a)。
简单来说，拉格朗日中值定理告诉我们，对于任意一段曲线，至少存在一个点，该点的切线斜率等于该曲线两个端点间的斜率之差。
为了更好地理解拉格朗日中值定理，我们可以通过一个具体的例子来说明。
假设有一个汽车在某段时间内行驶了一段距离，我们希望知道在这段时间内汽车的平均速度与某一刻的瞬时速度之间的关系。
根据拉格朗日中值定理，平均速度等于瞬时速度。
具体而言，在某一刻，汽车的瞬时速度等于汽车在该段时间内的总位移除以该段时间的长度，即平均速度。
拉格朗日中值定理的应用远不止于此，它可以用于证明很多重要的数学定理。
例如，利用拉格朗日中值定理，我们可以证明柯西中值定理、罗尔中值定理和费马定理等。
这些定理在微积分中具有重要的地位，并且被广泛应用于求解极值问题、证明函数的性质以及推导其他数学定理。
总之，高等数学拉格朗日中值定理是微积分中的一项基础且重要的定理。
通过该定理，我们可以了解函数在某个区间内的平均变化率与其导数在该区间内某点的值之间的关系。
此外，拉格朗日中值定理还可以用于证明其他重要的数学定理，为我们研究函数的性质和求解实际问题提供了有力的工具。
关于高等数学常见中值定理证明及应用
关于高等数学常见中值定理证明及应用中值定理是微积分中的重要定理之一，它包括了拉格朗日中值定理、柯西中值定理和罗尔中值定理。
这些定理在数学中有广泛的应用，尤其在求解函数的零点、证明不等式等问题上起到了重要的作用。
下面我将详细介绍这些中值定理的证明及应用。
1. 拉格朗日中值定理（Lagrange's Mean Value Theorem）：拉格朗日中值定理是微积分中最基本的中值定理之一、设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，则存在xi∈(a, b)，使得f'(xi) = (f(b) - f(a))/(b - a)。
换句话说，函数在开区间内其中一点的导数等于函数在闭区间两端的函数值之差与区间长度的比值。
证明：我们可以通过引入辅助函数g(x)=f(x)-kx来证明，其中k是一个常数，使得g(a)=g(b)。
然后根据罗尔中值定理，我们得到存在一个ξ∈(a, b)，使得g'(ξ)=0。
进而，我们得到f'(ξ)-k=0，即f'(ξ)=k。
由于k=(f(b)-f(a))/(b-a)，得到f'(ξ)=(f(b)-f(a))/(b-a)。
应用：拉格朗日中值定理常用来证明不等式、求解方程和不定积分等问题。
例如，若函数在区间[a, b]上连续且处处大于零，则存在一个ξ∈(a, b)，使得f(ξ)>(1/(b-a))∫[a,b]f(x)dx。
这可以直接利用拉格朗日中值定理证明。
2. 柯西中值定理（Cauchy's Mean Value Theorem）：柯西中值定理是拉格朗日中值定理的推广，它描述的是两个函数之间的关系。
设函数f(x)和g(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且g'(x)≠0，则存在xi∈(a, b)，使得(f'(xi)/g'(xi))=(f(b)-f(a))/(g(b)-g(a))。
高等数学中值定理的题型与解题方法
高等数学中值定理的题型与解题方法高数中值定理包含：1.罗尔中值定理rolle; 2.拉格朗日中值定理lagrange; 3.柯西中值定理cauchy; 还有经常用到的泰勒展开式taylor, 其中(,)a b ξ∈,一定是开区间.全国考研的学生都害怕中值定理,看到题目的求解过程看得懂,但是自己不会做,这里往往是在构造函数不会处理,这里给总结一下中值定理所涵盖的题型,保证拿到题目就会做; 题型一：证明：()0n f ξ=基本思路,首先考虑的就是罗尔定理rolle,还要考虑极值的问题; 例1. ()[,]f x C a b ∈在(,)a b 可导,()()0f a f b >>,()()02a bf a f +<, 证明：存在(,)a b ξ∈,使得'()0f ξ=.分析：由()()0f a f b >>,()()02a bf a f +<,容易想到零点定理; 证明：()()02a b f a f +<,∴存在1(,)2a bx a +∈,使得1()0f x =,又()()0f a f b >>,∴(),()f a f b 同号,∴()()02a bf b f +<,∴存在2(,)2a bx b +∈,使得2()0f x =,∴12()()0f x f x ==,所以根据罗尔中值定理：存在(,)a b ξ∈,使得'()0f ξ=.例2. ()[0,3]f x C ∈在(0,3)内可导,(0)(1)(2)3f f f ++=,(3)1f =, 证明：存在(0,3)ξ∈,使得'()0f ξ= 证明：1()[0,3]f x C ∈,∴()f x 在[0,3]使得上有最大值和最小值,M m ,∴根据介值性定理(0)(1)(2)3f f f m M ++≤≤,即1m M ≤≤∴存在[0,3]c ∈,使得()1f c =,2()(3)1f c f ==,所以根据罗尔中值定理：存在(,3)(0,3)c ξ∈⊂,使得'()0f ξ=.例3. ()f x 在(0,3)三阶可导,[0,1]x ∈,(1)0f =,3()()F x x f x = 证明：存在(0,1)ξ∈,使得'''()0F ξ= 证明：1(0)(1)0F F ==,∴存在1(0,1)ξ∈,使得1'()0F ξ=,223'()3()'()F x x f x x f x =+,所以1'(0)'()0F F ξ==,∴存在21(0,)ξξ∈,使得2''()0F ξ=,3223''()6()3'()3'()''()F x xf x x f x x f x x f x =+++,所以2''(0)''()0F F ξ==,∴存在2(0,)(0,1)ξξ∈⊂,使得'''()0F ξ=,例3. ()[0,1]f x C ∈在(0,1)内可导,[0,1]x ∈,(0)1f =,11()22f =,(1)2f =证明：存在(0,1)ξ∈,使得'()0f ξ= 证明：(0)1f =,11()22f =,(1)2f =∴存在(0,1)ξ∈,使得()f m ξ=,又()f x 在(0,1)内可导,∴存在(0,1)ξ∈,使得'()0f ξ=题型二：证明：含ξ,无其它字母 基本思路,有三种方法： 1还原法;''()[ln ()]()f x f x f x =能够化成这种形式 例1. ()[0,1]f x C ∈在(0,1)可导,(1)0f =,证明：存在(0,1)ξ∈,使得'()3()0f f ξξξ+=.分析：由3'()3'()3()00[ln ()]'(ln )'0()f x xf x f x f x x f x x+=⇒+=⇒+=, 证明：令 3()()x x f x ϕ=,(0)(1)1ϕϕ==存在(0,1)ξ∴∈,使得'()0ϕξ=,而23'()3()'()0f f ϕξξξξξ=+= 存在(0,1)ξ∈,使得'()3()0f f ξξξ+=例2. ()[,]f x C a b ∈在(,)a b 可导,()()0f a f b ==,证明：存在(,)a b ξ∈,使得'()2()0f f ξξ-=.分析：由2'()'()2()020[ln ()]'(ln )'0()x f x f x f x f x e f x --=⇒-=⇒+=, 证明：令 2()()x x f x e ϕ-=,()()0f a f b ==,()()0a b ϕϕ∴==存在(,)a b ξ∴∈,使得'()0ϕξ=,而 即存在(,)a b ξ∈,使得'()2()0f f ξξ-=例3. ()f x 在[0,1]上二阶可导,(0)(1)f f =,证明：存在(0,1)ξ∈,使得2'()''()1f f ξξξ=-. 分析：由22'()''()2''()0[ln '()]'[ln(1)]'01'()1f x f x f x f x x x f x x =⇒+=⇒+-=--, 证明：令 2()'()(1)x f x x ϕ=-,(0)(1)(0,1)f f c =⇒∃∈,使得'()0f c =,所以2()'()(1)0c f c c ϕ=-=,又因为(1)0ϕ=()(1)0c ϕϕ∴==∴由罗尔定理知,存在(0,1)ξ∈,使得2'()''()1f f ξξξ=-. 记：① '()()kx f kf x e f x ϕ+⇒=② '()()k f kf x x f x ξϕ+⇒= 2分组构造法;① ''()()f f ξξ=② ''()()10f f ξξ-+=还原法行不通例1. ()[0,1]f x C ∈,在(0,1)内可导,11(0)0,()1,(1)22f f f ===,证明：①存在(0,1)c ∈,使得()f c c =,②存在(0,1)c ∈,使得'()2[()]1f f ξξξ--=.证明：① 令 ()()x f x x ϕ=-,111(0)0,(),(1)222ϕϕϕ∴===-1()(1)02ϕϕ<,1(,1)(0,1)2c ∴∃∈⊂使得()0c ϕ=,即()f c c =② 分析'()2[()]1[()]'2[()]0f x f x x f x x f x x --=⇒---=令 2()[()]x h x e f x x -=-,(0)()0h h c ∴==∴存在(0,1)c ∈,使得'()2[()]1f f ξξξ--=.题型三：证明：含,ξη.分几种情形：情形1：结论中只有'(),'()()f f ξη⎧⎨⎩找三句次La gr a nge点两话两例1. ()[0,1]f x C ∈,在(0,1)内可导,(0)0,(1)1f f ==,证明：①存在(0,1)c ∈,使得()1f c c =-,②存在,(0,1)ξη∈,使得'()'()1f f ξη=.证明：① 令 ()()1x f x x ϕ=-+,(0)1,(1)1ϕϕ∴=-=(0)(1)0ϕϕ< (0,1)c ∴∃∈使得()1f c c =- ②(0,),(,1)c c ξη∃∈∈,使得()(0)1'()f c f cf c cξ--==(1)()'()11f f c cf c cη-==--,所以存在,(0,1)ξη∈,使得'()'()1f f ξη= 例2. ()[0,1]f x C ∈,在(0,1)内可导,(0)0,(1)1f f ==,证明：①存在(0,1)c ∈,使得1()2f c =,②存在,(0,1)ξη∈,使得112'()'()f f ξη+=. 证明：① 令 1()()2x f x ϕ=-,11(0),(1)22ϕϕ∴=-=,(0)(1)0ϕϕ<(0,1)c ∴∃∈,使得1()2f c =②(0,),(,1)c c ξη∃∈∈,使得()(0)1'()2f c f f c cξ-==, (1)()1'()12(1)f f c f c c η-==--,所以存在,(0,1)ξη∈,使得112'()'()f f ξη+=情形2：结论中含有,ξη,但是两者复杂度不同; 例1. ()[,]f x C a b ∈,在(,)(0)a b a >内可导证明：存在,(,)a b ξη∈,使得'()'()()2f f a b ηξη=+. 证明：① 令 2()F x x =,'()20F x x =≠由柯西中值定理(,)a b η∴∃∈使得22()()'()2f b f a f b a ηη-=-,所以()()'()()2f b f a f a b b a ηη-=+- (,)a b ξ∴∃∈使得()()'()f b f a f b aξ-=-,得证;例2. ()[,]f x C a b ∈,在(,)(0)a b a >内可导证明：存在,(,)a b ξη∈,使得2'()'()abf f ξηη=. 证明：① 令 1()F x x =-,21'()0F x x=-≠由柯西中值定理 (,)a b η∴∃∈使得2()()'()111f b f a f b a ηη-=-+,所以2()()'()f b f a ab f b a ηη-=-(,)a b ξ∴∃∈使得()()'()f b f a f b aξ-=-,得证;例3. ()[,]f x C a b ∈,在(,)a b 内可导, ()()1f a f b ==证明：存在,(,)a b ξη∈,使得['()()]1e f f ηξηη-+=. 分析：“留复杂”['()()]e f f ηηη+证明：① 令 ()()x x e f x ϕ=,由拉格朗日中值定理(,)a b η∴∃∈使得()()['()()]b a e f b e f a e f f b aηηη-=+-, ['()()],(,)b a e e e e f f a b b aξηηηξ-∴==+∈-,即['()()]1e f f ηξηη-+=. 题型四：证明：拉格朗日中值定理的两惯性思维; ()f x 可导①()()'()f b f a f b a ξ-=-②见到3点两次使用拉格朗日中值定理;例1. lim '()x f x e →∞=,且lim[()(1)]lim(),xx x x c f x f x x c→∞→∞+--=-则 c = 解：()(1)'()(1)f x f x f x x ξξ--=-<<,lim '()x f x e →∞=.又因为2lim 2222lim()lim[(1)]x x c c x x x c c c x c x cx x x c c e e x c x c→∞---→∞→∞+=+==-- 例2. '()0,''()0f x f x >>,且000'(),()(),0dy f x x y f x x f x x =∆∆=+∆-∆>,则,,0dy y ∆的大小关系;解：由拉格朗日中值定理知000'(),()y f x x x x x ξ∆=∆<<+∆,''()0,'()f x f x >∴单调递增又00,'()'()x f x f ξξ<∴<又因为00,'()'(),0x f x x f x dy y ξ∆>∴∆<∆∴<<∆例3. ()f x 在(,)a b 内可导,且'()f x M ≤,()f x 在(,)a b 内至少有一个零点;证明：()()()f a f b M b a +≤-证明：1因为()f x 在(,)a b 内至少有一个零点,所以(,),()0c a b f c ∃∈=2下边用两次拉格朗日中值定理11()()'()(),(,)f c f a f c a a c ξξ-=-∈,所以11()'()(),(,)f a f c a a c ξξ-=-∈'()f x M ≤,1()(),(,)f a M c a a c ξ∴≤-∈2()(),(,)f b M b c c b ξ≤-∈,()()()f a f b M b a ∴+≤- 例4. ()f x 在(,)a b 内二阶可导,有一条曲线()y f x =,如图 证明：(,)a b ξ∃∈,使得''()0f ξ=证明：112(,),(,)a c c b ξξ∃∈∈使得12()()()()'(),'()f c f a f b f c f f c a b cξξ--==-- 因为,,A C B 共线,所以12'()'()f f ξξ=,所以由罗尔定理知12(,)(,)a b ξξξ∃∈⊂,使得''()0f ξ=题型五：Taylor 公式的常规证明;例1. '''()[1,1]f x C ∈-,(1)0,'(0)0,(1)1f f f -===证明：存在(1,1)ξ∈-,使得'''()3f ξ=.题外分析：考虑什么时候该用泰勒公式什么时候不用()()(2)n f n ξ≥时考虑,但是()()0n f ξ=为题型一,考虑罗尔定理2n =时比较尴尬,有时候用拉格朗日中值定理,有时候不用,该怎么考虑呢,分情况：(),(),()''()'(),'(),'()'(),'(),'()f a f b f c lagrangef f a f b f c lagrange f a f b f c taylor ξ⎧⎧⎪⎨⎨⎩⎪⎩次拉格朗日中值定理解两决证明： 2311'''()''(0)(1)(0)(10)(10),(1,0)2!3!f f f f ξξ-=+--+--∈-, 两个式子相减得：12'''()'''()6f f ξξ∴+=12'''()[,]f x C ξξ∈,'''()f x ∴在12[,]ξξ上有,m M ,则122'''()'''()2m f f M ξξ∴≤+≤12'''()'''()32f f m M m M ξξ+∴≤≤⇒≤≤,所以根据介值定理得：存在12[,](1,1)ξξξ∈⊂-,使得'''()3f ξ=例2. ()f x ,在[0,1]二阶可导,(0)(1)0f f ==,01min ()1x f x ≤≤=-,证明：存在(0,1)ξ∈,使得''()8f ξ≥.证明：由01min ()1x f x ≤≤=-知,存在(0,1)c ∈,使得()1f c =-且'()0f c =由泰勒公式：211''()(0)()(0),(0,)2!f f f c c c ξξ=+-∈, ①111(0,]''()8,2c f ξξξ∈⇒≥=②221(,1)''()8,2c f ξξξ∈⇒≥=例3. ()f x 在[,]a b 上二阶可导,''()f x M ≤,()f x 在(,)a b 内取最大值; 证明：存在'()'()()f a f b M b a +≤-.证明：由()f x 在(,)a b 内取最大值知,存在(0,1)c ∈,使得'()0f c =所以存在'()'()()f a f b M b a +≤-.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
若结论是
f '' 0
1.在不同区间用
罗尔找到 1,2
2.在 1,2 用一
次罗尔
柯西中值 定理
1.同一字母同一 侧，分别积分， 找原函数 F,G 2.对 F,G 用柯西
泰勒定理
1.在 题 目 出 现 的
某点泰勒展开
2.带入其他点，寻
找与结论之间的
1
关系（有时会结合
介值定理）
1.闭区间上连续函数定理 ① ② ③ ④ 2.微分中值定理 ①
（1） 存在（0，1）内两个不同的点 , ，使得 f ' ( ) f ' () 2 .
（2）
存在（0，1）内两个不同的点 , ，使得
1 f ' ( )
1 f ' ()
2 .
（3） 存在（0，1）内两个不同的点 , ，使得 f ' ( ) f ' () 1 .
f ' ( ) （4） 存在（0，1）内两个不同的点 , 及大于零的常数 ，使得 f ' () （5） 对于任意的正整数 n，存在（0，1）内两个不同的点 , 及常数 0 ，
3
5.若 f (x) 在[0,1] 上可导，且当 x [0,1] 时有 0 f (x) 1，且 f (x) 1，证明：在 (0,1) 内有且仅有一个点 使得 f ( )
6.设 f (x) 在[0，1]上连续，在(0，1)内可导，且 f (0) = f (1) =0， f (1 ) =1。试证 2
②
③
④
3.积分中值定理 ① ②
不等式证明思路 构造函数（利用极值） 拉格朗日中值定理 函数凹凸性定义
2
1.若 f (x) 在 [a,b] 上连续，在 (a,b) 上可导， f (a) f (b) 0 ，证明： R ， (a,b) 使得： f ( ) f ( ) 0
2.设 a,b 0 ，证明： (a,b) ，使得 aeb bea (1 )e (a b)
至少存在一个 (0，1)，使 f ¢(x) =1
7.设 f (x) 在 [0,1] 上连续，在 (0,1) 内可导，且 f (0) f (1) 试证存在 和 .满足 0 1，使 f ( ) f () 0 .
8.设 f (x) 在[a,b] 上连续, (a,b) 内可导 (0 a b), f (a) f (b),
第三章 中值定理证明
题目类型
定 理
结论只包含
f , f ',
结论包含
1. f , f ', a,b, , 2. f ', g ', a, b, ,
结论包含 反对幂指三
+ f , f ', g, g',,
结论包含
f ', f '', f ''', a, b,
等式或不等式
罗尔定理
1.移项=0 2.构造函数 常微分方程 （C=F(x)） 不定积分 3.验证 F(a)=F(b) （结合零点/介值 /积分中值）
13.设 f x在-1,1具有三阶连续导数，且 f -1 0，f 1 1, f '0 0, 证明：在 -1,1 至少存在一点 ，使得 f ''' 3
14.设 f x 在 a,b，0 a b 上连续，在 a,b 内可导， 试证 , a,b ，使得 f ' 2 f '
ab
15.设 f x 在 0,1，上连续，在 0,1内可导，且
3.设 f (x) 在 (0,1) 内有二阶导数，且 f (1) 0 ，有 F (x) x2 f (x) 证明：在 (0,1) 内 至少存在一点 ，使得： F( ) 0
4.设 f (x) 在[0，2a]上连续， f (0) f (2a) ，证明在[0,a]上存在 使得 f (a ) f ( ) .
4
证明: , (a, b) 使
f
(
)
ab 2
f
( ).
9. 已知函数 f (x) 在[0 ,1]上连续，在（0 ，1）内可导， 0 a b ，证明存在 , (a, b) ，使 3 2 f / ( ) (a 2 ab b2 ) f / ()
10. 设 f (x) 在[0，1]上连续（0，1）内可导， f (0) 0 ， f (1) 1，试分别证明：
f ' ( ) 使得 f () = n( 1) .
5
11.设
f xLeabharlann 在0,1 上 连 续 ， 且
1 0
f xdx
0
，证明：至少存在一点
，使得
0
f
t dt
f
12.设 f x 在 a,b上连续，在 a,b内可导，且 f 'x 0, 试证 , a,b ，使得
f f
' '
eb b
ea a
e
6
f 1 0,
2
e f x
arctan
xdx
1
,
试证
0,1 ，使得
1 2
arc tan
f
'
1
0
2
7
16.设 f x 在 [a,) 上连续，在 (a,) 内可导，且方程 f x 0 在上有根，又
f a 0 ，证明方程 f x 0 在 a, a f x 内有唯一的实根.
k
17.设函数在 0，1上连续，并且对 0，1任意一点 x 有： 0 f x 1 ,求证：在上必 存在一点 ，使得 f .
18.设函数 f (x) 在[0,1]上连续，在(0,1)上可导， f (0) 0 ， f (1) 1.证明： (1)在(0,1)内存在 ，使得 f ( ) 1 ． (2) 在(0,1)内存在两个不同的点 ，使得f / ( ) f / () 1
8
拉格朗日 中值定理
一．
1.目 标 是 寻 找 区 间 里某点 C 2.在 两 个 区 间 分 别 用拉格朗日定理,带 入结论，找到确定 C 点的方法（零点或者 介值定理）
1.一柯 2.一拉+一拉 3.一拉+一柯
二． , 没有大小关
系 1.同一字母同一侧， 分别积分，找到 F,G 2.对 F,G 用拉格朗日 定理 3.比 较 跟 结 论 的 关 系