渐开线齿廓的形成与啮合特点
简述渐开线齿廓的啮合特点

简述渐开线齿廓的啮合特点渐开线齿廓是一种常见的齿轮啮合方式,其特点是具有曲率变化的齿廓。
在渐开线齿轮啮合中,两个齿轮的齿廓曲线是相互匹配的,使得齿轮之间可以顺畅地啮合,并传递动力。
渐开线齿廓的啮合特点可以从以下几个方面来描述:1. 齿廓曲线的特殊性:渐开线齿廓是一种特殊的曲线,具有曲率变化的特点。
与其他齿轮啮合方式相比,渐开线齿廓的曲率变化更加平滑,使得齿轮在啮合过程中的运动更加稳定。
这种平滑的曲线使得渐开线齿廓具有较高的传动效率和较低的噪声。
2. 齿廓的中心扩展:渐开线齿廓的中心扩展是指齿廓曲线中心的轨迹不是一个点,而是一个曲线。
这种中心扩展使得齿轮在啮合过程中可以实现相对滑动,减小了啮合时的摩擦和磨损,提高了齿轮的寿命和可靠性。
同时,中心扩展还可以使得渐开线齿轮在高速运动时具有更好的动平衡性能。
3. 齿廓的变位特性:渐开线齿轮的齿廓变位是指齿廓曲线在垂直于齿轮轴线方向上的变化。
齿廓变位可以使得齿轮在啮合过程中实现平稳的传动,减小冲击和振动。
同时,齿廓变位还可以改变齿轮的传动特性,如变速、变转矩等,提高了齿轮传动的灵活性和适应性。
4. 齿廓的接触特性:渐开线齿轮的齿廓接触是指齿轮齿廓之间的接触区域。
由于渐开线齿廓的特殊曲线形状,齿轮在啮合过程中的接触区域相对较大,使得齿轮传递的载荷分布更加均匀,减小了齿轮的磨损和损伤。
同时,齿廓接触还可以改善齿轮的传动效率和承载能力,提高齿轮传动的可靠性。
总的来说,渐开线齿廓具有曲率变化、中心扩展、变位特性和接触特性等特点,在齿轮传动中具有重要的应用价值。
通过合理设计和制造渐开线齿轮,可以实现高效稳定的传动,提高齿轮传动的可靠性和使用寿命。
渐开线齿廓的形成与啮合特点

渐开线齿廓的形成与啮合特点
形成原理:
渐开线齿廓是由齿轮齿侧面的直线(称为侧面线)和齿根圆的一部分(称为基圆)组成。
侧面线与基圆的交点构成了齿槽的啮合点。
渐开线齿
廓的形成主要是通过给定齿数、压力角和齿轮传动比等参数,利用特定的
公式计算而得。
啮合特点:
1.线接触。
渐开线齿廓的啮合面积较小,只有一个点或一小段线接触,这样能够实现对点接触的要求,减小了齿轮的摩擦和接触磨损,提高了传
动效率。
2.平稳传动。
渐开线齿廓具有相对平滑的啮合传动特性,能够减小振
动和冲击,使传动更加平稳。
3.轴向移动。
渐开线齿廓的特点使得齿轮在转动过程中能够自动沿轴
向方向进行微小的移动,可以自动适应齿轮间隙的变化。
这样能够保证齿
轮的啮合正常,并且减小了噪声和振动。
4.高承载能力。
渐开线齿廓的啮合传动是通过多点接触来实现的,使
得载荷能够均匀分布在齿面上,提高了齿轮的承载能力。
5.较小的齿根强度。
由于渐开线齿廓的齿根圆的一部分构成了齿轮的
齿槽,在齿根处可能出现较大的应力集中,降低了齿根的强度。
因此在设
计中需要合理选择齿廓参数,以确保齿轮的强度和可靠性。
6.减小中心距误差的影响。
由于渐开线齿轮通过自动的轴向移动来适应齿间隙变化,可以减小中心距误差对齿轮啮合性能的影响,提高传动的准确性。
总之,渐开线齿廓的形成和啮合特点使得其广泛应用于各种机械传动中,能够实现平稳、高效、可靠的传动效果。
齿轮机构的齿廓啮合基本规律特点和类型

d d
a f
(z 2ha* (z 2ha*
2x 2 )m
2c* 2x)m
为齿顶高削减系数。
30
第七节平行轴斜齿圆柱齿轮传动
一、齿廓曲面的形成及啮合特点
31
斜齿轮的轮齿啮合过 程比直齿轮长,同时参 与啮合的轮齿对数也比 直齿轮多。
因此,斜齿轮传动平稳、 承载能力强、噪声和冲击小。 适用于高速、大功率的齿轮 传动。
1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
二、根切现象和最少齿数
避免根切的条件: PB2≤PN
而:PB2= ha*m/sin α PN=PO sin α =mz/2sinα
有:Z≥2 ha*/sin2α ha* =1,a=200时
2.齿厚和齿槽宽
由于加工变位齿轮时,与轮坯分度圆相切的不再是刀具中线, 齿厚和齿槽宽为:
s m 2KJ ( 2x tan )m
2
2
e m 2KJ ( 2x tan )m
2
2
29
3.齿顶高和齿根高
hf ha*m c*m xm (ha* c* x)m ha ha*m xm (ha* x)m
7、标准直齿圆柱齿轮的分度圆半径 r=rb/cos α,db=d cos α=mZ cos α
16
返回
第四节 渐开线标准直齿 圆柱齿轮的啮合传动
一、正确啮合条件---一对齿相 邻两齿同侧齿廓间在啮合线上 的法线距离相等,pn1=pn2 。
渐开线的特性即pb1=pb2 推导: π db1/z1= π db2/z2
ha*=1, α=200时,εmax≈1.982 标准齿轮恒有1<ε<2,不必校核 但要理解其物理含义。
07-4第三十六讲渐开线齿廓的啮合特性(精)

O1 ω1 rb1 N1 P N2 rb2 ω2 O2 K C2 C1
= rb2 /rb1
——基圆之反比。
实际安装中心距略有变化时,不影响i12,这 一特性称为运动可分性,对加工和装配很有利。
由于上述特性,工程上广泛采用渐开线作为齿轮的齿 廓曲线。
JM
返回
第三十六讲 渐开线齿廓的啮合特性
1、渐开线齿廓能保证定传动比传动 两齿廓在任意点K啮合时,过K作两齿廓 的法线N1N2,是基圆的切线,为定直线。 两轮中心连线也为定直线,故交点 P必为定点。
N2 ω1 rb1 N1 P K C2 C1
K’
i12=ω 1/ω 2=O2P/ O1P=const
rb2
ω2 O2
工程意义:i12为常数可减少因速度变化所产生的附加动载荷、 振动和噪音,延长齿轮的使用寿命,提高机器的工作精度。 2、齿廓间正压力方向不变 N1N2是啮合点的轨迹,称为啮合线 该线又是接触点的法线,正压力总是沿法线方向, 故正压力方向不变。该特性对传动的平稳性有利。
JM
返回
3、运动可ห้องสมุดไป่ตู้性 △ O1N1P≌△O2N2P 故传动比又可写成: i12=ω 1/ω 2=O2P/ O1P
齿廓啮合基本定律
分度圆
分度圆
节线 (中线)
节线 中线
m m
2
2
中线
m m
2
2
(1)齿条刀中线与轮坯分度圆相离加工出的齿轮为正变位
齿轮,用x > 0表示正变位,切出的齿轮分度圆的齿厚s
大于齿槽宽e ,齿根高 hf < (ha*+c*)m,齿顶高h*a> ham。
分度圆
分度圆
节线 (中线)
节线 中线
m m
2
2
中线
m m
(5)基圆内无渐开线。
Σ3 Σ1
Σ2
N2 N1
rb1
K
KO2
o2 KO1 o1
(三)渐开线的方程式
以O为中心,以OK0为极轴 的渐开线K点的极坐标方程: Vk
发生线
rk
rb
cos κ
k K
θk inv κ tg κ κ
Pk rk
invk— 渐开线函数
(kNO 0K K
N rb k k
K0
N2
rb2 o2
З
1 rb1
N1
k1
r2'
2
3、中心距的变化不影响角速比
a a'
•渐开线齿廓啮合的中心
距可变性——— 当两齿
轮制成后,基圆半径便已
确定,以不同的中心距(a
或a')安装这对齿轮,其传
动比不会改变。
t
i12
1 2
o2P o1 P
rb 2 rb1
t'
N2
i1'2
1
' 2
o
' 2
p
'
渐开线齿轮
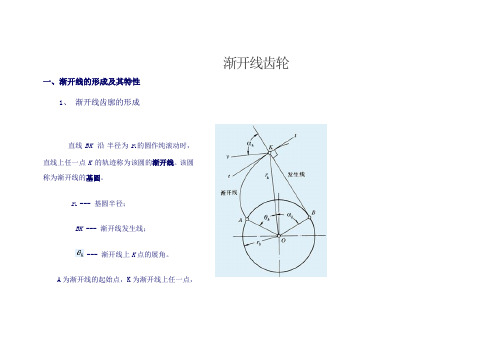
渐开线齿轮一、渐开线的形成及其特性1、渐开线齿廓的形成直线BK沿半径为r b的圆作纯滚动时,直线上任一点K 的轨迹称为该圆的渐开线。
该圆称为渐开线的基圆。
r b--- 基圆半径;BK --- 渐开线发生线;--- 渐开线上K点的展角。
A为渐开线的起始点,K为渐开线上任一点,其向径用r k表示。
渐开线齿轮的齿廓曲线是渐开线。
2、渐开线的特性1)发生线沿基圆滚过的长度,等于基圆上被滚过的圆弧长度。
由于发生线BK在基圆上作纯滚动,故2)渐开线上任一点的法线恒与基圆相切。
发生线BK沿基圆作纯滚动,它与基圆的切点B即为其速度瞬心,所以发生线BK即为渐开线在K点的法线。
又由于发生线恒切于基圆,故渐开线上任一点的法线恒与基圆相切。
3)渐开线上离基圆愈远的部分,其曲率半径愈大,渐开线愈平直。
发生线BK与基圆的切点B是渐开线在点K 的曲率中心,而线段KB是相应的曲率半径,故渐开线上离基圆愈远的部分,其曲率半径愈大,渐开线愈平直;渐开线初始点A处的曲率半径为零。
4)基圆内无渐开线。
5)渐开线的形状取决于基圆的大小。
基圆愈小,渐开线愈弯曲;基圆愈大,渐开线愈平直。
当基圆半径为无穷大时,其渐开线将成为一条直线。
二、渐开线齿廓的啮合特点一对齿轮传动,是依靠主动轮的齿廓依次推动从动轮的齿廓来实现的。
因此,要能实现预定的传动比,一个齿轮最关键的部位是轮齿的齿廓曲线。
图示为一对分别属于齿轮1和齿轮2的两条齿廓曲线G1、G2在点K 啮合接触的情况。
齿廓曲线G1绕O1点转动,G2绕O2 转动。
过K点所作的两齿廓的公法线nn与连心线 O1O2 相交于点C。
由三心定理知,点C是两齿廓的相对速度瞬心,齿廓曲线G1和齿廓曲线G2在该点有相同的速度:由此可得我们称点C为两齿廓的啮合节点,简称节点。
齿廓啮合基本定律:两齿廓在任一位置啮合接触时,过接触点所作的两齿廓的公法线必通过节点C,它们的传动比等于连心线O1O2被节点C 所分成的两条线段的反比。
《机械基础》课件——渐开线

渐开线上各点的齿形角不等
标准直齿圆柱齿轮 各部分的名称
《机械基础》第四章第三节
渐开线标准直齿圆柱齿轮各部分的名称
1.齿顶圆:通过轮齿顶部的圆周,直径用da表示。 2.齿根圆:通过轮齿根部的圆周,直径用df表示。 3.分度圆:轮齿上具有标准模数和标准齿形角的圆,直径用d表示。
7.齿宽:齿轮的有齿部分沿分度圆柱面直母线方向量取的宽度。用b表示。 8.齿顶高:齿顶圆与分度圆之间的径向距离。用ha表示。 9.齿根高:齿根圆与分度圆之间的径向距离。用hf表示。 10.齿高:齿顶圆与齿根圆之间的径向距离。用h表示。
h= ha+ hf
渐开线标准直齿圆柱齿轮各部分的名称
小结:
谢谢观看
渐开线标准直齿圆柱齿轮各部分的名称
4.齿厚:在端平面(垂直于齿轮轴线的平面)上,一个齿的两侧端面齿廓之间的 分度圆弧长。用s表示。
5.齿槽宽:在端平面上,一个齿槽的两侧端面轮廓之间的分度圆弧长。用e表示。 6.齿距:两个相邻且同侧端面齿廓之间的分度圆弧长。用p表示。
p=s+e
渐开线标准直齿圆柱齿轮各部分的名称
以同一个基圆上产 生的两条反向渐开线为 齿廓的齿轮就是渐开线 齿轮。
渐开线的形成及性质
二、渐开线的性质
(1)发生线在基圆上滚过的线段长度NK,等 于基圆上被滚过的圆弧长NA。
(2)渐开线上的任意一点K的法线必与基圆 相切。例如线段KN就是渐开线上K点的法线。
渐开线的形成及性质
(3)渐开线的形状取决于与基圆的大小, 如右图所示。基圆相同,渐开线的形状完全相同。 基圆越小,渐开线越弯曲;基圆越大,渐开线越 趋平直。当基圆半径无穷大时,渐开线将变成直 线,这种直线型的渐开线就是齿条的齿廓线,即 齿轮就变成齿条。
渐开线齿轮原理

渐开线齿轮原理一、引言渐开线齿轮是一种常见的机械传动元件,它通过齿轮的啮合来传递动力和运动。
渐开线齿轮原理的理解对于机械工程师和设计师来说至关重要。
本文将介绍渐开线齿轮的原理及其应用。
二、渐开线齿轮的定义渐开线齿轮是一种特殊形状的齿轮,其齿廓曲线为渐开线。
渐开线齿轮的齿廓曲线具有独特的性质,使得齿轮的啮合更加平稳,传动效率更高。
三、渐开线齿轮的原理1. 渐开线的定义:渐开线是一种特殊的曲线,其特点是在任意一点处的切线与该点到一个固定点的距离成正比。
在渐开线齿轮中,齿廓曲线正是由这样的渐开线构成。
2. 渐开线齿轮的齿廓曲线:渐开线齿轮的齿廓曲线是由渐开线与圆弧段组成的。
渐开线部分使得齿轮的啮合过程更加平稳,而圆弧段则用来实现齿轮的啮合。
四、渐开线齿轮的特点1. 平稳的啮合:由于渐开线齿轮的齿廓曲线特殊,使得齿轮的啮合过程更加平稳,减小了齿轮的噪声和振动。
2. 高效的传动:渐开线齿轮的齿廓曲线使得齿轮的传动效率更高,能够减小能量损失,提高传动效率。
3. 大扭矩传递能力:渐开线齿轮由于齿廓曲线的特殊性质,使得齿轮的接触面积更大,从而增加了齿轮的扭矩传递能力。
五、渐开线齿轮的应用1. 机械传动:渐开线齿轮广泛应用于各种机械传动系统中,如汽车变速器、工业机械等。
其平稳的啮合特性和高效的传动性能使其成为理想的传动元件。
2. 纺织机械:渐开线齿轮在纺织机械中的应用也非常广泛。
纺织机械中需要传递大扭矩和保持稳定的运动,渐开线齿轮能够满足这些要求。
3. 风力发电:在风力发电机组中,渐开线齿轮用于传递风力发电机的转动力和转速,保证风能转化为电能的高效率和稳定性。
六、总结渐开线齿轮作为一种常见的机械传动元件,具有平稳的啮合特性、高效的传动性能和大扭矩传递能力。
它在各种机械传动系统中得到广泛应用,如汽车变速器、工业机械、纺织机械和风力发电等领域。
了解渐开线齿轮的原理和特点对于机械工程师和设计师来说非常重要,能够帮助他们设计出更加高效和稳定的机械传动系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
古代齿轮的齿形是方形的
齿廓形状的发展
摆线齿轮 (17世纪70年代 , 丹麦)
圆弧齿轮
(20世纪50年代,前苏联)
渐开线齿轮
(17世纪90年代 ,法国)
渐开线齿廓及其啮合特性 《机械原理》
渐开线齿廓
渐开线齿廓及其啮合特性 《机械原理》
渐开线齿轮
渐开线
渐开线齿廓
渐开线的形成过程(动画)
渐开线齿廓及其啮合特性 《机械原理》
传动比恒定 中心距的可分性 传力方向不变 加工工艺成熟
渐开线齿轮的参数计算
渐开线齿廓及其啮合特性 《机械原理》
直齿圆柱齿轮
斜齿圆柱齿轮
圆锥齿轮
The end
谢谢!
渐开线齿廓及其啮合特性 《机械原理》
N′2
rb2
ω2
O2
O′2
渐开线齿廓的啮合特点
轮齿的传力方向是什么? 传力方向不变(动画)
工程意义: ◇ 提高机器运行的平稳性
渐开线齿廓及其啮合特性 《机械原理》
O1 ω1
K N1 C N2
ω2 O2
渐开线齿轮的一些性能数据
单级传动效率可达 99% 传递功率可达10 000 KW 转速可达10 000 r/min 圆周线速度可达300 m/s 齿轮直径范围 : 1 mm ~150 m
渐开线齿廓及其啮合特性
国徽上的“齿轮”
渐开线齿廓及其啮合特性 《机械原理》
国徽上艺术化的齿轮
齿轮传动的性能要求
渐开线齿廓及其啮合特性 《机械原理》
传动平稳:传动比恒定
i12
1 2
const
良好的传力性能
轮齿具有足够的强度和刚度
从动轮2
主动轮1
齿廓形状的发展
渐开线齿廓及其啮合特性 《机械原理》
K 渐开线
发生线
A
B
O
基圆
(
渐开线齿廓
渐开线的形成过程 渐开线的几何特性
— AB = KB B点为K点的曲率中心 — KB为K点的曲率半径 KB线 (发生线) : 渐开线上K点的法线 KB线(发生线) : 基圆的切线
渐开线齿廓及其啮合特性 《机械原理》
K 渐开线
发生线 A
B O
基圆
渐开线齿廓的啮合特点
渐开线齿廓及其啮合特性 《机械原理》
i
12
1 2
O2 C O1 C
rb2 rb1
const
O1
ω1
rb1
满足齿廓啮合基本定律,能实现定比传动
工程意义: ◇ 减少附加动载荷、振动和噪音 ◇ 提高机器的工作精度与使用寿命
N2
rb2
K N1 C
公法线 发生线
内公切线
ω2 O2
渐开线齿廓的啮合特点
i
12
1 2
O2 C O1 C
rb2 rb1
const
i
12Leabharlann 1 2 rb2 rb1
O2
C
=
const
O1 C
中心距的可分性
工程意义:
◇ 当两个齿轮的中心距产生误差时, 不会影响传动比
渐开线齿廓及其啮合特性 《机械原理》
O1
ω1
rb1
K N1N′1 CC′ N2
渐开线齿廓及其啮合特性 《机械原理》
机械手表
汽车自动变速器
发电站机组
喷气发动机
渐开线齿轮的一些性能数据
单级传动效率可达 99% 传递功率可达10 000 KW 转速可达10 000 r/min 圆周线速度可达300 m/s 齿轮直径范围 : 1 mm ~150 m
渐开线齿廓及其啮合特性 《机械原理》
