第四届全国组合数学与图论会议纪要
组合数学课件-第四章第三节波利亚(Polya)定理

波利亚定理的重要性
波利亚定理在几何学中有着广泛的应 用,它可以帮助我们解决一些与图形 和空间有关的问题。
例如,在几何图形中,我们可以通过 应用波利亚定理来判断一个点是否在 某个区域内,或者判断一个封闭曲线 是否与某个区域相交。
第二步
根据已知条件和数学原理,推导出与结论 相关的中间结论,这是证明的关键环节。
B
C
第三步
通过逻辑推理和数学推导,逐步推导出最终 结论,这一步需要严谨的逻辑推理和精确的 数学表达。
第四步
对推导出的结论进行验证,确保其正确性和 可靠性,这一步也是证明的重要环节。
D
定理证明的结论
波利亚定理的证明结论是:在一定条件下,一个数学问题可 以通过逐步转化和化简,最终转化为一个更简单或更易于解 决的问题,从而找到问题的解。
03
多变量版本的波利亚定理
该定理将单变量版本的波利亚定理扩展到多变量函数,提供了解决多变
量问题的新工具。
定理在其他数学领域的应用
在几何学中的应用
波利亚定理在几何学中有着广泛的应用,例如在计算几何形状的 面积和体积,解决几何问题等方面。
在组合数学中的应用
波利亚定理在组合数学中有着重要的应用,例如在解决组合问题、 计数问题、排列问题等方面。
B
C
波利亚定理的证明方法有多种,其中最常用 的是数学归纳法。
波利亚定理在数学教育中也具有重要意义, 它有助于培养学生的逻辑推理能力和数学思 维能力。
D
对波利亚定理的展望
随着数学的发展,波利亚定理的应用范围将不断扩大, 将有更多的数学问题可以通过波利亚定理得到解决。
抽屉原理在数学中的运用

抽屉原理在初等数学中的运用摘要:抽屉原理也称为鸽巢原理,它是组合数学中的一个最基本的原理.也是数学中的一个重要原理,抽屉原理的简单形式可以描述为:“如果把1+n 个球或者更多的球放进n 个抽屉,必有一个抽屉至少有两个球.”它的正确性十分明显,很容易被并不具备多少数学知识的人所接受,如果将其灵活地运用,则可得到一些意想不到的效果. 运用抽屉原理可以论证许多关于“存在”、“总有”、“至少有”的存在性问题。
学习抽屉原理可以用来解决数学中的许多问题,也可以解决生活中的一些现象。
如招生录取、就业安排、资源分配、职称评定等等,都不难看到抽屉原理的作用。
在解决数学问题时有非常重要的作用. 抽屉原理主要用于证明某些存在性问题及必然性题目,如几何问题、涂色问题等. 各种形式的抽屉原理在高等数学和初等数学中经常被采用,使用该原理的关键在于如何巧妙地构造抽屉,即如何找出合乎问题条件的分类原则,抽屉构造得好,可得出非常巧妙的结论.本文着重从抽屉的构造方法阐述抽屉原理在高等数学和初等数学(竞赛题)中的应用,同时指出了它在应用领域中的不足之处.关键词:抽屉原理;初等数学;应用一、 抽屉原理(鸽巢原理)什么是抽屉原理?先举个简单的例子说明,就是将3个球放入2个篮子里,无论怎么放,必有一个篮子中至少要放入2个球,这就是抽屉原理.或者假定有五个鸽子笼,养鸽人养了6只鸽子,当鸽子飞回巢中,那么一定至少有一个鸽笼里有两只鸽子,这就是著名的鸽巢原理.除了这种比较普遍的形式外,抽屉原理还经许多学者推广出其他的形式.比如陈景林、阎满富编著的中国铁道出版社出版的《组合数学与图论》一书中对抽屉原理给出了比较具体的定义,概括起来主要有下面几种形式:原理1 把多于n 个的元素按任一确定的方式分成n 个集合,则一定有一个集合中含有两个或两个以上的元素.原理2 把m 个元素任意放到n )(n m >个集合里,则至少有一个集合里至少有k 个元素,其中原理3 把无穷个元素按任一确定的方式分成有穷个集合,则至少有一个集合中仍含无穷个元素.卢开澄在《组合数学》(第三版)中将抽屉原理(书中称为鸽巢原理)又进行了推广[2].鸽巢原理:设k 和n 都是任意正整数,若至少有kn+1只鸽子分配在n 个鸽巢中,则至少存在一个鸽巢中有至少k+1只鸽子.二、抽屉的构造途径在利用抽屉原理解题时,首先要明确哪些是“球”,哪些是“抽屉”,而这两者通常不会现成存在于题目中,尤其是“抽屉”,往往需要我们用一些巧妙的方法去构造。
科大组合与图论专业三十五年

科大组合与图论专业三十五年------为科大校庆五十周年而写李乔、李炯生、徐俊明中国科学技术大学组合与图论专业从李乔发表的第一篇论文算起,经历了整整35年。
在这35年里,逐渐形成了自己的研究特色:组合矩阵论和组合网络理论。
发表学术论文300余篇,专著和教材16部。
获得1993年国家教委科技进步一等奖(合作)、2003年安徽省自然科学二等奖和2008年中国科学院首届教学成果二等奖。
培养硕士研究生57名,博士研究生26名,进站博士后5名,接收国内高校青年进修和访问学者9名。
回忆这段历史,科大组合学与图论专业的创立和发展大体上分为三个阶段。
一、创立阶段(1973-1985)中国科学技术大学数学系的组合学与图论研究始于上世纪七十年代初。
北京大学段学复教授向曾肯成建议:国内可由科大牵头研究组合与图论。
李乔和冯克勤凭借代数方面的深厚功底开始涉及组合与图论,在国内率先开展代数图论研究。
1973年,李乔在《中国科学技术大学学报》上发表的“关于偶图的极大对口”是本专业第一篇学术论文。
随后,李乔和冯克勤合作完成了 “关于树和其他图的联系矩阵”、“图的谱性质的若干结果”和“论图的最大特征根” 3篇论文,分别发表在《中国科学技术大学学报》(1976,1979)和《应用数学学报》(1979)上。
这些论文是国内代数图论研究最早的学术论文,现成为此研究领域的经典论文之一。
在此期间,李乔和冯克勤还从数学角度介入当时国内兴起的“量子化学的图论研究”,成为国内最早开展此项研究的学者。
1977年8月在上海举行的全国第一次量子化学学术会议上,李乔介绍了他与冯克勤在这方面的研究成果。
组合学是经典的数学分支,被人熟知。
图论是组合学的一个活跃分支,但当时数学界对它还不大了解。
1977年底,李乔对数学系师生做了题为《图论》的介绍性报告。
他以图论语言简洁证明“在任意六人中必存在三人, 要么都相识,要么都不相识”为开场,来介绍图论,生动有趣。
正是这个报告引起了不少人对图论的兴趣。
组合数学的基本概念与方法

汇报人:XX
目录
01
添加目录项标题
02
组合数学简介
03
组合数学的基本概念
04
组合数学的主要方法
05
组合数学中的问题与求解方法
06
组合数学与其他数学领域的联系
添加章节标题
PART 01
组合数学简介
PART 02
组合数学的定义
组合数学是研究离散对象组合性质和结构的数学分支
THANK YOU
汇报人:XX
特点:具有自相似性、层次性和规律性
定义:一个数学对象或系统通过自身子对象或子系统的递归方式进行描述或构造
组合数学的主要方法
PART 04
归纳法
定义:归纳法是从个别到一般的推理方法,通过对一些具体实例的分析,总结出一般规律。
应用:在组合数学中,归纳法常用于研究排列、组合、概率等问题,通过对具体问题的分析,归纳出一般性的结论。
注意事项:在应用反证法时,需要注意推理和演绎的严密性和准确性,避免出现逻辑错误。
构造法
定义:构造法是一种通过构造具体的实例或模型来解决问题的数学方法。
应用场景:在组合数学中,构造法常用于证明组合恒等式、求解组合问题等。
举例说明:例如,通过构造一个具体的组合模型来证明组合恒等式。
注意事项:使用构造法时需要注意构造的合理性和正确性,以及构造实例或模型的代表性和一般性。
数学归纳法
定义:数学归纳法是一种证明无限数学命题的推理方法,通过有限次验证和归纳推理来证明无限命题的正确性。
步骤:数学归纳法包括两个步骤:基础步骤和归纳步骤。基础步骤是验证命题在某个初始值成立,而归纳步骤则是假设在某个值成立,然后证明该假设对于下一个值也成立。
精选组合数学资料

图所示:
a1 a2
a3 a4
根据幻方的定义,它的幻和是5,于是 a1+ a2= a1+ a3=5,可得a2= a3,因为a1 ,a2,a3, a4必定彼此不同,所以不可 能,矛盾。因此不存在2阶幻方。
2019年10月8日
25
• 幻方的构造性问题
(1)奇数阶幻方的构造
连续摆放法(de la Loubère法)。 规则为:假定构造n阶(n为奇数)幻方。 •首先将1放在 (n+1)/2列第1行的方格中,
• 4阶幻方 • 分类枚举 • 基本形式有880个 • 变形有7040个
2019年10月8日
38
• 5阶幻方 • 基本形式有275305224个
• 6阶及以上幻方 • 即使通过大型计算机的计算仍 然难以获得精确的数字,目前只能估 计出它的取值范围
2019年10月8日
39
§1.2 拉丁方问题
•拉丁方是另一类典型的组合数学问题
2019年10月8日
46
3阶正交拉丁方
1 2 3 1 2 3 (1,1) (2,2) (3,3) 3 1 2 2 3 1 (3,2) (1,3) (2,1) 2 3 1 3 1 2 (2,3) (3,1) (1,2)
并置方阵
2019年10月8日
组合数学
吉林大学 计算机科学与技术学院
2009年9月
参考教材
组合数学,屈婉玲编。北京大学出版 社,1989年11月。
组合数学(第四版),卢开澄等。清 华大学出版社, 2006年12月。
组合数学(英文版·第5版) ,(美)布鲁迪 (Brualdi,R.A.)著。机械工业出版社, 2009年3月。
2019年10月8日
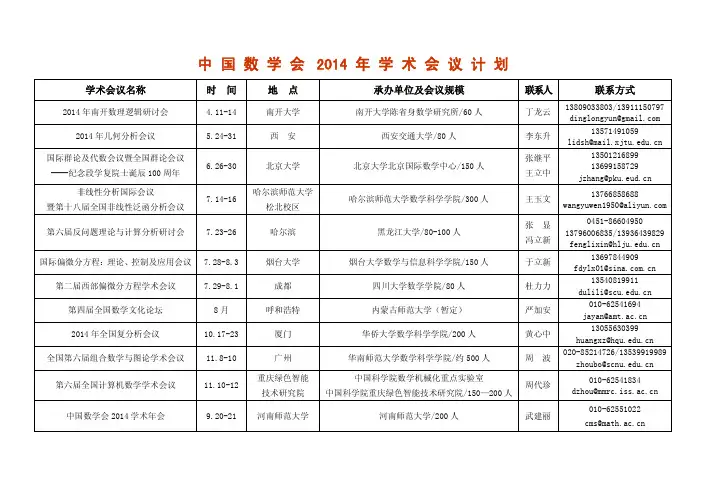
年度活动
010-62551022
第六届全国计算机数学学术会议
中国数学会 2014 学术年会
时间
4.11-14 5.24-31 6.26-30
7.14-16
7.23-26 7.28-8.3 7.29-8.1
8月 10.17-23 11.8-10 11.10-12 9.20-21
地点
南开大学 西安
北京大学 哈尔滨师范大学
13697844909 fdylx01@
13540819911 dulili@
010-62541694 jayan@
13055630399 huangxz@ 020-85214726/13539919989 zhoubo@
松北校区 哈尔滨
烟台大学 成都
呼和浩特 厦门 广州
重庆绿色智能 技术研究院 河南师范大学
承办单位及会议规模
南开大学陈省身数学研究所/60 人 西安交通大学/80 人
北京大学北京国际数学中心/150 人
哈尔滨师范大学数学科学学院/300 人
黑龙江大学/80-100 人
烟台大学数学与信息科学学院/150 人 四川大学数学学院/80 人 内蒙古师范大学(暂定)
华侨大学数学科学学院/200 人 华南师范大学数学科学学院/约 500 人
中国科学院数学机械化重点实验室 中国科学院重庆绿色智能技术研究院/150—200 人
河南师范大学/200 人
联系人
丁龙云 李东升 张继平 王立中 王玉文 张显 冯立新 于立新 杜力力 严加安 黄心中 周波
周代珍
武建丽
联系方式
13809033803/13911150797 dinglongyun@
2010年徐州师大国家社会科学基金和自然科学基金项目新突破
面上项 目 面上项 目 面上项 目
9
秦
盛
江苏沿海滩涂部分药用植物 内生放线菌多样性与活性初步 青年科学基金项 目
’
研究
1 郑维发 O
1 马晓冬 1
一氧化氮介导的桦褐孔菌多酚类化合物合成调控 的机理研究
江苏省乡村聚落地域类型、演化机理与优化模式研究
面上项 目
研究
面上项 目 面上项 目
5
石
枫
基于 a 硫氰基芳基乙酮的新型多组分反应的设计和新的杂 青年科学基金项 目 一 环骨架的有序构建
6 7 8
史延慧 屠树江 王 超
三齿吡咯后过渡金属配合物的合成及在氢胺化反应 的应用 基于多活性中心协同作用 的杂环骨架 的构筑 可控固/ 液界面环境下的电化学过程研究
面上项 目
1 康建荣 2 1 韩继光 3 1 张超金 4
山区煤矿开采引起的高陡边坡失稳机理研究 变变位系数偏心渐开线齿轮传动的研究 基于半导体纳米结构的极端非线性光学效应研究
面上项 目 面上项 目 青年科学基金项 目
另外,我校杨绪敏教授的 “ 张燧 《 经世挈要》点校 ” 、 张文德教授 的 “ 《 皇明四夷考》 《 四夷馆 考》校注 ” 和周棉教授的“ 清代留学档案史料整理 ” 分别获得全国高校古籍整理研究资助项 目。
1 2
当代中国马克思主义哲学研究范式创新研究 社会主义核心价值体系融入国民教育和精神文
明建设 全 过
陈延斌
3
4
2 世纪初中国传统社会 的转型与文学 的变革研究 0
金 文历 朔研 究
周
棉
一般项 目
一般 项 目
叶 正渤
自主招生认可奖项解读
1
2
3
丘成桐中学数学/物理奖受到复旦大学和南开大学高度认可,其他学校招生简章中没有特别提到,其适用范围远不及全国中学生数学竞赛。
4
自主招生认可奖项—学科竞赛类
力图用各种方法介绍数学竞赛中的14个专题,书中有对基本知识、基本问题以及解决这些问题的一些典型方法的讲解,还有由基本问题派生出来的教学方法和应用,相对易懂。
数学联赛推荐用书---进阶
《奥赛经典》,湖南师范大学出版社
这套书分为《奥林匹克数学中的组合问题》、《奥林匹克数学中的几何问题》、《奥林匹克数学中的代数问题》、《奥林匹克数学中的数论问题》、《奥林匹克数学中的真题分析》五册。
五大学科类竞赛详情—数学联赛
五大学科类竞赛详情—数学联赛时间流程
五大学科类竞赛详情—数学联赛时间流程
数学联赛推荐用书---入门
《奥数教程》,华东师范大学出版社 这套书按年级分为高一、高二、高三三套,每个年级包含教程、测试和学习手册三本,是比较基础、入门级的竞赛教程。
《奥数教程》从课本知识出发,由浅入深,逐步过渡到竞赛,内容涵盖了竞赛的全部考点和热点。每本书包含基础篇和拔高篇,基础篇主要是一试相关内容,拔高篇是二试相关内容。共30讲,每讲又分为“内容概述”、“例题精解”、“读一读”和“巩固训练”四个部分,系统地梳理了数学竞赛知识,比较适合刚接触竞赛的学生使用。
自主招生概述
3、自主招生有什么用? 获得加分,相当于降分录取。 比如,2017年北大的录取分数线是695分,某学生高考只考了670分,但他在北大的自主招生考试中表现优秀,获得30分加分,加分后为700分,高于北大的统招分数线,即可顺利进入北京大学。 4、自主招生可以加多少分? 一般来说,高校的自主招生加分,10分-30分是主流。只有少数优秀的学生可以拿到降分60或降到一本线录取。 所以,自主招生可以帮你更加稳定地进入符合自己实际水平学校,可以让你够到满意的热门专业,但绝不能让你弯道超车进入明显超过自己水平学校,不要抱有不切实际的幻想!
ch1-什么是组合数学-czm(1)
•
•
组合数学的历史
• 早在1303年,中国的朱世杰提出著名的 帕斯卡三角(Pascal三角),即杨辉三角; • 17世纪,学者帕斯卡和费马研究了与博弈相 关的组合问题, • 18世纪,拉普拉斯使用有利情形定义了概率; 欧拉结合著名的哥尼斯堡桥问题发明了图论; 而伯努利出版了第一本展示组合方法的书 《猜度术》; • 在18世纪和19世纪,哈密顿把组合数学应用 于拼图和游戏的研究中;
应用组合数学
曹霑懋 Caozhanmao@
章目录
• • • • • • • • • • • • • • • • • 第1章 什么是组合数学 第一部分 组合数学的基本工具 第2章 基本计数规则 第3章 图论概述 第4章 关系 第二部分 计数问题 第5章 生成函数及其应用 第6章 递推关系 第7章 容斥定理 第8章 波利亚计数理论 第三部分 存在问题 第9章 组合设计 第10章 编码理论 第11章 图论中的存在问题 第四部分 组合优化 第12章 匹配与覆盖 第13章 图和网络的优化问题
组合数学的应用
• 【例1.4 棋盘完美覆盖问题】8×8 的64个 正方形,每个牌可盖住两个格子, • ①32个牌可否不重叠地盖住所有格子?
–有,满足不重叠盖住的排列为完美覆盖。 –计算共有多少不同的完美覆盖?
• Fischer,1961年,12 988 816 =24×(901)2 • 3×3的棋盘不存在完美覆盖。
组合数学知识架构
• 例子一部分介绍 • 符号具有统一性 • 要有离散数学,算法设计等基础需要,没 有的可以退选 • 思想和方法和例子结合 • 适度练习
应用呼唤研究
• • • • • • • • DNA序列比对 蛋白质序列 生物种进化树重构 杂交 心理量 基因组图谱测绘 卫星通信 着色问题:移动通讯,交通灯…
(完整word版)组合数学第四版卢开澄标准答案-第四章
习题四4。
1。
若群G的元素a均可表示为某一元素x的幂,即a= x m,则称这个群为循环群.若群的元素交换律成立,即a , b G满足a b = b a则称这个群为阿贝尔(Abel)群,试证明所有的循环群都是阿贝尔群。
[证].设循环群(G,)的生成元是x0ÎG。
于是,对任何元素a ,b G,m,nÎN,使得a= x0m , b= x0n,从而a b = x0m x0n= x0m +n (指数律)= x0n +m (数的加法交换律)= x0n x0m(指数律)= b a故运算满足交换律;即(G, )是交换群.4.2。
若x是群G的一个元素,存在一个最小的正整数m,使x m=e,则称m为x的阶,试证:C={e,x,x2, ,x m—1}是G的一个子群。
[证].(1)非空性C :因为eÎG;(2)包含性C G:因为xÎG,根据群G的封闭性,可知x2, ,x m—1,(x m=)eÎG,故C G;(3)封闭性 a , b C a b C: a , b C,k,lÎN (0k〈m,0l〈m),使a = x k,b = x l,从而a b = x k x l = x(k+l)mod m C(因为0 (k+l) mod m〈m) ;(4)有逆元 a C a —1C: a C,kÎN (0k<m),使a = x k, 从而a -1= x m—k C(因为0 m-k < m)。
综合(1) (2)(3) (4),可知(C, )是(G, )的一个子群.4.3。
若G是阶为n的有限群,则G的所有元素的阶都不超过n。
[证]。
对任一元素xÎG,设其阶为m,并令C={e,x,x2,,x m-1},则由习题4.2.可知(C, )是(G, )的一个子群,故具有包含性C G。
因此有m = |C|£|G|= n所以群G的所有元素的阶都不超过n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四届全国组合数学与图论会议纪要
为促进我国组合数学与图论学科的进一步发展,加强国内同行的学术交流与合作,第四届全国组合数学与图论大会于2010年8月21日至25日在徐州师范大学举行。
会议由中国组合数学与图论学会主办,徐州师范大学承办,并得到了徐州师范大学和国家自然科学基金委天元基金的大力资助。
会议期间,来自国内外约160所大学和研究院所的约400位专家、学者和研究生共聚一堂, 积极讨论,相互交流。
福州大学范更华教授、同济大学邵嘉裕教授、中科院胡晓东教授、香港大学臧文安教授、南开大学高维东教授和北京交通大学常彦勋教授等作了6个大会报告(60分钟)。
另外,分四个分组进行了13个特邀报告(30分钟)以及近120个小组报告(15分钟)。
报告内容涉及组合数学与图论的各个领域。
其中包括结构图论、随机图论、代数图论、化学图论、图的染色、组合设计、组合优化、组合计数、组合矩阵、复杂网络、网络优化、代数组合论与应用图论等众多领域。
开幕式由徐州师范大学数学科学学院院长刘笑颖教授主持,徐州师范大学党委书记徐放鸣教授首先致开幕词,接着,中国组合数学与图论学会的理事长陈永川发表了热情洋溢的讲话。
本次会议还举行了中国组合数学与图论学会理事会的换届选举。
首先由上届正副理事长陈永川教授、李学良教授和王军教授(其中宝升教授因事缺席)提出新一届理事会的候选人名单。
然后经理事会充分讨论,并进行民主投票选举,产生了51位新任理事,并随后由新一届理事会选举产生了新一届常务理事会与正副理事长。
与会代表衷心感谢本次会议的东道主徐州师范大学的校、院各级领导对本次会议的大力支持,衷心感谢会务组的全体同志为本次会议的顺利召开而付出的辛勤劳动。
经新一届常务理事会讨论,决定下一届全国组合数学与图论大会于2012年在洛阳师范学院举行。
