同角三角比的关系和诱导公式沪教版课件
同角的三角比

2、单位圆中的有向线段:
设单位圆和角的终边的交点为 P( x, y) 考察角的各个三角比:
y
P(x, y)
O
x
第一象限: y
第二象限: y
T P
P
O MA x
MO
Ax
sin MP
T
cos OM tan AT
例:已知 ,且 cos 2 ,则角
2
的取值范围是_______________。
N x
有向线段QP
Q
P
若线段的方向和坐标轴的正方向一致,就规定这条线段是 正的,否则就规定它是负的。
所以图中有正向线段MN、PQ;负向线段NM、QP
1、有向线段: 坐标轴是规定了方向的直线
若线段的方向和坐标轴的正方向一致,就规定这条线段是 正的,否则就规定它是负的。
y
D2
C 1
A
B
|
|
|
o
1
23
AB 2 BA 2 CD 1 DC 1
csc
(5) sin2 cos2 1
2
2
典型例题:
例:sin2 cos2 1的充要条件是 。
sin2 cos2 5 1
2
2
cos 5
cos
?? 终边相同,所以三角比全对应相等
2
2
(终边相同的角,三角比对应相等)
知识要点:
(终边相同的角,三角比对应相等)
第一组诱导公式:
sin(2k ) sin cos(2k ) cos tan( 2k ) tan cot(2k ) cot
例:求 tan 25 的值
3
第一组诱导公式 (1) sin(2k ) sin (2) cos(2k ) cos (3) tan( 2k ) tan (4) cot(2k ) cot
5.3(2)同角三角比的关系与诱导公式

(1) 求sin a cos 的值; (2) 求sin cos 的值.
例
5 3. 若 tan cot , 求sin cos 的值. 2
二、例题选讲
例4. 已知 tan 2 ,求下列各式的值. sin cos (1) ; sin cos sin cos (2) sin 2 2 cos 2 (3)
三、课堂小结
1、同角三角比的八个其本关系式; 2、已知某角的一个三角比,求其他三角比值;
3、由三角比的符号确定角所在象限(符号看象限);
4、化简三角式的方法与技巧.
sin cos
化简与证明的一般方法与技巧:
(1)“化弦法”,即将正切、余切、正割、余割 都化为正弦、余弦 ;
(2“ )1 的妙用”,即将“ 1 ”化为sin 2 cos2 或sec2 tan2 或 csc2 cot2 等;
(3)三角式开偶次方时,要注意角的范围,以确定 正负号的选取.
一、复习
(2)商数关系: t an sin k k Ζ cos 2 cos k k Ζ cot sin
(3)平方关系: sin 2 cos2 1 R 2 2 1 tan sec k k Ζ 2 2 2 1 cot csc k k Ζ
说明: 本系列课件,经多次使用,修改,其中有部分 来自网络,它山之石可以攻玉,希望谅解。 为了一个课件,我们仔细研磨; 为了一个习题,我们精挑细选; 为了一点进步,我们竭尽全力; 没有最好,只有更好! 制作水平有限,错误难免,请多指教: 28275061@
第五章 三角比
(1)倒数关系:sin csc 1 k k Ζ cos sec 1 k k Ζ k 2 k Ζ tan cot 1
5.3(4)同角三角比的关系与诱导公式

第二组诱导公式
(the second group of induction formulas)
第三组诱导公式
(the third group of induction formulas)
第四组诱导公式
(the fourth group of induction formulas)
二、特殊角的三角比
α
sinα
0
6
4
3
2
2 3
3 4
5 6
cosαBiblioteka tanα例1、化简: cos(2 ) cot( ) tan( ) (1) ; sin( ) cot( 3 )
tan( ) cos( ) cos( ) (2) ; cot( ) sin( 2 )
1 (1)已知 sin x ,x [ 0, 2 ); 2
3 (2)已知 tan x ,x [, ); 3 1 (3)已知 sin x ,x在第一象限; 2
1 (4 )已知 sin x ,x在第三象限. 2
三、课堂小结
1、利用诱导公式,化简,求值;
2、利用诱导公式,根据三角比的值求出角的值.
说明: 本系列课件,经多次使用,修改,其中有部分 来自网络,它山之石可以攻玉,希望谅解。 为了一个课件,我们仔细研磨; 为了一个习题,我们精挑细选; 为了一点进步,我们竭尽全力; 没有最好,只有更好! 制作水平有限,错误难免,请多指教: 28275061@
第五章 三角比
一、复习回顾
第一组诱导公式
sin n tann (3) , n Z; cos2n
高考数学第一轮基础复习 同角三角函数的基本关系及诱导公式课件

解法 2:设 tanα1=185,α1 为锐角, 如图在 Rt△ABC 中,由 tanα1=185, 设 AC=8,BC=15,则 AB=17, ∴sinα1=187,
∵α 为第二象限角,∴sinα>0,从而 sinα=187. 解法 3:∵α 是第二象限角,∴sinα>0,排除 B、D, 又 tanα=csionsαα=-185,由勾股数组 8,15,17 知排除 A, ∴选 C.
已知
tan2α = - 2
2
,
且
满
足
π 4
<α<
π 2
,
则
2cos2α2-sinα-1 2sinπ4+α
的值为(
)
A. 2
B.- 2
C.-3+2 2
D.3-2 2
解析:2cos22sα2i-nπ4si+nαα- 1=csionsαα+-csoinsαα=1ta-nαta+nα1. 又 tan2α=-2 2=1-2tatannα2α
cos2
sin2
=sinα2+cosα2 -sinα2-cosα2
α2为第二象限角 α2为第四象限角
∴原式=± 2sinα2+π4. 答案:± 2sinα2+π4
利用诱导公式进行化简求值
[例 3] 设 f(x)=asin(πx+α)+bcos(πx+α),其中 a,b,
α∈R,且 ab≠0,α≠kπ (k∈Z).若 f(2009)=5,则 f(2010)
答案:C
点评:本题中由 sinθ+cosθ= 32-1两边平方扩大了 θ 的取值范围会引起增解,必须结合 0<θ<π 与 0<sinθ+ cosθ<1 得出π2<θ<π,进而得出|sinθ|>|cosθ|来去掉增解 tanθ =- 33,故变换时必须要等价,使用不等价变换时,一 定要检验.
高考数学复习同角三角函数的基本关系与诱导公式

第2讲 同角三角函数的基本关系与诱导公式 最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x +cos 2x =1,sin xcos x =tan x .2.借助单位圆的对称性,利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2,α±π的正弦、余弦、正切. 命题趋势 考查利用同角三角函数的基本关系、诱导公式解决条件求值问题,常与三角恒等变换相结合起到化简三角函数关系的作用,强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1.同角三角函数的基本关系 (1)平方关系:sin 2x +cos 2x =1.(2)商数关系:tan x =sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π+π2,k ∈Z .2.三角函数的诱导公式 组数 一 二 三 四 五 六 角 α+2k π (k ∈Z ) π+α -α π-α π2-α π2+α 正弦 sin α -sin__α -sin__α sin__α cos__α cos__α 余弦 cos α -cos__α cos__α -cos__α sin__α -sin__α正切tan αtan__α-tan__α-tan__α常用结论1.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍和偶数倍,变与不变指函数名称的变化.2.同角三角函数的基本关系式的几种变形 (1)sin 2α=1-cos 2α=(1+cos α)(1-cos α);cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. (2)sin α=tan αcos α⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z .(3)sin 2α=sin 2αsin 2α+cos 2α=tan 2αtan 2α+1;cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1.常见误区1.同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响,尤其是利用平方关系求三角函数值,进行开方时要根据角的范围,判断符号后,正确取舍.2.注意求值与化简后的结果一般要尽可能有理化、整式化.1.判断正误(正确的打“√”,错误的打“×”) (1)对任意的角α,β,都有sin 2α+cos 2β=1.( ) (2)若α∈R ,则tan α=sin αcos α恒成立.( )(3)sin(π+α)=-sin α成立的条件是α为锐角.( ) (4)若cos(n π-θ)=13(n ∈Z ),则cos θ=13.( ) 答案:(1)× (2)× (3)× (4)×2.(易错题)已知cos(π+α)=23,则tan α=( ) A .52 B .255 C .±52D .±255解析:选C.因为cos(π+α)=23, 所以cos α=-23,则α为第二或第三象限角,所以sin α=±1-cos 2α=±53.所以tan α=sin αcos α=±53-23=±52. 3.已知sin αcos α=12,则tan α+1tan α=( ) A .2 B .12 C .-2D .-12解析:选A.tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.4.sin 2 490°=________;cos ⎝ ⎛⎭⎪⎫-52π3=________.解析:sin 2 490°=sin(7×360°-30°)=-sin 30°=-12.cos ⎝ ⎛⎭⎪⎫-52π3=cos 52π3=cos ⎝ ⎛⎭⎪⎫16π+π+π3=cos ⎝ ⎛⎭⎪⎫π+π3=-cos π3=-12. 答案:-12 -125.化简cos ⎝ ⎛⎭⎪⎫α-π2sin ⎝ ⎛⎭⎪⎫52π+α·cos(2π-α)的结果为________.解析:原式=sin αcos α·cos α=sin α. 答案:sin α同角三角函数的基本关系式 角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角,且tan α=-34,则sinα=( )A .-35 B.35 C.45 D .-45 【解析】 因为tan α=sin αcos α=-34, 所以cos α=-43sin α ①.sin 2α+cos 2α=1 ②,由①②得sin 2α=925,又α是第四象限角,所以sin α<0,则sin α=-35,故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的.角度二 sin α,cos α的齐次式问题已知tan αtan α-1=-1,求下列各式的值:(1)sin α-3cos αsin α+cos α;(2)sin 2α+sin αcos α+2. 【解】 由已知得tan α=12. (1)sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.(2)sin 2α+sin αcos α+2=sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝ ⎛⎭⎪⎫122+12⎝ ⎛⎭⎪⎫122+1+2=135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α,求关于sin α与cos α的齐n次分式或齐二次整式的值.角度三sin α±cos α,sin αcos α之间的关系已知α∈(-π,0),sin α+cos α=1 5.(1)求sin α-cos α的值;(2)求sin 2α+2sin2α1-tan α的值.【解】(1)由sin α+cos α=1 5,平方得sin2α+2sin αcos α+cos2α=1 25,整理得2sin αcos α=-24 25.所以(sin α-cos α)2=1-2sin αcos α=49 25.由α∈(-π,0),知sin α<0,又sin α+cos α>0,所以cos α>0,则sin α-cos α<0,故sin α-cos α=-7 5.(2)sin 2α+2sin2α1-tan α=2sin α(cos α+sin α)1-sin αcos α=2sin αcos α(cos α+sin α)cos α-sin α=-2425×1575=-24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方,sin α+cos α,sin α-cos α,sin αcos α之间可建立联系,若令sin α+cos α=t ,则sin αcos α=t 2-12,sin α-cos α=±2-t 2(注意根据α的范围选取正、负号).(2)对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,可以知一求二.1.(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2+α=35,且α∈⎝ ⎛⎭⎪⎫π2,3π2,则tan α=( )A .43 B .34 C .-34D .±34解析:选B.因为cos ⎝ ⎛⎭⎪⎫π2+α=35,所以sin α=-35.又α∈⎝ ⎛⎭⎪⎫π2,3π2,所以cos α=-1-sin 2α=-45,所以tan α=sin αcos α=34.2.已知tan α=-34,则sin α(sin α-cos α)=( ) A.2125 B.2521 C.45D.54解析:选 A.sin α(sin α-cos α)=sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α=tan 2α-tan αtan 2α+1,将tan α=-34代入得原式=⎝ ⎛⎭⎪⎫-342-⎝ ⎛⎭⎪⎫-34⎝ ⎛⎭⎪⎫-342+1=2125.3.(一题多解)已知sin α-cos α=2,α∈(0,π),则tan α=( ) A .-1 B .-22 C .22D .1解析:选A.方法一:由⎩⎨⎧sin α-cos α=2,sin 2α+cos 2α=1,得2cos 2α+22cos α+1=0,即(2cos α+1)2=0, 所以cos α=-22.又α∈(0,π),所以α=3π4, 所以tan α=tan 3π4=-1.方法二:因为sin α-cos α=2, 所以2sin ⎝ ⎛⎭⎪⎫α-π4=2,所以sin ⎝ ⎛⎭⎪⎫α-π4=1.因为α∈(0,π),所以α=3π4,所以tan α=-1.法三:由sin α-cos α=2得1-sin 2α=2,所以sin 2α=-1. 设sin α+cos α=t ,所以1+sin 2α=t 2,所以t =0.由⎩⎨⎧sin α-cos α=2,sin α+cos α=0得sin α=22,cos α=-22, 所以tan α=-1.诱导公式的应用(1)sin(-1 200°)cos 1 290°=________.(2)已知角θ的顶点在坐标原点,始边与x 轴正半轴重合,终边在直线3x -y =0上,则sin ⎝ ⎛⎭⎪⎫3π2+θ+2cos (π-θ)sin ⎝ ⎛⎭⎪⎫π2-θ-sin (π-θ)等于________.【解析】 (1)原式=-sin 1 200°cos 1 290° =-sin(3×360°+120°)cos(3×360°+210°) =-sin 120°cos 210°=-sin(180°-60°)cos(180°+30°) =sin 60°cos 30°=32×32=34.(2)由题意可知tan θ=3,原式=-cos θ-2cos θcos θ-sin θ=-31-tan θ=32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变,则cos ⎝ ⎛⎭⎪⎫π2+θ-sin (-π-θ)cos ⎝ ⎛⎭⎪⎫11π2-θ+sin ⎝ ⎛⎭⎪⎫9π2+θ=________.解析:由题意可知tan θ=3, 原式=-sin θ+sin (π+θ)cos ⎝ ⎛⎭⎪⎫6π-π2-θ+sin ⎝ ⎛⎭⎪⎫4π+π2+θ =-sin θ-sin θcos ⎝ ⎛⎭⎪⎫π2+θ+sin ⎝ ⎛⎭⎪⎫π2+θ=-2sin θ-sin θ+cos θ=2tan θtan θ-1=2×33-1=3.答案:3(1)诱导公式用法的一般思路①化负为正,化大为小,化到锐角为止;②角中含有加减π2的整数倍时,用公式去掉π2的整数倍. (2)常见的互余和互补的角①常见的互余的角:π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等; ②常见的互补的角:π3+θ与2π3-θ;π4+θ与3π4-θ等.1.已知sin ⎝ ⎛⎭⎪⎫α-π3=13,则cos ⎝ ⎛⎭⎪⎫α+π6的值是( )A .-13 B.13 C.223 D .-223解析:选A.因为sin ⎝ ⎛⎭⎪⎫α-π3=13,所以cos ⎝ ⎛⎭⎪⎫α+π6=cos ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫α-π3=-sin ⎝ ⎛⎭⎪⎫α-π3=-13.2.(多选)已知A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α,则A 的值可以是( )A .3B .-3C .1D .-1解析:选AD.由已知可得,当k 为偶数时,A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α=sin αsin α+cos αcos α+tan αtan α=3;当k 为奇数时,A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α=-sin αsin α+-cos αcos α+tan αtan α=-1,所以A 的值可以是3或-1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角,且cos α=-1010. (1)求tan α的值;(2)化简并求cos (π-α)2sin (-α)+sin ⎝ ⎛⎭⎪⎫π2+α的值.【解】 (1)因为α是第三象限角,cos α=-1010, 所以sin α=-1-cos 2α=-31010,所以tan α=sin αcos α=3.(2)原式=-cos α-2sin α+cos α=cos α2sin α-cos α=12tan α-1,由(1)知tan α=3,所以原式=12×3-1=15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本 思路①分析结构特点,选择恰当公式; ②利用公式化成单角三角函数;③整理得最简形式化简 要求①化简过程是恒等变换;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值1.已知sin ⎝ ⎛⎭⎪⎫5π2+α=35,所以tan α的值为( )A .-43B .-34C .±43D .±34解析:选C.sin ⎝ ⎛⎭⎪⎫5π2+α=sin ⎝ ⎛⎭⎪⎫π2+α=cos α=35,所以sin α=±45,tan α=sin αcos α=±43.2.已知tan(π-α)=-23,且α∈⎝ ⎛⎭⎪⎫-π,-π2,则cos (-α)+3sin (π+α)cos (π-α)+9sin α的值为( )A .-15B .-37 C.15 D.37解析:选 A.因为tan(π-α)=-23,所以tan α=23,所以cos (-α)+3sin (π+α)cos (π-α)+9sin α=cos α-3sin α-cos α+9sin α=1-3tan α-1+9tan α=1-2-1+6=-15,故选A.[A 级 基础练]1.(多选)已知x ∈R ,则下列等式恒成立的是( ) A .sin(-x )=sin x B .sin ⎝ ⎛⎭⎪⎫3π2-x =cos xC .cos ⎝ ⎛⎭⎪⎫π2+x =-sin xD .cos(x -π)=-cos x解析:选CD.sin(-x )=-sin x ,故A 不成立;sin ⎝ ⎛⎭⎪⎫3π2-x =-cos x ,故B 不成立;cos ⎝ ⎛⎭⎪⎫π2+x =-sin x ,故C 成立;cos(x -π)=-cos x ,故D 成立.2.(多选)若sin α=45,且α为锐角,则下列选项中正确的有( )A .tan α=43 B .cos α=35 C .sin α+cos α=85D .sin α-cos α=-15解析:选AB.因为sin α=45,且α为锐角, 所以cos α=1-sin 2α=1-⎝ ⎛⎭⎪⎫452=35,故B 正确, 所以tan α=sin αcos α=4535=43,故A 正确,所以sin α+cos α=45+35=75≠85,故C 错误, 所以sin α-cos α=45-35=15≠-15,故D 错误.3.已知角α是第二象限角,且满足sin ⎝ ⎛⎭⎪⎫5π2+α+3cos(α-π)=1,则tan(π+α)=( )A . 3B .- 3C .-33D .-1解析:选B.由sin ⎝ ⎛⎭⎪⎫5π2+α+3cos(α-π)=1,得cos α-3cos α=1,所以cos α=-12, 因为角α是第二象限角,所以sin α=32, 所以tan(π+α)=tan α=sin αcos α=- 3.4.已知f (α)=sin (2π-α)cos ⎝ ⎛⎭⎪⎫π2+αcos ⎝ ⎛⎭⎪⎫-π2+αtan (π+α),则f ⎝ ⎛⎭⎪⎫π3=( ) A .12 B .22 C .32D .-12解析:选A.f (α)=sin (2π-α)cos ⎝ ⎛⎭⎪⎫π2+αcos ⎝ ⎛⎭⎪⎫-π2+αtan (π+α)=-sin α·(-sin α)sin α·tan α=sin 2αsin α·sin αcos α=cos α,则f ⎝ ⎛⎭⎪⎫π3=cos π3=12.5.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上一点A (2sin α,3)(sin α≠0),则cos α=( )A .12B .-12C .32D .-32解析:选A.由三角函数定义得tan α=32sin α,即sin αcos α=32sin α,得3cos α=2sin 2α=2(1-cos 2α),解得cos α=12或cos α=-2(舍去).故选A.6.计算:sin 11π6+cos 10π3的值为________.解析:原式=sin ⎝ ⎛⎭⎪⎫2π-π6+cos ⎝ ⎛⎭⎪⎫3π+π3=-sin π6-cos π3=-12-12=-1.答案:-17.已知sin ⎝ ⎛⎭⎪⎫-π2-αcos ⎝ ⎛⎭⎪⎫-7π2+α=1225,且0<α<π4,则sin α=________,cos α=________.解析:sin ⎝ ⎛⎭⎪⎫-π2-αcos ⎝ ⎛⎭⎪⎫-7π2+α=-cos α·(-sin α)=sin αcos α=1225.因为0<α<π4,所以0<sin α<cos α.又因为sin 2α+cos 2α=1,所以sin α=35,cos α=45.答案:35 45 8.化简1-2sin 40°cos 40°cos 40°-1-sin 250°=________. 解析:原式=sin 240°+cos 240°-2sin 40°cos 40°cos 40°-cos 50°=|sin 40°-cos 40°|sin 50°-sin 40°=|sin 40°-sin 50°|sin 50°-sin 40°=sin 50°-sin 40°sin 50°-sin 40°=1.答案:19.已知sin(3π+α)=2sin ⎝ ⎛⎭⎪⎫3π2+α,求下列各式的值:(1)sin α-4cos α5sin α+2cos α;(2)sin 2α+sin 2α.解:由已知得sin α=2cos α. (1)原式=2cos α-4cos α5×2cos α+2cos α=-16.(2)原式=sin 2α+2sin αcos αsin 2α+cos 2α=sin 2α+sin 2αsin 2α+14sin 2α=85.10.已知角θ的终边与单位圆x 2+y 2=1在第四象限交于点P ,且点P 的坐标为⎝ ⎛⎭⎪⎫12,y .(1)求tan θ的值;(2)求cos ⎝ ⎛⎭⎪⎫π2-θ+cos (θ-2π)sin θ+cos (π+θ)的值.解:(1)由θ为第四象限角,终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12,y ,得⎝ ⎛⎭⎪⎫122+y 2=1,y <0,解得y =-32,所以tan θ=-3212=- 3.(2)因为tan θ=-3, 所以cos ⎝ ⎛⎭⎪⎫π2-θ+cos (θ-2π)sin θ+cos (π+θ)=sin θ+cos θsin θ-cos θ=tan θ+1tan θ-1=-3+1-3-1=2- 3. [B 级 综合练]11.(多选)已知角θ的终边与坐标轴不重合,式子1-sin 2(π+θ)化简的结果为-cos θ,则( )A .sin θ>0,tan θ>0B .sin θ<0,tan θ>0C .sin θ<0,tan θ<0D .sin θ>0,tan θ<0解析:选BD.1-sin 2(π+θ)=1-sin 2θ=cos 2θ=|cos θ|=-cos θ,所以cos θ<0,角θ的终边落在第二或三象限,所以sin θ>0,tan θ<0或sin θ<0,tan θ>0,故选BD.12.(2020·陕西汉中月考)已知角α为第二象限角,则cos α·1+sin α1-sin α+sin 2α1+1tan 2α=( )A .1B .-1C .0D .2解析:选B.因为角α为第二象限角,所以sin α>0,cos α<0,所以cos α 1+sin α1-sin α=cos α(1+sin α)2cos 2α=cos α·1+sin α|cos α|=-1-sin α,sin 2α1+1tan 2α=sin 2α1+cos 2αsin 2α=sin 2αsin 2α+cos 2αsin 2α=sin 2α1sin 2α=sin 2α⎪⎪⎪⎪⎪⎪1sin α=sin α,所以cos α1+sin α1-sin α+sin 2α1+1tan 2α=-1-sin α+sin α=-1.故选B.13.是否存在α∈⎝ ⎛⎭⎪⎫-π2,π2,β∈()0,π使等式sin(3π-α)=2cos ⎝ ⎛⎭⎪⎫π2-β,3cos(-α)=-2cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.解:假设存在角α,β满足条件. 由已知条件可得⎩⎨⎧sin α=2sin β,①3cos α=2cos β,②由①2+②2,得sin 2α+3cos 2α=2.所以sin 2α=12,所以sin α=±22.因为α∈⎝ ⎛⎭⎪⎫-π2,π2,所以α=±π4. 当α=π4时,由②式知cos β=32, 又β∈(0,π),所以β=π6,此时①式成立; 当α=-π4时,由②式知cos β=32,又β∈(0,π), 所以β=π6,此时①式不成立,故舍去. 所以存在α=π4,β=π6满足条件. 14.在△ABC 中,(1)求证:cos 2A +B 2+cos 2 C2=1;(2)若cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan(C -π)<0,求证:△ABC 为钝角三角形.证明:(1)在△ABC 中,A +B =π-C , 所以A +B 2=π2-C2,所以cos A +B 2=cos ⎝ ⎛⎭⎪⎫π2-C 2=sin C 2,所以cos 2A + B 2+cos 2C2=1.(2)若cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan(C -π)<0,所以(-sin A )(-cos B )tan C <0, 即sin A cos B tan C <0.因为在△ABC 中,0<A <π,0<B <π,0<C <π且sin A >0, 所以⎩⎨⎧cos B <0,tan C >0或⎩⎨⎧cos B >0,tan C <0,所以B 为钝角或C 为钝角,所以△ABC 为钝角三角形.[C 级 创新练]15.(2020·山东肥城统考)公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现黄金分割比例为5-12≈0.618,这一数值也可以表示为m =2sin 18°.若m 2+n =4,则m n2cos 227°-1=( )A .4B .3C .2D .1解析:选C.因为m =2sin 18°,且m 2+n =4,所以n =4-m 2=4-4sin 218°=4(1-sin 218°)=4cos 218°,所以m n2cos 227°-1=2sin 18°4cos 218°cos 54°=4sin 18°cos 18°sin 36°=2.故选C.16.已知α,β∈(0,2π)且α<β,若关于x 的方程(x +sin α)(x +sin β)+1=0有实数根,则代数式3sin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2-β2-sin (π-α)cos ⎝ ⎛⎭⎪⎫3π2+β=________.解析:整理方程(x +sin α)(x +sin β)+1=0得x 2+x (sin α+sin β)+sin αsin β+1=0.由题意得Δ=(sin α+sin β)2-4sin αsin β-4≥0, 即(sin α-sin β)2≥4①.因为-1≤sin α≤1,-1≤sin β≤1,所以sin α-sin β∈[-2,2],从而(sin α-sin β)2≤4②.由①②得sin α-sin β=±2,所以⎩⎨⎧sin α=1,sin β=-1或⎩⎨⎧sin α=-1,sin β=1.因为α,β∈(0,2π)且α<β,所以α=π2,β=3π2,即⎩⎨⎧sin α=1,sin β=-1.因此3sin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2-β2-sin (π-α)cos ⎝ ⎛⎭⎪⎫3π2+β=3cos α-sin β2-sin αsin β=12+1=13.答案:13第2讲 同角三角函数的基本关系与诱导公式 最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x +cos 2x =1,sin xcos x =tan x .2.借助单位圆的对称性,利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2,α±π的正弦、余弦、正切. 命题趋势 考查利用同角三角函数的基本关系、诱导公式解决条件求值问题,常与三角恒等变换相结合起到化简三角函数关系的作用,强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1.同角三角函数的基本关系 (1)平方关系:sin 2x +cos 2x =1.(2)商数关系:tan x =sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π+π2,k ∈Z .2.三角函数的诱导公式 组数 一 二 三 四 五 六 角 α+2k π (k ∈Z ) π+α -α π-α π2-α π2+α 正弦 sin α -sin__α -sin__α sin__α cos__α cos__α 余弦 cos α -cos__α cos__α -cos__α sin__α -sin__α正切tan αtan__α-tan__α-tan__α常用结论1.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍和偶数倍,变与不变指函数名称的变化.2.同角三角函数的基本关系式的几种变形 (1)sin 2α=1-cos 2α=(1+cos α)(1-cos α);cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. (2)sin α=tan αcos α⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z .(3)sin 2α=sin 2αsin 2α+cos 2α=tan 2αtan 2α+1;cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1.常见误区1.同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响,尤其是利用平方关系求三角函数值,进行开方时要根据角的范围,判断符号后,正确取舍.2.注意求值与化简后的结果一般要尽可能有理化、整式化.1.判断正误(正确的打“√”,错误的打“×”) (1)对任意的角α,β,都有sin 2α+cos 2β=1.( ) (2)若α∈R ,则tan α=sin αcos α恒成立.( )(3)sin(π+α)=-sin α成立的条件是α为锐角.( ) (4)若cos(n π-θ)=13(n ∈Z ),则cos θ=13.( ) 答案:(1)× (2)× (3)× (4)×2.(易错题)已知cos(π+α)=23,则tan α=( ) A .52 B .255 C .±52D .±255解析:选C.因为cos(π+α)=23, 所以cos α=-23,则α为第二或第三象限角,所以sin α=±1-cos 2α=±53.所以tan α=sin αcos α=±53-23=±52. 3.已知sin αcos α=12,则tan α+1tan α=( ) A .2 B .12 C .-2D .-12解析:选A.tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.4.sin 2 490°=________;cos ⎝ ⎛⎭⎪⎫-52π3=________.解析:sin 2 490°=sin(7×360°-30°)=-sin 30°=-12.cos ⎝ ⎛⎭⎪⎫-52π3=cos 52π3=cos ⎝ ⎛⎭⎪⎫16π+π+π3=cos ⎝ ⎛⎭⎪⎫π+π3=-cos π3=-12. 答案:-12 -125.化简cos ⎝ ⎛⎭⎪⎫α-π2sin ⎝ ⎛⎭⎪⎫52π+α·cos(2π-α)的结果为________.解析:原式=sin αcos α·cos α=sin α. 答案:sin α同角三角函数的基本关系式 角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角,且tan α=-34,则sinα=( )A .-35 B.35 C.45 D .-45 【解析】 因为tan α=sin αcos α=-34, 所以cos α=-43sin α ①.sin 2α+cos 2α=1 ②,由①②得sin 2α=925,又α是第四象限角,所以sin α<0,则sin α=-35,故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的.角度二 sin α,cos α的齐次式问题已知tan αtan α-1=-1,求下列各式的值:(1)sin α-3cos αsin α+cos α;(2)sin 2α+sin αcos α+2. 【解】 由已知得tan α=12. (1)sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.(2)sin 2α+sin αcos α+2=sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝ ⎛⎭⎪⎫122+12⎝ ⎛⎭⎪⎫122+1+2=135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α,求关于sin α与cos α的齐n次分式或齐二次整式的值.角度三sin α±cos α,sin αcos α之间的关系已知α∈(-π,0),sin α+cos α=1 5.(1)求sin α-cos α的值;(2)求sin 2α+2sin2α1-tan α的值.【解】(1)由sin α+cos α=1 5,平方得sin2α+2sin αcos α+cos2α=1 25,整理得2sin αcos α=-24 25.所以(sin α-cos α)2=1-2sin αcos α=49 25.由α∈(-π,0),知sin α<0,又sin α+cos α>0,所以cos α>0,则sin α-cos α<0,故sin α-cos α=-7 5.(2)sin 2α+2sin2α1-tan α=2sin α(cos α+sin α)1-sin αcos α=2sin αcos α(cos α+sin α)cos α-sin α=-2425×1575=-24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方,sin α+cos α,sin α-cos α,sin αcos α之间可建立联系,若令sin α+cos α=t ,则sin αcos α=t 2-12,sin α-cos α=±2-t 2(注意根据α的范围选取正、负号).(2)对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,可以知一求二.1.(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2+α=35,且α∈⎝ ⎛⎭⎪⎫π2,3π2,则tan α=( )A .43 B .34 C .-34D .±34解析:选B.因为cos ⎝ ⎛⎭⎪⎫π2+α=35,所以sin α=-35.又α∈⎝ ⎛⎭⎪⎫π2,3π2,所以cos α=-1-sin 2α=-45,所以tan α=sin αcos α=34.2.已知tan α=-34,则sin α(sin α-cos α)=( ) A.2125 B.2521 C.45D.54解析:选 A.sin α(sin α-cos α)=sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α=tan 2α-tan αtan 2α+1,将tan α=-34代入得原式=⎝ ⎛⎭⎪⎫-342-⎝ ⎛⎭⎪⎫-34⎝ ⎛⎭⎪⎫-342+1=2125.3.(一题多解)已知sin α-cos α=2,α∈(0,π),则tan α=( ) A .-1 B .-22 C .22D .1解析:选A.方法一:由⎩⎨⎧sin α-cos α=2,sin 2α+cos 2α=1,得2cos 2α+22cos α+1=0,即(2cos α+1)2=0, 所以cos α=-22.又α∈(0,π),所以α=3π4, 所以tan α=tan 3π4=-1.方法二:因为sin α-cos α=2, 所以2sin ⎝ ⎛⎭⎪⎫α-π4=2,所以sin ⎝ ⎛⎭⎪⎫α-π4=1.因为α∈(0,π),所以α=3π4,所以tan α=-1.法三:由sin α-cos α=2得1-sin 2α=2,所以sin 2α=-1. 设sin α+cos α=t ,所以1+sin 2α=t 2,所以t =0.由⎩⎨⎧sin α-cos α=2,sin α+cos α=0得sin α=22,cos α=-22, 所以tan α=-1.诱导公式的应用(1)sin(-1 200°)cos 1 290°=________.(2)已知角θ的顶点在坐标原点,始边与x 轴正半轴重合,终边在直线3x -y =0上,则sin ⎝ ⎛⎭⎪⎫3π2+θ+2cos (π-θ)sin ⎝ ⎛⎭⎪⎫π2-θ-sin (π-θ)等于________.【解析】 (1)原式=-sin 1 200°cos 1 290° =-sin(3×360°+120°)cos(3×360°+210°) =-sin 120°cos 210°=-sin(180°-60°)cos(180°+30°) =sin 60°cos 30°=32×32=34.(2)由题意可知tan θ=3,原式=-cos θ-2cos θcos θ-sin θ=-31-tan θ=32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变,则cos ⎝ ⎛⎭⎪⎫π2+θ-sin (-π-θ)cos ⎝ ⎛⎭⎪⎫11π2-θ+sin ⎝ ⎛⎭⎪⎫9π2+θ=________.解析:由题意可知tan θ=3, 原式=-sin θ+sin (π+θ)cos ⎝ ⎛⎭⎪⎫6π-π2-θ+sin ⎝ ⎛⎭⎪⎫4π+π2+θ =-sin θ-sin θcos ⎝ ⎛⎭⎪⎫π2+θ+sin ⎝ ⎛⎭⎪⎫π2+θ=-2sin θ-sin θ+cos θ=2tan θtan θ-1=2×33-1=3.答案:3(1)诱导公式用法的一般思路①化负为正,化大为小,化到锐角为止;②角中含有加减π2的整数倍时,用公式去掉π2的整数倍. (2)常见的互余和互补的角①常见的互余的角:π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等; ②常见的互补的角:π3+θ与2π3-θ;π4+θ与3π4-θ等.1.已知sin ⎝ ⎛⎭⎪⎫α-π3=13,则cos ⎝ ⎛⎭⎪⎫α+π6的值是( )A .-13 B.13 C.223 D .-223解析:选A.因为sin ⎝ ⎛⎭⎪⎫α-π3=13,所以cos ⎝ ⎛⎭⎪⎫α+π6=cos ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫α-π3=-sin ⎝ ⎛⎭⎪⎫α-π3=-13.2.(多选)已知A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α,则A 的值可以是( )A .3B .-3C .1D .-1解析:选AD.由已知可得,当k 为偶数时,A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α=sin αsin α+cos αcos α+tan αtan α=3;当k 为奇数时,A =sin (k π+α)sin α+cos (k π+α)cos α+tan (k π+α)tan α=-sin αsin α+-cos αcos α+tan αtan α=-1,所以A 的值可以是3或-1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角,且cos α=-1010. (1)求tan α的值;(2)化简并求cos (π-α)2sin (-α)+sin ⎝ ⎛⎭⎪⎫π2+α的值.【解】 (1)因为α是第三象限角,cos α=-1010, 所以sin α=-1-cos 2α=-31010,所以tan α=sin αcos α=3.(2)原式=-cos α-2sin α+cos α=cos α2sin α-cos α=12tan α-1,由(1)知tan α=3,所以原式=12×3-1=15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本 思路①分析结构特点,选择恰当公式; ②利用公式化成单角三角函数;③整理得最简形式化简 要求①化简过程是恒等变换;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值1.已知sin ⎝ ⎛⎭⎪⎫5π2+α=35,所以tan α的值为( )A .-43B .-34C .±43D .±34解析:选C.sin ⎝ ⎛⎭⎪⎫5π2+α=sin ⎝ ⎛⎭⎪⎫π2+α=cos α=35,所以sin α=±45,tan α=sin αcos α=±43.2.已知tan(π-α)=-23,且α∈⎝ ⎛⎭⎪⎫-π,-π2,则cos (-α)+3sin (π+α)cos (π-α)+9sin α的值为( )A .-15B .-37 C.15 D.37解析:选 A.因为tan(π-α)=-23,所以tan α=23,所以cos (-α)+3sin (π+α)cos (π-α)+9sin α=cos α-3sin α-cos α+9sin α=1-3tan α-1+9tan α=1-2-1+6=-15,故选A.[A 级 基础练]1.(多选)已知x ∈R ,则下列等式恒成立的是( ) A .sin(-x )=sin x B .sin ⎝ ⎛⎭⎪⎫3π2-x =cos xC .cos ⎝ ⎛⎭⎪⎫π2+x =-sin xD .cos(x -π)=-cos x解析:选CD.sin(-x )=-sin x ,故A 不成立;sin ⎝ ⎛⎭⎪⎫3π2-x =-cos x ,故B 不成立;cos ⎝ ⎛⎭⎪⎫π2+x =-sin x ,故C 成立;cos(x -π)=-cos x ,故D 成立.2.(多选)若sin α=45,且α为锐角,则下列选项中正确的有( )A .tan α=43 B .cos α=35 C .sin α+cos α=85D .sin α-cos α=-15解析:选AB.因为sin α=45,且α为锐角, 所以cos α=1-sin 2α=1-⎝ ⎛⎭⎪⎫452=35,故B 正确, 所以tan α=sin αcos α=4535=43,故A 正确,所以sin α+cos α=45+35=75≠85,故C 错误, 所以sin α-cos α=45-35=15≠-15,故D 错误.3.已知角α是第二象限角,且满足sin ⎝ ⎛⎭⎪⎫5π2+α+3cos(α-π)=1,则tan(π+α)=( )A . 3B .- 3C .-33D .-1解析:选B.由sin ⎝ ⎛⎭⎪⎫5π2+α+3cos(α-π)=1,得cos α-3cos α=1,所以cos α=-12, 因为角α是第二象限角,所以sin α=32, 所以tan(π+α)=tan α=sin αcos α=- 3.4.已知f (α)=sin (2π-α)cos ⎝ ⎛⎭⎪⎫π2+αcos ⎝ ⎛⎭⎪⎫-π2+αtan (π+α),则f ⎝ ⎛⎭⎪⎫π3=( ) A .12 B .22 C .32D .-12解析:选A.f (α)=sin (2π-α)cos ⎝ ⎛⎭⎪⎫π2+αcos ⎝ ⎛⎭⎪⎫-π2+αtan (π+α)=-sin α·(-sin α)sin α·tan α=sin 2αsin α·sin αcos α=cos α,则f ⎝ ⎛⎭⎪⎫π3=cos π3=12.5.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上一点A (2sin α,3)(sin α≠0),则cos α=( )A .12B .-12C .32D .-32解析:选A.由三角函数定义得tan α=32sin α,即sin αcos α=32sin α,得3cos α=2sin 2α=2(1-cos 2α),解得cos α=12或cos α=-2(舍去).故选A.6.计算:sin 11π6+cos 10π3的值为________.解析:原式=sin ⎝ ⎛⎭⎪⎫2π-π6+cos ⎝ ⎛⎭⎪⎫3π+π3=-sin π6-cos π3=-12-12=-1.答案:-17.已知sin ⎝ ⎛⎭⎪⎫-π2-αcos ⎝ ⎛⎭⎪⎫-7π2+α=1225,且0<α<π4,则sin α=________,cos α=________.解析:sin ⎝ ⎛⎭⎪⎫-π2-αcos ⎝ ⎛⎭⎪⎫-7π2+α=-cos α·(-sin α)=sin αcos α=1225.因为0<α<π4,所以0<sin α<cos α.又因为sin 2α+cos 2α=1,所以sin α=35,cos α=45.答案:35 45 8.化简1-2sin 40°cos 40°cos 40°-1-sin 250°=________. 解析:原式=sin 240°+cos 240°-2sin 40°cos 40°cos 40°-cos 50°=|sin 40°-cos 40°|sin 50°-sin 40°=|sin 40°-sin 50°|sin 50°-sin 40°=sin 50°-sin 40°sin 50°-sin 40°=1.答案:19.已知sin(3π+α)=2sin ⎝ ⎛⎭⎪⎫3π2+α,求下列各式的值:(1)sin α-4cos α5sin α+2cos α;(2)sin 2α+sin 2α.解:由已知得sin α=2cos α. (1)原式=2cos α-4cos α5×2cos α+2cos α=-16.(2)原式=sin 2α+2sin αcos αsin 2α+cos 2α=sin 2α+sin 2αsin 2α+14sin 2α=85.10.已知角θ的终边与单位圆x 2+y 2=1在第四象限交于点P ,且点P 的坐标为⎝ ⎛⎭⎪⎫12,y .(1)求tan θ的值;(2)求cos ⎝ ⎛⎭⎪⎫π2-θ+cos (θ-2π)sin θ+cos (π+θ)的值.解:(1)由θ为第四象限角,终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12,y ,得⎝ ⎛⎭⎪⎫122+y 2=1,y <0,解得y =-32,所以tan θ=-3212=- 3.(2)因为tan θ=-3, 所以cos ⎝ ⎛⎭⎪⎫π2-θ+cos (θ-2π)sin θ+cos (π+θ)=sin θ+cos θsin θ-cos θ=tan θ+1tan θ-1=-3+1-3-1=2- 3. [B 级 综合练]11.(多选)已知角θ的终边与坐标轴不重合,式子1-sin 2(π+θ)化简的结果为-cos θ,则( )A .sin θ>0,tan θ>0B .sin θ<0,tan θ>0C .sin θ<0,tan θ<0D .sin θ>0,tan θ<0解析:选BD.1-sin 2(π+θ)=1-sin 2θ=cos 2θ=|cos θ|=-cos θ,所以cos θ<0,角θ的终边落在第二或三象限,所以sin θ>0,tan θ<0或sin θ<0,tan θ>0,故选BD.12.(2020·陕西汉中月考)已知角α为第二象限角,则cos α·1+sin α1-sin α+sin 2α1+1tan 2α=( )A .1B .-1C .0D .2解析:选B.因为角α为第二象限角,所以sin α>0,cos α<0,所以cos α 1+sin α1-sin α=cos α(1+sin α)2cos 2α=cos α·1+sin α|cos α|=-1-sin α,sin 2α1+1tan 2α=sin 2α1+cos 2αsin 2α=sin 2αsin 2α+cos 2αsin 2α=sin 2α1sin 2α=sin 2α⎪⎪⎪⎪⎪⎪1sin α=sin α,所以cos α1+sin α1-sin α+sin 2α1+1tan 2α=-1-sin α+sin α=-1.故选B.13.是否存在α∈⎝ ⎛⎭⎪⎫-π2,π2,β∈()0,π使等式sin(3π-α)=2cos ⎝ ⎛⎭⎪⎫π2-β,3cos(-α)=-2cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.解:假设存在角α,β满足条件. 由已知条件可得⎩⎨⎧sin α=2sin β,①3cos α=2cos β,②由①2+②2,得sin 2α+3cos 2α=2.所以sin 2α=12,所以sin α=±22. 因为α∈⎝ ⎛⎭⎪⎫-π2,π2,所以α=±π4. 当α=π4时,由②式知cos β=32,又β∈(0,π),所以β=π6,此时①式成立;当α=-π4时,由②式知cos β=32,又β∈(0,π),所以β=π6,此时①式不成立,故舍去.所以存在α=π4,β=π6满足条件.14.在△ABC 中,(1)求证:cos 2A +B 2+cos 2 C 2=1;(2)若cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan(C -π)<0,求证:△ABC 为钝角三角形. 证明:(1)在△ABC 中,A +B =π-C ,所以A +B 2=π2-C 2,所以cos A +B 2=cos ⎝ ⎛⎭⎪⎫π2-C 2=sin C 2, 所以cos 2A + B 2+cos 2C 2=1.(2)若cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan(C -π)<0, 所以(-sin A )(-cos B )tan C <0,即sin A cos B tan C <0.因为在△ABC 中,0<A <π,0<B <π,0<C <π且sin A >0,所以⎩⎨⎧cos B <0,tan C >0或⎩⎨⎧cos B >0,tan C <0, 所以B 为钝角或C 为钝角,所以△ABC 为钝角三角形.[C 级 创新练]15.(2020·山东肥城统考)公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现黄金分割比例为5-12≈0.618,这一数值也可以表示为m =2sin 18°.若m 2+n =4,则m n 2cos 227°-1=( ) A .4 B .3 C .2 D .1解析:选C.因为m =2sin 18°,且m 2+n =4,所以n =4-m 2=4-4sin 218°=4(1-sin 218°)=4cos 218°,所以m n 2cos 227°-1=2sin 18°4cos 218°cos 54°=4sin 18°cos 18°sin 36°=2.故选C.16.已知α,β∈(0,2π)且α<β,若关于x 的方程(x +sin α)(x +sin β)+1=0有实数根,则代数式3sin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2-β2-sin (π-α)cos ⎝ ⎛⎭⎪⎫3π2+β=________. 解析:整理方程(x +sin α)(x +sin β)+1=0得x 2+x (sin α+sin β)+sin αsin β+1=0.由题意得Δ=(sin α+sin β)2-4sin αsin β-4≥0,即(sin α-sin β)2≥4①.因为-1≤sin α≤1,-1≤sin β≤1,所以sin α-sin β∈[-2,2],从而(sin α-sin β)2≤4②.由①②得sin α-sin β=±2,所以⎩⎨⎧sin α=1,sin β=-1或⎩⎨⎧sin α=-1,sin β=1.因为α,β∈(0,2π)且α<β,所以α=π2,β=3π2,即⎩⎨⎧sin α=1,sin β=-1. 因此3sin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2-β2-sin (π-α)cos ⎝ ⎛⎭⎪⎫3π2+β=3cos α-sin β2-sin αsin β=12+1=13. 答案:13。
第三节 同角三角比关系和诱导公式
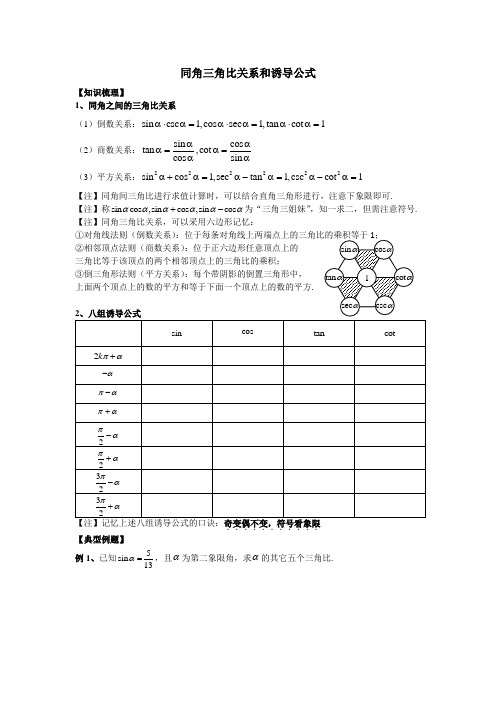
同角三角比关系和诱导公式【知识梳理】1、同角之间的三角比关系(1)倒数关系:sin csc 1,cos sec 1,tan cot 1α⋅α=α⋅α=α⋅α= (2)商数关系:sin cos tan ,cot cos sin ααα=α=αα(3)平方关系:222222sin cos 1,sec tan 1,csc cot 1α+α=α-α=α-α=【注】同角间三角比进行求值计算时,可以结合直角三角形进行,注意下象限即可.【注】称sin cos ,sin cos ,sin cos αααααα+-为“三角三姐妹”,知一求二,但需注意符号. 【注】同角三角比关系,可以采用六边形记忆: ①对角线法则(倒数关系)②相邻顶点法则(商数关系):位于正六边形任意顶点上的 三角比等于该顶点的两个相邻顶点上的三角比的乘积; ③倒三角形法则(平方关系):每个带阴影的倒置三角形中, 上面两个顶点上的数的平方和等于下面一个顶点上的数的平方.【注】记忆上述八组诱导公式的口诀:奇变偶不变,符号看象限...........【典型例题】 例1、已知5sin 13α=,且α为第二象限角,求α的其它五个三角比.【练习1】设)tan 01m α=<<,化简22sin sin cos cos m m αα++α-α.【练习2】化简:33sin (1cot )cos (1tan )x x x x +++.【练习3,2παπ⎛⎫∈ ⎪⎝⎭【练习4=,则角x 的终边在第_______象限. 【练习5】若1+=-,则x 的终边在第_______象限.【练习62sin101sin 10=--_________.【练习7】化简:2662222csc sin cos cot sin cos 11cot 1tan α-α-α-α⎛⎫αα-- ⎪+α+α⎝⎭【练习8例2、若4sin 2cos 23sin 4cos 3x x x x +=-,则tan x =__________.【练习】已知21sin 3sin cos x x x +=,则tan x =__________.例3、已知tan 2α=,求下列各式的值: (1)sin cos cos 2sin αααα-+(2)22sin sin cos 3cos αααα++ (3)22sin sin cos sin 1αααα++(4)2212sin cos sin 2cos x xx x+-(5)3323sin cos 4cos sin cos x xx x x +-例4、关于x 的方程()2tan cot 10x x -α+α+=的一个根是2sin cos αα=______.例5、(2008清华自招)sin cos x x +=x 的取值范围为________.【变式】(2005交大推优)8841sin cos ,0,1282x x x π⎛⎫+=∈ ⎪⎝⎭,则x =________.例6、已知()sin cos tan cot sec csc f x x x x x x x =+++++,求()f x 的最小值.例7、是否存在0,2π⎛⎫α∈ ⎪⎝⎭,使得关于x 的方程24cos 20x x -α+=和24sin 20x x -α-=有一个实数解相等?如果存在,求出α;不存在,请说明理由.例8、化简下列各式(1)()()()()22sin 42cot 25cot 65sin 48α+++ββ-+-α(2)()()()()tan 150cos 210cos660tan 240sin 330-⋅-⋅-⋅-(3)()()()()()()cos 90csc 270tan 180sec 360sin 180cot 90x x x x x x +⋅+⋅--⋅+⋅-(4)sin[(21)]sin[(21)]()sin(2)cos(2)k k k Z k k απαπαπαπ+++--∈--+(5)()4334cos cos 44k kk Z +-π+π∈例9、若3cos 5α=-,则()()cos 2sin 322tan 3cot 2π⎛⎫α-+π-α ⎪⎝⎭=π⎛⎫π+α+α+ ⎪⎝⎭_________.【变式1】若1tan 2α=-,则()72cos cos 52sin cos 22π⎛⎫α--π-α ⎪⎝⎭=ππ⎛⎫⎛⎫+α+α- ⎪ ⎪⎝⎭⎝⎭_________.【变式2】已知33cos()252ππααπ⎛⎫+=-<< ⎪⎝⎭,求tan(),sin(2).παπα--例10、若22tan 2tan 1α=β+,证明:22sin 2sin 1β=α-例11、证明下列恒等式:(1)4222sin sin cos cos 1α+αα+α= (2)222222cos cos sin sin cot cot α-β=αβα-β(3)cos 1sin 1sin cos x xx x+=- (4)1sec tan tan sec 11sec tan tan sec 1x x x x x x x x ++--=---+(5)6622csc cot 13csc cot x x x x -=+(6)tan sin tan sin tan sin tan sin ααα+α=α-ααα(7)1sec tan 1sin 1sec tan cos +α+α+α=+α-αα(8)()2cos sin cos sin 1sin 1cos 1sin cos α-ααα-=+α+α+α+α(9)()()cos 2sec tan sec 2tan 2cos 3tan αα+αα-α=α-α。
同角三角函数与诱导公式
同角三角函数与诱导公式同角三角函数是指在同一个角度下,不同三角函数之间的关系。
常见的同角三角函数有正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
这些函数在数学中起到重要的作用,可以帮助我们求解各种三角函数相关的问题。
在学习同角三角函数时,一个非常重要的概念就是诱导公式。
诱导公式是指根据已知的三角函数值,来求解其他三角函数值的公式。
通过诱导公式,我们可以快速地计算各种三角函数的值,从而简化计算步骤并提高计算效率。
下面我们将详细介绍同角三角函数以及它们之间的关系,以及常见的诱导公式。
1. 正弦函数(sin):在一个直角三角形中,正弦函数定义为对边与斜边的比值。
即sinθ = 对边/斜边。
2. 余弦函数(cos):余弦函数定义为邻边与斜边的比值。
即cosθ = 邻边/斜边。
3. 正切函数(tan):正切函数定义为对边与邻边的比值。
即tanθ = 对边/邻边。
4. 余切函数(cot):余切函数定义为邻边与对边的比值。
即cotθ = 邻边/对边。
5. 正割函数(sec):正割函数定义为斜边与邻边的比值。
即secθ = 斜边/邻边。
6. 余割函数(csc):余割函数定义为斜边与对边的比值。
即cscθ = 斜边/对边。
这些函数之间有着一定的关系,通过这些关系我们可以得到一些重要的诱导公式。
一、正弦函数与余弦函数的关系:根据勾股定理,我们知道对于一个直角三角形,有a² + b² = c²,其中a、b、c分别代表直角边的长度。
根据这个性质,我们可以得到sin²θ + cos²θ = 1,这就是著名的三角恒等式之一根据这个恒等式,我们可以得到以下诱导公式:sin(90° - θ) = cosθcos(90° - θ) = sinθsin(180° - θ) = sinθcos(180° - θ) = -cosθ二、正弦函数与正切函数的关系:根据正弦函数和正切函数的定义,我们可以得到以下关系:tanθ = sinθ/cosθ由此我们可以得到以下诱导公式:tan(θ - 90°) = -cotθtan(θ + 90°) = -cotθ三、余弦函数与正切函数的关系:根据余弦函数和正切函数的定义,我们可以得到以下关系:tanθ = cosθ/sinθ由此我们可以得到以下诱导公式:tan(90° - θ) = cotθtan(90° + θ) = -cotθ四、其他关系:除了上述关系之外,还有一些其他的关系,比如余切函数与正弦函数、正切函数与余切函数之间的关系。
同角三角函数与诱导公式
同角三角函数与诱导公式同角三角函数是指角度相等的两个三角函数值相等的关系。
在三角函数中,正弦函数、余弦函数和正切函数都存在同角关系。
首先,我们来看正弦函数和余弦函数的同角关系。
在一个单位圆上,取一个角度θ,将其对应的弧长作为一个新的线段,分别与x轴、y轴相交。
这样就得到一个角度为θ的直角三角形。
我们定义这个三角形上的三个边与θ的函数关系,分别为sinθ和cosθ,分别表示θ的对边和邻边的比值。
根据三角函数的定义,我们可以得到如下的同角关系:sinθ = y / rcosθ = x / r其中,x表示邻边的长度,y表示对边的长度,r表示斜边即半径的长度。
接下来,我们来看正切函数的同角关系。
正切函数tanθ定义为对边与邻边的比值,即:tanθ = y / x正弦函数和余弦函数之间的同角关系可以通过勾股定理推导得出。
根据勾股定理,我们有:r^2=x^2+y^2将x和y用sinθ和cosθ表示,我们有:r^2 = (r * cosθ)^2 + (r * sinθ)^2整理得:1 = cos^2θ + sin^2θ因此,我们有著名的三角恒等式:sin^2θ + cos^2θ = 1接下来,我们来看一下诱导公式,它是指由一个三角函数的导出另一个三角函数的关系。
我们知道,正弦函数和余弦函数是同角的,因此它们之间存在一种导数的关系。
根据导数的定义,我们有:(sinθ)' = lim(Δθ->0) (sin(θ + Δθ) - sinθ) / Δθ将sin(θ + Δθ)写成两个三角函数的和,有:sin(θ + Δθ) = sinθ cosΔθ + cosθ sinΔθ代入上式,我们得到:(sinθ)' = lim(Δθ->0) (sinθ cosΔθ + cosθ sinΔθ - sinθ) / Δθ整理得:(sinθ)' = lim(Δθ->0) sinθ (cosΔθ - 1) / Δθ +lim(Δθ->0) cosθ sinΔθ / Δθ根据求极限的定义,我们得到:(sinθ)' = cosθ这就是诱导公式,它表明sinθ的导数等于cosθ。
沪教版数学高一下-同角三角比的关系应用ppt下载
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
练习
2.求证: tan2αsin2α=tan2α-sin2α.
证明:因为tan2α-sin2α
sin cos
2
sin2
sin2
1
cos2
沪教版数学高一下-
求证:
cos2 cot2
cos2 cot2
sin2 sin2
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
小结:利用“同角三角比关系” 证明恒等式 掌握方法、了解思路、善用公式。
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
了解思路 一角二名三结构。转化思想方法,利
用三角公式进行化名,化角,使等式两端化 “异”为“同”。
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
沪教版数学高一下-同角三角比的关系 应用pp t下载 【PPT教 研课件 】
应用:利用同角三角比关系式证明三角恒等式
证明方法
(1)综合法: 已知到结论。
左右,右左,左右归一;
(2)作差法:A-B = 0 A = B;
(3)定义法:三角比定义应用; (4)转化命题法: 证明其等价命题; (5)几何法等.
沪教版数学高一下册5.3《同角三角比的关系》课件 (共40张PPT)
三角比关系图:
s in
cos
ta n
1
co t
sec
csc
1)对角线法则——倒数关系:位于每条对角线上两端点上的三角 比的乘积等于中心的1; 2)相邻顶点法则——乘积关系(商数关系):位于正六边形任意 顶点上的三角比等于该顶点的两个相邻顶点上的三角比的乘积; 3)三角形法则——平方关系:每个倒置三角形中,上面两个三角 比或数1的平方和等于下面一个顶点上的三角比或数1的平方。
例题讲解 例1 已知 sin
4 5
,且 是第二象限角,
求cos , cot 的值. tan , 解:因为 sin 2 cos 2 1 ,所以
cos
2
1 sin
2
1 ( )
5
4
2
9 25
,
cos 0
.
又因为α是第二象限角,所以 于是,
(广东高考题)
( B )
B .m 8
D .m 9
1 cos
2
若
[ 0 , 2 ], 且
1 sin
2
sin cos ,
则β的取值范围是 A .[0,0.5π] C.[π,1.5π]
( B.[0.5π,π] D.[1.5π,2π]
B)
同角三角比关系运用:求值
sin 1 cos
2
12 13
1 (
5 13
)
2
12 13
tan
sin cos
(
13 5
)
12 5
如果α是第三象限角,那么
sin 12 13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 12
②
设 sin 5 k,co s 1 2 k代入①式得:k 1
因此
s
i
n
cos
5 13 12
或
s
in
cos
5 13
12
解毕
13
1 3
13
课堂练习
1.已知 sin 1 ,且 是第三象限角,
3
求其余三角比.
2.已知 cot2,求 sin,cos,tan.
3.求证下列三角恒等式:
m2 1
m2 1
例3.已知 tan()3,求下列各式的值.
当角 使得等式两边都有意义时,上面
的等式称为三角恒等式.
例1.已知 c o s 4 ,且 是第四象限角,求其余 5
三角比.
解: sin2cos21且 sin0
sin1cos2 3
5
tan sin 3 cos 4
sec5,csc5,cot4 解毕
4
3
3
例1.已知 c o s 4 ,且 是第四象限角,求其余 5
当 k 为奇数时, k 与 终边关于原点对称:
s i n ( k ) s i n , c o s ( k ) c o s
综上:sin ( k ) ( 1 )ksin ,k Z
c o s( k ) ( 1 )kc o s,k Z
思考 tan(k)?
第五章 三角比
5.3.2 同角三角比的关系和诱导公式
一、角 与 的三角函数值的关系
角 与 终边关于原点对称,
第III组诱导公式
sin()sin
y
T
1P
cos()cos
M' O MA x
tan() tan
P'
作用:转化为锐角三角比
二、角 与 的三角函数值的关系
角 与 终边关于y 轴对称,
第IV组诱导公式
y
T
sin()sin
P'1 P
(3)
cos(2)cot()tan() sin()cot(3)
解:
(1)原式=
cossin sin(cos)
1
(2)原式= stain n ctaons csoisn1
例3.化简:
cos(180)sin(720)
(1) sin(180)cos(180)
(2) tsa in n(( ))tc ao ns((2 ))cso is n ((2 ))
42
cos( )
4
(3) tan(1560)tan1560 tan(4360120)
tan120 tan(18060) tan60 3
例2.利用诱导公式,化简求值:
(1) s in 1 1 sin(4 ) s i n 3
3
3
32
(2) cos225 cos(18045)cos45 2 2
cos2sin2 cos2sin2
1
例2.已知 tanm,求 cos,sin的值.
解:
sin mcos sin2 cos2 1
cos2
1 m2 1
当 的终边在第一、四象限或 x 正半轴时,
cos 1 ,sin m
m2 1
m2 1
当 的终边在第二、三象限或 x 负半轴时,
cos 1 ,sin m 解毕
第五章 三角比
5.2.3 任意角的三角比
5.3.1 同角三角比的关系和诱导公式
一、同角三角比的关系
y
在单位圆中,由三角比的定义
P1
及勾股定理可得:
sin2cos21
A
MO
x
tan sin (k,kZ)
T
cos
2
s i n c s c 1 , c o s s e c 1 , t a n c o t 1
5.3.3 同角三角比的关系和诱导公式
例1.化简:
(1) 1sin2110 cos2110 | cos110 | cos70
(2) csc2 80 1
1 sin2 80
1
cot2 80 cot80
(3) 2 c o s 2 1 1 2 sin 2
2cos2(sin2cos2) (sin2cos2)2sin2
三角比.
解法二:利用余弦线可知 的终边经过点( 4 , 3 )
55
即 x4, y3,r 1
y
5
5
1
由三角比的定义可知:
sin3,tan3
5
4
MA
O
x
PT
sec5,csc5,cot4 解毕
4
3
3
例2.已知tan 5 ,求 sin,cos
12
解:sin 2 cos 2 1 ①
sin cos
(1) cosx 1sinx (2) 1tan2sec2
1sinx cosx
课堂练习答案
1. cos2 2,tan 2
3
4
csc3,sec32,cot22
4
2. tan 1
2
当 是第二象限角时,sin 5,cos2 5
5
5
当 是第四象限角时,sin 5,cos2 5
5
5
课堂练习答案
3. 证:(1) cosx1sinxcos2x(1sin2x) 1sinx cosx (1sinx)cosx
cos()cos
tan()tan
M 'O M A x
作用:转化为锐角三角比
T'
例1.利用诱导公式,把下列三角比化为锐角三角比 后求值:
(1)s in 7 sin( ) s i n 1
6
6
62
(2) c o s 1 1 cos(2 3 ) c o s 3
4
4
4
cos 2
sin2 xcos2 x10 cosx 1sinx
(1sinx)cosx
1sinx cosx
(2) 1tan21c so in s2 2 sin2c o s2c os2
1 sec2 证毕 cos2
注意证明方法的选取及书写过程的规范性.
第五章 三角比
5.3.1 同角三角比的关系和诱导公式
5.3.2 同角三角比的关系和诱导公式
(3) tan(16 ) tan(16 ) tan(5 )
3
3
3
tan( ) ta n 3
33总结把任意角源自角比转化为锐角三角比的步骤例3.化简:
cos(180)sin(720)
(1) sin(180)cos(180)
(2) tsa in n(( ))tc ao ns((2 ))cso is n ((2 ))
(3)
cos(2)cot()tan() sin()cot(3)
coscot(tan) 解: (3)原式= sin(cot)
cos tan 1 解毕 sin
(选用)例4. 已知 k Z
求 sin ( k ),c o s( k )的值.
解:当 k 为偶数时, k 与 终边重合:
s i n ( k ) s i n ,c o s ( k ) c o s
