四川省绵阳南山中学2021届高三上学期10月月考试题 数学(理) Word版含答案
2021年高三上学期10月月考试题 数学(理) 含答案

2021年高三上学期10月月考试题 数学(理) 含答案(满分160分,考试时间120分钟)一、填空题:(本大题共14小题,每小题5分,共70分.)1. 已知集合M ={x |x <1},N ={x |lg(2x +1)>0},则M ∩N = .(0,1)2. 复数z =a +i 1-i为纯虚数,则实数a 的值为 .13. 不等式|x +1|·(2x ―1)≥0的解集为 . {x |x =―1或x ≥12}4. 函数f (x )=13x -1+a (x ≠0),则“f (1)=1”是“函数f (x )为奇函数”的条件(用“充分不必要”,“必要不充分”“充要”“既非充分又非必要”填写).5. 充要6. m 为任意实数时,直线(m -1)x +(2m -1)y =m -5必过定点_________.(9,-4)7. 向量a =(1,2)、b =(-3,2),若(k a +b )∥(a -3b ),则实数k =_________. 8. 由题意知,a 与b 不共线,故k ∶1=1∶(-3),∴k =-139. 关于x 的方程cos 2x +4sin x -a =0有解,则实数a 的取值范围是 . 10. [-4,4]11. 已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值是________.412. 解:x +2y =8-x ·(2y )≥8-⎝⎛⎭⎫x +2y 22,整理得(x +2y )2+4(x +2y )-32≥0,即(x +2y -4) (x+2y +8)≥0.又x +2y >0,∴x +2y ≥4.13. 已知点x ,y 满足不等式组⎩⎪⎨⎪⎧x ≥0y ≥02x +y ≤2,若ax +y ≤3恒成立,则实数a 的取值范围是__________.(-∞,3]14. 已知△ABC 是等边三角形,有一点D 满足→AB +12·→AC =→AD ,且|→CD |=3,那么→DA ·→DC= . 315. 若函数f (x )=mx 2+ln x -2x 在定义域内是增函数,则实数m 的取值范围是_________.[12,+∞)16. 解:f '(x )=2mx +1x -2≥0对x >0恒成立,2mx 2+1-2x ≥0∴2m ≥2x -1x 2=-1x 2+2x,令t =1x >0∴2m ≥-t 2+2t ,∵()-t 2+2t max =1,∴2m ≥1,∴m ≥12. 17. 已知函数f (x )=⎩⎨⎧-x 2+ax (x ≤1)2ax -5 (x >1),若x 1, x 2∈R ,x 1≠x 2,使得f (x 1)=f (x 2)成立,则实数a 的取值范围是 . (-∞,4)18. 将y =sin2x 的图像向右平移φ单位(φ>0),使得平移后的图像仍过点⎝⎛⎭⎫π3,32,则φ的最小值为_______.19. 解法一:点代入y =sin(2x -2φ)∴sin(2π3-2φ)=32∴-2φ+2π3=2k π+π3或-2φ+2π3=2k π+2π3∴φ=-k π+π6或φ=-k π∴φ的最小值为π6.20. 解法二:结合函数y =sin2x 的图形.21. 已知函数f (x )满足f (x )=f (1x ),当x ∈[1,3]时,f (x )=ln x ,若在区间[13,3]内,函数g (x )=f(x )-ax 与x 轴有三个不同的交点,则实数a 的取值范围是 . 22. ⎣⎡ln33,⎭⎫1e二、解答题(本大题共6小题,共90分解答应写出文字说明、证明过程或演算步骤) 23. (本小题满分14分) 24. 已知直线和.25. 问:m 为何值时,有:(1);(2).解:(1)∵,∴,得或;当m =4时,l 1:6x +7y -5=0,l 2:6x +7y =5,即l 1与l 2重合,故舍去. 当时,即 ∴当时,. ………7分 (2)由得或; ∴当或时,. ………14分 26. (本小题满分14分)27. 已知函数f (x )=sin(ωx +φ) (ω>0,0<φ<π),其图像经过点M ⎝⎛⎭⎫π3,12,且与x 轴两个相邻的交点的距离为π. 28. (1)求f (x )的解析式;29. (2)在△ABC 中,a =13,f (A )=35,f (B )=513,求△ABC 的面积.解:(1)依题意知,T =2π,∴ω=1,∴f (x )=sin(x +φ)∵f (π3)=sin(π3+φ)=12,且0<φ<π ∴π3<π3+φ<4π3 ∴π3+φ=5π6 即φ=π2∴f (x )=sin ⎝⎛⎭⎫x +π2=cos x . ………6分(2)∵f (A )=cos A =35,f (B )=cos B =513, ∴A ,B ∈(0,π2)∴sin A =45,sin B =1213 ………8分∴sin C =sin(A +B )=sin A cos B +cos A sin B =5665………10分 ∵在△ABC 中a sin A =bsin B ∴b =15. ………12分∴S △ABC =12ab sin C =12×13×15×5665=84. ………14分30. (本小题满分15分)31. 已知|a |=3,|b |=2,a 与b 的夹角为120º,当k 为何值时, 32. (1)k a -b 与a -k b 垂直;33. (2)|k a -2b |取得最小值?并求出最小值.解:(1)∵k a -b 与a -k b 垂直,∴(k a -b )·(a -k b )=0.∴k a 2-k 2a ·b -b ·a +k b 2=0.∴9k -(k 2+1)×3×2·cos120°+4k =0.∴3k 2+13k +3=0.∴k =-13±1336. ………7分(2)∵|k a -2b |2=k 2a 2-4k a ·b +4b 2=9k 2-4k ×3×2·cos120°+4×4 =9k 2+12k +16=(3k +2)2+12.∴当k =-23时,|k a -2b |取得最小值为23. ………15分34. (本小题满分15分)35. 如图①,一条宽为1km 的两平行河岸有村庄A 和供电站C ,村庄B 与A 、C 的直线距离都是2km ,BC 与河岸垂直,垂足为D .现要修建电缆,从供电站C 向村庄A 、B 供电.修建地下电缆、水下电缆的费用分别是2万元/km 、4万元/km .36. (1)已知村庄A 与B 原来铺设有旧电缆,但旧电缆需要改造,改造费用是0.5万元/km .现决定利用此段旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.37. (2)如图②,点E 在线段AD 上,且铺设电缆的线路为CE 、EA 、EB .若∠DCE =θ(0≤θ≤ π3),试用θ表示出总施工费用y (万元)的解析式,并求y 的最小值.解:(1)由已知可得△ABC 为等边三角形,∵AD ⊥CD ,∴水下电缆的最短线路为CD . 过D 作DE ⊥AB 于E ,可知地下电缆的最短线路为DE 、AB . ………3分又CD =1,DE =32,AB =2,故该方案的总费用为 1×4+32×2+2×0.5=5+ 3 (万元). …………6分 (2)∵∠DCE =θ (0≤θ≤ π3)∴CE =EB =1cos θ,ED =tan θ,AE =3-tan θ.则y =1cos θ×4+1cos θ×2+(3-tan θ)×2=2×3-sin θcos θ+2 3 ……9分令f (θ)=3-sin θcos θ (0≤θ≤ π3)则f '(θ)=-cos 2θ-(3-sin θ)(-sin θ)cos 2θ=3sin θ-1cos 2θ,……11分∵0≤θ≤ π 3,∴0≤sin θ≤32,记sin θ0=13,θ0∈(0, π 3)当0≤θ<θ0时,0≤sin θ<13,∴f '(θ)<0当θ0<θ≤ π 3时,13<sin θ≤32,∴f '(θ)>0∴f (θ)在[0,θ0)上单调递减,在(θ0, π3]上单调递增.……13分∴f (θ)min =f (θ0)=3-13223=22,从而y min =42+23,此时ED =tan θ0=24,答:施工总费用的最小值为(42+23)万元,其中ED =24. ……15分38. (本小题满分16分)39. 已知a 为实数,函数f (x )=a ·ln x +x 2-4x .40. (1)是否存在实数a ,使得f (x )在x =1处取极值?证明你的结论; 41. (2)若函数f (x )在[2, 3]上存在单调递增区间,求实数a 的取值范围; 42. (3)设g (x )=2a ln x +x 2-5x -1+ax,若存在x 0∈[1, e],使得f (x 0)<g (x 0)成立,求实数a 的取值范围.解:(1)函数f (x )定义域为(0,+∞),f '(x )=a x +2x -4=2x 2-4x +a x假设存在实数a ,使f (x )在x =1处取极值,则f '(1)=0,∴a =2, ……2分此时,f '(x )=2(x -1)2x,∴当0<x <1时,f '(x )>0,f (x )递增;当x >1时,f '(x )>0,f (x )递增. ∴x =1不是f (x )的极值点.故不存在实数a ,使得f (x )在x =1处取极值. ………4分(2)f '(x )=2x 2-4x +a x =2(x -1)2+a -2x,①当a ≥2时,∴f '(x )≥0,∴f (x )在(0,+∞)上递增,成立; ………6分②当a <2时,令f '(x )>0,则x >1+1-a 2或x <1-1-a2,∴f (x )在(1+1-a2,+∞)上递增,∵f (x )在[2, 3]上存在单调递增区间,∴1+1-a2<3,解得:6<a <2 综上,a >-6. ………10分(3)在[1,e]上存在一点x 0,使得成立,即在[1,e]上存在一点,使得,即函数在[1,e]上的最小值小于零.有22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x +--++-+'=--==①当,即时, 在上单调递减, 所以的最小值为,由可得,因为,所以; ………12分 ②当,即时,在上单调递增,所以最小值为,由可得; ………14分 ③当,即时,可得最小值为, 因为,所以,,故 此时不存在使成立.综上可得所求的范围是:或. ………16分解法二:由题意得,存在x ∈[1, e],使得a (ln x -1x )>x +1x成立.令m (x )=ln x -1x ,∵m (x )在[1, e]上单调递增,且m (1)=-1<0, m (e)=1-1e >0故存在x 1∈(1,e),使得x ∈[1, x 1)时,m (x )<0;x ∈(x 1, e]时,m (x )>0 故存在x ∈[1, x 1)时,使得a <x 2+1x ln x -1成立,·························(☆)或存在x ∈(x 1, e]时,使得a >x 2+1x ln x -1成立,·························(☆☆) ………12分记函数F (x )=x 2+1x ln x -1,F '(x )=(x 2-1)ln x -(x +1)2(x ln x -1)2当1<x ≤e 时,(x 2-1)ln x -(x +1)2=(x 2-1)·⎝⎛⎭⎪⎫ln x -x +1x -1∵G (x )=ln x -x +1x -1=ln x -2x -1-1递增,且G (e)=-2e -1<0∴当1<x ≤e 时,(x 2-1)ln x -(x +1)2<0,即F '(x )<0∴F (x )在[1, x 1)上单调递减,在(x 1, e]上也是单调递减, ………14分 ∴由条件(☆)得:a <F (x )max =F (1)=-2 由条件(☆☆)得:a >F (x )min =F (e)=e 2+1e -1综上可得,a >e 2+1e -1或a <-2. ………16分43. (本小题满分16分)44. 已知常数a >0,函数f (x )=13ax 3-4(1-a )x ,g (x )=ln(ax +1)-2x x +2.45. (1)讨论f (x )在(0,+∞)上的单调性;46. (2)若f (x )在⎝⎛⎭⎫-1a ,+∞上存在两个极值点x 1、x 2,且g (x 1)+g (x 2)>0,求实数a 的取值范围.解:(1)由题意可知:f '(x )=ax 2-4(1-a )当a ≥1时,f '(x )>0,此时,f (x )在区间(0,+∞)上单调递增. 当0<a <1时,由f '(x )=0得:x 1=2a (1-a )a (x 2=-2a (1-a )a<0舍去) 当x ∈(0, x 1)时,f '(x )<0;当x ∈(x 1,+∞)时,f '(x )>0.故f (x )在区间(0, x 1)上单调递减,在区间(x 1,+∞)上单调递增. 综上所述,当a ≥1时,f (x )在区间(0,+∞)上单调递增; 当0<a <1时,f (x )在区间(0,2a (1-a )a )上单调递减,在区间(2a (1-a )a,+∞)上单调递增. ………6分(2)由(1)知,当a ≥1时,f '(x )≥0,此时f (x )不存在极值点, 因而要使得f (x )有两个极值点,必有0<a <1. 又∵f (x )的极值点只可能是x 1=2a (1-a )a 和x 2=-2a (1-a )a, 由g (x )的定义可知,x >-1a 且x ≠-2,∴-2a (1-a )a >-1a 且2a (1-a )a x ≠2解得:0<a <12或12<a <1 【定义域在这里很重要】 ………8分此时,由(*)式易知,x 1, x 2分别是f (x )的极小值点和极大值点. 而g (x 1)+g (x 2)=ln(ax 1+1)(ax 2+1)-2x 1x 1+2-2x 2x 2+2=ln[a 2x 1x 2+a (x 1+x 2)+1]-4x 1x 2+4(x 1+x 2)x 1x 2+2(x 1+x 2)+4=ln(2a -1)2-4(a -1)2a -1=ln(2a -1)2-22a -1-2………10分令x =2a -1,由0<a <12且a ≠12知,当0<a <12时,-1<x <0;当12<a <1时,0<x <1 ,记h (x )=ln x 2+2x-2.①当-1<x <0时,h (x )=2ln(-x )+2x-2,设t =-x ∈(0,1), (t )=2ln t -2t -2单调递增 ∴ (t )< (1)=-4<0∴h (x )<-4<0,故当0<a <12时,g (x 1)+g (x 2)<0,不合题意,舍去.②当0<x <1时,h (x )=2ln x +2x -2,∴h '(x )=2x -2x 2=2x -2x2<0,∴h (x )在(0,1)上单调递减,∴h (x )>h (1)=0,故当12<a <1时,g (x 1)+g (x 2)>0.综上,a 的取值范围为⎝⎛⎭⎫12,1.………16分附加题(考试时间:30分钟 总分:40分)xx.1021.(选修4—2:矩阵与变换)(本小题满分10分) 已知矩阵(1)求;(2)满足AX =二阶矩阵X解:(1) ………5分(2) ………10分22.(选修4—4:坐标系与参数方程)(本小题满分10分)在极坐标系中,曲线C 的极坐标方程为ρ=2cos θ+2sin θ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l 的参数方程为⎩⎨⎧x =1+t ,y =3t(t 为参数),求直线l 被曲线C 所截得的弦长.解:曲线C 的直角坐标方程为x 2+y 2-2x -2y =0,圆心为(1,1),半径为2,(3分)直线的直角坐标方程为3x -y -3=0,(5分)所以圆心到直线的距离为d =||3-1-32=12,(8分)所以弦长=22-14=7.(10分)23.(本小题满分10分)如图,在三棱柱ABC -A 1B 1C 1中,AB =3,AA 1=AC =4,AA 1⊥平面ABC ; AB ⊥AC , (1)求二面角A 1-BC 1-B 1的余弦值;(2)在线段BC 1存在点D ,使得AD ⊥A 1B ,求BDBC 1的值.解: (1)如图,以A 为原点建立空间直角坐标系A -, 则B (0,3,0),A 1(0,0,4),B 1(0,3,4),C 1(4,0,4),设平面A 1BC 1的法向量为, 则,即,令,则,,所以.同理可得,平面BB 1C 1的法向量为, 所以.由题知二面角A 1-BC 1-B 1为锐角,所以二面角A 1-BC 1-B 1的余弦值为. ………5分(2)设D 是直线BC 1上一点,且. 所以.解得,,. 所以.由,即.解得.因为,所以在线段BC 1上存在点D , 使得AD ⊥A 1B .此时,. ………10分1C 1A 1B 1C ABC24.(本小题满分10分)(1)证明:①;②(其中);(2)某个比赛的决赛在甲、乙两名运动员之间进行,比赛共设局,每局比赛甲获胜的概率均为,首先赢满局者获胜(). ①若,求甲获胜的概率;②证明:总局数越多,甲获胜的可能性越大(即甲获胜的概率越大). 解:(1)①()()()()()()()()()111!1!!!()!1!(1)!1!()!1!1!11!r r n nr n n r n r n n C C r n r r n r r n r n C r n r +++++-⎡⎤⎣⎦+=+=-+--+-+==++-+……2分②由① ……3分(2)①若,甲获胜的概率()10156)1()1(2322242233+-=-+-+=p p p p p pC p p pC p P ……5分②证明:设乙每一局获胜的概率为,则. 记在甲最终获胜的概率为,则()nn nn n nn n nn n n n n n n n n n n qC q Cq Cpqp pC q p pC q p pC p P 2221122211...1...++++=++++=++++++所以,()()()()()[]()()[()][][]()()()0122)()()(...)1()1()11(......1...1...11...1...1 (112111212111212211122211212211122211212211211221)3221211212231321211222131222211112221312222111122213122222111<-=-=-=+--=+--+-+++-++-+-=+++++++++-++++=++++--++++=++++-++++=-++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++q C q p C qC q p C qC q p C qC C q p C q C C q C C C q C C q C C q p qC q C q C q q C q C q C qC q C q C p q C q C q C q qC q C q C p q C q C q C p q C q C q C p P P n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n nn n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n所以即总局数越多,甲获胜的可能性越大(即甲获胜的概率越大). ………10分 26545 67B1 枱Ay21102 526E 剮40664 9ED8 默33073 8131 脱 35752 8BA8 讨25121 6221 戡24143 5E4F 幏34944 8880 袀34497 86C1 蛁。
2021年高三10月月考数学理试题word版

2021年高三10月月考数学理试题word版一、选择题(40分)1、设{-1,1,。
3},则使函数的定义域是R,且为奇函数的所有的值是()A、1,3B、-1,1C、-1,3D、-1,1,32、函数的定义域是()A、{x|x<0}B、{x|x>0} A、{x|x<0且x≠-1} A、{x|x≠-0且x ≠-1}3、若m>0且m≠1,n>0,则“<0”是“(m-1)(n-1)<0”的()A、充要条件B、充分不必要条件C、必要不充分条件D、既不充分也不必要条件4、若方程2-x-1=0在(0,1)内恰有一解,则a的取值范围是()A、a<-1A、a>1 C、-1<a<1 D、0≤a<15、已知集合P={(x,y)|y=k},Q={(x,y)|y=+1},且Q=,那么k的取值范围是A、(-,1)B、(-,1]C、(1,+)D、(-,+)6、若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则a的取值范围是()A、a=-1或3B、a=-1C、a>3或a<-1D、-1<a37、已知函数f(x)满足f(x)=f(-x),且当x时,f(x)=x+sinx,则A、f(1)<f(2)<f(3)B、f(2)<f(3)<f(1)C、f(3)<f(2)<f(1)D、f(3)<f(1)<f(2)8、如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+的零点所在的区间是()A、()B、(,1)C、(1,2)D、(2,3)第II卷(非选择题,110分)二、填空题(30分)9、命题“若x2<1,则-1<x<1”的逆否命题是___________10、若函数f(x)=x2+ax+b的两个零点是-2和3,则不等式af(-2x)>0的解集是_____11、函数f(x)=x3-15x2-33x+6的极大值为____12、若函数f(a)=,则=___13、已知集合A={x|2},B=(),若AB,则实数a的取值范围是(c,+),其中c=____14、甲:函数f(x)是奇函数;乙:函数f(x)在定义域上是增函数,对于函数能使甲、乙均为真命题的所有函数的序号是____三、解答题(80分)15、(本小题满分12分)已知>3,且,命题p:指数函数f(x)=(2a-6)x在R上是单调函数,命题q:关于x的方程:x2-3ax+2a2+1=0的两个实根均大于3,若p或q为真,p且q为假,求实数a的取值范围。
2021年高三上学期10月月考数学(理)试题 含答案

xx学年第一学期10月月考高三年级数学试题(理科))李翠清本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(每小题5分,共60分.下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)1.已知集合M={x|﹣2<x<3},N={x|2x+1≥1},则M∩N等于()A.(﹣2,﹣1] B.(﹣2,1] C.[1,3)D.[﹣1,3)2.=()A.i B.-i C.1+i D.1﹣i3.设是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则且;④若,则,其中真题的个数是()A.0 B.1 C.2 D.34.命题p:;命题q:在中,若sinA>sinB,则A>B。
下列命题为真命题的是()A.pB.C.D.5.若的展开式中项系数为20,则的最小值为()A. 2B. 3C. 4D. 16.已知=则的值为()A.2B. 3C. 4D.167.一个算法的程序框图如图所示,若该程序输出的结果是,则判断框中应填入的结果是()A. B. C. D.8.函数y=xcosx+sinx的图象大致为()A.B.C.D.9.若等比数列的各项均为正数,且=2(e为自然对数的底数),则= ()A. 20B.30C.40D.5010. 已知变量满足约束条件若目标函数 (其中)仅在点(1,1)处取得最大值,则的取值范围为 ( )A. B. C. D.11.设直线:,圆,若在圆上存在两点,在直线上存在一点,使得,则的取值范围是( )A.B.C.D.12.右图为某四面体的三视图,其正视图、侧视图、俯视图均为边长为4的正方形,则该四面体的内切球的半径为()A. B. C. D.2021年高三上学期10月月考数学(理)试题含答案二、填空题(每题5分,共20分.把答案填在答题纸的横线........上)13.已知双曲线的一条渐近线方程为,则实数m的值为.14. 设向量ab若是实数,且,则的最小值为.15.已知,α是第四象限角,且tan(α+β)=1,则tanβ的值为.16.对于函数给出定义:设是函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”. 某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数,请你根据上面探究结果,计算1232016()()()()2017201720172017f f f f= .三、解答题(本大题共6个题,共70分.解答应写出文字说明、证明过程或演算步骤,写在答题纸的相应位置..........)17.(本小题满分10分)8个篮球队中有3个强队,任意将这8个队分成两组(每组4个队)进行比赛(1)求至少有两个强队分在组中的概率;(2)用表示分在组中强队的个数,求的分布列和数学期望。
2021年高三上学期10月月考理数试题含答案

2021年高三上学期10月月考理数试题含答案一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,集合,,则集合( )A .B .C .D .2.若,则下列不等式中不成立的是( )A .B .C .D .3.函数的零点有( )A .0个B .1个C .2个D .3个4.设,,,则的大小关系是( )A .B .C .D .5.下面几种推理过程是演绎推理的是( )A .两条直线平行,同旁内角互补,如果和是两条平行直线的同旁内角,则+=B .由平面三角形的性质,推测空间四面体的性质C .某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人D .在数列中,,,计算,由此推测通项6.已知函数的导函数为,且满足,则( )A .B .C .D .7.函数的定义域和值域都是,则( )A .B .C .D .8.函数满足,那么函数的图象大致为( )9.设函数是定义在上周期为3的奇函数,若,,则有( )A .且B .或C .D .10.已知,是互不相同的正数,且,则的取值范围是( )A .B .C .D .Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请把答案填在题中横线上11..12.设实数满足则的最大值为.13.观察下列式子:,,,…,根据上述规律,第个不等式应该为.14.在等式“”的两个括号内各填入一个正整数,使它们的和最小,则填入的两个数依次为、.15.下列四个命题:①命题“若,则”的否命题是“若,则”;②若命题,则;③若命题“”与命题“或”都是真命题,则命题一定是真命题;④命题“若,则”是真命题.其中正确命题的序号是.(把所有正确的命题序号都填上)三、解答题:本大题有6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤16.(本题满分12分)已知集合,,.(Ⅰ)求集合;(Ⅱ)若,求实数的取值范围.17.(本题满分12分)设命题:函数在上是增函数,命题:,如果是假命题,是真命题,求的取值范围.18.(本题满分12分)已知函数.(Ⅰ)若函数的图象在处的切线方程为求的值;(Ⅱ)若函数在上是增函数,求实数的最大值.19.(本题满分12分)已知二次函数.(Ⅰ)若且函数的值域为求函数的解析式;(Ⅱ)若且函数在上有两个零点,求的取值范围.20.(本题满分13分)某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度(单位:毫克/立方米)随着时间(单位:天)变化的函数关系式近似为,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒个单位的去污剂,要使接下来的4天中能够持续有效去污,试求的最小值(精确到,参考数据:取).21.(本题满分14分)设,函数.(Ⅰ)求的单调递增区间;(Ⅱ)设问是否存在极值,若存在,请求出极值;若不存在,请说明理由;(Ⅲ)设是函数图象上任意不同的两点,线段的中点为直线的斜率为.证明:.高三数学试题(理科)参考答案及评分标准一、选择题:ABADA BCCBD二、填空题:11.8 12.4 13.14.4,12 15.②③三、解答题16.解:(Ⅰ)由,得.…………………………2分由不等式得所以.…………………………4分所以.…………………………6分(Ⅱ)因为,所以,…………………………8分所以…………………………9分解得.…………………………11分所以,实数的取值范围是.…………………………12分17.解:∵函数在上是增函数,∴,…………………………2分由得方程有解,………………4分∴,解得或…………………………5分∵是假命题,是真命题,∴命题一真一假,…………………………6分①若真假,则∴;…………………………8分②若假真,则解得,…………………………10分综上可得的取值范围为…………………………12分18.解:(Ⅰ)∵∴.于是由题知解得.…………………………2分∴.∴,于是,解得.…………………………4分(Ⅱ)由题意即恒成立,∴恒成立;……………6分减函数极小值增函数∴…………………………11分∴.∴的最大值为…………………………12分19.解:(Ⅰ)因为所以…………………………2分因为函数的值域为所以方程有两个相等的实数根,…………………………3分即有等根,故.…………………………5分所以;…………………6分(Ⅱ)解法一:因为在上有两个零点,且,所以有……8分(图正确,答案错误,扣2分)通过线性规划可得.……12分(若答案为,则扣1分)解法二:设的两个零点分别为,所以;…………8分不妨设,因为,且,所以,…………………………10分因为,所以.…………………………12分20.解:(Ⅰ)因为一次喷洒4个单位的去污剂,所以空气中释放的浓度为…………………………2分当时,令,解得,所以.当时,令,解得,所以.于是得,…………………………5分即一次投放4个单位的去污剂,有效去污时间可达8天.…………………………6分(Ⅱ)设从第一次喷洒起,经天,浓度.…………………………8分因为,而,所以,…………………………10分故当且仅当时,有最小值为.令,解得,…………………………12分所以的最小值为.…………………………13分21.解:在区间上,.…………………………1分(Ⅰ) .(1)当时,∵,∴恒成立,的单调增区间为;………2分(2)当时,令,即,得∴的单调增区间为…………………………3分综上所述:当时,的单调增区间为;当时,的单调增区间为…………………………4分(Ⅱ)得…………………………5分当时,恒有∴在上为单调增函数,故在上无极值;…………………………6分当时,令,得单调递增,单调递减.∴无极小值…………………………8分综上所述:时,无极值时,有极大值无极小值.…………………………9分29922 74E2 瓢25903 652F 支{28051 6D93 涓>31261 7A1D 稝11[~29029 7165 煥p31708 7BDC 篜21076 5254 剔20099 4E83 亃。
高三上学期10月月考数学(理)试题Word版含答案
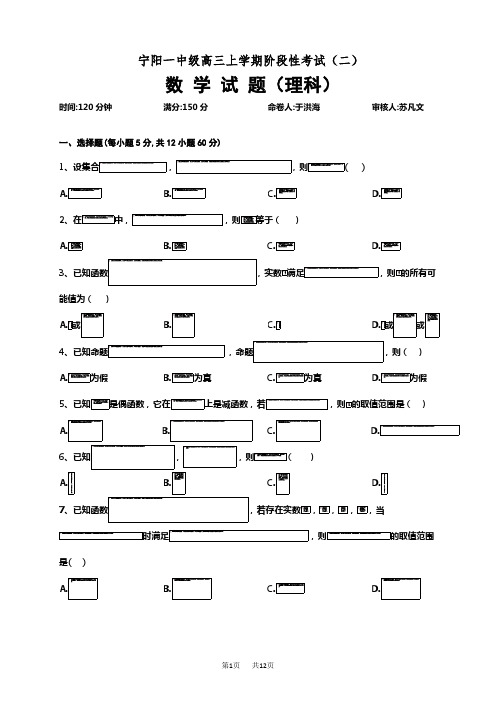
时间:120 分钟宁阳一中级高三上学期阶段性考试(二)数 学 试 题(理科)满分:150 分命卷人:于洪海审核人:苏凡文一、选择题(每小题 5 分,共 12 小题 60 分)1、设集合,,则()A.B.C.D.2、在中,,则 等于( )A.B.C.D.3、已知函数,实数 满足,则 的所有可能值为( )A. 或B.C.D. 或或4、已知命题,命题,则( )A.为假B.为真C.为真D.为假5、已知 是偶函数,它在上是减函数,若,则 的取值范围是( )A.B.C.D.6、已知,,则()A.B.C.D.7、已知函数,若存在实数 , , , ,当时满足,则的取值范围是( )A.B.C.D.第1页 共12页8、函数 A.的图象大致是( ) B.C.D.9、使得函数有零点的一个区间是( )A.B.C.D.10、定义在 上的函数 的导函数为,已知是偶函数,且.若,且,则与的大小关系是( )A.B.C.D.不确定11、已知是定义在 上的减函数,那么实数 的取值范围是()A.B.C.D.12、已知函数的部分图像如图所示,则的图象可由的图象( )第2页 共12页A.向右平移 个长度单位 B.向左平移 个长度单位 C.向右平移 个长度单位 D.向左平移 个长度单位二、填空题(每小题 5 分,共 4 小题 20 分)13、已知向量,满足,,则__________.14、已知函数的图象向左平移 个单位后与函数的图象重合,则正数 的最小值为__________.15、已知 为锐角,,则__________.16、若函数在上有最小值,则实数 的取值范围为__________.三、解答题(第 17 题 10 分,第 18 题 12 分,第 19 题 12 分,第 20 题 12 分,第 21 题 12 分,第 22 题 12 分,共 6 小题 70 分)17、已知命题,且,命题,且.(Ⅰ)若,求实数 的值;(Ⅱ)若 是 的充分条件,求实数 的取值范围.18、已知向量,,函数,且 图象上一个最高点的坐标为,与之相邻的一个最低点的坐标为.(1)求 的解析式;(2)在中,是角所对的边,且满足,求角 的大小以及的取值范围.第3页 共12页19、设函数(1)求函数的单调区间;(2)若关于 的方程(3)当时,证明:是自然对数的底数)在区间上恰有两相异实根,求 的取值范围;20、设函数,其中.(Ⅰ)当时,求曲线在原点处的切线方程;(Ⅱ)试讨论函数 极值点的个数;21、已知函数(其中(Ⅰ)求函数 的单调区间;(Ⅱ)若函数 与函数值范围.且),函数 在点处的切线过点 .的图像在 有且只有一个交点,求实数 的取22、已知函数.(1)判断函数 的奇偶性,并证明;(2)若对于任意,不等式值范围.恒成立,求正实数 的取宁阳一中 2016 级高三上学期阶段性考试(二)第4页 共12页数学理科答案解析第 1 题答案 D 解析由已知得,故.第 2 题答案 D 因为,所以,所以,所以.第 3 题答案 A ∵,∴,∴,当时,,,.当 时,,∴ 或.第 4 题答案 C 当 时,,即命题 为真命题,当 时,,即命题 为假命题,则 为真, 为假, 为假, 为真,则为真;故选 C.第 5 题答案 C 因为 是偶函数,它在上是减函数,则,所以 的取值范围是,故选 C.第 6 题答案 D 由①, 所以②由①②可得③由①③得,.第 7 题答案 D 如下图所示,设从左往右的零点依次为,则,又∵,∴,,故选 D第 8 题答案 B 因为,易知,当时,第5页 共12页,当时,,排除 A、C;又易知当时,,此时当时,,此时 单调递减.第 9 题答案, 单调递增,∴,由零点存在定理,可知选 C第 10 题答案 C由可知,当 时,函数递减.当增.因为函数是偶函数,所以,对称轴为 .所以若,则.若,此时由,即,选 C.第 11 题答案 C 依题意,有且,解得,当 时,,所以.时,函数递,即函数的,则必有,则,综上,又当 ,解得时, .故第 12 题答案 A 根据题中所给的图像,可知第 13 题答案 由,即 .,故选 A. ,即,所以第6页 共12页第 14 题答案将的图象向左平移 个单位后,得到函数的图象,又的图象与的图像重合,故,,所以(),又,故当 时, 取得最小值,为.第 15 题答案因为 为锐角,所以,,所以.因为,所以,所以.第 16 题答案,令得或,令得,所以函数 的单调递增区间为和,减区间为.所以要使函数在上有最小值,只需,即.第 17 题答案(1)∵,————2 分(1)若,则有,解得: .————5 分(2) 是 的充分条件,即分两种情况,或,解得: 或、a 4 ——------------10 分.第 18 题答案(1);(2),(1)--------------------1 分. --------------------2 分∵ 图象上一个最高点的坐标为,与之相邻的一个最低点的坐标为.第7页 共12页∴,∴,于是---------------------5 分.所以. ---------------6 分(2)∵,∴. ------------7 分又,∴,----------------------------------8 分∴. ---------------------------------9 分∵,∴,于是,----------------10∴,所以.-------------------------12 分第 19 题答案(1) 的递增区间为 递减区间为(2)第 19 题解析(1)------------------1 分当时当时--------------2 分的递增区间为 递减区间为----------3 分(2)由方程得------------4 分令则-----------5 分当时,递减当时,递增-------------------------7 分又-------------------------9 分(3)要证原不等式成立,只需证明成立---------------10 分第8页 共12页由(1)可知当 时,故即又 时,--------11 分---------------------------12 分第 20 题答案(Ⅰ)(Ⅱ)当时,无极值点;当时,有 2 个极值点;当 时,有 1 个极值点第 20 题解析(Ⅰ)当时,-----------1 分,则,-----2 分∴,---------------3 分∴曲线在原点处的切线方程为;---------4 分(Ⅱ),--------------5 分令当时,,所以,则,所以在上为增函数,所以无极值点;-------------6 分当时,,所以,则,所以 在上为增函数,所以无极值点;----------------------7 分当时,,令,则,-------------9 分当时,,,此时有 2 个极值点;-----10 分当 时,,此时有 1 个极值点;-------------11 分综上:当时,无极值点;当时,有 1 个极值点;当 时,有 1 个极值点.第9页 共12页--------------12 分第 21 题答案见解析第 21 题解析(Ⅰ),∴∴----------------------------------------1 分∴函数 在处的切线方程为,∵切线过点 ,∴,即,------------------2 分∴,令,解得----------3 分①当时,单调递增,单调递减,-----------------4 分②当时,单调递减,单调递增-----------------5分.(Ⅱ)原题等价方程在 只有一个根,即在 只有一个根,令,等价函数 在 与 轴只有唯一的交点,------------6 分∴①当 时, 在递减,递增,当 趋近于趋近于正无穷要是函数 在 与 轴只有唯一的交点需或,所以或-------------------------------------8 分②当时, 在递增,递减,递增因为,当 趋近于 , 趋近于负无穷,因为第10页 共12页所以 在与 轴只有唯一的交点----------------------10 分③当 时, 在 的递增,∵,,∴函数 在 与 轴只有唯一的交点,-------------------------------11 分综上所述, 的取值范围是或或.-------------12 分第 22 题答案(1) 在定义域上是奇函数;(2) 的取值范围是.第 22 题解析(1)由,得且,∴函数的定义域为,------------------1 分当时,,,-----------------5 分所以,∴ 在定义域上是奇函数--------------------6 分(2)由于,当或时,恒成立,所以在上是减函数,-----------7 分因为且,所以x x1 10,(xm 1)2 (7x)0-----------------------8分由及在上是减函数,第11页 共12页所以,-----------------9 分因为,所以在恒成立.---------10 分设,,则,所以,所以当时,.所以在 上是增函数,.--------------11 分综上知符合条件的 的取值范围是.-------------------------------12 分第12页 共12页。
四川省绵阳南山中学2024届高三上学期10月月考理科数学试卷及答案

2023年10月绵阳南山中学高2021级高三上期10月月考试题理科数学命题人:杜晓英审题人:周莉莎一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,1.已知集合A .{}2,0−3.设正项等比数列{}n a 的前n 项和为n S ,若321238S a a =+,则公比=q ( ) A .2B .32−C .2或32−D .2或324.如图所示的ABC ∆中,点D 是线段AC 上靠近A 的三等分点,点E 是线段AB 的中点,则=DE ( )A .BC BA 6131−−B .BC BA 3161−−C . BC BA 3165−−D .BC BA 3165+−5.纳皮尔是苏格兰数学家,其主要成果有球面三角中的纳皮尔比拟式、纳皮尔圆部法则(1614)和纳皮尔算筹(1617),而最大的贡献是对数的发明,著有《奇妙的对数定律说明书》,并且发明了对数表,可以利用对数表查询出任意对数值.现将物体放在空气中冷却,如果物体原来的温度是1T (℃),空气的温度是0T (℃),经过t 分钟后物体的温度T (℃)可由公式()()310304log log t T T T T =−−−⎡⎤⎣⎦得出;现有一杯温度为70℃的温水,放在空气温度为零下10℃的冷藏室中,则当水温下降到10℃时,经过的时间约为( ) 参考数据:lg 20.301≈,lg 30.477≈.A .3.048分钟B .4.048分钟C .5.048分钟D .6.048分钟6.已知命题p :函数()af x x =在()0,∞+上单调递减;命题:q x R ∀∈,都有220ax x a −+≤.若p q ∨为真命题,p q ∧为假命题,则实数a 的取值范围为( ) A .()1,0− B .[]0,1 C .(]()10,−∞−+∞, D .(](),11,−∞−⋃+∞7.函数xx y cos )1ln(2+=的图象可能为( )A B C D8.已知()3sin cos sin 2παπαα⎛⎫−+−= ⎪⎝⎭,则22sin sin cos ααα−=( )A .2110B .32C .2D .29.已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减,则ω的取值范围是( )A .13[,]24B . 15[,]24C .1(0,]2D .(0,2]11.定义在R 上的奇函数()f x 满足(2)(2)f x f x +=−,且当[0,2]x ∈时,1π()sin 24f x x =,则方程1()8f x x =−在[4,20]−上所有根的和为( ) A .32B .48C .64D .8013.已知,x y 满足约束条件1021010x y x y x y −−≤⎧⎪−+≥⎨⎪++≥⎩,则目标函数2z x y =−+的最小值为 . 14.已知向量(23),(31)a t b =−=−,,,且()b b a//2+,则=a. 15.已知定义在),0(+∞上的函数)(x f 的导函数为()f x ',若()2f x '<,且5)4(=f ,则不等式3log )(log 222−>x x f 的解集是______________. 16.已知函数()2cos()f x x ωϕ=+(0ω>,2πϕ<)的部分图象如图所示,则满足条件0)34()()47()(>⎪⎭⎫⎝⎛−⎪⎭⎫ ⎝⎛−−ππf x f f x f 的最小正整数x 为________.三、解答题:共 70 分。
2021年高三10月月考数学(理)试卷 含解析

2021年高三10月月考数学(理)试卷含解析一、填空题(共14小题,每小题5分,满分70分)1.已知复数z=(1+i)(2﹣i)(i为虚数单位),则= .2.设集合 M={x|x2+x﹣6<0},N={x|1≤x≤3},则M∩N=.3.某算法流程图如图所示,则输出k的值是.4.已知α是第二象限角,且sinα=,则tan(α+)= .5.曲线y=2lnx在点(e,2)处的切线(e是自然对数的底)与y轴交点坐标为.6.已知函数,则的值为.7.对任意的θ∈(0,),不等式+≥|2x﹣1|恒成立,则实数x的取值范围是.8.求“方程3x+4x=5x的解”有如下解题思路:设,则f(x)在R上单调递减,且f(2)=1,所以原方程有唯一解x=2.类比上述解题思路,方程的解为.9.如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则•的值为.10.若函数,则函数y=f(f(x))的值域是.11.已知函数f(x)=(a∈R).若存在实数m,n,使得f(x)≥0的解集恰为[m,n],则a的取值范围是.12.设曲线y=(ax﹣1)e x在点A(x0,y1)处的切线为l1,曲线y=(1﹣x)e﹣x在点B(x0,y2)处的切线为l2.若存在,使得l1⊥l2,则实数a的取值范围为.13.已知f(x)是定义在[1,+∞]上的函数,且f(x)=,则函数y=2xf(x)﹣3在区间(1,xx)上零点的个数为.14.若存在α,β∈R,使得,则实数t的取值范围是.二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(15分)已知函数.(1)设,且,求θ的值;(2)在△ABC中,AB=1,,且△ABC的面积为,求sinA+sinB的值.16.(15分)已知二次函数f(x)=ax2﹣bx+1.(1)若f(x)<0的解集是(,),求实数a,b的值;(2)若a为正整数,b=a+2,且函数f(x)在[0,1]上的最小值为﹣1,求a的值.17.(15分)如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC.(1)设∠MOD=30°,求三角形铁皮PMN的面积;(2)求剪下的铁皮三角形PMN面积的最大值.18.(15分)已知函数f(x)=+,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y﹣3=0.(Ⅰ)求a、b的值;(Ⅱ)证明:当x>0,且x≠1时,f(x)>.19.(15分)心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量;若在t(t>4)天时进行第一次复习,则此时存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”(1)若a=﹣1,t=5,求“二次复习最佳时机点”;(2)若出现了“二次复习最佳时机点”,求a的取值范围.20.(15分)已知函数f(x)=x3+ax2+b(a,b∈R).(1)试讨论f(x)的单调性;(2)若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,)∪(,+∞),求c的值.xx学年江苏省连云港市灌南县华侨双语学校高三(上)10月月考数学试卷(理科)参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(xx•江苏模拟)已知复数z=(1+i)(2﹣i)(i为虚数单位),则=3﹣i.【考点】复数的代数表示法及其几何意义.【专题】数系的扩充和复数.【分析】利用复数的运算法则、共轭复数的定义即可得出.【解答】解:由z=(1+i)(2﹣i)=3+i,∴=3﹣i.故答案为:3﹣i.【点评】本题考查了复数的运算法则、共轭复数的定义,考查了计算能力,属于基础题.2.(xx•江苏三模)设集合M={x|x2+x﹣6<0},N={x|1≤x≤3},则M∩N=[1,2).【考点】交集及其运算.【专题】计算题.【分析】求出集合M中不等式的解集,确定出集合M,找出M与N解集的公共部分,即可求出两集合的交集.【解答】解:由集合M中不等式x2+x﹣6<0,分解因式得:(x﹣2)(x+3)<0,解得:﹣3<x<2,∴M=(﹣3,2),又N={x|1≤x≤3}=[1,3],则M∩N=[1,2).故答案为:[1,2)【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.(xx•江苏模拟)某算法流程图如图所示,则输出k的值是5.【考点】程序框图.【专题】计算题;算法和程序框图.【分析】根据题意,模拟程序框图的运行过程,即可得出该程序运行后输出的结果.【解答】解:模拟程序框图的运行过程,得;k=1,S=10﹣1=9;k=2,S=9﹣2=7;k=3,S=7﹣3=4;k=4,S=4﹣4=0;S≤0,输出k=4+1=5.故答案为:5.【点评】本题考查了循环结构的程序框图应用问题,解题时应模拟程序的运行过程,是基础题目.4.(xx•江苏四模)已知α是第二象限角,且sinα=,则tan(α+)=.【考点】两角和与差的正切函数.【专题】三角函数的求值.【分析】由同角三角函数基本关系可得tanα,代入两角和的正切公式可得.【解答】解:∵α是第二象限角sinα=,∴cosα=﹣=﹣,∴tanα==﹣,∴tan(α+)==.故答案为:【点评】本题考查两角和的正切公式,涉及同角三角函数基本关系,属基础题.5.(xx秋•仪征市期末)曲线y=2lnx在点(e,2)处的切线(e是自然对数的底)与y轴交点坐标为(0,0).【考点】利用导数研究曲线上某点切线方程.【专题】导数的综合应用.【分析】求出曲线方程的导函数,把切点横坐标代入导函数中表示出的导函数值即为切线的斜率,由切点坐标和斜率表示出切线方程,把x=0代入切线方程中即可求出y轴交点坐标.【解答】解:对y=2lnx求导得:y′=,∵切点坐标为(e,2),所以切线的斜率k=,则切线方程为:y﹣2=(x﹣e),把x=0代入切线方程得:y=0,所以切线与y轴交点坐标为(0,0).故答案为:(0,0).【点评】本题的解题思想是把切点的横坐标代入曲线方程的导函数中求出切线的斜率,进而写出切线方程.6.(xx•盐城三模)已知函数,则的值为.【考点】二倍角的正弦;同角三角函数基本关系的运用;二倍角的余弦.【专题】计算题.【分析】利用公式tanx=、sin2α=2sinαcosα、cos2α=2cos2α﹣1即可化简求值.【解答】解:因为f(x)==,所以f()=.【点评】本题考查同角三角函数的基本关系及正余弦的倍角公式.7.(xx•江苏模拟)对任意的θ∈(0,),不等式+≥|2x﹣1|恒成立,则实数x的取值范围是[﹣4,5] .【考点】基本不等式.【专题】转化思想;综合法;三角函数的求值;不等式.【分析】θ∈(0,),可得+=(sin2θ+cos2θ)=5+,利用基本不等式的性质即可得出最小值.根据对任意的θ∈(0,),不等式+≥|2x﹣1|恒成立,可得|2x﹣1|≤,即可得出.【解答】解:∵θ∈(0,),∴+=(sin2θ+cos2θ)=5+≥=9,当且仅当tanθ=时取等号.∵对任意的θ∈(0,),不等式+≥|2x﹣1|恒成立,∴|2x﹣1|≤=9,∴﹣9≤2x﹣1≤9,解得﹣4≤x≤5.∴实数x的取值范围是[﹣4,5].故答案为:[﹣4,5].【点评】本题考查了基本不等式的性质、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.8.(xx春•姜堰市期中)求“方程3x+4x=5x的解”有如下解题思路:设,则f(x)在R上单调递减,且f(2)=1,所以原方程有唯一解x=2.类比上述解题思路,方程的解为﹣1或1.【考点】类比推理.【专题】计算题;推理和证明.【分析】类比求求“方程3x+4x=5x的解”的解题思路,设f(x)=x3+x,利用导数研究f(x)在R上单调递增,从而根据原方程可得x=,解之即得方程的解.【解答】解:类比上述解题思路,设f(x)=x3+x,由于f′(x)=3x2+1≥0,则f(x)在R 上单调递增,∵,∴x=,解之得,x=﹣1或1.故答案为:﹣1或1.【点评】本题主要考查了类比推理,考查了导数与单调性的关系,函数单调性的应用,属于中档题.9.(xx•江苏模拟)如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则•的值为72.【考点】平面向量数量积的运算.【专题】计算题;平面向量及应用.【分析】由三角形的重心的向量表示,可得=﹣(+),由向量的三角形法则,代入向量OC,再由向量垂直的条件和勾股定理,计算即可得到所求值.【解答】解:连接CO延长交AB于M,则由O为重心,则M为中点,且=﹣2=﹣2×(+)=﹣(+),由OA⊥OB,AB=6,则=0,+==36.则•=(﹣)•(﹣)=(2+)(2+)=5+2(+)=0+2×36=72.故答案为:72.【点评】本题考查三角形重心的向量表示,考查向量垂直的条件,考查向量的平方即为模的平方,考查运算能力,属于中档题.10.(2011•江苏二模)若函数,则函数y=f(f(x))的值域是.【考点】指数函数的定义、解析式、定义域和值域;函数的值域.【专题】计算题;分类讨论.【分析】讨论x的正负,代入相应的解析式,然后求出函数f(x)的值域,再代入相应的解析式,求出y=f(f(x))的值域,即可求出所求.【解答】解:设x<0,则f(x)=2x∈(0,1)∴y=f(f(x))=f(2x)当x∈(0,1)时f(x)=﹣2﹣x∈(﹣1,﹣)设x>0,则f(x)=﹣2﹣x∈(﹣1,0)∴y=f(f(x))=f(﹣2﹣x)当x∈(﹣1,0)时f(x)=2x∈(,1)综上所述:y=f(f(x))的值域是故答案为:【点评】本题主要考查了指数函数的值域,以及复合函数的值域问题,同时考查了分类讨论的思想,属于中档题.11.(xx•徐州三模)已知函数f(x)=(a∈R).若存在实数m,n,使得f(x)≥0的解集恰为[m,n],则a的取值范围是(0,).【考点】利用导数求闭区间上函数的最值.【专题】函数的性质及应用;导数的综合应用.【分析】分别讨论a的取值范围,利用参数分离法,结合导数研究函数的最值即可得到结论.【解答】解:当a=0时,f(x)==>0,则不存在f(x)≥0的解集恰为[m,n],当a<0时,f(x)=>0,此时函数f(x)单调递减,则不存在f(x)≥0的解集恰为[m,n],当a>0时,由f(x)≥0得,当x<0,>0,,此时(x)=>0,则f(x)≥0的解集为(﹣∞,0),不满足条件,当x>0时,不等式等价为a,设g(x)=,则g,当x>1时,g′(x)<0,当0<x<1时,g′(x)>0,即当x=1时,g(x)取得极大值,同时也是最大值g(1)=,∴若存在实数m,n,使得f(x)≥0的解集恰为[m,n],则必有a,即0<a,故答案为:(0,)【点评】本题主要考查导数的综合应用,考查分类讨论的数学思想,综合性较强,难度较大.12.(xx•徐州模拟)设曲线y=(ax﹣1)e x在点A(x0,y1)处的切线为l1,曲线y=(1﹣x)e﹣x在点B(x0,y2)处的切线为l2.若存在,使得l1⊥l2,则实数a的取值范围为.【考点】利用导数研究曲线上某点切线方程;函数的值域;两条直线垂直与倾斜角、斜率的关系.【专题】计算题.【分析】根据曲线方程分别求出导函数,把A和B的横坐标x0分别代入到相应的导函数中求出切线l1和切线为l2的斜率,然后根据两条切线互相垂直得到斜率乘积为﹣1,列出关于等式由解出,然后根据为减函数求出其值域即可得到a的取值范围.【解答】解:函数y=(ax﹣1)e x的导数为y′=(ax+a﹣1)e x,∴l1的斜率为,函数y=(1﹣x)e﹣x的导数为y′=(x﹣2)e﹣x∴l2的斜率为,由题设有k1•k2=﹣1从而有∴a(x02﹣x0﹣2)=x0﹣3∵得到x02﹣x0﹣2≠0,所以,又a′=,另导数大于0得1<x0<5,故在(0,1)是减函数,在(1,)上是增函数,x0=0时取得最大值为=;x0=1时取得最小值为1.∴故答案为:【点评】此题是一道综合题,考查学生会利用导数求切线的斜率,会求函数的值域,掌握两直线垂直时斜率的关系.13.(xx•崇川区校级一模)已知f(x)是定义在[1,+∞]上的函数,且f(x)=,则函数y=2xf (x)﹣3在区间(1,xx)上零点的个数为11.【考点】函数零点的判定定理.【专题】计算题;函数的性质及应用.【分析】令函数y=2xf(x)﹣3=0,得到方程f(x)=,从而化函数的零点为方程的根,再转化为两个函数的交点问题,从而解得.【解答】解:令函数y=2xf(x)﹣3=0,得到方程f(x)=,当x∈[1,2)时,函数f(x)先增后减,在x=时取得最大值1,而y=在x=时也有y=1;当x∈[2,22)时,f(x)=f(),在x=3处函数f(x)取得最大值,而y=在x=3时也有y=;当x∈[22,23)时,f(x)=f(),在x=6处函数f(x)取得最大值,而y=在x=6时也有y=;…,当x∈[210,211)时,f(x)=f(),在x=1536处函数f(x)取得最大值,而y=在x=1536时也有y=;综合以上分析,将区间(1,xx)分成11段,每段恰有一个交点,所以共有11个交点,即有11个零点.故答案为:11.【点评】本题考查了函数的零点与方程的根的关系及函数的交点的应用,属于基础题.14.(xx•泰州二模)若存在α,β∈R,使得,则实数t的取值范围是[,1] .【考点】三角函数中的恒等变换应用.【专题】计算题;函数思想;综合法;导数的综合应用;三角函数的求值.【分析】由α≤α﹣5cosβ,得到cosβ<0,由已知α≤t,即,令,则f′(t)=,令f′(t)=0,则sinβ=0,当sinβ=0时,f(t)取得最小值,然后由t≤α﹣5cosβ,即,令,则.令f′(t)=0,则sinβ=0.当sinβ=0时,f(t)取得最大值.【解答】解:∵α≤α﹣5cosβ,∴0≤﹣5cosβ.∴cosβ<0.∵α≤t,∴,即.令,则f′(t)==,令f′(t)=0,则sinβ=0.∴当sinβ=0时,f(t)取得最小值.f(t)=.∵t≤α﹣5cosβ,∴α≥t+5cosβ.∴即.令,则.令f′(t)=0,则sinβ=0.当sinβ=0时,f(t)取得最大值.f(t)=.则实数t的取值范围是:[,1].故答案为:[,1].【点评】本题考查了三角函数的恒等变换应用,考查了导数的综合运用,计算量大,具有一定的难度,是难题.二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(15分)(xx•河南校级二模)已知函数.(1)设,且,求θ的值;(2)在△ABC中,AB=1,,且△ABC的面积为,求sinA+sinB的值.【考点】余弦定理;同角三角函数基本关系的运用;两角和与差的余弦函数;正弦定理.【专题】计算题.【分析】(1)利用二倍角公式及辅助角公式对函数化简可得,f(x)=2cos(x+)+,由可得,cos(θ+)=,结合已知可求θ的值;(2)由(1)知由已知面积可得,从而有由余弦定理得可得a2+b2=再由正弦定理得可求.【解答】解:(1)==.(3分)由得于是(k∈Z)因为所以(7分)(2)因为C∈(0,π),由(1)知.(9分)因为△ABC的面积为,所以,于是.①在△ABC中,设内角A、B的对边分别是a,b.由余弦定理得,所以a2+b2=7.②由①②可得或于是.(12分)由正弦定理得,所以.(14分)【点评】(1)考查了二倍角公式的变形形式的应用,辅助角公式可以把函数化为一个角的三角函数,进而可以研究三角函数的性(2)考查了正弦定理及余弦定理及三角形的面积公式的综合运用.16.(15分)(xx秋•徐州期中)已知二次函数f(x)=ax2﹣bx+1.(1)若f(x)<0的解集是(,),求实数a,b的值;(2)若a为正整数,b=a+2,且函数f(x)在[0,1]上的最小值为﹣1,求a的值.【考点】一元二次不等式的解法;二次函数在闭区间上的最值.【专题】计算题.【分析】(1)由一元二次不等式的解集与一元二次方程的根的关系可以得出,ax2﹣bx+1=0的解是x1=,x2=,由根系关系即可求得实数a,b的值;(1)将已知中函数f(x)化为顶点式的形式,再结合函数f(x)的最小值为﹣1,易得一个关于a的方程,解方程即可求出答案.【解答】解:(1)不等式ax2﹣bx+1>0的解集是(,),故方程ax2﹣bx+1=0的两根是x1=,x2=,所以=x1x2=,=x1+x2=,所以a=12,b=7.(2)∵b=a+2,∴f(x)=ax2﹣(a+2)x+1=a(x﹣)2﹣+1,对称轴x==+,当a≥2时,x==+∈(,1],∴f(x)min=f()=1﹣=﹣1,∴a=2;当a=1时,x==+=,∴f(x)min=f(1)=﹣1成立.综上可得:a=1或a=2.【点评】本题考查的知识点是二次函数的性质,二次函数在闭区间上的最值,其中熟练掌握二次函数的性质是解答本题的关键.17.(15分)(xx•信阳一模)如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC.(1)设∠MOD=30°,求三角形铁皮PMN的面积;(2)求剪下的铁皮三角形PMN面积的最大值.【考点】两角和与差的正弦函数.【专题】应用题;三角函数的图像与性质.【分析】(1)设MN交AD交于Q点由∠MOD=30°,利用锐角三角函数可求MQ,OQ,=MN•AQ可求进而可求MN,AQ,代入S△PMN(2)设∠MOQ=θ,由θ∈[0,],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代=MN•AQ=(1+sinθ)(1+cosθ)展开利用换元法,转化为二次入三角形的面积公式S△PMN函数的最值求解【解答】解:(1)设MN交AD交于Q点∵∠MOD=30°,∴MQ=,OQ=(算出一个得2分)=MN•AQ=××(1+)=…(6分)S△PMN(2)设∠MOQ=θ,∴θ∈[0,],MQ=sinθ,OQ=cosθ=MN•AQ=(1+sinθ)(1+cosθ)∴S△PMN=(1+sinθcosθ+sinθ+cosθ)….(11分)令sinθ+cosθ=t∈[1,],=(t+1+)∴S△PMNθ=,当t=,的最大值为.…..…(14分)∴S△PMN【点评】本题主要考查了三角函数的定义的应用及利用三角函数求解函数的最值,换元法的应用是求解的关键18.(15分)(2011•新课标)已知函数f(x)=+,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y﹣3=0.(Ⅰ)求a、b的值;(Ⅱ)证明:当x>0,且x≠1时,f(x)>.【考点】利用导数研究曲线上某点切线方程;导数在最大值、最小值问题中的应用.【专题】综合题;压轴题;分类讨论;转化思想.【分析】(I)据切点在切线上,求出切点坐标;求出导函数;利用导函数在切点处的值为切线的斜率及切点在曲线上,列出方程组,求出a,b的值.(II)构造新函数,求出导函数,通过研究导函数的符号判断出函数的单调性,求出函数的最值,证得不等式.【解答】解:(I).由于直线x+2y﹣3=0的斜率为﹣,且过点(1,1)所以解得a=1,b=1(II)由(I)知f(x)=所以考虑函数,则所以当x≠1时,h′(x)<0而h(1)=0,当x∈(0,1)时,h(x)>0可得;当从而当x>0且x≠1时,【点评】本题考查导函数的几何意义:在切点处的导数值为切线的斜率、考查通过判断导函数的符号求出函数的单调性;通过求函数的最值证明不等式恒成立.19.(15分)(2011•江苏二模)心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量;若在t(t>4)天时进行第一次复习,则此时存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”(1)若a=﹣1,t=5,求“二次复习最佳时机点”;(2)若出现了“二次复习最佳时机点”,求a的取值范围.【考点】函数模型的选择与应用.【专题】综合题;函数的性质及应用.【分析】(1)第一次复习后的存留量是y2,不复习时的存留量为y1,复习后与不复习的存留量差是y=y2﹣y1;把a、t代入,整理即得所求;(2)求出知识留存量函数y=+﹣(t>4,且t、a是常数,x是自变量),y取最大值时对应的t、a取值范围即可.【解答】解:(1)设第一次复习后的存留量与不复习的存留量之差为y,由题意,第一次复习后的存留量是,不复习的存留量为;∴;当a=﹣1,t=5时,=≤=,当且仅当x=14时取等号,所以“二次复习最佳时机点”为第14天.(2)知识留存量函数=≤,当且仅当时取等号,由题意,所以﹣4<a<0.【点评】本题考查了含有字母参数的函数类型的应用,题目中应用基本不等式a+b≥2(a >0,b>0)求出最值,有难度,是综合题.20.(15分)(xx•江苏)已知函数f(x)=x3+ax2+b(a,b∈R).(1)试讨论f(x)的单调性;(2)若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,)∪(,+∞),求c的值.【考点】利用导数研究函数的单调性;函数零点的判定定理.【专题】综合题;导数的综合应用.【分析】(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣)=+b,则函数f(x)有三个不同的零点等价于f(0)f(﹣)=b(+b)<0,进一步转化为a>0时,﹣a+c>0或a<0时,﹣a+c<0.设g(a)=﹣a+c,利用条件即可求c的值.【解答】解:(1)∵f(x)=x3+ax2+b,∴f′(x)=3x2+2ax,令f′(x)=0,可得x=0或﹣.a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;a>0时,x∈(﹣∞,﹣)∪(0,+∞)时,f′(x)>0,x∈(﹣,0)时,f′(x)<0,∴函数f(x)在(﹣∞,﹣),(0,+∞)上单调递增,在(﹣,0)上单调递减;a<0时,x∈(﹣∞,0)∪(﹣,+∞)时,f′(x)>0,x∈(0,﹣)时,f′(x)<0,∴函数f(x)在(﹣∞,0),(﹣,+∞)上单调递增,在(0,﹣)上单调递减;(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣)=+b,则函数f(x)有三个不同的零点等价于f(0)>0,且f(﹣)<0,∴b>0且+b<0,∵b=c﹣a,∴a>0时,﹣a+c>0或a<0时,﹣a+c<0.设g(a)=﹣a+c,∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,)∪(,+∞),∴在(﹣∞,﹣3)上,g(a)<0且在(1,)∪(,+∞)上g(a)>0均恒成立,∴g(﹣3)=c﹣1≤0,且g()=c﹣1≥0,∴c=1,此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],∵函数有三个零点,∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,解得a∈(﹣∞,﹣3)∪(1,)∪(,+∞),综上c=1.【点评】本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,考查分类讨论的数学思想,难度大.28094 6DBE 涾37302 91B6 醶39449 9A19 騙E21759 54FF 哿20781 512D 儭31582 7B5E 筞31135 799F 禟Q29265 7251 牑35431 8A67 詧32475 7EDB 绛。
2021年高三10月月考数学(理)试题含答案

2021年高三10月月考数学(理)试题含答案一、选择题:(本大题共12小题,每小题5分,共60分.在每题给出的四个选项中,只有一个是符合题目要求的.)1.设U ={1,2,3,4,5},A ={1,2,3},B ={2,3,4},则下列结论中正确的是( )A .A ⊆B B .A ∩B ={2}C .A ∪B ={1,2,3,4,5}D .A ∩()={1}2.,,,,5.0log ,3,5.035.03c b a c b a 则若===的大小关系是( )A. B. C. D.3.下列命题中,假命题是( )A .B .C .D .4.函数的一个零点落在下列哪个区间( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)5.若函数)10()(≠>==a a a y x f y x ,且是函数的反函数,且 ( )A. B . C . D .6.函数的图象大致是( )7.已知函数)()2())((x f x f R x x f y =+∈=满足,且,则的交点的个数为()A .4B .5C .6 D.78.若函数在区间[2,+∞)上单调递增,则实数的取值范围是( )A. B. C. D.9.曲线在点处的切线与坐标轴所围三角形的面积为( )A. B. C. D .10.设函数在上均可导,且,则当时,有( )A .B .C .D .第Ⅱ卷(共100分)二、填空题: (本大题5小题,每小题5分,共25分)中学联盟网11、函数是幂函数且在上单调递减,则实数的值为 .12. = .13. 函数f (x )=x 3+3ax 2+3[(a +2)x +1]有极值,则 a 的取值范围是________. 14.已知函数,若f (x )在上单调递增,则实数a 的取值范围为____ ____.15.定义在上的偶函数满足,且在上是增函数,下面是关于的判断:①的图像关于点P()对称 ②的图像关于直线对称;③在[0,1]上是增函数; ④.其中正确的判断是____________________(把你认为正确的判断都填上)三、解答题:(本大题共6题,满分75分.解答须写出文字说明、证明过程和演算步骤)16.(本小题满分12分 )已知,,且是的必要不充分条件,求实数的取值范围.17. (本小题满分12分)已知,设命题上的单调递减函数;命题R ax axx g q 的定义域为:函数)122lg()(2++=.是假命题,求实数的取值范围.18.(本小题满分12分)山东中学联盟网已知函数f (x )=ax +1x 2 ( x ≠0,常数a ∈ R). (1)讨论函数f (x )的奇偶性,并说明理由;(2)若函数f (x )在x ∈ [3,+∞)上为增函数,求a 的取值范围.19. (本小题满分12分 )已知函数(1)求函数的极值点;(2)若直线过点(0,—1),并且与曲线相切,求直线的方程;20. (本小题满分13分 )有两个投资项目,根据市场调查与预测,A 项目的利润与投资成正比,其关系如图甲,B 项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)(1)分别将两个投资项目的利润表示为投资(万元)的函数关系式;(2)现将万元投资项目, 万元投资项目.表示投资A 项目所得利润与投资项目所得利润之和.求的最大值,并指出为何值时, 取得最大值21. (本小题满分14分 )设函数(e=2.718 28……是自然对数的底数).(I)判断的单调性;(1I)当在(0,+∞)上恒成立时,求a 的取值范围;(Ⅲ)证明:当(0,+∞)时,.高三理科数学阶段检测一参考答案xx.10一、选择题:1-5:DABBD 6-10: DCADB二、填空题:11. 2 12. 13. a >2或a <-1 14. (2,3] 15.①②④三、解答题:16.解:由,得,或.由,得. 中学联盟网或是的必要不充分条件,.17.解:当命题, 因为上的单调递减函数,所以 --------------------2分当命题,因为R ax ax x g 的定义域为函数)122lg()(2++=所以当 ----------------4分当20084002<<⎩⎨⎧<-=∆>≠a a a a a ,解得时,则有 所以,当命题---------------8分因为是假命题,所以一真一假当--------------9分当0212010=<≤⎩⎨⎧<≤≥≤a a a a a q p 或,解得或真时,有假-----------11分综上所述的取值范围是 ----------------12分18.解:(1)定义域(-∞,0 )∪ ( 0,+∞),关于原点对称.当a =0时,f(x)=1x 2,满足对定义域上任意x ,f(-x)=f(x),∴ a =0时,f(x)是偶函数;当a≠0时,f(1)=a +1,f(-1)=1-a ,若f(x)为偶函数,则a +1=1-a ,a =0矛盾;若f(x)为奇函数,则1-a =-(a +1),1=-1矛盾,∴ 当a≠0时,f(x)是非奇非偶函数.(2) 在[3,+∞)上恒成立.[)max 33222y=3+27a y x x ∴≥∞∴=即恒成立 又在区间,上递减. ≥ 227 19.(1)解: (1)>0.………………………………………………………1分而>0lnx+1>0><0<00<<所以在上单调递减,在上单调递增.………………4分所以是函数的极小值点,极大值点不存在.…………………6分(2)设切点坐标为,则切线的斜率为所以切线的方程为……………………8分又切线过点,所以有解得所以直线的方程为………………………………………………12分20.解:(1)设投资为万元,A 项目的利润为万元,B 项目的利润为万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2022年10月绵阳南山中学2022年秋季高2021届10月月考 数 学 试 题 (理工类)1、试题说明:本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.第II 卷的22、23、24小题是选考内容,务必先选后做.考试范围:绵阳一诊考试内容. 2、命题人:张家寿,审题人:蔡晓军.第Ⅰ卷(选择题,共60分)留意事项:必需使用2B 铅笔在答题卡上将所选答案对应的标号涂黑.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}Z x x y y M ∈==,|2,{}R x x x N ∈≥-=,63|,全集R U =,P 是N 的补集,则PM 的真子集个数是( ).A 15 .B 7.C 16 .D 82.已知()3sin f x x x π=-,命题:(0,),()02p x f x π∀∈<,则( ).A p 是假命题;:(0,),()02p x f x π⌝∀∈≥ .B p 是真命题; 00:(0,),()02p x f x π⌝∃∈≥.C p 是真命题;:(0,),()02p x f x π⌝∀∈> .D p 是假命题; 00:(0,),()02p x f x π⌝∃∈≥ 3.“0>x ” 是“111<+x ”的( )条件 .A 充分不必要 .B 必要不充分 .C 充要条件 .D 既不充分也不必要4. ABC ∆中,AB 边的高为CD ,若CB a =,CA b =,0a b ⋅=,1,2a b ==,则AD =( )11.33A a b - 22.33B a b - 33.55C a b - 44.55D a b -5.函数2||()2x f x x =-的图像为( )6.函数)sin()(ϕω+=x A x f 的图象如下图所示,为了得到x A x g ωcos )(-=的图像,可以将)(x f 的图像( ).A 向右平移12π个单位长度 .B 向右平移125π个单位长度 .C 向左平移12π个单位长度 .D 向左平移125π个单位长度 7.设121333211(),(),(),,,333a b c a b c===则的大小关系( ).A a c b >> .B a b c >> .C c a b >> .D b c a >>8.若函数2()(1)2f x x m x m =--+在[]0,1上有且只有一个零点,则实数m 的取值范围为( ) .A (]2,0- .B ()1,0- .C []2,0- .D ()2,1-- 9.定义在R 上的奇函数f x (),0)3(=f ,且对任意不等的正实数1x ,2x 都满足:[])()(21x f x f -0)(12<-x x ,则不等式0)(3>-⋅x f x 的解集为( ).A )30()03(,,⋃- .B )3()3(∞+⋃--∞,, .(,3)(0,3)C -∞-⋃ .D )3()03(∞+⋃-,,10.某厂生产的甲、乙两种产品每件可获利润分别为30元、20元,生产甲产品每件需用A 原料2 kg 、B 原料4 kg ,生产乙产品每件需用A 原料3 kg 、B 原料2 kg.A 原料每日供应量限额为60 kg ,B 原料每日供应量限额为80 kg.要求每天生产的乙种产品不能比甲种产品多超过10件,则合理支配生产可使每日获得的利润最大为( ).500A 元 .B 700元 .C 400元 .D 650元11.已知)(x f 是定义在R 上的奇函数,当0>x 时,⎪⎩⎪⎨⎧>-≤<-=-2),2(2120,12)(1x x f x x f x ,则函数1)()(-=x xf x g 在[)+∞-,6上的全部零点之和等于( ).7A .B 8 .C 9 .D 1012.定义在R 上的函数()f x 满足)(2)5(,1)1()(,0)0(x f x f x f x f f ==-+=,且当1201x x ≤≤≤时,12()()f x f x ≤,则)121(f 等于( ) 1.2A .B 14 .C 18 .D 116第Ⅱ卷 (非选择题,共90分)留意事项:必需使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答。
作图时可先用铅笔会出,确认后再用0.5毫米黑色墨迹签字笔描清楚。
答在试题卷、草稿纸上无效。
本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必需作答。
第22题~24题为选考题,考生依据要求作答。
二、填空题:本大题共4小题,每小题5分,共20分.13.若向量(2cos ,1),(sin ,1)a b αα==,且//a b ,则sin 2α等于 .14.已知幂函数223*()()m m f x x m N --=∈的图象关于y 轴对称,且在(0,+∞)上是减函数, 则m 的值为________.15.已知数列{}n a 的通项公式是22n a n kn =++,若对全部的*n N ∈,都有1n n a a +>成立,则实数k的取值范围是________. 16.下列命题中:(1)若1x 满足522=+xx ,2x 满足5)1(log 222=-+x x ,则421=+x x ;(2)函数)10(1)3(log 3≠>-+=a a x y 且的图象恒过定点A ,若A 在02=++ny mx 上,其中0>mn ,则n m 11+的最小值是2223+;(3)设)(x g 是定义在R 上,以1为周期的函数,若)(2)(x g x x f +=在[]1,0上的值域为[]3,1-,则)(x f 在区间[]3,0上的值域为[]7,1-;(4)函数x xy -=42log 2图象的对称中心为()1,2;其中真命题序号为 .三、解答题:本大题共6小题,前5个题每个12分,选做题10分,共70分.解答应写出文字说明、证明过程或演算步骤.前五题各12分. 17.(本小题满分12分)已知向量)sin ,1(x a =,)sin ),32(cos(x x b π+=,函数x b a x f 2cos 21)(-⋅=(Ⅰ)求函数)(x f 的解析式及其单调递增区间;(Ⅱ)当]3,0[π∈x 时,求函数)(x f 的值域.18.(本小题满分12分)已知数列{}n a 的前n 项和为n S,11a =,且1323n n a S ++= (n 为正整数).(Ⅰ)求数列{}n a的通项公式;(Ⅱ)若对任意正整数n ,32nk S ≤恒成立,求实数k 的最大值.19.(本小题满分12分)已知定义在区间[0,2]上的两个函数()f x 和()g x ,其中2()24f x x ax =-+(1)a ≥,2()1x g x x =+. (Ⅰ)求函数()y f x =的最小值()m a ;(Ⅱ)若对任意1x 、2[0,2]x ∈,21()()f x g x >恒成立,求a 的取值范围.20.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且满足(2)cos cos 0c a B b A --=. (Ⅰ)若7,13b a c =+=,求此三角形的面积;(Ⅱ)求)6sin(sin 3π-+C A 的取值范围. 21.(本小题满分12分)已知函数1()1lna f x x x =-+(a 为实常数)。
(Ⅰ)当1a =时,求函数()()2g x f x x =-的单调区间; (Ⅱ)若函数()f x 在区间(0,2)上无极值,求a 的取值范围;(Ⅲ)已知n N *∈且3n ≥,求证:n+11111ln<++++3345n ⋅⋅⋅.请考生在第22、23、24题中任选一题作答,假如多做,则按所做的第一题计分。
作答时用2B 铅笔在答题卡上把所选题目题号涂黑。
22.(本小题满分10分)选修4-1:几何证明选讲如图,ABC ∆中,AB AC =,O 经过点A ,与BC 相切于B ,与AC 相交于D ,若1AD CD ==,求O 的半径r .23.(本小题满分10分)选修4-4:坐标系与参数方程已知直线11cos :()sin x t C t y t αα=+⎧⎨=⎩为参数,圆2cos :()sin x C y θθθ=⎧⎨=⎩为参数.(1)当=3πα时,求12C C 与的交点的直角坐标;(2)过坐标原点O 作1C的垂线,垂足为A ,P 为OA 的中点,当α变化时,求P 点轨迹的参数方程,并指出它是什么曲线.24.( 本小题满分10分)选修4-5:不等式选讲 已知函数.3)(,212)(+=++-=x x g a x x x f(1)当2-=a 时,求不等式)()(x g x f <的解集;(2)设1->a ,且当⎪⎭⎫⎢⎣⎡-∈21,2a x 时,)()(x g x f ≤,求a 的取值范围. 2021届10月月考参考答案16BBADCB - 712ACADBB - 13.5414.1 15.(-3,+∞) 16.(2)(3)(4) 17.(1)x x x b a x f 2cos 21sin )32cos()(2-++=⋅=π)62sin(21π+-=x 由2326222πππππ+≤+≤+k x k 得326ππππ+≤≤+k x k 单调递增区间为]32,6[ππππ++k k ,Z k ∈(2)当]3,0[π∈x 时,则]65,6[62πππ∈+x ,]1,21[)62sin(∈+πx 故)(x f 的值域是⎥⎦⎤⎢⎣⎡-0,2118. (1)a n =a 1q n -1=(13)n -1(n ∈N *);(2)由(1)知,S n =a 11-qn1-q=1-13n1-13=32[1-(13)n ]. 又对∀n ∈N *恒有32k ≤32 [1-(13)n ]得k ≤1-(13)n .∵数列{1-(13)n}单调递增,∴当n =1时,数列中的最小项为23,∴必有k ≤23,即实数k 的最大值为23.19.(1)2412,()84 2.a a m a a a ⎧-<=⎨-⎩≤≥ (2)1()(1)21g x x x =++-+,当[0,2]x ∈时,1[1,3]x +∈,又()g x 在区间[0,2]上单调递增(证明略),故4()0,3g x ⎡⎤∈⎢⎥⎣⎦. 由题设,得2min 1max ()()f x g x >,故212,443a a <⎧⎪⎨->⎪⎩≤或2,484,3a a ⎧⎪⎨->⎪⎩≥ 解得261a <≤为所求的范围.20.解:(1)△ABC 的面积S =12ac sin B =10 3.(2)3sin A +sin ⎝⎛⎭⎪⎫C -π6=2sin ⎝ ⎛⎭⎪⎫A +π6∈(]1,2. 21(Ⅰ)()g x 在10,2x ⎛⎫∈ ⎪⎝⎭时递增;在1,2x ⎛⎫∈+∞ ⎪⎝⎭时递减。
