方差分析—田间试验统计
田间试验与统计分析之方差分析

5.19 4.18 5.36
不同药剂处理水稻苗高平均数比较(q法)
鱼增重平均数
差异显著性
0.05
0.01
31.18
a
A
27.96
b
AB
26.28
b
AB
24.74
b
B
(2)新复极差法
新复极差法,又称最短显著极差法(shortest
significant range,SSR法),与q 法相似。计算 LSRα值查的是SSRα值(附表6)而不是q 表。
bc
B
c
B
2.最小显著极差法
定义:把平均数的差数看成平均数的极差,
根据极差范围内在显著水平ɑ上依秩次距k
的不同而采用的不同的检验尺度叫最小显著 极差,记LSRɑ,k。 秩次距:极差范围内所包含的处理数。
一般,有k 个平均数相互比较,就有k-1 种 秩次距,即k,k-1,k-2 …,2,因而需求得 k-1个最小显著极差LSRɑ,k ,分别作为判断
a
0
F
Fa (1 , 2 )
F 界值表
分母自由 度υ2 1
2
25
附表4 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分子的自由度,υ1
1
2
3
4
5
6
161
200
216
225
230
234
4052
4999
5403
5625
5764
5859
18.51 19.00 19.16 19.25 19.30 19.33
当秩次距k=2时,取等号;秩次距k>3时,取
值时,总是将要测验的那一项变异因素的均方作 分子,而以另一项变异(如误差项)作分母。
田间试验与统计分析教学大纲

田间试验与统计分析教学大纲(农学类专业专科学生)第一部分课程的性质和任务田间试验与统计分析,是运用数理统计理论与方法研究农业科学研究和技术工作中,所需的田间试验设计、实施和试验资料统计分析方法的一门应用学科,是农学类专业的专业基础课。
本课程在高等数学、线性代数、概率论初步等课程的基础上,介绍数理统计的基本概念和基本原理,讲解田间试验的基本要求、设计实施和试验资料统计分析方法。
本课程既涉及一些严谨的数学理论和方法,又紧密结合农业生产和科学研究实践。
通过学习为进一步学习遗传学、作物栽培学、作物育种学等专业基础课和专业课打下坚实的基础,同时学会如何利用这一工具进行农业科学研究和技术工作方法。
第二部分基本要求通过本课程的学习,学生应达到以下要求:1. 有关试验数据分析的基本技能,如整理数据和计算平均数、变异数等,对试验结果有一个数量概念。
2.有关从试验数据进行归纳的统计推断原理和程序。
3. 掌握试验设计的基本原则和各种设计的要点及特点。
4.能根据所给试验条件,能够正确选用试验设计方法,并做出试验设计。
5.掌握EXCEL常见函数主要功能和数据分析工具。
第三部分教学说明及学时分配本课程总共60学时,讲授44学时,实验8个计16学时。
本课程以概率论、数理统计为基础,介绍田间试验与统计分析的基本概念、基本知识和基本方法,着重讲解农学类专业常用田间试验的设计、实施和统计分析方法。
本课程概念较多、理论抽象、系统严密、实践性强、公式复杂、符号繁多、计算量大,除课堂讲授外,要求学生认真完成习题作业,并结合农业生产和科学研究实践,有针对性的安排上机实习和田间实习,注意培养学生运用所学知识和技能分析问题和解决问题的能力。
(一)教学环节1、课堂讲授着重讲解基本概念、基本原理和基本方法,突出重点和难点。
各种统计分析方法的介绍主要结合例题来讲解。
2、实验及习题实验对于帮助学生巩固和加深理解教学的基本内容是很有作用的。
本课程拟安排八个实验,利用EXCEL所提供函数和数据分析工具实现所授统计方法计算。
田间试验统计方法

田间试验统计方法
田间试验统计方法是在农田或田间进行的实验中,采用统计学原理和方法对数据进行分析和推断的一种方法。
它可以帮助农业科研人员或农田经营者评估不同农业实践、品种、肥料、农药等对农作物产量和质量的影响。
田间试验统计方法通常包括以下几个步骤:
1. 设计试验:选择合适的试验设计,如完全随机设计、区组设计、分组区组设计等,确保试验能够提供可靠的结果。
2. 样本选择:根据试验设计和样本容量计算方法,确定需要监测或采集的样本数量,并随机选择样本。
3. 数据采集:在试验期间或收获时,采集或记录相关数据,如生长状况、产量、植株高度、籽粒重量等。
4. 数据处理:对采集的数据进行整理和处理,计算平均值、标准差、方差等统计量,并进行适当的数据转换或修正。
5. 假设检验:根据试验目的和假设,选择合适的统计检验方法,如t检验、方差分析、回归分析等,判断不同条件下的差异是否显著。
6. 结果解释:根据统计分析的结果,得出结论并解释试验结果的意义,评估不同处理或因素对农作物生长和产量的影响。
田间试验统计方法可以帮助农业科研人员或农田经营者了解农作物的生长规律、评估不同管理措施的效果、优化农田管理方案,从而提高农业生产效益和可持续发展能力。
田间试验与统计分析

田间试验与统计分析概论:1.生物统计的内容包括哪三个方面?①统计原理②统计方法③试验设计2.生物统计的作用是什么?①提供试验或调查的方法②提供整理或分析资料的方法3.通常把样本容量小于或等于30的样本称为小样本。
样本容量大于30的样本称为大样本。
4.生物统计:应用概率论和数据统计原理方法来确定生物界数量变化的学科。
根据研究目的确定的研究对象的全体称为总体。
总体的一部分称为样本。
由总体计算的特征数称为参数。
是真值,不受抽样变动的影响。
由样本计算的特征数称为统计量,是参数的估计值,受抽样变动的影响。
准确性:也叫准确度,指在试验或调查中某一试验指标或性状的观测值与其真值接近的程度。
精确性:也叫精确度,指在试验或调查中同一试验指标或性状的重复观测值彼此接近的程度。
随机误差也叫抽样误差,这是由于许多无法控制的内在和外在的偶然因素所造成。
系统误差也叫片面误差,这是由于试验的初始条件相差较大,其条件未控制相同,测量的仪器不准,操作错误等所引起。
(影响准确性)第一章1.田间试验:指在田间土壤、自然气候等环境条件下栽培作物,并进行与作物有关的各种科学研究试验。
试验指标:在试验中具体测定的性状或观测项目称为试验指标。
试验因素:指试验中人为控制的、影响试验指标的原因。
因素水平:对试验因素所设定的量的不同级别或质的不同状态称为因素水平。
试验处理:事先设计好的实施在试验单位上的具体项目叫试验处理。
试验小区:安排一个试验处理的小块地段称为试验小区。
试验单位:指施加试验处理的材料单位,也称为试验单元。
2.田间试验的特点?要求?特点:①田间试验研究的对象和材料是农作物,以农作物生长发育的反应作为试验指标研究其生长发育规律、各项栽培技术或条件的效果。
②田间试验具有严格的地区性和季节性。
田间试验普遍存在试验误差。
要求:①试验目的要明确②试验要有代表性和先进性③试验结果要正确可靠④试验结果要具有重演性3.土壤差异的表现形式:梯度变化斑块状变化4.田间试验对照的设置形式:空白对照互为对照标准对照试验对照自身对照肥底对照5.田间试验设计?常用的田间试验设计方法有哪几种?田间试验设计:按照试验的目的要求和试验地的具体情况,将各试验小区在试验地上作最合理的设置和排列,称为田间试验设计。
对田间试验数据的统计处理方法 格拉布斯准则和应用进行方差分析 多重比较

谢谢观看
我们也注意到,对于不同类型的数据和不同的研究问题,可能需要采用不同的 统计方法。在实际科研工作中,我们需要根据具体情况选择最合适的方法进行 分析。另外,我们还需要注意数据处理过程中的伦理和隐私问题,并采取适当 的措施加以保护。
总之,本次演示重点探讨了田间试验数据的统计处理方法——格拉布斯准则及 其应用。通过案例演示了其数据分析过程,并讨论了结果解释、结论与展望。 希望这些内容能够为相关领域的研究者提供一定的参考和借鉴意义。
首先,田间试验数据的统计处理方法在科学研究中的作用不言而喻。正确、科 学的数据分析方法能够客观地评价试验结果,揭示作物产量、品质、生理生化 等指标的变异性及其影响因素。在海量数据背景下,如何准确、高效地处理和 分析数据成为一个亟待解决的问题。本次演示重点探讨了格拉布斯准则这一数 据处理方法的应用。
我们也注意到,对于不同类型的数据和不同的研究问题,可能需要采用不同的 统计方法。在实际科研工作中,我们需要根据具体情况选择最合适的方法进行 分析。另外,我们还需要注意数据处理过程中的伦理和隐私问题,并采取适当 的措施加以保护。
总之,本次演示重点探讨了田间试验数据的统计处理方法——格拉布斯准则及 其应用。通过案例演示了其数据分析过程,并讨论了结果解释、结论与展望。 希望这些内容能够为相关领域的研究者提供一定的参考和借鉴意义。
在数据处理过程中,首先计算出数据系列的平均值,然后计算每个数据点与平 均值的差异。将这些差异从小到大排序后,选取最大的差异值作为异常值的界 限。在本案田间试验数据的统计处理方法对科研工作者的决策和结论产生重要 影响。本次演示详细阐述了如何使用格拉布斯准则进行数据分析,通过案例演 示了其应用过程,并讨论了结果解释、结论与展望。
数据处理:在兽医科研中,数据可能来自于各种来源,包括动物实验、临床病 例记录等。这些数据可能包括定量数据如体重、血液指标等,也可能包括定性 数据如诊断结果、治疗措施等。在进行分析前,需要对数据进行预处理,如数 据清洗、缺失值处理、异常值检测与处理等。此外,还需要对数据进行合适的 量纲转换和标准化处理,以保证数据分析的可靠性。
田间试验和统计分析

均方的计算:
ST2
SST nk 1
St2
SSt k 1
Se2
SSe k(n 1)
第一节 方差分析的基本原理和方法
田间试验和统计分析
第一节 方差分析的基本原理和方法
方差分析表
变异来源 平方和SS
处理间
SSt
处理内/误差 SSe
总变异
SST
自由度DF 均方MS
K-1
第三章 方差分析
Chapter 3 ANOVA (Analysis of Variance)
田间试验和统计分析
第三章 方差分析
方差是平方和除以自由度的商。
2 (xi )2
N
2 x
2
/
n
方差分析是判断多组数据( K≥3 )之间平均数差异是 否显著的一种假设测验方法。2个样本平均数可用 t 或U测验 的方法来评定其差数的显著性。如果有K个平均数,且K≥3, 若仍然用两两比较的方法来测验,则需要作K(K-1)/2次测验, 如果K=10,则需要45次测验,不但测验程序繁琐,而且在 理论上,其显著水平已经扩大了。因此,对于多样本平均数 的假设测验,需采用一种更为合适的统计方法,即方差分析 法(Fisher, 1923)。
推断:接受HA,即测验药剂间变异显著地大 于药剂内变异,不同药剂对水稻苗高具有不 同效应。
田间试验和统计分析
第一节 方差分析的基本原理和方法
方差分析表
变异来源 处理间 误差 总变异
自由度DF 平方和SS 均方MS F值
K-1
SSt
St2= SSt/df1 F=St2/ Se2
K(n-1)
SSe
Se2= Sse/df2
21
田间试验与统计分析课后习题解答及复习资料

名师精编优秀资料田间试验与统计分析-习题集及解答1. 2. 3. 在种田间试验设计方法中,属于顺序排列的试验设计方法为:对比法设计、 间比法 若要控制来自两个方面的系统误差,在试验处理少的情况下,可采用:拉丁 方设计 如果处理内数据的标准差或全距与其平均数大体成比例,或者效应为相 乘性, 则在进行方差分析之前, 须作数据转换。
其数据转换的方法宜采用: 对数转换。
对于百分数资料,如果资料的百分数有小于 30%或大于 70%的,则在进 行方差分析之前,须作数据转换。
其数据转换的方法宜采用:反正弦转换 (角度转换)。
样本平均数显著性测验接受或否定假设的根据是: 小概率事件实际不可能性 原理。
对于同一资料来说,线性回归的显著性和线性相关的显著性:一定等价。
为了由样本推论总体,样本应该是:从总体中随机地抽取的一部分 测验回归和相关显著性的最简便的方法为:直接按自由度查相关系数显著 表。
选择多重比较的方法时,如果试验是几个处理都只与一个对照相比较,则应 选择:LSD 法。
如要更精细地测定土壤差异程度,并为试验设计提供参考资料,则宜采用: 空白试验 = = (两样本 所属的总体方差同质)时,作平均数的假设测验宜用的方法为:t 测验 因素内不同水平使得试验指标如作物性状、特性发生的变化,称为:效应 若算出简单相差系数 大于 1 时,说明:计算中出现了差错。
田间试验要求各处理小区作随机排列的主要作用是: 获得无偏的误差估计值 正态分布曲线与 轴之间的总面积为:等于 1。
描述总体的特征数叫:参数,用希腊字母表示;描述样本的特征数叫:统计 数,用拉丁字母表示。
确定 分布偏斜度的参数为:自由度4.5. 6. 7. 8. 9. 10.11. 当总体方差为末知,且样本容量小于 30,但可假设 12. 13. 14. 15. 16. 17.18. 用最小显著差数法作多重比较时,当两处理平均数的差数大于 LSD0.01 时, 推断两处理间差异为:极显著 19. 要比较不同单位, 或者单位相同但平均数大小相差较大的两个样本资料的变 异度宜采用:变异系数 20. 选择多重比较方法时,对于试验结论事关重大或有严格要求的试验,宜用: q 测验。
田间试验统计分析
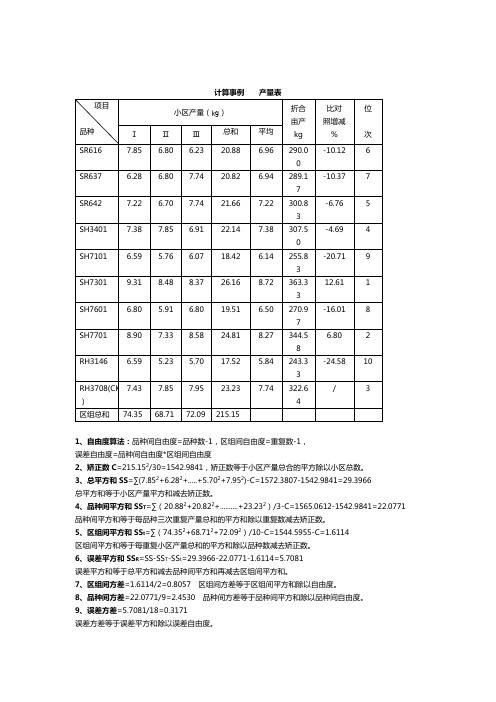
1、自由度算法:品种间自由度=品种数-1,区组间自由度=重复数-1,误差自由度=品种间自由度*区组间自由度2、矫正数C=215.152/30=1542.9841,矫正数等于小区产量总合的平方除以小区总数。
3、总平方和SS=∑(7.852+6.282+.....+5.702+7.952)-C=1572.3807-1542.9841=29.3966总平方和等于小区产量平方和减去矫正数。
4、品种间平方和SS T=∑(20.882+20.822+..........+23.232)/3-C=1565.0612-1542.9841=22.0771 品种间平方和等于每品种三次重复产量总和的平方和除以重复数减去矫正数。
5、区组间平方和SS t=∑(74.352+68.712+72.092)/10-C=1544.5955-C=1.6114区组间平方和等于每重复小区产量总和的平方和除以品种数减去矫正数。
6、误差平方和SS R=SS-SS T-SS t=29.3966-22.0771-1.6114=5.7081误差平方和等于总平方和减去品种间平方和再减去区组间平方和。
7、区组间方差=1.6114/2=0.8057 区组间方差等于区组间平方和除以自由度。
8、品种间方差=22.0771/9=2.4530 品种间方差等于品种间平方和除以品种间自由度。
9、误差方差=5.7081/18=0.3171误差方差等于误差平方和除以误差自由度。
10、区组间F 值=0.8057/0.3171=2.45408,品种间F 值=2.4530/0.3171=7.7357 F 值等于区组间和品种间方差分别除以误差方差。
F 0.05和F 0.01的数据从表中查得,如果F 值小于 F 0.05,则不显著;如果F 值在F 0.05和F 0.01之间,则显著;11、标准误差=0.3171/3=0.33,标准误差等于误差方差除以重复数的开方。
12、SSR 0.05和SSR 0.01由新复极差表中查得LSR 0.05=SSR 0.05*标准误差,LSR 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
29 =21
1、总变异
把表中的全部观察值作为一个组看待
[即把4个处理(4组、每组有4个观察值)合并
成一组,共有16个观察值],根据前面讲过的
计算平方和的公式 ,可以计算出总变异的平
方和和自由度
SST ( y i y ) 2 y 2 ( y ) 2 nk
2 336 182 212 322 602 4 4
5.1
方差分析的基本原理
5.1.1
5.1.2
自由度和平方和的分解
F分布与F测验
上章介绍了一个或两个样本平均数的假设测验方
法。本章将介绍k(k≥3)个样本平均数的假设测验方 法,即方差分析(analysis of variance)。这种方 法的基本特点是:将所有k个样本的观察值和平均数
作为一个整体加以考虑,把观察值总变异的自由度
2
2
2 T22 92 202 24 2 262 22 2 20 n 4
2 药剂C内:SSe ( y3 j y3 ) y3 j
3
2
2 T32 56 102 152 17 2 14 2 26 n 4
药剂D内: SS e ( y 4 j y 4 ) y 4 j
其中:
( y ) 2 nk
T2 nk
称为矫正数,用C表示。
自由度
DFT=nk-1=4×4-1=15。
表中的每一个观察值,即包括有处理的
效应(不同药剂对苗高的影响)又受到误
差的影响。
2、误差效应
表中处理内(组内)各观察值之间,若不存在误
差,则各观察值应该相等,由于误差是客观存
在的,因而处理内(组内)各观察值之间必然是
和平方和分解为不同变异来源的自由度和平方和, 进而获得不同变异来源的总体方差估计值。
其中,扣除了各种试验原因所引起的变异后的
剩余变异提供了试验误差的无偏估计,作为假 设测验的依据。
上一章学习一个或两个样本平均数的假设测验方法本章将学习k≥3个样 本平均数的假设测验方法。在k≥3个样本能否用统计推断的方法进行两 两测验呢?回答是不可取的。主要原因是会提高犯第一类错误的概率。 例如,用一对一比较的方法检验5个平均数之间的相等性,共检验10对。 假设每一对检验接受无效假设的概率都是 1-α=0.95,而且这些检验都是 独立的,那末,10对都接受的概率是0.9510=0.60, α′=1-0.6=0.40,犯 第一类错误的概率明显增加。解决这一问题的一种统计方法,叫做方差 分析法。此法将所有k个样本的观察值和平均数作为一个整体加以考虑, 把观察值总变异的自由度和平方和分解为不同变异来源的自由度和平方 和,进而获得不同变异来源的总体方差估值。计算这些估值的适当的 F值, 就测验假设H0: µ1=µ2=µ3=……µk(各总体平均数相等),方差分析是科
2 2 1
k
2
(14 21) (29 21) ] 504
2 2
SSt
Ti
n
2
72 92 56 116 C 7056 504 4
2 2 2 2
SST SS t SS e ,
DFT DFt DFe
本例中 自由度:
平方和:602=504+98 15=3+12
2
4
2
T42 1162 2 2 2 2 28 27 29 32 14 n 4
从理论上讲,这4个误差平方和除以相应的 自由度得的误差均方都可以作为总体误差 方差的无偏估计值。但是,用它们的加权 平均值来估计总体误差方差,则效果更佳。 所以:
SS e ( yij yi ) 38 20 26 14 98
学的实验设计和分析中的一个十分重要工具。
5.1.1
自由度和平方和的分解
方差是平方和除以自由度的商。要将一个试验资
料的总变异分解为各个变异来源的相应变异,首先必
须将总自由度和总平方和分解为各个变异来源的相应 部分。因此,自由度和平方和的分解是方差分析的第 一步。
下面我们首先用一个例子来说明这一问题。
因此误差平方和可以采用简单的办法计算
SSe=SST-SSt=602-504=98。
进而可得均方:
SS t 504 MS t s 168.00 df t 3
2 t
SS e 98 MS e s 8.17 df e 12
2 e
将上述例子推广到一般,设有k组数据,每组皆 具n个观察值,则资料共有nk个观察值,其数据 分组如表6.1(P99)。
SS t 需要注意的是, df 系样本平均数的方差,
t
是
2
n 的估值,而
SS e
df e
2 则是 的估值
为了进行正确的F 测验,必须使它们都是估
计同一参数
应为:
2 。因而,处理 (组间)平方和
SSt nSSt n ( yi y )
2 1
k
2 T i
n
C
SSt n ( yi y ) 4 [(18 21) (23 21)
有剂A内: SSe ( y1 j y1 ) y1 j
1
2
2 T12 72 182 212 202 132 38 n 4
SS e ( y 2 j y 2 ) 2 y 2 j 药剂B内:
[例5.1]以A、B、C、D4种药剂处理水稻种 子,其中A为对照,每处理各得4个苗高观 察值(cm),试分解其自由度和平方和。
药剂 A B 18 20 苗高观察值 yi 21 24 20 26 13 22 总和Ti 72 92 平均数 18 23
C
D
10
28
15
27
17
29
14
32
56
116
14
T=336
2 1 1
k
n
每个组内(处理内)的自由度为:n -1=4-1=3,
所以误差的自由度为:DFe=k(n-1)=4(4-1)=12
3、处理效应 如果没有处理效应,表中各个处理(组)平均数
yi
从理论上讲均应该相等, 因此可以用 y i
来度量处理效应。
SS t ( yi y ) ,
2 1
k
DFt (k 1)
