勾股数的规律
勾股数规律的探究

勾股数的规律能够组成一个直角三角形的三边长的正整数,叫做勾股数。
如“勾三股四弦为五”(3,4,5)再如常见的(6,8,10)(5,12,13)、(7,24,25),熟记一些勾股数利于我们更快、更准的解决于直角三角形有关的实际问题。
下面就勾股数的三个正整数之间的规律进行探究:规律一:在勾股数(3,4,5)、(5,12,13)、(7,24,25)(9,40,41)中,我们发现由(3,4,5)有: 32=9=4+5由(5,12,13)有: 52=25=12+13由(7,24,25)有: 72=49=24+25由(9,40,41)有: 92=81=40+41.即在一组勾股数中,当最小边为奇数时,它的平方刚好等于另外两个连续的正整数之和。
其论证如下:数a为大于1的正数,则2a+1为奇数数,则有∵(2a+1)2=4a2+4a+1=(2a2+2a)+(2a2+2a+1)∴(2a +1)2+(2a 2+2a)2=(2a2+2a+1)2因此,我们把它推广到一般,从而可得出勾股数公式一:(2a+1,2a2+2a,2a2+2a+1)(a为正整数)或整理为:对于一个大于1的整奇数m,构成的勾股数为(m,,)规律二:在勾股数(6,8,10)、(8,15,17)、(10,24,26)中,我们发现由(6,8,10)有: 62=36=2×(8+10)由(8,15,17)有: 82=64=2×(15+17)由(10,24,26)有: 102=100=2×(24+26)即在一组勾股数中,当最小边为偶数时,它的平方刚好等于两个连续且相差为2的整数之和的二倍。
其论证如下:数a为大于1的正数,则2a为偶数,则有∵(2a)2=4a2=2[(a2-1)+(a2+1)]∴(2a)2+(a2-1)2=(a2+1)2(a≥2且a为正整数)因此,我们把它推广到一般,从而可得出勾股数公式二:(2a,a2-1,a2+1)(a≥2且a为正整数)或整理为:对于一个大于1的整偶数m,构成的勾股数为(m,,)。
探索勾股数的规律
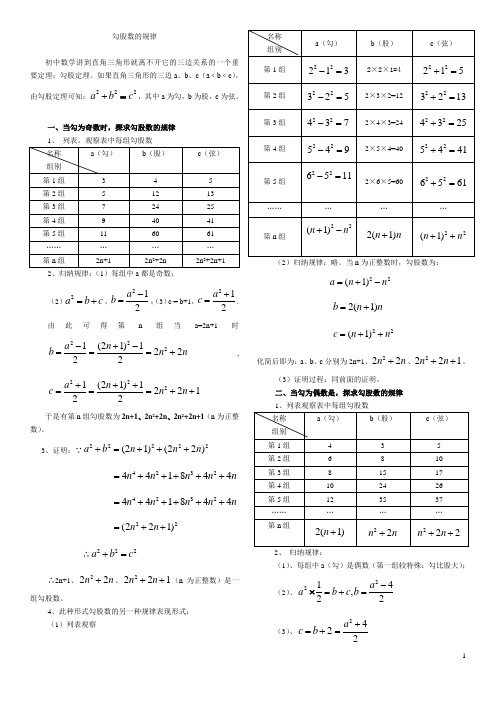
勾股数的规律初中数学讲到直角三角形就离不开它的三边关系的一个重要定理:勾股定理。
如果直角三角形的三边a 、b 、c (a ﹤b ﹤c ),由勾股定理可知:222a b c +=,其中a 为勾,b 为股,c 为弦。
一、当勾为奇数时,探求勾股数的规律 1、 列表,观察表中每组勾股数2、归纳规律:(1)每组中a 都是奇数;(2)2a b c =+,212a b -=;(3)c = b+1,212a c +=.由此可得第n 组当a=2n+1时2221(21)12222a n b n n-+-===+,2221(21)122122a n c n n +++===++于是有第n 组勾股数为2n+1、2n 2+2n 、2n 2+2n+1(n 为正整数)。
3、证明:∵22222(21)(22)ab n n n +=+++4232441844n n n n n =+++++ 4232441844n n n n n =+++++22(221)n n =++∴222ab c +=∴2n+1、222n n +、2221n n ++(n为正整数)是一组勾股数。
4、此种形式勾股数的另一种规律表现形式: (1)列表观察(2)归纳规律:略。
当n 为正整数时,勾股数为:22(1)a n n =+-2(1)b n n =+22(1)c n n =++化简后即为:a 、b 、c 分别为2n+1、222nn +、2221n n ++。
(3)证明过程:同前面的证明。
二、当勾为偶数是,探求勾股数的规律 1、列表观察表中每组勾股数 2、 归纳规律:(1)、每组中a (勾)是偶数(第一组较特殊:勾比股大);(2)、2214,22a abc b -=+=⨯(3)、2c b =+242a +=由此可得第n 组中的2(1)a n =+时,则:2224[2(1)]4224a n b n n -+-===+2224[2(1)]42224a n c n n +++===++[或22c=b+2=(n2n)+2=n 2n+2++],于是有第n 组勾股数为2(1)n +、22n n +、222n n ++(n为正整数)。
勾股数规律

勾股数规律
规律一:在勾股数(3,4,5)、(5,12,13)、(7,24,25)(9,40,41)中,发现:
由(3,4,5)有: 32=9=4+5
由(5,12,13)有: 52=25=12+13
由(7,24,25)有: 72=49=24+25
由(9,40,41)有: 92=81=40+41.
即在一组勾股数中,当最小边为奇数时,它的平方刚好等于另外两个连续的正整数之和。
因此,我们把它推广到一般,从而可得出以下公式:
∵(2n+1)2=4n2+4n+1=(2n2+2n)+(2n2+2n+1)
∴(2n+1)2+(2n2+2n)2=(2n2+2n+1)2(n为正整数)
勾股数公式一:(2n+1,2n2+2n,2n2+2n+1)(n为正整数)
规律二:在勾股数(6,8,10)、(8,15,17)、(10,24,26)中,发现:
由(6,8,10)有: 62=36=2×(8+10)
由(8,15,17)有: 82=64=2×(15+17)
由(10,24,26)有: 102=100=2×(24+26)
即在一组勾股数中,当最小边为偶数时,它的平方刚好等于两个连续整数之和的二倍,推广到一般,从而可得出另一公式:
∵(2n)2=4n2=2[(n2-1)+(n2+1)]
∴(2n)2+(n2-1)2=(n2+1)2(n≥2且n为正整数)
勾股数公式二:(2n,n2-1,n2+1)(n≥2且n为正整数)
利用以上两个公式,我们可以快速写出各组勾股数。
常见勾股数大全

常见勾股数大全勾股数,又称直角三角形的边长,是指一个三角形中的三条边中,满足勾股定理的关系,即a² + b² = c²。
在数学中,勾股数是一种特殊的整数,它们之间存在着一些特殊的规律和性质。
下面我们来总结一下常见的勾股数大全,希望对大家有所帮助。
1. 3、4、5勾股数。
3、4、5勾股数是最简单的勾股数之一,满足3² + 4² = 5²。
它是勾股数中最小的一组,也是最早被人们发现的勾股数之一。
在古代,人们就已经知道了这组勾股数的存在,并且应用于建筑、农业等方面。
2. 5、12、13勾股数。
5、12、13勾股数是另一组常见的勾股数,满足5² + 12² = 13²。
它也是一个较小的勾股数组合,可以在实际生活中找到很多应用场景,比如房屋建筑、道路规划等。
3. 7、24、25勾股数。
7、24、25勾股数是另一组常见的勾股数,满足7² + 24² = 25²。
它是一个稍大一些的勾股数组合,同样可以在实际生活中找到很多应用场景,比如航天工程、城市规划等。
4. 8、15、17勾股数。
8、15、17勾股数是另一组常见的勾股数,满足8² + 15² = 17²。
它也是一个较小的勾股数组合,可以在实际生活中找到很多应用场景,比如建筑设计、农业规划等。
5. 9、40、41勾股数。
9、40、41勾股数是另一组常见的勾股数,满足9² + 40² = 41²。
它是一个稍大一些的勾股数组合,同样可以在实际生活中找到很多应用场景,比如航天工程、城市规划等。
6. 11、60、61勾股数。
11、60、61勾股数是另一组常见的勾股数,满足11² + 60² = 61²。
它也是一个较小的勾股数组合,可以在实际生活中找到很多应用场景,比如建筑设计、农业规划等。
勾股数顺口溜100句

勾股数顺口溜如下:1. 勾股定理要记牢,3,4,5是诀窍。
2. 根号下开出2来,6,8,10来寻找。
3. 根号下开出3来,9,12,15来寻找。
4. 根号下开出5来,15,20,25来寻找。
5. 根号下开出6来,24,30,36来寻找。
6. 勾股数在图形中,三角形里他最灵。
7. 勾股定理真奇妙,三边关系它指导。
8. 直角三角形边勾股,斜边直角紧相邻。
9. 勾股定理是定理,作图验证最明现。
10. 验证之后最明了,三边关系都明了。
11. 勾股定理有前提,必须直角三边形里。
12. 直角三角形三边长,勾股定理最能帮。
13. 已知直角三角形边长,求另两边长用勾股。
14. 已知直角三角形边长,求角度也用它。
15. 已知直角三角形角度,求边长也用它。
16. 勾股定理作用大,计算长度都靠它。
17. 勾股定理有妙用,数形结合是宝招。
18. 已知两边求第三边,勾股定理最方便。
19. 已知三边求角度,余弦定理不可少。
20. 已知角度求两边,正弦定理少不了。
21. 勾股定理是基础,三边关系紧相连。
22. 直角三角形常出现,勾股定理最方便。
23. 已知三边求角度,余弦定理不可少。
24. 已知角度求边长,正弦定理少不了。
25. 勾股定理在图形,直角三角形最明现。
26. 勾股定理是基石,三角函数是依靠。
27. 勾股定理在计算,长度角度最方便。
28. 勾股定理是宝招,数形结合不可少。
29. 勾股定理作用大,数学计算都靠它。
30. 勾股定理真奇妙,数学世界离不了。
31. 勾股定理很简单,理解概念是关键。
32. 勾股定理要记牢,应用广泛不可少。
33. 勾股定理是基石,数学计算都靠它。
34. 勾股定理是妙招,解决问题离不了。
35. 勾股定理用途广,数形结合最妙招。
36. 勾股定理很神奇,生活实际都靠它。
37. 直角三角形三边长,勾股定理最妙用。
38. 勾股定理有妙用,生活处处离不了。
39. 勾股定理作用大,数学世界都靠它。
40. 勾股定理是宝招,数学计算离不了。
勾股数组成规律

八年级学了勾股定理后,我们知道了勾3,股4,弦5。
也就是在一个直角三角形中,三条直角边的长,都是正整数时,我们称这三个数就是一组勾股数。
现在考试题型中,和勾股数有关的题型也越来越多。
本文重点讲述勾股数之间的构造规律
我们还总结出来一个方便理解和记忆的方法:
在一组勾股数中,若第一个数是奇数,则另外两个数,一个数是它的平方减1的一半,一个数是它的平方加1的一半。
在一组勾股数中,若第一个数是奇数,则另外两个数,一个数是它的平方减1的一半,一个数是它的平方加1的一半。
在一组勾股书中,当一个数是偶数时,则另外两个数,一个数是它的一半的平方减1,另一个数是它一半的平法加1.。
勾股数的规律详解

勾股数的规律详解勾股数又名毕氏三元数凡是可以构成一个直角三角形三边的一组正整数,称之为勾股数。
①观察3,4,5;5,12,13;7,24,25;…发现这些勾股数都是奇数,且从3起就没有间断过。
计算0.5(9-1),0.5(9+1)与0.5(25-1),0.5(25+1),并根据你发现的规律写出分别能表示7,24,25的股和弦的算式。
②根据①的规律,用n的代数式来表示所有这些勾股数的勾、股、弦,合情猜想他们之间的两种相等关系,并对其中一种猜想加以说明。
③继续观察4,3,5;6,8,10;8,15,17;…可以发现各组的第一个数都是偶数,且从4起也没有间断过,运用上述类似的探索方法,之间用m的代数式来表示它们的股合弦。
设直角三角形三边长为a、b、c,由勾股定理知a^2+b^2=c^2,这是构成直角三角形三边的充分且必要的条件。
因此,要求一组勾股数就是要解不定方程x^2+y^2=z^2,求出正整数解。
例:已知在△abc中,三边长分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1),求证:∠c=90°。
此例说明了对于大于2的任意偶数2n(n>1),都可构成一组勾股数,三边分别是:2n、n2-1、n2+1。
如:6、8、10,8、15、17,10、24、26…等。
再来看下面这些勾股数:3、4、5,5、12、13,7、24、25,9、40、41,11、60、61…这些勾股数都是以奇数为一边构成的直角三角形。
由上例已知任意一个大于2的偶数可以构成一组勾股数,实际上以任意一个大于1的奇数2n+1(n>1)为边也可以构成勾股数,其三边分别是2n+1、2n2+2n、2n2+2n+1,这可以通过勾股定理的逆定理获证。
观察分析上述的勾股数,可看出它们具有下列二个特点:1、直角三角形短直角边为奇数,另一条直角边与斜边是两个连续自然数。
2、一个直角三角形的周长等于短直角边的平方与短边自身的和。
掌握上述二个特点,为解一类题提供了方便。
勾股数规律

(5)勾股数组的规律满足不定方程a 2+b 2=c 2的三个正整数称为勾股数组。
古巴比伦公元前2000年左右就发现了很多勾股数组。
成书于西汉时期的《周髀算经》中记载的(3,4,5)无疑是中国数学史上发现最早的一组勾股数组。
公元一世纪,我国古代数学著作《九章算术》中对于具体的数据(如勾股和、弦长等)给出了求勾股弦三个数的具体算法。
有人推测,九章算术已经给出了勾股数的一般规律:若给了两个数m 、n ,则)(2122n m -、mn 、)(2122n m +就是一组勾股数,刘徽更明确了所有的勾股数组的比率满足这一规律,但从文字看还只是具体数据的,尚不能明确。
公元前6世纪毕达哥拉斯学派发现:任取一个奇数,把它的平方数分为相差1的两个数,那么这三个数就是勾股数. 若m 为大于1的奇数,则(m ,212-m ,212+m )便是一组勾股数组。
因此,国外人们习惯把勾股数组叫做毕达哥拉斯三元数组。
欧几里得也曾给出求勾股数组的方法:m 、n 是整数,(2222,2,m n m mn n +-)是一组勾股数。
实际上,可以证明:在三个数互质的情况下,勾股数组都可以写成(2222,2,m n m mn n +-)的形式,或者说勾股数组都可以写成()(,2),k(m 2222n m k kmn n +-)的形式。
◎勾股数组的规律,可能真是一个“下金蛋的母鸡”勾股数组的规律,太复杂了,学生哪能探究?是的,学生要完全探究出这些规律确实困难,但也许学生探究的过程中会有很多收获哟。
当年,被称为“业余数学家之王”的法国数学家费马,在阅读丢番图的《算术》一书中“分一个给定的平方数为两个平方数的和”这个问题时,写下了著名的旁注:“一个立方数不可能分解成两个立方数的和,一个四次方数不能分解成两个四次方数的和,一般地说,大于2的任意次幂的数都不能分解为两个同次幂的数的和。
我找到了这个命题的一个真正奇妙的证明,但书上空白的地方太窄,写不下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选范本
所谓勾股数,就是当组成一个直角三角形的三边长都 为正整数时,我们就称这一组数为勾股数
那么,组成一组勾股数的三个正整数之间, 是否具有一定的规律 可寻呢?下面我们一起来观察几组勾股数:
规律一:在勾股数(3, 4, 5)、( 5,12,13)、( 7,
24, 25)( 9, 40,41)中,我们发现
由(3, 4, 5)有:
3 2=9=4+5 由(5, 12, 13)有:
5 =25=12+13 由(7, 24, 25)有:
7 =49=24+25 由(9, 40, 41)有: 92=81=40+41.
即在一组勾股数中,当最小边为奇数时,它的平方刚好 等于
另外两个连续的正整数之和。
因此,我们把它推广到一般,从而 可得出以下公式:
2 2 2 2
•••(2n+1) =4n+4n+仁(2n +2n ) + (2n+2n+1)
2 2 2 2 2
•••(2n+1) + (2n+2n ) = (2n+2n+1)
(n 为正整数) 勾股数公式一:(2n+1, 2n 2+2n , 2n 2+2n+1)(n 为正整数) 等于两个连续整数之和的二倍,推广到一般,从而可得出另一公式:
2 2 2 2
•••(2n ) =4n =2[ (n-1 ) + (n+1)]
•••(2n ) + (n-1 ) = (n +1) (n 》2 且 n 为正整数)
勾股数公式二:(2n , n 2-1 , n 2+1)( n 》2且n 为正整 数)
禾U 用以上两个公式,我们可以快速写出各组勾股数。
规律二:在勾股数(6, 8, 26)中,我们发现 由(6, 8, 10)有: 由(8, 15, 17)有: 由(10, 24, 26)有: 即在
一组勾股数中, 10)、( 8, 15, 17)、( 10, 24,
2 6 =36=2X( 8+10)
82=64=2X( 15+17)
2 10 =100=2X( 24+26) 当最小边为偶数时,它的平方刚好。
