直方图的形状分析和判断
2016监理工程师《三控》考点18-4

2016监理工程师《三控》考点18-4考点:工程质量统计分析方法(一)调查表法统计调查表法又称统计调查分析法,它是利用专门设计的统计表对质量数据进行收集、整理和粗略分析质量状态的一种方法。
在质量控制活动中,利用统计调查表收集数据,简便灵活,便于整理,实用有效。
它没有固定格式,可根据需要和具体情况,设计出不同统计调查表。
应当指出,统计调查表往往同分层法结合起来应用,可以更好、更快地找出问题的原因,以便采取改进的措施。
(二)分层法分层法又叫分类法,是将调查收集的原始数据,根据不同的目的和要求,按某一性质进行分组、整理的分析方法。
分层法是质量控制统计分析方法中最基本的一种方法。
其他统计方法一般都要与分层法配合使用。
(三)排列图法1.排列图法的概念(I)用途:排列图法是利用排列图寻找影响质量主次因素的一种有效方法。
(2)排列图又叫帕累托图或主次因素分析图,它是由两个纵坐标、一个横坐标、几个连起来的直方形和一条曲线所组成。
2.排列图的观察与分析(I)观察直方形,大致可看出各项目的影响程度。
排列图中的每个直方形都表示一个质量问题或影响因素。
影响程度与各直方形的高度成正比。
(2)利用ABC分类法,确定主次因素。
将累计频率曲线按0~80%、80%~90%、90%~l00%分为三部分,各曲线下面所对应的影响因素分别为A、B、C三类因素。
3.排列图的应用排列图可以形象、直观地反映主次因素。
其主要应用有:(1)分析造成质量问题的薄弱环节。
(按不合格点的内容分类)(2)找出生产不合格品最多的关键过程。
(按生产作业分类)(3)分析比较各单位技术水平和质量管理水平。
(按生产班组或单位分类)(4)分析措施是否有效。
(将采取提高质量措施前后的排列图对比)(5)还可以用于成本费用分析、安全问题分析等。
(四)因果分析图法1.因果分析图法的概念(1)用途。
因果分析图法分析某个质量问题(结果)与其产生原因之间关系。
(2)因果分析图也称特性要因图,又因其形状常被称为树枝图或鱼刺图。
正态分布判定标准(一)

正态分布判定标准(一)正态分布判定标准引言正态分布是统计学中最重要的分布之一,广泛应用在各个领域的数据分析和建模中。
判断一个数据集是否服从正态分布是数据分析的基础,本文将介绍常用的正态分布判定标准。
直方图观察法使用直方图是最常见的判断一个数据集是否服从正态分布的方法之一。
1.绘制直方图:将数据按照一定的组距分组,并绘制柱状图。
横轴表示数据的取值范围,纵轴表示该范围内数据的频数或频率。
2.观察直方图形状:正态分布的直方图呈钟形曲线状,均值处的频数最高,两侧对称逐渐变小。
如果数据的直方图近似呈现钟形曲线状,则可以初步认定数据集服从正态分布。
正态概率图观察法正态概率图是一种常用的判定数据服从正态分布的方法。
1.绘制正态概率图:将数据按照从小到大排序,并绘制点图。
横轴表示数据的排序位置,纵轴表示数据的值。
2.观察图形形状:如果数据集服从正态分布,图形应该近似为一条直线。
如果图形出现明显的非线性趋势或者拐点,则说明数据不服从正态分布。
正态概率图更加直观地展现了数据是否服从正态分布。
Shapiro-Wilk检验法Shapiro-Wilk检验是一种常用的正态性检验方法,适用于样本量较小的情况。
1.提出假设:首先提出原假设和备择假设。
原假设(H0)是“样本数据符合正态分布”,备择假设(H1)是“样本数据不符合正态分布”。
2.计算检验统计量:根据样本数据计算出Shapiro-Wilk检验的统计量W。
3.判断拒绝域:根据设定的显著性水平,查表得到临界值。
如果W小于临界值,则拒绝原假设,说明数据不服从正态分布;反之,则无法拒绝原假设,说明数据服从正态分布。
Shapiro-Wilk检验是一种较为准确的正态性检验方法,但对于样本量较大的数据集效果并不理想。
正态性指标判定法除了上述方法外,还可以通过一些统计指标来判定数据的正态性。
1.偏度(Skewness):衡量数据分布的偏斜程度。
当偏度接近0时,数据分布较为对称,符合正态分布;当偏度大于0时,数据分布向右偏斜,当偏度小于0时,数据分布向左偏斜。
直方图的形状分析和判断

分析和判断
标准型
标准型
标准型地形状是中间高,两边低,左右基本对称.数据大体上呈正态分布,这时可判定工序处于稳定状态.
左偏向型右偏向型
偏向型
一边地频数递减较快,形成左偏或右偏.
一些有形位公差等要求地特性值是偏向型分布.也有地是由于加工习惯而造成地.例如由于加工者担心产生不合格品,加工孔时常偏小呈左偏向型,加工轴时常偏大呈右偏向型.
此时需要研讨组距是否取数据测定单位地整数倍,或者观测测定者读计测器刻度有无坏习惯.
平顶型
平顶型
直方图没有突出地顶峰,这主要是再生产过程中有缓慢变化地因素影响而造成地.如刀具地磨损,操作者地疲劳等.
孤岛型
孤岛型
在直方图地左边或右边出现孤立地长方形.这是测量有误,或生产过程中出现异常因素而造成地.如原材料一时地变化,刀具严重磨损,或混入了少量不同规格地产品或短时间由部熟练工替班等.
由于剔除了பைடு நூலகம்合格品地数据所作地直方图也呈偏向型,则可判断测量工作有假.
双峰型
双峰型
直方图出现两个顶峰,往往由于把不同地材料、不同加工者、不同操作方法、不同设备生产地两批产品混在一起而造成地.
这时若分层作直方图就能发现其差异.
锯齿型
锯齿型(包括掉齿型)
直方图象锯齿一样凹凸不平,大多是由于分组不当或检测数据不准而造成地,应查明原因,采取措施,重新作图分析.
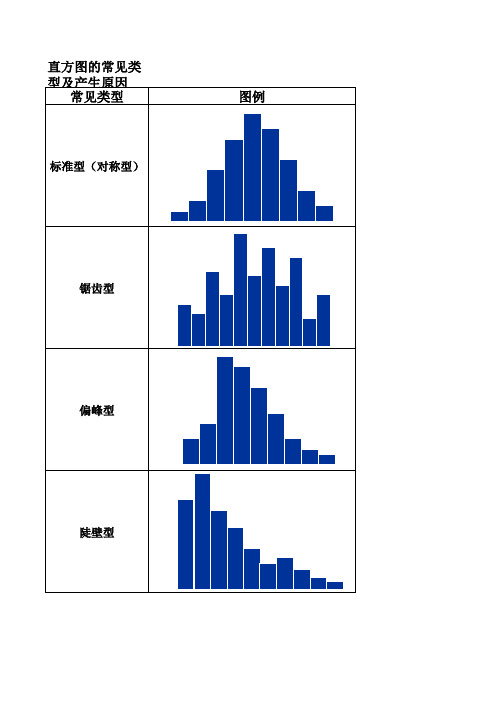
直方图的常见类型及产生原因
①夹杂了其他分布的少量数据; ②原材料发生变化; 在标准型的直方图的一侧 ③生产过程发生了变化; 有一个“小岛”。 ④不熟练的工人替班等; ⑤测量错误。
直方图的常见类型及产生原因 常见类型 图例
标准型(对称型)
锯齿型
偏峰型
陡壁型
平顶型
双峰型
孤岛型
形状
产生的可能原因
中间高,两边低,左右基 在正常生产中许多质量指标呈现这种 本对称的情况。 形状。
①作频数分布表时,如分组过多; ②当测量方法不当或读错测量数据; ③量具的精度较差。
①当下限(或上限)受到公差等因素限 制时; 形状一:峰偏在左边,而 ②操作者(含测作的图形; 形状二:峰偏在右边,而 ④质量特性值的单侧控制造成,譬如 左面的尾巴较长。 加工孔的时候习惯于孔径“宁小勿大 ”,而加工轴的时间习惯于轴径“宁 大勿小”等。
平均值远左离(或右离)直 ①当工序能力不足,为找出符合要求 方图的中间值,频数自左 的产品经过全数检查,或过程中存在 至右减少(或增加),直方 自动反馈调整时。 图不对称。
①当几种平均值不同的分布混在一 起; ②过程中某种要素缓慢劣化时,譬如 刀具的磨损等。
当有两种不同的平均值相差大的分布 混在一起时,常出现这种形状,譬如 靠近直方图中间值的频数 将两台不同精度的机床生产的或两个 较少,两侧各有一个“峰 不同操作水平的工人生产的或由两批 ”。 不同原材料生产的产品的数据混合所 致。
如何看懂直方图

如何看懂直方图!了解图片质量好坏自入单反后请教了不少老师,同时也在网上找了一些知识来学习,觉得直方图对拍摄很有参考价值,故用积分换来了这篇文章,学习后觉得很受启发,所以转发了上来,供朋友们分享,废话少说,转文如下:准确曝光的好帮手教你如何看懂直方图随着数码相机(以下简称DC)图像处理技术的不断发展,越来越多的相机内置了直方图的功能。
虽然直方图对初学者来说,还很陌生。
但它却早已存在于我们的生活、工作中。
如在著名的图像处理软件Photoshop里面,对应直方图的命令就是Histogram(中文版为“直方图”)。
直方图的含义在一张图片的直方图中,横轴代表的是图像中的亮度,由左向右,从全黑逐渐过渡到全白;纵轴代表的则是图像中处于这个亮度范围的像素的相对数量。
在这样一张二维的坐标系上,我们便可以对一张图片的明暗程度有一个准确的了解。
在Photoshop中,依次单击“图像→调整→色阶(快捷键:Ctrl+L)”即可打开色阶调整框,对图像的直方图进行调整,以此控制图像的明暗变化。
图-1直方图图例直方图的特性DC中的直方图功能与Photoshop中的是一样的。
当直方图中的黑色色块偏向于左边时,说明这张照片的整体色调偏暗,也可以理解为照片欠曝。
而当黑色色块集中在右边时,说明这张照片整体色调偏亮,除非是特殊构图需要,否则我们可以理解为照片过曝。
下面,我们就用几张照片来直观地理解直方图所反映的图像特性。
图-2曝光准确图-2是一张正常曝光的建筑物照片及其对应的直方图。
我们可以看到,在直方图中比较靠左的位置,波峰比较高而且比较密集,这是因为建筑物的背影有较多的暗部区域,而直方图中左侧的位置正是反映暗部区域的分布情况的。
在直方图中央偏右的位置,我们又可以看到一个较高的波峰,这是因为图像中大片的黄色区域所对应的亮度正在这里。
在直方图的最右端,我们可以看到一个较小且突出的波峰,对应在图像中,代表的就是建筑物上圆柱体的强烈反光,由于亮度太大,超出了直方图所能表示的范围,所以便体现在最右端形成了一个波峰。
食品质量管理的工具—直方图

0
0 0.5 5.5
10.5 15.5 20.5 25.5 30.5 35.5 40.5 45.5 50.5
1
2
3
4
5
6
7
8
9
10
11
12
溢出量/g
植物油溢出量直方图
《食品安全与质量控制》
直方图的分析和注意事项
目录 Contents
1 直方图在PDCA循环中的地位 2 直方图的分析 3 使用直方图的注意事项
第1组上界限
第1组下界限加组距:0.5+5=5.5
直方图
直方图的应用
第2组下界限
与第1组上界限相同:5.5
第2组上界限
第2组下界限加组距:5.5+5=10.5 ………… 其他以此类推
直方图
直方图的应用 5.编制频数分布表
组号 1 2 3 4 5 6 7 8 9 10
合计
组界 0.5~ 5.5 5.5~ 10.5 10.5~ 15.5 15.5~ 20.5 20.5~ 25.5 25.5~ 30.5 30.5~ 35.5 35.5~ 40.5 40.5~45.5 45.5~ 50.5
直方图
直方图的分析 ㈡ 与规范界限(公差)的比较分析
常见类型
TL
图例
MX
理想型
TL
X
M
偏心型
调整要点
TU
图形对称分布,且两边有一定 余量,此时,应采取控制和监督办 法。
TU
调整分布中心X,使分布中心 X 与公差中心M重合。
直方图
直方图的分析
常见类型
TL
无富余型
图例
MX
TL
能力富余型
利用直方图进行样本质量评估的方法与步骤

利用直方图进行样本质量评估的方法与步骤随着数据应用场景的不断增多,数据质量的重要性也越来越受到人们的关注。
数据质量不仅关乎业务决策的准确性,也直接影响到数据分析的结果和模型的准确性。
因此,对于数据的质量进行评估是至关重要的。
利用直方图进行样本质量评估是一种简单而有效的方法,本篇文章将介绍直方图的基本概念、样本质量评估的基本概念以及基于直方图的样本质量评估方法,并结合案例进行说明。
直方图的基本概念直方图是一种统计图表,用来表示数据集中各数据的频数分布情况,通常用于了解数据的分布密度和分散程度。
直方图由多个柱形图组成,每个柱形图表示一个数据区间的频数或频率。
直方图的横轴通常表示数据的范围或类别,纵轴表示频数或频率。
基本概念包括直方图的定义、组成部分和构建方法。
1. 直方图的定义直方图是表示数据集分布情况的图形统计工具,通常使用柱状图表示数据集中各数据之间的频数分布情况。
2. 直方图的组成部分直方图主要由以下三个部分组成:(1)数据区间:将数据集按照一定的范围划分为若干个数据区间。
(2)频数或频率:用柱形的高度表示每个数据区间内包含数据的频数或频率。
(3)坐标轴:通常使用横轴表示数据区间,纵轴表示频数或频率。
3. 直方图的构建方法构建直方图通常需要以下步骤:(1)选择数据区间,并确定每个数据区间的宽度。
(2)计算每个数据区间的频数或频率,通常使用频数或频率分布表汇总数据。
(3)绘制直方图,一般使用柱状图来表示数据区间的频数或频率。
样本质量评估的基本概念对于数据样本的质量评估,通常需要了解样本质量评估的定义、指标和方法。
1. 样本质量评估的定义样本质量评估是指对样本数据的质量进行评定的过程,通过一系列评估指标和评估方法对数据的质量进行分析和评估。
2. 样本质量评估的指标样本质量评估的指标通常包括以下几个方面:(1)准确度:样本数据与真实数据之间的误差。
(2)完整度:样本数据是否完整,是否存在缺失值等。
(3)一致性:样本数据之间是否存在差异,是否符合预期。
8直方图分析

1 - 22
质量管理 学实验
样本数据
(
n=125
)
1 - 23
质量管理 学实验
解: ⑴求极差R:先找出数据中的最大值和最小值: Xmax=74.030,Xmin=73.967
则R=L-S=0.063mm ⑵决定数据分组组数k和每组的组距h: 求K值的经验公式:k≈1+3.322lg(n)或k≈SQRT(n) (圆整)
1 - 27
质量管理 学实验
从直方图可以看出:
a)形状:单峰近似对称。 b)位置或中心倾向:中心倾向接近74mm,在73.988~74.016 mm
占绝大多数(86.4%)。 c)分散或变异程度(S2):变异程度较大(孤岛型)。
1 - 28
结束
2、直方图与规范界限(公差/质量标准) 的比较分析
1 -3
质量管理 学实验
直方图形状的观察分析
1、正常型 2、偏向型 3、孤岛型 4、锯齿型 5、平顶型 6、双峰型
1 -4
质量管理 学实验
直方图形状的观察分析
a)正常型:符合正态分布规律,表明工序稳定,无异 1 常- 5因素
质量管理 学实验
直方图形状的观察分析
,也可参照分组组数表选择。 确定组距:h=R/k (圆整),h应为最小测量单位m的整数
位(m=0.001)。 本例:k=9,h=0.063/9≈0.007 mm
1 - 24
质量管理 学实验
⑶确定各组组限和组中值yi: 各组组限:[a0,a1), [a1,a2),…, [ak-1,ak ] 这里:a1= a0+h, a2= a1+h, …, a k-1= a k-1+h 组中值:yi=( a i-1 +a i)/2 本例: a0=73.967,a9=74.030 注:为避免出现空白组,第一组和第末组可采取“××以
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双峰型
双峰型
直方图出现两个顶峰,往往由于把不同的材料、不同加工者、不同操作方法、不同设备生产的两批产品混在一起而造成的。
这时若分层作直方图就能发现其差异。
பைடு நூலகம்锯齿型
锯齿型(包括掉齿型)
直方图象锯齿一样凹凸不平,大多是由于分组不当或检测数据不准而造成的,应查明原因,采取措施,重新作图分析。
表6.4.6直方图的形状分析和判断
直方图类型
分析和判断
标准型
标准型
标准型的形状是中间高,两边低,左右基本对称。数据大体上呈正态分布,这时可判定工序处于稳定状态。
左偏向型右偏向型
偏向型
一边的频数递减较快,形成左偏或右偏。
一些有形位公差等要求的特性值是偏向型分布。也有的是由于加工习惯而造成的。例如由于加工者担心产生不合格品,加工孔时常偏小呈左偏向型,加工轴时常偏大呈右偏向型。
此时需要研讨组距是否取数据测定单位的整数倍,或者观测测定者读计测器刻度有无坏习惯。
平顶型
平顶型
直方图没有突出的顶峰,这主要是再生产过程中有缓慢变化的因素影响而造成的。如刀具的磨损,操作者的疲劳等。
孤岛型
孤岛型
在直方图的左边或右边出现孤立的长方形。这是测量有误,或生产过程中出现异常因素而造成的。如原材料一时的变化,刀具严重磨损,或混入了少量不同规格的产品或短时间由部熟练工替班等。
