证明抛物线焦点弦的18个结论
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论重庆市开县临江中学张帮军2011.08/复习备考【内容摘要】关于抛物线的焦点弦到底有哪些结论呢?总结一下有四大类共18个结论,第一类是常见的基本结论;第二类是与圆有关的结论;第三类是由焦点弦得出有关直线垂直的结论;第四类是由焦点弦得出有关直线过定点的结论。
【关键词】证明抛物线焦点弦现在通过下面的例题来证明这些结论。
例:过抛物线y 2=2px (p >0)的焦点F 的一条直线AB 和此抛物线相交于A ,B 两点(α是直线AB 的倾斜角),准线l 的方程:x =-p 2,设点A (x 1,y 1),B(x 2,y 2),则有关抛物线的焦点弦有以下八个基本结论:(1)x 1x 2=p 24;(2)y 1y 2=-p 2;(3)|AF |=x 1+p 2;|BF |=x 2+p2(4)|AB |=x 1+x 2+p ;(5)|AB |=2p sin α;(6)|AF||BF|=p 2sin 2α;(7);1|AF |+1|BF |=2p(8)S △AOB =p22sin α证明:如图若α≠π2,则k =tan α因为点F(p 2,0),所以设直线AB 的方程为y =k (x -p 2)由y =k (x -p 2)y 2=2p px得k 2x 2-p (k 2+2)x +k 2p 24=0由根与系数的关系得:x 1x 2=p 24;x 1+x 2=p (k 2+2)k2∴(1)式得证∵A ,B 两点都在直线y 2=2px 上∴y 12=2px 1;y 22=2px 2∴(y 1y 2)2=4p 2x 1x 2=p 4∵y 1y 2<0,∴y 1y 2=-p 2即(2)式得证过点A ,B 分别作AA 1,BB 1与直线l 垂直,垂足为A 1,B 1即A 1(-p 2,y 1),B 1(-p 2,y 2)由抛物线定义知|AF |=|AA 1|=x 1+p 2;|BF |=|BB 1|=x 2+p 2即(3)式得证∵|AB |=|AF |+|BF |=x 1+x 2+p ∴(4)式得证∵x 1+x 2=p (k 2+2)k2,k =tan α∴|AB |=x 1+x 2+p =2p (k 2+1)k 2=2p (tan 2α+1)tan 2α=2p sin 2α即(5)式得证∵|AF ||BF |=(x 1+p 2)·(x 2+p 2)=x 1·x 2+p 2(x 1+x 2)+p 24=p 2(x 1+x 2+p )=p 2·2p sin 2α=p 2sin 2α∴(6)式得证∵1|AF |+1|BF |=|AF |+|BF ||AF |·|BF |=|AB ||AF |·|BF |=2psin 2α·sin 2αp 2=2p∴(7)式得证∵点O 到直线AB 的距离d 就是△AOB 的高∴h =d =p|k|21+k2姨=p sin α2∴S △AOB =12|AB|·h =12·2psin 2αp sin α2=p 22sin α∴(8)式得证下面来探究焦点弦与圆有关的四条结论:(1)以AB 为直径的圆M 与准线相切;(2)以AF 为直径的圆C 与y 轴准线相切;(3)以BF 为直径的圆D 与y 轴准线相切;(4)分别以AB ,AF ,BF 为直径的圆关系有:圆C 与圆D 外切;圆C 与圆D 既与y 轴相切又圆M 相内切。
很全抛物线焦点弦的有关结论附答案

很全抛杨线焦A孩的有关结E沦附答案[很 全]抛物线焦点 弦的有 关结论知识点1:若A3是过抛物线y 2 = IpX(P > 0)的焦点F 的弦。
设A(X^y I ∖ B(x 2,y 2),2则(1) X l Xy = — ; (2) y 1y-> =-p 2"4 …λλ,x2 =T- 综上:ArV2 =T-但儿儿<0,・・・儿儿=_1「 (2)另证:设 AB ∙.x = ιny+ 与),=2/x 联立,得J 2 一 2Pmy- P I = 0.Λy l >,2 = -P 2知识点2:若A3是过抛物线y 2 = 2∕ΛV (∕? > 0)的焦点F 的弦。
设A(X^y I ∖ β(x 2,y 2), 则(!)吩+5;⑵设直线細的倾斜角为S 则I 件鵲 证明:(1)山抛物线的定义知(2)若α = 90°,M ∣Jx 1 =x 2=-,由(1)矢Π∣AB ∣=2p = 2若 QH 90°,设AB : y = k(x-f),与y' =2px 联立,得.∙.召 + * /忙+2),.网=H- ⅛±1), k k知识点3:若A3是过抛物线y 2 = 2/9x(/? > 0)的焦点F 的弦,则以A3为直径的圆与 抛物线的准线相切。
证明:如图,(1)若AB 的斜率不存在时,依题意 X 1=X 2=-. :. X 1X 2 2若A3的斜率存在时,设为人则AB:(2) ∙.∙ X I = 2J :2 = P A 亠儿儿=±/『,得2〃而k = tanσ ,证明:过点A 、B 分别向抛物线的准线引垂线,垂足分别为A P 坊,过中点M 向准线引垂线,垂足为N,设以A3为直径的圆的半径为几・••以AB 为直径的圆与抛物线的准线相切。
接Ao 并延长交该抛物线的准线于点C,则BCHOF.证明:设 A(X H y l ), B(X 29y 2)9 则2 由知识点 1 知 y l y∖ = -P I:. y c = J >,2逆定理:若A3是过抛物线y 2 = 2∕zv(p > 0)的焦点F 的弦,过点B 作BC 〃OF 交抛 物线准线于点C 则A 、C 、O 三点共线。
抛物线焦点弦的八大结论推导过程

抛物线焦点弦的八大结论推导过程抛物线焦点弦是一个重要研究课题,它可以帮助我们理解抛物线的切线、焦点、双曲线、点到弦距离等微积分概念。
抛物线焦点弦推导过程通常被认为是一个好方向,它具有很多有益的特点,例如微积分知识的运用。
该过程包括以下步骤:一、首先,要确定抛物线的方程,它可以是一元二次方程,也可以是一般的双曲线方程。
二、然后,求解出抛物线的焦点和弦长,可以利用不同的函数求解方法来求解,或者可以利用几何的推导原理。
三、然后,可以运用微积分来求解抛物线的切线,可以利用极限的方法来求解抛物线的切线,同时也可以利用微分形式来求解抛物线的切线。
四、然后,可以利用数学分析的方法,用一元二次型或者双曲线型去绘制抛物线的切线,来求解抛物线焦点弦。
五、接着可以利用微积分中的定义来计算抛物线焦点弦的弧长,可以利用定积分的方法来计算抛物线弦的长度。
六、然后,利用向量的知识来求解抛物线焦点弦的方向,即利用向量的几何性质,推导出抛物线焦点弦的方向。
七、最后,可以利用抛物线焦点弦的方向和弦长,来进一步检验焦点弦是否符合抛物线的法则。
八、完成全部推导后,可以得到抛物线焦点弦的八个结论:1)抛物线的焦点和弦长可以用一元二次方程或者双曲线函数来求解。
2)抛物线的切线可以通过极限的方法和微分来求解。
3)焦点弦的长度可以通过定积分的方法来求解。
4)焦点弦的方向可以通过向量的几何性质来求解。
5)焦点弦的长度与抛物线的焦点和切线总是垂直。
6)距离抛物线在不同点上的距离是固定的,与抛物线的焦点和弦长相关。
7)抛物线在每个焦点点处均有弦,其长度总是相等的。
8)抛物线的弦长和焦点会满足正弦和余弦函数方程的要求。
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论
抛物线是一种椭圆形的函数图形,它是由抛物线焦点弦决定的。
抛物线焦点弦是指抛物线的两个焦点和连接它们的弦段。
围绕抛物线焦点弦可以建立18个结论。
1. 两个焦点之间的距离与抛物线弦段长度相同,即它们之间的距离等于抛物线弦段的1倍。
2. 弦段连接抛物线的两个焦点,因此,任何一点的垂直距离都等于其焦点的距离。
3. 对抛物线的焦点取中对称,则其两点之间的距离一定是直线的1倍.
5. 相对于一个焦点而言,另一个焦点总是处于弦段的同一边,而且位于弦段上面。
6. 抛物线是对称的,即抛物线的对称轴是连接两个焦点的直线段。
8. 抛物线准线与切线交于抛物线的焦点。
12. 对任意点A而言,从A点向任意点B连线便构成一条直线,此直线连接A点和B 点的距离有正有负,正值表示线段到抛物线焦点的距离是它的弦段长度所乘以2倍的直线段距离,负值则表示抛物线焦点到线段的距离也是它的弦段长度乘以2倍的直线段距离。
17. 抛物线的对称轴与它的弦段垂直,因此它的弦段将对称轴分为2个相等的距离。
以上就是抛物线焦点弦的十八个结论,也是其对称性规律、准确性和完整性的总结。
抛物线焦点弦的这些结论,既给抛物线函数提供了数学化的更直观的解释,又为描述抛物线的属性提供了一定的参考依据。
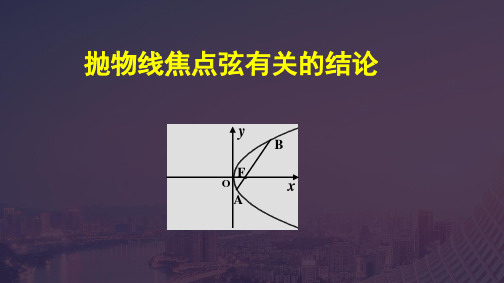
抛物线的焦点弦的性质全
1 cos
1 cos
FA FB p
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2),
思考:若直线AB与x轴的夹角为,焦点∆AOB的面积如何用表示
结论(4)
SAOB
p2
2sin
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2), 思考:以线段AB为直径的圆与准线有怎样的位置关系? 思考:以线段AF为直径的圆与y轴有怎样的位置关系?
抛物线焦点弦有关的结论
y
B
F
O
x
A
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2), 思考:A,B两点的横坐标之间有怎样的关系?纵坐标呢?
结论:(1)x1x2=p2/4; y1y2= -p2;
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2), 思考:如何求弦长|AB|,其最小值是多少?
2.已知抛物线C: y2=2px(p>0)的焦点为F,过F的直线与该抛物线交于P,Q两个 不同的点,P,Q两点在抛物线的准线上的射影分别为M,N,若|MF|=4, |NF|=4, 则p=( )
3.过抛物线C: y2=4x的焦点F的直线与抛物线交于A,B两点,若 |AF|=2 |BF|,则|AB|等于 ( )
结论:(2)|AB|=x1+x2+p 通径长为2 p 过焦点的所有弦中,通径最短
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2),
(完整版)抛物线的焦点弦_经典性质及其证明过程
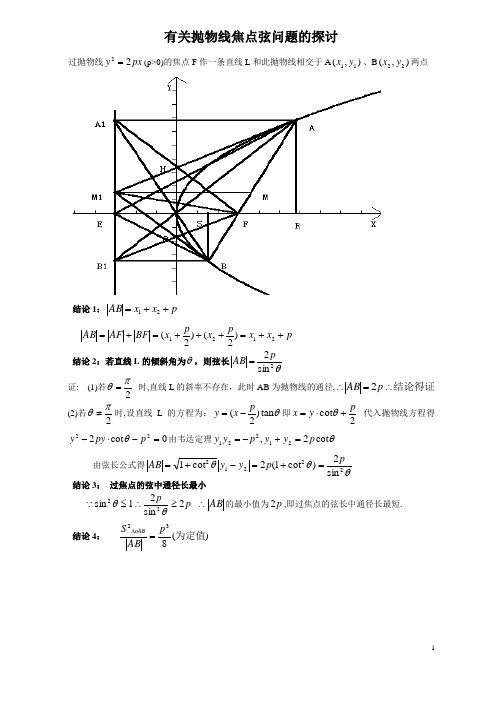
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
[很全]抛物线焦点弦的有关结论
![[很全]抛物线焦点弦的有关结论](https://img.taocdn.com/s3/m/ef2d77a3c1c708a1284a44ba.png)
p2 .
4
综上: x1x2
p2 .
4
(2)Q x1
y12 2p
,
x2
y22 2p
, y12 y2 2
p4
y1 y2
p2,
但 y1 y2 0, y1 y2 p 2
(2)另证:设
AB :
x
my
p 2
与
y2
2 px 联立,得
y2
2 pmy
p2
0,
y1 y2
y 2 2 px
t
y2
2 pay
2 pt
0
y1 y2 2 pt ②
由①②得 t p 2
AB 恒过焦点 p ,0 2
5
抛物线 y 2 2 pxp 0
成立。
,过(2p,0)的直线与之交于 A、B 两点,则 OA⊥OB。反之也
小结: (1)抛物线中的焦点弦问题很多都可以转化为这个直角梯形中的问题,在解决这类问题 时注意对这个梯形的运用; (2)万变不离其宗,解决问题的关键仍然是抛物线定义.
m
n
mn
sin y1 y2 mn
S AOB
1 m nt
2
y1 y2 1 m nt
mn 2 mn
y1 y2
而 S AOB
p2 4
n m
m n
1 2
m n
mn
p2 2
t
y1 y2
p2 2
①
l : x ay 又可设
抛物线焦点弦的有关结论

[很全]抛物线焦点弦的有关结论知识点1:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1)4221p x x =;(2)221p y y -=证明:如图,(1)若AB 的斜率不存在时,依题意,221px x ==4221p x x =∴若AB 的斜率存在时,设为,k 则⎭ ⎝⎛=2:k y AB()042222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k.4221p x x =∴ 综上:.4221p x x =(2)p y x p y x 2,2222211== ,,22142221p y y p y y ±=⇒=∴但22121,0p y y y y -=∴< (2)另证:设2:pmy x AB +=与px y 22=联立,得22122,02p y y p pmy y -=∴=-- 知识点2:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1);21p x x AB ++=(2)设直线AB 的倾斜角为α证明:(1)由抛物线的定义知,2,221px BF p x AF +=+=p x x BF AF AB ++=+=∴21 (2)若,2,90210p x x ===则α由(1)知2p AB ==若px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝⎛-=≠与设α联立,得()042222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k(),22221k k p x x +=+∴()222112k k p p x x AB +=++=∴,而αtan =k ,()ααα222sin 2tan tan 12pp AB =+=∴ 知识点3:若AB 是过抛物线()022>=p px y 的焦点F 的弦,则以AB 为直径的圆与抛物线的准线相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明抛物线焦点弦的18个结论
重庆市开县临江中学
张帮军
2011.08/复习备考
【内容摘要】关于抛物线的焦点弦到底有哪些结论呢?总结一下有四大类共18个结论,第一类是常见的基本结论;第二类是与圆有关的结论;第三类是由焦点弦得出有关直线垂直的结论;第四类是由焦点弦得出有关直线过定点的结论。
【关键词】证明抛物线焦点弦
现在通过下面的例题来证明这些结论。
例:过抛物线y 2=2px (p >0)的焦点F 的一条直线AB 和此抛物线相交于A ,B 两点(α是直线AB 的倾斜角),准线l 的方程:x =-p 2
,设点A (x 1,y 1),B
(x 2,y 2),则有关抛物线的焦点弦有以下八个基本结论:
(1)x 1x 2=p 2
4
;
(2)y 1y 2=-p 2;(3)|AF |=x 1+p 2;|BF |=x 2+p
2
(4)|AB |=x 1+x 2+p ;(5)|AB |=2p sin α
;
(6)|AF||BF|=p 2
sin 2α;(7);1|AF |+1|BF |=2
p
(8)S △AOB =p
2
2sin α
证明:如图若α≠π2,则k =tan α因为点F(p 2
,0),
所以设直线AB 的方程为y =k (x -p 2
)
由
y =k (x -p 2)y 2=2p p
x
得k 2x 2-p (k 2+2)x +k 2p 2
4
=0由根与系数的关系得:x 1x 2=p 24;x 1+x 2=p (k 2
+2)k
2
∴(1)式得证
∵A ,B 两点都在直线y 2=2px 上∴y 12=2px 1;y 22=2px 2
∴(y 1y 2)2=4p 2x 1x 2=p 4
∵y 1y 2<0,∴y 1y 2=-p 2即(2)式得证过点A ,B 分别作AA 1,BB 1与直线l 垂直,垂足为A 1,B 1即A 1(-p 2,y 1),B 1(-p 2
,y 2)
由抛物线定义知|AF |=|AA 1|=x 1+p 2
;|BF |=|BB 1|=
x 2+p 2
即(3)式得证
∵|AB |=|AF |+|BF |=x 1+x 2+p ∴(4)式得证
∵x 1+x 2=p (k 2
+2)k
2,k =tan α∴|AB |=x 1+x 2+p =2p (k 2+1)k 2=2p (tan 2
α+1)tan 2
α=2p sin 2α
即(5)式得证
∵|AF ||BF |=(x 1+p 2)·(x 2+p 2)=x 1·x 2+p 2
(x 1+x 2
)+p 24=p 2(x 1+x 2
+p )=p 2·2p sin 2α=p 2
sin 2α
∴(6)式得证∵1|AF |+1|BF |=|AF |+|BF ||AF |·|BF |=|AB ||AF |·|BF |=2p
sin 2α
·sin 2
αp 2=2p
∴(7)式得证
∵点O 到直线AB 的距离d 就是△AOB 的高∴h =d =p|k|21+k
2姨=p sin α
2∴S △AOB =12|AB|·h =12·2p
sin 2αp sin α2=p 2
2sin α
∴(8)式得证
下面来探究焦点弦与圆有关的四条结论:(1)以AB 为直径的圆M 与准线相切;(2)以AF 为直径的圆C 与y 轴准线相切;(3)以BF 为直径的圆D 与y 轴准线相切;(4)分别以AB ,AF ,BF 为直径的圆关系有:
圆C 与圆D 外切;圆C 与圆D 既与y 轴相切又圆M 相内切。
B 1
A 1
l y
x
O F A
B M 1
M
C 1
C D 1
D 证明:(1)过点M 作MM 1,所以MM 1是梯形AA 1B 1B 的中位
线,由抛物线定义知|AA 1|=|AF ||BB 1|=|BF |
53
建设高效课堂的几点思考
江苏省连云港市灌云县实验中学
尹
好
【内容摘要】建设高效课堂是教育工作者的追求,那什么样的课堂才是高效课堂呢?高效课堂首先是有效的课堂,高效课堂必须是
面向全体的课堂,高效课堂还应该是轻松快乐的课堂,高效课堂更应该是放眼学生未来成长的课堂。
那么怎样才能打造高效课堂呢?良好的课堂秩序是高效课堂的基石,高效课堂需要培养学生良好的学习习惯,高效课堂必须让学生成为课堂的主人,高效课堂必然是重视学习方法指导的课堂。
【关键词】高效课堂特征打造策略思考
在大力推行课程改革、全面实施素质教育的背景下,传统教学那种靠加班加点、题海战术提高教学质量的做法显然行不通了。
特别是随着江苏省“五严”、连云港市“六严”规定的出台并实施,我们明显感觉到教学时间较以前大幅度减少了,而教学内容却没有跟着调整。
此种情况下,要想在有限的时间里完成既定的教学任务,提高课堂教学效率就显得非常重要。
建设高效课堂成了教育工作者迫在眉睫的任务。
那什么样的课堂才是高效课堂呢?
高效课堂首先是有效的课堂。
课堂的有效性取决于学生收获了多少,而不是取决于教师讲解了多少。
有些教师为了完成教学任务而不顾学生实际,一味追求教学进度,看起来把该讲的都讲完了,可学生没有掌握你所讲的知识,你怎么能说完成了教学任务?如果说完成了,那么教学任务到底是什么?学生没有掌握,你讲得再多也是无效的知识,你的劳动也只能是无效劳动。
人们常说,老师要给学生一碗水,自己需要拥有一桶水。
可是老师拥有一桶水就一定能给学生一碗水吗?当然不是。
那种只顾将自己的
“桶”扳倒倒水,不顾学生“碗”放在哪,甚至不知学生有没有拿出“碗”来的老师,即使将自己的一桶水全倒出去,也不可能倒满学生一碗水,甚至可能学生的碗都是空的。
高效课堂必须是面向全体的课堂。
检验课堂教学效果不能只看几个班级尖子生,而应该看全体学生至少是大多数学生对教学内容的掌握情况。
班级少数尖子生不用老师教也能掌握课堂教学内容,说不定要让他们自学的话还能学得更快更好。
所以他们的成绩不是老师教出来的,至少不能全算是老师的教学效果,倒是那些中等生尤其是学困生,他们的每一点收获都是老师的功劳,他们对教学内容的掌握情况最能反映老师的教学效果。
∴|MM 1|=12(|AA 1|+|BB 1|)=12(|AF |+|BF |)=12
|AB |
即以|AB 为直径的圆M 与准线相切,同理可证(2),(3)。
(4)∵|AF |+|BF |=|AB |,∴以分别以AB ,AF ,BF 为直径的圆有以下关系。
即圆C 与圆D 既与y 轴相切又圆M 相内切。
接下来探究由焦点弦得出有关直线垂直关系有四条结论。
(1)以AB 为直径的圆的圆心在准线上的射影M 1与A ,B 两点的连线互相垂直;
(2)以AF 为直径的圆的圆心在y 轴上的射影C 1与A ,F 两点的连线互相垂直;
(3)以BF 为直径的圆的圆心在y 轴上的射影D 1与B ,F 两点的连线互相垂直;
(4
)A 1F 与B 1F 的连线互相垂直。
B 1
A 1
l y
x
O F A
B M 1
M
C 1
C D 1
D 证明:∵准线与圆M 相切和y 轴与圆C 和圆D 相切
∴圆M 的圆心在准线上的射影就是切点,∵直径所对的圆周角是直角∴AM 1⊥BM 1同理可证AC 1⊥FC 1,FD 1⊥BD 1
(4)由抛物线定义可知AA 1=AF BB 1=BF
∵BB 1//NF //AA 1∴∠AA 1F =∠AFA 1=∠A 1FN ;∠BB 1F =∠BFB 1=∠B 1FN
而∠AFA 1+∠A 1FN +∠BFB 1+∠B 1FN =π∴∠A 1FN +∠NFB 1=π2
即A 1F ⊥B 1F
最后由焦点弦得出有关直线过定点有两条的结论。
(1)以A 1B 1为直径的圆必过点F 。
(2)直线AB 1必过原点。
证明:(1)∵直径所对的圆周角是直角∴以A 1B 1为直径的圆必过点F 。
(2)由焦点弦的基本结论知:x 1x 2=p 2
4
;y 1y 2=-p 2
k OA =y 1x 1=-p
2
y 2p 24x 2
=-4x 2y 2=-4y 222p y 2=-2y 2
p
∵BB 1⊥l ∴点B 的坐标为
(-p 2
,y 2)∴k OB =-y 2-p
2
=-2y 2p =k OA
故直线AB 1必过原点。
参考文献
[1]董丽.有关抛物线的焦点弦问题及其应用[M].中外教育研究,2009,4.
54。
