西工大,西电 孙肖子版 模电 第五章 连续系统复频域分析--答案
自动控制原理课后习题答案 西北工业大学出社
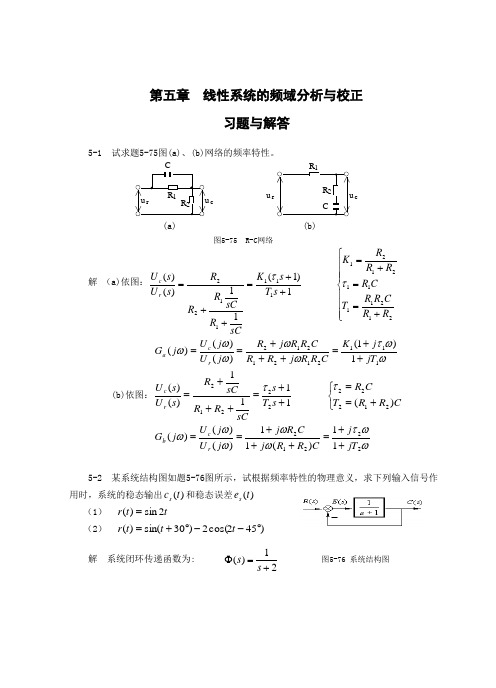
第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。
u rR 1u cR 2CCR 2R 1u ru c(a) (b)图5-75 R-C 网络解 (a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图:⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c)(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如题5-76图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s (1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时, 2=ω,r m =1则 ,35.081)(2==Φ=ωωj ο45)22arctan()2(-=-=j ϕο4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(οο-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(ο+=-Φ=t t j r e e e m ss ϕ (2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωωο5.26)21arctan()1(45.055)1(-=-===Φj j ϕ ο4.18)31arctan()1(63.0510)1(====Φj j e e ϕ )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+-⋅Φ-++⋅Φ=οο)902cos(7.0)4.3sin(4.0οο--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+-⋅Φ-++⋅Φ=οο )6.262cos(58.1)4.48sin(63.0οο--+=t t5-3 若系统单位阶跃响应 )0(8.08.11)(94≥+-=--t e e t h tt试求系统频率特性。
《信号与系统》第五章 连续系统的s域分析

例3: 求下图所示信号的单边拉氏变换。
第5-23页
西安邮电大学通信与信息工程学院
信号与系统
5.2 拉普拉斯变换性质
解: f1(t)(t)(t1)
f2(t)(t1 )(t 1 )
F1(s)F2(s)1s(1es)
例4:e2(t1)(t) e 2
s 2
f1 (t )
1
t
01
f2(t)
1
-1 0 1 t
第5-14页
西安邮电大学通信与信息工程学院
信号与系统
5.1 拉普拉斯变换
(3)满足
limf(t)et
t
0,(0)的信号称为指数
阶信号,指数阶信号的单边拉氏变换一定存在;
(4) e t 2 等信号比指数函数增长快,找不到收敛坐标,
为非指数阶信号,无法进行拉氏变换;
(5)有界的非周期信号的拉氏变换一定存在;
f( t) e s a t F ( s s a ) , R e [ s ]0 a
例7:
已知因果信号
f
( t ) 的象函数F (s)
s s2 1
求 et f (3t 2) 的象函数。
(s
s 1 1)2
西工大高频课后习题部分答案

解:( 1 )Tr1为不平衡--平衡变换器,Tr6为反相功率分配器,Tr2、Tr3为9:1 阻抗变换器, Tr7 为反相功率合成器, Tr4 为平衡—不平衡变换器, Tr5为 l : 4 1-23 图P1 — 23所示为工作在( 2~30 )MHz频段上、输出功率为 阻抗变化器 。 50w的反相功率合成电路,试指出各传输线变压器功能及 ( 2 ) Trl 输出端呈现的电阻为50Ω ,经 9:1阻抗变化器后的电阻为 —Tr3 传输线变压器的特性阻抗,并估算功率晶体管输入阻 50Tr1 Ω/9=5.6 Ω,因此晶体管 T1、T2 的输入电阻均为2.8Ω。 Ll、L2的作用不予考虑。 ( 抗和集电极等效负载阻抗。图中, 3 )输出负载为50Ω。经Tr4和Tr5变换后的电阻为 50Ω/4 =12.5Ω因此,T1、 T2管的输出负载电阻均为6.25Ω。 ( 4 ) Tr1~ Tr5的特性阻抗:Zc1=50Ω,Zc4=12.5Ω, Zc5=25 Ω Zc2=Zc3=1/3Ri=1/3*50Ω=16.7Ω。
I
.
2014-11-8
19
3-5 试判断图 NP3-5 所示交流通路中,哪些可能产生振荡,哪
些不能产生振荡:若能产生振荡,则说明属于哪种振荡电路。
解:(a)不振。同名端 接反,不满足正反馈;
( b )能振。变压器耦合反馈振荡器;
2014-11-8
20
(C)不振。不满足三点式振荡 电路的组成法则;
2014-11-8
15
2-14 根据图( a )所示的谐振功率放大器原理电路,按下列要 求画出它的实用电路。( l )两级放大器共用一个电源; ( 2 ) T2管的集电极采用并馈电路,基极采用自给偏置电路; ( 3 ) T1 管的集电极采用串馈电路,基极采用分压式偏置电路。
模拟电路第五章课后习题答案

模拟电路第五章课后习题答案案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
西安电子科技大学数电答案第五章1

波形如图解 5-1 所示。
2. 按钮开关在转换的时候由于弹簧片的颤动使信号也出现抖动,因此实际使用时往往需 要加上防抖动电路。RS 触发器是常用的电路之一,其连接如图 P5-2 所示。试说明其 工作原理,并画出对应于图中输入波形的输出波形。
图 P5-2 解: 设 Q 的初态为 0, 开关打至 (即 接地) 后松开, 信号有抖动, 由于 R 1 , S R 01 时,Q 置 1, S R 11 时 Q 保持置 1 状态,输出信号波形如图解 5-2 所示。可见该电路可
电路(a)当 A=1 时, Q1 输出(脉宽与 B 的周期相同)单脉冲。电路(b)当 A=0 时
Q3 输出(脉宽与 B 的周期相同)单脉冲。
6. 在图 P5-6 所示的电路中, FF1 为 JK 触发器, FF2 为 D 触发器,初始状态均为 0,试 画出在 CP 的作用下 Q1 , Q 2 的波形。
Q1 至 Q8 的波形图如图解 5-4 所示。
5. 在图 P5-5 所示的触发器电路中,A 和 B 的波形已知,对应画出 Q 0 , Q1 , Q 2 和 Q3 的波 形,设各触发器的初始状态为 0.
图 P5-5 解:图 (a) :Q0
n 1
Q 0 ,触发器在 A 的上升沿翻转, 因 RD 0 Q1 ,故 Q 0 0 时,Q0 0 。
9. 试设计一个单脉冲产生电路,该电路输入为时钟脉冲 CP,有一按钮开关(开关的结构 可自选) ,人工每按一次按钮开关,该电路输出一个时钟脉冲。画出电路,说明其工作 原理,注意要考虑人工按键时可能产生的抖动。 解:电路如图解 5-9 所示,电路的状态转移真值表(状态表)如表解 5-9 所示,开关自然状 态时接 R, 此时 S=1, Q 保持 0, 当开关按下 (R=1,S=0) 时, Q 输出 1, 即使有抖动 (RS=11) ,Q 仍可保持 1,开关松开(R=0,S=1), Q 输出 0,即实现了人工每按一次按钮开关,该电路输 出一个时钟脉冲。
《信号与系统》考研试题解答第五章 连续系统的s域分析

第五章 连续系统的s 域分析一、单项选择题X5.1(浙江大学2002年考研题))()cos(0t t εω的拉氏变换为 。
(A )[])()(200ωωδωωδπ-++ (B )[])()(00ωωδωωδπ-++(C )202ω+s s (D )220ωω+s X5.2(北京邮电大学2004年考研题)信号⎰-=td t h t f 0)()(τττ的拉氏变换为 。
(A ))(1s H s (B ))(12s H s (C ))(13s H s (D ))(14s H sX5.3(北京邮电大学2003年考研题)信号)()(2t e t f tε=的拉氏变换及收敛域为 。
(A )2]Re[,21)(->+=s s s F (B )2]Re[,21)(-<-=s s s F (C )2]Re[,21)(>-=s s s F (D )2]Re[,21)(<+=s s s FX5.4(北京邮电大学2003年考研题)已知某信号的拉氏变换αα+=+-s e s F Ts )()(,则该信号的时间函数为(A ))()(T t e T t ---εα (B ))(T t e t --εα(C ))(αεα--t et(D ))()(T t e t ---εααX5.5(西安电子科技大学2005年考研题)单边拉普拉斯变换4)(2+=-s se s F s的原函数是 。
(A ))1()2sin(-t t ε (B ))1()1(2sin --t t ε (C ))1()1(2cos --t t ε (D ))1()2cos(-t t εX5.6(西安电子科技大学2001年考研题)单边拉普拉斯变换se ss s F 2212)(-+=的原函数是 。
(A ))(t t ε (B ))2(-t t ε (C ))()2(t t ε- (D ))2()2(--t t ε X5.7(东南大学2000年考研题)若线性时不变因果系统的H (j ω),可由其系统函数H (s )将其中的s 换成j ω来求取,则要求该系统函数H (s )的收敛域应为 。
西工大,西电 孙肖子版 模电 第五章 连续系统复频域分析--答案

五章 习 题5.1 求下列各时间函数()t f 的像函数()s F 。
(1) ()()()t U e t f at--=1 (2) ()()()t U t t f φω+=sin(3) ()()()t U at e t f at-=-1 (4)()()()t U e a t f at --=11(5)()()t U t t f 2= (6) ()()()()t t U t t f δ32++= (7) ()()t tU t t f ωcos = (8)()()()t U at e t f at 1-+=-答案5.2 求下列各像函数()s F 的原函数()t f 。
(1) ()()()()()4231++++=s s s s s s F (2) ()()()126516222++++=s s s s s F(3) ()2399222++++=s s s s s F (4) ()()ss s s s F 2323++=答案(1)42)(321++++=s K s K s K s F83)4)(2()3)(1(01=⨯++++==s s s s s s s K41)2()4)(2()3)(1(22=+++++=-=s s s s s s s K83)4()4)(2()3)(1(43=+++++=-=s s s s s s s K48324183)(++++=s s s s F )()834183()(42*t U e e t f t t -++=(2)1245152393425121232)(321+++-++=+++++=s s s s K s K s K s F )()45152934512()(1232t U e e e t f tt t ---+-=(3)21122)2)(1(532)(++++=++++=s s s s s s F)()2()(2)(2t U e e t t f tt --++=δ (4)24111)2)(1(23123)(22+-++=+++-=++=s s s s s s s s s F )()4()()(2t U e e t t f tt ---+=δ5.3 求下列各像函数()s F 的原函数()t f 。
《模拟电子技术基础》课后习题答案完美第五章到第七章

第五章 放大电路的频率响应自 测 题一、选择正确答案填入空内。
(1)测试放大电路输出电压幅值与相位的变化,可以得到它的频率响应,条件是 。
A.输入电压幅值不变,改变频率B.输入电压频率不变,改变幅值C.输入电压的幅值与频率同时变化(2)放大电路在高频信号作用时放大倍数数值下降的原因是 ,而低频信号作用时放大倍数数值下降的原因是 。
A.耦合电容和旁路电容的存在B.半导体管极间电容和分布电容的存在。
C.半导体管的非线性特性D.放大电路的静态工作点不合适(3)当信号频率等于放大电路的f L 或f H 时,放大倍数的值约下降到中频时的 。
A.0.5倍B.0.7倍C.0.9倍 即增益下降 。
A.3dBB.4dBC.5dB (4)对于单管共射放大电路,当f = f L 时,与相位关系是 o U &iU &。
A.+45˚B.-90˚C.-135˚当f = f H 时,与的相位关系是 oU &i U &。
A.-45˚ B.-135˚ C.-225˚ 解:(1)A (2)B ,A (3)B A (4)C C二、电路如图T5.2所示。
已知:V C C =12V ;晶体管的C μ=4pF ,f T = 50MHz ,=100Ω, β'bb r 0=80。
试求解: (1)中频电压放大倍数; smu A & (2);'πC (3)f H 和f L ;(4)画出波特图。
图T5.2解:(1)静态及动态的分析估算: ∥178)(mA/V2.69k 27.1k 27.1k 17.1mV26)1(V 3mA 8.1)1(Aμ 6.22c m bee b'i s ismTEQ m b be i e b'bb'be EQe b'c CQ CC CEQ BQ EQ bBEQCC BQ −≈−⋅+=≈=Ω≈=Ω≈+=Ω≈+=≈−=≈+=≈−=R g r r R R R A U I g R r R r r r I r R I V U I I R U V I u &ββ(2)估算:'πCpF1602)1(pF214π2)(π2μc m 'μTe b'0μπe b'0T ≈++=≈−≈+≈C R g C C C f r C C C r f πππββ(3)求解上限、下限截止频率:Hz14)π(21kHz 175π21567)()(i s L 'πH s b b'e b'b s b b'e b'≈+=≈=Ω≈+≈+=CR R f RC f R r r R R r r R ∥∥∥(4)在中频段的增益为dB 45lg 20sm≈u A & 频率特性曲线如解图T5.2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五章 习 题5.1 求下列各时间函数()t f 的像函数()s F 。
(1) ()()()t U e t f at--=1 (2) ()()()t U t t f φω+=sin(3) ()()()t U at e t f at-=-1 (4)()()()t U e a t f at --=11(5)()()t U t t f 2= (6) ()()()()t t U t t f δ32++= (7) ()()t tU t t f ωcos = (8)()()()t U at e t f at 1-+=-答案5.2 求下列各像函数()s F 的原函数()t f 。
(1) ()()()()()4231++++=s s s s s s F (2) ()()()126516222++++=s s s s s F(3) ()2399222++++=s s s s s F (4) ()()ss s s s F 2323++=答案(1)42)(321++++=s K s K s K s F83)4)(2()3)(1(01=⨯++++==s s s s s s s K41)2()4)(2()3)(1(22=+++++=-=s s s s s s s K83)4()4)(2()3)(1(43=+++++=-=s s s s s s s K48324183)(++++=s s s s F )()834183()(42*t U e e t f t t -++=(2)1245152393425121232)(321+++-++=+++++=s s s s K s K s K s F )()45152934512()(1232t U e e e t f tt t ---+-=(3)21122)2)(1(532)(++++=++++=s s s s s s F)()2()(2)(2t U e e t t f tt --++=δ (4)24111)2)(1(23123)(22+-++=+++-=++=s s s s s s s s s F )()4()()(2t U e e t t f tt ---+=δ5.3 求下列各像函数()s F 的原函数()t f 。
(1) ()8666223++++=s s s s s s F (2) ()()2211+=s s s F答案(1)4422)(+-+++=s s s s F)()42()()(42t U e e t t f tt ---+'=δ (2)s s s s s s K s K s K s K s K s F 3113)2(2)1(11)1()1()(2232222113212311-+++++++=+++++++=)()3()()321()()33221()(22t U t t U e t t t U t e te e t t f t t t t -+++=-+++=----5.4 求下列各像函数()s F 的原函数()t f 。
(1) ()()()41221+-+=--s e s F s (2) ()()se s s F --=11 (3) ()21⎥⎦⎤⎢⎣⎡-=-s e s F s答案(1)因22)1(222)1(2212)1(2)(+-⨯++-=--s e s s F s 又因有42)(2sin 2+↔s t tU故由时移性有 se s t U t -+↔--42)1()1(2sin 2又由复频移性有)1(24)1(2)1()1(2sin --+-↔--s t es t U t e故 )1()1(2sin 21)(2sin )(--+=t U t e t tU e t f t t(2)s e s s F --⨯=111)( 故 ∑∑∞=∞=-=-*=0)()()()(n k K t U K t t U t f δ, N K ∈(3)s e e s F s s ---⨯-=121)(因有 )1(1)1()(s e s t U t U --↔--故[][])2()2()1()1(2)()1()()1()()(--+---=--*--=t U t t U t t tU t U t U t U t U t f5.5 用留数法求像函数()()()321617422++++=s s s s s F 的原函数()t f 。
答案令)(s F 的分母0)3()2(2=++s s ,得到一个单极点31-=s 和一个二重极点22-=s 。
下面求各极点上的留数。
[]ts st s ste e s s s es s F s 332231)2(16174)3)((Re --=-==⎥⎦⎤⎢⎣⎡+++=+=[]=⎭⎬⎫⎩⎨⎧+-=-=22)2)(()!12(1Re s st e s s F dt d s=⎥⎦⎤⎢⎣⎡+++-=22)316174(s st e s s s ds d =⎥⎦⎤⎢⎣⎡++++++++-=22223161749635244s st st e s s s t e s s s s t t te t te e222)23()2(3----=-+故[])()23()(23t U e t e t f tt ---+=5.6 求下列各像函数()s F 的原函数()t f 的初值()+0f 与终值()∞f 。
(1) ()112232+--++=s s s s s s F (2) ()123++=s s s s F(3) ()s s s s s F 231223+++= (4) ()()4122+-=-s s e s F s答案初值定理应用的条件是,)(s F 必须是真分式;终值定理应用的条件式:(1))(s F 的极点必须在s 平面的左半开平面;(2)在0=s 处,)(s F 只能有一阶极点。
也就是说,终值定理只有在)(t f 有终值的情况下才能应用。
例如,当)(t f 维周期函数时就,终值定理就不能适用了。
(1))1()1()1()1)(1()1(112)(2222232+-+=--+=+--++=s s s s s s s s s s s s F 由于)(s F 在s 的右半开平面上有二阶极点1=s ,故)(t f 的终值不存在。
1lim )1()1()1(lim )0(3322==+-+=∞→∞→+s s s s s s f s s(2)1lim )(230=++=∞→s s s s f s又111)(2+++-=s s s s F故 011lim )0(2=++=∞→+s s sf s(3)212312lim )(330=+++=∞→s s s s sf s 02312lim )0(23=+++=∞→+s s s s sf s(4))4(1lim )0(22=+-=-∞→+s s e s f ss因)(s F 在j ω轴上有一对共轭极点,故)(s F 对应的()f t 不存在终值。
5.7 已知系统的微分方程为()()()()()t f t f t y t y t y 323''''+=++ 激励()()t U e t f t 3-=系统的初始状态为()10=-y ,()20'=-y 。
试求系统全响应()t y 的初始值()+0y 和()+0'y 。
答案系统全响应的初始值(0)y +是等于(0)y -加上零状态响应()f y t 的初始值()f y t +,即)0()0()0(+-++=f y y y )0()0()0(+-+'+'='f y y y在零状态条件下对原微分方程等号两边同时求拉普拉斯变换,得)(3)()(2)(3)(2s F s sF s Y s sY s Y s f f f +=++令31)(+=s s F ,代入上式有131331)()23(2=+++=++s s ss Y s s f故231)(2++=s s s Y f故得零状态响应)(t y f 的初始值为0231lim )0(2=++=∞→+s s sy s f因21()()32f f y t sY s ss s '⎡⎤==⎣⎦++故得1231lim )0(2=++⨯='∞→+s s ss y s f故得全响应得初始值为101)0()0()0(=+=+=+-+f y y y 312)0()0()0(=+='+'='+-+f y y y5.8 图题5-8(a)所示电路,已知激励()t f 的波形如图题5-8(b)所示。
求响应()t u ,并画出()t u 的波形。
)(t f +-Ω1NΩ1+-1F)(t u (a)(b)图题5-8答案图题5-8(a )所示电路的开关等效电路,如图题5-8(c )所示。
0t <时S 在1,电路已工作于稳态,电容C 相当于开路,故有(0)1u -=-V 。
0t >时S 在2,故可作出0t >时的s 域电路模型,如图题5-8(d )所示。
故可列写出节点N 的KCL 方程为s s s s s s U s 31113)()1111(+-=-+=++故22523)2(3)(++=++==s s s s s s U 故得 )()2523()(2t U e t u t --= ()u t 得波形入图题5-8(e )所示。
)(t f +-Ω1NΩ1+-1F)(t u (a)(b)Ω1+-)(t u 1S (c)s3+-Ω1NΩ1+-)(t U (d)s1s1-+-(e)图题5-85.9 图题5-9所示零状态电路,激励()()V t U t f =,求电路的单位阶跃响应()t u。
+-)(t图题5-9答案图题5-9(a )电路的s 域电路模型,如图5-9(b )所示。
故得411212212)(2+=⨯+⨯=s s s s ss s U 故得 )(2sin )(t tU t u =+-)(t (a)+-)(s (b)图题5-95.10 图题5-10所示电路,已知()A i 10=-,()V u 10=-,()()V t tU u sin 0=-。
求全响应()t u 。
u图题5-10答案图题5-10(a )电路的s 域电路模型,如图题5-10(b )所示,其中11)(2+=s s F 。
故可列写节点N 的KCL 方程为(a)u+-(b)Ω1()F s +-Ns 32s 2Ω1s132+-)(s U图题5-10s s s U ss 12111)()2321111(2-++=+++ 故15215128.212)1)(3)(1(232)1)(34(232)(222232223+++++++-=+++-+-=+++-+-=s s ss s s s s s s s s s s s s s s U故得[])()43.63cos(447.08.22)()sin 52cos 518.22()(22t U t e e t U t t e e t u t t t t -++-=+++-=----(V )5.11 图题5-11(a)所示电路,已知激励()t f 的波形如图题5-11(b)所示,()()()[]V t U e t U t f t -+-=22。
