介电常数计算公式知识讲解
tion介电常数

介电常数什么是介电常数?在物理学中,介电常数是描述物质对电场响应的一个重要参数。
它衡量了物质在外加电场下的极化程度。
当一个物体被置于电场中时,原子或分子会发生重新排列,形成一个局部的正负极化。
这种极化现象导致了物体内部的电位移,从而产生了一定的电容性质。
介电常数就是用来衡量这种极化效应的。
介电常数的定义和计算方法介电常数可以通过下面的公式来计算:其中,是介电常数,是带有介质时的总电容,是不带有介质时的总电容。
介质和真空真空是一种没有任何物质存在的状态,在真空中不存在任何原子或分子。
因此,在真空中没有极化现象发生,也就是说真空中的介电常数为1(近似值)。
而对于其他物质来说,它们都有自己特定的介电常数。
这是因为物质中的原子或分子会受到电场的作用而发生极化,从而导致介电常数的存在。
不同物质的介电常数可以有很大的差异,这取决于其分子结构和性质。
介质对电场的影响介质对电场有着重要的影响。
当一个物体被置于电场中时,电场会在介质中传播,并且会引起极化现象。
这种极化现象使得物体内部产生了一个与外加电场方向相反的局部电场,从而减弱了外加电场。
具体来说,外加电场在介质中传播时会与介质中的原子或分子相互作用。
这种相互作用导致了一种抵消效应,使得外加电场在介质中逐渐减弱。
因此,在带有介质时,总体上看到的电场强度要比没有介质时要小。
介质常见特性除了介电常数之外,介质还有其他一些常见特性:1. 介磁性某些材料在外加磁场下也会发生极化现象,形成局部磁化。
这种磁化效应称为介磁性。
介磁性与介电性类似,也可以用介磁常数来描述。
2. 导电性一些材料不仅具有介电效应,还具有导电效应。
这种材料称为导电介质。
导电介质的导电特性使得它们在外加电场下不仅会发生极化,还会发生电流的传导。
3. 耗散因子当一个物体处于交变电场中时,由于分子内部的摩擦和能量损耗,会产生热量。
这个过程被称为耗散。
耗散因子是一个衡量该过程强度的物理量。
应用领域介电常数在许多领域都有重要的应用:•电容器设计:了解物质的介电常数可以帮助工程师设计更高效的电容器。
介电常数计算公式

电容与介电常数的转换
2
00r d C S d C r ⋅⋅⋅=⋅⋅=πεεε 9
14.3854.8104110⨯⨯⋅⋅⋅=⋅⋅=d C S d C r εε 0ε=8.854⨯10-12(F/m )
r ε为陶瓷样品的相对介电系数
C 为薄膜样品的电容(F)
S 为薄膜样品的面积(m 2)
d 为薄膜样品的厚度(nm)
r 为电极半径(mm )
0ε为真空介电系数(8.854×10-12F/m)。
=100000000000*(C*4*400)/(8.854*3.14*9)
利用阻抗图谱计算介电常数:
ω=2πf
f 为测得阻抗频率值 电容C=-1/(ω*Z”)
Z” 为测得阻抗虚部值 电容C=S*ε/4πKd
介电常数ε=4πKdC/S
K 为静电常数 9E+09
d 为薄膜厚度
S 为薄膜面积
介电损耗D=1/tanθ=Z'/Z"
Z’ 为测得阻抗实部值
利用LCR 仪计算介电常数:
电容量与电极极板面积和电介质介电常数成正比,与极板间距(电介质的厚度)成反比: s C=4kd επ
式中,s 为极板面积,d 为电极间距离。
介电损耗直接可读。
介电常数计算公式

介电常数计算公式介电常数计算公式是一种应用在物理学、材料学和电子学领域的公式,它可以用来计算某一介质中的介电常数ε。
介电常数是指介质中能够发生电磁耦合的特性,其表示物质对外界电磁场的相应程度。
一般情况下,我们将介电常数ε定义为一个比例常数,即:ε = E/D其中,E表示介质中的电场强度,D表示介质中的电位差。
因此,介电常数ρ可以通过测量介质中的电场强度和电位差来计算得出。
介电常数的计算公式可以描述如下:ε = (V1-V2)/(I1R1+I2R2)其中,V1和V2分别表示两端的电压;I1和I2分别表示两端的电流;R1和R2分别表示两端的电阻。
介电常数计算公式不仅可以用于传统的电气介质,也可以用于新型介质,如纳米材料和纳米结构。
与传统介质不同,纳米材料和纳米结构通常具有更高的介电常数,并且其介电常数随着介质结构的变化而变化。
根据介电常数ρ的定义,可以使用下面的公式来计算介质的介电常数:ε = (V1-V2)/(I1R1+I2R2)其中,V1和V2分别表示两端的电压;I1和I2分别表示两端的电流;R1和R2分别表示两端的电阻。
计算介电常数时,需要知道介质中的电场强度和电流大小。
为了获得电场强度,可以使用电场力矩计算器,它可以测量介质中的电场强度,也可以测量电流大小。
此外,介电常数ρ还可以用Cauer-Kelvin方法来计算。
Cauer-Kelvin方法是一种基于电路理论的方法,用于计算介质的介电常数。
该方法的基本原理是:介质的介电常数ε可以通过测量电流和电压之间的关系,然后根据Ohm定律来计算。
因此,介电常数ρ的计算公式可以概括为:ε = (V1-V2)/(I1R1+I2R2)其中,V1和V2分别表示两端的电压;I1和I2分别表示两端的电流;R1和R2分别表示两端的电阻。
介电常数计算公式是用来计算介质中的介电常数ε的常用公式,它可以用来计算传统介质、纳米材料和纳米结构的介电常数。
此外,Cauer-Kelvin方法也可以用来计算介质的介电常数。
介电常数

29
离子间作用力强,相同外电场使离 子产生位移困难; 离子间作用力弱,相同外电场使离 子产生位移容易。 离子位移极化所需的时间10-12 10-13秒。
30
外电场频率>1013赫兹时,时间 <10-13秒,离子位移极化来不及完成, 不再产生离子位移极化,而产生电 子位移极化。(极化时间10-14 10-15秒)
14
如下图被电场极化了的介质表面
出现感应电荷,这些电荷不会跑到
极板上而被束缚在介质表面,称为 表面束缚电荷。
15
16
极化的微观本质就是介质内部带电质点产 生位移。但由于介质内部质点的束缚力很强, 在电场作用下沿一定方向的相对位移是有限 度的,是在平衡位置附近的很小的位移,因 而它不是载流子,不形成电流。
33
与离子位移极化的区别: 离子位移极化只在平衡位置附 近移动。 离子松弛极化,离子是从一个 平衡位置运动到另一个新的平衡 位置。
34
离子松弛极化可用下述过程描 述,若在某缺陷附近有两个平衡 位置1及2,中间隔有势垒u(下图 a),当离子热运动能超过势垒高 度u时,离子就从1迁移至2,反之, 离子也可以从2迁移至1.在一定 温度下离子迁移的几率与势垒u有 关。
6
各种材料室温时的介电常数为: 装置瓷、电阻瓷及电真空瓷:212 Ⅰ型电容器瓷:6 1500; Ⅱ型电容器瓷:200 3万; Ⅲ型电容器瓷:7000 几十万; 压电陶瓷:50 20000 干燥空气;1.000585; 真空:1。
7
由上可知,电子陶瓷的介电 常数数值范围很大。介电常数大 的材料,可以制造容量大、体积 小的电容器;介电常数小的材料, 用来制造装置另件。
第二节
介电常数
电子陶瓷除具有绝缘性质外,还能储 存电荷。 介电常数就是衡量其储存电荷能力的 参数,又叫介电系数或电容率。 一、介质极化和介电常数 设有一个真空中的平行板电极系统,电 极面积为s,两极板间的距离为 l ,在两 极板间加上直流电压U,则极板上将充有 电荷Q0一 陶瓷介质,而极板的面积s和距离l不变; 或在厚度为l的平板形陶瓷介质两面被上 面积为s的电极。在电压U不变的情况下, 极板上电荷由Q0增加到Q。 电荷增加是由于陶瓷介质在电场作 用下发生极化的结果。这一现象叫介质 的宏观极化。它是介质微观质点极化的 外部表现。极板上电荷增加的过程也就 是微观质点极化的过程。
折射角度介电常数计算公式

折射角度介电常数计算公式介电常数是材料对电场的响应能力的量度,它描述了材料在电场作用下的极化程度。
在光学中,介电常数也被用来描述光在材料中传播时的速度和折射角度。
折射角度介电常数计算公式是一种用来计算光在不同介质中的折射角度的公式,它可以帮助我们理解光在不同介质中的传播规律。
折射角度介电常数计算公式可以用来计算光在不同介质中的折射角度,它的形式如下:n = c / v。
其中,n是介质的折射率,c是光在真空中的速度,v是光在介质中的速度。
介质的折射率决定了光在介质中传播时的速度和折射角度,而介电常数则是影响介质折射率的重要因素之一。
介电常数可以通过以下公式来计算:ε = ε0 εr。
其中,ε是介质的介电常数,ε0是真空的介电常数,εr是介质的相对介电常数。
介质的相对介电常数描述了介质相对于真空的极化能力,它是介质在电场作用下的极化程度与真空的比值。
折射角度介电常数计算公式可以通过介电常数来计算介质的折射率,从而进一步计算光在介质中的折射角度。
介质的折射率决定了光在介质中传播时的速度和折射角度,因此折射角度介电常数计算公式对于理解光在不同介质中的传播规律具有重要意义。
在实际应用中,折射角度介电常数计算公式可以帮助我们设计和制造光学元件,优化光学系统的性能。
通过计算不同介质的折射率和折射角度,我们可以选择合适的材料来制造透镜、棱镜、光纤等光学元件,从而实现光的传输、聚焦和分离。
此外,折射角度介电常数计算公式也可以帮助我们研究光在不同介质中的传播规律,探索光在材料中的能量传递和损耗机制。
通过计算不同介质的折射率和折射角度,我们可以深入理解光在材料中的传播特性,为光学材料的研发和应用提供理论支持。
总之,折射角度介电常数计算公式是一种重要的光学公式,它可以帮助我们计算光在不同介质中的折射角度,进而理解光在材料中的传播规律。
通过介电常数的计算,我们可以优化光学系统的性能,研究光在材料中的传播特性,推动光学材料的应用和发展。
介电常数与真空介电常数和相对介电常数公式

介电常数与真空介电常数和相对介电常数公式介电常数是描述材料中电场作用下电荷极化程度的物理量。
它与真空介电常数和相对介电常数有密切关系。
真空介电常数,通常用符号ε0表示,是自然界中的一个常数。
它定义为真空中单位体积的电容率,其数值约为8.85×10-12 F/m。
真空介电常数是一个普遍适用于所有材料的参考值,因为在真空中不存在其他物质,因此电场作用下电荷极化的唯一影响来自于空气中的电荷。
相对介电常数,通常用符号εr表示,是一种材料特有的物理量。
它定义为材料在电场作用下电容率与真空电容率之比。
相对介电常数是描述材料对电场的响应能力的一个参数。
对于相同的电场强度,材料的相对介电常数越大,说明材料极化程度越高。
根据介电常数的定义,可以将材料中的电场作用下的电荷极化过程分为两个部分:一部分是电场作用下电子的位移极化,另一部分是电场作用下离子的位移极化。
对于电子的位移极化,当材料中存在电场时,电子会受到电场力的作用,发生位移。
这种位移导致电子云的形状发生变化,从而使材料中的电子产生了极化。
电子的位移极化可以通过介电常数来描述,其数值与材料的相对介电常数有关。
对于离子的位移极化,当材料中存在电场时,离子会受到电场力的作用,发生位移。
这种位移导致离子云的形状发生变化,从而使材料中的离子产生了极化。
离子的位移极化同样可以通过介电常数来描述,其数值与材料的相对介电常数有关。
通过介电常数的定义可以看出,介电常数与真空介电常数和相对介电常数之间存在着密切的关系。
真空介电常数是一个普遍适用于所有材料的参考值,而相对介电常数则是描述材料特性的一个参数。
在实际应用中,通过测量材料的相对介电常数,可以间接地得到材料中的电子和离子的位移极化程度,从而进一步了解材料的电学性质。
介电常数是描述材料中电场作用下电荷极化程度的物理量,它与真空介电常数和相对介电常数密切相关。
真空介电常数是一个普遍适用于所有材料的参考值,而相对介电常数则是描述材料特性的一个参数。
介电常数
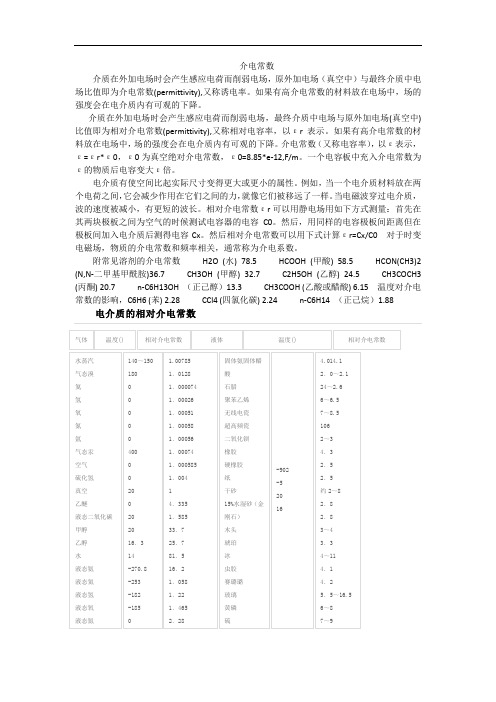
介电常数介质在外加电场时会产生感应电荷而削弱电场,原外加电场(真空中)与最终介质中电场比值即为介电常数(permittivity),又称诱电率。
如果有高介电常数的材料放在电场中,场的强度会在电介质内有可观的下降。
介质在外加电场时会产生感应电荷而削弱电场,最终介质中电场与原外加电场(真空中)比值即为相对介电常数(permittivity),又称相对电容率,以εr表示。
如果有高介电常数的材料放在电场中,场的强度会在电介质内有可观的下降。
介电常数(又称电容率),以ε表示,ε=εr*ε0,ε0为真空绝对介电常数,ε0=8.85*e-12,F/m。
一个电容板中充入介电常数为ε的物质后电容变大ε倍。
电介质有使空间比起实际尺寸变得更大或更小的属性。
例如,当一个电介质材料放在两个电荷之间,它会减少作用在它们之间的力,就像它们被移远了一样。
当电磁波穿过电介质,波的速度被减小,有更短的波长。
相对介电常数εr可以用静电场用如下方式测量:首先在其两块极板之间为空气的时候测试电容器的电容C0。
然后,用同样的电容极板间距离但在极板间加入电介质后测得电容Cx。
然后相对介电常数可以用下式计算εr=Cx/C0对于时变电磁场,物质的介电常数和频率相关,通常称为介电系数。
附常见溶剂的介电常数H2O (水) 78.5 HCOOH (甲酸) 58.5 HCON(CH3)2 (N,N-二甲基甲酰胺)36.7 CH3OH (甲醇) 32.7 C2H5OH (乙醇) 24.5 CH3COCH3 (丙酮) 20.7 n-C6H13OH (正己醇)13.3 CH3COOH (乙酸或醋酸) 6.15 温度对介电常数的影响,C6H6 (苯) 2.28 CCl4 (四氯化碳) 2.24 n-C6H14 (正己烷)1.88"介电常数" 在工具书中的解释1.又称电容率或相对电容率,表征电介质或绝缘材料电性能的一个重要数据,常用ε表示。
它是指在同一电容器中用同一物质为电介质和真空时的电容的比值,表示电介质在电场中贮存静电能的相对能力。
复合材料介电常数计算公式

复合材料介电常数计算公式
复合材料是一种由两种或两种以上不同材料组成的材料,具有独特的性能和应用领域。
其中一个重要的性能指标就是介电常数,它对复合材料的电性质和电磁波传播具有重要影响。
复合材料的介电常数是由其组成材料的介电常数和体积分数决定的。
介电常数是材料在电场作用下的响应能力,反映了材料分子之间的电荷传导行为。
复合材料的介电常数可以通过如下公式计算:
ε_c = ε_m * V_m + ε_f * V_f
其中,ε_c为复合材料的介电常数,ε_m和ε_f分别为组成材料的介电常数,V_m和V_f分别为组成材料的体积分数。
在这个公式中,我们可以看到复合材料的介电常数是由组成材料的介电常数和体积分数加权平均得到的。
这意味着当组成材料的体积分数不同时,复合材料的介电常数也会发生变化。
通过调整组成材料的体积分数,我们可以改变复合材料的介电常数,从而实现对其电性质和电磁波传播性能的调控。
这对于一些特定应用领域来说非常重要,比如电子器件中的电磁屏蔽材料、微波器件中的微波吸收材料等。
在实际应用中,我们可以通过实验测量的方法来确定复合材料的介电常数。
一种常用的方法是使用介电常数测试仪进行测量,根据测
量结果可以得到复合材料的介电常数。
另外,还可以通过模拟计算的方法来预测复合材料的介电常数,这需要借助计算机模拟软件进行建模和计算。
复合材料的介电常数是由其组成材料的介电常数和体积分数决定的。
通过调整组成材料的体积分数,可以改变复合材料的介电常数,从而实现对其电性质和电磁波传播性能的调控。
这对于复合材料在电子器件、微波器件等领域的应用具有重要意义。
