逻辑斯谛(Logistic)映射
逻辑斯蒂(logistic)回归深入理解、阐述与实现

逻辑斯蒂(logistic)回归深⼊理解、阐述与实现第⼀节中说了,logistic 回归和线性回归的区别是:线性回归是根据样本X各个维度的Xi的线性叠加(线性叠加的权重系数wi就是模型的参数)来得到预测值的Y,然后最⼩化所有的样本预测值Y与真实值y'的误差来求得模型参数。
我们看到这⾥的模型的值Y是样本X各个维度的Xi的线性叠加,是线性的。
Y=WX (假设W>0),Y的⼤⼩是随着X各个维度的叠加和的⼤⼩线性增加的,如图(x为了⽅便取1维):然后再来看看我们这⾥的logistic 回归模型,模型公式是:,这⾥假设W>0,Y与X各维度叠加和(这⾥都是线性叠加W)的图形关系,如图(x为了⽅便取1维):我们看到Y的值⼤⼩不是随X叠加和的⼤⼩线性的变化了,⽽是⼀种平滑的变化,这种变化在x的叠加和为0附近的时候变化的很快,⽽在很⼤很⼤或很⼩很⼩的时候,X叠加和再⼤或再⼩,Y值的变化⼏乎就已经很⼩了。
当X各维度叠加和取⽆穷⼤的时候,Y趋近于1,当X各维度叠加和取⽆穷⼩的时候,Y趋近于0.这种变量与因变量的变化形式就叫做logistic变化。
(注意不是说X各个维度和为⽆穷⼤的时候,Y值就趋近1,这是在基于W>0的基础上,(如果W<0,n那么Y趋近于0)⽽W是根据样本训练出来,可能是⼤于0,也可能是⼩0,还可能W1>0,W2<0…所以这个w值是样本⾃动训练出来的,也因此不是说你只要x1,x2,x3…各个维度都很⼤,那么Y值就趋近于1,这是错误的。
凭直觉想⼀下也不对,因为你连样本都还没训练,你的模型就有⼀个特点:X很⼤的时候Y就很⼤。
这种强假设肯定是不对的。
因为可能样本的特点是X很⼤的时候Y就很⼩。
)所以我们看到,在logistic回归中,X各维度叠加和(或X各维度)与Y不是线性关系,⽽是logistic关系。
⽽在线性回归中,X各维度叠加和就是Y,也就是Y与X就是线性的了。
逻辑斯蒂回归在分类问题中的应用

逻辑斯蒂回归在分类问题中的应用逻辑斯蒂回归(Logistic Regression)是一种常用的分类算法,尤其在二分类问题中得到广泛应用。
逻辑斯蒂回归通过将线性回归模型的输出映射到一个概率范围内,从而实现对样本进行分类。
本文将介绍逻辑斯蒂回归的原理、优缺点以及在分类问题中的具体应用。
### 一、逻辑斯蒂回归原理逻辑斯蒂回归是一种广义线性回归模型,其模型形式为:$$P(y=1|x) = \frac{1}{1+e^{-(w^Tx+b)}}$$其中,$P(y=1|x)$表示在给定输入$x$的情况下,输出为类别1的概率;$w$和$b$分别为模型的参数,$w$为权重向量,$b$为偏置项;$e$为自然对数的底。
逻辑斯蒂回归通过对线性回归模型的输出进行Sigmoid函数的映射,将输出限制在0到1之间,表示样本属于某一类别的概率。
### 二、逻辑斯蒂回归优缺点1. 优点:- 实现简单,计算代价低;- 输出结果具有概率意义,便于理解和解释;- 可以处理非线性关系。
2. 缺点:- 容易受到异常值的影响;- 对特征工程要求较高;- 无法很好地处理多分类问题。
### 三、逻辑斯蒂回归在分类问题中的应用逻辑斯蒂回归在分类问题中有着广泛的应用,以下是一些常见的应用场景:1. 金融风控在金融领域,逻辑斯蒂回归常用于信用评分和风险控制。
通过构建逻辑斯蒂回归模型,可以根据客户的个人信息、财务状况等特征,预测其违约概率,从而制定相应的风险控制策略。
2. 医疗诊断在医疗领域,逻辑斯蒂回归可用于疾病诊断和预测。
通过医疗数据的特征提取和逻辑斯蒂回归模型的构建,可以帮助医生判断患者是否患有某种疾病,提前进行治疗和干预。
3. 市场营销在市场营销中,逻辑斯蒂回归可用于客户分类和营销策略制定。
通过分析客户的购买行为和偏好,构建逻辑斯蒂回归模型,可以预测客户的购买意向,从而制定个性化的营销方案。
4. 文本分类在自然语言处理领域,逻辑斯蒂回归可用于文本分类任务。
逻辑斯蒂回归参数估计

逻辑斯蒂回归参数估计
逻辑斯蒂回归(Logistic Regression)是一种常见的分类模型,它使用一个逻辑函数对输入特征进行建模并预测输出类别。
在给定训练数据和标签的情况下,我们可以通过最大似然估计方法来估计逻辑斯蒂回归模型的参数。
假设我们有一个二分类问题,输入特征为 x,标签为 y,逻辑斯蒂回归模型可以表示为:
h(x) = P(y=1|x) = 1 / (1 + exp(-wx))
h(x) 是通过逻辑函数(sigmoid函数)将输入特征与权重参数 w 结合后的预测结果。
我们的目标是通过最大似然估计方法来估计参数 w。
为了方便计算,我们引入对数似然函数:
L(w) = sum(y*log(h(x)) + (1-y)*(1-log(h(x))))
接下来,我们可以使用梯度下降算法来最大化对数似然函数,从而估计出参数 w。
梯度下降算法的更新规则如下:
w := w + alpha * sum((y - h(x)) * x)
alpha 是学习率,用于控制更新的步长。
通过重复执行上述更新规则,直到满足终止条件(如达到最大迭代次数或参数收敛),我们就可以得到逻辑斯蒂回归模型的参数估计值 w。
需要注意的是,在进行参数估计时,我们需要对输入特征进行适当的预处理(如标准化、归一化等),以确保模型的准确性和稳定性。
以上便是逻辑斯蒂回归参数估计的基本原理和方法,希望对您有所帮助。
逻辑斯蒂增长模型
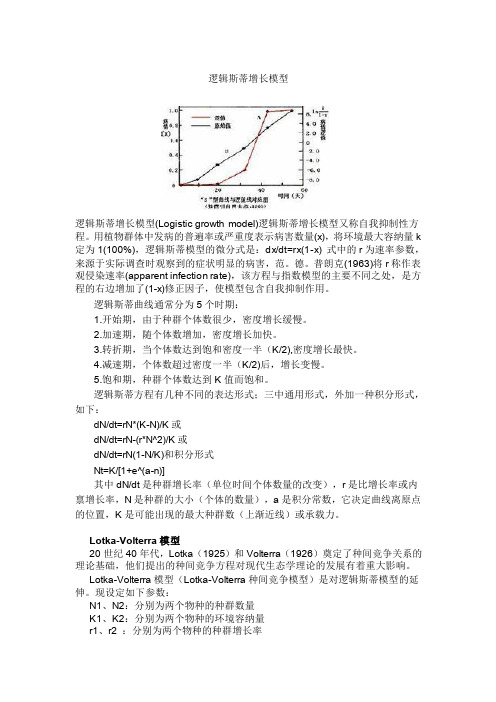
逻辑斯蒂增长模型逻辑斯蒂增长模型(Logistic growth model)逻辑斯蒂增长模型又称自我抑制性方程。
用植物群体中发病的普遍率或严重度表示病害数量(x),将环境最大容纳量k 定为1(100%),逻辑斯蒂模型的微分式是:dx/dt=rx(1-x) 式中的r为速率参数,来源于实际调查时观察到的症状明显的病害,范。
德。
普朗克(1963)将r称作表观侵染速率(apparent infection rate),该方程与指数模型的主要不同之处,是方程的右边增加了(1-x)修正因子,使模型包含自我抑制作用。
逻辑斯蒂曲线通常分为5个时期:1.开始期,由于种群个体数很少,密度增长缓慢。
2.加速期,随个体数增加,密度增长加快。
3.转折期,当个体数达到饱和密度一半(K/2),密度增长最快。
4.减速期,个体数超过密度一半(K/2)后,增长变慢。
5.饱和期,种群个体数达到K值而饱和。
逻辑斯蒂方程有几种不同的表达形式;三中通用形式,外加一种积分形式,如下:dN/dt=rN*(K-N)/K或dN/dt=rN-(r*N^2)/K或dN/dt=rN(1-N/K)和积分形式Nt=K/[1+e^(a-n)]其中dN/dt是种群增长率(单位时间个体数量的改变),r是比增长率或内禀增长率,N是种群的大小(个体的数量),a是积分常数,它决定曲线离原点的位置,K是可能出现的最大种群数(上渐近线)或承载力。
Lotka-Volterra模型20世纪40年代,Lotka(1925)和Volterra(1926)奠定了种间竞争关系的理论基础,他们提出的种间竞争方程对现代生态学理论的发展有着重大影响。
Lotka-Volterra模型(Lotka-Volterra种间竞争模型)是对逻辑斯蒂模型的延伸。
现设定如下参数:N1、N2:分别为两个物种的种群数量K1、K2:分别为两个物种的环境容纳量r1、r2 :分别为两个物种的种群增长率依逻辑斯蒂模型有如下关系:dN1 / dt = r1 N1(1 - N1 / K1)其中:N/K可以理解为已经利用的空间(称为“已利用空间项”),则(1-N/K)可以理解为尚未利用的空间(称为“未利用空间项”)当两个物种竞争或者利用同一空间时,“已利用空间项”还应该加上N2种群对空间的占用。
逻辑斯蒂回归模型

逻辑斯蒂回归模型
逻辑斯蒂回归(Logistic Regression)是一种广泛使用的机器学习方法,属于分类算法,它可以用来预测一个样本属于哪一类。
它早在19上世纪60年代就被发明出来了。
在实际应用中,逻辑斯蒂回归是一种用二元逻辑(0和1)来预测分类问题的统计模型,通过分析给定的特征来判断是否属于特定的类。
其实,逻辑斯蒂回归是概率模型,数学原理是最大似然估计,它的模型在实际问题中有着众多的优缺点。
逻辑斯蒂回归模型的主要优点是速度快且易于实现,而且非常适用于一对多(即多分类)分类问题,而且更倾向于低维度的特征,这使得它易于识别重要特征。
由于其易于实现,因此可以节省大量的时间和工作量。
此外,逻辑斯蒂回归不仅可以处理事件类别,而且还可以应用于连续结果;另外,它还可以捕获事件之间的依赖性,解释变量的影响,并对协变量开展校正,这在传统的统计方法中是困难的。
然而,逻辑斯蒂回归模型也有缺点,其中最明显的是模型仅包括线性项,因此它不适用于样本特征具有非线性关系的情况。
此外,由于逻辑斯蒂回归模型只能返回二元逻辑(0和1)的结果,因此它不适用于半边的分类问题,即对实际解决的问题没有很好的应用。
另外,需要注意的是,如果样本中有较多的偏斜或独立变量,模型的精度也会受到影响。
简述种群增长的逻辑斯谛模型及其主要参数的生物学意义

简述种群增长的逻辑斯谛模型及其主要参数的生物学意义在一定条件下,生物种群增长并不是按几何级数无限增长的。
即开始增长速度快,随后速度慢直至停止增长(只是就某一值产生波动),这种增长曲线大致呈“S”型,这就是统称的逻辑斯谛(Logistic)增长模型。
意义当一个物种迁入到一个新生态系统中后,其数量会发生变化.假设该物种的起始数量小于环境的最大容纳量,则数量会增长.增长方式有以下两种:(1) J型增长若该物种在此生态系统中无天敌,且食物空间等资源充足(理想环境),则增长函数为N(t)=n(p^t).其中,N(t)为第t年的种群数量,t为时间,p为每年的增长率(大于1).图象形似J形。
(2) S型增长若该物种在此生态系统中有天敌,食物空间等资源也不充足(非理想环境),则增长函数满足逻辑斯谛方程。
图象形似S形.逻辑斯谛增长模型的生物学意义和局限性逻辑斯谛增长模型考虑了环境阻力,但在种群数量较小时未考虑随机事件的影响。
比较种群指数增长模型和逻辑斯谛增长模型指数型就是通常所说的J型增长,是指在理想条件下,一个物种种群数目所呈现的趋势模型,但其要求食物充足,空间丰富,无中间斗争的情况,通常是在自然界中不存在的,当然,科学家为了模拟生物的J型增长,会在实验室中模拟理想环境,不过仅限于较为简单的种群(如细菌等)逻辑斯谛型是指通常所说的S型曲线,其增长通常分为五个时期1.开始期,由于种群个体数很少,密度增长缓慢。
2.加速期,随个体数增加,密度增长加快。
3.转折期,当个体数达到饱和密度一半(K/2),密度增长最快。
4.减速期,个体数超过密度一半(K/2)后,增长变慢。
5.饱和期,种群个体数达到K值而饱和自然界中大部分种群符合这个规律,刚开始,由于种群密度小,增长会较为缓慢,而后由于种群数量增多而环境适宜,会呈现J型的趋势,但随着熟练进一步增多,聚会出现种类斗争种间竞争的现象,死亡率会加大,出生率会逐渐与死亡率趋于相等,种群增长率会趋于0,此时达到环境最大限度,即K值,会以此形式达到动态平衡而持续下去。
logistic回归模型

Logistic回归模型
• 列联表中的数据是以概率的形式把属性变量联系 起来的,而概率p的取值在0与1之间,因此,要把
概率 p (x)与 x 之间直接建立起函数关系是不合
适的。即 (x) x
Logistic回归模型
• 因此,人们通常把p的某个函数f(p)假设为变量的 函数形式,取 f ( p) ln (x) ln p
1 (x) 1 p
• 称之为logit函数,也叫逻辑斯蒂变换。 • 因此,逻辑斯蒂变换是取列联表中优势的对数。
当概率在0-1取值时,Logit可以取任意实数,避免 了线性概率模型的结构缺陷。
Logistic回归模型
假设响应变量Y是二分变量,令 p P(Y 1) ,影响Y
的因素有k个 x1, xk,则称:
多项logit模型
• 前面讨论的logit模型为二分数据的情况,有时候 响应变量有可能取三个或更多值,即多类别的属 性变量。
• 根据响应变量类型的不同,分两种情况:
–响应变量为定性名义变量; –响应变量为定性有序变量;
• 当名义响应变量有多个类别时,多项logit模型应 采取把每个类别与一个基线类别配成对,通常取 最后一类为参照,称为基线-类别logit.
• 为二分数据的逻辑斯ln 1蒂pp回归g(模x1,型,,xk简) 称逻辑斯蒂 回归模型。其中的k个因素称为逻辑斯蒂回归模型 的协变量。
• 最重要的逻辑斯蒂回归模型是logistic线性回归模 型,多元logit模型的形式为:
ln
p 1 p
0
1x1
k xk
Logistic回归模型
• 其中,0, 1, , k 是待估参数。根据上式可以得到
多项logit模型
logistic 分类算法

logistic 分类算法Logistic分类算法是一种常用的分类算法,广泛应用于机器学习和数据分析领域。
它是基于逻辑斯蒂回归模型的一种分类算法,可以用于解决二分类和多分类问题。
下面我们将介绍Logistic分类算法的原理、应用和优缺点。
一、Logistic分类算法原理Logistic分类算法是建立在逻辑斯蒂回归模型的基础上的。
逻辑斯蒂回归模型是一种广义线性模型,它可以用来描述因变量和自变量之间的关系。
逻辑斯蒂回归模型的核心思想是通过一个Sigmoid函数将线性回归的结果映射到0和1之间,从而实现分类。
Sigmoid函数的表达式为:$$ g(z) = \frac{1}{1+e^{-z}} $$其中,z为线性回归的结果。
如果z大于0,则预测结果为1,否则为0。
Sigmoid函数的特点是在z趋近于正无穷时,函数值趋近于1;在z趋近于负无穷时,函数值趋近于0。
这样就实现了将线性回归结果映射到0和1之间的效果。
二、Logistic分类算法应用Logistic分类算法可以应用于很多领域,特别是在二分类问题中应用较为广泛。
下面我们列举了一些常见的应用场景。
1. 信用评估:通过客户的个人信息和历史信用记录,预测客户是否具有偿还贷款的能力。
2. 垃圾邮件过滤:通过邮件的主题、正文和附件等信息,判断邮件是否为垃圾邮件。
3. 疾病诊断:通过患者的体征和病史等信息,判断患者是否患有某种疾病。
4. 情感分析:通过文本数据分析,判断用户对某个产品或事件的情感倾向。
三、Logistic分类算法优缺点Logistic分类算法具有以下优点:1. 算法简单:Logistic分类算法是一种简单而有效的分类算法,不需要太多的计算资源和存储空间。
2. 可解释性强:通过逻辑斯蒂回归模型,可以清晰地解释自变量对于分类结果的影响。
3. 鲁棒性好:Logistic分类算法对异常值和噪声数据具有较好的鲁棒性,不会对结果产生较大的影响。
但是,Logistic分类算法也存在一些缺点:1. 无法处理非线性关系:Logistic分类算法只能处理线性可分的问题,对于非线性关系的问题效果较差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4 从倍周期分定走向混沌
4-1 逻辑斯谛(Logistic )映射
我们将以一个非常简单的数学模型来加以说明从倍周期分定走向混沌现象。
该模型称为有限环境中无世代交替昆虫生息繁衍模型。
若昆虫不加以条件控制,每年增加λ倍,我们将一年作为一代,把第几代的虫日记为,则有:
i N o i i i N N N 11++==λλ (4-1)
i N ,1>λ增长很快,发生“虫口爆炸”,但虫口太多则会由于争夺有限食物和生存空间,
以及由于接触传染导致疾病曼延,使虫口数目减少,它正比于,假定虫口环境允许的最大虫口为,并令2
i N o N o
i
i N N x =
,则该模型由一个迭代方程表示: 21i i i N N N λλ−=+
即为:
)1(1i i i x x x −=+λ (4-2)
其中:]4,0[],
1,0[∈∈λi x 。
(4-2)式就是有名的逻辑斯谛映射。
4-2 倍周期分歧走向混沌
借助于对这一非线性迭代方程进行迭代计算,我们可以清楚地看到非线性系统通过倍周期分岔进入混沌状态的途径。
(一)迭代过程
迭代过程可以用图解来表示。
图4-1中的水平轴表示,竖直轴表示,抛物线表示(4-2)式右端的迭代函数。
45º线表示n x 1+n x n n x x =+1的关系。
由水平轴上的初始点作竖直线,找到与抛物线的交点,A 的纵坐标就是。
由点
)0,(0x R ),(10x x A 1x
),(10x x A 作水平直线,求它与45º线的交点,经B 点再作竖直线,求得与抛物
线的交点,这样就得到了。
仿此做法可得到所迭代点。
),(11x x B ),(21x x 2x 从任何初始值出发迭代时,一般有个暂态过程。
但我们关心的不是暂态过程,而是这所趋向的终态集。
终态集的情况与控制参数λ有很大关系。
增加λ值就意味着增加系统的非线性的程度。
改变λ值,不仅仅改变了终态的量,而且也改变了终态的质。
它所影响的不仅仅是终态所包含的定态的个数和大小,而且也影响到终态究竟会不会达到稳定。
(二)终态性质
①当31<<γ时,迭代结果的归宿是一个确定值,趋于一个不动点,即抛物线与45º线的交点,这相当于系统处于一个稳定态,如图4-2(a)所示。
此值与λ有关,且与λ值有一一对应关系。
当4.2=λ时,12/711==+i x x 。
迭代的结果为一个不动点的情况,其周期为1,这表示从出发,迭代一次就回到。
i x i x ②当449.33<<γ时,迭代的终态在一个正方形上循环,亦即在两个值之间往复跳跃,与一个i x λ值对应将有两个值,即其归宿轮流取两个值,如图4-2(b)所示。
当i x 2.3=λ时,此值为i i x x =⇔+2,7995.05130.0周期为2,表示从出发,迭代二次后回到。
所以,从图3-12(a)到3-12(b)中间发生了一个倍周期分岔,一个稳定态分裂成为两
i x i x
图4-2 叠代过程
种状态,而系统便在两个交替变动的值间来回振荡。
③当544.3449.3<<λ时,最终在四个值之间循环跳跃,如图4-2(c)所示。
+4,即终态集是个四周期解,表示从出发,迭代四次后回到。
所以,从图4-2(b)
到3-12(c),中间又发生了一个倍周期分岔,两种状态分裂成四种状态,而系统便在四个交
i x i i x x i x i x =
替变动的值间来回振荡。
当5.3=λ时,四个值为
④当
4
569.3
<<λ,周期变为,最后归宿可取无穷多的各种不同值,即出现混沌象。
图4-2(d)表示∞0.4=λ现时的具体迭代过程,此时系统已进入混沌,没有稳定的周期轨道,相点几乎可以通过相空间中的任何一点。
图4-2 叠代过程
、分岔图
由于逻辑斯谛映射的计算非常简单,因而人们对它进入混沌区的过程研究得非常细致。
计算表明,第一次分岔开始发生在
三3=λ的地方,其后发生一个无穷系列的倍周期分岔,再次开始分岔的参数值为3.449, 3.544, 3.564, …间隔越来越小,到, 其间了极限值
569.3=λ的地方进入混沌区(见
图4-3)。
在λ从3.569到4的参数范围内,情况是极为复杂的,这里基本上是混沌区。
但
在其中有无穷多个稳定的周期解的“窗口”,窗口里又有无情况可以图4-4中看出来。
此图反映的是逻辑斯谛映射穷多个倍周期分岔系列,这些的终态集随参数λ变化的情况,它 叫做映射的分岔图。
4-3 鲍姆数
978年美国物理学家费根鲍姆(Feigenbaum )发现若用
图4-4 映射的分岔图。
费根1了有关倍周期分岔系列的一些性质。
m λ代表第m 次分岔出现的λ值,则相继分岔的间距之比趋于一个常数,即有 6692.4lim lim
1
11
==∆∆−−+∞→+−∞→δλλλλm m m m m m m m
(4-3)
上式表明,随着λ的增加,两相邻分岔的间距L 21,∆∆越来越小(见图4-5),倍周期的来临越来越快,这一几何级数的收敛的,92,越到后来越精确。
纵轴方向的分岔宽度收敛的比率4.66L ,,21εε渐进地按照因子5029.2=α衰减,即
5029.2/lim 1==+∞
→m m m εεα
(4-4)
也就是说,前一次的分岔宽度大约是下一次的分岔宽度的2.5029倍,越到后来越精确。
整个系统的运行在越来越小的尺度上重复出现近似的自相似结构,由大到小的自相似的缩不比率就是一个普适的费根鲍姆数。
表4-1清楚地表明迭代系统)1(i i i x x x −=λ的周期倍增分岔现象中分岔间距比值1+∆<∆m m 趋向6692.4=δ的情形。
表4-1 分岔间距比值的变化情况
m 分岔情况 分岔值m λ
间距比值1/+∆∆m m 1 2 1分为2 2分为4 为64
周期解→ 3
3.449 4899 743 9 691 610
4.751 466 4.668 74 .669 1
4.669 201 609
3 4 5 6
4分为8 8分为16 16分为32 32分 3.544 090 359 3.564 407 266 3.568 759 420 3.56 4.656 251 4.668 242 4M ∞
M
混沌
3.569 945 972
M M
由此表沌是有不是混乱这:“混沌非周期的有序性”,“混沌是确定性的非周期流”。
这就是说,混沌并不是简单的有序态,而是一种没有确期性和性的有特别值意的是明混规律的,的。
所以有人又样定义混沌是或定周明显对称序态。
得注,常数δ和α并不限于这类映射,对不同的非线性系统,例如正弦映射in(1i i x x )s πλ=+1i x ,
指数映射1(exp[i x x −)]=+λ,得到δ值和α值都精确地相同。
可见,非线代系统可以很遵循同向混沌。
这反映出沿倍周期分岔系列通向混沌的道路中具有的某种普适性。
不仅是上述映射较简单的数学模型具有这种普适性,在某些真实的物理实验中也具有这种普适性。
年ab 为精致,也在其中发出 分别按因子性迭的本身结构不相同,但却样的方式走1977利布沙伯(Libch er )做了一个极的液氦对流实验了倍周期分岔系列,验算了倍周期分岔的实验数据,所得结果和费根鲍姆数比较接近。
据单摆实验的倍周期分岔序列算出的结果和费根鲍姆数比较,其差值也在计算误差范围内。
费根鲍姆数反映出通向混沌道路中的有序性,它揭示出周期倍增分岔时分岔间距和分岔宽度αδ和衰减的规律,依据费根鲍姆数可以预料参数值为多少时发生2, 4, 8等等的售周期分岔。
随着控制参数λ的增大,当λ达到∞λ时,周期倍增分岔导致“稳定的”∞
2周期解。
注意∞=∞
2,而周期无穷大就等于没有周期,所以系统从此就进入了混
沌状态。
