第1章质点运动学与牛顿定律
大学物理(西南交大)作业参考答案1
NO.1 质点运动学和牛顿定律班级 姓名 学号 成绩一、选择1. 对于沿曲线运动的物体，以下几种说法中哪种是正确的： [ B ] (A) 切向加速度必不为零． (B) 法向加速度必不为零（拐点处除外）． (C) 由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零． (D) 若物体作匀速率运动，其总加速度必为零．(E) 若物体的加速度a为恒矢量，它一定作匀变速率运动．2．一质点作一般曲线运动，其瞬时速度为V ，瞬时速率为V ，某一段时间内的平均速度为V，平均速率为V ，它门之间的关系为：[ D ]（A ）∣V ∣=V ，∣V ∣=V ； （B ）∣V ∣≠V ，∣V∣=V ； （C ）∣V ∣≠V ，∣V ∣≠V ； （D ）∣V ∣=V ，∣V∣≠V .3.质点作曲线运动，r 表示位置矢量，v 表示速度，a表示加速度，S 表示路程，a τ表示切向加速度，下列表达式中， [ D ](1) d /d t a τ=v ， (2) v =t r d /d ， (3) v =t S d /d ， (4) d /d t a τ=v ．(A) 只有(1)、(4)是对的． (B) 只有(2)、(4)是对的．(C) 只有(2)是对的． (D) 只有（1）、(3)是对的．（备注：经过讨论认为（1）是对的）4.某物体的运动规律为t k t 2d /d v v -=，式中的k 为大于零的常量．当0=t 时，初速为0v ，则速度v 与时间t 的函数关系是 [ C ](A) 0221v v +=kt , (B) 0221v v +-=kt , (C) 02121v v +=kt , (D) 02121v v +-=kt 5.质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任一时刻质点的速率) [ D ](A) t d d v ．(B) 2v R ． (C) R t 2d d vv +．(D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v ．6．质点沿x 方向运动，其加速度随位置的变化关系为：a=31+3x 2. 如在x=0处，速度v 0=5m.s -1，则在x=3m处的速度为：[ A ]（A ）9 m.s -1； （B ）8 m.s -1； （C ）7.8 m.s -1； （D ）7.2 m.s -1 .7.如图所示，假设物体沿着竖直面上圆弧形轨道下滑，轨道是光滑的，在从A 至C 的下滑过程中，下面哪个说法是正确的？[ E ](A) 它的加速度大小不变，方向永远指向圆心． (B) 它的速率均匀增加．(C) 它的合外力大小变化，方向永远指向圆心． (D) 它的合外力大小不变．(E) 轨道支持力的大小不断增加．8．物体作圆周运动时，正确的说法是：[ C ] （A ）加速度的方向一定指向圆心；（B ）匀速率圆周运动的速度和加速度都恒定不变； （C ）必定有加速度，且法向分量一定不为零；（D ）速度方向一定在轨道的切线方向，法向分速度为零，所以法向加速度一定为零；9．以下五种运动形式，a保持不变的运动是 [ E ]A（A ）单摆的运动；（B ）匀速圆周运动；（C ）圆锥摆运动；（D ）行星的椭圆轨道运动；（E ）抛体运动； 二、填空1．已知一质点在Oxy 平面内运动，其运动学方程为22(192)r ti t j =++；r的单位为m ，t 的单位为s ，则位矢的大小rv = 24i t j + ，加速度a =4(/)j m s 。
第1章-质点运动学
z A.
(t )
.B
的变化情况，定义：质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即：质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数，或等于矢径 r 对时
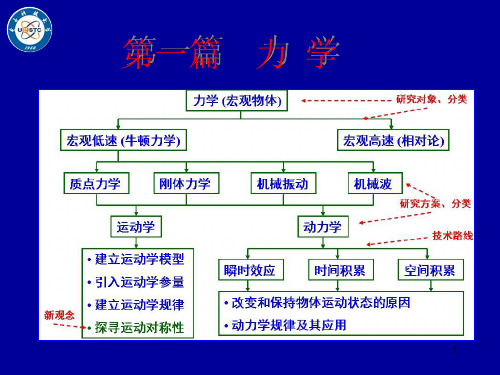
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论：关于物质运动属性的两种哲学论断 赫拉克利特：“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得：x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示，质点沿曲线C运动。时刻t在A点，时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r，称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
大学物理C复习提纲
第一章 质点运动学 第二章牛顿定律1、掌握质点运动学第二类问题的计算。
2、掌握牛顿定律的应用举例。
练习：1、已知一质量为m 的质点在x 轴上运动，质点只受到指向原点的引力作用，引力大小与质点离原点的距离x 的平方成反比，即2/x k f −=，k 是比例常数．设质点在A x =时的速度为零，求质点在4/A x =处的速度的大小。
2、质量为m 的子弹以速度0v 水平射入沙土中，设子弹所受阻力与速度成正比，比例系数为k ，忽略子弹的重力,求(1)子弹射入沙土后,，速度随时间变化的函数关系式；(2) 子弹射入沙土的最大深度。
第三章 动量守恒定律和能量守恒定律1、掌握冲量的概念。
2、掌握动量守恒定律。
3、掌握保守力的概念及保守力作功的特点：保守力做功只与始末位置有关，而与路径无关。
练习：1、在一定时间间隔内质点系的动量守恒，则在该时间间隔内，质点系所受A 、外力矩始终为零B 、外力做功始终为零C 、外力矢量和始终为零D 、内力矢量和不为零2、以下说法正确的是A 、大力的冲量一定比小力的冲量大B 、小力的冲量有可能比大力的冲量大C 、速度大的物体动量一定大D 、质量大的物体动量一定大第四章 刚体的转动1、掌握力矩的定义。
2、理解合外力矩与合外力的关系。
3、掌握决定刚体转动惯量大小的因素。
4、掌握转动定律。
5、刚体定轴转动的角动量：JW L =及角动量守恒定律。
练习：1、一质量为m 的质点作半径为r 的匀速圆周运动，则作用于质点的合力F 相对于圆心的力矩M= 。
2、刚体定轴转动惯量的大小由刚体的质量、质量分布和转轴位置决定。
3、以下说法正确的是A 、合外力为零，合外力矩一定为零B 、合外力为零，合外力矩一定不为零C 、合外力为零，合外力矩可以不为零D 、合外力不为零，合外力矩一定不为零4、在定轴转动中，如果合外力矩的方向与角速度方向一致，则以下说法正确的是A 、合力矩增大时，物体角速度一定增大B 、合力矩减小时，物体角速度一定减小C 、合力矩减小时，物体角加速度不一定变小D 、合力矩增大时，物体角加速度不一定增大5、芭蕾舞演员可绕过脚尖的铅直轴旋转,当她伸长两手时的转动惯量为J 0，角速度为ω0，当她突然收臂使转动惯量减小为J 0/2时，其角速度应为A 、ω0/4B 、4ω0C 、ω0/2D 、2ω0第五章 静电场 第六章 静电场中的导体与电介质1、 掌握静止电荷在其周围空间中只产生电场，而运动电荷在其周围空间既产生电场，又产生磁场。
1 质点运动学
en
2.切向加速度
法向加速度
v dv
d
；t+dt时刻：B点 t时刻：A点 v v dv dt时间内经过弧长ds ds对应圆心角角度d
B
R
A
v
ˆ dr dset
ˆ dv d v ( t )e t a dt dt
例1．路灯距地面高H ，行人高h ，若人以速率 u从路 灯正下方背向路灯运动时，求人头顶影子的运动方程 （以路灯的正下方为原点）。
解：
x ut
H x h x x H H x x ut H h H h
§1.2 位移 速度 加速度
位移（displacement）： 位置矢量的变化量 r(t)
ˆ ˆ d( xi yˆ zk ) j ˆ ˆ v vx i v y ˆ vz k j dt
速度的大小：
v v v v
2 2 x y
2 z
速度的方向：为轨迹切线的方向，指向时间 t 值增 大的一方。
注意：
s r , d s d r
r r , d r d r
r | r |
2 2
2 2
2 2
2 1
2 1
2 1
路程（path）： 位置矢量末端运动轨迹 s 的长度
位移与路程的区别： （A）位移是矢量，路程是标量。 （B）一般情况，位移大小不等于路程。
r s
（C）两点间的路程是不唯一的，而位移是唯一的。
r ？s
什么情况下
1. 不改变方向的直线运动;
大小： 方向：
r
4 2 ( 4) 2 5.65m
4 arctg 4 4
第1章--质点运动学与牛顿定律
习题1 选择题1.1一质点在平面上运动,已知质点位置矢量的表达式为 r = a t 2 i + b t 2 j (其中a 、b 为常量), 则该质点作( ) (A) 匀速直线运动 (B) 变速直线运动 (C) 抛物线运动 (D) 一般曲线运动解 首先要判断的是质点的轨迹，由质点的位置矢量表达式 r = a t 2 i + b t 2 j 知2x at =，2y bt =。
消去t 可得质点的轨迹方程为by x a=，由此可知质点的轨迹为直线。
其次要判断的是状态的变化，也就是考察速度和加速度，22d at bt dt==+rυi j ，22a b =+a i j 。
由此可知质点作变速直线运动，故选B 。
1.2 如图所示，用水平力F 把木块压在竖直的墙面上并保持静止。
当F 逐渐增大时，木块所受的摩擦力( )（A ）不为零， 但保持不变（B ）随F 成正比地增大（C ）开始随F 增大， 达到某一最大值后， 就保持不变 （D ）无法确定解 由题意可知物体的状态是静止，根据牛顿第二定律物体所受的合外力为零。
在竖直方向上物体受重力和摩擦力两个力的作用，两个力大小相等 、方向相反。
故选A 。
1.3一质点沿x 轴运动，其速度与时间的关系为：24m/s t =+v ，当3s t =时，质点位于9m x =处，则质点的运动方程为( )(A)214123x t t =+- (B)2142x t t =+(C)23x t =+ (D)314123x t t =++解 因为质点沿x 轴运动，由dx dtυ=有dx dt υ=，通过积分2(4)dx dt t dt υ==+⎰⎰⎰得到2143x t t C =++。
当3s t =时，质点位于9m x =处，可求得12C =-。
故选A 。
1.4 质点作曲线运动，其瞬时速度为υ，瞬时速率为υ，平均速度为υ，平均速率为υ，则它们之间的下列四种关系中哪一种是正确的? ( ) （A ）,υυ==υυ （B ）,υυ≠=υυ习题1.2图（C ）,υυ=≠υυ （D ）,υυ≠≠υυ 解 ,,,d d s sd t d t t tυυ∆∆====∆∆r r υυ；d d s =r s ∆≠∆r 。
理论力学知识总结
学生整理，时间有限，水平有限，仅供参考，如有纰漏，请以老师、课本为主。
第一章质点力学（1）笛卡尔坐标系 位置：k z j y i x ++=r速度：k z j y i x dtr d ...v ++== 加速度：k z j y i x dtv d ......a ++== （2）极坐标系坐标：j i e r θθsin cos += j i e θθθcos sin +-= r e r =r 速度：r r .v = .v θθr =加速度:2...θr r a r -= .....2θθθr r a += （3）自然坐标系（0>θd ） 坐标：ds r d e t =θd e d e t n = θρd ds = 速度：t e v v = 加速度：n t e v e v ρ2.a +=（4）相对运动（5）牛顿运动定律 牛顿第一定律：惯性定律 牛顿第二定律：)(a m v m P dtP d dt v d m F ==== 牛顿第三定律：2112F F -= （6）功、能量vF dt rd F dt dW P rFd dA ⋅=⋅=== （7）（7）有心力第二章 质点动力学的基本定理知识点总结： 质点动力学的基本方程质点动力学可分为两类基本问题:. (1) .已知质点的运动，求作用于质点的力; (2) 己知作用于质点的力，求质点的运动。
动量定理 动量：符号动量定理微分形式动量守恒定律：如果作用在质点系上的外力主失恒等于零，质点系的动量保持不变。
即：质心运动定理：质点对点O 的动量矩是矢量mv r J i ⨯= 质点系对点0的动量矩是矢量i ni nii i i v m r J J ∑∑=⨯==1若z 轴通过点0，则质点系对于z 轴的动量矩为∑==ni z z z J M J ][若C 为质点系的质心，对任一点O 有 c c c J mv r J +⨯=02. 动量矩定理∑∑=⨯=⨯=nie i i n i i i i M F r v m r dt d dt dJ )()( 动量矩守恒：合外力矢量和为零，则动量矩为常矢量。
《大学物理1》内容提要(PDF)
1.参考系：描述物体运动时用作参考的其它物体和一套同步的钟.2.位矢和位移一运动的描述➢运动方程kt z j t y i t x t r r)()()()(++==➢位移)()(t r t t r r−∆+=∆注意: 一般rr ∆≠∆ 3.速度和速率tsd d =v k t z j dt y i t x t rd d d d d d d ++==v ➢速度➢速率（速度合成）第一章质点运动学3.加速度任意曲线运动都可以视为沿x ，y ，z 轴的三个各自独立的直线运动的叠加（矢量加法）.——运动的独立性原理或运动叠加原理.kj i t r t a z y x tv t v t v v d d d d d d d d d d 22++===二. 匀加速运动=a常矢量初始条件:or v ,0ta +=0v v 2021ta t r++=0v r➢匀加速直线运动at+=0v v 2021att x ++=0v x ax22=−20v v ➢抛体运动0=x a ga y −=θcos 0x v v =gty −=θsin 0vv t⋅=θcos 0v x 221sin gtt −⋅=θ0vy 三. 圆周运动➢角速度Rt v ==d d θω➢角加速度td d ωβ=➢速度tt t d d e r e e ts ω===v vnn t t e a e a a +=➢圆周运动加速度22nt a a a +=切向加速度22t d d d d ts r t a ===αv 法向加速度rr a 22n v v ===ωω（指向圆心）（沿切线方向）➢力学的相对性原理:动力学定律在一切惯性系中都具有相同的数学形式.四. 相对运动➢伽利略速度变换u+='v v第二章牛顿定律一牛顿运动定律第一定律：惯性和力的概念，惯性系的定义.第二定律：tp F d d =vm p =当时，写作c <<v a m F=第三定律2112F F−=力的叠加原理+++=321F F F F 二国际单位制力学基本单位m 、kg 、s量纲：表示导出量是如何由基本量组成的关系式.t mma F xx x d d v ==tmma F yy y d d v ===直角坐标表达形式自然坐标表达形式d d t t F ma mt ==vn n F ma mρ==2v牛顿第二定律的数学表达式am t p F ==d d 一般的表达形式nn t t y x e F e F j F i F F +=+=（1）万有引力r221e r m m G F−=重力gm P =三几种常见的力(3）摩擦力滑动摩擦力静摩擦力Nf F F μ=N0f0m 0f F F F μ=≤（2）弹性力：弹簧弹力（张力、正压力和支持力）kxF−=四应用牛顿定律解题的基本思路1）确定研究对象，几个物体连在一起需作隔离体，把内力视为外力；2）受力分析：画受力图；3）建立坐标系，列方程求解；(用分量式)4）先用文字符号求解，后代入数据计算结果.第三章动量守恒定律和能量守恒定律一动量、冲量、动量定理vm p =——机械运动的量度质点的动量力的冲量——力对时间的累计⎰=21d t tt F I1221d v v m m t F t t −=⎰质点的动量定理：质点所受合外力的冲量等于质点在此时间内动量的增量。
大学物理所有公式
大学物理所有公式第一章质点运动学和牛顿运动定律1.1平均速度v =t △△r1.2 瞬时速度v=lim 0△t →△t △r =dt dr1. 3速度v=dt ds==→→lim lim 0△t 0△t △t △r1.6 平均加速度a =△t △v1.7瞬时加速度（加速度）a=lim 0△t →△t △v =dt dv 1.8瞬时加速度a=dt dv =22dt rd1.11匀速直线运动质点坐标x=x 0+vt1.12变速运动速度 v=v 0+at1.13变速运动质点坐标x=x 0+v 0t+21at 21.14速度随坐标变化公式:v 2-v 02=2a(x-x 0)1.15自由落体运动 1.16竖直上抛运动===gy v at y gt v 22122 -=-=-=gyv v gt t v y gtvv 2212022001.17 抛体运动速度分量-==gta v v a v v y x sin cos 001.18 抛体运动距离分量-?=?=20021sin cos gt t a v y tav x1.23向心加速度 a=R v 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =R v 21.27切向加速度只改变速度的大小a t =dt dv1.28 ωΦR dtd R dt ds v ===1.29角速度dt φωd = 1.30角加速度 22dt dtd d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR RR R v == a t =αωR dt d R dt dv ==牛顿第一定律：任何物体都保持静止或匀速直线运动状态，除非它受到作用力而被迫改变这种状态。
牛顿第二定律：物体受到外力作用时，所获得的加速度a 的大小与外力F 的大小成正比，与物体的质量m 成反比；加速度的方向与外力的方向相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题1 选择题一质点在平面上运动,已知质点位置矢量的表达式为 r = a t 2 i + b t 2 j (其中a 、b 为常量), 则该质点作( ) (A) 匀速直线运动 (B) 变速直线运动 (C) 抛物线运动 (D) 一般曲线运动解 首先要判断的是质点的轨迹，由质点的位置矢量表达式 r = a t 2 i + b t 2 j 知2x at =，2y bt =。
消去t 可得质点的轨迹方程为by x a=，由此可知质点的轨迹为直线。
其次要判断的是状态的变化，也就是考察速度和加速度，22d at bt dt==+rυi j ，22a b =+a i j 。
由此可知质点作变速直线运动，故选B 。
如图所示，用水平力F 把木块压在竖直的墙面上并保持静止。
当F 逐渐增大时，木块所受的摩擦力( )（A ）不为零， 但保持不变（B ）随F 成正比地增大（C ）开始随F 增大， 达到某一最大值后， 就保持不变 （D ）无法确定解 由题意可知物体的状态是静止，根据牛顿第二定律物体所受的合外力为零。
在竖直方向上物体受重力和摩擦力两个力的作用，两个力大小相等 、方向相反。
故选A 。
一质点沿x 轴运动，其速度与时间的关系为：24m/s t =+v ，当3s t =时，质点位于9m x =处，则质点的运动方程为( )(A)214123x t t =+- (B)2142x t t =+(C)23x t =+ (D)314123x t t =++解 因为质点沿x 轴运动，由dx dtυ=有dx dt υ=，通过积分2(4)dx dt t dt υ==+⎰⎰⎰得到2143x t t C =++。
当3s t =时，质点位于9m x =处，可求得12C =-。
故选A 。
质点作曲线运动，其瞬时速度为υ，瞬时速率为υ，平均速度为υ，平均速率为υ，则它们之间的下列四种关系中哪一种是正确的 ( )（A ）,υυ==υυ （B ）,υυ≠=υυ习题图（C ）,υυ=≠υυ （D ）,υυ≠≠υυ 解 ,,,d ds sdt dt t tυυ∆∆====∆∆r r υυ；d ds =r s ∆≠∆r 。
故选C 。
以下五种运动形式中，a 保持不变的运动是( ) (A) 单摆的运动 (B) 匀速率圆周运动 (C) 行星的椭圆轨道运动 (D) 抛体运动(E) 圆锥摆运动解 a 保持不变表明物体所受的合外力恒定不变。
单摆的运动、行星的椭圆轨道运动、圆锥摆运动合外力的大小和方向都在不断的改变；匀速率圆周运动合外力的大小不变，但方向不断地改变；作抛体运动的物体只受重力作用，大小和方向都不变，故选D 。
对于沿曲线运动的物体，以下几种说法中哪一种是正确的( ) (A) 切向加速度必不为零。
(B) 法向加速度必不为零（拐点处除外）。
(C) 由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零。
(D) 若物体作匀速率运动，其总加速度必为零。
(E) 若物体的加速度a 为恒矢量，它一定作匀变速率运动。
解 对于沿曲线运动的物体，2,n d a a dt τυυρ==。
当0υ=时，a τ可以等于零；当0υ≠时，0n a ≠；故选B 。
一运动质点在某瞬时位于矢径(),x y r 的端点处, 其速度大小为( )(A)t r d d (B) d d tr(C) d d tr(D)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 解 因为 d dx dy dt dt dt ==+r υi j ，所以速度的大小为22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 。
故选D 。
水平地面上放一物体A ，它与地面间的滑动摩擦系数为．现加一恒力F 如图所示．欲使物体A 有最大加速度，则恒力F 与水平方向夹角应满足( )(A) sin ＝． (B) cos ＝． (C) tg ＝． (D) ctg＝．解 欲使物体A 有最大加速度，对物体进行受力解，物体共受到,,F N P 三个力的作用，FθA习题图所受合外力是()cos sin F P F θθμ--，根据牛顿第二定律()cos sin F P F a mθθμ--=，令()'0a θ=，可求得tg μθ=时物体A 有最大加速度。
故选C 。
在相对地面静止的坐标系内，A 、B 二船都以12m s -⋅速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x 、y 方向单位矢用i 、j 表示)，那么在A 船上的坐标系中，B 船的速度（以m/s 为单位）为( ) (A) 2i ＋2j (B) 2i ＋2j(C) －2i －2j (D) 2i －2j解 这是一个相对运动的问题，要求的是B 船相对A 船的速度，由题意可知()12A m s -=⋅υi ，()12B m s -=⋅υj ，'22BB A =-=-υυυj i ，故选B 。
如图所示，一轻绳跨过一个定滑轮，两端各系一质量分别为m 1和m 2的重物，且m 1>m 2．滑轮质量及轴上摩擦均不计，此时重物的加速度的大小为a ．今用一竖直向下的恒力gm F 1=代替质量为m 1的物体，可得质量为m 2的重物的加速度为的大小a ′，则( ) (A) a ′= a (B) a ′> a(C) a ′< a (D) 不能确定.1m 2解 对12,m m 两物体进行受力解，1m 受力1,P T ；2m 受力2,P T 。
根据牛顿第二定律 有1122,P T m a T P m a -=-=，可求得()1212m m g a m m -=+；当用一竖直向下的恒力g m F 1=代替质量为m 1的物体，可得质量为m 2的重物的加速度为的大小()12'2m m g a m -=。
由此可知a ′> a ，故选B 。
习题图2 填空题在xoy 平面内有一运动的质点，其x ,y 分量的运动方程分别为10cos(5)x t =，10sin(5)y t =(SI)，t 时刻其速率υ =__________， 其切向加速度的大小a τ=______________；其法向加速度的大小n a =_________。
解 根据,x y dx dydt dtυυ==可得()()50sin 5,50cos 5x y t t υυ=-=，t 时刻质点的速率为 22150x y m s υυυ-=+=⋅，切向加速度的大小0d a dtτυ==，法向加速度的大小22250n a m s Rυ-==⋅。
在x 轴上作变加速直线运动的质点,已知其初速度为0υ,初始位置为0x ,加速度为a=C t 2 (其中C 为常量),则其速度与时间的关系υ= ， 运动方程为x= 。
解 根据,d adt dx dt υυ==，通过积分02t d Ct dt υυυ=⎰⎰可得3013Ct υυ=+；通过积分03001()3x t x dx Ct dt υ=+⎰⎰可得400112x x t Ct υ=++。
灯距地面高度为H ,一个人身高为h , 在灯下以匀速率υ沿水平直线行走, 如图所示.则他的头顶在地上的影子M 点沿地面移动的速度M υ= 。
解 建立如下坐标，设时刻t 影子M 点在地面的位置为x ，人在地面的位置为t υ，由几何关系知x H x t h υ=-，将此式对t 求导得dx dx h H dt dt υ=-，因为M dx dt υ=，所以M H H hυυ=+。
H M习题图 HMOx如图,一质点P 从O 点出发以匀速率11m s -⋅作顺时针转向的圆周运动, 圆的半径1m,如图所示,当它走过34圆周时, 走过的路程是 ，这段时间内的平均速度大小 ，方向是 。
解 质点P 从O 点出发以匀速率11m s -⋅作顺时针转向的圆周运动, 当它走过34圆周到达B 时，走过的路程是33242m ππ⨯=，1223OB m s t π-==⋅υ，方向与ox 轴成45。
一质点沿半径为R 的圆周运动, 在t = 0时经过P 点, 此后它的速率υ按υ=A+B t (A 、B 为正的已知常量)变化, 则质点沿圆周运动一周再经过P 点时的切向加速度a t = ，法向加速度a n = 。
解 d a B dtτυ==，22()n A Bt a R R υ+==。
以一定初速度斜向上抛出一个物体, 如果忽略空气阻力, 当该物体的速度υ与水平面的夹角为 时，它的切向加速度a τ的大小为a τ= ， 法向加速度a n 的大小为a n = 。
解 因为忽略空气阻力，物体只受重力作用，所以物体的加速度就是重力加速度g ，将g 分解为沿速度方向和与速度垂直方向即得到sin ,cos n a g a g τθθ==。
如图所示装置中，若两个滑轮与绳子的质量以及滑轮与其轴之间的摩擦都忽略不计，绳子不可伸长，则在外力F 的作用下，物体m 1和m 2的加速度为a =______________________，m 1与m 2间绳子的张力T =________________________。
·O P xyTm 1m 2· O P xyB习题图解 因为两个滑轮与绳子的质量以及滑轮与其轴之间的摩擦都忽略不计，绳子不可伸长，对12,m m 两物体进行受力解，1m 受力1,P T,F ；2m 受力2,P T 。
根据牛顿第二定律 有1122,F P T m a T P m a +-=-=，可求得1212212122,m g m g F m m g Fm a T m m m m -++==++。
在如图所示的装置中，两个定滑轮与绳的质量以及滑轮与其轴之间的摩擦都可忽略不计，绳子不可伸长，m 1与平面之间的摩擦也可不计，在水平外力F 的作用下，物体m 1与m 2的加速度a ＝______________，绳中的张力T ＝_________________。
解 因为两个滑轮与绳子的质量以及滑轮与其轴之间的摩擦都忽略不计，绳子不可伸长， 对12,m m 两物体进行受力解，1m 水平方向受力,F T ；2m 受力2,P T 。
根据牛顿第二定律有122,F T m a T P m a -=-=，可求得21221212,F m g m m g Fm a T m m m m -+==++。
3 计算题已知质点位矢随时间变化的函数形式为22t t =+r i j ，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。
解 (1)由d dt =r υ，有：22t =+υi j ，d dt=υa ，有：2=a i （2）而υ=υ，有速率：υ==∴d a dtτυ==，利用222n a a a τ=+有：n a ==一质点沿x 轴作直线运动,它在t 时刻的坐标是234.52x t t =-，式中x 以米计，t 以秒计，试求习题图 习题图(1) 1=t s 和2=t s 时刻的瞬时速度；（2）第二秒内所通过的路程；（3）第二秒内的平均加速度以及s t 1=和 s t 2=时刻的瞬时加速度。