三次函数对称中心
三次函数常见的性质及应用

三次函数常见的性质及应用
一、性质
1、三次函数的图像一定是一个闭合曲线,其中心点为原点(0,0);
2、三次函数的图像具有左右对称性;
3、三次函数图像的极值点(即最大值点和最小值点)一定位于曲线的拐点处;
4、三次函数的导数存在,其单调性与函数的单调性相反;
5、三次函数的二阶导数存在,其值大于等于0;
二、应用
1、三次函数可以用来描述经济学中的供求关系;
2、三次函数可以用来描述物理学中的力学变化;
3、三次函数可以用来描述数学中的曲线图形;
4、三次函数可以用来描述自然现象中的变化趋势;
5、三次函数可以用来描述计算机科学中的数据处理。
三次函数的图像和性质

三次函数的图像和性质 知识回顾:定义:形如()()0,23≠+++=a d cx bx ax x f 的函数叫做三次函数;定义域:R ;值域:R ;图像:对称性:中心对称图形,对称中心⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--a b f a b O 3,3;三次多项式因式分解:()()()32123x x x x x x a d cx bx ax ---=+++方法一:试根,待定系数因式分解;方法二:代数基本定理:d s a r i i ,,则多项式的所有有理数根一定在ii r s 中取得;典例1:三次函数单调区间和极值 1. 已知函数()1223-+-=x x x x f(1)求函数的单调区间和极值;(2)判断函数的零点个数;典例2:三次函数的零点问题1. 已知函数()λ--+-=1223x x x x f ,若函数存在三个零点,则实数λ的取值范围 ;2. 已知奇函数()x f 是R 的单调函数,若函数()()213--++=x f x f y λ至少有两个零点,求实数a 的取值范围.变式训练:设函数()a ax x x x f ++-=2331有三个零点,求实数a 的取值范围.典例3:三次函数的切线问题1. 设函数()()1,3+==x x g x x f λ(1)若曲线()x g与函数()x f 的图像相切,求实数λ的值; (2)若()()x g x f =有三个根,求实数λ的值;2. 已知函数()x x x f 323-=. (1)求()x f 的对称中心以及对称中心处的切线方程;(2)若过点()t P,1存在3条直线与曲线()x f 相切,求实数t 的取值范围; (3)讨论过点()()R n m n m ∈,,,存在几条直线与曲线()x f 相切;经验分享:一般的三次函数的切线条数有如下规律:三次函数()()0,23≠+++=a d cx bx ax x f 的图像和其相应过对称中心⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--a b f a b O 3,3的切线l 将平面分为如下四个区域:(1)过区域①,③内的点可作3条与曲线()x f 相切的直线; (2)过曲线()x f 或直线l 上且不在O 处的点可作2条与曲线()x f 相切的直线;(3)过O 或区域②,④内的点可作1条与曲线()x f 相切的直线;•O ② ③④ O •①② ④。
三次函数的对称性中心问题

三次函数的对称性中心问题而)3()3()3()3]()3(3[)3(2323a b c a b b d a b a a b c a b a d a b a -++-=-++-)3(ab f -=)0()(23≠+++=a d cx bx ax x f 的图象关于))3(,3(a b f a b --对称。
证明3:设函数)0()(23≠+++=a d cx bx axx f 的对称中心为(m ,n )。
按向量),(a n m --=将函数的图象平移,则所得函数n m x f y -+=)(是奇函数,所以2)()(=-+-++n m x f m x f+++++++d m x c m x b m x a )()()(23dm x c m x b m x a ++-++-++-)()()(23-2n=0化简得:上式对恒成立,故⎩⎨⎧=-+++=+00323n d cm bm am b am 得,。
所以,函数的对称中心是()。
定理3:若三次函数有极值,则它的对称中心是两个极值点的中点证明:不妨设0232=++c bx ax 为)(x f 的导方程,判别式01242>-=∆ac b ,设)(x f 两极值点为))(,()),(,(2211x f x B x f x A[][]acx x a b x x d x x c x x x x b x x x x x x a dx x c x x b x x a d cx bx ax d cx bx ax x f x f 3,322)(2)(3)()(2)()()()()(2121212122121221212122213231222321213121=-=++++-++-++=++++++=+++++++=+∴ 又dabc a b b a b a da b c a c b a b b a c a b a a b a x f x f 2)3(2)3(2)3(22)32(32323)32(332)()(232321+-+-+-=+-+-⎪⎭⎫⎝⎛-+--⎪⎭⎫ ⎝⎛-=+∴)3(2)(21ab f x x f -=+∴所以此时的对称中心是两个极值点的中点,同时也是函数)(x f 的拐点。
高考数学考点 三阶函数的对称中心

结合三个函数的图像,我们能得到一个这样的结论:三次函数的对称点所在的直线是导函数的对称轴所在的直线,还是二阶导函数的零点所在的直线,如图中的C点所在的垂直于x轴的直线,在高中阶段我们不研究B点,在大学微积分中B点叫做拐点,即B点是函数凸凹性发生改变的点,关于凸凹性在函数性质中提到过,因此我们求三次函数的对称点只需要求三次函数的二阶导数的零点即可,即:
很显然二阶导数为y=3x²-8x+1,我们把导函数图像和三次函数图像作在一起:
从上面图中可以看出二次函数的正负决定三次函数的增减,又因为二次函数是对称的平滑函数,所以三次函数必定也是对称函数,我们在导数中研究的是导函数的零点就是三次函数的极值点,但是我们没有研究过导函数的对称轴与三次函数是什么关系,初步猜测,导函数对称轴所在的直线与三次函数的交点处就是三次函数的对称点,如图上的B点,我们研究了三次函数的导函数,不妨再看看三次函数的二阶导函数,下面将三次函数、导函数、二阶导函数放在同一个图中:
结合三个函数的图像,我们能得到一个这样的结论:三次函数的对称点所在的直线是导函数的对称轴所在的直线,还是二阶导函数的零点所在的直线,如图中的C点所在的垂直于x轴的直线,在高中阶段我们不研究B点,在大学微积分中B点叫做拐点,即B点是函数凸凹性发生改变的点,关于凸凹性在函数性质中提到过,因此我们求三次函数的对称点只需要求三次函数的二阶导数的零点即可,即:
上述结论如在考试中遇到,直接用就行。
看一个有意思的关于三次函数对称性的题目:。
三次函数性质的再探索凸凹性拐点及对称中心——教师用卷
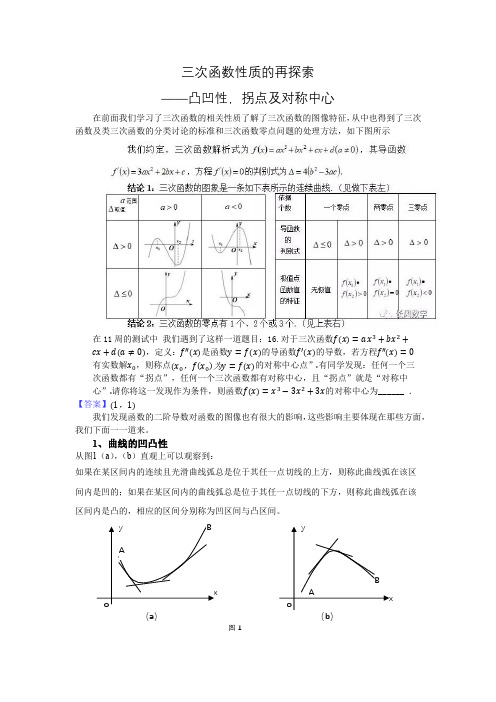
三次函数性质的再探索——凸凹性,拐点及对称中心在前面我们学习了三次函数的相关性质了解了三次函数的图像特征,从中也得到了三次函数及类三次函数的分类讨论的标准和三次函数零点问题的处理方法,如下图所示在11周的测试中我们遇到了这样一道题目:16.对于三次函数,定义:是函数的导函数的导数,若方程有实数解,则称点,为的对称中心点”有同学发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是“对称中心”请你将这一发现作为条件,则函数的对称中心为______ .【答案】,我们发现函数的二阶导数对函数的图像也有很大的影响,这些影响主要体现在那些方面,我们下面一一道来。
1、曲线的凹凸性从图1(a),(b)直观上可以观察到:如果在某区间内的连续且光滑曲线弧总是位于其任一点切线的上方,则称此曲线弧在该区间内是凹的;如果在某区间内的曲线弧总是位于其任一点切线的下方,则称此曲线弧在该区间内是凸的,相应的区间分别称为凹区间与凸区间。
2、曲线的凹凸性的定义定义1 设)(x f 在区间I 上连续,如果对于I 上任意的两点21,x x ,恒有()()222121x f x f x x f +<⎪⎭⎫ ⎝⎛+ 那么称)(x f 在I 上的图形是凹的; 如果恒有 ()()222121x f x f x x f +>⎪⎭⎫⎝⎛+,那么称)(x f 在I 上的图形是凸的。
从图1还可以看到如下事实:对于凹的曲线弧,其切线的斜率)(x f '随着x 的增大而增大,即)(x f '单调增加;对于凸的曲线弧,其切线的斜率)(x f '随着x 的增大而减少,即)(x f '单调减少.而函数)(x f '的单调性又可用它的导数,即)(x f 的二阶导数)(x f ''的符号来判定,故曲线)(x f y =的凹凸性与)(x f ''的符号有关。
三次函数性质总结-三次函数的性质

三次函数性质的探索我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一闭区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.其中运用的较多的一次函数不等式性质是:在上恒成立的充要条件接着,我们同样学习了二次函数,利用已学知识归纳得出:当时(如图1)对称轴;当时(图2)的左侧单调递增、右侧单调递减,对称轴在某一区间取得最大值与最小值.其中决定函数的开口方向,同时决定对称轴,决定函数与轴相交的位置.总结:一次函数只有一个单调性,二次函数有两个单调性,那么三次函数是否就有三个单调性呢?三次函数专题一、定义定义1 的函数,称为“三次函数”(从函数解析式的结构上命名)。
定义 2 ,把叫做三次函数导函数的判别式。
由于三次函数的导函数是二次函数,而二次函数是高中数学中的重要内容,所以三次函数的问题,已经成为高考命题的一个新的热点和亮点。
系列探究1:开始反思1的相关性质呢?反思2的相关性质呢?反思3的相关性质呢?例题 1.(2012天津理4)函数内的零点个数是( ) (A)0 (B)1 (C)2 (D)3探究一般三次函数先求导1、单调性:(1,此时函数()f x在R上是增函数;(2,令两根为12,x x且,则上单调递增,在上单调递减。
2、零点(1) 032≤-acb,则恰有一个实根;(2) ,且,则恰有一个实根;(3) ,且有两个不相等的实根;(4) ,且,则有三个不相等的实根.说明:(1)(2) 与轴只相交一次,即在上为单调函数或两极值同号.(3)0)(=x f 有两个相异实根的充要条件是曲线)(x f y =与x 轴有两个公共点且其中之一为切点,所以032>-ac b ,且0)()(21=⋅x f x f ;(4)0)(=x f 有三个不相等的实根的充要条件是曲线)(x f y =与x 轴有三个公共点,即)(x f 有一个极大值,一个极小值,且两极值异号.所以032>-ac b 且0)()(21<⋅x f x f .3、奇偶性:函数当且仅当时是奇函数。
三次函数的对称性中心问题

三次函数再探讨---对称中心问题武汉市长虹中学 郭永清三次函数存在对称中心吗?我们先从几个特殊的函数入手,三次函数cx ax x f +=3)((0≠a )是奇函数,其图象关于)0,0(对称,三次函数d bx ax x f ++=3)((0≠a )的图象关于点),0(d 对称,那么对于一般的三次函数)0()(23≠+++=a d cx bx ax x f 有没有对称中心呢?答案是肯定的,有对称中心,其对称中心是))3(,3(ab f a b --。
在证明之前,先回忆一个结论: 定理1:函数)(x f y =的图像关于点),(b a M 对称,则在b x a f x f 2)2()(=-+ 证明:设),(y x A 是)(x f y =图像上任意一点,则A 关于点),(b a M 的对称点)2,2(y b x a B --也在函数)(x f y =图像上,即)2(2x a f y b -=-, 又)(x f y =,所以b x a f x f 2)2()(=-+ 定理2:三次函数)0()(23≠+++=a d cx bx ax x f 的对称中心是))3(,3(ab f a b -- 证明1:设),(y x A 是)(x f y =图像上任意一点,只要能证明点))3(2,32-(y a b f x a b B --- 也在函数图像上。
cx bx ax d a bc a b d cx abc bx a x b a b ax bx x a b a b d x ab c x a b b x a b a x a b f ---+-=+--+++----=+--+--+--=--23232223322232332274323494234278)32()32()32()32( d cx bx ax x f y d ab c a b b a b a a b f +++==+-+-+-=-2323)()3()3()3()3(cx bx ax d a bc a b d cx bx ax d a b c a b b a b a y a b f ---+-=----+-+-+-=--23232323322742)3(2)3(2)3(2)3(2 所以)3(2)32()(ab f x a b f x f -=--+ 所以三次函数)0()(23≠+++=a d cx bx ax x f 的对称中心是))3(,3(ab f a b --证明2:因为)0()(3≠+=a bx ax x f 的对称中心是(0,0),所以0030)()()(y x x b x x a x f +-+-=的对称中心为),(00y x ,即))(,(00x f xdcx bx ax x f +++=23)(d cx ab a x a b a a b x a b x a b x a ++--+++=323223)3()3(3])3()3(333[ d ab a xc a b a a b x a +---+=323)3(])3(3[)3( )3]()3(3[)3()3]()3(3[)3(2323a b c a b ad a b a a b x c a b a a b x a -++-+--+= 而)3()3()3()3]()3(3[)3(2323a b c a b b d a b a a b c a b a d a b a -++-=-++-)3(ab f -= )0()(23≠+++=a d cx bx ax x f 的图象关于))3(,3(a b f a b --对称。
三次函数图象一定是中心对称图形吗?

b , ≠0 d ) ≠0 c , ≠0.
三、 交流与合作
)中≠ (凸0 其 )
在以上两个小组研 究的基础上, 我组织他们 进行 了交流和答辩 等合作 活动. 1第二小组的同学对第一小组的研究提出一 . 点质疑, 他们指出, 第一小组的研究在 “ 设三次函
论, 更重要的是, 学生获得了研究问题 的一些途径
的图象 为中心对图形, 对称中心为P x, (o . o , 上任意一点M(l (1 (l ) 厂 ) 则C ( ) x, z) X ∈R I ) 关于 P x ,(o 的对称 点 M 20 一 1 (oIz) ) ( 5 , 2 (o 一. )都在 上, Iz) 厂 1 ( ) 也就是说, 对任意
n
放在一起来看, 就大有文章了. 究的兴趣和热 研 情一下子调动起来了.
一
由( 式得 X =一2. 3 ) O 。 = 。
将 ( 式分别代入 ( 、5, 6 ) 4 ( 经化简验证, ) ) 此 时( 、5两式均成立, O 同时满足对 4 ( ) ) 即X:一 称中心的条件( 、4、5, 3 ( ( 所以, ) ) ) 三次函数 Iz =a 3 x +c +d( ≠0 () x +b a )
一
般地, 设三次 函数解析式为
IZ =a 3 x +c +d ( ≠0, () x +b a )
先研 究简单特殊 的情况.
Iz =a 3 x +c ( ) x +b +d ( ≠0 a )
1当a≠0 c , = d 时, . , ≠0 b =0
维普资讯
由以上两点, 同学们大胆类 比、联想、猜 请 测, 有什么想法? 同学们觉得以上这两份材料虽然简单, 可是
