MATLAB_-_05_-_二维数组及其应用_修改_
MATLAB程序设计及应用实例
c=input('请输入一个字符','s'); if c>='A' & c<='Z'
disp(setstr(abs(c)+1)); elseif c>='a'& c<='z'
disp(setstr(abs(c)-1)); elseif c>='0'& c<='9'
disp(abs(c)-abs('0')); else
disp(c); end
5.1.4 选择结构- switch语句
switch语句
其语句格式为： switch 表达式 case 值1 语句组1 case 值2 语句组2 …… case 值m 语句组m otherwise 语句组m+1 end
5.1.4 选择结构- switch语句
例 某商场对顾客所购买的商品实行打折销售，已知打折标 准，求所售商品的实际销售价格
例 矩阵乘法运算要求两矩阵的维数相容，否则会出错。 先求两矩阵的乘积，若出错，则自动转去求两矩阵的点乘
MATLAB课件-第二讲
A（r,c）
访问A的由r指定行和c指定列上元素构 成的子数组；r，c可取多行或列
A（r, :）
访问A的r指定行上全部元素构成的子 数组；此处冒号表示全部列
A（:,c）
访问A的c指定列上全部元素的子数 组；此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组，以形成更大 的数组
在总元素数不变的前提下，改变数组的“行数、列 数” 以数组“水平中线”为对称轴，交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴，交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数，导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.
matlab教程(第3讲-数组)
2.1数值表示、变量及表达式 （续）
运算符和表达式
运算
加 减 乘 除 幂
数学表达式
a+b a-b axb a/b或a\b
MATLAB运算符
+ * /或 \ ^
MATLAB表达式
a+b a-b a*b a/b或a\b a^b
第二种方法：使用冒号“:”操作符
〘例2-2〙创建以1~10顺序排列整数为元素的 行向量b。>>b=1:10 b=1 2 3 4 5 6 7 8 9 10
2016/11/22 Application of Matlab Language 10
所有的向量元素必须在操作符“[ ]”之内； 向量元素间用空格或英文的逗点“,”分开。
计算
z
z3
z1=3+4*i, z2=1+2*i, z3=exp(i*pi/6), z=z1*z2/z3 z_real=real(z), z_image=imag(z), z_angle=angle(z), z_length=abs(z),
2016/11/22
Application of Matlab Language
第四种方法：利用函数logspace 列向量的创建
通过实验认识该函数的功能。
使用方括号“[ ]”操作符，使用分号“;”分 割行。
〘例2-5〙键入并执行x= [1; 2; 3] X=1 2 3
使用冒号操作符
〘例2-6〙键入并执行x= (1:3)‟ % “ ‟ ”表示矩阵的转 置
2016/11/22 Application of Matlab Language 13
MATLAB数据及其运算
补：两个多维数组的 点运算。
3. MATLAB常用数学函数
函数使用说明：
(1) 三角函数以弧度为单位计算。 (2) abs函数可以求实数的绝对值、复数的 模、字符串的ASCII码值。 (3) 用于取整的函数有fix、floor、ceil、 round，要注意它们的区别。 (4) rem与mod函数的区别。rem(x,y)和 mod(x,y)要求x,y必须为相同大小的实矩阵 或为标量。
p25
A=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ]
[1 3 5 11 13 15 ]
A( [1,3],[1 3 5] )
可以利用 一般向量 和 end 运算符来表示矩阵下标， 从而获得子矩阵。end表示某一维的末尾元素下标。
A( [1,end-பைடு நூலகம்],[1 :2:end] ) ?
例2.3 建立5阶方阵A，判断A的元素是否能被3整 除。
A =[24,35,13,22,63;23,39,47,80,80; ... 90,41,80,29,10;45,57,85,62,21;37,19,31,88,76]
P = rem(A,3)==0
其中，rem(A,3)是矩阵A的每个元素除以3的余数 矩阵。此时，0被扩展为与A同维数的零矩阵，P 是进行等于(==)比较的结果矩阵。
A(3,2)=200
采用矩阵元素的序号(Index)来引用矩阵元素。
1 矩阵元素的序号就是相应元素在内存中的排列顺序。在
4
MATLAB中，矩阵元素按列存储，先第一列，再第二列，依 次类推。例如
2 A=[1,2,3 ;
matlab教程ppt(完整版)
矩阵的数学运算
总结词
详细描述
总结词
详细描述
掌握矩阵的数学运算，如求逆 、求行列式、求特征值等。
在MATLAB中，可以使用inv() 函数来求矩阵的逆，使用det() 函数来求矩阵的行列式，使用 eig()函数来求矩阵的特征值。 例如，A的逆可以表示为 inv(A)，A的行列式可以表示 为det(A)，A的特征值可以表 示为eig(A)。
• 总结词：了解特征值和特征向量的概念及其在矩阵分析中的作用。 • 详细描述：特征值和特征向量是矩阵分析中的重要概念。特征值是满足Ax=λx的标量λ和向量x，特征向量是与特征值对
应的非零向量。特征值和特征向量在许多实际问题中都有应用，如振动分析、控制系统等。
04
MATLAB图像处理
图像的读取与显示
变量定义
使用赋值语句定义变量，例如 `x = 5`。
矩阵操作
学习如何创建、访问和操作矩 阵，例如使用方括号 `[]`。
函数编写
学习如何创建自定义函数来执 行特定任务。
02
MATLAB编程
变量与数据类型
01
02
03
变量命名规则
MATLAB中的变量名以字 母开头，可以包含字母、 数字和下划线，但不应与 MATLAB保留字冲突。
了解矩阵的数学运算在实际问 题中的应用。
矩阵的数学运算在许多实际问 题中都有应用，如线性方程组 的求解、矩阵的分解、信号处 理等。通过掌握这些运算，可 以更好地理解和解决这些问题 。
矩阵的分解与特征值
• 总结词：了解矩阵的分解方法，如LU分解、QR分解等。
• 详细描述：在MATLAB中，可以使用lu()函数进行LU分解，使用qr()函数进行QR分解。这些分解方法可以将一个复杂的 矩阵分解为几个简单的部分，便于计算和分析。
MATLAB之(一)数组、矩阵和函数及运算
说明 4位小数
3.14159265358979 15位小数
3.14
2位小数
355/113
最接近的有理数
format short e,t =pi 3.1416e+000
科学计数
format long e ,t =pi 四、函数
3.141592653589793e+000
MATLAB提供了大量的函数，按照起用法分为标量函数、 向量函数和矩阵函数。
14
b= 1 3 5 7
c=6:-3:-6(从6到-6公差为-3的等差数组)
c=
6 3 0 -3 -6 e=[0:2:8,ones(1,3)](等差数组和行向量的拼接)
e=
0 2468111
2数组的运算
数组除作为1×n矩阵（行向量）遵循矩阵运算外，
MATLAB还为数组提供了一些特殊运算。两个数组间的
的最重要特征是按元素进行运算。
2021/4/14
13
1 数组的输入 ⑴可以像1×n矩阵（即行向量）一样输入，如： a=[2,3,4,5] a=
2345
⑵数组常用“：”来方便地生成一些特殊的数组。如：
a=1:5(从1到5公差为1的等差数组)
a=
12345
b=1:2:7(从1到7公差为2的等差数组)
2021/4/14
（5） randn（生成正态分布随机矩阵）； U=ones(3)
W=zeros(2,3) V=eye(2,4)
U=
W=
V=
111
000
2021/4/14
000
1000 0100
111
9
111
X=rand(2,3)
X=
matlab教程ppt(完整版)
汇报人：可编辑
2023-12-24
目录
• MATLAB基础 • MATLAB编程 • MATLAB矩阵运算 • MATLAB数值计算 • MATLAB可视化 • MATLAB应用实例
01
CATALOGUE
MATLAB基础
MATLAB简介
MATLAB定义
MATLAB应用领域
菜单栏
包括文件、编辑、查看、主页 、应用程序等菜单项。
命令窗口
用于输入MATLAB命令并显示 结果。
MATLAB主界面
包括命令窗口、当前目录窗口 、工作空间窗口、历史命令窗 口等。
工具栏
包括常用工具栏和自定义工具 栏。
工作空间窗口
显示当前工作区中的变量。
MATLAB基本操作
变量定义
使用变量名和赋值符号（=）定义变 量。
详细描述
直接输入：在 MATLAB中，可以直 接通过输入矩阵的元 素来创建矩阵。例如 ，`A = [1, 2, 3; 4, 5, 6; 7, 8, 9]`。
使用函数创建： MATLAB提供了多种 函数来创建特殊类型 的矩阵，如`eye(n)`创 建n阶单位矩阵， `diag(v)`创建由向量v 的元素构成的对角矩 阵。
使用bar函数绘制柱状图 ，可以自定义柱子的宽
度、颜色和标签。
使用pie函数绘制饼图， 可以自定义饼块的比例
和颜色。
三维绘图
01
02
03
04
三维线图
使用plot3函数绘制三维线图 ，可以展示三维空间中的数据
点。
三维曲面图
使用surf函数绘制三维曲面图 ，可以展示三维空间中的曲面
。
三维等高线图
实验一_MATLAB_软件环境及基本操作
实验⼀_MATLAB_软件环境及基本操作实验⼀ MATLAB 软件环境及基本操作⼀、实验⽬的熟悉 MATLAB 软件的⼯作环境，练习 MATLAB 命令窗⼝的基本操作。
⼆、实验内容1、命令窗⼝（Command Window ）运⾏⼊门（1）最简单的计算器使⽤法【例 1】求[12 + 2×(7- 4)]÷32的算术运算结果。
1）⽤键盘在 MATLAB 命令窗⼝中命令提⽰符>>后输⼊以下内容：(12+2*(7-4))/3^22）在上述表达式输⼊完成后，按【Enter 】键，执⾏命令。
3）MA TLAB 命令窗⼝中将显⽰以下结果：ans =【例 2】简单矩阵的输⼊步骤。
123A=4567891）在键盘上输⼊下列内容A = [1,2,3; 4,5,6; 7,8,9]2）按【Enter 】键执⾏命令。
3）在命令执⾏后，MATLAB 命令窗⼝中将显⽰以下结果：A =1 2 34 5 67 8 9【例 3】矩阵的分⾏输⼊A=[1 2 34 5 67 8 9]（显⽰结果同例2）【例 4】命令的续⾏输⼊。
…是续⾏符号，表明下⼀⾏是本⾏的接续。
S = 1 – 1/2 + 1/3 –1/4 + 1/5 – 1/6 ... + 1/7 – 1/8S =0.6345 （2）复数和复数矩阵【例1】复数z1 = 3+ 4i，z2 =1+ 2i，z3 = 2eπi/6表达，及计算123z z zz（1）直⾓坐标表⽰法z1= 3 + 4iz1 =3.0000 +4.0000i（2）采⽤运算符构成的直⾓坐标表⽰法和极坐标表⽰法>> z2 = 1 + 2 * i %运算符构成的直⾓坐标表⽰法。
z2 =1.0000 +2.0000i>> z3=2*exp(i*pi/6) %运算符构成的极坐标表⽰法z3 =1.7321 + 1.0000i>> z=z1*z2/z3z =0.3349 + 5.5801i【例-2】复数矩阵的⽣成及运算>> A=[1,3;2,4]-[5,8;6,9]*iB=[1+5i,2+6i;3+8*i,4+9*i]C=A*BA =1.0000 - 5.0000i 3.0000 - 8.0000i2.0000 - 6.0000i 4.0000 - 9.0000iB =1.0000 + 5.0000i2.0000 + 6.0000i3.0000 + 8.0000i4.0000 + 9.0000iC =1.0e+002 * 0.9900 1.1600 - 0.0900i1.1600 + 0.0900i 1.3700【例3】求上例复数矩阵C 的实部、虚部、模和相⾓。
MATLAB使用说明
t=linspace(0,4*pi,512); plot(t,sin(t),t,cos(t),'-.'); title('my figure'); xlabel('t'); legend('sin(t)','cos(t)');
八、plot函数——绘图函数(continuous) plot函数 函数——绘图函数 绘图函数(continuous)
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0
1
2
3
4
5
6
7
8
9
10
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0
1
2
3
4
567Fra bibliotek89
10
一、基本信号的MATLAB表示 基本信号的MATLAB表示
% rectpuls t=0:0.001:4; T=1; ft=rectpuls(t−2*T,T); plot(t,ft) axis([0,4,−0.5,1.5])
计算机软件及应用matlab
2024/10/14
Matlab Language
4
2.2.2、创建一维数组变量（续）
列向量的创建
使用方括号“[ ]”操作符，使用分号“;”分 割行。
【例2-5】键入并执行x= [1; 2; 3]
X=1 2 3
使用冒号操作符
【例2-6】键入并执行x= (1:3)’ % “ ’ ”表示矩阵的转 置
>>a=[1 2 3]; b=[2 3 4]; >>c=[a;b]; >>c1=[a b];
第二种方法：函数方法
函数ones(生成全1矩阵)、zeros (生成全0矩阵) 、reshape “help elmat”获得基本的矩阵生成和操作函数列表 【例3-4】创建全1的3x3数组。 >>ones(3) 【例3-5】创建全1的3x4数组。 >>ones(3,4)
该函数生成一个由n个元素组成的行向量； x1为其第一个元素； x2为其最后一个元素； x1、x2之间元素的间隔=(x2-x1)/(n-1)。 如果忽略参数n，则系统默认生成100个元素的行向量。
【例2-4】键入并执行x= linspace(1,2,5) x=1.0000 1.2500 1.5000 1.7500 2.0000
ans = 1.0000 3.2500 10.0000
2024/10/14
Matlab Language
13
4、数组元素的标识与寻访 （续）
>>a(1:3) %寻访前3个元素组成的子数组
ans =
1.0000 3.2500 5.5000
>>a(3:-1:1) %由前3个元素倒序构成的子数组
《MATLAB仿真技术》实验指导书2016附问题详解
实验项目及学时安排实验一 MATLAB环境的熟悉与基本运算 2学时实验二 MATLAB数值计算实验 2学时实验三 MATLAB数组应用实验 2学时实验四 MATLAB符号计算实验 2学时实验五 MATLAB的图形绘制实验 2学时实验六 MATLAB的程序设计实验 2学时实验七 MATLAB工具箱Simulink的应用实验 2学时实验八 MATLAB图形用户接口GUI的应用实验 2学时实验一 MATLAB环境的熟悉与基本运算一、实验目的1．熟悉MATLAB开发环境2．掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下：（1）变量名可以由英语字母、数字和下划线组成（2）变量名应以英文字母开头（3）长度不大于31个（4）区分大小写MATLAB中设置了一些特殊的变量与常量，列于下表。
MATLAB运算符，通过下面几个表来说明MATLAB的各种常用运算符4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验容1、学习使用help命令，例如在命令窗口输入help eye，然后根据帮助说明，学习使用指令eye（其它不会用的指令，依照此方法类推）2、学习使用clc、clear，观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习，新建M-file，保存（自己设定文件名，例如exerc1、exerc2、 exerc3……），学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
matlab()用法
matlab()用法MATLAB()用法MATLAB是一种高级技术计算语言和环境，主要用于数值计算、数据可视化和算法开发。
在MATLAB中，“()”是一种重要的运算符，它可以用于多种场景。
下面是一些常见的MATLAB()用法：1. 索引和切片在MATLAB中，可以使用”()“来对数组或矩阵进行索引和切片操作。
有以下几种用法：•使用单个索引获取数组或矩阵中的元素。
例如，a = [1, 2, 3];a(2)将返回2。
•使用多个索引获取数组或矩阵中的多个元素。
例如，a = [1, 2, 3]; a([1, 3])将返回[1, 3]。
•使用冒号操作符（：）进行切片操作。
例如，a = [1, 2, 3];a(1:2)将返回[1, 2]。
2. 函数调用MATLAB中的函数调用也需要使用”()“。
使用”()“来传递参数给函数，并获取函数的返回值。
例如：result = max(1, 2);上述代码中，“max()”是MATLAB内置的函数，用来获取两个数中的较大值。
函数调用通过”()“来传递参数1和2，并将返回值赋给变量result。
3. 创建矩阵在MATLAB中，可以使用”()“来创建矩阵。
有以下几种用法：•使用方括号和分号创建矩阵。
例如，a = [1, 2; 3, 4]将创建一个2x2的矩阵。
•使用冒号操作符创建矩阵。
例如，a = 1:5将创建一个包含1到5的矩阵。
4. 修改数组或矩阵除了索引和切片操作外，用”()“也可以对数组或矩阵进行修改。
以下是一些常见的用法：•使用单个索引修改数组或矩阵中的元素。
例如，a = [1, 2, 3];a(2) = 4将把2替换为4。
•使用冒号操作符（：）进行切片赋值操作。
例如，a = [1, 2, 3]; a(1:2) = [4, 5]将把1和2替换为4和5。
5. 调用类方法在MATLAB中，可以使用”()“来调用类的方法。
类是一种面向对象的编程概念，在MATLAB中也得到了支持。
matlab 二维数组 定义
matlab 二维数组定义二维数组是一种常见的数据结构，它由多行多列的元素组成。
在Matlab中，我们可以使用矩阵来表示二维数组。
本文将从定义、特性、操作等方面介绍二维数组在Matlab中的应用。
一、定义二维数组是由相同类型的元素按照行和列排列形成的矩形表格。
在Matlab中，我们可以使用方括号和分号来定义二维数组。
例如，下面的代码定义了一个3行4列的二维数组A：A = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12];二、特性1. 二维数组的元素可以是任意类型，包括数字、字符、字符串等。
2. 二维数组的行和列的数目可以不相等，但同一行或同一列的元素个数必须相等。
3. 二维数组的行和列的索引从1开始，行在前，列在后。
4. 二维数组可以通过行和列的索引来访问和修改元素。
三、操作1. 访问元素我们可以使用行和列的索引来访问二维数组中的元素。
例如，要访问二维数组A中的第2行第3列的元素，可以使用下面的代码：A(2, 3)2. 修改元素我们可以通过赋值的方式来修改二维数组中的元素。
例如，要将二维数组A中的第1行第2列的元素修改为10，可以使用下面的代码：A(1, 2) = 103. 求和我们可以使用sum函数来对二维数组的元素进行求和。
例如，要求二维数组A中每一列的和，可以使用下面的代码：sum(A)4. 求最大值和最小值我们可以使用max函数和min函数来求二维数组的最大值和最小值。
例如，要求二维数组A中的最大值和最小值，可以使用下面的代码：max(A)min(A)5. 求平均值我们可以使用mean函数来求二维数组的平均值。
例如，要求二维数组A中每一行的平均值，可以使用下面的代码：mean(A, 2)6. 转置我们可以使用'运算符来对二维数组进行转置操作。
例如，要将二维数组A进行转置，可以使用下面的代码：A'四、应用举例下面通过一个简单的例子来展示二维数组在Matlab中的应用。
Matlab 数组
第一章 MATLAB入门与基础 • 1.3.1 数组
1.3.1 数组
数组（array）：就是相同数据类型的元素按一 定顺序的集合，把有限个类型相同的变量用 一个名字命名，然后用编号区分他们的变量 的集合，这个名字称为数组名，编号称为下 标。组成数组的各个变量称为数组的分量， 也称为数组的元素，有时也称为下标变量。
ans(:,:,2) = 6 33 26 17 7 34 21 12 2 29 22 13
ans(:,:,3) = 19 10 24 15 23 14 25 16 27 18 20 11
表1.3-1 特殊矩阵构建函数
1.3.1 数组
函数名称
函数功能
ones(n)
构建一个n*n的1矩阵（矩阵元素全部是1）
构建构建一个和A大小相同的下三角矩阵，该矩阵的第k条对角线 以上元素与A相同，其余元素均为0
数组的创建
⑤创建标准数组 • 全0数组，zeros(m,n) • 全1数组，ones(m,n)
或ones(m,n,k) m—数组行数，n—数组列数， k—数组页数;
1.3.1 数组
数组的创建
⑤创建标准数组 • 单位矩阵
数组的创建
④创建三维数组 例12，创建一个3行4列2页
的三维数组。
1.3.1 数组
数组的创建
④创建三维数组
例12，创建一个3 行4列2页的三 维数组。
1.3.1 数组
数组的创建
④创建三维数组
cat(dim,A,B)在dim维上将 A与B数组联结起来。
例12，创建一个3行4列2 页的三维数组。
1.3.1 数组
数组的创建
1.3.ቤተ መጻሕፍቲ ባይዱ 数组
一 Matlab基本操作方法
例如 format long 1.35^2-cos(2/3*pi)+sqrt(12.35)/1.2 ans = 5.25104723180093 4．指令中的标点符号 ． 空格 用于输入量与输入量的分隔符，数组行元素 间的分隔符。 逗号‘，’ 指令之间的分隔符，其余作用同‘空 格’ 分号‘；’ 数组间的行分隔符，指令结尾，则不 显示运行结果。 百分号‘%’ 后面为注释。 括号[ ] 用于数组输入时用。
x=linspace(2,5,12) x = 2.0000 2.2727 2.5455 2.8182 3.0909 3.3636 3.6364 3.9091 4.1818 4.4545 4.7273 5.0000 2）矩阵输入的基本方法 ） 输入一个小矩阵最简单的方法是用直接列出矩 阵元素的方式。矩阵用方括号括起，元素之间 用空格或逗号分隔，矩阵行与行之间用分号隔 开。大的矩阵可以分行输入，用回车键代替分 号。
5．输入输出语句 ． （1） 键盘输入参数的值 x=input('请输入参数 x='); （2）输出语句 ） 直接输出： x 或 disp(x); fprintf(' M=%.5f, a(%.0f)=%.5f \n ',M,i,a(i)),对 于‘‘，其中%前为提示符，按字符串显示， f指显示为实数，%与f之间的数字表示要显示 的数小数点后面的位数，如5为小数点后面5 位，0为小数点后面0位，\n为换行命令，后 面的字母对应为要显示的数字。
反双曲函 asinh acosh 数 指数和对 数 复数运算 数值运算 整数函数 exp abs fix lcm log angle floor gcd
其中： log(x)：求x的自然对数ln(x)，loga(x): 求x以a为底的 对数 angle(x)：求复数x的辐角，conj(x): 求x的共轭复数， real(x)和imag(x)分别表示求x的实部和虚部 fix(x): 求实数x最接近0的整数值 floor(x)：求x最接近负无穷的整数值 ceil(x): 求x最接近正无穷的整数值 round(x)：求x最接近x的整数值 rem(x，y): 求x除y的余数 lcm(a，b): 返回整数值a和b的最小公倍数，gcd(a， b)返回正整数a和b的最大公约数
第一章 Matlab中的数组操作
zeros(m): m阶全零方阵 zeros(m,n): m×n阶全零方阵 eye(m): m阶单位阵 ones(m): m阶全1方阵 ones(m,n): m×n阶全1方阵 rand(m): m阶均匀分布随机方阵 randn(m): m阶正态分布随机方阵
4.元胞数组的创建 元胞数组是MATLAB的一种特殊数据类型， 可以将元胞数组看做一种无所不包的通用矩阵， 或者叫做广义矩阵。 组成元胞数组的元素可以是任何一种数据类型的 量，每一个元素也可以具有不同的尺寸，每一个元素 的内容也可以完全不同，元胞数组的元素叫做元胞。 建立元胞数组：{ } a={'matlab',20;ones(2,3),1:10}
A=[0,0,2,-1,3,0,0,5,0,6,-7,0,0,9]; b1=find(A,3) b2=find(A,2, 'last') b1=3 4 5 b2=11 14 B=[0,1,0;2,3,0;4,0,0] c1=find(B) c1 = m= [m,n]=find(B) 2 2
B= 0 2 4 1 3 0 0 0 0
b1 = 16.2000 12.4000 b2 = 12.40 16.20 20.00 8.6000 4.8000
二维数组A的元素的提取： 由于数组A有两种编址方法，matlab会根据接受的指 令，先判断是哪一种编址方法，然后再进行元素的提取。 如： A=[1,2,3,4,5;0,1,2,3,4;-1,0,1,2,3;-2,-1,0,1,2]
x=0:2:10, y=[-2,-5,-8], xx=[x,y] xx = 0 2 4 6 8 10 -2 -5 -8 yy=[xx([2,5]);y(2:3)] yy = 2 8 -5 -8
二维数组元素的存储顺序matlab
一、介绍二维数组二维数组是一种常见的数据结构，它由多行和多列的元素组成。
在Matlab中，二维数组也称为矩阵，它是一个重要的数据类型，常用于存储和处理二维数据。
二、二维数组的存储顺序在Matlab中，二维数组的存储是按列优先的方式进行的。
这意味着数组的元素是按照列的顺序依次存储的，而不是按照行的顺序。
这一点与其他编程语言中的存储方式可能有所不同，需要注意。
三、优点和缺点1. 优点按列优先的存储方式有利于Matlab进行矩阵运算和向量化操作。
由于在实际应用中，矩阵运算和向量化操作是Matlab经常需要进行的操作，这种存储方式可以提高运算效率和性能。
2. 缺点但是，按列优先的存储方式在访问数组元素时可能会导致不连续访问内存，从而降低缓存命中率，影响性能。
另外，在某些特定场景下，按行优先的存储方式可能更加高效。
四、存储顺序的影响存储顺序的不同可能会对代码性能产生影响。
在Matlab中，如果对一个二维数组进行迭代操作，尤其是较大规模的数组，需要注意存储顺序对性能的影响。
1. 一般性建议通常情况下，Matlab中的许多函数和操作都是针对按列优先的存储方式进行优化的，因此在大多数情况下，存储顺序的影响并不明显。
但在性能要求较高的场景下，还是需要仔细评估存储顺序的影响。
2. 特殊场景注意如果在Matlab中遇到需要自己手动对二维数组进行迭代的情况，例如使用循环逐个处理数组元素，需要考虑存储顺序对性能的影响。
在这种情况下，可以对数组进行转置，以适应按行优先的存储方式。
五、如何确定存储顺序在Matlab中，可以使用函数`isrowmajor`来确定存储顺序。
这个函数会返回一个逻辑值，表示数组的存储方式是按行优先还是按列优先。
通过这个函数，可以帮助我们更好地理解数组的存储方式，并在需要时进行适当的调整。
六、总结在Matlab中，二维数组的存储顺序是按列优先的。
这种存储方式对于矩阵运算和向量化操作有利，但在某些特定场景下可能会对性能产生影响。
Matlab二维数组及其应用
Matlab:二维数组及其应用二维数组实际上也是一个矩阵。
应此直接创建一个矩阵就行。
创建的方法你应该会吧，就是直接按行方式输入每个元素：同一行中的元素用逗号（，）或者用空格符来分隔，且空格个数不限；不同的行用分号（；）分隔。
所有元素处于一方括号（[ ]）内。
比如，创建一个3×5的矩阵（对应3×5的二维数组）A = [12 62 93 -8 22; 16 2 87 43 91; -4 17 -72 95 6]A =12 62 93 -8 2216 2 87 43 91-4 17 -72 95 6当然也可以用专门用来创建多维数组的cat函数来创建。
具体如下：函数cat格式A=cat(n,A1,A2,…,Am)说明n=1和n=2时分别构造[A1；A2]和[A1，A2]，都是二维数组，而n=3时可以构造出三维数组。
例如：>> A1=[1,2,3;4,5,6;7,8,9];A2=A1';>> A3=cat(2,A1,A2)A3 =1 2 3 1 4 74 5 6 2 5 87 8 9 3 6 9这样A3就是一个二维数组此外还有诸如特殊矩阵的创建方法等这里就不列举了你可以百度或者Google一下二维数组的变换我还不太确定你的意思：这里就提供几个矩阵的操作：1.矩阵的变维矩阵的变维有两种方法，即用“：”和函数“reshape”，前者主要针对2个已知维数矩阵之间的变维操作；而后者是对于一个矩阵的操作。
（1）“：”变维例1-48> A=[1 2 3 4 5 6;6 7 8 9 0 1]A =1 2 3 4 5 66 7 8 9 0 1>> B=ones(3,4)B =1 1 1 11 1 1 11 1 1 1>> B(:)=A(:)B =1 7 4 06 3 9 62 8 5 1（2）Reshape函数变维格式 B = reshape(A,m,n) %返回以矩阵A的元素构成的m×n矩阵BB = reshape(A,m,n,p,…) %将矩阵A变维为m×n×p×…B = reshape(A,[m n p…]) %同上B = reshape(A,siz) %由siz决定变维的大小，元素个数与A中元素个数相同。
matlab 二维数组最大值
matlab 二维数组最大值二维数组是在数学和计算机科学中常见的数据结构，它由一系列元素组成，这些元素按照两个坐标（行和列）进行排列。
而我们今天要讨论的是如何找到二维数组中的最大值，并通过Matlab来实现这个过程。
在Matlab中，我们可以使用max函数来找到二维数组中的最大值。
这个函数可以接受一个矩阵作为输入，并返回该矩阵中的最大值。
下面我们将通过一个实例来演示如何使用max函数找到二维数组的最大值。
我们需要创建一个二维数组。
在Matlab中，我们可以使用矩阵的方式来表示二维数组。
例如，我们可以通过以下代码创建一个3行4列的二维数组：```matlabA = [1 2 3 4; 5 6 7 8; 9 10 11 12];```接下来，我们可以使用max函数来找到这个二维数组中的最大值。
例如，我们可以通过以下代码找到这个二维数组的最大值：```matlabmax_value = max(max(A));```在这个例子中，我们首先使用max函数找到每一列的最大值，然后再使用max函数找到这些最大值中的最大值。
最后，我们将结果保存在max_value变量中。
除了找到整个二维数组的最大值之外，我们还可以找到每一行或每一列的最大值。
例如，我们可以使用max函数的第二个参数来指定维度。
例如，我们可以通过以下代码找到每一行的最大值：```matlabmax_value_row = max(A, [], 2);```在这个例子中，我们将第二个参数设置为2，表示我们要找到每一行的最大值。
最后，我们将结果保存在max_value_row变量中。
同样地，我们也可以找到每一列的最大值。
例如，我们可以通过以下代码找到每一列的最大值：```matlabmax_value_column = max(A, [], 1);```在这个例子中，我们将第二个参数设置为1，表示我们要找到每一列的最大值。
最后，我们将结果保存在max_value_column变量中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
与二维数组相关的函数
cmax = max(A) rmax = max(A,[],2)
返回cmax为一个行数组，元素为A中每个列的最大值 返回rmax为一个列数组，元素为A中每个行的最大值
[cmax,index] = max(A)
[rmax,index] = max(A,[],2) max(A,B)
三维网格图: mesh, meshc, meshz
mesh(X,Y,Z,C) 绘制由矩阵 X,Y,Z 所确定的曲面网格图，矩阵 C 用于
确定网格颜色，省略时 C=Z
meshc(X,Y,Z,C) 调用方式与 mesh 相同，在 mesh 基础上增加等高线 meshz(X,Y,Z,C) 调用方式与 mesh 相同，在 mesh 基础上屏蔽边界面
对子数组A(r,c)进行赋值：B的“行、列” A(r,c) = B 必须与A(r,c)的“行、列”相同
二维数组的子数组 的寻访和赋值
使用“单下标”方式
A(:) A(s)
由A的各列按自左到右的次序，首尾相接而生成 的“一维长列”数组 引用A中由一维数组s指定的元素。s若是行（或 列），则A(s)就是长度相同的行（或列） 全元素赋值方式。结果：保持A的“行宽、列长” 不变。条件：A、D两个数组的总元素相等，但 “行宽、列长”不一定相同 对A的部分元素重新赋值。结果：保持A的“行 宽、列长”不变。条件：s单下标数组的长度必 须与“一维数组”B的长度相等，但是s、B不一 定同是“行数组”或“列数组”
返回A中每个列向量的平均值 返回A中每个行向量的平均值
median(A) 返回A中每个列向量的中值 Median(A,2) 返回A中每个行向量的中值
std(A) std(A,2)
返回A中每个列向量的标准差 返回A中每个行向量的标准差
sum(A) sum(A,2)
计算A中每个列向量的元素的和 计算A中每个行向量的元素的和
0 0 0 1 1 1 0 0 0 1 1 1
B= 1 0 0 0 -4 0 0 0
0 2 0 0 0 -3 0 0 0 0 3 0 0 0 -2 0 0 0 0 4 0 0 0 -1
已知一维数组x和y： x [ x1 , x2 , x3 , x4 , x5 ] [1, 0, 1, 2,3]， y [ y1 , y2 , y3 , y4 , y5 ] [3, 2,1, 1, 2] 在matlab生成下面的二维数组： x1 x2 x3 x4 x5 1 x 2 x 3 x 4 x 5 x
A(r,c)
2、“单下标”标识： Linear Index 只用一个下标来指明元素在数组中的位置： 把二维数组的所有列，按先左后右的次序， 首尾相接排成“一维长列”，然后，自上往下 对元素位置进行标号。
A(ind)
“单下标”与“全下标”的转化
1、全下标→单下标 ind = sub2ind(siz,r,c) 2、单下标→全下标 [r,c] = ind2sub(siz,ind)
A = [1,2,3; 4,5,6; 7,8,9] （2）按【Enter】键，指令被执行。 （3）在指令执行后，MATLAB指令窗中将显示以下结果： A = 1 2 3 4 5 6 说明：直接输入矩阵时，每行元素用 7 8 9 空格或逗号分隔，矩阵行用分号分隔， 整个矩阵放在方括号里，标点符号一 定要在英文状态下输入。
sort(A)
对A中列向量进行升序排序
sort(A,’descend’) 对A中列向量进行降序排序 sort(A,2)
对A中行向量进行升序排序
sort(A,2,’descend’) 对A中行向量进行降序排序
当只有一个输出参数时，size函数返 sz=size(A) 回的是一个行向量，该行向量的第一 个元素是数组的行数，第二个元素是 数组的列数。 当有两输出参数时，size函数将数组 [r,c]=size(A) 的行数返回到第一个输出变量，将数 组的列数返回到第二个输出变量。
2 1 2 2 2 3 2 4 2 5
x1 y1 x2 y2 x3 y3 x4 y4 x5 y5
y1 /1 x1 y5 y2 / 2 x2 y4 y3 / 3 x3 y3 y4 / 4 x4 y2 y5 / 5 x5 y1
二维数组操作函数
把“大小”相同的若干数组，沿“指 cat(dim, A, B) 定维”方向，串接成高维数组 。行 （dim=1） 列（dim=2）
由一维数组创建二维数组
A = [1,3,5] B = [2,4,6] C = [3,5,7]
D = [A;B] E = [A;B;C] F = [A’,B’] G = [A’,B’,C’]
由函数创建二维数组
zeros(m,n)
ones(m,n) eye(m,n)
生成一个 m 行 n 列的零矩阵，m=n 时可简写为 zeros(n)
二维数组的转置运算
• A.’：转置 • A’：共轭转置
两个维数相同的 二维数组之间的数组运算
• • • • • • A + B：加，对应位置的数组元素相加 A - B：减，对应位置的数组元素相减 A.*B：点乘，对应位置的数组元素相乘 A./B：右点除，对应位置的数组元素相除 A.\B：左点除 A.^B：点幂，对应位置的数组元素做幂运算
二维数组的与标量 的运算
• • • • • • • A + c ：A的每个元素加c A - c： A的每个元素减c A.*c：点乘， A的每个元素乘c A./c：右点除， A的每个元素除c A.\c：左点除，c除A的每个元素 A.^c：点幂， A的每个元素做幂运算 c.^A：点幂，c做幂运算
函数作用在二维数组上的 运算规则
利用二维数组在同一坐标轴中同时绘制下列函 数的图形：
y k cos x , x 0,2 , k 1,2,3
plot用二维数组绘图的细节
你想要是下面的哪一种图形？怎样绘制出这两种图形？
3
3
2
2
1
1
0
0
-1
-1
-2
-2
-3
0
1
2
3
4
5
6
7
-3
0
1
2
3
4
5
6
7
补充：plot绘图的细节
二维数组的单个元素 的引用和赋值
• X＝magic(6) • 单个元素寻访 X(2,3) X(5,5) X(16) • 单个元素的赋值 X (2,3) = 0 X (5,5) = 7 X (16) = 8
二维数组的子数组 的寻访和赋值
使用“双下标”方式
A(r,:)
A(:,c) A(r,c)
由A的“r行”和“全部列”上的元素组 成 由A的“全部行”和“c列”上的元素组 成 由A的“r行”和“c列”上的元素组成
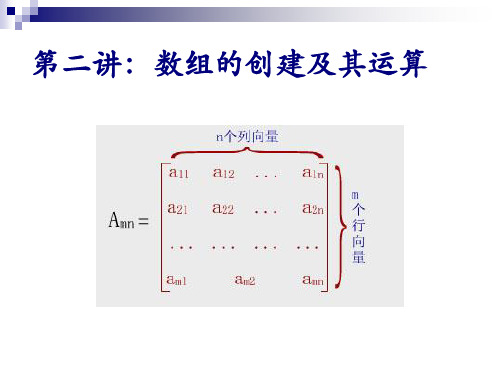
x11 x 21 X ... xm1 x12 x22 ... xm 2 ... x1n ... x2 n xij ... ... ... xmn
mn
mn
f X f xij
如何引用二维数组的元素？
1、“全下标”标识： 即指出是“第几行，第几列”的元素
r=size(A,1)
返回数组 A 的行数
c=size(A,2) 返回数组 A 的列数 length(A)
返回数组的长度(行数或列数的较大值)
numel(A)
返回数组元素的个数
练习
函数f x 的定义如下： x2 x 6 2 f ( x) x 5 x 6 x2 x 1 , , , x 0且x 4 0 x 10 , x 2且x 3 其它
diag(A,k) flipud(A) fliplr(A) kron(A,B)
A 是矩阵，则 diag(A,k) 返回A的第k 条对角线向量，默认k=0 以数组“水平中线”为对称轴，交换 上下对称位置上的数组元素 以数组“垂直中线”为对称轴，交换 左右对称位置上的数组元素
按Kronecker乘法规则（直积）产生 “积”数组
编写一个Matlab函数实现该函数，且要求函数能够 处理输入参数为一维、二维数组的情况，即要求: f xij f xij mn mn
二维数组在2d绘图中的应用
plot(x,y)
若x, y 都是二维数组，则将 x 的列和 y 中 相应的列相组合，绘制多条平面曲线。此时 x, y 必须具有相同的大小。
A(:) = D(:)
A(s) = B
二维数组的子数组 的寻访和赋值
使用“逻辑数组”方式
A(L)
“逻辑数组”寻访，生成“一维”列数组： 由与A同样大小的“逻辑数组”L中的“1元 素”选出A的对应元素；按“单下标”次序 排成长列组成
4 2 0 2 4 例：找出数组A 3 1 1 3 5 中所有绝对值大于3的元素。
A中每个列向量的累加和，维数与A相同 A中每个行向量的累加和，维数与A相同
cumsum(A) cumsum(A,2)
prod(A) prod(A,2) cumprod(A) cumprod(A,2)
计算A中每个列向量的元素的积 计算A中每个行向量的元素的积
A中每个列向量的累乘积，维数与A相同 A中每个行向量的累乘积，维数与A相同
生成一个 m 行 n 列的元素全为 1 的矩阵, m=n 时可写为 ones(n) 生成一个主对角线全为 1 的 m 行 n 列矩阵, m=n 时可简写为 eye(n)，即为 n 维单位矩阵 生成魔方数组，各行、列之和 = (1+2+……+n2 )/n
magic(n) diag(v,k)
rand(m,n) randn(m,n)
二维数组操作函数
repmat(A,m,n) rot90(A,k)