2016年开封市九年级一模数学试卷

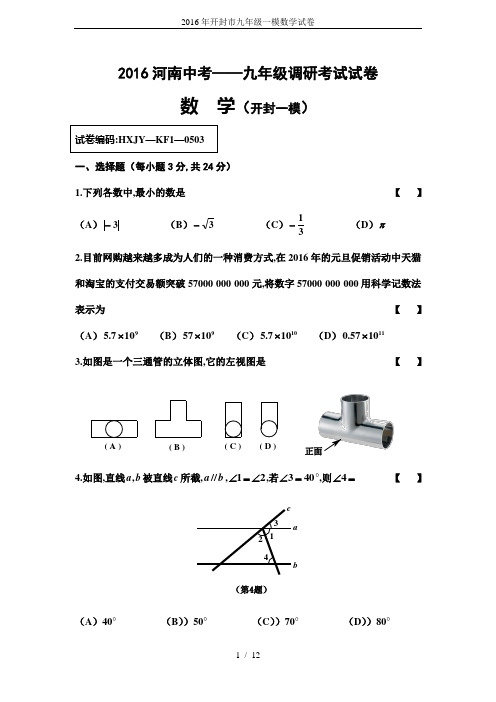
2016河南中考——九年级调研考试试卷
数 学（开封一模）
一、选择题（每小题3分,共24分）
1.下列各数中,最小的数是 【 】 （A ）3- （B ）3- （C ）3
1
-
（D ）π 2.目前网购越来越多成为人们的一种消费方式,在2016年的元旦促销活动中天猫和淘宝的支付交易额突破57000 000 000元,将数字57000 000 000用科学记数法表示为 【 】 （A ）9107.5⨯ （B ）91057⨯ （C ）10107.5⨯ （D ）111057.0⨯ 3.如图是一个三通管的立体图,它的左视图是
【
】
正面
( D )
( C )( B )( A )
4.如图,直线b a ,被直线c 所截,b a //,21∠=∠,若403=∠°,则=∠4 【
】
b
a
（第4题）
（A ）40° （B ））50° （C ））70° （D ））80°
图（12）N
F
E B
A
C D
M
5.下列运算正确的是 【 】 （A ）623a a a =⋅ （B ）()
3362a a = （C ）()222
b a b a -=- （D ）22223a a a =-
6.不等式组⎩⎨⎧≥+-->+03312x x 的整数解的个数是 【 】
（A ）5 （B ）4 （C ）3 （D ）无数个 7.如图（12）所示,在△ABC 中,AD 平分∠BAC,按如下步骤作图: 第一步:分别以点A 、D 为圆心,以大于2
1
AD 的长为半径在AD 两 侧作弧,交于两点M 、N;
第二步:连结MN 分别交AB 、AC 于点E 、F; 第三步:连结DE 、DF.
若BD=6, AF=4, CD=3,则BE 的长是 【 】 （A ）2 （B ）4 （C ）6 （D ）8
8.如图,等边三角形ABC 的边长为3,N 为AC 的三等分点,三角形边上的动点M 从点A 出发,沿A →B →C 的方向运动,到达点C 时停止.设点M 运动的路程为x ,MN 2=y ,则y 关于x 的函数图象大致为
【 】
（第14题）
C
D A
O
B
二、填空题（每小题3分,共21分） 9.
(
)
=⎪
⎭
⎫
⎝⎛+--+-︒1
2130sin 122π
________.
10.学校组织春游活动,安排给九年级三辆车,小刚和小行都可以从这三辆客车中任选一辆搭乘,小刚和小行同车的概率是________. 11.如下图,A 、B 是双曲线x
k
y =
上的两点,过点A 作AC x ⊥轴于点C,交OB 于D 点,若△ADO 的面积为1,D 为OB 的中点,则k 的值为________.
（第11题）
y
x
（第13题）...
A 3
C 3
A 2
C 2
A 1
C 1
O
12.正多边形的一个外角是72︒,则这个多边形的内角和的度数是________.
13.如上图,一段抛物线:)2(-=x x y (0≤x ≤2),记为1C ,它与x 轴交于点O ,1A ;将
1C 绕点1A 旋转︒180得2C ,交x 轴交于点2A ;将2C 绕点2A 旋转︒180得3C ,,交x 轴
交于点3A ; … , 如此进行下去,直至得2016C .若),4031
(a P 在第2016段抛物线2016C 上,则=a ________.
14.如图,在圆心角为︒90的扇形OAB 中, 半径OA=2 cm,C 为弧AB 的中点,D 、E
分别是OA 和OB 的中点,则图中阴影部 分的面积为________cm 2.
（第15题）
15.在菱形ABCD 中,AB=5, AC=8, 点P 是 AC 上的一个动点,过点P 作EF 垂直于AC 交AD 于点E,交AB 于点F,将△AEF 沿EF 折叠,使点A 落在点A′处,当△A′CD 是直角 三角形时,AP 的长为________.
三、解答题（本题共8小题,共75分）
16.（8分）先化简,再求值:242212+-÷
⎪⎭⎫ ⎝⎛+-+x x
x x ,其中34+-=x .
17.（7分）某研究小组为了了解本市出租车司机工作情况,随机抽取本市100名出租车司机进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图. 请根据以上信息解答下列问题:
（1）出租车司机工作情况扇形统计图中,“经常加班”所对应的圆心角度数为________;
（2）请补全条形统计图;
（3）该市共有1000名出租车司机,请估计全市出租车司机中经常加班且工作时间超过10小时的人数;
（4）小明认为“全市所有出租车司机中,工作时间为9小时的人数约为
130100
13
1000=⨯
”,请你判断这种说法是否正确,并说明理由. 35﹪20
﹪
时间
经常加班的出租车司机工作时间情况 条形统计图
出租车司机工作情况 扇形统计图
从不加班偶尔加班
经常加班
18.（9分）如图（1）,线段AB=4,以线段AB 为直径画⊙O,C 为⊙O 上的动点,连接OC,过点A 作⊙O 的切线与BC 的延长线交于点D,E 为AD 的中点,连接CE. （1）求证: CE 是⊙O 的切线;
（2）①当CE=________时,四边形AOCE 为正方形? ②当CE=________时,△CDE 为等边三角形?
图（2）
图（1）
C
B
E O
D
19.（9分）已知关于x 的一元二次方程2)3)(1(m x x =--. （1）求证:对于任意实数m ,方程总有两个不相等的实数根; （2）若方程的一个根是4,求m 的值及方程的另一根.
20.（9分）如图,为了测量山顶铁塔AE 的高,小明在27 m 高的楼CD 底部D 测得塔顶A 的仰角为45°,在楼顶C 测得塔顶A 的仰角为36°52′,已知山高BE 为80 m,楼底部D 与山脚在同一水平线上,求该铁塔的高AE. （参考数据:75.05236tan ,60.05236sin ''≈≈︒︒）
21.（10分）某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
（1）求每台电冰箱与空调的进价分别是多少?
（2）现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,且购进电冰箱少于40台,请确定获利最大的方案以及最大利润;
（3）实际进货时,厂家对电冰箱出厂价下调k元,若商场保持这两种家电的售价不变,请你根据以上信息及（2）中条件,设计出使这100台家电销售总利润最大的进货方案.
22.（10分）在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD,将线段AD 绕点A 逆时针旋转90°得到AE,连接EC.
问题发现
（1）如果AB=AC,∠BAC=90°,当点D 在线段BC 上时（不与点B 重合）,如图1,请你判断线段CE,BD 之间的位置．．关系和数量．．
关系____________; 拓展探究
（2）如果AB=AC,∠BAC=90°,当点D 在线段BC 的延长线上时,如图2,请判断（1）中的结论是否仍然成立,如成立,请证明你的结论;
问题解决
（3）如图3,A B≠AC, ∠BAC≠90°,若点D 在线段BC 上运动,试探究:当锐角∠ACB 等于________度时,线段CE 和BD 之间的位置关系仍然成立（点C 、E 重合除外）.此时若作DF ⊥AD 交线段CE 于点F,AC=23,线段CF 长的最大值是________.
图3
图2
图1
E
A
B
C
23.（11分）如图,抛物线c bx x y ++-=2与直线12
1
+=
x y 交于A 、B 两点,其中A 在y 轴上,点B 的横坐标为4,P 为抛物线上一动点,过点P 作PC 垂直于AB,垂足为C.
（1）求抛物线的解析式;
（2）若点P 在直线AB 上方的抛物线上,设P 的横坐标为m ,用m 的代数式表示线段PC 的长,并求出线段PC 的最大值及此时点P 的坐标;
（3）若点P 是抛物线上任意一点,且满足PAB ∠<︒0≤︒45,请直接写出: ①点P 的横坐标的取值范围;
②纵坐标为整数的点P 为“巧点”, “巧点”的个数.
y
x
C
B
A O
P。