上海交通大学附属中学10-11学年高二下学期期末考试(数学)
2019-2020学年上海市上海交通大学附属中学高二下学期期末数学试题解析

2019-2020学年上海市上海交通大学附属中学高二下学期期末数学试题一、单选题1.空间中,“直线l 平行于平面α上的一条直线”是“直线//l 平面α”的( )条件.A .充分非必要B .必要非充分C .充分必要D .非充分非必要答案:B由线面平行的判断定理和性质定理判断即可得出结论. 解:由线面平行的判定定理可知,当直线l 在平面α内,l 平行于平面α上的一条直线,则不能得出结论“直线//l 平面α”,故“直线l 平行于平面α上的一条直线”是“直线//l 平面α”不充分条件;由直线和平面平行性质定理可知,“直线//l 平面α”则经过直线l 的平面和平面α相交,那么直线l 和交线平行,所以能得出“直线l 平行于平面α上的一条直线”,故“直线l 平行于平面α上的一条直线”是“直线//l 平面α”必要条件. 故选:B 点评:本题考查直线和平面平行的判断定理和性质定理,考查理解辨析能力,属于基础题. 2.在平行六面体1111ABCD A B C D -中,M 为11A C 与11B D 的交点,若,AB a AD b ==,1AA c =,则与BM 相等的向量是( )A .1122a b c ++ B .1122a b c --+ C .1122a b c -+ D .1122-++a b c 答案:D根据空间向量的线性运算,用,,a b c 作基底表示BM 即可得解. 解:根据空间向量的线性运算可知11BM BB B M =+ 11112AA B D =+()1111112AA B A A D =++()112AA AB AD =+-+因为,AB a AD b ==,1AA c=, 则()112AA AB AD +-+ 1122a b c =-++即1122BM a b c =-++,故选:D. 点评:本题考查了空间向量的线性运算,用基底表示向量,属于基础题.3.一间民房的屋项有如图三种不同的盖法:①单向倾斜;②双向倾斜;⑤四向倾斜.记三种盖法是屋项面积分别为1P 、2P 、3P ,若屋顶倾斜面与水平面所成的角都是θ,则( )A .321P P P >>B .321P P P >=C .321P P P =>D .321P P P ==答案:D因为三种盖法的屋顶斜面与水平面所成二面角都相等,且三种盖法的屋顶在水平面上的射影面积均相等,由面积射影公式S 影=S 侧cos θ⋅,知屋顶面积1P 、2P 、3P ,均相等.解:∵三种盖法的屋顶斜面与水平面所成二面角都是θ,三种盖法的屋顶在水平面上的射影面积都相同,射影面积可设为S ,则由面积射影公式,得:123P cos S P cos S P cos S θθθ⋅=⋅=⋅=,,, ∴321P P P ==. 故选:D . 点评:本题是二面角知识在实际生活中的应用,由面积射影公式S 影=S 侧cos θ⋅,容易得出结论,是基础题.4.如图为某水晶工艺品示意图,该工艺品由一个半径为R 的大球放置在底面半径和高均为R 的圆柱内,球与圆柱下底面相切为增加观赏效果,设计师想在圆柱与球的空隙处放入若干大小相等的实心小球,且满足小球恰好与圆柱底面、圆柱侧面及大球都相切,则该工艺品最多可放入( )个小球.A .14B .15C .16D .17答案:B圆柱与球的空隙处放入若干大小相等的实心小球,且满足小球恰好与圆柱底面、圆柱侧面及大球都相切,过球心与圆柱体底面圆心的平面截得该图形的平面图,利用几何关系计算即可. 解:如图,过球心与圆柱体底面圆心的平面截得该图形的平面图,设球的半径为R ,实心小球的半径为r 22r r R R ++=,解得:(32)R r =+,因为小球球心在以E 为圆心,EF 为半径的圆上,2EF =,周长为2EF π, 所以22rn EF π≤,即()(22(322)22222215.16222r r R r EFn rr rπππππ⎡⎤+++⎣⎦≤====+≈.故该工艺品最多可放入15个小球. 故选:B.点评:本题考查空间几何体与球接、切问题的求解方法.求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.二、填空题5.随机扔一个硬币三次,数字朝上恰好出现一次的概率是______. 答案:38由随机扔一个硬币,每次数字朝上的概率均为12,且相互独立,结合独立重复试验的概率计算公式,即可求解. 解:由题意,随机扔一个硬币,每次数字朝上的概率均为12,且相互独立, 所以数字朝上恰好出现一次的概率为123113(1)228P C =⨯⨯-=. 故答案为:38.点评:本题主要考查了独立重复试验的概率的计算,其中解答中正确理解题意,合理利用独立重复试验的概率计算公式进行求解是解答的关键,着重考查分析问题和解答问题的能力.6.将边长为1的正方形ABCD 沿对角线AC 折叠,使得点B 和D 的距离为1,则二面角B AC D --的大小为______. 答案:2π设翻折前AC 与BD 相交于点O ,则OB AC ⊥,OD AC ⊥,作出翻折后的图形,由二面角的定义可知BOD ∠即为所求,易证BOD ∆为等腰直角三角形,故2BOD π∠=,从而得解. 解:设翻折前AC 与BD 相交于点O ,则OB AC ⊥,OD AC ⊥,而翻折之后的图形如图所示,BOD ∴∠为二面角B AC D --的平面角.2OB OD ==1BD =, BOD ∴为等腰直角三角形,且2BOD π∠=,∴二面角B AC D --的大小为2π. 故答案为:2π. 点评:本题考查二面角的求法,理解二面角的定义是解题的关键,考查学生的空间立体感、作图能力和逻辑推理能力,属于基础题.7.圆锥的底面半径是3,高是4,则圆锥的侧面积是__________. 答案:15π分析:由已知中圆锥的底面半径是3,高是4,由勾股定理,我们可以计算出圆锥的母线长,代入圆锥侧面积公式S rl π=,即可得到结论. 详解:圆锥的底面半径是3r =,高是4h =,圆锥的母线长5l =,则圆锥侧面积公式15S rl ππ==,故答案为15π.点睛:本题主要考查圆锥的性质与圆锥侧面积公式,意在考查对基本公式的掌握与理解,属于简单题.8.若6a x ⎛- ⎝⎭的展开式的常数项为60,则a =_____答案:4先求出二项式展开式的通项公式,再令x 的系数等于0,求得r 的值,即可求得展开式中的常数项的值,再由展开式的常数项为60,求出常数a 的值. 解:∵62x x ⎛- ⎝⎭展开式的通项公式为T r+1=66(r r r C x -=⋅⋅•x ﹣2r =r r 6(C ⋅•x 6﹣3r ,令6﹣3r =0,可得 r =2,∴展开式的常数项为226(C ⋅=60,解得a =4.故答案为4. 点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.9.某校开设A 类选修课5门,B 类选修课4门,一位同学从中供选3门,若要求两类课程中至少选一门,则不同的选法共有______.种 答案:70根据分类计数原理,3门功课可分成2种情况,分别求方法种数. 解:由条件可知3门课程可以分成以下两种情况:A 类2门,B 类1门,共有215440C C =种,或A 类1门,B 类2门,共有1254C C 30=,所以不同的选法共有403070+=种方法.故答案为:70 点评:本题考查分类计数原理,组合知识,重点考查分类讨论的思想,属于基础题型. 10.如图,在正四棱锥P ABCD -中,60APC ∠=︒,则二面角A PB C --的平面角的余弦值为______.答案:17-设AB a ,则2AC a =,过A 作AE PB ⊥,垂足为E ,连CE ,则根据PAB PCB ≅△△,可得CE PB ⊥,所以AEC ∠为二面角A PB C --的平面角,在AEC 中,用余弦定理可求得结果.解:设AB a ,则2AC a =,因为60APC ∠=︒,所以2PA PC a ==,过A 作AE PB ⊥,垂足为E ,连CE ,则根据PAB PCB ≅△△,可得CE PB ⊥, 如图:所以AEC ∠为二面角A PB C --的平面角,在PAB △中,2cos 4AB aPBA PB ∠===,所以sin 4PBA ∠==, 所以在直角AEB △中,sin AE AB EBA =⋅∠=,同理CE =, 在AEC 中,222cos 2AE CE AC AEC AE CE +-∠=⋅222214142161614216a a a a +-=⨯17=-. 故答案为:17-.点评:本题考查了正四棱锥的结构特征,考查了二面角的求法,按照作、证、求这三个步骤做题是解题关键,属于中档题.11.在由二项式系数所构成的杨辉三角形,第________行中从左至右第14与第15个数的比为2:3; 答案:34依题意有1314C 2C 3nn =,()()!13!13!142!13314!14!n n n n n -==--,解得34n =. 点评:本题主要考查二项式系数与杨辉三角的对应关系,考查组合数的计算公式.二项式展开式的二项式系数为01C ,C ,,C n n n n ,由于计数是从0开始的,故第14,与15项的比为1314C 2C 3nn =,在用阶乘表示组合数的计算公式,约分后解方程可求得n 对应的数值.12.集合{}*110,,S x x x N n N=≤≤∈∈共有120个三元子集()1,2,...,120iA i =,若将i A 的三个元素之和记为()1,2,...,120i a i =,则12120...a a a +++=______. 答案:1980根据题意,将所有元素在子集中的个数算出,然后再求和即可. 解:因为集合{}{}*110,,1,2,3,4,5,6,7,8,9,10S x x x N n N=≤≤∈∈=,所以含元素1的子集有29C ,同理含2,3,4,5,6,7,8,9,10的子集也各有29C ,所以2121209...(123...10)a a a C +++=++++⨯,()1011098198022+⨯=⨯=. 故答案为:1980 点评:本题主要考查集合的新定义以及组合问题,还考查了分析推理的能力,属于中档题. 13.太阳光线照于地面,与地面成角02παα⎛⎫<<⎪⎝⎭.调整木棍角度可改变其在水平地面的影子长度.则长度为d 的木棍在水平地面的影子最长为______. 答案:sin dα太阳光与水平面所成的角是不变量, 设BAC θ∠=,利用正弦定理公式可得,()sin sin d AC αθα=+影子长为()sin sin d AC θαα+=,α是不变量 ,且sin α确定,只需要()sin θα+最大,计算即可得出结果.解:光线照于地面,与地面成角02παα⎛⎫<<⎪⎝⎭.调整木棍角度可改变其在水平地面的影子长度.则长度为d ,如图所示:AB d =,C α=,设BAC θ∠=,影子长为AC ,根据正弦定理:()sin sin d AC αθα=+,则()sin sin d AC θαα+=, 因为α是不变量 ,且sin α确定,只需要()sin θα+最大, 故有2πθα+=,此时,木棍在水平地面的影子最长为sin dα. 故答案为:sin dα点评:本题考查了线面角中的最小角定理,还考查了学生们的空间想象能力及把生活中的实例用数学的思想加以解释的能力,即建模能力.14.在一个密闭的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是.答案:15, 66⎛⎫ ⎪⎝⎭解:试题分析:如图,正方体ABCD-EFGH,此时若要使液面不为三角形,则液面必须高于平面EHD,且低于平面AFC.而当平面EHD平行水平面放置时,若满足上述条件,则任意转动该正方体,液面的形状都不可能是三角形.所以液体体积必须>三棱柱G-EHD的体积16,并且<正方体ABCD-EFGH体积-三棱柱B-AFC体积15166-=【考点】1.棱柱的结构特征;2.几何体的体积的求法15.气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22℃.现有甲、乙、丙三地连续5天的日平均温度的记录数据:(记录数据都是正整数)①甲地5个数据的中位数为24,众数为22;②乙地5个数据的中位数为27,总体均值为24;③丙地5个数据中有一个数据是32,总体均值为26,总体方差为10.8.则肯定进入夏季的地区有_____.答案:①③根据数据的特点进行估计甲、乙、丙三地连续5天的日平均气温的记录数据,分析数据的可能性进行解答即可得出答案.解:①甲地:5个数据的中位数为24,众数为22,根据数据得出:甲地连续5天的日平均温度的记录数据可能为:22、22、24、25、26,其连续5天的日平均气温均不低于22;②乙地:5个数据的中位数为27,总体均值为24,当5个数据为19、20、27、27、27,可知其连续5天的日平均温度有低于22,故不确定;③丙地:5个数据中有一个数据是32,总体均值为26,若有低于22,假设取21,此时方差就超出了10.8,可知其连续5天的日平均温度均不低于22,如22、25、25、26、32,这组数据的平均值为26,方差为10.8,但是进一步扩大方差就会超过10.8,故③对.则肯定进入夏季的地区有甲、丙两地,故答案为①③. 点评:本题考查中位数、众数、平均数、方差的数据特征,简单的合情推理,解答此题应结合题意,根据平均数的计算方法进行解答、取特殊值即可.16.有7个评委各自独立对A 、B 两位选手投票表决,两位选手旗鼓相当,每位评委公平投票且不得弃权.若7位评委依次揭晓票选结果,则A 选手在每位评委投票揭晓后票数始终保持领先的概率是______. 答案:532将比分分为7:0,6:1,5:2,4:3四种情况讨论计算概率. 解:由条件可知前两名投票的都投给选手A ,并且投给每位选手的概率是12P =. 若投票给A 、B 两位选手的比分为7:0,则概率为712⎛⎫ ⎪⎝⎭, 若比分为6:1,则投给选手B 的方法有155C =种,所以概率为7152⎛⎫⋅ ⎪⎝⎭若比分为5:2,则投给选手B 的两票不能在第三和第四的位置,有2519C -=种,所以概率为7192⎛⎫⋅ ⎪⎝⎭, 若比分为4:3,则投给A 的票不能是最后一位,且不能占5,6位,有2415C -=种,所以概率为7152⎛⎫⋅ ⎪⎝⎭, 所以概率()7151595232P ⎛⎫=+++⋅=⎪⎝⎭. 故答案为:532点评:本题考查独立事件同时发生的概率,重点考查分类的思想,属于中档题型.三、解答题17.某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(1)记A 为事件“一续保人本年度的保费不高于基本保费”.求()P A 的估计值; (2)求续保人本年度平均保费的估计值. 答案:(1)1120;(2)1.1925a . (1)求出A 为事件:“一续保人本年度的保费不高于基本保费”的人数.总事件人数,即可求()P A 的估计值;(2)利用人数与保费乘积的和除以总续保人数,可得本年度的平均保费估计值. 解:(1)记A 为事件:“一续保人本年度的保费不高于基本保费”. 事件A 的人数为:60+50=110,该险种的200名续保,()P A 的估计值为:1101120020=; (2)续保人本年度的平均保费估计值为0.856050 1.2530 1.530 1.75202101.1925200a a a a a a x a ⨯+⨯+⨯+⨯+⨯+⨯==点评:本题考查样本估计总体的实际应用,考查计算能力.属于基础题.18.如图,正方形ABCD 的边长为2,E 、F 分别是边AB 及BC 的中点,将AED 、BEF 及DCF 折起,使A 、B 、C 三点重合于1A 点.(1)求三棱锥1A EFD -的体积; (2)求1A D 与平面DEF 所成角的大小. 答案:(1)13;(2)1arcsin 3.(1)首先证明1A D ⊥平面1A EF ,再求三棱锥的体积;(2)首先证明平面1A MD ⊥平面EFD ,再说明1A D 与平面DEF 所成角为1A DM ∠,并求角的大小. 解:(1)由条件可知11A E A D ⊥,11A F A D ⊥,且111A E A F A ⋂=1A D ∴⊥平面1A EF ,1A EF 是等腰直角三角形,1111122A EFS∴=⨯⨯=, 1111111123323A EFD D A EFA EF V V S A D --∴==⨯⨯=⨯⨯=; (2)取EF 的中点M ,连结1A M ,DM ,11A E A F =,1A M EF ∴⊥,同理,DM EF ⊥,且1A MEF M =EF ∴⊥平面1A MD ,又EF ⊂平面1A MD ,∴平面1A MD ⊥平面EFD ,且平面1A MD 平面EFD MD =,∴1A D 与平面DEF 所成角为1A DM ∠,1A D ⊥平面1A EF ,11A D A M ∴⊥ 1122A M EF ==,()222212325222DM DE EF ⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭, 111sin 3A M A DM MD ∴∠==, 即11arcsin 3A DM ∠= ,1A D 与平面DEF 所成角为1arcsin 3.点评:本题考查垂直关系,几何体的体积,线面角,重点考查直观想象能力,计算能力,推理证明能力,属于基础题型. 19.(1)已知()2fx kx =+,不等式()3f x <的解集为()1,5-,不等式()1xf x ≥的解集为A .求集合A ;(2)解关于x 的不等式()2220ax a x +--≥.答案:(1)[)1,2;(2)见解析(1)由题意得,23523k k ⎧-+=⎪⎨+=⎪⎩,由此可求得()2f x x =-+,代入后转化为一元二次不等式即可求出答案;(2)分类讨论法解不等式即可. 解:解:(1)∵()2f x kx =+,不等式()3f x <的解集为()1,5-, ∴方程23kx +=的解集为1,5,∴23523k k ⎧-+=⎪⎨+=⎪⎩,解得1k =-,∴()2f x x =-+,∴()112x x f x x ≥⇔≥-+()2102x x -⇔≤-()()12020x x x ⎧--≤⇔⎨-≠⎩, 解得12x ≤<, ∴[)1,2A =;(2)∵()2220ax a x +--≥,①当0a =时,原不等式化为220x --≥,解得1x ≤-; 当()2010a a x x a ⎛⎫≠∴-+≥ ⎪⎝⎭, ②当0a >时,原不等式化为()210x x a ⎛⎫-+≥ ⎪⎝⎭, 解得1x ≤-,或2x a≥; ③当0a <时,原不等式化为()210x x a ⎛⎫-+≤ ⎪⎝⎭, 1︒当21a =-即2a =-时,原不等式化为()210x +≤,解得1x =-; 2︒当21a <-即20a -<<时,解得21x a≤≤-; 3︒当21a >-即2a <-时,解得21x a-≤≤;综上:当2a <-时,原不等式的解集为21,x a ⎡⎤∈-⎢⎥⎣⎦;当2a =-时,原不等式的解集为{}1x ∈-; 当20a -<<时,原不等式的解集为2,1x a ⎡⎤∈-⎢⎥⎣⎦; 当0a =时,原不等式的解集为(],1x ∈-∞-; 当0a >时,原不等式的解集为(]2,1,x a ⎡⎫∈-∞-+∞⎪⎢⎣⎭. 点评:本题主要考查一元二次不等式的解法,考查分式不等式的解法,考查转化与化归思想,考查分类讨论法,属于中档题.20.如图,为正六棱柱111111ABCDEF A B C D E F -,底面边长AB a ,高1AA h =.(1)若a h =,求异面直线1BD 和1CF 所成角的大小; (2)计算四面体11BCD F 的体积(用,a h 来表示);(3)若正六棱柱为一容器(有盖),且底面边长a 和高h 满足:23h a k +=(k 为定值),则当底面边长a 和高h 分别取得何值时,正六棱柱的表面积与体积之比最小? 答案:(1)5;(223h ;(3)3a k =,14h k =,取得最小.(1)延长,EF BA 相交于G 点,延长1111,E F B A 相交于H 点,连接GH , 得111BCFGB C F H 是直四棱柱,证明1//CF BH ,所以异面直线1BD 和1CF 所成角的大小即为直线1BD 和BH 所成角的大小.解三角形可得.(2)建立空间直角坐标系,求出平面1BF C 法向量,求出1D 到平面1BF C 的距离,可得四面体11BCD F 的体积. (3)求出正六棱柱的表面积2633Sha a , 正六棱柱的体积233Va h ,利用已知条件,转化为二次函数求得最值,得解.解:(1)补形如图:延长,EF BA 相交于G 点,延长1111,E F B A 相交于H 点,连接GH 由正六边形性质知BCFG 是平行四边形,从而得111BCFGB C F H 是直四棱柱,则1//BC HF 且1=BC HF 所以四边形1BCF H 是平行四边形,所以1//CF BH ,所以异面直线1BD 和1CF 所成角的大小即为直线1BD 和BH 所成角的大小. 在三角形1BD H 中,由平面几何知识和余弦定理得:17D Ha ,5BHa ,12BD a ,22222211115cos 210252BH BD HD HBD BH BD a a15arccosHBD(2)如图,建立分别以1,FB FE FF ,为,,x y z 轴的空间直角坐标系,则 (3,0,0)B a ,3,,0)C a a ,133,)2a aD h ,1(0,0,)F h (0,,0)BCa ,1(3,0,)BF a h ,13(,,)22a aCD h 设平面1BF C 法向量为(,,)n x y z =100n BC n BF ⎧⋅=⎪⎨⋅=⎪⎩ , 030ay ax hz =⎧⎪⎨-+=⎪⎩,令3x =,则3az h,0y = 3(3,0,)a n h所以1D 到平面1BF C 的距离1222233302292393a a a hn CD h dna h a h又2214FC a h ,BC a =,2213BF a h ,22211BC BF F C122111322BF CSBC BF a a h11122221113332239D BF CBF C V S d a a h h h (3)由题知,正六棱柱的表面积221626sin 606332S ha a haa正六棱柱的体积221336sin 6022V a ha h 2222332633423423h V a h ah Sha a ha a h a又2h k = 22221()22416V hk h h h k kh Skkk 所以当=4k h 时,VS 有最大值,也即SV取得最小值, 此时=4k h ,6a k = 点评:本题考查异面直线所成角,利用空间向量求四面体体积及利用表面积与体积之比转化为函数求其最值问题,属于较难题. 21.对任意*n N ∈,定义(1nn a b +=+n a ,n b 为正整数.(1)求33a b +,44a b +的值; (2)求证:2221n n a b -=; (3)设nn na cb =是否存在实数0λ>,使得()()10n n c c λλ+--<对任意*n N ∈恒成立?若存在,求出λ的值,若不存在,请说明理由. 答案:(1)12,29;(2)证明见解析;(3)存在,λ=(1)分别令3n =和4n =,将3(1+和4(1+展开,求得3344,,,a b a b 的值,进而求得结果;(2)分别列出n a 和n b 的值,列出关系,得到222(1)nn n a b -=-,从而证得结果;(3)假设存在实数0λ>,满足条件,根据题意找关系,确定出nn na cb =的极限,求得结果. 解:(1)(31167=++=+所以337,5a b ==,所以3312a b +=,(411624417+=+⨯+⨯=+,所以4417,12a b ==,4429a b +=;(2)12233(11(2)n nn n n n n C C C C =+⋅+++,所以224361222n n n n a C C C =++++,132522n n nn b C C C =+++,所以222()()n n n n n n a b a a -=224361325224361325[(1222)2(22)][(1222)2(22)]n n n n n nnnnn nnC C C C C C C C C C C C =++++++++⋅++++-+++12232[(1(2)]n n n n n n C C C C =+⋅+⋅++2233[1(]nn n n n C C C C ⋅-⋅-⋅++-(1(1[(1(1)n n n n =-=+=-,所以2221nn a b -=;(3)由(2)知,2221n n a b -=,设2221n n a b -=,== 可以发现132522n n n n b C C C=+++会随着n 的增大而增大,=n的增大而减小,并且会越来越接近与1,所以nn na cb =要大; 当2221n n a b -=-时,== 同理可以确定nn na cb =会随着会随着n ,从而可以得出满足()()10n n c c λλ+--<的λ.点评:该题考查的是有关二项式定理的有关问题,涉及到的知识点有二项式定理和数列的综合题,在解题的过程中,注意极限的思想的应用,属于难题.。
2023年上海交通大学附属中学高二下期中数学试卷及答案

上海市交通大学附属中学2022-2023学年高二下期中数学试卷一、填空题(1-6每题4分,7-12每题5分,共54分)1.已知集合{}2|680A x x x =-+≤,{||1|2,Z}B x x x =-<∈,则A B = ___________.2.已知(1,0)a = ,(3,4)b = ,则向量a 在向量b 方向上的数量投影为___________.3.已知直线1:10l mx y -+=,直线2:420l x my -+=,若12//l l ,则m =_____________.4.已知复数z 满足i 34i z =+(i 是虚数单位),则z =___________.5.函数2y =的最小值是______.6.母线长为10的圆锥的侧面展开图的圆心角等于8π5,则该圆锥的体积为___________.7.直线l 过点(2,3)P ,当原点到直线l 的距离最大时,直线l 的方程为___________.8.设常数a使方程sin x x a +=在闭区间[]0,2π上恰有三个不同的解123,,x x x ,则实数a 的取值为___________.9.设随机变量()12,X B p ~,若()8E X ≤,则()D X 的最大值为___________.10.研究人员开展甲、乙两种药物的临床抗药性研究实验,事件A 为“对药物甲产生抗药性”,事件B 为“对药物乙产生抗药性”,事件C 为“对甲、乙两种药物均不产生抗药性”.若()415P A =,()215P B =,()710P C =,则()P B A =______.11.已知椭圆2222:1(0)x y C a b a b +=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE V 的周长是________________.12.如图,探测机器人从O 点出发,准备探测道路OA 和OB 所围的三角危险区域.已知机器人在道路OA 和OB 上探测速度可达每分钟2米,60AOB ∠=︒,在AOB ∠内为危险区域,探测速度为每分钟1米.假设机器人可随时从道路进入危险区域且可在危险区域各方向自由行动(不考虑转向耗时),则理论上,5分钟内机器人可达到探测的所有危险区域内的点组成的区域面积为___________.二、选择题(13、14每题4分,15、16每题5分,共18分)13.已知222:O x y r += ,直线223l x y r +=:,若l 与⊙O 相离,则()A.点(2,3)P 在l 上B.点(2,3)P 在O 上C.点(2,3)P 在O 内D.点(2,3)P 在O 外14.某教学软件在刚发布时有100名教师用户,发布5天后有1000名教师用户.如果教师用户人数()R t 与天数t 之间满足关系式:()0e ktR t R =,其中k 为常数,0R 是刚发布时的教师用户人数,则教师用户超过20000名至少经过的天数为()(参考数据:lg20.3010≈)A.9B.10C.11D.1215.给定下列四个命题:①图像不经过点(1,1)-的幂函数一定不是偶函数;②若一条直线垂直于平面内的无穷多条直线,则这条直线垂直于这个平面;③有两个相邻的侧面是矩形的棱柱是直棱柱;④设数列{}n a 的前n 项和为n S ,若{}n a 是递增数列,则数列{}n S 也是递增数列;以上命题是真命题的序号是()A.①②B.②③C.③④D.①③16.等轴双曲线Γ的焦点(,0)c ±,圆222:()C x c y r -+=(0,0)r c >>,则()A.对于任意r ,存在c ,使圆C 与双曲线Γ右支恰有两个公共点B.对于任意r ,存在c ,使圆C 与双曲线Γ右支恰有三个公共点C.存在c ,使对于任意r ,圆C 与双曲线Γ右支至少有一个公共点D.存在c ,使对于任意r ,圆C 与双曲线Γ右支至多有两个公共点三、解答题(本大题共5道小题,共78分)17.某校学生利用解三角形有关知识进行数学实践活动.A 处有一栋大楼,某学生选(与A 在同一水平面的)B 、C 两处作为测量点,测得BC 的距离为50m ,=45ABC ∠︒,105BCA ∠=︒,在C 处测得大楼楼顶D 的仰角α为75︒.(1)求,A C 两点间的距离;(2)求大楼的高度.(第(2)问不计测量仪的高度,计算结果精确到1m )18.已知双曲线22:1C x y -=,及直线:1l y kx =-.(1)若l 与C 有且只有一个公共点,求实数k 的值;(2)若l 与C 的左右两支分别交于A 、B 两点,且OAB ,求实数k 的值.19.设a 为实数,函数2()||1,f x x x a x R =+-+∈.(1)讨论函数()f x 的奇偶性并说明理由;(2)求()f x 的最小值.20.直线l 与抛物线24y x =交于A 、B 两点,O 为坐标原点,直线OA 、OB 的斜率之积为1-,以线段AB 为半径的圆与直线l 交于P 、Q 两点.(1)求证:直线l 过定点;(2)求AB 中点的轨迹方程;(3)设()6,0M ,求22MP MQ +的最小值.21.已知ABC 的三个顶点都在椭圆22:143x y Γ+=上.(1)设它的三条线段AB ,BC ,AC 的中点分别为D ,E ,M ,且三条边所在线的斜率分别为123,,k k k ,且123,,k k k 均不为0.点O 为坐标原点,若直线OD ,OE ,OM 的斜率之和1.求证:123111k k k ++为定值;(2)当O 是ABC 的重心时,求证:ABC 的面积是定值;(3)如图,设ABC 的边AB 所在直线与x 轴垂直,垂足为椭圆右焦点F ,过点F 分别作直线12,l l 与椭圆交于,,,C D E G (不同于A ,B 两点),连接,CG DE 与AB 分别交于,M N ,求证:FM FN =.上海市交通大学附属中学2022-2023学年高二下期中数学试卷一、填空题(1-6每题4分,7-12每题5分,共54分)1.已知集合{}2|680A x x x =-+≤,{||1|2,Z}B x x x =-<∈,则A B = ___________.【答案】{}2【解析】【分析】解一元二次不等式化简集合A ,再解含绝对值符号的不等式化简集合B ,再利用交集的定义求解作答.【详解】解不等式2680x x -+≤,得(2)(4)0x x --≤,解得24x ≤≤,即{|24}A x x =≤≤,解不等式|1|2x -<,得212x -<-<,解得13x -<<,即{0,1,2}B =,所以{2}A B = .故答案为:{}22.已知(1,0)a = ,(3,4)b = ,则向量a在向量b 方向上的数量投影为___________.【答案】35##0.6【解析】【分析】利用向量的数量积转化求解向量a ,b在方向上的数量投影即可.【详解】解:设向量a 与b 的夹角是θ,则向量a 在b方向上的数量投影为:3||cos 5||a b a b θ⋅==.故答案为:353.已知直线1:10l mx y -+=,直线2:420l x my -+=,若12//l l ,则m =_____________.【答案】2-【解析】【分析】根据两直线平行的充要条件求解.【详解】因为12//l l ,所以2424m m ⎧-=-⎨≠⎩,解得2m =-.故答案为:2-4.已知复数z 满足i 34i z =+(i 是虚数单位),则z =___________.【答案】5【解析】【分析】根据复数的除法运算和共轭复数、模长的定义求解即可.【详解】由i 34i z =+可得()2i 34i 34i 43i i iz ++===-,所以43i z =+,5z ==,故答案为:55.函数2y =的最小值是______.【答案】2【解析】【分析】将函数化为y =++,注意运用基本不等式和二次函数的最值,同时注意最小值取得时,x 的取值要一致,即可得到所求最小值.【详解】解:函数22y ====++= .当且仅当=0x =,取得等号.则函数的最小值为2.故答案为:2.【点睛】本题考查基本不等式的运用:求最值,注意求最值的条件:一正二定三等,属于中档题和易错题.6.母线长为10的圆锥的侧面展开图的圆心角等于8π5,则该圆锥的体积为___________.【答案】128π【解析】【分析】求出侧面展开图的弧长和底面圆半径,再求出圆锥的高,由此计算圆锥的体积.【详解】因为母线长为10的圆锥的侧面展开图的圆心角等于8π5,所以侧面展开图的弧长为:810π16π5⨯=.设该圆锥的底面圆的半径为r ,所以2π16πr =,解得8r =,所以该圆锥的高6h ==,所以该圆锥的体积2211ππ86128π33V r h ==⨯⨯=.故答案为:128π.7.直线l 过点(2,3)P ,当原点到直线l 的距离最大时,直线l 的方程为___________.【答案】23130x y +-=【解析】【分析】作图分析可知,当原点到直线l 的距离最大时,OP l ⊥,求出l 的斜率,根据点斜式即可求出直线l 的方程.【详解】由题意知,OP l ⊥,32OP k =,所以直线l 的斜率23k =-,所以直线l 的方程为:()2323y x -=--,即23130x y +-=.故答案为:23130x y +-=.8.设常数a 使方程sin x x a +=在闭区间[]0,2π上恰有三个不同的解123,,x x x ,则实数a 的取值为___________.【解析】【分析】利用辅助角公式得到方程的解的个数即为在[]0,2π上直线y a =与三角函数π2sin3y x ⎛⎫=+ ⎪⎝⎭图象的交点的个数,画出图象,数形结合得到当且仅当a =与三角函数图象恰有三个交点,得到答案.【详解】∵13πsin 2sin 2sin 223x x x x x a ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,∴方程的解即为在[]0,2π上直线y a =与三角函数π2sin 3y x ⎛⎫=+⎪⎝⎭图象的交点的横坐标,∵[]0,2πx ∈,∴ππ7π,333x ⎡⎤+∈⎢⎥⎣⎦,令π3z x =+,画出函数2sin y z =在π7π,33z ⎡⎤∈⎢⎥⎣⎦上的图象,如下:由图象可知当且仅当a =.9.设随机变量()12,X B p ~,若()8E X ≤,则()D X 的最大值为___________.【答案】3【解析】【分析】根据二项分布的数学期望得p 的范围,再根据方差运算公式结合基本不等式求得()D X 的最大值.【详解】随机变量()12,X B p ~,由()8E X ≤可得0128p <≤,所以203p <≤又()()211211232p p D X p p +-⎛⎫=-≤⨯= ⎪⎝⎭当且仅当12p =时,“”=成立,故()D X 的最大值为3.故答案为:3.10.研究人员开展甲、乙两种药物的临床抗药性研究实验,事件A 为“对药物甲产生抗药性”,事件B 为“对药物乙产生抗药性”,事件C 为“对甲、乙两种药物均不产生抗药性”.若()415P A =,()215P B =,()710P C =,则()P B A =______.【答案】38##0.375【解析】【分析】求出()P A B ,结合()()()()P A B P A P B P AB =+- 求出()P AB ,进而利用求条件概率公式求出答案.【详解】由题意可知()()710P C P A B =⋂=,则()()73111010P A B P A B ⋃=-⋂=-=.又()()()()P A B P A P B P AB =+- ,所以()()()()423115151010P AB P A P B P A B =+-⋃=+-=,则()()()13104815P AB P B A P A ===.故答案为:3811.已知椭圆2222:1(0)x y C a b a b+=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE V 的周长是________________.【答案】13【解析】【分析】利用离心率得到椭圆的方程为222222213412043x y x y c c c+=+-=,即,根据离心率得到直线2AF 的斜率,进而利用直线的垂直关系得到直线DE 的斜率,写出直线DE 的方程:x c =-,代入椭圆方程22234120x y c +-=,整理化简得到:221390y c --=,利用弦长公式求得138c =,得1324a c ==,根据对称性将ADE V 的周长转化为2F DE △的周长,利用椭圆的定义得到周长为413a =.【详解】∵椭圆的离心率为12c e a ==,∴2a c =,∴22223b a c c =-=,∴椭圆的方程为222222213412043x y x y c c c+=+-=,即,不妨设左焦点为1F ,右焦点为2F ,如图所示,∵222AF a OF c a c ===,,,∴23AF O π∠=,∴12AF F △为正三角形,∵过1F 且垂直于2AF 的直线与C 交于D ,E 两点,DE 为线段2AF 的垂直平分线,∴直线DE 的斜率为33,直线DE 的方程:x c =-,代入椭圆方程22234120x y c +-=,整理化简得到:221390y c --=,判别式()22224139616c c ∆=+⨯⨯=⨯⨯,∴12226461313cDE y =-=⨯=⨯⨯⨯=,∴138c =,得1324a c ==,∵DE 为线段2AF 的垂直平分线,根据对称性,22AD DF AE EF ==,,∴ADE V 的周长等于2F DE △的周长,利用椭圆的定义得到2F DE △周长为222211*********DF EF DE DF EF DF EF DF DF EF EF a a a ++=+++=+++=+==.故答案为:13.12.如图,探测机器人从O 点出发,准备探测道路OA 和OB 所围的三角危险区域.已知机器人在道路OA 和OB 上探测速度可达每分钟2米,60AOB ∠=︒,在AOB ∠内为危险区域,探测速度为每分钟1米.假设机器人可随时从道路进入危险区域且可在危险区域各方向自由行动(不考虑转向耗时),则理论上,5分钟内机器人可达到探测的所有危险区域内的点组成的区域面积为___________.【答案】5033【解析】【分析】讨论机器人探测的路线,结合直线与圆的关系计算三角形面积即可.【详解】如图所示,机器人只在道路上前进可到达AB 点,则OA =OB =10米,作AOB ∠的角平分线OC ,过A 作AD ⊥OB ,垂足为D 点,交OC 于C 点,设机器人先在道路OA 上前进t 分钟到达P 点,此时2OP t =,AP=102t -,后进入危险区域,其能探测到达的点组成以P 为圆心,以()5t -为半径的圆弧 QR,由题意可知:1sin 2r OAD AP ==∠,即AD 与该圆弧相切,设切点为E ,故随P 点从O 移动到A ,机器人可探测的区域为OAD △,结合对称性,机器人5分钟能到达的点围成区域有OAD △与OBF ,即图中阴影部分,其面积为2OAC S ,易知OAC 为含120°的等腰三角形,所以区域面积为:215032sin12023OA ⨯⨯⨯=.故答案为:5033【点睛】本题关键在于对题意的理解,然后结合直线与圆的位置关系,利用角的对称性得出区域形状,再解三角形求区域面积,极容易出错,需要仔细审题.二、选择题(13、14每题4分,15、16每题5分,共18分)13.已知222:O x y r += ,直线223l x y r +=:,若l 与⊙O 相离,则()A.点(2,3)P 在l 上B.点(2,3)P 在O 上C.点(2,3)P 在O 内D.点(2,3)P 在O 外【答案】C 【解析】【分析】根据l 与O2r >,即可推出||r OP >,即可得答案.【详解】由已知l 与O 相离,可知圆心到直线的距离大于半径,不妨设r 为222:O x y r +=22r =>,故r >,由于(2,3)P,则OP =||r OP >,则点(2,3)P 在O 内,故选:C .14.某教学软件在刚发布时有100名教师用户,发布5天后有1000名教师用户.如果教师用户人数()R t 与天数t 之间满足关系式:()0e ktR t R =,其中k 为常数,0R 是刚发布时的教师用户人数,则教师用户超过20000名至少经过的天数为()(参考数据:lg20.3010≈)A.9 B.10 C.11D.12【答案】D 【解析】【分析】根据已知条件求得()ln105e 100t R t =,结合()20000R t >及指对数关系、对数运算性质求解集,即可得结果.【详解】由题设0050(0)e 100(5)e 1000kR R R R ⎧==⎨==⎩,可得0100ln105R k =⎧⎪⎨=⎪⎩,所以()ln105e100R t =,则ln105e10020000t >,故5ln 2005lg 2005(lg 22)11.50511ln10t ===⨯+≈>,所以教师用户超过20000名至少经过12天.故选:D15.给定下列四个命题:①图像不经过点(1,1)-的幂函数一定不是偶函数;②若一条直线垂直于平面内的无穷多条直线,则这条直线垂直于这个平面;③有两个相邻的侧面是矩形的棱柱是直棱柱;④设数列{}n a 的前n 项和为n S ,若{}n a 是递增数列,则数列{}n S 也是递增数列;以上命题是真命题的序号是()A.①②B.②③C.③④D.①③【答案】D 【解析】【分析】对①利用幂函数和偶函数特点即可判断,对②和④举反例即可,对③利用线面垂直的判定结合直棱柱的定义即可判断.【详解】对①, 幂函数的图象都过(1,1),偶函数的图象关于y 轴对称,∴图象不经过点(1,1)-的莫函数一定不是偶函数,故①正确;对②,若平面内的无数条直线互相平行,则这条直线可以不垂直这个平面,故②错误;对③,若有两个相邻的侧面是矩形,则两侧面的交线即一条侧棱垂直于底面两相交的直线,则这条侧棱垂直于底面,根据棱柱侧棱互相平行,则所有侧棱均垂直于底面,则棱柱为直棱柱,故③正确;对④,当7n a n =-时,满足数列{}n a 是递增数列,116S a ==-,2126511S a a =+=--=-,则12S S >,不满足数列{}n S 是递增数列,故④不正确;故选:D.16.等轴双曲线Γ的焦点(,0)c ±,圆222:()C x c y r -+=(0,0)r c >>,则()A.对于任意r ,存在c ,使圆C 与双曲线Γ右支恰有两个公共点B.对于任意r ,存在c ,使圆C 与双曲线Γ右支恰有三个公共点C.存在c ,使对于任意r ,圆C 与双曲线Γ右支至少有一个公共点D.存在c ,使对于任意r ,圆C 与双曲线Γ右支至多有两个公共点【答案】AD 【解析】【分析】联立方程可得2224420x cx c r -+-=,构建()222442f x x cx c r =-+-,根据二次函数讨论()f x 在[],c r c r -+上的零点分布,并结合对称性分析C 与Γ右支的交点个数.【详解】设双曲线方程为:2222c x y -=,联立方程()2222222c x y x c y r ⎧-=⎪⎨⎪-+=⎩,消去y 得2224420x cx c r -+-=,由圆222:()C x c y r -+=可知:x 的取值范围为[],c r c r -+,构建()222442f x x cx c r =-+-,[],x c r c r ∈-+,则()f x 的对称轴2cx c c r =<<+,且()()()222222,20,2402c f c r r c c f r f c r r cr c ⎛⎫-=--=-<+=++>⎪⎝⎭,当()02f c r c c r ⎧-<⎪⎨-≥⎪⎩即2122c c r ⎛-<≤ ⎝⎭时()f x 有且只有一个零点()0,x c r c r ∈-+,当()02f c r c c r ⎧-=⎪⎨-≥⎪⎩即212r c ⎛⎫=- ⎪ ⎪⎝⎭时()f x 有且只有一个零点0212x c ⎛⎫=- ⎪ ⎪⎝⎭.当()02f c r c c r ⎧->⎪⎨-≥⎪⎩即2012r c ⎛⎫<<- ⎪ ⎪⎝⎭时()f x 无零点.当()02f c r c c r ⎧->⎪⎨-<⎪⎩即212r c ⎛⎫>+ ⎪ ⎪⎝⎭时()f x 有且只有两个零点()01,,x x c r c r ∈-+.当()02f c r c c r ⎧-=⎪⎨-<⎪⎩即12r c ⎛⎫=+ ⎪ ⎪⎝⎭时()f x有且只有两个零点()011,,2x c x c r c r ⎛⎫=+∈-+ ⎪ ⎪⎝⎭.当()02f c r c c r ⎧-<⎪⎨-<⎪⎩即2122c r c ⎛⎫<<+ ⎪ ⎪⎝⎭时有且只有一个零点()0,x c r c r ∈-+.注意到当212r c ⎛⎫=- ⎪ ⎪⎝⎭,C 与Γ的交点坐标为21,02c ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,当212r c ⎛⎫=+ ⎪ ⎪⎝⎭时,C 与Γ的交点坐标有21,02c ⎛⎫⎛⎫+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,即会出现交点在对称轴上,结合C 与Γ的对称性可得:当012r c ⎛⎫<<- ⎪ ⎪⎝⎭时,使C 与Γ没有公共点,即C 与Γ的右支没有公共点;当212r c ⎛⎫=-⎪ ⎪⎝⎭时,使C 与Γ有且仅有一个公共点,即C 与Γ的右支有且仅有一个公共点;当221122c r c ⎛⎫⎛⎫-<<+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭时,使C 与Γ有两个公共点,此时C 与Γ有且仅有两个公共点;当12r c ⎛⎫=+ ⎪ ⎪⎝⎭时,使C 与Γ有三个公共点,此时C 与Γ有且仅有两个公共点;当212r c ⎛⎫>+ ⎪ ⎪⎝⎭时,使C 与Γ有四个公共点,此时C 与Γ有且仅有两个公共点.对A :对于任意r ,存在c ,使得212r c ⎛⎫>-⎪ ⎪⎝⎭,此时圆C 与双曲线Γ右支恰有两个公共点,A 正确;对B :对于任意r ,存在c ,使得12r c ⎛⎫>-⎪ ⎪⎝⎭,此时圆C 与双曲线Γ右支至多有两个公共点,B 错误;对C :存在c ,使对于任意r ,使得212r c ⎛⎫<- ⎪ ⎪⎝⎭,此时圆C 与双曲线Γ右支没有公共点,C 错误;对D :存在c ,使对于任意r ,使得12r c ⎛⎫>- ⎪ ⎪⎝⎭,此时圆C 与双曲线Γ右支至多有两个公共点,D 正确.故选:AD.三、解答题(本大题共5道小题,共78分)17.某校学生利用解三角形有关知识进行数学实践活动.A 处有一栋大楼,某学生选(与A 在同一水平面的)B 、C 两处作为测量点,测得BC 的距离为50m ,=45ABC ∠︒,105BCA ∠=︒,在C 处测得大楼楼顶D 的仰角α为75︒.(1)求,A C 两点间的距离;(2)求大楼的高度.(第(2)问不计测量仪的高度,计算结果精确到1m )【答案】(1)m (2)264m 【解析】【分析】(1)根据题意,先求出BAC ∠,然后利用正弦定理计算即可求解;(2)根据题意结合(1)的结果可直接求出AD = ,然后利用两角和的正切公式计算即可.【小问1详解】由已知得1801054530BAC ∠=︒-︒-︒=︒,在ABC 中,因为sin sin BC ACBAC ABC=∠∠,即50sin30sin45AC︒︒=,所以AC =,所以,A C两点间的距离为m.【小问2详解】在DCA △中,因为90,tan ADDAC AC∠α==,所以tan75AD AC == ,又因为()tan75tan 4530=+31tan45tan30321tan45tan3033++==+-所以2AD =+=141.4122.45263.85264≈+=≈,答:楼高约为264m .18.已知双曲线22:1C x y -=,及直线:1l y kx =-.(1)若l 与C 有且只有一个公共点,求实数k 的值;(2)若l 与C 的左右两支分别交于A 、B 两点,且OAB,求实数k 的值.【答案】(1)1k =±或k =(2)0k =【解析】【分析】(1)联立方程组,消元后得到()221220k xkx -+-=,分210k -=、210k -≠两种情况求解即可;(2)先由题意可得11k -<<,令直线l 与y 轴交于点(0,1)D -,从而得到1212111222=+=+=-= OAB OAD OBD S S S x x x x .【小问1详解】由2211x y y kx ⎧-=⎨=-⎩,消去y ,得()221220k x kx -+-=①,当210k -=,即1k =±时,方程①有一解,l 与C 仅有一个交点(与渐近线平行时).当()22210,Δ4810k k k ⎧-≠⎪⎨=+-=⎪⎩,得22,==k k l 与C 也只有一个交点(与双曲线相切时),综上得k 的取值是1k =±或k =【小问2详解】设交点()()1122,,,A x y B x y ,由2211x y y kx ⎧-=⎨=-⎩,消去y ,得()221220k x kx -+-=,首先由()22210,Δ4810k k k ⎧-≠⎪⎨=+->⎪⎩,得k <<且1k ≠±,并且12122222,11--+==--k x x x x k k ,又因为l 与C 的左右两支分别交于A 、B 两点,所以120x x <,即22020,11k k-<->-,解得11k -<<,故11k -<<.因为直线l 与y 轴交于点(0,1)D -,所以1212111222=+=+=-= OAB OAD OBD S S S x x x x ,故22121212222248,4811--⎛⎫⎛⎫-=∴+-=-= ⎪ ⎪--⎝⎭⎝⎭k x x x x x x k k .解得0k =或62k =±.因为11k -<<,所以0k =.19.设a 为实数,函数2()||1,f x x x a x R =+-+∈.(1)讨论函数()f x 的奇偶性并说明理由;(2)求()f x 的最小值.【答案】(1)当0a =时,函数是偶函数,当0a ≠时,函数是非奇非偶函数;(2)当12a 时,min 3()4f x a =-;当1122a -<<时,2min ()1f x a =+;当12a 时,min 3()4f x a =+.【解析】【分析】(1)考查函数的奇偶性,用特殊值法判断函数及不是奇函数又不是偶函数;(2)先判断函数的单调性再求最值.【详解】解:(1)当0a =时,函数2()()||1()f x x x f x -=-+-+=此时,()f x 为偶函数当0a ≠时,()21f a a =+,2()2||1f a a a -=++,()()f a f a ≠-,()()f a f a ≠--此时()f x 既不是奇函数,也不是偶函数(2)①当x a时,2213()1(24f x x x a x a =-++=-++当12a ,则函数()f x 在(-∞,]a 上单调递减,从而函数()f x 在(-∞,]a 上的最小值为()21f a a =+.若12a >,则函数()f x 在(-∞,]a 上的最小值为13(24f a =+,且1(()2f f a.②当x a时,函数2213()1()24f x x x a x a =+-+=+-+若12-a ,则函数()f x 在[a ,)∞+上的最小值为13()24f a -=-;若12a >-,则函数()f x 在[a ,)∞+上单调递增,从而函数()f x 在[a ,)∞+上的最小值为()21f a a =+.综上,当12-a 时,函数()f x 的最小值为34a -当1122a -< 时,函数()f x 的最小值为21a +当12a >时,函数()f x 的最小值为34a +.【点睛】本题为函数的最值和奇偶性的考查;是高考常考的知识点之一;而求最值时需要注意的是先判断函数的单调性.20.直线l 与抛物线24y x =交于A 、B 两点,O 为坐标原点,直线OA 、OB 的斜率之积为1-,以线段AB 为半径的圆与直线l 交于P 、Q 两点.(1)求证:直线l 过定点;(2)求AB 中点的轨迹方程;(3)设()6,0M ,求22MP MQ +的最小值.【答案】(1)证明见解析;(2)2142x y =+;(3)10.【解析】【分析】(1)设直线l 的方程为x my t =+,设点()11,A x y 、()22,B x y ,将直线l 的方程与抛物线的方程联立,列出韦达定理,分析可知0OA OB ⋅=,利用平面向量的数量积的坐标运算并结合韦达定理求出t 的值,即可证得结论成立;(2)设线段AB 的中点为(),N x y ,可得出2242x m y m⎧=+⎨=⎩,消去m 可得出线段AB 的中点的轨迹方程;(3)利用平面向量的数量积推导出()222224MP MQMO PQ '+=+,结合两点间的距离公式以及二次函数的基本性质可求得22MP MQ +的最小值.【详解】(1)设直线AB 的方程为x my t =+,设点()11,A x y 、()22,B x y ,由24y x x my t⎧=⎨=+⎩得2440y my t --=,所以()()22141606t m t m∆++==>,所以124y ym +=,124y y t =-,所以()21212242x x m y y t m t +=++=+,222121216y y x x t ⋅==,因为直线OA 、OB 的斜率之积为1-,所以0OA OB ⋅=,所以2121240x x y y t t +=-=,所以4t =,所以直线AB 的方程为4x my =+,过定点()4,0;(2)21248x x m +=+ ,直线l 中点为圆心()224,2O m m +',设线段AB 的中点为(),N x y ,可得2242x m y m⎧=+⎨=⎩,消去m 得228y x =-,因此,线段AB 的中点的轨迹方程为2142x y =+;(3)如下图所示,易知圆心O '为线段PQ 的中点,()()111222MO MP PO MP PQ MP MQ MP MQ MP ''=+=+=+-=+ ,所以,2MO MP MQ '=+ ,所以,()()222222422MO PQ MQ MP MQ MP MQ MP '+=++-=+ ,即()(222222244MP MQMO PQ MO ''+=+=+()()2222422144148161816202m m m m m ⎛⎫⎡⎤=-++=-++=-+ ⎪⎢⎥⎣⎦⎝⎭,所以222218102MP MQ m ⎛⎫+=-+ ⎪⎝⎭,所以当22m =±时,22MP MQ +的最小值为10.【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.21.已知ABC 的三个顶点都在椭圆22:143x y Γ+=上.(1)设它的三条线段AB ,BC ,AC 的中点分别为D ,E ,M ,且三条边所在线的斜率分别为123,,k k k ,且123,,k k k 均不为0.点O 为坐标原点,若直线OD ,OE ,OM 的斜率之和1.求证:123111k k k ++为定值;(2)当O 是ABC 的重心时,求证:ABC 的面积是定值;(3)如图,设ABC 的边AB 所在直线与x 轴垂直,垂足为椭圆右焦点F ,过点F 分别作直线12,l l 与椭圆交于,,,C D E G (不同于A ,B 两点),连接,CG DE 与AB 分别交于,M N ,求证:FM FN =.【答案】(1)证明见解析(2)证明见解析(3)证明见解析【解析】【分析】(1)设出点的坐标,代入椭圆方程,利用点差法得出斜率与中点坐标的关系即可得证;(2)点的坐标代入椭圆方程,化简得1212346x x y y +=-,再由椭圆的参数方程化简可得cos()αβ-,再由重心可得3ABC AOB S S = 求证即可;(3)根据直线CD 、EG 的方程及点在椭圆上可得曲线系()()2211221043x y y k x k y k x k λ+-+-+-+=,取1x =,可由方程根的关系得证.【小问1详解】设()()()()()()112233112233,,,,,,,,,,,A x y B x y C x y D s t E s t M s t ,因为,A B 在椭圆上,所以222211221,14343x y x y +=+=,两式相减得:121211*********y y x x s k x x y y t -+==-⨯=-⨯-+,即111413t k s =-,同理可得3222334411,33t t k s k s =-=-,则31212312311143t t t k k k s s s ⎛⎫++=-++ ⎪⎝⎭因为直线OD OE OM 、、的斜率之和为1,所以12311144133k k k ++=-⨯=-,即123111k k k ++为定值.【小问2详解】设()()()112233,,,,,A x y B x y C x y 因为ABC 的重心为O ,故1231230x x x y y y ++=++=又A B C 、、都在椭圆22143x y +=上,故()()222222121211221,1,1434343x x y y x y x y +++=+=+=化简得1212346x x y y +=-,设11222cos ,,2cos ,x y x y ααββ====,代入上式可得:2cos cos 2sin sin 1αβαβ+=-,即()1cos 2αβ-=-,()122139322ABC AOB S S x y x y αβ==-=-=△△,即ABC 的面积为定值92.【小问3详解】设直线CD 方程为:()11y k x =-,直线EG 的方程为:()21y k x =-,直线CD 与直线EG 上所有点对应的曲线方程为:()()11220y k x k y k x k -+-+=,又C D E G 、、、都在椭圆上,则同时过C D E G 、、、的二次曲线系可设为:()()2211221043x y y k x k y k x k λ+-+-+-+=,取1x =,得213034y λ⎛⎫+-= ⎪⎝⎭,易知该方程的两根分别为,M N y y ,由韦达定理可知,0M N y y +=,则FM FN =.【点睛】关键点点睛:根据点在椭圆上,结合重心化简得1212346x x y y +=-,利用椭圆的参数方程,结合重心的性质找出3ABC AOB S S = ,并且能应用三角函数求出AOB S 的大小,是研究三角形面积为定值的关键,本题困难,不易解答.。
上海交大附中高二期末考试数学真题

上海交大附中高二期末考试数学真题近年来,随着教育的不断发展和进步,学生们面临着越来越大的学习压力。
而对于高中生来说,期末考试则是一个非常重要的环节。
今天,我们就来一起解析一下上海交大附中高二期末考试的数学真题。
第一部分:选择题题目一:若函数f(x)=x^2-x,则f(-1)的值为多少?解析:根据题目中给出的函数f(x)=x^2-x,我们只需要将x替换为-1,得到f(-1)=(-1)^2-(-1)=1+1=2。
因此,f(-1)的值为2。
题目二:已知三角形ABC中,∠B=90°,AB=3,BC=4,则AC的长度为多少?解析:根据题目中给出的信息可知,三角形ABC是一个直角三角形,且已知两个边的长度为AB=3和BC=4。
我们可以使用勾股定理来计算AC的长度。
根据勾股定理,直角三角形的斜边的长度等于两个直角边的平方和的平方根。
因此,AC的长度为√(3^2+4^2)=√(9+16)=√25=5。
第二部分:填空题题目三:已知函数f(x)=4x^2+6x+2,求f(-2)的值。
解析:根据题目中给出的函数f(x)=4x^2+6x+2,我们只需要将x替换为-2,得到f(-2)=4(-2)^2+6(-2)+2=4(4)-12+2=16-12+2=6。
因此,f(-2)的值为6。
题目四:在平面直角坐标系中,已知一点A(3,4),则该点关于y轴的对称点的坐标是(____, ____)。
解析:根据题目中给出的点A的坐标为(3,4),我们可以通过求解对称点的坐标来确定。
由于点A关于y轴对称,因此对称点的x坐标不变,y坐标取相反数。
所以,对称点的坐标为(-3,4)。
第三部分:解答题题目五:已知函数f(x)满足f(x+1)=f(x)+2x,且f(1)=1,求f(5)的值。
解析:我们可以使用递推的方法来解决这道题。
首先,将x替换为1,得到f(2)=f(1)+2(1)=1+2=3。
然后,将x替换为2,得到f(3)=f(2)+2(2)=3+4=7。
上海交通大学附属中学高二下学期质量检测一数学试题

交大附中 高二年级 第二学期 质量检测一2017.03.14一、填空题(1-6题每小题4分,7-12题每小题5分,共54分)1、直线032=-+y x 的倾斜角为_______2、增广矩阵为⎪⎪⎭⎫ ⎝⎛+-411211k k 的方程中,若解x 与y 相等,则k 的值为______ 3、抛物线x y 162=的焦点与双曲线19222=-y a x 的一个焦点重合,则双曲线的实轴长为____ 4、已知复数233)3(2)()1(i a i a i z --+=(i 为虚数单位),且32||=z ,则实数a 的值为______ 5、已知⎪⎭⎫ ⎝⎛++-=21cos log 21sin 2ααi z ,i 为虚数单位,若z 为纯虚数,则____=α 6、若点),(y x P 在直线042=-+y x 上,则y x --+42的最小值是_____7、若1||=z ,则|1|i z -+的最大值为_______8、如图,六个相等的小正方形可以拼成一个正方体,则正方体中,直线AB 与CD 所成角的大小为______9、设函数⎩⎨⎧>+-≤<=51050)(ln x x x e x f x ,若方程k x f =)((k 为常数)有三个不同的实数解c b a ,,,且c b a <<,则abc 的取值范围是_______10、在复数范围内写出求方程z z 22=的解集_______11、设),(n n n y x P 是直线))(1(23*N n x n y ∈-=+与椭圆13422=+y x 在第一象限的交点,则极限_____123lim =--∞→n n n x y 12、已知复数集⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧≤≤≤=1|)Im(|2)Re(0z z z U ,集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧=-≤≤≤=1|1|,|)Re(||)Re(|)Re()Re(0w w z w z z M ,则集合M C U 在复平面上表示区域的面积为________二、选择题(每小题5分,共20分)12、两个圆0222:221=-+++y x y x C 与0124:222=+--+y x y x C 的公切线有且仅有 ( )A. 1条B. 2条C. 3条D. 4条14、如图,D C B A ,,,是某长方体四条棱的中点,则直线AB 和直线CD的位置关系是 ( )A. 相交B. 平行C. 异面D. 垂直15、设21,z z 均是复数,则下列命题中的真命题是 ( )A. “21z z >”是“021>-z z ”的必要不充分条件B. “121>z ”是“),1()1,(1+∞--∞∈ z ”的充分必要条件C. “02221=+z z ”是“021==z z ”的充分非必要条件D. “R z z ∈+21”是“21z z =”的既不充分也不必要条件 16、已知曲线Γ的参数方程为⎩⎨⎧++=-=)1ln(cot 23t t y t t t x ,其中参数R t ∈,则曲线Γ ( ) A. 关于x 轴对称 B. 关于y 轴对称C. 关于原点对称D. 没有对称性三、解答题(共5大题,共76分)17、(第1小题7分,第2小题7分,共14分)已知关于t 的方程)(0342C z i zt t ∈=++-有实数根;(1)设)(,5R a ai z ∈+=,求a 的值;(2)求||z 的取值范围;18、(第1小题7分,第2小题7分,共14分)已知数列}{n a 中,211=a ,点)2,(1n n a a n -+在直线x y =上,其中,...3,2,1=n ; (1)令11--=+n n n a a b ,求证:数列}{n b 是等比数列;(2)求数列}{n a 的通项;19、(第1小题6分,第2小题8分,共14分)如图,空间四边形ABCD 中,H G F E CD AB ,,,,8==分别是线段DB AD CA BC ,,,的中点,6=FH ;(1)求证:直线EG 与直线FH 相互垂直;(2)求异面直线AB 与CD 所成角的大小;已知10,z z 均为复数,且00111z z z -+=,记10,z z 在复平面上对应的点分别为Q P ,; (1)若10z z =,求0z 的值;(2)若点P 在y 轴上运动,求点Q 的轨迹方程;(3)点P 在圆)0()1(:2221>=+-r r y x C 上运动,点Q 的轨迹记为曲线D ,求r 的值,使得圆C 与曲线D 只有一个公共点;设椭圆)0,(1:2222>=+Γb a by a x 过点)1,6(),2,2(N M ; (1)求椭圆Γ的方程;(2)21,F F 为椭圆的左、右焦点,直线l 过1F 与椭圆交于B A ,两点,求AB F 2∆面积的最大值;。
【推荐下载】上海交大附中高二数学下册期末测试卷答案

[键入文字]
上海交大附中高二数学下册期末测试卷答案
为了帮助考生们了解更多高中信息,分享了高二数学下册期末测试卷答案,供您参考!
高二数学下册期末测试卷答案
(满分150分,120分钟完成,答案一律写在答题纸上)
一、填空题(本大题共14题,每题4分,满分56分)
1.设复数满足,则______ ______。
2.三个平面最多把空间分割成8 个部分。
3.若圆锥的侧面展开图是半径为2、圆心角为180的扇形,则这个圆锥的体积是。
4.如图,在正三棱柱中, ,异面直线与所成角
的大小为,该三棱柱的体积为。
5. 的展开式中的常数项是60 。
1。
2022年上海交大附属中学高二数学理期末试题含解析

2022年上海交大附属中学高二数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 点P是曲线x2﹣y﹣2ln=0上任意一点,则点P到直线4x+4y+1=0的最小距离是()A.B.C.D.参考答案:B【考点】导数的运算;两条直线平行的判定;两条平行直线间的距离.【分析】求出函数的导函数,令导函数等于已知直线的斜率求出x的值,即与直线4x+4y+1=0平行的切线的切点横坐标,代入曲线方程求出切点坐标,利用点到直线的距离公式求出切点到直线的距离,即最小距离.【解答】解:即∴又4x+4y+1=0即为y=﹣x令得与直线4x+4y+1=0平行的切线的切点为∴点P到直线4x+4y+1=0的最小距离是故选B2. 黑白两种颜色的正六边形地面砖块按如图的规律拼成若干个图案,则第五个图案中有白色地面砖()块.A.27B.22C.20D.23参考答案:B3. 某班m名学生在一次考试中数学成绩的频率分布直方图如图,若在这m名学生中,数学成绩不低于100分的人数为33,则m等于()A.45 B.48 C.50 D.55参考答案:D【考点】频率分布直方图.【分析】根据频率分布直方图,求出数学成绩不低于100分的频率,再根据数学成绩不低于100分的人数为33求得m.【解答】解:由频率分布直方图知,数学成绩不低于100分的频率为(0.030+0.020+0.010)×10=0.6,∵在这m名学生中,数学成绩不低于100分的人数为33,∴m=33÷0.6=55.故选:D.4. 已知f(x)为R上的可导函数,且?x∈R,均有f(x)+f'(x)<0,则以下判断正确的是()A.e2017?f(2017)>f(0)B.e2017?f(2017)=f(0)C.e2017?f(2017)<f(0)D.e2017f(2017)与f(0)的大小无法确定参考答案:C【考点】6A:函数的单调性与导数的关系.【分析】令g(x)=e x f(x),求出函数的导数,根据函数的单调性,可得结论.【解答】解:令g(x)=e x f(x),则g′(x)=e x[f(x)+f′(x)]<0,故g(x)在R递减,故g(2017)<g(0),即e2017f(2017)<f(0),故选:C.【点评】本题考查了函数的单调性问题,考查导数的应用,是一道基础题.5. 下列函数中与为同一函数的是()A、 B、 C、 D、参考答案:C略6. 将一枚质地均匀的硬币连续抛掷3次,出现“2次正面向上,1次反面向上”的概率为A. B. C.D.参考答案:C略7. ,已知,则= ( )A、-3B、-1C、 0D、2参考答案:A8. 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使在C塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔高AB的高度为()A.10 B.10C.10D.10参考答案:D【考点】解三角形的实际应用.【分析】先在△ABC中求出BC,再△BCD中利用正弦定理,即可求得结论.【解答】解:设塔高AB为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,从而有BC=x,AC=x在△BCD中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30°由正弦定理可得, =∴BC==10∴x=10∴x=故塔高AB=9. 随机变量的分布列为0 1 2 3 4 5P,则( )A.B.C.D.参考答案:B10. 的展开式中的常数项为 ()A.-1320 B.1320 C.-220 D.220参考答案:C略二、填空题:本大题共7小题,每小题4分,共28分11. 在平面直角坐标系中,正方形的中心坐标为(1,0),其一边AB所在直线的方程为x﹣y+1=0,则边CD所在直线的方程为.参考答案:x﹣y﹣3=0【考点】待定系数法求直线方程.【分析】求出直线x﹣y+1=0上的点关于(1,0)的对称点,设出直线CD的方程,根据待定系数法求出直线CD的方程即可.【解答】解:直线x﹣y+1=0上的点(﹣1,0)关于点(1,0)对称点为(3,0),设直线CD的方程为x﹣y+m=0,则直线CD过(3,0),解得m=﹣3,所以边CD所在直线的方程为x﹣y﹣3=0,故答案为:x﹣y﹣3=0.【点评】本题考查了求直线方程问题,考查直线的平行关系以及关于点对称问题,是一道中档题.12. 若曲线f(x)=ax2+lnx存在平行于x轴的切线,则实数a的取值范围是.参考答案:(﹣∞,0)【考点】导数的几何意义.【专题】计算题;转化思想;转化法;导数的概念及应用.【分析】求函数的导数,根据导数的几何意义进行求解即可.【解答】解:若f(x)=ax2+lnx存在平行于x轴的切线,则等价为f′(x)=0有解,即f′(x)=2ax+=0,则(0,+∞)上有解,即2a=﹣,∵x>0,∴﹣<0,则2a<0,则a<0,故答案为:(﹣∞,0),【点评】本题主要考查函数的导数的几何意义的应用,根据条件转化为f′(x)=0有解是解决本题的关键.13. 椭圆的两个焦点是,为椭圆上与不共线的任意一点,为的内切圆圆心,延长交线段于点,则。
上海交通大学附属中学10-11学年度高二上学期期末试卷(数学)
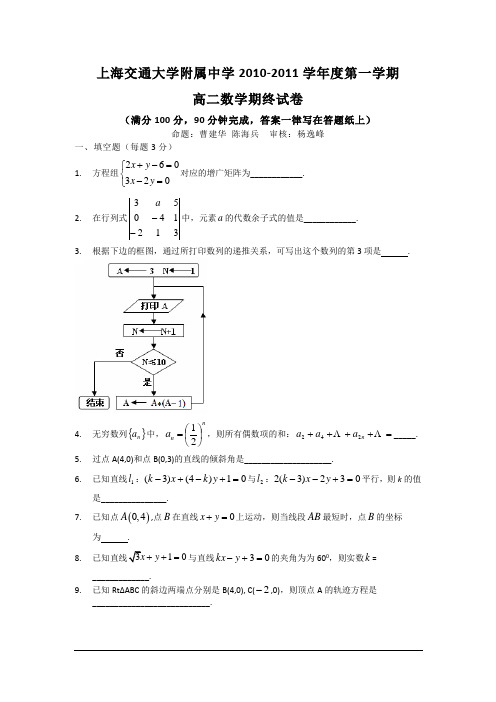
上海交通大学附属中学2010-2011学年度第一学期高二数学期终试卷(满分100分,90分钟完成,答案一律写在答题纸上)命题:曹建华 陈海兵 审核:杨逸峰一、填空题(每题3分)1. 方程组260320x y x y +-=⎧⎨-=⎩对应的增广矩阵为____________. 2. 在行列式31214053--a 中,元素a 的代数余子式的值是____________.3. 根据下边的框图,通过所打印数列的递推关系,可写出这个数列的第3项是 .4. 无穷数列{}n a 中,nn a ⎪⎭⎫ ⎝⎛=21,则所有偶数项的和:=++++ΛΛn a a a 242_____. 5. 过点A(4,0)和点B(0,3)的直线的倾斜角是____________________.6. 已知直线1l :01)4()3(=+-+-y k x k 与2l :032)3(2=+--y x k 平行,则k 的值是_______________.7. 已知点()0,4A ,点B 在直线0x y +=上运动,则当线段AB 最短时,点B 的坐标为 .8. 310x y ++=与直线03=+-y kx 的夹角为为600,则实数k = _____________.9. 已知RtΔABC 的斜边两端点分别是B(4,0), C(2-,0),则顶点A 的轨迹方程是___________________________.10. 已知椭圆221102x y m m +=--,长轴在y 轴上. 若焦距为4,则m = . 11. 与圆22(2)1x y +-=相切,且在两坐标轴上截距相等的直线共有________条.12. 若关于x 的方程212+=-kx x 恰有两个实根,则k 的取值范围是_________________.13. 在等差数列{a n }中,1a 为首项,n S 是其前n 项的和,将2)(1n a a S n n +=整理为12121a a n S n n +=后可知:点ΛΛ),,(,),2,(),1,(222111nS a P S a P S a P n n n (n 为正整数)都在直线12121a x y +=上,类似地,若{n b }是首项为1b ,公比为)1(≠q q 的等比数列,n T 是其前n 项的和,则点ΛΛ),,(,),,(),,(222111n n n T b P T b P T b P (n 为正整数)在直线__________________________________上.14. 在ABC ∆中,设a 、b 、c 分别是A ∠、B ∠、C ∠所对的边长,且满足条件a b c 2,2==,则ABC ∆面积的最大值为________________.二、选择题(每题3分)15. 设{(,)|(2)()0}A x y x y x y =+--=,2{(,)|}0x y B x y x y +=⎧=⎨-=⎩则“x A ∈”是“x B ∈”的( )A 、充分不必要条B 、必要不充分条件C 、充要条件D 、既不是充分条件,也不是必要条件16. 点()M x y 00,是圆()0222>=+a a y x 内不为圆心的一点,则直线200a y y x x =+与该圆的位置关系是 ( )A 、相切B 、相交C 、相离D 、相切或相交17. 已知直线2x =及4x =与函数2log y x =图像的交点分别为,A B ,与函数lg y x =图像的交点分别为,C D ,则直线AB 与CD ( )A 、相交,且交点在第I 象限B 、相交,且交点在第II 象限C 、相交,且交点在第IV 象限D 、相交,且交点在坐标原点18. 在ABC ∆中,O 是平面ABC 上的一点,点P 满足()++=λ,),0(+∞∈λ,则直线AP 过ABC ∆的( )A 、垂心B 、重心C 、内心D 、外心三、解答题(10分+12分+12分+12分)19. 求圆心在直线0=+y x 上,且过圆02410222=-+-+y x y x 与圆082222=-+++y x y x 的交点的圆的方程。
上海交大附中2023-2024学年高二下学期期中考试数学试题

上海交通大学附属中学2023-2024学年度第二学期高二数学期中考试卷(本试卷共4页,满分150分,120分钟完成.答案一律写在答题纸上)一、填空题(本大题共有12题,满分54分,第16题每题4分,第7~12题每题5分)考生应在答题纸的相应位置直接填写结果.1.设函数()()sin 12f x x =+,则()f x ′=__________.2.4对双胞胎站成一排,要求每对双胞胎都相邻,则不同的站法种数是__________.(结果用数字作答)3.设事件A B 、是互斥事件,且()()14P A P B ==,则()P A B ∪=__________. 4.已知函数()2ln f x ax x =+的导函数()f x ′满足()13f ′=,则a 的值为__________. 5.若从正方体的6个面的12条面对角线中,随机选取两条,则它们成异面直线的概率是__________. 6.为了弘扬我国古代的“六艺文化”,某学校欲利用每周的社团活动课开设“礼”“乐”“射”“御”“书”“数”六门课程,每周开设一门,每门课都要开,连续开设六周,若课程“射”不排在第二周,课程“乐”不排在第五周,则所有可能的排法种数为__________.7.一家药物公司试验一种新药,在500个病人中试验,其中307人有明显疗效,120人有疗效但疗效一般,剩余的人无疗效,则没有明显疗效的频率是__________.8.某篮球运动员的罚球命中率为80%,假设每次罚球的结果是独立的,则他在3次罚球中至少进1球的概率是__________.9.设()f x 是定义在R 上的偶函数,()f x ′为其导函数,()20240f =,当0x >时,有()()xf x f x ′>恒成立,则不等式()0xf x >的解集为__________.10.小张一次买了三电冰糖葫芦,其中一串有两颗冰糖葫芦,一串有三颗冰糖葫芦,一串有五颗冰糖葫芦.若小张每次随机从其中一串中吃一颗,每一电只能从上往下吃,那么不同的吃完的顺序有__________种.(结果用数字作答)11.为庆祝70周年校庆,学校开设A B C 、、三门校史课程培训,现有甲、乙、丙、丁、戊、已六位同学题名参加学习,每位同学仅报一门,每门课至少有一位同学报名,则不同报名方法有__________种.12.设点P 在曲线()Γ:ln 22x y x =+上,点Q 在直线:1l y x =−上,平面上一点M 满足13QM MP = ,则M 到坐标原点O 的距离的最小值为__________.二、题题题(本大题共有4题,第13、14题每题4分,第15、16题每题5分)每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑.13.抛一枚硬币的试验中,下列对“伯努利大数定律”的理解正确的是( )A.大量的试验中,出现正面的频率为0.5.B.不管试验多少次,出现正面的概率始终为0.5C.试验次数增大,出现正面的经验概率为0.5D.试验次数每增加一次,下一次出现正面的频率一定比它前一次更接近于0.514.某城市新修建的一条道路上有12个路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的4盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有( )A.47CB.48CC.49CD.48P15.抛一枚骰子,记事件A 表示事件“出现奇数点”,事件B 表示事件“出现4点或5点”,事件C 表示事件“点数不超过3”,事件D 表示事件“点数大于4”,有下列四个结论:①事件A 与B 是独立事件;②事件B 与C 是互斥事件;③事件C 与D 是对立事件;③D A B ⊆∩;其中正确的结论是( )A.①②B.②③C.③④D.①④16.对于函数()y f x =和()y g x =,及区间D ,若存在实数k b 、,使得()()f x kx b g x ≥+≥对任意x D ∈恒成立,则称()y f x =在区间D 上“优于”()y g x =.有以下两个结论:①()2log f x x =在区间[]1,2D =上优于()2(1)g x x =−; ②()32f x x =+在区间[]1,1D −上优于()e x g x =.那么( )A.①、②均正确B.①正确,②错误C.①错误,②正确D.①、②均错误三、解答题(本大题共有5题,满分78分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.17.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.如图,在直三棱柱111ABC A B C −中,D 是AC 的中点.(1)证明:1AB ∥平面1BC D .(2)若1,90,45AB BC ABC B AB ∠∠===,求二面角11B C D B −−的余弦值.18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.已知函数()()22ln f x a x x ax =−+−. (1)当3a =时,求函数()y f x =的单调区间;(2)若函数()y f x =在区间[]1,e 上恰有一个零点,求a 的取值范围.19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.某次数学考试中只有两道题目,甲同学答对每题的概率均为p ,乙同学答对每题的概率均为()q p q >,且每人各题答题结果互不影响.已知每题甲、乙同题答题的概率为12,恰有一人答对的概率为512. (1)求p 和q 的值; (2)设事件i A =“甲同学答对了i 道题”,事件i B =“乙同学答对了i 道题”,其中0,1,2i =,试求甲答对的题数比乙多的概率.20.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.设12,F F 分别为椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,P 是椭圆C 短轴的一个顶点,已知12PF F1213F PF ∠=.如图,,,M NG 是椭圆上不重合的三个点,原点O 是MNG 的重心.(1)求椭圆C 的方程;(2)求点M 到直线NG 的距离的最大值;(3)判断MNG 的面积是否为定值,并说明理由.21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.已知函数()e 2e x x f x a −=++.(1)若直线3y x =+是曲线()y f x =的切线,求实数a 的值;(2)若()21f x x x ≥−+对任意实数x 恒成立,求a 的取值范围; (3)若12e e 3x x +=,且()()()12123f x f x x x k ⋅≥++,求实数k 的最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海交通大学附属中学2010-2011学年度第二学期高二数学期末试卷(满分150分,120分钟完成。
答案一律写在答题纸上)命题:陈海兵 审核:杨逸峰一. 填空题(本大题满分56分)本大题共有14题,考生应在答题纸上相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1. 如果复数=z 421ii -+(其中i 为虚数单位),那么z Im (即z 的虚部)为__________。
2. 在二项式8)1(xx -的展开式中,含5x 的项的系数是 (用数字作答). 3. 顶点在原点,以x 轴为对称轴且经过点)3,2(-M 的抛物线的标准方程为____________. 4. 双曲线m y x =-222的一个焦点是)3,0(,则m 的值是__________.5. 已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程是y =,它的一个焦点与抛物线216y x =的焦点相同。
则双曲线的方程为 。
6.则总体标准差的点估计值为 (结果精确到0.01).7. 某展室有9个展台,现有3件不同的展品需要展出,要求每件展品独自占用1个展台,并且3件展品所选用的展台既不在两端又不相邻,则不同的展出方法有______种;8. 把4个不同的球任意投入4个不同的盒子内(每盒装球数不限),则无空盒的概率为________. 9. 若z C ∈且221z i +-=,则12z i --的最大值是_______.10. 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑。
已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,则每根铁筋的长度为________米.11. △ABC 的三个顶点A 、B 、C 到平面α的距离分别为2 cm 、3 cm 、4 cm ,且A,B,C 在平面α的同侧,则△ABC 的重心到平面α的距离为___________。
12. 过点(4,4)P 且与双曲线221169x y -=只有一个公共点的直线有 条。
13. △ABC 的三边长分别是3,4,5,P 为△ABC 所在平面外一点,它到三边的距离都是2,则P 到α的距离为_________.14. 如图,平面α⊥平面β,α∩β=l ,DAα,BC α,且DA ⊥l 于A ,BC ⊥l 于B ,AD=4,BC=8,AB=6,在平面β内不在l 上的动点P ,记PD 与平面β所成角为1θ,PC 与平面β所成角为2θ,若21θθ=,则△PAB 的面积的最大值是 。
二. 选择题(本大题满分20分)本大题共有4题,每题只有一个正确答案,选对得5分,答案代号必须填在答题纸上.注意试题题号与答题纸上相应编号一一对应,不能错位. 15. 下列四个命题: ①满足zz 1=的复数只有±1,±I; ②若a,b 是两个相等的实数,则(a -b)+(a +b)i 是纯虚数; ③|z+z |=2|z|;④复数z ∈R 的充要条件是z=z ;其中正确的有( )(A)0个 (B)1个 (C)2个 (D)3个 16. 平面αβ⊥,直线b α,m β,且b m ⊥,则b 与β( ) A.b β⊥ B.b 与β斜交 C.//b β D.位置关系不确定17. 在正方体1111D C B A ABCD -的侧面11A ABB 内有一动点P 到直线11B A 与直线BC 的距离相等,则动点P 所在的曲线的形状为 ( ) 18. 已知点(1,0),(1,0)A B -及抛物线22y x =,若抛物线上点P 满足PA m PB =,则m 的最大值为( )(A )3 (B )2 (C(D三、解答题19. (本题满分12分)第一题满分5分,第二题满分7分. 已知复数i z +=31,||2z =2,221z z ⨯是虚部为正数的纯虚数。
(1)求221z z ⨯的模;(2)求复数2z 。
A B 1BA(A)AB 1B(B)AB 1B(C)AB 1BA(D)20. (本题满分14分)第一题满分7分,第二题满分7分. 已知n n x x f )1()(+=,(1)若20112011012011()f x a a x a x =+++ ,求2011200931a a a a ++++ 的值; (2)若)(3)(2)()(876x f x f x f x g ++=,求)(x g 中含6x 项的系数;21. (本题满分14分)第一题满分4分,第二题满分4分,第三题满分6分.甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将4张扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张。
(1)设(,)i j分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示),写出甲乙二人抽到的牌的所有情况;(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;若甲抽到的牌的牌面数字不比乙大,则乙胜。
你认为此游戏是否公平,说明你的理由。
22. (本题满分16分)第一题满分4分,第二题满分6分,第三题满分6分. 已知动圆过定点P (1,0),且与定直线1:-=x l 相切。
(1)求动圆圆心的轨迹M 的方程;(2)设过点P ,且倾斜角为0120的直线与曲线M 相交于A ,B 两点,A ,B 在直线l 上的射影是11,A B 。
求梯形11AA B B 的面积;(3)若点C 是(2)中线段11A B 上的动点,当△ABC 为直角三角形时,求点C 的坐标。
23. (本题满分18分)第一题满分5分,第二题满分5分,第三题满分8分.如图,有一公共边但不共面的两个三角形ABC 和A 1BC 被一平面DEE 1D 1所截,若平面DEE 1D 1分别交AB,AC,A 1B,A 1C 于点D,E,D 1,E 1。
(1)讨论这三条交线ED,CB, E 1 D 1的关系。
(2)当BC//平面DEE 1D 1时,求EACEC E E A AD BD DB AD ⋅⋅⋅111111的值;(3)当BC 不平行平面DEE 1D 1时,EACEC E E A AD BD DB AD ⋅⋅⋅111111的值变化吗?为什么?上海交通大学附属中学2010-2011学年度第二学期高二数学期末试卷答案1、 3-2、 283、 x y 292-= 4、 -25、112422=-y x 6、 17.60 7、 608、 323 9、 4 10、 6.5 m 11、 3 12、 4 13、314、 12 (解析:)由条件可得:PB=2PA ,即P 到B 的距离为到A 的距离的2倍在平面β内以AB 为x 轴,AB 的中垂线为y 轴,建立平面直角坐标系设P (x ,y )则22)3(2y x ++=22)3(y x +-∴()22964y x x +++=2296y x x ++- ∴223303y x x +++27=0 ∴91022-=++y x x ∴22)5(y x ++=16∴平面β内P 点轨迹为以(5-,0)为圆心,4为半径的圆(与x 轴的交点除外) ∴高的最大值为4, ∴面积的最大值为246⨯=12 15、B 16、D 17、B 18、C19、解:(1)|221z z ⨯|=|1z ||22z |=|1z ||2z |2=8;(2)221z z ⨯是虚部为正数的纯虚数∴221z z ⨯=i 822z =ii+38=()438ii -=i 322+ 设复数2z =bi a +(R b a ∈,)=+-abi b a 222i 322+⎪⎩⎪⎨⎧==-322222ab b a 解之得⎩⎨⎧==13b a 或⎩⎨⎧-=-=13b a ∴)3(2i z +±=20、解:(1)因为n n x x f )1()(+=,所以20112011()(1)f x x =+,又20112011012011()f x a a x a x =+++ ,所以20112011012011(1)2f a a a =+++= (1)20110120102011(1)0f a a a a -=-++-= (2)(1)-(2)得:201113200920112()2a a a a ++++= 所以:201013200920112011(1)2a a a a f ++++== (2)因为)(3)(2)()(876x f x f x f x g ++=,所以678()(1)2(1)3(1)g x x x x =+++++)(x g 中含6x 项的系数为667812399C C +⨯+=21、 解:(1)甲乙二人抽到的牌的所有情况(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示)为: (2,3)、(2,4)、(2,4’)、(3,2)、(3,4)、(3,4’)、 (4,2)、(4,3)、(4,4’)、(4’, 2)、(4’,3)(4’,4) 共12种不同情况(没有写全面时:只写出1个不给分,2—4个给1分,5—8个给2分,9—11个给3分) (2)甲抽到3,乙抽到的牌只能是2,4,4’ 因此乙抽到的牌的数字大于3的概率为23(3)由甲抽到的牌比乙大的有(3,2)、(4,2)、(4,3)、(4’,2)、(4’,3)5种,甲胜的概率1512p =,乙获胜的概率为2757,121212p =< ∴此游戏不公平。
22、解: (1)曲线M 是以点P 为焦点,直线l 为准线的抛物线,其方程为x y 42=.(2)由题意得,直线AB的方程为21)1),4y x y x y x⎧=-⎪=-⎨=⎪⎩由 消y 得 .3,31,03103212===+-x x x x 解出于是, A 点和B 点的坐标分别为A )332,31(,B (3,32-),所以11||A B ==111216||||2.3AA BB x x +=++=11111(||||)||2S AA BB A B =+=(3)设C (-1,y )使△ABC 成直角三角形, 2222334928)332()311(||y y y AC +-=-+--=,22223428)32()13(||y y y BC ++=+++=,9256)316(||22==AB .(i) 当090A ∠=时,方法一:当222||||||BC AC AB =+时,22282562899y y y ++=++,即,y CAB =∠为直角. C 点的坐标是(1,-方法二:当090A ∠=时,得直线AC 的方程为1)3y x -,求得C 点的坐标是(1,-。
