2007年各地中考压轴题汇编(3)
2007年全国各地中考数学试题压轴题精选全解五

2007年全国各地中考试题压轴题精选全解之五82.(四川省德阳市)25.如图,已知与x 轴交于点(10)A ,和(50)B ,的抛物线1l 的顶点为(34)C ,,抛物线2l 与1l 关于x 轴对称,顶点为C '.(1)求抛物线2l 的函数关系式;(2)已知原点O ,定点(04)D ,,2l 上的点P 与1l 上的点P '始终关于x 轴对称,则当点P 运4OD = ,22654m m ∴-+=,即2652m m -+=±.当2652m m -+=时,解得3m = 当2652m m -+=-时,解得3m =.∴当点P 运动到(3或(3或(32)-或(32)-时,P P OD '∥,以点D O P P ',,,为顶点的四边形是平行四边形.(3)满足条件的点M 不存在.理由如下:若存在满足条件的点M 在2l 上,则90AMB ∠= ,30BAM ∠= (或30ABM ∠= ), 114222BM AB ∴==⨯=. 过点M 作ME AB ⊥于点E ,可得30BME BAM ∠=∠=.1121EB BM ∴==⨯=,EM =,4OE =.点,经过A 、B 、C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴交于D ,抛物线的顶点为E . (1)求m 的值及抛物线的解析式;(2)设∠DBC = α,∠CBE = β,求sin (α-β)的值;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCE 相似?若存在,请指出点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.x解:(1)由题意可知C (0,-3),12=-ab, ∴ 抛物线的解析式为y = ax 2-2ax -3(a >0), 过M 作MN ⊥y 轴于N ,连结CM ,则MN = 1,5=CM ,∴ CN = 2,于是m =-1.、C84.(南充市)25.如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线216y x bx c =++过点A 和B ,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象. (2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.3∵Q (8,m )抛物线上,∴m =2.过点Q 作QK ⊥x 轴于点K ,则K (8,0),QK =2,AK =6, ∴AQ =又∵B (6,0)与A (2,0)关于对称轴l 对称, ∴PQ +PB 的最小值=AQ =.行于x 轴,B C D ,,三点在抛物线2425y x =上,DC 交y 轴于N 点,一条直线OE 与AB 交于E 点,与DC 交于F 点,如果E 点的横坐标为a ,四边形ADFE 的面积为1352.(1)求出B D ,两点的坐标; (2)求a 的值;(3)作ADN △的内切圆P ,切点分别为M K H ,,,求tan PFM ∠的值.设⊙P 的半径为r ,则12521)13125(21⨯⨯=++=∆r S AND ,r =2 在正方形PMNK 中,PM =MN =2∴413452=+=+=NF MN MF 在Rt △PMF 中,tan ∠PMF =1384132==MF PM图(13)A m 又∵ 抛物线P 过(2,0)、(-2,-4),则由抛物线的对称性可知, 点A 、B 、C 的坐标分别为 A(2,0),B(-4,0),C(0,-4) . (2)由题意,AD DGAO OC=,而AO=2,OC=4,AD=2-m ,故DG=4-2m , ···· 又BE EFBO OC=,EF=DG ,得BE=4-2m ,∴ DE=3m , ∴SDEFG=DG·DE=(4-2m) 3m=12m-6m 2(0<m <2) .注:也可通过解Rt△BOC 及Rt △AOC ,或依据△BOC 是等腰直角三角形建立关系求解. (3)∵SDEFG=12m-6m 2(0<m <2),∴m=1时,矩形的面积最大,且最大面积是6 . 当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0), 设直线DF 的解析式为y=kx+b ,易知,k=23,b=-23,∴2233y x =-, 又可求得抛物线P 的解析式为:2142y x x =+-,61b 三角形MND (D 为抛物线的顶点)是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.解:(1)证明:∵抛物线y =x 2-2ax +b 2经过点(0)M a c +,∴22()2()0a c a a c b +-++= ∴22222220a ac c a ac b ++--+=∴222b c a +=由勾股定理的逆定理得: ABC △为直角三角形(2)解:①如图所示; ∵3MNP NOP S S =△△∴3MN ON = 即4MO ON =∴2c c = 又c >0,∴c =1由于c =53a b =54a ∴a =35b =34∴当a =35,b =34,c =1时,MNP △为等腰直角三角形。
2007年全国各地中考试题压轴题精选全解之二

25.(杭州市)24.在直角梯形 中, ,高 (如图1)。动点 同时从点 出发,点 沿 运动到点 停止,点 沿 运动到点 停止,两点运动时的速度都是 。而当点 到达点 时,点 正好到达点 。设 同时从点 出发,经过的时间为 时, 的面积为 (如图2)。分别以 为横、纵坐标建立直角坐标系,已知点 在 边上从 到 运动时, 与 的函数图象是图3中的线段 。
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点.
(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明).
解:(1)∵ ,
设正方形的边长为 ,
∴ , 或 (舍去).
(2) .
.
(3)①当0≤ <4时,重叠部分为三角形,如图①.
可得△ ∽△ ,
∴ , = .
∴ .
②当4≤ <6时,重叠部分为直角梯形,如图②.
.
③当6≤ <8时,重叠部分为五边形,如图③.
可得, , .
= .
④当8≤ <10时,重叠部分为五边形,如图④.
(3)分两种情况讨论:
①当
②当
综上所述,当x为2.5秒或3.1秒时, 为直角三角形。
28.(金华市)如图1,在平面直角坐标系中,已知点 ,点 在 正半轴上,且 .动点 在线段 上从点 向点 以每秒 个单位的速度运动,设运动时间为 秒.在 轴上取两点 作等边 .
(1)求直线 的解析式;
(2)求等边 的边长(用 的代数式表示),并求出当等边 的顶点 运动到与原点 重合时 的值;
2007年全国100多个地区中考数学试题分类汇编 点、线、相交、平行
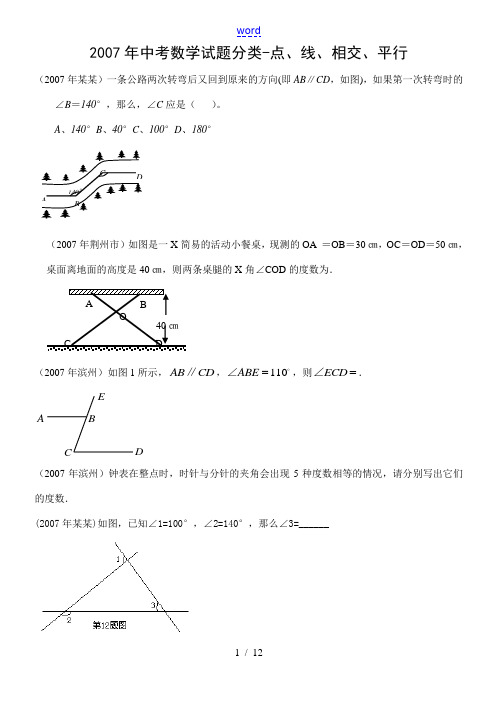
2007年中考数学试题分类-点、线、相交、平行(2007年某某)一条公路两次转弯后又回到原来的方向(即AB ∥CD ,如图),如果第一次转弯时的∠B =140°,那么,∠C 应是( )。
A 、140°B 、40°C 、100°D 、180°(2007年荆州市)如图是一X 简易的活动小餐桌,现测的OA =OB =30㎝,OC =OD =50㎝,桌面离地面的高度是40㎝,则两条桌腿的X 角∠COD 的度数为.(2007年滨州)如图1所示,AB CD ∥,110ABE =∠,则ECD =∠.(2007年滨州)钟表在整点时,时针与分针的夹角会出现5种度数相等的情况,请分别写出它们的度数.(2007年某某)如图,已知∠1=100°,∠2=140°,那么∠3=______ABCD EODCBA40㎝ ABCD140°(2007年某某市)如图所示,直线a b ∥,112330'=∠,则2=∠.(2007年某某市)如图2,直线a b ∥,则A ∠的度数是( ) A.28B.31C.39D.42(2007年某某市)如图,AB CD ∥,40A ∠=,45D ∠=,则1∠=.(2007年某某市)如图12,平面内有公共端点的六条射线OA ,OB ,OC ,OD ,OE ,OF ,从射线OA 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…. (1)“17”在射线上.(3分)(2)请任意写出三条射线上数字的排列规律.(3分) (3)“2007”在哪条射线上?(3分)ABCDab70°31°abc12.(2007年某某省)图10-1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm ).将它们拼成如图10-2的新几何体,则该新几何体的体积为cm 3.(计算结果保留 )(2007年某某省)用M ,N ,P ,Q 各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.图6-1—图6-4是由M ,N ,P ,Q 中的两种图形组合而成的(组合用“&”表示).那么,下列组合图形中,表示P&Q 的是( )(2007年某某省)如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )图10-2图10-1M&PN&PN&QM&Q图6-1图6-2图6-3图6-4A .B .C .D .A .50°B .60°C .140°D .160°(2007年某某市)如图,已知a b ∥,170∠=,则2∠=.(2007年某某市)如图1,直线c 截二平行直线a 、b ,则下列式子中一定成立的是 ( ) A .∠1=∠5 B . ∠1=∠4 C . ∠1=∠3 D . ∠1=∠2(2007年某某市)如图,能判定EB ∥AC 的条件是( )。
2007年全国各地中考数学试题压轴题精选全解之四

2007年全国各地中考试题压轴题精选全解之四63.(某某市)26. 如图,ABCD 中,4AB =,3BC =,120BAD =∠,E 为BC 上一动点(不与B 重合),作EF AB ⊥于F ,FE ,DC 的延长线交于点G ,设BE x =,DEF △的面积为S .(1)求证:BEF CEG △∽△;(2)求用x 表示S 的函数表达式,并写出x 的取值X 围; (3)当E 运动到何处时,S 有最大值,最大值为多少? 解: (1)证明略;(2)由(1)DG 为DEF △中EF 边上的高,在Rt BFE △中,60B =∠,sin EF BE B x ==, 在Rt CEG △中,3CE x =-,3(3)cos602xCG x -=-=, 112xDG DC CG -∴=+=,213288S EF DG x x ∴==-+, 其中03x <≤. (3)308a =-<,对称轴112x =,∴当03x <≤时,S 随x 的增大而增大,∴当3x =,即E 与C 重合时,S 有最大值.S =最大64.(某某省某某) 27.如图,矩形ABCD 中,AB =3,BC =4,将矩形ABCD 沿对角线AC 平移,平移后的矩形为EFGH (A 、E 、C 、G 始终在同一条直线上),当点E 与C 重合时停止移动.平移中EF 与BC 交于点N ,GH 与BC 的延长线交于点M ,EH 与DC 交于点P ,FG 与DC 的延长线交于点Q .设S 表示矩形PCMH 的面积,S '表示矩形NFQC 的面积. (1) S 与S '相等吗?请说明理由.(2)设AE =x ,写出S 和x 之间的函数关系式,并求出x 取何值时S 有最大值,最大值AC B DEF G是多少?(3)如图11,连结BE ,当AE 为何值时,ABE ∆是等腰三角形.解: (1)相等理由是:因为四边形ABCD 、EFGH 是矩形, 所以,,EGH EGF ECN ECP CGQ CGM S S S S S S ∆∆∆∆∆∆===所以,EGH ECP CGM EGF ECN CGQ S S S S S S ∆∆∆∆∆∆--=-- 即:S S '=(2)AB =3,BC =4,AC =5,设AE =x ,则EC =5-x ,34(5),,55PC x MC x =-=所以12(5)25S PC MC x x ==-,即21212(05)255S x x x =-+≤≤ 配方得:2125()3252S x =--+,所以当52x =时, S 有最大值3(3)当AE =AB =3或AE =BE =52或AE =3.6时,ABE ∆是等腰三角形65.(某某省某某市)28. 两个直角边为6的全等的等腰直角三角形Rt AOB △和Rt CED △按图1所示的位置放置A 与C 重合,O 与E 重合. (1)求图1中,A B D ,,三点的坐标.(2)Rt AOB △固定不动,Rt CED △沿x 轴以每秒2个单位长的速度向右运动,当D 点运动到与B 点重合时停止,设运动x 秒后Rt CED △和Rt AOB △重叠部分面积为y ,求y 与x 之间的函数关系式.(3)当Rt CED △以(2)中的速度和方向运动,运动时间4x =秒时Rt CED △运动到如图2所示的位置,求经过A G C ,,三点的抛物线的解析式. (4)现有一半径为2,圆心P 在(3)中的抛物线上运动的动圆,试问P 在运动过程中是xN MQ PHGFEDCBA图11QPNM HGF ED CB A 图10否存在P 与x 轴或y 轴相切的情况,若存在请求出P 的坐标,若不存在请说明理由.解:(1)(06)A ,,(60)B ,,(60)D -, (2)当03x <≤时,位置如图A所示,作GH DB ⊥,垂足为H ,可知:2OE x =,EH x =,62DO x =-,6DH x =-,22()GHD IOD IOHG y S S S ∴==-△△梯形22112(6)(62)22x x ⎡⎤=---⎢⎥⎣⎦223263122x x x x ⎛⎫=-+=-+ ⎪⎝⎭当36x ≤≤时,位置如图B所示. 可知:122DB x =-212DGBy S DB ⎫∴==⎪⎪⎝⎭△2212)12362x x x ⎤=-=-+⎥⎣⎦(求梯形IOHG 的面积及DGB △的面积时只要所用方法适当,所得结论正确均可给分)y ∴与x 的函数关系式为:22312(03)1236(36)x x x y x x x ⎧-+<⎪=⎨-+⎪⎩≤≤≤ (3)图2中,作GH OE ⊥,垂足为H ,当4x =时,28OE x ==,1224DB x =-=122GH DH DB ∴===,1666242OH HB DB =-=-=-=图B∴可知:(06)A ,,(42)G ,,(86)C ,∴经过A G C ,,三点的抛物线的解析式为:221(4)22644x y x x =-+=-+ (4)当P 在运动过程中,存在P 与坐标轴相切的情况,设P 点坐标为00()x y ,当P 与y 轴相切时,有02x =,02x =±,由02x =-得:011y =,1(211)P ∴-,由02x =,得03y =,2(23)P ∴,当P 与x 轴相切时,有02y = 21(4)204y x =-+>02y ∴=,得:04x =,3(42)P ∴,综上所述,符合条件的圆心P 有三个,其坐标分别是:1(211)P -,,2(23)P ,,3(42)P ,66.(某某省永州市) 25、在梯形ABCD 中,AB CD ∥,90ABC ∠=°,5AB =,10BC =,tan 2ADC ∠=.(1)求DC 的长;(2)E 为梯形内一点,F 为梯形外一点,若BF DE =,FBC CDE ∠=∠,试判断ECF △的形状,并说明理由.(3)在(2)的条件下,若BE EC ⊥,:4:3BE EC =,求DE 的长.解(1)过A 点作AG DC ⊥,垂足为G90AB CD BCD ABC ∴∠=∠=∥, ∴四边形ABCG 为矩形510CG AB AG BC ∴====,tan 2AGADG DG∠==510DG DC DG CG ∴=∴=+=,(2)DE BF FBC CDE BC DC =∠=∠=,,DEC BFC ∴△≌△EC CF ECD FCB ∴=∠=∠,9090BCE ECD ECF ∠+∠=∠=,ECF ∴△是等腰直角三角形(3)过F 点作FH BE ⊥BE EC CF CE CE CF =⊥,⊥,∴四边形ECFH 是正方形,6FH EC ∴==:4:390BE EC BEC =∠=, 222BC BE EC ∴=+68ECBE ∴==,2BH BE EH ∴=-=DE BF ∴===67.(某某省某某市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
2007年全国各地中考数学试题压轴题精选全解之二

2007年全国各地中考试题压轴题精选全解之二25.(某某市)24. 在直角梯形ABCD 中,90C ∠=︒,高6CD cm =(如图1)。
动点,P Q 同时从点B 出发,点P 沿,,BA AD DC 运动到点C 停止,点Q 沿BC 运动到点C 停止,两点运动时的速度都是1/cm s 。
而当点P 到达点A 时,点Q 正好到达点C 。
设,P Q 同时从点B 出发,经过的时间为()t s 时,BPQ ∆的面积为()2y cm (如图2)。
分别以,t y 为横、纵坐标建立直角坐标系,已知点P 在AD 边上从A 到D 运动时,y 与t 的函数图象是图3中的线段MN 。
(1)分别求出梯形中,BA AD 的长度; (2)写出图3中,M N 两点的坐标;(3)分别写出点P 在BA 边上和DC 边上运动时,y 与t 的函数关系式(注明自变量的取值X 围),并在图3中补全整个运动中y 关于t 的函数关系的大致图象。
解: (1)设动点出发t 秒后,点P 到达点A 且点Q 正好到达点C 时,BC BA t ==,则1630,102BPQ S t t ∆=⨯⨯=∴=(秒)则()()10,2BA cm AD cm ==; (2)可得坐标为()()10,30,12,30M N (3)当点P 在BA 上时,()213sin 010210y t t B t t =⨯⨯⨯=≤<; 当点P 在DC 上时,()()1101859012182y t t t =⨯⨯-=-+<≤ 图象略(图1)(图2)26.(某某市)27.四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.(1)如图2,画出菱形ABCD的一个准等距点.(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP 交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点.(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明).解:(1)如图2,点P即为所画点.(答案不唯一,但点P不能画在AC中点)。
2007年广东省中考数学压轴题全解全析

2007年广东省中考数学压轴题全解全析2008年中考在即,备受广大师生关注的中考数学中的压轴题,因为这些试题有较强的选拔性,往往在很大的程度上决定了考试的成败,为帮助大家迎接今年的中考,特对2007年广东省各市中考数学压轴题加以整理,希望对大家有所帮助。
1.(深圳) 如图7,在平面直角坐标系中,抛物线2164y x =-与直线12y x =相交于A B ,两点.(1)求线段A B 的长.(2)若一个扇形的周长等于(1)中线段A B 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少? (3)如图8,线段A B 的垂直平分线分别交x 轴、y 轴于C D ,两点,垂足为点M ,分别求出O M O C O D ,,的长,并验证等式222111+=是否成立.(4)如图9,在R t AB C △中,90A C B=∠,C D A B ⊥,垂足为D ,设B C a =,A C b =,A B c =.C D b =,试说明:222111abh+=.解(1) ∴A (-4,-2),B (6,3)分别过A 、B 两点作x AE ⊥轴,y BF ⊥轴,垂足分别为E 、F∴AB =OA+OB 22223624+++=55=(2)设扇形的半径为x ,则弧长为)255(x -,扇形的面积为y则)255(21x x y -=x x5252+-=16125)455(2+--=x∵01<-=a ∴当455=x 时,函数有最大值16125=最大y(3)过点A 作AE ⊥x 轴,垂足为点E ∵CD 垂直平分AB ,点M 为垂足∴255225521=-=-=OA AB OM ∵COM EOA OMC AEO ∠=∠∠=∠,图7 图8图9D∴△AEO ∽△CMO ∴COAO OMOE =∴CO52254=∴45415225=⋅⋅=CO同理可得 25=OD∴542520)52()54(112222==+=+OD OC∴5412=OM∴222111OMODOC=+(4)等式222111hba=+成立.理由如下:∵AB CD ACB⊥=∠,90∴2222121b aABh AB ab +=⋅=∴h c ab ⋅=∴ 2222h cba ⋅= ∴22222)(h b aba += ∴22222222222)(hb a hb a hb a ba +=∴222221ba bah+=∴222111bah+=∴222111hba=+2. (梅州 11分)如图12,直角梯形A B C D 中,90643A B C D A A B A D D C ∠====∥,°,,,,动点P 从点A 出发,沿A D C B →→→方向移动,动点Q 从点A 出发,在A B 边上移动.设点P 移动的路程为x ,点Q 移动的路程为y ,线段P Q 平分梯形A B C D 的周长. (1)求y 与x 的函数关系式,并求出x y ,的取值范围; (2)当P Q A C ∥时,求x y ,的值;(3)当P 不在B C 边上时,线段P Q 能否平分梯形A B C D 的 面积?若能,求出此时x 的值;若不能,说明理由.解:(1)过C 作C E A B ⊥于E ,则34C D A E C E ===,,可得5B C =,所以梯形A B C D 的周长为18. ····················································································· 1分 P Q 平分A B C D 的周长,所以9x y +=, ··································································· 2分 因为06y ≤≤,所以39x ≤≤, 所求关系式为:939y x x =-+,≤≤. ················ 3分(2)依题意,P 只能在B C 边上,79x ≤≤. 126P B x B Q y =-=-,,因为P Q A C ∥,所以B P Q B C A △∽△,所以B P B Q B CB A=,得 ······································ 4分12656x y --=,即6542x y -=, 解方程组96542x y x y +=⎧⎨-=⎩, 得87121111x y ==,. ······ 6分 ABCD P Q图12(3)梯形A B C D 的面积为18. ························································································ 7分 当P 不在B C 边上,则37x ≤≤(a )当34x <≤时,P 在A D 边上,12A P Q S x y =△.如果线段P Q 能平分梯形A B C D 的面积,则有192x y =······················································· 8分 可得:918.x y x y +=⎧⎨=⎩,解得36x y =⎧⎨=⎩,;(63x y ==,舍去). ····················································· 9分(b )当47x ≤≤时,点P 在D C 边上,此时14(4)2A D P Q S x y =⨯-+.如果线段P Q 能平分梯形A B C D 的面积,则有14(4)92x y ⨯-+=,可得92217.x y x y +=⎧⎨+=⎩,此方程组无解. 所以当3x =时,线段P Q 能平分梯形A B C D 的面积.11分3. (韶关 9分)如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
2007年全国各地中考数学试题压轴题精选全解之三

2007年全国各地中考试题压轴题精选全解之三45.(某某省某某市)24. 已知:如图,在平面直角坐标系中,ABC △是直角三角形,90ACB ∠=,点A C ,的坐标分别为(30)A -,,(10)C ,,3tan 4BAC ∠=. (1)求过点A B ,的直线的函数表达式;(2)在x 轴上找一点D ,连接DB ,使得ADB △与ABC △相似(不包括全等),并求点D 的坐标;(3)在(2)的条件下,如P Q ,分别是AB 和AD 上的动点,连接PQ ,设AP DQ m ==,问是否存在这样的m 使得APQ △与ADB △相似,如存在,请求出m 的值;如不存在,请说明理由.解:(1)点(30)A -,,(10)C ,4AC ∴=,3tan 434BC BAC AC =⨯=⨯=∠,B 点坐标为(13),设过点A B ,的直线的函数表达式为y kx b =+,由0(3)3k b k b=⨯-+⎧⎨=+⎩ 得34k =,94b =∴直线AB 的函数表达式为3944y x =+ (2)如图1,过点B 作BD AB ⊥,交x 轴于点D , 在Rt ABC △和Rt ADB △中,BAC DAB =∠∠Rt Rt ABC ADB ∴△∽△,D ∴点为所求又4tan tan 3ADB ABC ==∠∠, 49tan 334CD BC ADB ∴=÷=÷=∠第24题图第24题图1134OD OC CD ∴=+=,1304D ⎛⎫∴ ⎪⎝⎭,(3)这样的m 存在在Rt ABC △中,由勾股定理得5AB = 如图1,当PQ BD ∥时,APQ ABD △∽△则133413534mm+-=+,解得259m =如图2,当PQ AD ⊥时,APQ ADB △∽△则133413534mm+-=+,解得12536m =46.(某某市)24. 已知:如图,△ABC 是边长3cm 的等边三角形,动点 P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 方向匀速移 动,它们的速度都是1cm/s ,当点P 到达点B 时,P 、Q 两 点停止运动.设点P 的运动时间为t (s ),解答下列问题:(1)当t 为何值时,△PBQ 是直角三角形?(2)设四边形APQC 的面积为y (cm 2),求y 与t 的关系式;是否存在某一时刻t ,使四边形APQC 的面积是△ABC 面积的三分之二?如果存在,求出相应的t 值;不存在,说明理由;(3)设PQ 的长为x (cm ),试确定y 与x 之间的关系式. 解:⑴根据题意:AP =tcm ,BQ =tcm . △ABC 中,AB =BC =3cm ,∠B=60°, ∴BP=(3-t)cm .△PBQ 中,BP =3-t ,BQ =t ,若△PBQ 是直角三角形,则∠BQP=90°或∠BPQ=90°. 当∠BQP=90°时,BQ =12BP .第24题图2A P即t =12(3-t),t =1(秒).当∠BPQ=90°时,BP =12BQ .3-t =12t ,t =2(秒).答:当t =1秒或t =2秒时,△PBQ 是直角三角形.⑵过P 作PM⊥BC 于M . Rt△BPM 中,sin∠B=PM PB,∴PM=PB·sin∠B=2(3-t).∴S △PBQ =12BQ·PM=12· t ·2(3-t).∴y=S △ABC -S △PBQ=12×322-122(3-t)2444.∴y 与t 的关系式为: y 2444-+.假设存在某一时刻t ,使得四边形APQC 的面积是△ABC 面积的23, 则S 四边形APQC =23S △AB C .2444=23×12×322.∴t 2-3 t +3=0. ∵(-3) 2-4×1×3<0 ∴方程无解.∴无论t 取何值,四边形APQC 的面积都不可能是△ABC 面积的23.⑶在Rt△PQM 中, MQ =BM BQ -=()312t -.MQ 2+PM 2=PQ 2.∴x 2=[32(1-t)]2+2(3-t)]2=()()2293219644t t t t -++-+ =()23412124t t -+=3t 2-9t +9.∴t 2-3t =()2193x -.2444+,)234t t -()21943x -+212x .∴y 与x 的关系式为:y 212x .47.(某某省某某市) 29.如图①,Rt ABC △中,90B ∠=,30CAB ∠=.它的顶点A 的坐标为(100),,顶点B 的坐标为(5,10AB =,点P 从点A 出发,沿A B C →→的方向匀速运动,同时点Q 从点(02)D ,出发,沿y 轴正方向以相同速度运动,当点P 到达点C 时,两点同时停止运动,设运动的时间为t 秒.(1)求BAO ∠的度数.(2)当点P 在AB 上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分,(如图②),求点P 的运动速度.(3)求(2)中面积S 与时间t 之间的函数关系式及面积S 取最大值时点P 的坐标. (4)如果点P Q ,保持(2)中的速度不变,那么点P 沿AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小,当点P 沿这两边运动时,使90OPQ ∠=的点P 有几个?请说明理由.解: (1)60BAO =∠.(2)点P 的运动速度为2个单位/秒. (3)(10)P t -(05t ≤≤)1(22)(10)2S t t =+-2912124t ⎛⎫=--+ ⎪⎝⎭. ∴当92t =时,S有最大值为1214, 此时112P ⎛ ⎝⎭.(4)当点P 沿这两边运动时,90OPQ =∠的点P 有2个. ①当点P 与点A 重合时,90OPQ <∠,当点P 运动到与点B 重合时,OQ 的长是12单位长度, 作90OPM =∠交y 轴于点M ,作PH y ⊥轴于点H ,由OPH OPM △∽△得:11.53OM ==, 所以OQ OM >,从而90OPQ >∠.所以当点P 在AB 边上运动时,90OPQ =∠的点P 有1个.(第29题图①)Ax t (第29题图②)②同理当点P 在BC 边上运动时,可算得1217.83OQ =+=.而构成直角时交y 轴于03⎛⎫ ⎪ ⎪⎝⎭,,20.217.83=>, 所以90OCQ <∠,从而90OPQ =∠的点P 也有1个. 所以当点P 沿这两边运动时,90OPQ =∠的点P 有2个.48.(某某省东营市)24. 根据以下10个乘积,回答问题:11×29; 12×28; 13×27; 14×26; 15×25; 16×24; 17×23; 18×22; 19×21; 20×20.(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;(2)将以上10个乘积按照从小到大的顺序排列起来; (3)试由⑴、⑵猜测一个一般性的结论.(不要求证明) 解:⑴11×29=202-92;12×28=202-82;13×27=202-72;14×26=202-62;15×25=202-52;16×24=202-42; 17×23=202-32;18×22=202-22;19×21=202-12; 20×20=202-02.例如,11×29;假设11×29=□2-○2, 因为□2-○2=(□+○)(□-○); 所以,可以令□-○=11,□+○=29. 解得,□=20,○=9.故229202911-=⨯. (或11×29=(20-9)(20+9)=202-92. ⑵ 这10个乘积按照从小到大的顺序依次是:1129122813271426⨯<⨯<⨯<⨯<152516241723⨯<⨯<⨯<182219212020⨯<⨯<⨯.⑶ ① 若40=+b a ,a ,b 是自然数,则ab ≤202=400. ② 若a +b =40,则ab ≤202=400.③ 若a +b =m ,a ,b 是自然数,则ab ≤22m ⎛⎫⎪⎝⎭.④ 若a +b =m ,则ab ≤22m ⎛⎫⎪⎝⎭.⑤ 若a 1+b 1=a 2+b 2=a 3+b 3=…=a n +b n =40.且 | a 1-b 1|≥|a 2-b 2|≥|a 3-b 3|≥…≥| a n -b n |, 则 a 1b 1≤a 2b 2≤a 3b 3≤…≤ a n b n .⑥若a 1+b 1=a 2+b 2=a 3+b 3=…=a n +b n =m .且 | a 1-b 1|≥|a 2-b 2|≥|a 3-b 3|≥…≥| a n -b n |, 则a 1b 1≤a 2b 2≤a 3b 3≤…≤ a n b n .49.(某某枣庄)25. 已知:如图,在△ABC 中,D 为A 月边上一点,∠A =36°,AC =BC ,AC 2=AB ·AD . (1)试说明:△ADC 和△BDC 都是等腰三角形, (2)若AB =1,求AC 的长,(3)试构造一个等腰梯形,要求该梯形连同它的两条对角线所形成的8个三角形中有尽可能多的等腰三角形.解:(1)在△ABC 中,AC =BC ,∠A =36°,∴∠B =∠A =36°,∠ACB =108°在△ABC 与△CAD 中,∠A =∠B =36°. ∵AC 2=AB ·AD ,∴AC AD ADAB AC BC==. ∴△ABC ∽△CAD . ∴∠ACD =∠B =36°.∴∠CDB =72°,∠DCB =108°-36°=72°. ∴△ADC 和△BDC 都是等腰三角形. (2)设AC =x ,则AD =1-BD =1-BC =1-2x ∴x 2=1×(1-x ),即x 2+x -1=0.解得121515,22x x -+--== (舍去).∴512AC -=(3)说明:按照画出的梯形中,有4个,6个和8个等腰三角形三种情况分类得分. ①有4个等腰三角形,得1分; ②有6个等腰三角形,得2分; ③有8个等腰三角形,得4分.50.(某某省滨州市)26. 如图12-1所示,在ABC △中,2AB AC ==,90A =∠,O 为BC 的中点,动点E 在BA 边上自由移动,动点F 在AC 边上自由移动.(1)点E F ,的移动过程中,OEF △是否能成为45EOF =∠的等腰三角形?若能,请指出OEF △为等腰三角形时动点E F ,的位置.若不能,请说明理由.(2)当45EOF =∠时,设BE x =,CF y =,求y 与x 之间的函数解析式,写出x 的取值X 围.(3)在满足(2)中的条件时,若以O 为圆心的圆与AB 相切(如图12-2),试探究直线EF 与O 的位置关系,并证明你的结论.图12-1AEF 图12-2A BOEF解:如图,(1)点E F ,移动的过程中,OEF △能成为45EOF ∠=°的等腰三角形. 此时点E F ,的位置分别是: ①E 是BA 的中点,F 与A 重合.②BE CF ==E 与A 重合,F 是AC 的中点(2)在OEB △和FOC △中,135EOB FOC ∠+∠=°,135EOB OEB ∠+∠=°,FOC OEB ∠=∠∴.又B C ∠=∠∵,OEB FOC ∴△∽△. BE BOCO CF=∴. BE x =∵,CF y =,OB OC === 2(12)y x x=∴≤≤. (3)EF 与O 相切.OEB FOC ∵△∽△,BE OECO OF =∴. BE OEBO OF =∴. 即BE BO OE OF =. 又45B EOF ∠=∠=∵°,A EFOCB AEFOC B(图12-1)(图12-2)BEO OEF ∴△∽△. BEO OEF ∠=∠∴.∴点O 到AB 和EF 的距离相等. AB ∵与O 相切,∴点O 到EF 的距离等于O 的半径. EF ∴与O 相切.51.(日照市)24. 如图,直线EF 将矩形纸片ABCD 分成面积相等的两部分,E 、F 分别与BC 交于点E ,与AD 交于点F (E ,F 不与顶点重合),设AB=a,AD=b,BE=x .(Ⅰ)求证:AF=EC ;(Ⅱ)用剪刀将纸片沿直线EF 剪开后,再将纸片ABEF 沿AB 对称翻折,然后平移拼接在梯形ECDF 的下方,使一底边重合,直腰落在边DC 的延长线上,拼接后,下方的梯形记作EE′B′C .(1)求出直线EE ′分别经过原矩形的顶点A 和顶点D 时,所对应的 x ︰b 的值;(2)在直线EE ′经过原矩形的一个顶点的情形下,连接B E′,直线BE ′与EF 是否平行?你若认为平行,请给予证明;你若认为不平行,请你说明当a 与b 满足什么关系时,它们垂直? 解: (Ⅰ)证明:∵AB=a ,AD=b ,BE=x ,S 梯形ABEF =S 梯形CDFE . ∴21a (x +AF )=21a (EC +b -AF ), ∴2AF =EC +(b -x ). 又∵EC =b -x , ∴2AF =2EC ,即AF=EC ;(Ⅱ)(1)当直线EE′经过原矩形的顶点D 时,如图(一), ∵EC ∥E ′B ′, ∴B E EC ''=BD DC'.由EC =b -x ,E ′B ′=EB =x ,DB ′=DC +CB ′=2a , 得aax x b 2=-, ∴x ︰b =32;当直线E′E 经过原矩形的顶点A 时,如图(二), 在梯形AE ′B ′D 中,∵EC ∥E ′B ′,点C 是DB ′的中点,∴CE =21(AD + E ′B ′), 即b -x =21(b +x ),∴x ︰b =31.(2) 如图(一), 当直线EE′ 经过原矩形的顶点D 时,BE ′∥EF . 证明:连接BF . ∵FD ∥BE , FD =BE ,∴四边形FBED 是平行四边形,∴FB ∥DE , FB =DE ,又∵EC ∥E ′B ′, 点C 是DB ′的中点, ∴DE =EE ′,∴FB ∥EE ′, FB = EE ′, ∴四边形BE ′EF 是平行四边形 ∴BE ′∥EF .如图(二), 当直线EE′ 经过原矩形的顶点A 时,显然BE ′与EF 不平行,设直线EF 与BE ′交于点G .过点E ′作E ′M ⊥BC 于M , 则E ′M =a ..∵x ︰b =31, ∴EM =31BC =31b .若BE′与EF 垂直,则有∠GBE +∠BEG =90°,又∵∠BEG =∠FEC =∠MEE ′, ∠MEE ′+∠ME ′E =90°, ∴∠GBE =∠ME ′E .在R t△BME ′中,tan ∠E ′BM = tan ∠GBE =BM M E '=b a32.在R t△EME ′中,tan ∠ME ′E =M E EM '=ab31,∴b a 32=a b 31. 又∵a >0,b >0,=ba32, ∴当=ba32时,BE′与EF 垂直.52.(某某省聊城市)25. 某市为了进一步改善居民的生活环境,园林处决定增加公园A 和公园B 的绿化面积.已知公园A B ,分别有如图1,图2所示的阴影部分需铺设草坪,在甲、乙两地分别有同种草皮21608m 和21200m 出售,且售价一样.若园林处向甲、乙两地购买草皮,其路程和运费单价见下表:公园A公园B路程(千米)运算单价(元)路程(千米)运费单价(元) 甲地 30 0.25 32 0.25 乙地220.3300.3(注:运费单价指将每平方米草皮运送1千米所需的人民币)65m 12060图1图2(1)分别求出公园A B ,需铺设草坪的面积;(结果精确到21m ) (2)请设计出总运费最省的草皮运送方案,并说明理由.解:(1)设公园A B ,需铺设草坪的面积分别为12S S ,,根据题意,得16232622322221800S =⨯-⨯-⨯+⨯=.设图2中圆的半径为R ,由图形知,圆心到矩形较长一边的距离为252, 所以25cos302R =°,有R =.于是,2212012565252π2100836022S =⨯-⨯⨯-⨯≈.所以公园A B ,需铺设草坪的面积分别为21800m 和10082m .(2)设总运费为y 元,公园A 向甲地购买草皮x 2m ,向乙地购买草皮(1800)x -2m . 由于公园A B ,需要购买的草皮面积总数为180010082808+=(2m ), 甲、乙两地出售的草皮面积总数为2160812002808(m )+=. 所以,公园B 向甲地购买草皮2(1608)m x -, 向乙地购买草皮21200(1800)(600)(m )x x --=-.于是,有01608018001200x x ⎧⎪⎨-⎪⎩,.≤≤≤≤所以6001608x ≤≤. 又由题意,得300.25220.3(1800)320.25(1608)300.3(600)y x x x x =⨯+⨯-+⨯-+⨯-···1.919344x =+.因为函数 1.919344y x =+随x 的增大而增大,所以,当600x =时,有最小值 1.96001934420484y =⨯+=(元).因此,公园A 在甲地购买6002m ,在乙地购买2180********(m )-=;公园B 在甲地购买16086001008-=(2m ). 此时,运送草皮的总运费最省.53.(某某省某某市非课改区)26. 如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,E 是BC 边上的一个动点(不与B C ,重合),EF AB ⊥,EG AC ⊥,垂足分别为F G ,.(1)求证:EG CGAD CD=; (2)FD 与DG 是否垂直?若垂直,请给出证明;若不垂直,请说明理由; (3)当AB AC =时,FDG △为等腰直角三角形吗?并说明理由.解: (1)证明:在ADC △和EGC △中Rt ADC EGC ∠=∠=∠,C C ∠=∠ADC EGC ∴△∽△EG CGAD CD∴=(2)FD 与DG 垂直 证明如下:在四边形AFEG 中,90FAG AFE AGE ∠=∠=∠= ∴四边形AFEG 为矩形AF EG ∴=由(1)知EG CGAD CD=AF CGAD CD∴=EB (第26题)EB (第26题)ABC △为直角三角形,AD BC ⊥ FAD C ∴∠=∠ AFD CGD ∴△∽△ ADF CDG ∴∠=∠又90CDG ADG ∠+∠=90ADF ADG ∴∠+∠=即90FDG ∠=FD DG ∴⊥(3)当AD AC =时,FDG △为等腰直角三角形, 理由如下:AB AC =,90BAC ∠= AD DC ∴=由(2)知:AFD CGD △∽△1FD ADGD DC ∴== FD DG ∴= 又90FDG ∠=FDG ∴△FDG ∴△为等腰直角三角形54.(某某省某某市)23. 已知:如图14,在ABC △中,D 为AB 边上一点,36A ∠=,AC BC =,2AC AB AD =.(1)试说明:ADC △和BDC △都是等腰三角形; (2)若1AB =,求AC 的值;(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)解:(1)在ABC △中,AC BC =,36108B A ACB ∴∠=∠=∠=,.在ABC △与CAD △中,36A B ∠=∠=;ADB图142AC AB AD =,AC AB ABAD AC BC ∴==. ABC CAD ∴△∽△ 721083672CDB DCB ∴∠=∠=-=,.ADC ∴△和BDC △都是等腰三角形.4分(2)设AC x =,则()211x x =⨯-,即210x x +-=.解得x x =∴=(负根舍去).55.(某某省实验区) 23.如图,对称轴为直线72x =的抛物线经过点A (6,0)和B (0,4). (1)求抛物线解析式及顶点坐标;(2)设点E (x ,y )是抛物线上一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形.求平行四边形OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值X 围;①当平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形?②是否存在点E ,使平行四边形OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由.36363636 363672 72108(有8个等腰三角形)解:(1)由抛物线的对称轴是72x =,可设解析式为27()2y a x k =-+. 把A 、B 两点坐标代入上式,得227(6)0,27(0) 4.2a k a k ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解之,得225,.36a k ==- 故抛物线解析式为22725()326y x =--,顶点为725(,).26- (2)∵点(,)E x y 在抛物线上,位于第四象限,且坐标适合22725()326y x =--,∴y<0,即 -y>0,-y 表示点E 到OA 的距离. ∵OA 是OEAF 的对角线, ∴2172264()2522OAES SOA y y ==⨯⨯⋅=-=--+.因为抛物线与x 轴的两个交点是(1,0)的(6,0),所以,自变量x 的 取值X 围是1<x <6.① 根据题意,当S = 24时,即274()25242x --+=.化简,得271().24x -=解之,得123, 4.x x == 故所求的点E 有两个,分别为E 1(3,-4),E 2(4,-4). 点E 1(3,-4)满足OE = AE ,所以OEAF 是菱形; 点E 2(4,-4)不满足OE = AE ,所以OEAF 不是菱形.② 当OA ⊥EF ,且OA = EF 时,OEAF 是正方形,此时点E 的 坐标只能是(3,-3).而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E , 使OEAF 为正方形.56.(某某市) 如图①,在平面直角坐标系中,Rt △AOB ≌Rt △CDA ,且A(-1,0)、B(0,2),抛物线y =ax 2+ax -2经过点C 。
2007年中考数学压轴题及答案

2007年广东省各市数学中考压轴题解析1、(2007 广东省中山市)第22题:如图,正方形ABCD 的边长为3a ,两动点E 、F分别从顶点B 、C 同时开始以相同速度沿BC 、CD 运动,与△BCF 相应的△EGH 在运动过程中始终保持△EGH ≌△BCF ,对应边EG =BC ,B 、E 、C 、G 在一直线上。
(1)若BE =a ,求DH 的长;(2)当E 点在BC 边上的什么位置时,△DHE 的面积取得最小值?并求该三角形面积的最小值。
解:(1)连结EF ,则FH ∥BE 且FH=BE ,在Rt △DFH 中,DF=3a -a=2a ,FH=a ,∠DFH=900所以,DH=a FH DF DH 522=+= (2)设BC=x ,△DHE 的面积为y , 依题意得,EG H CD H G CD E S S S y ∆∆-+=梯形x a x x a x a a ⨯⨯-⨯++-⨯⨯=321)3(21)3(321 22292321a ax x +-=故2222827)23(21292321a a x a ax x y +-=+-= 当时a x 23=,即BE=BC 21=时,E 是BC 的中点,y 取最小值。
△DHE 的面积y 的最小值是2827a 2、(2007 广东省佛山市)第24题:如图,隧道的截面由抛物线AED 和矩形ABCD 构成,矩形的长BC 为8m ,宽AB 为2m ,以BC 所在的直线为x 轴,线段BC 的中垂线为y 轴,建立平面直角坐标系,y 轴是抛物线的对称轴,顶点E 到坐标原点O 的距离为6m . (1)求抛物线的解析式;(2)一辆货运卡车高4.5m ,宽2.4m ,它能通过该隧道吗?(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设有0.4m 的隔离带,则该辆货运卡车还能通过隧道吗?解:(1)根据题意,A (-4,2);D (4,2);E (0,6) 设物线的解析式为c ax y +=2,将A (-4,2);E (0,6)D(第22题图)BCAE FGH3a3a第24题图代入caxy+=2得,⎪⎩⎪⎨⎧=-=641ca,故6412+-=xy(2)取,2.1=x解得5454.56)2.1(412=+⨯-=y>4.5,则该辆货运卡车能安全通过隧道。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年各地中考压轴题汇编(3)19、(浙江义乌)如图,抛物线223y x x =--与x 轴交A 、B 两点(A点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F , 使A 、C 、F 、G 这样的四个点为顶点的四边形是 平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.解:(1)令y=0,解得11x =-或23x =(1分) ∴A (-1,0)B (3,0);(1分)将C 点的横坐标x=2代入223y x x =--得y=-3,∴C (2,-3)(1分) ∴直线AC 的函数解析式是y=-x-1(2)设P 点的横坐标为x (-1≤x ≤2)(注:x 的范围不写不扣分) 则P 、E 的坐标分别为:P (x ,-x-1),(1分) E (2(,23)x x x --(1分)∵P 点在E 点的上方,PE=22(1)(23)2x x x x x -----=-++(2分) ∴当12x =时,PE 的最大值=94(1分)(3)存在4个这样的点F ,分别是1234(1,0),(3,0),(4(4F F F F -+-(结论“存在”给1分,4个做对1个给1分,过程酌情给分) 20、(湖北天门)如图所示,在平面直角坐标系内,点A 和点C 的坐标分别为(4,8)、(0,5),过点A 作AB ⊥x 轴于点B ,过OB 上的动点D 作直线y =kx +b 平行于AC ,与AB 相交于点E ,连结CD ,过点E 作EF ∥CD 交AC 于点F 。
(1)求经过A 、C 两点的直线的解析式;(2)当点D 在OB 上移动时,能否使四边形CDEF 成为矩形?若能,求出此时k 、-b 的指;若不能,请说明理由;(3)如果将直线AC 作上下平移,交y 轴于C ’,交AB 于A ’,连结DC ’,过点E 作EF ’∥DC ’,交A ’C ’于F ’,那么能否使四边形C ’DEF ’为正方形?若能,请求出正方形的面积;若不能,请说明理由。
21、(江西南昌)实验与探究(1)在图1,2,3中,给出平行四边形A B C D 的顶点A B D ,,的坐标(如图所示),写出图1,2,3中的顶点C 的坐标,它们分别是 , , ;(2)在图4中,给出平行四边形A B C D 的顶点A B D ,,的坐标(如图所示),求出顶点C 的坐标(C 点坐标用含a b c d e f ,,,,,的代数式表示);归纳与发现(3)通过对图1,2,3,4的观察和顶点C 的坐标的探究,你会发现:无论平行四边形A B C D 处于直角坐标系中哪个位置,当其顶点坐标为()()()()A a b B c d C m n D e f ,,,,,,,(如图4)时,则四个顶点的横坐标a c m e ,,,之间的等量关系为 ;纵坐标b d n f ,,,之间的等量关系为 (不必证明); 运用与推广(4)在同一直角坐标系中有抛物线2(53)y x c x c =---和三个点15192222G c c S c c ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,,,,(20)H c ,(其中0c >).问当c 为何值时,该抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形?并求出所有符合条件的P 点坐标.解:(1)(52),,()e c d +,,()c e a d +-,. ···························································· 2分 (2)分别过点A B C D ,,,作x 轴的垂线,垂足分别为1111A B C D ,,,, 分别过A D ,作1AE BB ⊥于E ,1D F C C ⊥于点F . 在平行四边形A B C D 中,C D B A =,又11BB C C ∥,180EBA ABC BCF ABC BCF FCD ∴∠+∠+∠=∠+∠+∠=.x图1x图2x图3)x图4)xDE B AF C D ∴∠=∠.又90BEA CFD ∠=∠= ,B E AC FD ∴△≌△. ·································································································· 5分 AE DF a c ∴==-,B E C F d b ==-.设()C x y ,.由e x a c -=-,得x e c a =+-.由y f d b -=-,得y f d b =+-.()C e c a f d b ∴+-+-,. ································ 7分 (此问解法多种,可参照评分)(3)m a c e +=+,n b d f +=+或m c e a =+-,n d f b =+-.························· 9分 (4)若G S 为平行四边形的对角线,由(3)可得1(27)P c c -,.要使1P 在抛物线上, 则有274(53)(2)c c c c c =--⨯--,即20c c -=.10c ∴=(舍去),21c =.此时1(27)P -,. ································································ 10分 若SH 为平行四边形的对角线,由(3)可得2(32)P c c ,,同理可得1c =,此时2(32)P ,. 若G H 为平行四边形的对角线,由(3)可得(2)c c -,,同理可得1c =,此时3(12)P -,. 综上所述,当1c =时,抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形.符合条件的点有1(27)P -,,2(32)P ,,3(12)P -,. ······················································ 12分22、(浙江温州)在A B C ∆中,,4,5,D BC CD 3cm,C Rt AC cm BC cm ∠=∠==点在上,且以=现有两个动点P 、Q 分别从点A 和点B 同时出发,其中点P 以1cm/s 的速度,沿AC 向终点C 移动;点Q 以1.25cm/s 的速度沿BC 向终点C 移动。
