数列裂项相消法例子
数列裂项相消知识点

数列裂项相消是一种常用的数列求和技巧,可以帮助我们简化数列求和的过程。
在本文中,我将为大家介绍数列裂项相消的基本原理和应用方法。
一、数列裂项相消的基本原理在求和过程中,我们经常会遇到连续数列,即数列中的元素相差固定的值。
假设我们有一个连续数列{a, a+d, a+2d, a+3d, …},其中a为首项,d为公差。
如果我们将这个数列从头和从尾开始相加,会发现很多项会相消掉,最后只剩下首项和尾项。
二、数列裂项相消的应用方法假设我们要求解连续数列{1, 3, 5, 7, 9, 11, 13, 15}的和。
我们可以使用数列裂项相消的方法来简化求和过程。
首先,我们可以将这个数列分为两部分:{1, 3, 5, 7}和{9, 11, 13, 15}。
接下来,我们将这两个数列从头和从尾开始相加:1 + 15 = 16 3 + 13 = 16 5 + 11 = 16 7 + 9 = 16可以发现,这四组数的和都是16。
而在原始数列中,这四组数分别位于数列的首项和尾项,所以它们的和也等于数列的和。
所以,我们只需要计算数列的首项和尾项,然后将它们相加,即可得到数列的和。
在这个例子中,首项为1,尾项为15,所以数列的和为1 + 15 = 16。
三、数列裂项相消的推广数列裂项相消不仅适用于连续数列,还可以推广到其他类型的数列。
例如,对于等差数列{a, a+d, a+2d, a+3d, …},我们可以将它裂为两部分:{a, a+d, a+2d, …}和{a+3d, a+4d, a+5d, …}然后将这两个数列从头和从尾开始相加,最后只剩下首项和尾项。
对于等比数列{a, ar, ar^2, ar^3, …},同样可以使用数列裂项相消的方法来简化求和过程。
四、数列裂项相消的优势数列裂项相消的方法在求和过程中可以大大简化计算,特别是对于长数列来说。
通过将数列分为两部分,并从头和从尾开始相加,我们可以消除大部分中间项,只保留首项和尾项,从而大幅度减少计算量。
裂项相消法在数列求和中的应用
c1 c2
cn =(1+
1 d
) (
1 b1
1 b2
)
(1 b2
1 b3
)
(1 bn2
1 )( 1
bn1
bn1
1 bn
)
(1+ 1 ) ( 1 1 ) (1+ 1 ) (1 1 )
d b1 bn
d
bn
b1 1 0, d 0,bn 0
c1 c2
cn
(1+
1 ) (1 d
1 bn
1 16
二:裂项相消法与不等式的证明
(二)先放缩再求和
例6:已知an
n2
n (n 1)2
, 求证:a1
a2
an
1 2
总结:
1.三种常见裂项相消的通项特征
(一)等差型(一次函数)
(二)等比型
an
(2n
b)
1 (2n1
b)
=
1 2n
1
1
( 2 n b 2n1 b)
(三)无理式型
an
1
n
n 1 (
=
1 2
(11
1) 3
(
1 2
1 4
)
(1 3
1) 5
( 1 n 1
1) n 1
(1 n
n
1
2 )
=
1 2
1+
1 2
n
1 1
n
1
2
3 4
1 2
(
1 n
1
n
1
) 2
( 1 1) n2 n
裂项相消法在数列求和中 的应用
13.裂项相消法

求数列的 1 1 1 1 1 3 2 4 3 5 n n2
前n项和
注:裂项相消法常用于
三、裂项相消法
常见的拆项公式:
1 1 5. ( n k n) nk n k
1 1 1 求和:sn 1 3 3 5 2n 1 2n 1
晚修练习: 1、练习册P23 第6题 P33 第6题 2、试卷分两个晚上完成,周三交
裂项相消法
1.把数列中的每一项“一拆为二”,即 每一项拆成两项之差,使它们在相加时 能消去一些项,最终达到求和的目的。 2.消项的规律:前面保留第几项, 后面则保留倒数第几项,符号相反。
把下列数列的通项拆成两项之差
1 = (2n 1) (2n 1)
————————————
1 1 1 ( ) 2 2n 1 2n 1
积极思考
冷静分析
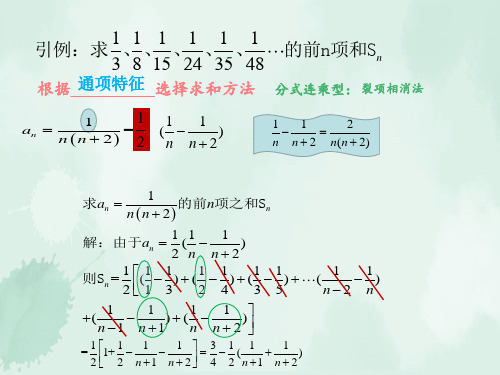
1 例 1: 求数列 的前n项和。 n (n 1)
裂项相消法
裂项相消法的基本思想是设法把数 列中的每一项“一拆为二”,即每一项 拆成两项之差,使它们在相加时能消去 一些项,最终达到求和的目的。
1 练习:求数列 的前n项和 n (n 2)
1 1 1 1 ( ) = 4 4n 1 4n 3 ———————————— (4n 1) (4n 3) 1 1 1 1 ( ) 6 6n 5 6n 1 (6n 5) (6n 1) = ————————————
1 例2:求数列 的前n项和。 n n 1
数列求和裂项相消法例题

数列求和裂项相消法例题【原创实用版】目录1.引言:裂项相消法求和2.例题 1:奇数项和偶数项的等差数列求和3.例题 2:绝对值不等的正负数列求和4.例题 3:具有规律的数列求和5.总结:裂项相消法的应用和注意事项正文一、引言:裂项相消法求和数列求和是数学中的一个重要知识点,它应用于各种实际问题中,如求解等差数列、等比数列的和等。
在求和过程中,裂项相消法是一种常用的方法,它可以有效地简化计算过程。
下面我们通过几个例题来介绍裂项相消法求和。
二、例题 1:奇数项和偶数项的等差数列求和假设有一个等差数列,其中奇数项和偶数项的公差分别为 a 和-b (a,b 均为正数),现在需要求解该数列的前 n 项和。
解法:我们可以将奇数项和偶数项分别求和,然后用总和减去偶数项的和,得到奇数项的和。
具体计算如下:设奇数项和为 S1,偶数项和为 S2,则S1 = a + a + 2 + a + 4 +...+ a + (2k-1)S2 = b + b + 2 + b + 4 +...+ b + (2k-1)将 S1 和 S2 相加,得到:S1 + S2 = (a + b) + (a + b + 2) + (a + b + 4) +...+ (a + b + 2k-2)观察发现,S1 + S2 中的每一项都等于 a + b,因此:S1 + S2 = (a + b) * k所以奇数项和 S1 = (a + b) * k - S2通过裂项相消法,我们成功地将等差数列求和问题简化为求解两个等差数列的和,从而降低了计算难度。
三、例题 2:绝对值不等的正负数列求和现在考虑一个由正数和负数构成的数列,其中正数的绝对值和负数的绝对值不相等,求该数列的前 n 项和。
解法:我们可以将数列中的正数和负数分别提取出来,然后分别求和。
具体计算如下:设正数和为 S1,负数和为 S2,则S1 = a1 + a2 + a3 +...+ anS2 = -b1 - b2 - b3 -...- bn其中,ai 和 bi 分别为数列中的正数和负数,a1, a2, a3,..., an 和b1, b2, b3,..., bn 分别为它们的绝对值。
高一数学必修5数列经典例题(裂项相消法)

2.(2014•成都模拟)等比数列{a n}的各项均为正数,且2a1+3a2=1,a32=9a2a6,(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a1+log3a2+…+log3a n,求数列{}的前n项和.解:(Ⅰ)设数列{a n}的公比为q,由a32=9a2a6有a32=9a42,∴q2=.由条件可知各项均为正数,故q=.由2a1+3a2=1有2a1+3a1q=1,∴a1=.故数列{a n}的通项式为a n=.(Ⅱ)b n=++…+=﹣(1+2+…+n)=﹣,故=﹣=﹣2(﹣)则++…+=﹣2[(1﹣)+(﹣)+…+(﹣)]=﹣,∴数列{}的前n项和为﹣.7.(2013•江西)正项数列{a n}满足﹣(2n﹣1)a n﹣2n=0.(1)求数列{a n}的通项公式a n;(2)令b n=,求数列{b n}的前n项和T n.解:(1)由正项数列{a n}满足:﹣(2n﹣1)a n﹣2n=0,可有(a n﹣2n)(a n+1)=0∴a n=2n.(2)∵a n=2n,b n=,∴b n===,T n===.数列{b n}的前n项和T n为.6.(2013•山东)设等差数列{a n}的前n项和为S n,且S4=4S2,a2n=2a n+1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设数列{b n}满足=1﹣,n∈N*,求{b n}的前n项和T n.解:(Ⅰ)设等差数列{a n}的首项为a1,公差为d,由S4=4S2,a2n=2a n+1有:,解有a1=1,d=2.∴a n=2n﹣1,n∈N*.(Ⅱ)由已知++…+=1﹣,n∈N*,有:当n=1时,=,当n≥2时,=(1﹣)﹣(1﹣)=,∴,n=1时符合.∴=,n∈N*由(Ⅰ)知,a n=2n﹣1,n∈N*.∴b n=,n∈N*.又T n=+++…+,∴T n=++…++,两式相减有:T n=+(++…+)﹣=﹣﹣∴T n=3﹣.28.(2010•山东)已知等差数列{a n}满足:a3=7,a5+a7=26.{a n}的前n项和为S n.(Ⅰ)求a n及S n;(Ⅱ)令(n∈N*),求数列{b n}的前n项和T n.解:(Ⅰ)设等差数列{a n}的公差为d,∵a3=7,a5+a7=26,∴有,解有a1=3,d=2,∴a n=3+2(n﹣1)=2n+1;S n==n2+2n;(Ⅱ)由(Ⅰ)知a n=2n+1,∴b n====,∴T n===,即数列{b n}的前n项和T n=.25.(2008•四川)在数列{a n}中,a1=1,.(Ⅰ)求{a n}的通项公式;(Ⅱ)令,求数列{b n}的前n项和S n;(Ⅲ)求数列{a n}的前n项和T n.解:(Ⅰ)由条件有,又n=1时,,故数列构成首项为1,公式为的等比数列.∴,即.(Ⅱ)由有,,两式相减,有:,∴.(Ⅲ)由有.∴T n=2S n+2a1﹣2a n+1=.3.(2010•四川)已知等差数列{a n}的前3项和为6,前8项和为﹣4.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=(4﹣a n)q n﹣1(q≠0,n∈N*),求数列{b n}的前n项和S n.解:(1)设{a n}的公差为d,由已知有解有a1=3,d=﹣1故a n=3+(n﹣1)(﹣1)=4﹣n;(2)由(1)的解答有,b n=n•q n﹣1,于是S n=1•q0+2•q1+3•q2+…+n•q n﹣1.若q≠1,将上式两边同乘以q,有qS n=1•q1+2•q2+3•q3+…+n•q n.上面两式相减,有(q﹣1)S n=nq n﹣(1+q+q2+…+q n﹣1)=nq n﹣于是S n=若q=1,则S n=1+2+3+…+n=∴,S n=.4.(2010•四川)已知数列{a n}满足a1=0,a2=2,且对任意m、n∈N*都有a2m﹣1+a2n﹣1=2a m+n﹣1+2(m﹣n)2(1)求a3,a5;(2)设b n=a2n+1﹣a2n﹣1(n∈N*),证明:{b n}是等差数列;(3)设c n=(a n+1﹣a n)q n﹣1(q≠0,n∈N*),求数列{c n}的前n项和S n.解:(1)由题意,令m=2,n=1,可有a3=2a2﹣a1+2=6再令m=3,n=1,可有a5=2a3﹣a1+8=20(2)当n∈N*时,由已知(以n+2代替m)可有a2n+3+a2n﹣1=2a2n+1+8于是[a2(n+1)+1﹣a2(n+1)﹣1]﹣(a2n+1﹣a2n﹣1)=8即b n+1﹣b n=8∴{b n}是公差为8的等差数列(3)由(1)(2)解答可知{b n}是首项为b1=a3﹣a1=6,公差为8的等差数列则b n=8n﹣2,即a2n+1﹣a2n﹣1=8n﹣2另由已知(令m=1)可有a n=﹣(n﹣1)2.∴a n+1﹣a n=﹣2n+1=﹣2n+1=2n于是c n=2nq n﹣1.当q=1时,S n=2+4+6++2n=n(n+1)当q≠1时,S n=2•q0+4•q1+6•q2+…+2n•q n﹣1.两边同乘以q,可有qS n=2•q1+4•q2+6•q3+…+2n•q n.上述两式相减,有(1﹣q)S n=2(1+q+q2+…+q n﹣1)﹣2nq n=2•﹣2nq n=2•∴S n=2•综上所述,S n=.16.(2009•湖北)已知数列{a n}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16(1)求数列{a n}的通项公式;(2)数列{a n}和数列{b n}满足等式a n=(n∈N*),求数列{b n}的前n项和S n.解:(1)设等差数列{a n}的公差为d,则依题意可知d>0由a2+a7=16,有,2a1+7d=16①由a3a6=55,有(a1+2d)(a1+5d)=55②由①②联立方程求,有d=2,a1=1/d=﹣2,a1=(排除)∴a n=1+(n﹣1)•2=2n﹣1(2)令c n=,则有a n=c1+c2+…+c na n+1=c1+c2+…+c n+1两式相减,有a n+1﹣a n=c n+1,由(1)有a1=1,a n+1﹣a n=2∴c n+1=2,即c n=2(n≥2),即当n≥2时,b n=2n+1,又当n=1时,b1=2a1=2∴b n=于是S n=b1+b2+b3+…+b n=2+23+24+…2n+1=2n+2﹣6,n≥2,.。
高中数学裂项相消法例题

高中数学裂项相消法例题1.已知等差数列{}n a 的公差0d ≠,前n 项和为4,10n S S =,且248,,a a a 成等比数列.(1)求数列{}n a 的通项公式n a ;(2)设()*21n n n b n N a a +=∈,求数列{}n b 的前n 项和n T .【答案】(1)n a n=(2)()()3234212n n T n n +=-++【分析】(1)结合等差数列前n 项、等差数列通项公式和等比数列性质,解关于1,a d 的方程即可求解n a ;(2)由(1)结合裂项公式得11122n b n n ⎛⎫- +⎝⎭=,采用累加法即可求解n T .(1)因为248,,a a a 成等比数列,则2428a a a =⋅,即()()()211137a d a d a d +=++,化简得:21d a d =,10,d d a ≠∴= ,①又410S =,则1434102a d ⨯+=,即1235a d +=,②联立①②解得:11a d ==,()11n a a n d n ∴=+-=.(2)当*n ∈N 时,()211111222n n n b a a n n n n +⎛⎫=== ++⎝⎭11111111111112324352112n T n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥--++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦()()11113231.22124212n n n n n +⎛⎫=+--=- ⎪++++⎝⎭所以*n ∈N 时,()()3234212n n T n n +=-++.2.已知数列{}n a ,{}n b 满足112n n n a a b +-=,122n n n b b a +-=+,且11a =,14b =.(1)写出2a ,2b ,并求{}n a 的通项公式;(2)记数列1n n n b a a +⎧⎫⎨⎬⎩⎭的前n 项和为n S ,数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和为n T ,证明:4n n S T >.【答案】(1)23a =,28b =,21n n a =-(2)证明见解析【分析】(1)由两数列的关系,{}n b 的递推关系,得到数列{}n a 的递推关系,再从基本定义出发构造等比数列{}1n a +,得到通项公式;(2)利用裂项相消法求和n S ,由等比数列的前n 项和公式得n T 后可得不等式成立.(1)因为11a =,14b =,所以211132a ab =+=,211228b a b =++=.由112n n n a a b +-=得,()12n n n b a a +=-,又122n n n b b a +-=+,所以()()2112222n n n n n a a a a a +++---=+,得()21121n n a a +++=+,得()1121n n a a ++=+,所以数列{}1n a +是以2为首项,2为公比的等比数列,.所以12n n a +=,21n n a =-.(2)由(1)可知,12n n b +=.所以()()1111211221212121n n n n n n n n b a a ++++⎛⎫==- ⎪----⎝⎭,所以数列1n n n b a a +⎧⎫⎨⎬⎩⎭得前n 项和111111112121337212121n n n n S ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-=- ⎪ ⎪ ⎪ ⎪⎢⎥---⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.数列1n b ⎧⎫⎨⎩⎭的前n 项和21112211112212n n n T ⎡⎤⎛⎫-⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦==-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-,所以14212n n T ⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.易知()()1111112122142220221221221n n n n n n n n n n n S T ++++---⎛⎫-=-=⨯=⨯> ⎪---⎝⎭,所以4n n S T >.3.已知数列{}n a 的前n 和22,n S n n =+记[lg ],n n b a =其中[]x 表示不超过x 的最大整数,如[0.9]0,[lg 99] 1.==(1)求数列{}n a 的通项公式;(2)设11,n n n c a a +=求数列{}n c 的前n 项和;n T (3)求数列{}n b 的500项和.【答案】(1)21n a n =+;(2)n T =11646n -+;(3)948.【分析】(1)由22n S n n =+,可知当2n ≥时,21(1)2(1)n S n n -=-+-,再利用()12n n n a S S n -=-≥,即可求出数列{}n a 的通项公式;(2)由(1)得,n c =1111((21)(23)22123n n n n =-++++,再利用裂项相消法即可求出n T ;(3)由(1)知[lg ]n n b a =[lg(21)]n =+,结合题意可求出12340b b b b ====,567491b b b b ===⋯==,505152534992b b b b b ====⋯==,5003b =,即可求出数列{}n b 的500项和.(1)解:22n S n n =+ ,①∴当2n ≥时,21(1)2(1)n S n n -=-+-,②由①-②得21(2)n a n n =+≥,当1n =时,113a S ==,满足上式,∴数列{}n a 的通项公式为:21n a n =+.(2)解:由(1)知,n c =1111()(21)(23)22123n n n n =-++++,所以数列{n c }前n 项和为:n T =1111111[()()()]235572123n n -+-++-++ =11646n -+.(3)解:由(1)知[lg ]n n b a =[lg(21)]n =+,14549504995003,9,11,99,101,999,1001a a a a a a a ======= ,由于lg y x =在(0,)+∞上单调递增,且lg10,lg101,lg1002,lg10003,====∴12340b b b b ====,567491b b b b ===⋯==,505152534992b b b b b ====⋯==,5003b =,数列{}n b 的前500项和为:4045145023948⨯+⨯+⨯+=.4.在①550S =,②1S 、2S 、4S 成等比数列,③()6632S a =+.这三个条件中任选两个,补充到下面问题中,并解答本题.问题:已知等差数列{}n a 的公差为()0d d ≠,前n 项和为n S ,且满足___________.(1)求n a ;(2)若()122n n n b b a n --=≥,且111b a -=,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)条件选择见解析,42n a n =-(2)21n n T n =+【分析】(1)根据所选条件,得出关于1a 、d 的方程组,解出这两个未知数的值,即可得出数列{}n a 的通项公式;(2)利用累加法可求得数列{}n b 的通项公式,再利用裂项相消法可求得n T .(1)解:①:因为1S 、2S 、4S 成等比数列,则2214S S S =,即()()2111246a d a a d +=+,因为0d ≠,可得12d a =.②:5151050S a d =+=,可得1210a d +=.③:()6632S a =+,可得()11615352a d a d +=++,可得12a =.若选①②,则有112210d a a d =⎧⎨+=⎩,可得124a d =⎧⎨=⎩,则()1142n a a n d n =+-=-;若选①③,则124d a ==,则()1142n a a n d n =+-=-;若选②③,则122210a d d +=+=,可得4d =,所以,()1142n a a n d n =+-=-.(2)解:()12284n n n b a n b n -=--=≥,且111b a -=,则13b =,所以,当2n ≥时,则有()()()121321n n n b b b b b b b b -=+-+-++- ()()()28412131220843412n n n n -+-=++++-=+=- ,13b =也满足241n b n =-,故对任意的n *∈N ,241n b n =-,则()()11111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭,所以,11111111112335212122121n n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥-+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.5.已知数列{}n a 的前n 项和n S 满足()236n n S a n n *=-∈N (1)证明:数列{}3n a +为等比数列;(2)若数列{}n b 为等差数列,且31b a =,122b a =,求数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)证明见解析(2)44nn +【分析】(1)由n S 与n a 的关系,利用等比数列的定义证明即可;(2)由(1)求出n b ,再利用裂项相消法求解即可(1)当1n =时,11236a a =-,16a ∴=.()236n n S a n n N *=-∈ ,∴当2n ≥时,()112361n n S a n --=--,12336n n n a a a -∴=--,()1333n n a a -∴+=+,∴数列{}3n a +是以139a +=为首项、以3为公比的等比数列.(2)由(1)得,113933n n n a -++=⨯=,即133n n a +=-,316b a ∴==,31223324b a ==-=.设等差数列{}n b 的公差为d ,则126b d +=,11124b d +=,12b d ∴==,2n b n ∴=,()11111122141n n b b n n n n +⎛⎫∴==- ⎪⨯++⎝⎭,1111111412231n T n n ⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-+⋅⋅⋅+-= ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦1114144n n n ⎛⎫-= ⎪++⎝⎭6.已知数列{}n a 的前n 项和为n S ,11a =,141n n S a +=+,设12n n n b a a +=-.(1)证明数列{}n b 是等比数列并求数列{}n b 的通项:(2)数列{}n c 满足1log3n nc b =+,设1223341n n n T c c c c c c c c +=++++ ,求n T .【答案】(1)证明见解析,2n n b =(2)5(25)n n T n =+【分析】(1)当2n ≥时,由141n n S a +=+得出141n n S a -=+,两式相减得出1144n n n a a a +-=-,然后利用等比数列的定义可证明出数列{}n b 为等比数列,并求数列{}n b 的通项公式;(2)由数列{}n b 的通项公式,求出n c ,然后利用裂项相消法即求.(1)当2n ≥时,由141n n S a +=+①,得141n n S a -=+②①-②得1144n n n a a a +-=-,所以()11222n n n n a a a a +--=-,又12n n n b a a +=-,所以12n n b b -=.因为11a =,且12141a a a +=+,所以21314a a =+=,所以12122b a a =-=,故数列{}n b 是首项为2,公比为2的等比数列,∴2n n b =.(2)由2n n b =,则()11log 323n n c n b n *==∈++N ,∴111111232522325n n c c n n n n +⎛⎫=⨯=- ⎪++++⎝⎭∴122334111111157792325n n n T c c c c c c c c n n +=++++=⨯+⨯++⨯++ 11111111112577923252525n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 5(25)nn =+∴5(25)n n T n =+.7.已知数列{}n a 满足()1123123(1)22n n a a a na n n N +*++++=-⋅+∈ .(1)求数列{}n a 的通项公式;(2)设()()111n n n n a b a a +=++,求数列{}n b 的前n 项和n S .【答案】(1)*1=12,2n n n a n n N ⎧=⎨≥∈⎩,且(2)131=1021n n S +-+【分析】(1)1n =时,可得11a =,2n ≥时,代入1n -,两式相减可得通项公式;(2)利用裂项相消法可求.(1)因为()1123123(1)22n n a a a na n n N +*++++=-⋅+∈ ,当1n =时,可得11121a a +==, ;当2n ≥时,可得1231123(1)(2)22n n a a a n a n -++++-=-⋅+ ,()1123123(1)22n n a a a na n n N +*++++=-⋅+∈ 两式相减得1(1)2(2)22n n n n na n n n +=-⋅--⋅=⋅,即2(2)n n a n =≥,所以数列{}n a 的通项公式为*1=12,2n n n a n n N⎧=⎨≥∈⎩,且(2)当1n =时,()()()()112121*********a b a a ===++++,当2n ≥时,()()()()1112111121212121n n n n n n n n n a b a a +++===-++++++,则23341111111212121212121110n n n S +-+-++-+++=++++ 1111131()105211021n n ++=+-=-++.8.已知数列{}2n a 是公比为4的等比数列,且满足2a ,4a ,7a 成等比数列,n S 为数列{}n b 的前n 项和,且n b 是1和n S 的等差中项,记231(1)n n n n n a c a a ++=-,求数列{}n c 的前2n 项和.【答案】11466n -+【分析】先根据条件推出{}n a 是等差数列,求出{}n a 的通项公式,代入到231(1)n n n n n a c a a ++=-中,可以用裂项相消法求出{}n c 的前2n 项和【详解】∵数列{}2n a 是公比为4的等比数列∴1242n na a +=即124n n a a +-=∴12n n a a +-=∴{}n a 是等差数列,且公差为2∵2a ,4a ,7a 成等比数列∴2427a a a =则()()()21116212a a a +=++解得:16a =∴()62124n a n n =+-=+∴()()()()231(1)(1)(410251111242622322)(1)3n n n n n n n n n n n n a c n n n a a n ++++⎛⎫==⨯+ ⎪++++++-=-⎝--⎭=设数列{}n c 的前2n 项和为2n T ,21111111111111123424525622223466n T n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++++=- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭ 9.已知数列{}n a 的前n 项和为n S ,其中11a =,满足121n n a a +=+.(1)证明数列{}1n a +为等比数列;(2)求数列1121n n n S S ++⎧⎫-⎨⎬⎩⎭的前n 项和n T .【答案】(1)证明见解析;(2)222423n n n n ++----.【分析】(1)由121n n a a +=+可得()1121n n a a ++=+,即可证明;(2)可得21n n a =-,12(2)n n S n +=-+,11121212121112(2)2(3)2(2)2(3)n n n n n n n n S S n n n n +++++++--==--+-+⎡⎤⎡⎤-+-+⎣⎦⎣⎦,然后可算出答案.【详解】(1)由121n n a a +=+可得()1121n n a a ++=+,因为11a =,所以112a +=所以数列{}1n a +是首项为2,公比为2的等比数列(2)根据(1)可得:()11112221n n n n n a a a -+=+⨯=⇒=-,所以()12122(2)12n n n S n n +-=-=-+-,所以11121212121112(2)2(3)2(2)2(3)n n n n n n n n S S n n n n +++++++--==--+-+⎡⎤⎡⎤-+-+⎣⎦⎣⎦,所以21222111111241144112(2)2(3)2(3)23n n n n n n n T n n n n +++++--=-+-+⋅⋅⋅+-=-=-+-+-+--.10.已知n S 是等差数列{}n a 的前n 项和,若2929a a +=,48S a =.(1)求数列{}n a 的通项公式n a ;(2)记11n n n b a a +=,数列{}n b 的前n 项和为n T ,()331nn n c n T =+,求数列{}n c 的前n 项和n K .【答案】(1)()*32n a n n N =-∈;(2)()1*313424n n n K n N +⎛⎫=+-⋅∈ ⎪⎝⎭.【分析】(1)根据已知条件可得出关于等差数列{}n a 的首项和公差的方程组,解出这两个量的值,即可求得等差数列{}n a 的通项公式;(2)利用裂项相消法可求得n T ,进而得出3nn c n =⋅,再利用错位相减法可求得数列{}n c 的前n 项和n K .【详解】(1)设等差数列{}n a 的首项为1a ,公差为d ,由题意294829a a S a +=⎧⎨=⎩,得111292943472a d a d a d +=⎧⎪⎨⨯+=+⎪⎩,解得113a d =⎧⎨=⎩,所以,()()*1132n a a n d n n N =+-=-∈;(2)由(1)知()()111111323133231n n n b a a n n n n +⎛⎫===- ⎪-+-+⎝⎭,所以,11111111113447323133131n n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-=-=⎪ ⎪ ⎪⎢⎥-+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,所以,()3313n nn n c n T n =+=⋅,则()1211323133n nn K n n -=⨯+⨯+⋅⋅⋅+-⋅+⋅①,()23131323133n n n K n n +=⨯+⨯+⋅⋅⋅+-⋅+⋅②,①-②,得()2311131331233333331322n nn n n n K n n n +++--=+++⋅⋅⋅+-⋅=-⋅=-⎛⎪-+⋅⎫⎝⎭- ,解得()1*313424n n n K n N +⎛⎫=+-⋅∈ ⎪⎝⎭.11.已知首项为1的数列{}n a 的前n 项和为n S ,且11331n n n n n a S S a a +++=++.(1)求证:数列11n a ⎧⎫⎨⎬+⎩⎭为等差数列;(2)记数列()(){}323111n n a a -+++的前n 项和为n T ,求n T .【答案】(1)证明见解析;(2)431=+n nT n .【分析】(1)由题可得+1111121n n aa =+++,利用等差数列的定义可证;(2)利用裂项相消法即求.【详解】(1)依题意,1131n n n n a a a a ++=++,则+113n n n a a a -=+,两边都加1可得,()+12113n n n a a a ++=+,故()+113121111212121n n n n n a aa a a ⎛⎫+==+=+ ⎪++++⎝⎭,则+1111112n n a a -=++,故数列11n a ⎧⎫⎨⎬+⎩⎭是首项为12,公差为12的等差数列;(2)由(1)可知,112n na =+,故21n a n +=,则()()()()3231224411113231323133231n n a a n n n n n n -+⎛⎫++==- ⎪-+-+-+⎝⎭,故4111111414131447323133131n nT n n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪-+++⎝⎭⎝⎭.12.已知数列{}n a 的前n 项和为n S ,且0n a >,6742021a =,()()612n n n S a a =++,*N n ∈.(1)求{}n a 的通项公式;(2)若数列{}n b 满足152n n n b b a --=+,2n ≥,*N n ∈,192b =,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)31n a n =-;(2)()()1232312n n T n n +=-++.【分析】(1)令1n =可求得11a =或12a =,当2n ≥时,可得2111623n n n S a a ---+=+与已知条件两式相减可得{}n a 是等差数列,再由6742021a =可确定1a 的值,进而可得{}n a 的通项公式;(2)利用累加法以及等差数列求和公式可得n b ,进而可得1nb ,利用裂项求和即可求解.【详解】(1)()()261232n n n n n S a a a a =++=++,当2n ≥时,可得2111623n n n S a a ---+=+,两式相减可得2211336n n n n n a a a a a ---+-=,化简得()()()1113n n n n n n a a a a a a ---+-=+.因为0n a >,则10n n a a -+≠,所以13n n a a --=,故数列{}n a 是以3为公差的等差数列.在2632n n n S a a =++中,令1n =,2111632a a a =++,即211320a a -+=,可得11a =或12a =.当11a =时,()13132n a n n =+-=-,674367422020a =⨯-=,不符合题意;当12a =时,()23131n a n n =+-=-,6742021a =,符合题意.综上所述:31n a n =-.(2)因为152n n n b b a --=+,所以12152n n n b b a ----=+,23252n n n b b a ----=+,…21252b b a -=+,累加可得:()1122512n n n n b b a a a a n ---=+++⋅⋅⋅++-,故()()()()112313255912122222n n n n n n b S a n b n +-+=-+-+=-+-+=(2n ≥),经检验192b =也满足上式,所以()322n n n b +=,则()121113232n b n n n n ⎛⎫==- ⎪++⎝⎭.所以1111111113324352n T n n ⎛⎫=-+-++⋅⋅⋅+- ⎪+⎝⎭111113212n n ⎛⎫=+-- ⎪++⎝⎭()()1232312n n n +=-++.13.数列{}n a 对于任意*n N ∈,满足()()1428n n a a ++-=,且12a =.()1求n a ;()2若12n n n n b a a +=,求数列{}n b 的前n 项和.【答案】()1221n n a =-;()214421n +--.【分析】()1根据已知条件化简并凑项,即可得出21n a ⎧⎫+⎨⎬⎩⎭是以2为首项,2为公比的等比数列,进而写出通项公式;()2由()1中221n n a =-,可得1111242121nn n n n n b a a ++⋅⎛⎫==- ⎪--⎝⎭,进而利用裂项相消法求数列{}n b 的前n 项和.【详解】解:()1由题意()()1428n n a a ++-=,即118428n n n n a a a a ++-+-=,1124n n n n a a a a ++-=,1241n na a +-=,1241n na a +=+,122211n n a a +⎛⎫=+- ⎪⎝⎭,122121n n a a +⎛⎫+=+ ⎪⎝⎭12a =,∴1212a +=则21n a ⎧⎫+⎨⎬⎩⎭是以2为首项,2为公比的等比数列.∴212n na +=,则221n n a =-()2由()1中221n n a =-,可得()()1122222121n n n n n n n b a a ++⨯⋅⋅==--()()114211421212121n n n n n ++⨯⎛⎫==-⎪----⎝⎭.设数列{}n b 的前n 项和为n S ,则123n nS b b b b =++++ 121231111114212121212121n n +⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎡⎤⎛⎫=-+-++- ⎪⎢⎥------⎝⎭⎣⎭⎦ 114121n +⎛⎫=- ⎪-⎝⎭14421n +=--.14.已知数列{}n a 的前n 项和为n S ,首项为1a ,且12nn S a a n-=.(1)证明:{}n a 为等差数列;(2)若{}n a 的首项和公差均为1,求数列()()122121n nn a a a +⎧⎫⎪⎪⎨⎬--⎪⎪⎩⎭的前n 项和n T .【答案】(1)证明见解析;(2)11121n n T +=--.【分析】(1)利用1n n n a S S -=-消去n S ,利用等差中项法证明等差数列;(2)先求出n a n =,把()()122121n n n a a a +--转化为()()1121121212121n n n a n n a a ++=-----,利用裂项相消法求和.【详解】解:(1)由题意得()()11112211n nn n S na na S n a n a --=+⎧⎨=-+-⎩(2n ≥)两式相减得()()1121n n n a a n a --+=-从而()()()1111211n n n nn a a n a n a a na -+⎧-+=-⎪⎨-+=⎪⎩再两式相减得()()()111122n n n n a n a n a +--+-=-又10n -≠∴112n n n a a a +-+=,于是{}n a 为等差数列.(2)由(1)可得{}n a 为等差数列,又11a d ==,∴n a n =.于是()()()()1112211212121212121n n nn n n n n a a +++==-------则2231111111111212121212121n n n n T ++⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-=- ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭.15.已知数列{}n a 是递增等比数列,n S 为其前n 项和,且1428a a +=,2327a a ⋅=.(1)求数列{}n a 的通项公式;(2)设数列{}n b 满足212n n n n a b S S +++=⋅,求其前n 项和n T .【答案】(1)13-=n n a ;(2)212431n n T +=--.【分析】(1)由已知条件可得出关于1a 、4a 的方程组,解出这两个量的值,可求得等比数列{}n a 的公比,可求得等比数列{}n a 的通项公式;(2)求出312n n S -=,可得出121123131n n n b ++⎛⎫=- ⎪--⎝⎭。
裂项相消法求和

裂项相消法求和裂项相消法是一种求和的方法,它通过将一系列相邻或相对数之间的差值相消,得到最终的和。
这种方法在高中数学中常常被用到,可以简化复杂的求和过程,使得计算更加简便和高效。
裂项相消法的基本思想是利用数列中的对称性,找出相邻项之间的差值,并通过相消的方式将它们消去。
这样一来,原来复杂的数列求和问题就变得相对简单起来。
举个例子来说明裂项相消法的使用。
假设我们要求和的数列是1-2+3-4+5-6+...+99-100。
一般情况下,我们可以使用等差数列求和公式来计算,但这里我们尝试使用裂项相消法来解决。
我们可以观察到数列中的对称性。
每两个相邻的数之间的差值都是1,所以我们可以分别将这些差值相加,即(1-2)+(3-4)+(5-6)+...+(99-100)。
接下来,我们可以发现每一对差值之和都是-1。
所以这个数列的和就等于差值的个数乘以-1,即有50个差值,所以和为50*(-1)=-50。
通过这个简单的例子,我们可以看出裂项相消法的优势。
它可以将原本复杂的数列求和问题转化为一系列简单的差值相加,从而得到最终的和。
而且,这种方法通常比直接使用求和公式更容易理解和计算。
除了对称性外,裂项相消法还可以利用数列中的其他特点来简化求和过程。
比如,如果数列中存在重复的项,我们可以将它们相加后再相消。
又或者,如果数列中存在周期性的规律,我们可以根据规律性质来简化求和。
这些都是裂项相消法的应用技巧,可以根据具体情况进行灵活运用。
裂项相消法是一种简化数列求和问题的方法。
它通过利用数列中的对称性和其他特点,将原本复杂的求和过程转化为简单的差值相加,从而得到最终的和。
在解决一些特定的数列求和问题时,裂项相消法可以帮助我们更加高效地计算,提高求解的准确性和速度。
所以,在数学学习中,掌握和运用裂项相消法是非常重要的。
数列裂项相消典型例题

一个典型的数列裂项相消的例题如下:
例题:考虑数列{1, 1, 2, 3, 5, 8, 13, ...},其中每一项等于前两项的和。
给定一个正整数N,计算数列的前N项之和。
解题思路:
这个数列是著名的斐波那契数列,它的定义是F(1) = 1,F(2) = 1,F(n) = F(n-1) + F(n-2)(n >= 3)。
我们可以使用裂项相消的方法来解决这个问题。
首先,我们可以设S为数列的前N项和。
那么S的表达式可以写为:
S = 1 + 1 + 2 + 3 + 5 + 8 + ... + F(N-1) + F(N)
然后,我们观察数列中每一项与它前一项的关系,即F(n) = F(n-1) + F(n-2)。
根据这个关系,我们可以发现S的表达式中的一些项可以相互抵消,通过相消的方式简化求解过程。
具体来说,我们可以将S的表达式中的项分为两组,一组是从F(1)到F(N-2)的项,另一组是F(N-1)和F(N)。
对于第一组,我们可以看到F(n)等于它的前两项之和,所以这些项可以两两抵消。
因此,我们可以得到:
S = F(N-1) + F(N)
对于第二组,我们可以看到F(N)等于F(N-1)和F(N-2)的和,所以这两项仍然保留在S中。
综合上述分析,我们可以得到以下简化后的表达式:
S = F(N) + F(N-1)
因此,这个问题的答案就是数列中第N项和第N-1项的和,即F(N) + F(N-1)。
我们可以通过计算斐波那契数列的第N项和第N-1项的值,然后求和来得到最终的答案。
希望这个解题思路能够帮助到你解决数列裂项相消的典型例题!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列裂项相消法
数列裂项相消法是一种常用的数学技巧,用于求解一些复杂的数列求和问题。
以下是几个例子,说明该方法的应用。
例1:已知等差数列{an},其中a1=1,d=2,求前n项和Sn。
解:首先,我们可以将等差数列的通项公式表示为an=a1+(n-1)d=1+2(n-1)=2n-1。
然后,我们可以将前n项和表示为Sn=a1+a2+...+an。
接下来,我们使用裂项相消法,将相邻两项相加,得到:
Sn=(1+3)+(3+5)+...+[(2n-3)+(2n-1)]
=2+4+ (2)
=n(n+1)
例2:已知等比数列{an},其中a1=1,q=2,求前n项和Sn。
解:首先,我们可以将等比数列的通项公式表示为an=a1*q^(n-1)=2^(n-1)。
然后,我们可以将前n项和表示为Sn=a1+a2+...+an。
接下来,我们使用裂项相消法,将相邻两项相减,得到:
Sn=(1-2)+(2-4)+...+[2^(n-2)-2^(n-1)]+2^(n-1)
=-1-1-...-1+2^(n-1)
=-(n-1)+2^(n-1)
=(2^n)-1-(n-1)
=(2^n)-n
例3:已知数列{an},其中an=n^2,求前n项和Sn。
解:首先,我们可以将数列的通项公式表示为an=n^2。
然后,我们可以将前n项和表示为Sn=a1+a2+...+an。
接下来,我们使用裂项相消法,将相邻两项相减,得到:
Sn=(1^2-0^2)+(2^2-1^2)+...+[n^2-(n-1)^2]
=1+3+5+...+(2n-1)
=n^2
通过以上例子可以看出,裂项相消法是一种非常实用的数学技巧,可以用于求解各种复杂的数列求和问题。
需要注意的是,在使用该方法时,需要根据具体的数列类型和题目要求来选择合适的裂项方式。
