ADAMS魔术公式的轮胎模型
ADAMS CAR不同轮胎模型的整车平顺性分析实例
ADAMS/CAR不同轮胎模型的整车平顺性分析实例在相同条件下，对使用不同轮胎模型的整车模型进行平顺性仿真。
仿真结束后，在后处理模块获得汽车底盘质心处x 、y 、z 三个轴向的加速度曲线。
为了确定路面引起汽车振动所在的频率范围，还需获取相应的加速度功率谱密度。
最后，求加速度加权均方根值，评价振动对人体的影响。
目录第一章、参考资料 (1)第二章、建模说明 (5)一、生成5.2.1前轮胎模型 (5)二、生成5.2.1后轮胎模型 (9)三、生成其他三个轮胎模型 (10)四、生成整车模型 (12)第三章、仿真分析 (16)一、平顺性仿真概述 (16)二、随机路面生成 (16)三、平顺性仿真条件设置 (16)四、仿真过程 (17)第四章、结果分析 (19)一、概述 (19)二、操作说明 (20)三、同等条件下，不同轮胎模型的汽车平顺性比较 (27)四、同等条件下，不同车速的汽车平顺性比较 (34)五、同等条件下，不同路面的汽车平顺性比较 (37)第一章、参考资料在ADAMS虚拟样机仿真软件中按照实际使用情况可将轮胎模型分为操作性分析轮胎模型、耐久性分析即3D接触分析轮胎模型以及摩托车用轮胎模型三大类。
由于本文中主要研究的是轮胎与路面间垂直力所引起的冲击振动情况，故应选用操纵性分析轮胎模型，其使用的是point follower的方式来计算轮胎由于路面不平激励所引起的垂直力。
在操纵性分析轮胎模型组中提供了MF-tyre、Pacejka ’89、Pacejka ’94、PAC2002、Fiala、5.2.1以及UA等轮胎模型，用户可以根据实际需要对模型数据进行修改。
通过修改软件自带的轮胎模型文件来生成轮胎模型能够保证车辆仿真要求的一致性，从而保证仿真结果的可靠性。
第二章、建模说明一、生成5.2.1前轮胎模型为建立轮胎模型，需先将acar共享文件中需要的轮胎数据复制到个人文件夹，本文进行汽车平顺性分析，适用于平顺性分析的轮胎模型有MF-tyre、Pacejka ’89、Pacejka ’94、PAC2002、Fiala、5.2.1以及UA等轮胎模型，本文选取4种类型：521_equation、mdi_fiala01、mdi_pac94、uat。
ADAMS培训 第八章 轮胎 tire
• ADAMS/Tire操纵性轮胎模块采用 point-follower 的方法计算轮胎的 正压力并且限于二维的路面模型。 注释：* Pacejka 轮胎模型中所使用计算公式来源于 H.B. Pacejka 博士公开发表的文献，在汽车行业通常指的是 Pacejka 模型。Dr. Pacejka 本人既没有参与这些轮胎模型的开发，也未 以任何方式资助其开发。
• 所有的轮胎模块都支持 ADAMS/Linear 的功能。
MSC Confidential
ADAMS/Tire 模块
• ADAMS/Tire 模块的特色
• 下表列出了 ADAMS/Tire 中各轮胎模块的特色。
MSC Confidential
ADAMS/Tire 模块
• 你应该使用什么类型的轮胎？
• • • • • ADAMS/Tire Handling Module Adams/Tire 3D Shell Road – 先前称为3D Contact Adams/Tire 3D Spline Road –先前称为3D Smooth Road model Specific Tire Models Features in ADAMS/Tire Modules
• ADAMS/Tire 允许你在一个车辆模型中最多可以有 40 个 轮胎。
MSC Confidential
ADAMS/Tire 模块
• ADAMS/Tire 有一系列的轮胎模块，你可以结合 ADAMS/View、 ADAMS/Solver、ADAMS/Car和 ADAMS/Chassis使用。这些模 块使你能够模拟常见的各种车辆如：轿车、卡车或飞机上的橡胶 轮胎。特别是，这些轮胎模块可以模拟轮胎上产生的力以使车辆 加速、制动或转向等。在 ADAMS/Tire 中可以用的轮胎模块有：
用魔术公式建立轮胎模型
用魔术公式建立轮胎模型根据资料，通过给定的参数以及对一些比例因子的设定，用魔术公式建立如下轮胎模型。
1.纯纵滑情况：%% Longitudinal Force (pure longitudinal slip)%% k is input value, means slip ratio%% Fx0 is output value, means longitudinal forcek=linspace(-1,1,300);dfz=(Fz-Fz0)/Fz0;C_x=P_Cx1; %取lam(Cx)=1 shape factoru_x=(P_Dx1+P_Dx2*dfz)*0.9; %取lam(ux*)=0.9 composite friction scaling fatorD_x=u_x*Fz; %zeta(1-8)都取1S_Hx=(P_Hx1+P_Hx2*dfz); %取lam(Hx)=1 horizontal shiftk_x=k+S_Hx;E_x=(P_Ex1+P_Ex2*dfz+P_Ex3*dfz^2)*(1-P_Ex4*sign(k_x)); %取lam(Ex)=1 curvature factorK_xk=Fz*(P_Kx1+P_Kx2*dfz)*exp(P_Kx3*dfz); %取lam(Kxk)=1 break slip stiffnessB_x=K_xk/(C_x*D_x+0.1); %取epsilon=0.1S_vx=Fz*(P_Vx1+P_Vx2*dfz)*(V0/(0.1+V0)); %lam(Vx),lam(ux),zeta1=1,epsil on=0.1Fx0=D_x*sin(C_x*atan(B_x*k_x-E_x.*(B_x*k_x-atan(B_x*k_x))))+S_vx;figure(1);plot(k,Fx0,'linewidth',1.5);gridxlabel('纵向滑移率');ylabel('纵向力/（N）');title('纵向力--滑移率(纯纵滑)');2.纯侧滑情况：%% Lateral Force and Torque (pure side slip)%% a is input value, means slip angle%% Fy0 is output value, means side force%% Mz0 is output value, means aligning torquea=linspace(-15,15,300); %侧偏角取-15-15 度ta=tan(a*pi/180);sr=sin(r); %r是外倾角，sr 表示r*C_y=P_Cy1; %取lam(Cy)=1u_y=(P_Dy1+P_Dy2*dfz)/(1+P_Dy3*sr^2); %取lam(uy*)=1D_y=u_y*Fz; %zeta(1-8)都取1K_ya=P_Ky1*Fz0*sin(P_Ky4*atan(Fz/((P_Ky2+P_Ky5*sr^2)*Fz0)))/(1+P_Ky3*sr^2); %取lam（Kya）=1 zeta(3)=1B_y=K_ya/(C_y*D_y); %取epsilony=0；K_yr0=Fz*(P_Ky6+P_Ky7*dfz); %取lam（Kyr)=1S_Vyr=Fz*(P_Vy3+P_Vy4*dfz)*sr;%lam(kyr)=1, camber force stiffness 后面的修正系数全部取1S_Hy=(P_Hy1+P_Hy2*dfz)+(K_yr0*sr-S_Vyr)/(K_ya+0.1); %zeta(0,4)都取1 epsilon(k)=0.1 S_Vy=Fz*(P_Vy1+P_Vy2*dfz)+S_Vyr; %lam(Vy,uy)=1,zeta(2)=1ay=ta+S_Hy; %tan(sa)表示横向侧偏角a*E_y=(P_Ey1+P_Ey2*dfz)*(1+P_Ey5*sr^2-(P_Ey3+P_Ey4*sr)*sign(ay)); %lam(ey)=1Fy0=D_y*sin(C_y*atan(B_y*ay-E_y.*(B_y*ay-atan(B_y*ay))))+S_Vy;figure(2);plot(a,Fy0,'linewidth',1.5);gridxlabel('侧偏角');ylabel('侧向力/（N）');title('侧向力-侧偏角(纯侧滑)');C_r=1;C_t=q_Cz1;B_t=(q_Bz1+q_Bz2*dfz+q_Bz3*dfz^2)*(1+q_Bz5*abs(sr)+q_Bz6*sr^2);S_Ht=q_Hz1+q_Hz2*dfz+(q_Hz3+q_Hz4*dfz)*sr;a_t=ta+S_Ht;B_r=(q_Bz9+q_Bz10*B_y*C_y);E_t=(q_Ez1+q_Ez2*dfz+q_Ez3*dfz^2)*(1+(q_Ez4+q_Ez5*sr)*(2/pi)*atan(B_t*C_t*a_t));S_Hf=S_Hy+S_Vy/K_ya;ar=ta+S_Hf;D_t0=Fz*(R0/Fz0)*(q_Dz1+q_Dz2*dfz); %取lambda(t)=1D_t=D_t0*(1+q_Dz3*abs(sr)+q_Dz4*sr^2);t0=D_t*cos(C_t*atan(B_t*a_t-E_t.*(B_t*a_t-atan(B_t*a_t))));D_r=Fz*R0*(q_Dz6+q_Dz7*dfz)+(q_Dz8+q_Dz9*dfz)*sr+(q_Dz10+q_Dz11*dfz)*sr*abs(sr);M_zr0=D_r*cos(C_r*atan(B_r*ar)); M_z0=M_zr0-t0.*Fy0;figure(3);plot(a,M_z0,'linewidth',1.5);grid on;xlabel('侧偏角');ylabel('回正力矩/（N）');title('回正力矩-侧偏角(纯侧滑)')3.组合滑移情况：%% Longitudinal Force (combined slip)%% aS is input value, means slip angle%% Fx is output value, means longitudinal forceS_Hxa=r_Hx1;E_xa=r_Ex1+r_Ex2*dfz;C_xa=r_Cx1;B_xa=(r_Bx1+r_Bx3*sr^2)*cos(atan(r_Bx2*k)); %lam(xa)=1,influence on Fx 矩阵aS=ta+S_Hxa; %矩阵G_xa0=cos(C_xa*atan(B_xa*S_Hxa-E_xa*(B_xa*S_Hxa-atan(B_xa*S_Hxa))));G_xa=cos(C_xa*atan(B_xa.*aS-E_xa*(B_xa.*aS-atan(B_xa.*aS))))./G_xa0;Fx=G_xa.*Fx0;figure(4);plot(a,Fx,'linewidth',1.5);grid on;xlabel('侧偏角');ylabel('纵向力/（N）');title('纵向力-侧偏角(混合滑移)');%% Lateral Force (combined slip)%% kS is input value, means slip ratio%% Fy is output value, means longitudinal forceC_yk=r_Cy1;E_yk=r_Ey1+r_Ey2*dfz;B_yk=(r_By1+r_By4*sr^2)*cos(atan(r_By2*(k-r_By3))); %lam(yk)=1D_Vyk=u_y*Fz*(r_Vy1+r_Vy2*dfz+r_Vy3*sr)*cos(atan(r_Vy4*ta)); %zeta(2)=1S_Vyk=D_Vyk.*sin(r_Vy5*atan(r_Vy6*k)); %取lam（Vyk）=1 S_Hyk=r_Hy1+r_Hy2*dfz;kS=k+S_Hyk;G_yk0=cos(C_yk*atan(B_yk*S_Hyk-E_yk*(B_yk*S_Hyk-atan(B_yk*S_Hyk))));G_yk=cos(C_yk*atan(B_yk.*kS-E_yk*(B_yk.*kS-atan(B_yk.*kS))))/G_yk0;Fy=G_yk.*Fy0+S_Vyk;figure(5);plot(k,Fy,'linewidth',1.5);grid on;xlabel('纵向滑移率');ylabel('侧向力/（N）');title('侧向力-纵向滑移率(混合滑移)');%% Aligning Torque (combined slip)%% ateq is input value, means slip angle%% Mz is output value, means Aligning Torqueateq=(sqrt(a_t.^2+(K_xk/K_ya)^2*(k.^2))).*sign(a_t);areq=(sqrt(ar.^2+(K_xk/K_ya)^2*(k.^2))).*sign(ar);M_zr=D_r*(C_r*atan(B_r*areq));s=R0*(S_sz1+S_sz2*(Fy/Fz0)+(S_sz3+S_sz4*dfz)*sr); %取lambda(s)=1 F_yy=Fy-S_Vyk;t=D_t*cos(C_t*atan(B_t*ateq-E_t.*(B_t*ateq-atan(B_t*ateq))));M_zz=-t.*F_yy;Mz=M_zz+M_zr+s.*Fx;figure(6);plot(a,Mz,'linewidth',1.5);grid on;xlabel('侧偏角');ylabel('回正力矩/（N）');title('回正力矩-侧偏角(混合滑移)');。
轮胎模型-PPT精品文档
• 二、 用于耐久性分析的轮胎模型
• 三维接触模型，考虑了轮胎胎侧截面的几何特性，并把轮 胎沿宽度方向离散，用等效贯穿体积的方法来计算垂直力， 可以用于三维路面。该模型是一个单独的License，但是如 果用户只购买Durability TIRE，只能用Fiala模型计算操稳。 • 除了上述两类模型以外，还有环模型，作为子午线轮胎的 近似，研究轮胎本身的振动特性，成为国际上仿真轮胎在 短波不平路面动特性的主流模型，是目前发展比较成熟和 得到商业化应用的轮胎模型，其中具有代表性的是F-tire和 SWIFT轮胎模型。
• SWIFT模型（Short Wave Intermediate Frequency TIRE Model） • SWIFT 模型是由荷兰 Delft 工业大学和 TNO 联合开发的，是 一个刚性环模型，在环模型的基础上只考虑轮胎的 0阶转动 和1阶错动这两阶模态，此时轮胎只作整体的刚体运动而并 不发生变形。在只关心轮胎的中低频特性时可满足要求。由 于不需要计算胎体的变形，刚性环模型的计算效率大大提高， 可用于硬件在环仿真进行主动悬架和ABS的开发。在处理面 外动力学问题时，SWIFT使用了魔术公式。
轮胎模型
一、轮胎模型简介 二 、ADAMS/TIRE 三、轮胎的特性文件
严金霞
2009年1月
• 轮胎是汽车重要的部件，它的结构参数和力学特性决定 着汽车的主要行驶性能。轮胎所受的垂直力、 纵向力、 侧向力和回正力矩对汽车的平顺性、 操纵稳定性和安全 性起重要作用。 • 轮胎模型对车辆动力学仿真技术的发展及仿真计算结果 有很大影响，轮胎模型的精度必须与车辆模型精度相匹 配。因此，选用轮胎模型是至关重要的。由于轮胎具有 结构的复杂性和力学性能的非线性，选择符合实际又便 于使用的轮胎模型是建立虚拟样车模型的关键。
ADAMS轮胎试验台(Tire Testrig)使用方法
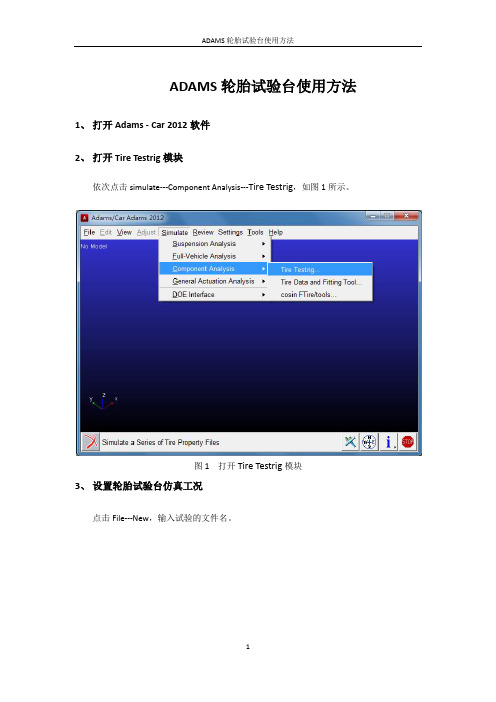
ADAMS轮胎试验台使用方法1、打开Adams - Car 2012软件2、打开Tire Testrig模块依次点击simulate---Component Analysis---Tire Testrig，如图1所示。
图1 打开Tire Testrig模块3、设置轮胎试验台仿真工况点击File---New，输入试验的文件名。
图2 新建试验台1、选择轮胎标签2、选择轮胎特性文件3、设置轮胎质量、转动惯量图3 轮胎设置图4 路面设置图5 轮胎运动设置 1、选择路面标签 2、选择路面类型，如平路面、凸块、路面文件3、设定路面运动方式1、选择轮胎运动标签2、轮胎纵向初速度3、轮胎旋转运动，可以设置纵向滑移率1、选择轮胎负载标签2、设置垂向力或运动3、设置纵向力或运动4、设置制动力矩图6 轮胎负载的设置1、选择平台输出标签2、设置平台侧向输入3、设置平台倾角图7 试验平台输出设置图8 弹簧、减震器设置4、 轮胎试验仿真在任意界面点击Run It ，如图9所示。
本试验工况为：轮胎特性文件为pac2002_195_65R15.tir ；路面为平路面；车轮质心纵向速度为20m/s ，车轮质心垂直加载为3000N ；轮胎侧偏角按正弦波变化，波峰为15度。
图9 开始仿真5、 仿真结果仿真结束后会自动进入ADAMS 后处理模块，点击File---Import---Requestrian File，如图1、选择弹簧阻尼标签3、设置弹簧刚度4、设置阻尼2、设置垂向预加载10所示。
在出现的对话框的File Name，右击选择Search，选择结果文件所在的文件夹，如图11所示。
选中结果文件，点击打开，如图12所示。
图10 导入结果文件图11 选择结果文件图12 选中结果文件图13 后处理曲线选择Requests 设置曲线纵坐标设置曲线横坐标图14 轮胎侧偏角与时间曲线图15 轮胎侧向力与时间曲线图16 轮胎侧向力与侧偏角曲线。
ADAMS轮胎试验台(Tire Testrig)使用方法
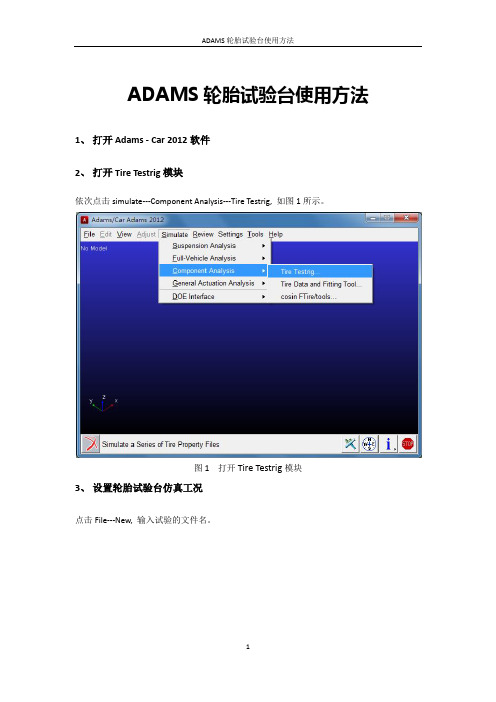
ADAMS轮胎试验台使用方法1、打开Adams - Car 2012软件2、打开Tire Testrig模块依次点击simulate---Component Analysis---Tire Testrig, 如图1所示。
图1 打开Tire Testrig模块3、设置轮胎试验台仿真工况点击File---New, 输入试验的文件名。
图2 新建试验台1、选择轮胎标签2、选择轮胎特性文件3、设置轮胎质量、转动惯量图3 轮胎设置图4 路面设置图5 轮胎运动设置 1、选择路面标签 2、选择路面类型，如平路面、凸块、路面文件3、设定路面运动方式1、选择轮胎运动标签2、轮胎纵向初速度3、轮胎旋转运动，可以设置纵向滑移率1、选择轮胎负载标签2、设置垂向力或运动3、设置纵向力或运动4、设置制动力矩图6 轮胎负载的设置1、选择平台输出标签2、设置平台侧向输入3、设置平台倾角图7 试验平台输出设置图8 弹簧、减震器设置4、 轮胎试验仿真在任意界面点击Run It, 如图9所示。
本试验工况为：轮胎特性文件为pac2002_195_65R15.tir ；路面为平路面；车轮质心纵向速度为20m/s, 车轮质心垂直加载为3000N ；轮胎侧偏角按正弦波变化, 波峰为15度。
图9 开始仿真5、 仿真结果仿真结束后会自动进入ADAMS 后处理模块, 点击File---Import---Requestrian File, 如图10所1、选择弹簧阻尼标签3、设置弹簧刚度4、设置阻尼2、设置垂向预加载示。
在出现的对话框的File Name, 右击选择Search, 选择结果文件所在的文件夹, 如图11所示。
选中结果文件, 点击打开, 如图12所示。
图10 导入结果文件图11 选择结果文件图12 选中结果文件图13 后处理曲线选择Requests 设置曲线纵坐标设置曲线横坐标图14 轮胎侧偏角与时间曲线图15 轮胎侧向力与时间曲线图16 轮胎侧向力与侧偏角曲线。
使用魔术公式的轮胎模型
使用魔术公式的轮胎模型使用魔术公式的轮胎模型主要有Pacejka ’89、Pacejka ’94、MF-Tyre 、MF-Swift 四种。
Pacejka ’89和’94轮胎模型Pacejka ’89 和’94轮胎模型是以魔术公式主要提出者H. B. Pacejka 教授命名的，根据其发布的年限命名。
目前有两种直接被ADAMS 引用。
魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式就可以完整地表达轮胎的纵向力F x 、侧向力F y 、回正力矩M z 、翻转力矩M x 、阻力矩M y 以及纵向力、侧向力的联合作用工况，故称为“魔术公式”。
魔术公式的一般表达式为：()()(){}[]Bx Bx E Bx C D x Y arctan arctan sin --=式中Y(x)可以是侧向力，也可以是回正力矩或者纵向力，自变量x 可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B 、C 、D 依次由轮胎的垂直载荷和外倾角来确定。
Pacejka ’89轮胎模型认为轮胎在垂直、侧向方向上是线性的、阻尼为常量，这在侧向加速度常见范围≤0.4g ，侧偏角≤5°的情景下对常规轮胎具有很高的拟合精度。
此外，由于魔术公式基于试验数据，除在试验范围的高精度外，甚至在极限值以外一定程度仍可使用，可以对有限工况进行外推且具有较好的置信度。
魔术公式正在成为工业标准，即轮胎制造商向整车厂提供魔术公式系数表示的轮胎数据，而不再是表格或图形。
基于魔术公式的轮胎模型还有较好的健壮性，如果没有某一轮胎的试验数据，而使用同类轮胎数据替代仍可取得很好的效果。
图 基于魔术公式的轮胎模型的输入和输出变量Pacejka ’89轮胎力与力矩的计算 轮胎纵向力计算公式为：()()()()()V X S BX BX E BX C D F +--=111arctan arctan sin其中X 1为纵向力组合自变量：X 1=(κ+S h )，κ为纵向滑移率（负值出现在制动态，-100表示车轮抱死）C ——曲线形状因子，纵向力计算时取B 0值：C = B 0D ——巅因子，表示曲线的最大值：Z Z F B F B D 221+= BCD ——纵向力零点处的纵向刚度：()ZF B Z Z e F B F B BCD 5423-⨯+=B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：109B F B S Z h += S v ——曲线的垂直方向漂移：S v =0E ——曲线曲率因子，表示曲线最大值附近的形状：8726BF B F B E Z Z ++=图 轮胎属性文件中的纵向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎侧向力计算公式为：()()()()()V Y S BX BX E BX C D F +--=111arctan arctan sin此时的X 1为侧向力计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，侧向力计算时取A 0值：C = A 0 D ——巅因子，表示曲线的最大值：Z Z F A F A D 221+= BCD ——侧向力零点处的侧向刚度：()γ5431arctan2sin A A F A BCD Z-⨯⎪⎪⎭⎫ ⎝⎛= B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：γ8109A A F A S Z h ++=曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数曲线曲率因子计算系数S v ——曲线的垂直方向漂移：131211A F A F A S Z Z V ++=γE ——曲线曲率因子，表示曲线最大值附近的形状：76AF A E Z +=图 轮胎属性文件中的侧向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎回正力矩计算公式为：()()()()()V Z S BX BX E BX C D M +--=111arctan arctan sin此时的X 1为回正力矩计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，回正力矩计算时取C 0值：C = C 0 D ——巅因子，表示曲线的最大值：Z Z F C F C D 221+=BCD ——回正力矩零点处的扭转刚度：()()ZF C Z Z e C F C F C BCD 564231-⨯-⨯+=γB – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：131211C F C C S Z h ++=γ曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数 曲线曲率因子计算系数 曲线垂直漂移计算系数S v ——曲线的垂直方向漂移：()171615214C F C F C F C S Z Z Z V +++=γE ——曲线曲率因子，表示曲线最大值附近的形状：()()γ1098271C C F C F C E Z Z -⨯++=图 轮胎属性文件中的回正力矩计算系数数据块图 Pacejka ’89轮胎回正力矩示例侧偏刚度（Lateral Stiffness ）侧偏刚度在Pacejka ’89和’94轮胎模型中假定是一个常量，在轮胎属性文件的参数PARAMETER 数据段中通过LATERAL_STIFFNESS 语句设定。
轮胎模型 PPT课件
• FTire是高分辨率物理轮胎模型，需要每秒数百万次评价路 面，为了实现空间和时间分辨率，路面模型选择很重要。 RGR路面（规则的栅格路面）是一个高分辨率的路面模型， 它采用等距网格避免寻找三角单元的节点，可选带有弧形中 心线，是特别适合以满足需求的效率，准确性和灵活性的路 面模型。因此，除了简单的几何参数的障碍路面模型，RGR 路面是FTire的首选路面描述方法。
• 5）Fiala模型 是弹性基础上的梁模型，不考虑外倾和松弛长 度。当不把内倾角作为主要因数且把纵向滑移和横向滑移分 开对待的情况下，对于简单的操纵性分析可得到合理的结果。
• 适用范围：有效频率到0.5Hz，可以用于二维和三维路面， 当与2D路面作用时是点接触；当与3D路面作用时，等效贯 穿体积的方法来计算垂直力。
二维路面、三维路面，还支持3D三角网格路面；RGR路面 文件（规则的栅格路面）；所有COSIN/ev 路面模型，包括 大量的被参数化的障碍定义的路面文件、滚筒的旋转鼓路 面和空间的试验场地 。 • 这些路面模型可在所有环境中的支持FTire ，且不需要单独 的许可证。
• 以下的路面模型需要各自软件的安装环境和许可证
5.80 MB 5.91 MB
0.21 s
0.28 s
•相对于不规则三角网格路面，RGR道路提供大量和可扩展 的减少文件大小，减小内存的需求，减少文件加载时间和 CPU评价的时间。
• FTire提供了一个辅助程序FTire/roadtools工具箱来产生， 分 析 和 处 理 所 有 的 道 路 文 件 ， 包 括 RGR 路 面 模 型 。
ADAMS轮胎模型简介
详细介绍轮胎模型，主要是自己做课题时，用到的整理汇总出来的，轮胎这部分的资料比较少的，记录下来帮助大家一起学习一起进步；主要分以下两部分介绍一、轮胎模型简介轮胎是汽车重要的部件，它的结构参数和力学特性决定着汽车的主要行驶性能。
轮胎所受的垂直力、纵向力、侧向力和回正力矩对汽车的平顺性、操纵稳定性和安全性起重要作用。
轮胎模型对车辆动力学仿真技术的发展及仿真计算结果有很大影响，轮胎模型的精度必须与车辆模型精度相匹配。
因此，选用轮胎模型是至关重要的。
由于轮胎具有结构的复杂性和力学性能的非线性，选择符合实际又便于使用的轮胎模型是建立虚拟样车模型的关键。
一、轮胎模型简介轮胎建模的方法分为三种：1）经验—半经验模型针对具体轮胎的某一具体特性。
目前广泛应用的有Magic Formula公式和吉林大学郭孔辉院士利用指数函数建立的描述轮胎六分力特性的统一轮胎半经验模型UniTire，其主要用于车辆的操纵动力学的研究。
2）物理模型根据轮胎的力学特性，用物理结构去代替轮胎结构，用物理结构变形看作是轮胎的变形。
比较复杂的物理模型有梁、弦模型。
特点是具有解析表达式，能探讨轮胎特性的形成机理。
缺点是精确度较经验—半经验模型差，且梁、弦模型的计算较繁复。
3）有限元模型基于对轮胎结构的详细描述 ,包括几何和材料特性，精确的建模能较准确的计算出轮胎的稳态和动态响应。
但是其与地面的接触模型很复杂，占用计算机资源太大，在现阶段应用于不平路面的车辆动力学仿真还不现实，处于研究阶段。
主要用于轮胎的设计与制造二、ADAMS/TIRE轮胎不是刚体也不是柔体，而是一组数学函数。
由于轮胎结构材料和力学性能的复杂性和非线性以及适用工况的多样性，目前还没有一个轮胎模型可适用于所有工况的仿真，每个轮胎模型都有优缺点和适用的范围。
必须根据需要选择合适的轮胎模型。
ADAMS/TIRE分为两大类：一）.用于操稳分析的轮胎模型魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式完整地表达轮胎的纵向力、侧向力、回正力矩、翻转力矩、阻力矩以及纵向力、侧向力的联合作用工况，主要包括以下的前四种模型。
轮胎模型
• FTire提供了一个辅助程序FTire/roadtools工具箱来产生， 分 析 和 处 理 所 有 的 道 路 文 件 ， 包 括 RGR 路 面 模 型 。 FTire/roadtools易于使用的图形用户界 三维接触模型，考虑了轮胎胎侧截面的几何特性，并把轮 胎沿宽度方向离散，用等效贯穿体积的方法来计算垂直力， 可以用于三维路面。该模型是一个单独的License，但是如 果用户只购买Durability TIRE，只能用Fiala模型计算操稳。 • 除了上述两类模型以外，还有环模型 环模型，作为子午线轮胎的 环模型 近似，研究轮胎本身的振动特性，成为国际上仿真轮胎在 短波不平路面动特性的主流模型，是目前发展比较成熟和 得到商业化应用的轮胎模型，其中具有代表性的是F-tire和 和 SWIFT轮胎模型。 轮胎模型。 轮胎模型
• 适用范围 适用范围：有效频率高达120-150Hz；可用于短波不平路 面，即障碍物的尺寸可以小于轮胎的印迹；可对不同的种 类的振动激励作出响应；可在相对运动的地面和各种各样 的试验台上进行仿真；可在三维路面上进行耐久性分析； 在水平路面和随机路面上对车辆的牵引和操纵性进行仿真 分析；可进行高动力悬浮控制系统对轮胎影响的评估 。 • 主要是针对乘坐舒适性（不平路面的制动、侧偏，不同速 度的越过障碍物以及4柱激励试验台）、耐久性以及操纵 性能（ABS制动时的制动距离，汽车的原地转向等）方面 的应用而设计的。此外，该模型的逼真度、细节和计算速 度之间提供了一个有效的折衷方法，在频域提供了有效地 分析结果，容易从轮胎的测量数据中获得模型参数。
• 可用于研究一些复杂的工况, 例如:不平路面的侧偏和ABS 制动。在处理轮胎-地面的接触问题时, SWIFT采用了等效 路形的方法，所用的等效路形是由一个专门的包容模型算 出来的。所以, SWIFT模型要自带一个包容模型来提供等 效路形，这也是它的缺点之一。 • 适用范围：有效频率为60-100Hz，可用于短波不平路面。 • 注： SWIFT模型所用到的路面模型要有合适的采样间隔， 否则会应用以内插值替换的数据，采样间隔一般为 0.1~0.2 m 或者更大。
ADAMS轮胎模型简介
详细介绍轮胎模型，主要是自己做课题时，用到的整理汇总出来的，轮胎这部分的资料比较少的，记录下来帮助大家一起学习一起进步；主要分以下两部分介绍一、轮胎模型简介轮胎是汽车重要的部件，它的结构参数和力学特性决定着汽车的主要行驶性能。
轮胎所受的垂直力、纵向力、侧向力和回正力矩对汽车的平顺性、操纵稳定性和安全性起重要作用。
轮胎模型对车辆动力学仿真技术的发展及仿真计算结果有很大影响，轮胎模型的精度必须与车辆模型精度相匹配。
因此，选用轮胎模型是至关重要的。
由于轮胎具有结构的复杂性和力学性能的非线性，选择符合实际又便于使用的轮胎模型是建立虚拟样车模型的关键。
一、轮胎模型简介轮胎建模的方法分为三种：1）经验—半经验模型针对具体轮胎的某一具体特性。
目前广泛应用的有 Magic Formula公式和吉林大学郭孔辉院士利用指数函数建立的描述轮胎六分力特性的统一轮胎半经验模型UniTire ，其主要用于车辆的操纵动力学的研究。
2）物理模型根据轮胎的力学特性，用物理结构去代替轮胎结构，用物理结构变形看作是轮胎的变形。
比较复杂的物理模型有梁、弦模型。
特点是具有解析表达式，能探讨轮胎特性的形成机理。
缺点是精确度较经验—半经验模型差，且梁、弦模型的计算较繁复。
3）有限元模型基于对轮胎结构的详细描述 , 包括几何和材料特性，精确的建模能较准确的计算出轮胎的稳态和动态响应。
但是其与地面的接触模型很复杂，占用计算机资源太大，在现阶段应用于不平路面的车辆动力学仿真还不现实，处于研究阶段。
主要用于轮胎的设计与制造二、 ADAMS/TIRE轮胎不是刚体也不是柔体，而是一组数学函数。
由于轮胎结构材料和力学性能的复杂性和非线性以及适用工况的多样性，目前还没有一个轮胎模型可适用于所有工况的仿真，每个轮胎模型都有优缺点和适用的范围。
必须根据需要选择合适的轮胎模型。
ADAMS/TIRE分为两大类：一） .用于操稳分析的轮胎模型魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式完整地表达轮胎的纵向力、侧向力、回正力矩、翻转力矩、阻力矩以及纵向力、侧向力的联合作用工况，主要包括以下的前四种模型。
基于_魔术公式_的轮胎动力学仿真分析_郑香美
Ｃ 为曲 线 形 状 因 子 ； Ｅ 为 曲 线 曲 率 因 子； Ｓ ｈ 为曲线 水平方向漂移 ； Ｓ ｖ 为曲线垂直方向漂移 。
１． １ 纯转弯工况 轮胎的侧偏特性是轮胎力学特性的一个重要组 成部分 ， 侧偏特性主要是指侧偏力 、 回正力矩与侧偏 角的关系 ， 忽略了回正力矩的影响 ， 针对侧偏力与侧 偏角的关系进行了仿真分析 。 当轮 胎 处 于 一 边 滚 动 一 边 侧 滑 状 态 时 ， 在轮胎 上会发生摩擦力 。 此摩擦力在轮胎侧向的分力是侧 向力 ， 切向的分力是滚动阻力 ， 在与轮胎前进方向成 直角的分力为侧偏 力 ， 而在前进方向的分力是侧偏 且随着侧偏角没有太大 阻力 。 由于滚动阻 力 较 小 ， 的变化 ， 故可以 略 而 不 计 。 因 此 在 侧 偏 角 小 的 情 况 下， 侧向力和侧偏力大体上可以看作是同样的值 。 由“ 魔术公式 ” 的 一 般 形 式， 得到在纯转弯单一 、 其侧向力 Ｆ 轮胎所受到的地 工况下 ， ０ 与 侧 偏 角α ｙ 面垂直载荷 Ｆ ｚ 之间的关系为 ： ｛ ［ Ｆ ０＝ （ Ｄｙ ｓ ｉ ｎ Ｃ ａ ｒ ｃ ｔ ａ ｎ Ｂｙ ｘ－Ｅｙ （ Ｂｙ ｘ－ ｙ 烄ｙ ］ ｝ （ ） Ｂｙ ｘ） ＋Ｓ ２ ａ ｒ ｃ ｔ ａ ｎ ｖ 烅 ｘ＝ α＋Ｓ ｈ 烆 ２ 其中 ； Ｃ ． ３； Ｄｙ ＝ａ Ｆ Ｆ Ｂｙ Ｃｙ Ｄｙ ＝ １ ｚ ＋ａ ２ ｚ； ｙ ＝１ ］（ ； ａ ｓ ｉ ｎ［ ａ ａ ｒ ｃ ｔ ａ ｎ（ ａ Ｆ １－ａ Ｂｙ ＝ γ︱ ） ３ ４ ５ ｚ） １ ２︱ ２ ／ ； ； Ｂｙ Ｃｙ Ｄｙ Ｃ Ｄｙ Ｅｙ ＝ａ Ｆ ａ Ｆ ａ ａ Ｓ γ； ６ ｚ＋ ７ ｚ＋ ８ Ｓ ｈ＝ ９ ｖ ｙ
５］ 。 工况下的力学特性曲线 ［
使用魔术公式的轮胎模型
使用魔术公式的轮胎模型使用魔术公式的轮胎模型主要有Pacejka ’89、Pacejka ’94、MF-Tyre 、MF-Swift 四种。
Pacejka ’89和’94轮胎模型Pacejka ’89 和’94轮胎模型是以魔术公式主要提出者H. B. Pacejka 教授命名的，根据其发布的年限命名。
目前有两种直接被ADAMS 引用。
魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式就可以完整地表达轮胎的纵向力F x 、侧向力F y 、回正力矩M z 、翻转力矩M x 、阻力矩M y 以及纵向力、侧向力的联合作用工况，故称为“魔术公式”。
魔术公式的一般表达式为：()()(){}[]Bx Bx E Bx C D x Y arctan arctan sin --=式中Y(x)可以是侧向力，也可以是回正力矩或者纵向力，自变量x 可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B 、C 、D 依次由轮胎的垂直载荷和外倾角来确定。
Pacejka ’89轮胎模型认为轮胎在垂直、侧向方向上是线性的、阻尼为常量，这在侧向加速度常见范围≤0.4g ，侧偏角≤5°的情景下对常规轮胎具有很高的拟合精度。
此外，由于魔术公式基于试验数据，除在试验范围的高精度外，甚至在极限值以外一定程度仍可使用，可以对有限工况进行外推且具有较好的置信度。
魔术公式正在成为工业标准，即轮胎制造商向整车厂提供魔术公式系数表示的轮胎数据，而不再是表格或图形。
基于魔术公式的轮胎模型还有较好的健壮性，如果没有某一轮胎的试验数据，而使用同类轮胎数据替代仍可取得很好的效果。
图 基于魔术公式的轮胎模型的输入和输出变量Pacejka ’89轮胎力与力矩的计算 轮胎纵向力计算公式为：()()()()()V X S BX BX E BX C D F +--=111arctan arctan sin其中X 1为纵向力组合自变量：X 1=(κ+S h )，κ为纵向滑移率（负值出现在制动态，-100表示车轮抱死）C ——曲线形状因子，纵向力计算时取B 0值：C = B 0D ——巅因子，表示曲线的最大值：Z Z F B F B D 221+= BCD ——纵向力零点处的纵向刚度：()ZF B Z Z eF B F B BCD 5423-⨯+=B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：109B F B S Z h += S v ——曲线的垂直方向漂移：S v =0E ——曲线曲率因子，表示曲线最大值附近的形状：8726BF B F B E Z Z ++=图 轮胎属性文件中的纵向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎侧向力计算公式为：()()()()()V Y S BX BX E BX C D F +--=111arctan arctan sin此时的X 1为侧向力计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，侧向力计算时取A 0值：C = A 0 D ——巅因子，表示曲线的最大值：Z Z F A F A D 221+=BCD ——侧向力零点处的侧向刚度：()γ5431arctan 2sin A A F A BCD Z -⨯⎪⎪⎭⎫⎝⎛= B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：γ8109A A F A S Z h ++=曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数曲线曲率因子计算系数S v ——曲线的垂直方向漂移：131211A F A F A S Z Z V ++=γE ——曲线曲率因子，表示曲线最大值附近的形状：76AF A E Z +=图 轮胎属性文件中的侧向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎回正力矩计算公式为：()()()()()V Z S BX BX E BX C D M +--=111arctan arctan sin此时的X 1为回正力矩计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，回正力矩计算时取C 0值：C = C 0 D ——巅因子，表示曲线的最大值：Z Z F C F C D 221+=BCD ——回正力矩零点处的扭转刚度：()()ZF C Z Z e C F C F C BCD 564231-⨯-⨯+=γB – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：131211C F C C S Z h ++=γ曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数 曲线曲率因子计算系数 曲线垂直漂移计算系数S v ——曲线的垂直方向漂移：()171615214C F C F C F C S Z Z Z V +++=γE ——曲线曲率因子，表示曲线最大值附近的形状：()()γ1098271C C F C F C E Z Z -⨯++=图 轮胎属性文件中的回正力矩计算系数数据块图 Pacejka ’89轮胎回正力矩示例侧偏刚度（Lateral Stiffness ）侧偏刚度在Pacejka ’89和’94轮胎模型中假定是一个常量，在轮胎属性文件的参数PARAMETER 数据段中通过LATERAL_STIFFNESS 语句设定。
魔术轮胎公式
2.3.3“魔术公式”轮胎模型“魔术公式”轮胎模型用三角函数的组合公式拟合实验轮胎数据，用一套形式相同的公式就能完整的表达纵向力、侧向力、回正力矩以及纵向力、侧向力联合作用的工况。
该模型统一性强，能描述轮胎所有稳态力学特性，编程方便；可从实际轮胎实验获得，且需拟合的参数少，有实际的物理意义；简单实用，模拟精度高，并能最大限度地反映出车辆的实际运作状况。
故本文采用“魔术公式”轮胎模型一起建立整车系统动力学模型[14]。
“魔术公式”的一般表达式为：SY=Dsin(Carctan(Bφ))+v(2.17)φ=（1-E)(X+h S）+(E/B）arctan(B(X+h S))(2.18)其中，D—峰值因子，表示曲线的最大值；B—刚度因子，B=BCD/(CD)；E—曲线曲率因子，决定曲线最大值附近的形状；C—曲线形状因子，决定曲线的形状特性，即曲线是表示侧向力、纵向力还是回正力矩；S—水平方向漂移；hS—垂直方向漂移；v而Y表示侧向力、纵向力或回正力矩，X表示侧偏角α或滑移率λ。
F和侧倾角γ的函除曲线的形状因子C外，其余每一个参数都是垂直载荷z数用参数拟合的方法得到，一般选代数多项式进行拟合。
曲线零点的水平漂移和垂直漂移用来描述由于轮胎制造误差而造成的轮胎圆锥效应和帘布层转向效应。
一般地，曲线零点的水平方向漂移和垂直方向漂移与轮胎侧倾角有关，本文将不考虑轮胎力特性曲线的水平方向漂移和垂直方向漂移，主要从纯滑移及纯侧偏两方面考虑：①纯滑移条件下纵向力公式为：F(λ)=x D sin(x C arctan(x Bλ-x E(x Bλ-arctan(x Bλ))))x0(2.19)式中，x C =1.65；x D =z z F a F a 221+；x B =)exp()5425z z z F a F a F a -+（/(x C x D )；x E =8726a F a F a z z ++；λ—车轮滑移率；x0F (λ)—由纯滑移条件下计算出的纵向力的值。
ADAMS CAR不同轮胎模型的整车平顺性分析实例
ADAMS/CAR不同轮胎模型的整车平顺性分析实例在相同条件下，对使用不同轮胎模型的整车模型进行平顺性仿真。
仿真结束后，在后处理模块获得汽车底盘质心处x 、y 、z 三个轴向的加速度曲线。
为了确定路面引起汽车振动所在的频率范围，还需获取相应的加速度功率谱密度。
最后，求加速度加权均方根值，评价振动对人体的影响。
目录第一章、参考资料 (1)第二章、建模说明 (5)一、生成5.2.1前轮胎模型 (5)二、生成5.2.1后轮胎模型 (9)三、生成其他三个轮胎模型 (10)四、生成整车模型 (12)第三章、仿真分析 (16)一、平顺性仿真概述 (16)二、随机路面生成 (16)三、平顺性仿真条件设置 (16)四、仿真过程 (17)第四章、结果分析 (19)一、概述 (19)二、操作说明 (20)三、同等条件下，不同轮胎模型的汽车平顺性比较 (27)四、同等条件下，不同车速的汽车平顺性比较 (35)五、同等条件下，不同路面的汽车平顺性比较 (38)第一章、参考资料在ADAMS虚拟样机仿真软件中按照实际使用情况可将轮胎模型分为操作性分析轮胎模型、耐久性分析即3D接触分析轮胎模型以及摩托车用轮胎模型三大类。
由于本文中主要研究的是轮胎与路面间垂直力所引起的冲击振动情况，故应选用操纵性分析轮胎模型，其使用的是point follower的方式来计算轮胎由于路面不平激励所引起的垂直力。
在操纵性分析轮胎模型组中提供了MF-tyre、Pacejka ’89、Pacejka ’94、PAC2002、Fiala、5.2.1以及UA等轮胎模型，用户可以根据实际需要对模型数据进行修改。
通过修改软件自带的轮胎模型文件来生成轮胎模型能够保证车辆仿真要求的一致性，从而保证仿真结果的可靠性。
第二章、建模说明一、生成5.2.1前轮胎模型为建立轮胎模型，需先将acar共享文件中需要的轮胎数据复制到个人文件夹，本文进行汽车平顺性分析，适用于平顺性分析的轮胎模型有MF-tyre、Pacejka ’89、Pacejka ’94、PAC2002、Fiala、5.2.1以及UA等轮胎模型，本文选取4种类型：521_equation、mdi_fiala01、mdi_pac94、uat。
ADAMS路面模型和轮胎UA模型中各全参数含义
2D Road TypesThe available road types are:•DRUM - Tire test drum (requires a zero-speed-capable tire model). •FLAT - Flat road.•PLANK - Single plank perpendicular, or in oblique direction relative to x-axis, with or without bevel edges. • POLY_LINE - Piece-wise linear description of the road profile. The profiles for the left and right track are independent. •POT_HOLE - Single pothole of rectangular shape. •RAMP - Single ramp, either rising or falling. •ROOF - Single roof-shaped, triangular obstacle. •SINE - Sine waves with constant wave length. •SINE_SWEEP - Sine waves with decreasing wave lengths.•STOCHASTIC_UNEVEN - Synthetically generated irregular road profiles that match measured stochastic properties of typical roads. The profiles for left and right track are independent, or may have a certain correlation. Examples of 2D RoadsSample files for all the road types for Adams/Car are in the standard Adams/Car database:install_dir /shared_car_database.cdb/roads.tbl/Sample files for all the road types for Adams/Tire are in: install_dir /solver/atire/Sample files for all the road types for Adams/Chassis are in: install_dir /achassis/examples/rdf/Note that you must select a specific contact method, such as point-follower or equivalent plane, to define how the roads will interact with the tires. Not allcombinations of road, tire, and contact methods are permitted. Allowable combinations are explained in Tire Models help under the description of the specific tire model.2D Road Model ParametersThe [PARAMETERS] block must contain the following data, some of which are independent of the type of road. Learn about parameters:•Independent of Road Type •Drum •Flat •Plank •Polyline•Pothole•Ramp•Roof•Sine•Sweep•Stochastic UnevenParameters Independent of Road TypeThe following parameters are required regardless of the road type.If ROAD_TYPE = drum, then define the following parameters:If ROAD_TYPE = flat, then no further parameters are required.Parameters for Road Type of PlankIf ROAD_TYPE = plank, then define the following parameters:If ROAD_TYPE = poly_line, then the [PARAMETERS] block must have a (XZ_DATA) subblock. The subblock consists of three columns of numerical data:•Column one is a set of x-values in ascending order.•Columns two and three are sets of respective z-values for left and right track.The following is an example of the full [PARAMETERS] Body for a road type of polyline: $---------------------------PARAMETERS[PARAMETERS]OFFSET = 0ROTATION_ANGLE_XY_PLANE = 180$(XZ_DATA)0 0 01000 100 502000 -1000 1003000 -100 1003001 50 04000 -100 100The XZ_DATA subblock can be extremely large. In this case, only the portion that is needed at the moment is loaded. To facilitate efficient reloading while simulation is running, do not use any comment lines in a subblock that contains more than 2000 lines. Parameters for Road Type of PotholeIf ROAD_TYPE = pot_hole, then the parameters are:If ROAD_TYPE = ramp, then the parameters are:If ROAD_TYPE = roof, then the parameters are:If ROAD_TYPE = sine, then the parameters are:amplitude Amplitude of sine wave (a).wave_lengthWave length of sine wave ().start Start of sine waves (traveldistance) (s s).The road height, z, is given by:Parameters for Road Type of Stochastic UnevenA stochastic uneven road profile both for left and right wheels is generated, with properties very close to measured road profiles.In a first step, discrete white noise signals are formed on the basis of nearly uniformly distributed random numbers. Two of these numbers are assigned to every 10 mm of travel path. The distribution of these random numbers is approximated by summing several equally distributed random numbers, taking advantage of the ‘law of large numbers’ of mathematical statistics.Next, these values are integrated with respect to travel distance, using a simplefirst order time-discrete integration filter. The independent variable of that filter is not time, but travel path. That is why the filter cutoff frequency is controlled by a path constant instead of a time constant. The filter process results in two approximate realizations of white velocity noise; that is, two signals, thederivatives of which are close to white noise. Signals with that property are known as road profiles with waviness 2. Several investigations in the past showed that the waviness derived from measured road spectral densities ranges from about 1.8 to 2.2. The last step is to linearly combine the two realizations of the aboveprocess:,, resulting in the left and right profile,. This is done such that the two signals are completely independent if , and identical if:If ROAD_TYPE = stochastic_uneven, then the parameters are:The parameter: Indicates:intensity Variable to control intensity of white velocity noise, whichapproximates measured spectra of road profiles fairly well.path_constant Variable to control high-pass integration filter.correlation_rl Variable to control correlation between left and right track:•If 0, no correlation.•If 1, complete correlation (that is, left track = right track). Can be any value between 0 and 1.startStart of unevenness (travel distance).Parameters for Road Type of SweepIf ROAD_TYPE = sine_sweep, then the parameters are:[PARAMETERS] Data for Road Type of Sine Sweep The parameter: Indicates:start Start of swept sine wave (travel distance) (). endEnd of swept sine wave (travel distance) ().amplitude_at_sta rtAmplitude of swept sine wave at start travel distance (). amplitude_at_end Amplitude of swept sine wave at end travel distance ().wave_length_at_s tartWave length of swept sine wave a start travel distance ().wave_length_at_e ndWave length of swept sine wave at end travel distance. Must be less than or equal to wave_length_at_start ().sweep_type•sweep_type = 0: frequency increases linearly with respect to travel distance. •sweep_type = 1: wave length decreases by a constant factor per cycle. Depending on the value of sweep_type, the road height is given by the following functions, where:• Linear sweep: (sweep_type = 0) The frequency increases linearly with respect to travel distance. The road height value z (s) as function of travel distance s is alculated as follows:Note the factor 2 in the denominator is not an error. The actual frequency (= derivative of the sine function argument with respect to travel path, divided by ; this is not equal to that factor that is multiplied by in the sine function) is given by thefollowing:•Logarithmic sweep: (sweep_type = 1) with every cycle, the wave length decreases by a constant factor. The road height value is calculated as follows:where:is the travel path where theoretically an infinitely high frequency was reached, measured relative to sweep start . Theactual frequency is given by:Using the UA-Tire ModelLearn about using the University of Arizona (UA) tire model:•Background Information •Tire Model Parameters •Force Evaluation •Operating Mode: USE_MODE •Tire Carcass Shape •Property File Format ExampleBackground Information for UA-TireThe University of Arizona tire model was originally developed by Drs. P.E. Nikravesh and G. Gim. Reference documentation: G. Gim, Vehicle Dynamic Simulation with aComprehensive Model for Pneumatic Tires, PhD Thesis, University of Arizona, 1988. The UA-Tire model also includes relaxation effects, both in the longitudinal and lateral direction.The UA-Tire model calculates the forces at the ground contact point as a function of the tire kinematic states, see Inputs and Output of the UA-Tire Model. A description of the inputs longitudinal slip k, side slip a and camber angle can be found in About Tire Kinematic and Force Outputs. The tire deflection and deflection velocity are determined using either a point follower or durability contact model. For more information, see Road Models in Adams/Tire . A description of outputs, longitudinal force Fx, lateral force Fy, normal force Fz, rolling resistance moment My and self aligningmoment Mz is given in About Tire Kinematic and Force Outputs. The required tire model parameters are described in Tire Model Parameters.Inputs and Output of the UA-Tire ModelDefinition of Tire Slip QuantitiesSlip Quantities at Combined Cornering and Braking/TractionThe longitudinal slip velocity Vsx in the SAE-axis system is defined using thelongitudinal speed Vx, the wheel rotational velocity , and the effective rolling radius Re:The lateral slip velocity is equal to the lateral speed in the contact point with respect to the road plane:The practical slip quantities (longitudinal slip) and (slip angle) are calculated with these slip velocities in the contact point:When the UA Tire is used for the force calculation the slip quantities during positive Vsx (driving) are defined as:The rolling speed Vr is determined using the effective rolling radius Re:Note that for realistic tire forces the slip angle is limited to 45 degrees and thelongitudinal slip Ss (= ) in between -1 (locked wheel) and 1.Lagged longitudinal and lateral slip quantities (transient tire behavior)In general, the tire rotational speed and lateral slip will change continuously because of the changing interaction forces in between the tire and the road. Often the tire dynamic response will have an important role on the overall vehicle response. For modeling this so-called transient tire behavior, a first-order system is used both forthe longitudinal slip as the side slip angle, . Considering the tire belt as a stretched string, which is supported to the rim with lateral spring, the lateral deflection of the belt can be estimated (see also reference [1]). The figure below shows a top-view of the string model.Stretched String Model for Transient Tire BehaviorWhen rolling, the first point having contact with the road adheres to the road (no sliding assumed). Therefore, a lateral deflection of the string will arise that depends on the slip angle size and the history of the lateral deflection of previous points having contact with the road.For calculating the lateral deflection v1 of the string in the first point of contact with the road, the following differential equation is valid during braking slip:with the relaxation length in the lateral direction. The turnslip can be neglected at radii larger than 10 m. This differential equation cannot be used at zero speed, but when multiplying with Vx, the equation can be transformed to:When the tire is rolling, the lateral deflection depends on the lateral slip speed; at standstill, the deflection depends on the relaxation length, which is a measure for the lateral stiffness of the tire. Therefore, with this approach, the tire is responding to a slip speed when rolling and behaving like a spring at standstill. When the UA Tire is used for the force calculations, at positive Vsx (traction) the Vx should be replaced by Vr in these differential equations.A similar approach yields the following for the deflection of the string in longitudinal direction:Now the practical slip quantities, ’ and ’, are defined based on the tire deformation:These practical slip quantities and are used instead of the usual and definitions for steady-state tire behavior. kVlow_x and kVlow_y are the damping rates at low speed applied below the LOW_SPEED_THRESHOLD speed. For the LOW_SPEED_DAMPING parameter in the tire property file yields:kVlow_x= 100 · kVlow_y= LOW_SPEED_DAMPINGNote: If the tire property file's REL_LEN_LON or REL_LEN_LAT = 0, then steady-state tire behavior is calculated as tire response on change of the slip and .Tire Model ParametersSymbol: Name in tire propertyfile: Units*: Description:r1 UNLOADED_RADIUS L Tire unloaded radiuskz VERTICAL_STIFFNESS F/L Vertical stiffnesscz VERTICAL_DAMPING FT/L Vertical dampingCr ROLLING_RESISTANCE L Rolling resistance parameter Cs CSLIP F Longitudinal slip stiffness,C CALPHA F/A Cornering stiffness,C CGAMMA F/ACamber stiffness,UMIN UMIN - Minimum friction coefficient(Sg=1)UMAX UMAX - Maximum friction coefficient(Ssg=0)x REL_LEN_LON L Relaxation length inlongitudinal directiony REL_LEN_LAT L Relaxation length in lateraldirection* L=length, F=force, A=angle, T=timeForce Evaluation in UA-Tire•Normal Force•Slip Ratios•Friction CoefficientNormal ForceThe normal force F z is calculated assuming a linear spring (stiffness: k z ) and damper (damping constant c z ), so the next equation holds:If the tire loses contact with the road, the tire deflection and deflection velocity become zero so the resulting normal force F z will also be zero. For very small positive tire deflections the value of the damping constant is reduced and care is taken to ensure that the normal force Fz will not become negative.In stead of the linear vertical tire stiffness cz , also an arbitrary tire deflection - load curve can be defined in the tire property file in the section[DEFLECTION_LOAD_CURVE], see also the Property File Format Example. If a section called [DEFLECTION_LOAD_CURVE] exists, the load deflection datapoints with a cubic spline for inter- and extrapolation are used for the calculation of the vertical force of the tire. Note that you must specify VERTICAL_STIFFNESS in the tire property file but it does not play any role.Slip RatiosFor the calculation of the slip forces and moments a number of slip ratios will be introduced:Longitudinal Slip Ratio: SsThe absolute value of longitudinal slip ratio, Ss, is defined as:Where k is limited to be within the range -1 to 1.Lateral Slip Ratios: Sa , Sg , SagThe lateral slip ratio due to slip angle, S, is defined as:The lateral slip ratio due to inclination angle, S, is defined as:A combined lateral slip ratio due to slip and inclination angles, S, is defined as:where is the length of the contact patch.Comprehensive Slip Ratio: SsagA comprehensive slip ratio due to longitudinal slip, slip angle, and inclination angle may be defined as:Friction CoefficientThe resultant friction coefficient between the tire tread base and the terrain surfaceis determined as a function of the resultant slip ratio (Ss) and friction parameters (UMAX and UMIN ). The friction parameters are experimentally obtained data representing the kinematic property between the surfaces of tire tread and the terrain.A linear relationship between Ss and , the corresponding road-tire friction coefficient, is assumed. The figure below depicts this relationship.Linear Tire-Terrain Friction ModelThis can be analytically described as:m = UMAX - (UMAX - UMIN) * SsagThe friction circle concept allows for different values of longitudinal and lateralfriction coefficients (x and y) but limits the maximum value for both coefficientsto . See the figure below.Friction Circle ConceptThe relationship that defines the friction circle follows:or andwhere:Slip Forces and MomentsTo compute longitudinal force, lateral force, and self-aligning torque in the SAE coordinate system, you must perform a test to determine the precise operating conditions. The conditions of interest are:•Case 1: 0•Case 2: 0 and C S C S•Case 3: 0 and C S C S•Forces and moments at the contact pointThe lateral force Fh can be decomposed into two components: Fha and Fhg. The twocomponents are in the same direction if a· g < 0 and in opposite direction if 0. Case 1. ag < 0Before computing the longitudinal force, the lateral force, and the self-aligning torque, some slip parameters and a modified lateral friction coefficient should bedetermined. If a slip ratio due to the critical inclination angle is denoted by S c, then it can be evaluated as:If Ssc represents a slip ratio due to the critical (longitudinal) slip ratio, then it can be evaluated as:If a slip ratio due to the critical slip angle is denoted by S c, then it can be determined as:when Ss Ssc.The term critical stands for the maximum value which allows an elastic deformation of a tire during pure slip due to pure slip ratio, slip angle, or inclination angle. Whenever any slip ratio becomes greater than its corresponding critical value, an elastic deformation no longer exists, but instead complete sliding state representsthe contact condition between the tire tread base and the terrain surface.A nondimensional slip ratio Sn is determined as:where:A nondimensional contact patch length is determined as:A modified lateral friction coefficient is evaluated as:where is the available friction as determined by the friction circle.To determine the longitudinal force, the lateral force, and the self-aligning torque, consider two subcases separately. The first case is for the elastic deformation state, while the other is for the complete sliding state without any elastic deformation of a tire. These two subcases are distinguished by slip ratios caused by the critical values of the slip ratio, the slip angle, and the inclination angle. Specifically, if all of slip ratios are smaller than those of their corresponding critical values, then there exists an elastic deformation state, otherwise there exists only completesliding state between the tire tread base and the terrain surface.(i) Elastic Deformation State: S S c, Ss Ssc, and S S cIn the elastic deformation state, the longitudinal force F, the lateral force F, and three components of the self-aligning torque are written as functions of the elastic stiffness and the slip ratio as well as the normal force and the friction coefficients, such as:where:•is the offset between the wheel plane center and the tire treadbase.•is set to zero if it is negative.•the length of the contact patch.Mz is the portion of the self-aligning torque generated by the slip angle . Mzsand Mzs are other components of the self-aligning torque produced by thelongitudinal force, which has an offset between the wheel center plane and the tire tread base, due to the slip angle and the inclination angle , respectively. The self-aligning torque Mz is determined as combinations of Mz, Mzs and Mzs.(ii) Complete Sliding State: S S c, Ss Ssc, and S S cIn the complete sliding state, the longitudinal force, the lateral force, and three components of the self-aligning torque are determined as functions of the normal force and the friction coefficients without any elastic stiffness and slip ratio as:Case 2:0 and C S C SAs in Case 1, a slip ratio due to the critical value of the slip ratio can be obtained as:A slip ratio due to the critical value of the slip angle can be found as:when Ss Ssc.The nondimensional slip ratio Sn, is determined as:where:The nondimensional contact patch length ln is found from the equation ln = 1 - Sn, and the modified lateral friction coefficient is expressed as:For the longitudinal force, the lateral force and the self-aligning torque two subcases should also be considered separately. A slip ratio due to the critical value of the inclination angle is not needed here since the required condition for Case 2,C S C S, replaces the critical condition of the inclination angle.(i) Elastic Deformation State: Ss Ssc and S SacIn the elastic deformation state:(ii) Complete Sliding State: Ss Ssc and S SacCase 3:0 and C S C SSimilar to Cases 1 and 2, slip ratios due to the critical values of the inclination angle and the slip ratio are obtained as:The nondimensional slip ratio Sn, is expressed as:where:For the longitudinal force, the lateral force, and the self-aligning torque, two subcases should also be considered similar to Cases 1 and 2. A slip ratio due to the critical value of the slip angle is not needed here since the required condition forCase 3, C S C S, replaces the critical condition of the slip angle. (i) Elastic Deformation State: S S c and Ss SscIn the elastic deformation state, F and Mz can be written:(ii) Complete Sliding State: S S c and Ss SscIn the complete sliding state, F, F, Mz, Mzs, and Mzs can be determined by using:respectively. The longitudinal force F , the lateral force F, and three componentsof the self-aligning torques, Mz , Mzs , and Mzs , always have positive values, but they can be transformed to have positive or negative values depending on the slip ratio s, the slip angle , and the inclination angle in the SAE coordinate system. Tire Forces and Moments in the SAE Coordinate SystemFor the general formulations of the longitudinal force Fx, lateral force Fy, and self-aligning torque Mz, in the SAE coordinate system, the three possible combinations of the slip ratio, the slip angle, and the inclination angle are also considered. Longitudinal Force:Fx = sin(k) F , for all cases Lateral Force: F y = -sin() F, for cases 1 and 2F y = sin() F , for case 3 Self-aligning Torque:M z = sin() M z - sin() [-sin() M zs + sin()M zs ]Rolling Resistance Moment:My = -Cr Fz, for a forward rolling tire. My = Cr Fz , for a backward rolling tire.Operating Mode: USE_MODEYou can change the behavior of the tire model through the switch USE_MODE in the [MODEL] section of the tire property file.•USE_MODE = 0: Steady-state forces and moments • The tire forces and moments react instantaneously to changes in the tire kinematic states. •USE_MODE = 1: Transient tire behavior • The tire will have a lagged response because of the so-called relaxation length in both longitudinal and lateral direction. See Lagged Longitudinal and Lateral Slip Quantities (transient tire behavior).•The effect of the relaxation lengths will be most pronounced at low forward velocityand/or high excitation frequencies. •USE_MODE = 2: Smoothing of forces and moments on startup of the simulation •When you indicate smoothing by setting the value of use mode in the tire property file, Adams/Tire smooths initial transients in the tire force over the first 0.1seconds of simulation. The longitudinal force, lateral force, and aligning torque are multiplied by a cubic step function of time. (See STEP in the Adams/Solver online help.) Longitudinal Force FLon = S*FLon Lateral Force FLat = S*FLat Aligning Torque Mz = S*MzTire Carcass ShapeYou can optionally supply a tire carcass cross-sectional shape in the tire property file in the [SHAPE] block. The 3D-durability, tire-to-road contact algorithm uses this information when calculating the tire-to-road volume of interference. If you omit the [SHAPE] block from a tire property file, the tire carcass cross-section defaults to the rectangle that the tire radius and width define.You specify the tire carcass shape by entering points in fractions of the tire radius and width. Because Adams/Tire assumes that the tire cross-section is symmetrical about the wheel plane, you only specify points for half the width of the tire. The following apply:•For width, a value of zero (0) lies in the wheel center plane. •For width, a value of one (1) lies in the plane of the side wall. •For radius, a value of one (1) lies on the tread. For example, suppose your tire has a radius of 300 mm and a width of 185 mm and that the tread is joined to the side wall with a fillet of 12.5 mm radius. The tread then begins to curve to meet the side wall at >+/- 80 mm from the wheel center plane. If you define the shape table using six points with four points along the fillet, the resulting table might look like the shape block that is at the end of the property format example (see SHAPE ).Property File Format Example$--------------------------------------------------------MDI_HEADER [MDI_HEADER]FILE_TYPE = 'tir' FILE_VERSION = 2.0 FILE_FORMAT = 'ASCII'(COMMENTS) {comment_string} 'Tire - XXXXXX''Pressure - XXXXXX' 'TestDate - XXXXXX' 'Test tire''New File Format v2.1'$-------------------------------------------------------------units [UNITS] LENGTH= 'meter' FORCE= 'newton'ANGLE= 'rad'MASS= 'kg'TIME= 'sec'$-------------------------------------------------------------model [MODEL]! use mode123! ------------------------------------------! relaxation lengthsX! smoothingX !PROPERTY_FILE_FORMAT= 'UATIRE'USE_MODE= 2$---------------------------------------------------------dimension [DIMENSION]UNLOADED_RADIUS= 0.295WIDTH= 0.195ASPECT_RATIO= 0.55$---------------------------------------------------------parameter [PARAMETER]VERTICAL_STIFFNESS= 190000VERTICAL_DAMPING= 50ROLLING_RESISTANCE= 0.003CSLIP= 80000CALPHA= 60000CGAMMA= 3000UMIN= 0.8UMAX= 1.1REL_LEN_LON= 0.6REL_LEN_LAT= 0.5$-------------------------------------------------------------shape[SHAPE]{radial width}1.0 0.01.0 0.21.0 0.41.0 0.61.0 0.80.9 1.0$---------------------------------------------------------------------load_curve $ For a non-linear tire vertical stiffness (optional)$ Maximum of 100 points[DEFLECTION_LOAD_CURVE]{penfz}0.0000.00.001212.00.002428.00.003648.00.0051100.00.0102300.00.0205000.00.0308100.0。
ADAMS魔术公式的轮胎模型
使用魔术公式的轮胎模型使用魔术公式的轮胎模型主要有Pacejka ’89、Pacejka ’94、MF-Tyre 、MF-Swift 四种。
Pacejka ’89和’94轮胎模型Pacejka ’89 和’94轮胎模型是以魔术公式主要提出者H. B. Pacejka 教授命名的，根据其发布的年限命名。
目前有两种直接被ADAMS 引用。
魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式就可以完整地表达轮胎的纵向力F x 、侧向力F y 、回正力矩M z 、翻转力矩M x 、阻力矩M y 以及纵向力、侧向力的联合作用工况，故称为“魔术公式”。
魔术公式的一般表达式为：()()(){}[]Bx Bx E Bx C D x Y arctan arctan sin --=式中Y(x)可以是侧向力，也可以是回正力矩或者纵向力，自变量x 可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B 、C 、D 依次由轮胎的垂直载荷和外倾角来确定。
Pacejka ’89轮胎模型认为轮胎在垂直、侧向方向上是线性的、阻尼为常量，这在侧向加速度常见范围≤0.4g ，侧偏角≤5°的情景下对常规轮胎具有很高的拟合精度。
此外，由于魔术公式基于试验数据，除在试验范围的高精度外，甚至在极限值以外一定程度仍可使用，可以对有限工况进行外推且具有较好的置信度。
魔术公式正在成为工业标准，即轮胎制造商向整车厂提供魔术公式系数表示的轮胎数据，而不再是表格或图形。
基于魔术公式的轮胎模型还有较好的健壮性，如果没有某一轮胎的试验数据，而使用同类轮胎数据替代仍可取得很好的效果。
图 基于魔术公式的轮胎模型的输入和输出变量Pacejka ’89轮胎力与力矩的计算 轮胎纵向力计算公式为：()()()()()V X S BX BX E BX C D F +--=111arctan arctan sin其中X 1为纵向力组合自变量：X 1=(κ+S h )，κ为纵向滑移率（负值出现在制动态，-100表示车轮抱死）C ——曲线形状因子，纵向力计算时取B 0值：C = B 0D ——巅因子，表示曲线的最大值：Z Z F B F B D 221+= BCD ——纵向力零点处的纵向刚度：()ZF B Z Z eF B F B BCD 5423-⨯+=B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：109B F B S Z h += S v ——曲线的垂直方向漂移：S v =0E ——曲线曲率因子，表示曲线最大值附近的形状：8726BF B F B E Z Z ++=图 轮胎属性文件中的纵向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎侧向力计算公式为：()()()()()V Y S BX BX E BX C D F +--=111arctan arctan sin此时的X 1为侧向力计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，侧向力计算时取A 0值：C = A 0 D ——巅因子，表示曲线的最大值：Z Z F A F A D 221+=BCD ——侧向力零点处的侧向刚度：()γ5431arctan 2sin A A F A BCD Z -⨯⎪⎪⎭⎫⎝⎛= B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：γ8109A A F A S Z h ++=曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数曲线曲率因子计算系数S v ——曲线的垂直方向漂移：131211A F A F A S Z Z V ++=γE ——曲线曲率因子，表示曲线最大值附近的形状：76AF A E Z +=图 轮胎属性文件中的侧向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎回正力矩计算公式为：()()()()()V Z S BX BX E BX C D M +--=111arctan arctan sin此时的X 1为回正力矩计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，回正力矩计算时取C 0值：C = C 0 D ——巅因子，表示曲线的最大值：Z Z F C F C D 221+=BCD ——回正力矩零点处的扭转刚度：()()ZF C Z Z e C F C F C BCD 564231-⨯-⨯+=γB – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：131211C F C C S Z h ++=γ曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数 曲线曲率因子计算系数 曲线垂直漂移计算系数S v ——曲线的垂直方向漂移：()171615214C F C F C F C S Z Z Z V +++=γE ——曲线曲率因子，表示曲线最大值附近的形状：()()γ1098271C C F C F C E Z Z -⨯++=图 轮胎属性文件中的回正力矩计算系数数据块图 Pacejka ’89轮胎回正力矩示例侧偏刚度（Lateral Stiffness ）侧偏刚度在Pacejka ’89和’94轮胎模型中假定是一个常量，在轮胎属性文件的参数PARAMETER 数据段中通过LATERAL_STIFFNESS 语句设定。
Magic_Formula轮胎模型
Fx
x
Fx0 , Fy
y
Fy 0
2 x
2 y
,
x
1
,
y
tan 1
MF模型简介
在Matlab/Simulink中建立的轮胎动力学模型：
工作计划
继续完成仿真工作，完善轮胎模型的参数辨 识； 学习整车模型的建立； 结合FPGA学习卡尔曼算法和非线性观测器。
谢谢！
MF模型简介
Magic Formula 模型：
用特殊正弦函数建立的轮胎纵向力、侧向力和自回正力矩模型。
用一个通过拟合实验数据而得到的三角函数公式来与轮胎实验数 据相吻合, 完全能够表达不同驱动情况时的轮胎特性。
只用一套公式就完整地表达了纯工况下轮胎的力学特性,故称为 魔术公式。
可对轮胎模型的特性进行良好描述,不但可以用函数表述轮胎的 转向力、回复力矩和驱动/制动力,也可以直接利用轮胎实验数据。
MF模型简介
MF公式：
Y=y+Sv y=Dsin{Carctan[Bx-E(Bx-arctanBx)]} x=X+Sh
式中, Y表示侧向力或纵向力,X表示侧偏角α或滑移率k。 B为刚度因子,C为形状因子,D为峰值因子,E为曲率因子Sv为垂 直偏移,Sh为水平偏移。除C外,该公式中的参数都是垂直载荷Fz
和侧偏角α的函数。 若计算回正力矩 Mz=-t*Fy+Mzr t(αt)=Dtcos[Ctarctan{Btαt-Et(Btαt-arctan(Btαt))}]cos(α) αt = α + Sht Mz表示回正力矩，t为气胎拖矩，Mzr为残余回正力矩。
MF模型简介
输入量：侧偏角α 纵向滑移率κ 侧倾角γ 垂直载荷Fz
1.纯制动/驱动条件 2.纯转向条件 3.联合工况（制动/驱动转向）
ADAMS仿真轮胎选择(转自simwe论坛)
一）.用于操稳分析的轮胎模型魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式完整地表达轮胎的纵向力、侧向力、回正力矩、翻转力矩、阻力矩以及纵向力、侧向力的联合作用工况，主要包括以下的前四种模型。
1）魔术公式轮胎模型（MF—Tyre）根据仿真工况的不同可在稳态和非稳态之间切换模型，考虑了轮胎高速旋转时陀螺耦合、侧偏和纵滑的相互影响，外倾对侧偏和纵滑的影响。
适用范围：有效频率到8Hz，是点接触模型，只能用于平路面（路面起伏的波长必须大于轮胎的周长）。
2）Pacejka89、Pacejka94 由提出者Pacejka教授根据其发布年命名的，是稳态侧偏模型，不能用于非稳态工况。
适用范围：有效频率到0.5Hz，当与2D路面作用时是点接触；当与3D路面作用时，等效贯穿体积的方法来计算垂直力，等效法假设轮胎胎体是圆筒，必须在轮胎文件的[形状]模块输入了轮胎胎体横剖面。
3）PAC2002模型Pacejka的后期发展, PAC2002和MF—Tyre具有相同的功能，但改善了模型的翻转力矩，已经取代了MF—Tyre。
适用范围：有效频率到8Hz，主要用于操稳的仿真分析。
4）PAC MC模型，是专门用于摩托车轮胎模型，有效频率到8Hz，适合于大外倾角的工况。
5）Fiala模型是弹性基础上的梁模型，不考虑外倾和松弛长度。
当不把内倾角作为主要因数且把纵向滑移和横向滑移分开对待的情况下，对于简单的操纵性分析可得到合理的结果。
适用范围：有效频率到0.5Hz，可以用于二维和三维路面，当与2D路面作用时是点接触；当与3D路面作用时，等效贯穿体积的方法来计算垂直力。
6）UA模型考虑了非稳态效果，通过摩擦圆考虑了侧偏和纵滑的相互影响，也考虑了外倾和松弛长度，在只需要有限几个参数的情况下，有非常好的精度。
适用范围：有效频率到8Hz，是点接触模型，只能用于平路面（路面起伏的波长必须大于轮胎的周长）。
7）5.2.1轮胎模型是ADAMS早期发布的轮胎模型，现已很少使用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
使用魔术公式的轮胎模型使用魔术公式的轮胎模型主要有Pacejka ’89、Pacejka ’94、MF-Tyre 、MF-Swift 四种。
Pacejka ’89和’94轮胎模型Pacejka ’89 和’94轮胎模型是以魔术公式主要提出者H. B. Pacejka 教授命名的，根据其发布的年限命名。
目前有两种直接被ADAMS 引用。
魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式就可以完整地表达轮胎的纵向力F x 、侧向力F y 、回正力矩M z 、翻转力矩M x 、阻力矩M y 以及纵向力、侧向力的联合作用工况，故称为“魔术公式”。
魔术公式的一般表达式为：()()(){}[]Bx Bx E Bx C D x Y arctan arctan sin --=式中Y(x)可以是侧向力，也可以是回正力矩或者纵向力，自变量x 可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B 、C 、D 依次由轮胎的垂直载荷和外倾角来确定。
Pacejka ’89轮胎模型认为轮胎在垂直、侧向方向上是线性的、阻尼为常量，这在侧向加速度常见范围≤0.4g ，侧偏角≤5°的情景下对常规轮胎具有很高的拟合精度。
此外，由于魔术公式基于试验数据，除在试验范围的高精度外，甚至在极限值以外一定程度仍可使用，可以对有限工况进行外推且具有较好的置信度。
魔术公式正在成为工业标准，即轮胎制造商向整车厂提供魔术公式系数表示的轮胎数据，而不再是表格或图形。
基于魔术公式的轮胎模型还有较好的健壮性，如果没有某一轮胎的试验数据，而使用同类轮胎数据替代仍可取得很好的效果。
图 基于魔术公式的轮胎模型的输入和输出变量Pacejka ’89轮胎力与力矩的计算 轮胎纵向力计算公式为：()()()()()V X S BX BX E BX C D F +--=111arctan arctan sin其中X 1为纵向力组合自变量：X 1=(κ+S h )，κ为纵向滑移率（负值出现在制动态，-100表示车轮抱死）C ——曲线形状因子，纵向力计算时取B 0值：C = B 0D ——巅因子，表示曲线的最大值：Z Z F B F B D 221+= BCD ——纵向力零点处的纵向刚度：()ZF B Z Z eF B F B BCD 5423-⨯+=B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：109B F B S Z h += S v ——曲线的垂直方向漂移：S v =0E ——曲线曲率因子，表示曲线最大值附近的形状：8726BF B F B E Z Z ++=图 轮胎属性文件中的纵向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎侧向力计算公式为：()()()()()V Y S BX BX E BX C D F +--=111arctan arctan sin此时的X 1为侧向力计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，侧向力计算时取A 0值：C = A 0 D ——巅因子，表示曲线的最大值：Z Z F A F A D 221+=BCD ——侧向力零点处的侧向刚度：()γ5431arctan 2sin A A F A BCD Z -⨯⎪⎪⎭⎫⎝⎛= B – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：γ8109A A F A S Z h ++=曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数曲线曲率因子计算系数S v ——曲线的垂直方向漂移：131211A F A F A S Z Z V ++=γE ——曲线曲率因子，表示曲线最大值附近的形状：76AF A E Z +=图 轮胎属性文件中的侧向力计算系数数据块图 Pacejka ’89轮胎纵向力示例轮胎回正力矩计算公式为：()()()()()V Z S BX BX E BX C D M +--=111arctan arctan sin此时的X 1为回正力矩计算组合自变量：X 1=(α+S h )，α为侧偏角 C ——曲线形状因子，回正力矩计算时取C 0值：C = C 0 D ——巅因子，表示曲线的最大值：Z Z F C F C D 221+=BCD ——回正力矩零点处的扭转刚度：()()ZF C Z Z e C F C F C BCD 564231-⨯-⨯+=γB – 刚度因子：B=BCD/(C ×D)S h ——曲线的水平方向漂移：131211C F C C S Z h ++=γ曲线形状因子巅因子计算系数 BCD 计算系数 曲线水平漂移计算系数 曲线曲率因子计算系数 曲线垂直漂移计算系数S v ——曲线的垂直方向漂移：()171615214C F C F C F C S Z Z Z V +++=γE ——曲线曲率因子，表示曲线最大值附近的形状：()()γ1098271C C F C F C E Z Z -⨯++=图 轮胎属性文件中的回正力矩计算系数数据块图 Pacejka ’89轮胎回正力矩示例侧偏刚度（Lateral Stiffness ）侧偏刚度在Pacejka ’89和’94轮胎模型中假定是一个常量，在轮胎属性文件的参数PARAMETER 数据段中通过LATERAL_STIFFNESS 语句设定。
侧向形变D e ：D e ＝F y /LATERAL_STIFFNESS ； 翻转力矩：M x ＝ -F z ×D e ；纵向力和侧偏角联合作用的回正力矩M z ；M Z = M Z,MF + Fx ×D e ，这里M Z,MF 为魔术公式计算所得的回正力矩。
滚动阻力（Rolling resistance ）滚动阻力系数R R 同样是在轮胎属性文件中规定的具体值，滚动阻力矩M y ： M y = F z ×R e ×R R曲线形状因子巅因子计算系数BCD 计算系数曲线水平漂移计算系数曲线曲率因子计算系数曲线垂直漂移计算系数这里：R e为轮胎的滚动半径；R R为滚动阻力系数；F z垂直载荷（kN）。
平滑过渡（Smoothing）是否使用平滑过渡也在轮胎属性文件中规定：✧USE_MODE = 1 或2：关闭平滑过渡✧USE_MODE = 3 或4：使用平滑过渡轮胎属性文件TR_rear_pac89.tir全文（示例整车模型MDI_Demo_Vehicle.asy使用的）：$---------------------------------------------------------------------MDI_HEADER[MDI_HEADER]FILE_TYPE = 'tir'FILE_VERSION = 2.0FILE_FORMAT = 'ASCII'(COMMENTS){comment_string}'Tire - XXXXXX''Pressure - XXXXXX''Test Date - XXXXXX''Test tire''New File Format v2.1'$--------------------------------------------------------------------------UNITS[UNITS]LENGTH = 'mm'FORCE = 'newton'ANGLE = 'radians'MASS = 'kg'TIME = 'sec'$--------------------------------------------------------------------------MODEL[MODEL]! use mode 1 2 3 4! -------------------------------------------! smoothing X X! combined X X!PROPERTY_FILE_FORMAT = 'PAC89' 轮胎模型关键词FUNCTION_NAME = 'TYR900' 解算器函数USE_MODE = 4.0 平滑过渡模式$----------------------------------------------------------------------DIMENSION [DIMENSION]UNLOADED_RADIUS = 340.6 轮胎自由半径WIDTH = 255.0 轮胎宽度ASPECT_RATIO = 0.35 高宽比$----------------------------------------------------------------------PARAMETER [PARAMETER]VERTICAL_STIFFNESS = 310.0 纵向刚度系数VERTICAL_DAMPING = 3.1 纵向阻尼系数LATERAL_STIFFNESS = 190.0 侧偏刚度ROLLING_RESISTANCE = 0.0 滚动阻力系数$-----------------------------------------------------------LATERAL_COEFFICIENTS [LATERAL_COEFFICIENTS]a0 = 1.65000a1 = -34.0a2 = 1250.00a3 = 3036.00a4 = 12.80a5 = 0.00501a6 = -0.02103a7 = 0.77394a8 = 0.0022890a9 = 0.013442a10 = 0.003709a11 = 19.1656a12 = 1.21356a13 = 6.26206$-------------------------------------------------------------------longitudinal [LONGITUDINAL_COEFFICIENTS]b0 = 2.37272b1 = -9.46000b2 = 1490.00b3 = 130.000b4 = 276.000b5 = 0.08860b6 = 0.00402b7 = -0.06150b8 = 1.20000b9 = 0.02990b10 = -0.17600$----------------------------------------------------------------------aligning [ALIGNING_COEFFICIENTS]c0 = 2.34000c1 = 1.4950c2 = 6.416654c3 = -3.57403c4 = -0.087737c5 = 0.098410c6 = 0.0027699c7 = -0.0001151c8 = 0.1000c9 = -1.33329c10 = 0.025501c11 = -0.02357c12 = 0.03027c13 = -0.0647c14 = 0.0211329c15 = 0.89469c16 = -0.099443c17 = -3.336941注意：属性文件中的单位数据块[UNITS]不用于魔术公式的系数a,b,c。