夫琅禾费双缝衍射的原理
第3章光的衍射2(光栅夫琅禾费)_168209982

a0 -- 单缝衍射 = 0
处的振幅
9
图示光栅衍射的物理机制
1
再进行 一次多 光束干 涉
2
f
f
π sin sin N d sin A a0 sin
10
sin N A A0 sin
光栅衍射的光强: 1)单缝衍射和多光束干涉的结果共同决定。 2)干涉主极大处受到衍射极小的影响,导 致所谓的“缺级”现象。
12
四. 光栅夫琅禾费衍射光强分布特点 (1)各干涉主极大受到单缝衍射的调制。
I0 I单 单缝衍射光强曲线 -2 -1 多光束干涉因子 N2 0
例 N 4 , d 4a
2
sin
sin N sin
单缝衍射因子
2
多光束干涉因子
11
光强分布与缺级现象
sin I I0
2
sin N sin
2
π
a sin
π d sin
内的干涉主极大个数减少, 若出现缺级的话,
则缺级的级次变低。
15
▲
若 d 不变 各干涉主极大位置不变;
单缝中央亮 a 减小 单缝衍射的轮廓线变宽, 纹内的干涉主极大个数增加,缺级的级次变高。 当 a 时,单缝衍射的轮廓线变 极端情形: 为很平坦,第一暗纹在距中心 处, 此时各 干涉主极大光强几乎相同。
§3.3 多缝的夫琅禾费衍射
一. 光栅(grating) 光栅是现代科技中常用的重要光学元件。 光通过光栅衍射可以产生明亮尖锐的亮纹, 复色光入射可产生光谱,用以进行光谱分析。
光的衍射原理与夫琅禾费衍射

光的衍射原理与夫琅禾费衍射夫琅禾费衍射是一种重要的光学现象,它是基于光的衍射原理而发展起来的。
光的衍射原理是指当光通过一个孔径或者绕过一条障碍物时,会发生弯曲现象从而形成衍射图样。
光的衍射原理是基于赫兹的波动理论建立的。
赫兹认为,光是一种波动,它的传播与声波等物质波有相似之处。
当光波传播到一个开口或者经过一个细缝时,由于波长与孔径的比值非常接近,光波会在孔径或细缝周围发生弯曲和干涉现象,进而产生衍射。
由于夫琅禾费衍射是基于光的波动性质而产生的,因此它也具有波动的特点。
夫琅禾费衍射是通过一个或多个光源,使光经过一个有规则的孔径或者障碍物后,形成衍射图样的现象。
这个孔径或者障碍物可以是光透过的物体,也可以是光透过的光栅。
夫琅禾费衍射现象的发生与孔径或细缝的大小有关。
当孔径或细缝的大小与光波的波长相当时,衍射图样会显示出明暗交替的条纹。
夫琅禾费衍射的特点是衍射波束比原来波束更加扩大,这是由于波像不单纯是简单的传播而已,波超出了衍射孔的范围。
夫琅禾费衍射的应用非常广泛,尤其在光学仪器和光学测量中得到了广泛的应用。
例如在显微镜中,通过夫琅禾费衍射观察样品的细微结构,可以获得更加清晰和详细的图像。
在衍射光栅中,夫琅禾费衍射图样的特点被用于测量光波的波长和频率。
此外,夫琅禾费衍射还被应用于激光器、干涉仪和光纤通信等领域。
除了夫琅禾费衍射,光的衍射还有其他形式的表现,如菲涅尔衍射和菲涅尔-半圆衍射。
这些衍射现象都是基于光的波动性质而产生的,它们加深了我们对光的认识和理解。
光的衍射现象不仅仅是一种物理现象,更是一种美妙的艺术。
通过对光的衍射原理的深入研究和理解,我们可以创造出各种各样的光影效果,从而使艺术作品更具表现力和魅力。
光的衍射不仅在艺术领域有所应用,还在建筑设计中得到了广泛的应用。
通过合理的设计和利用光的衍射原理,我们可以创造出独特的建筑形式和室内光环境。
总之,光的衍射原理与夫琅禾费衍射是光学领域中的核心概念。
大学物理实验丨利用单丝衍射测量细丝直径
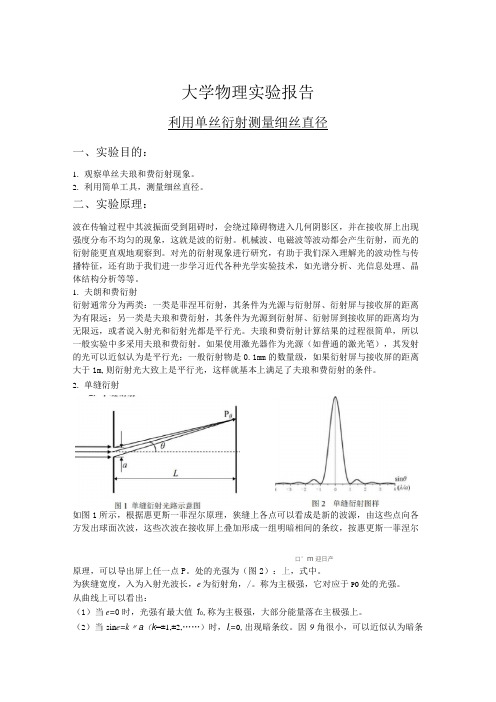
大学物理实验报告利用单丝衍射测量细丝直径一、实验目的:1.观察单丝夫琅和费衍射现象。
2.利用简单工具,测量细丝直径。
二、实验原理:波在传输过程中其波振面受到阻碍时,会绕过障碍物进入几何阴影区,并在接收屏上出现强度分布不均匀的现象,这就是波的衍射。
机械波、电磁波等波动都会产生衍射,而光的衍射能更直观地观察到。
对光的衍射现象进行研究,有助于我们深入理解光的波动性与传播特征,还有助于我们进一步学习近代各种光学实验技术,如光谱分析、光信息处理、晶体结构分析等等。
1.夫朗和费衍射衍射通常分为两类:一类是菲涅耳衍射,其条件为光源与衍射屏、衍射屏与接收屏的距离为有限远;另一类是夫琅和费衍射,其条件为光源到衍射屏、衍射屏到接收屏的距离均为无限远,或者说入射光和衍射光都是平行光。
夫琅和费衍射计算结果的过程很简单,所以一般实验中多采用夫琅和费衍射。
如果使用激光器作为光源(如普通的激光笔),其发射的光可以近似认为是平行光;一般衍射物是0.1mm的数量级,如果衍射屏与接收屏的距离大于1m,则衍射光大致上是平行光,这样就基本上满足了夫琅和费衍射的条件。
2.单缝衍射如图1所示,根据惠更斯一菲涅尔原理,狭缝上各点可以看成是新的波源,由这些点向各方发出球面次波,这些次波在接收屏上叠加形成一组明暗相间的条纹,按惠更斯一菲涅尔口°m迎日产原理,可以导出屏上任一点P。
处的光强为(图2):上,式中。
为狭缝宽度,入为入射光波长,e为衍射角,/。
称为主极强,它对应于P0处的光强。
从曲线上可以看出:(1)当e=0时,光强有最大值10,称为主极强,大部分能量落在主极强上。
(2)当sin e=k〃a(k=±1,±2,……)时,I e=0,出现暗条纹。
因9角很小,可以近似认为暗条纹在e=k刀a的位置上。
还可看到主极强两侧暗纹之间的角距离是A e=2〃a,而其他相邻暗纹之间的角距离均相等(均为A e=川a)。
(3)两相邻暗纹之间都有一个次极强。
夫琅禾费衍射的实验报告

一、实验目的1. 理解夫琅禾费衍射的基本原理和现象。
2. 通过实验验证夫琅禾费衍射的光强分布规律。
3. 掌握单缝衍射和双缝衍射实验的基本操作和数据处理方法。
二、实验原理夫琅禾费衍射是波动光学中的一个重要现象,当光波通过狭缝或圆孔时,由于光的波动性,光波会绕过障碍物并在其后方产生衍射现象。
当衍射光到达一个远处的屏幕上时,会形成一系列明暗相间的衍射条纹,这种现象称为夫琅禾费衍射。
夫琅禾费衍射的原理基于惠更斯-菲涅耳原理,即光波在传播过程中,波前的每一点都可以看作是次级波源,这些次级波源发出的波在空间中传播并相互干涉,最终在屏幕上形成衍射图样。
三、实验仪器与材料1. 夫琅禾费衍射实验装置(包括单缝和双缝狭缝装置、光源、透镜、屏幕等)。
2. 单色光源(如氦氖激光器)。
3. 光具座。
4. 刻度尺。
5. 记录纸。
四、实验步骤1. 单缝衍射实验- 将单缝狭缝装置固定在光具座上,调整光源使其发出平行光。
- 将透镜置于狭缝装置后,使衍射光通过透镜聚焦到屏幕上。
- 移动屏幕,观察并记录屏幕上的衍射条纹。
- 使用刻度尺测量条纹间距,并计算条纹间距与狭缝间距之间的关系。
2. 双缝衍射实验- 将双缝狭缝装置固定在光具座上,调整光源使其发出平行光。
- 将透镜置于狭缝装置后,使衍射光通过透镜聚焦到屏幕上。
- 移动屏幕,观察并记录屏幕上的衍射条纹。
- 使用刻度尺测量条纹间距,并计算条纹间距与狭缝间距之间的关系。
五、实验数据与结果分析1. 单缝衍射实验- 根据实验数据,绘制单缝衍射的光强分布曲线。
- 分析光强分布曲线,验证夫琅禾费衍射的光强分布规律。
2. 双缝衍射实验- 根据实验数据,绘制双缝衍射的光强分布曲线。
- 分析光强分布曲线,验证夫琅禾费衍射的光强分布规律。
- 通过观察双缝衍射条纹的间距,验证杨氏双缝干涉公式。
六、实验总结1. 通过本次实验,我们成功地验证了夫琅禾费衍射的光强分布规律。
2. 实验结果表明,单缝衍射和双缝衍射的光强分布曲线与理论公式相符。
双缝干涉条纹变宽的原理

双缝干涉条纹变宽的原理
双缝干涉是一种经典的光学现象,它的条纹变宽可以通过以下几个方面来解释:
1. 光的波动性,根据光的波动性理论,当光通过双缝时,每个缝都成为次波源,这些次波源发出的波会相互干涉。
由于波峰和波谷的叠加,会产生明暗条纹。
当条纹变宽时,说明波峰和波谷之间的距离增大,这可能是由于光波在传播过程中发生了衍射,导致光束的扩散,从而使得干涉条纹变宽。
2. 波长和缝宽的关系,根据夫琅禾费衍射原理,干涉条纹的宽度与波长和缝宽之间的关系有关。
当波长增大或者缝宽减小时,干涉条纹会变宽。
这是因为波长增大会导致波的传播范围变大,从而使得条纹变宽;而缝宽减小会导致衍射效应更加显著,也会使得条纹变宽。
3. 光源的宽度,双缝干涉实验中所使用的光源如果具有一定的宽度,会导致干涉条纹变宽。
这是因为光源的宽度增大会导致从不同部分发出的光波相位不同,从而使得干涉条纹变宽。
总的来说,双缝干涉条纹变宽是由于光的波动性、波长和缝宽的关系以及光源的宽度等因素共同作用所导致的。
这些因素相互影响,共同决定了干涉条纹的宽度。
夫琅禾费衍射实验报告

夫琅禾费衍射和菲涅尔衍射班级:物理1903 姓名:王高文 学号:41721176 同组人员:修为轩实验目的:测量单缝衍射的光强分布,验证光强分布理论;观察几类夫琅禾费衍射现象,加深对光的衍射现象和理论的理解。
实验原理:A 单缝衍射光强分布 202sin uI I u ,其中sin a u;a 为单缝宽度, 为光波波长,为衍射角。
当 =0时,u=0,此时光强为最大,这是中央零级亮条纹,称为主级强。
当sin ka时,u k ,这时 I =0,出现暗条纹。
实际上 很小,可以认为sin ,即暗条纹在ka的位置出现。
其他的亮条纹所在位置:sin 1.43, 2.46 3.47a a a,,,,次级强相对于主级强的强度分别为0.047,0.017,0.008...I I B 矩形孔衍射光强分布 22022sin sin I ,I,其中sin sin a b a b;,a 和b 为矩形孔边长, 为光波波长,a 和b 为衍射角。
C 圆孔衍射光强分布 2102J u I I u,式中, 1J u 为一阶贝塞尔函数;2sin a u;a 为圆孔半径, 为光波波长, 为衍射角。
根据贝塞尔函数的性质,当u=0时,即 =0时, 00I I I .这说明圆孔衍射的中心始终是一个亮点,并且强度取最大值,其他各级次强度极大值位置:'''123sin 0.819,sin 1.333,sin 1.84a a a,,,极小值位置123sin 0.610,sin 1.116,sin 1.619a a a,,,次级强相对主级强的相对强度分别为0.0175,0.0042,0.0016...I I D 双缝或双孔夫琅禾费衍射设狭缝宽度或圆孔半径为a,两狭缝或两圆孔的间距为d,双缝 220sin ()cos u I I u ,式中sin sin a b;, 为光波波长,为衍射角。
双孔 2120'2cos 'J I I,式中 1'J 为一阶贝塞尔函数;2sin 'a,sin b, 为光波波长, 为衍射角。
光的衍射问题

ba
1500(nm) 4500(nm)
(a b)sin
(2) k
2 10 理论上观察到最高
max
级次是第十级, 但最多只能观察到第九级。
(3) 由k a b k k 1,2, a k 4,8缺级 即第八级也缺级
实际呈现的条纹共15条:0, 1, 2, 3, 5, 6, 7, 9
※分辨率: 最小分辨角的倒数.
1
/
0
[ 1.22
D
] 1
•可见提高分辨率: ※增大孔径(天文、摄影) ※用紫光或紫外线作光源 ※电子显微镜(利用电子束的波动性成像)
X射线的衍射
# X 射线是波长很短的电磁波。
# 在电磁场中不发生偏转。 # X 射线的波长: 0.01 ~ 10nm
X射线管
阴极
阳极 (对阴极)
光的衍射问题的历史由来:
➢1818 年,巴 黎 科 学 院 举 行 了 一 次 以 解 释 衍 射 现 象 为 内 容 的 科 学 竞赛。 菲 涅 耳以惠更斯的波振面作图以及杨的 干涉原理相结合方式建立了一般的衍射理 论。
惠更斯-菲涅耳原理: 1)子波只能向前传播,且传播方向上任
一点的振幅与距离成反比; 2)传播方向上任一点的强度,决定于所
2
➢干涉与衍射的区别与联系
1、从根本上讲,都是波的相干叠加,没 有原则区别。
n
2、干涉:E Ei ,衍射:E dE
i 1
s
例:在单缝夫朗和费衍射实验中,屏上第3级暗纹 对应的单缝处波面可划分为——6 —个半波带?若 将缝宽缩小一半,原来第3级暗纹处将是明——纹。
例:波长为600nm的单色平行光,垂直入射到 缝宽为b=0.60mm的单缝上,缝后有一焦距 f=60cm的透镜。在透镜焦平面上观察衍射图 样.
夫琅禾费双缝衍射的原理

双缝衍射原理图1双缝衍射装置Fig.1. Double-slit diffraction equipment双缝衍射的实验装置如图1所示:一光栅有N 条缝,透光的缝宽度为a ,不透光的挡板宽度为b ,入射光波为λ。
双缝间距为d=a+b ,d 称为光栅常数。
如图,在θ方向,相邻两条缝之间的光程差为δ=dsin θ,相位差为λθπλδπϕsin 22d ==∆,假设每一个单缝引起的光波振幅为'A ∆,根据多个等幅同频振动的合振幅公式:()()2/sin 2/sin ϕϕ∆∆∆=n A A ,所有缝在θ方向产生的振幅为()()v Nv A N A A sin sin 2/sin 2/sin '''∆=∆∆∆=ϕϕ,其中λθπsin d v =。
汇聚点的光强为2'0)sin sin (vNv I I =,其中2''0A I ∆=。
当N=1,可知:'0I 是单缝引起的光强。
根据单缝衍射的公式20)sin (uu I I =,可得光栅衍射的光强公式20)sin (u u I I =2)sin sin (vNv ,其中u=λθπsin a 。
(1)当N=1时,光强公式变为单缝衍射的公式20)sin (uu I I =,因此2)sin (u u 称为单缝衍射因子。
(2)当N=2时,根据光栅衍射公式可得:v uu I I 220cos 4)sin (=[2]。
3双缝衍射的强度分布和谱线图仍利用MATLAB 软件,根据双缝衍射的算法,输入程序,得到的衍射强度分布和谱线图。
下面改变参数对双缝衍射进行讨论分析。
3.2.1改变缝宽a 观察双缝衍射图样变化图3光栅衍射的光强曲线和谱线(a ) 图4光栅衍射的光强曲线和谱线(b) Fig.3Grating diffraction intensity Fig.4Grating diffraction intensity curves and lines (a) curves and lines (b)图3和图4是双缝衍射的光强曲线和谱线,两图不同之处就是缝宽和波长的比值不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双缝衍射原理
图1双缝衍射装置
Fig.1. Double-slit diffraction equipment
双缝衍射的实验装置如图1所示:一光栅有N 条缝,透光的缝宽度为a ,不透光的挡板宽度为b ,入射光波为λ。
双缝间距为d=a+b ,d 称为光栅常数。
如图,在θ方向,相邻两条缝之间的
光程差为δ=dsin θ,相位差为λ
θπλδπϕsin 22d ==∆,假设每一个单缝引起的光波振幅为'A ∆,根据多个等幅同频振动的合振幅公式:()()2/sin 2/sin ϕϕ∆∆∆=n A A ,所有缝在θ方向产生的振幅为()()v Nv A N A A sin sin 2/sin 2/sin ''
'∆=∆∆∆=ϕϕ,其中λθπsin d v =。
汇聚点的光强为2'0)sin sin (v
Nv I I =,其中2''0A I ∆=。
当N=1,可知:'0I 是单缝引起的光强。
根据单缝衍射的公式20)sin (u
u I I =,可得光栅衍射的光强公式20)sin (u u I I =2)sin sin (v
Nv ,其中u=λθπsin a 。
(1)当N=1时,光强公式变为单缝衍射的公式20)sin (u
u I I =,因此2)sin (u u 称为单缝衍射因子。
(2)当N=2时,根据光栅衍射公式可得:v u
u I I 220cos 4)sin (
=[2]。
3双缝衍射的强度分布和谱线图
仍利用MATLAB 软件,根据双缝衍射的算法,输入程序,得到的衍射强度分布和谱线图。
下面改变参数对双缝衍射进行讨论分析。
3.2.1改变缝宽a 观察双缝衍射图样变化
图3光栅衍射的光强曲线和谱线(a ) 图4光栅衍射的光强曲线和谱线(b) Fig.3Grating diffraction intensity Fig.4Grating diffraction intensity curves and lines (a) curves and lines (b)
图3和图4是双缝衍射的光强曲线和谱线,两图不同之处就是缝宽和波长的比值不同。
由图3图4可知 ,当缝宽a 变小,变到与波长相等时,衍射图样逐渐接近双缝干涉图样,变成明暗相同的等亮度条纹。
可以这样解释:当a 逐渐变
小时,由双缝衍射公式v u u I I 220cos 4)sin (=可知,当u
u sin 1→(u=λθπsin a )时,)2sin 22(2cos 4cos 42020v d I v I I ===∆∆=→θλ
πδλπϕϕ。
双缝衍射光强分布就向双缝干涉2
cos 421ϕ∆=I I 过渡[7]。
在实验中,当两条缝宽比波长大得多时,我们发现衍射现象较明显,慢慢的调窄缝宽,当其小于光波长,但在一个数量级时,单缝衍射的调制作用消失,双缝衍射图样过渡到双缝干涉图样,可以说双缝干涉是双缝衍射在缝宽很小时的特例。
3.2.2减小双缝间距d 观察双缝衍射图样变化
图5光栅衍射的光强曲线和谱线(c) 图6光栅衍射的光强曲线和谱线(d) Fig.5Grating diffraction intensity Fig.6Grating diffraction intensity curves and lines (c) curves and lines (d)
以上上两图的缝宽一致,不同的是双缝间距,图5中双缝间距大于图6。
根据式v u
u I I 220cos 4)sin (=中的第二个因子可知 ,当缝宽a 不变 ,而减小双缝
间隔时,即d 减小时,20)sin (
u u I I →,)2sin 22(v d ===∆θλ
πδλπϕ。
从图5和图6观察可知中央最大包络线的宽度不变 ,最大包络线内的分裂条纹的间隙变大。
故在中央最大包络线内看到的亮细条纹数目减少,且变的很粗。
此时双缝衍射向单缝衍射过渡,双缝干涉因子2
cos 2ϕ∆逐渐趋向于1 ,作用消失。
双缝衍射光强分布变成了单缝衍射[8]。
[ 1] 石明吉, 张定群. 大学物理实验教学中存在的问题及
应对策略[J ] . 南阳师范学院学报, 2011, 10(9):97
-101.
[ 2] 王竞争, 刘显龙, 殷文金, 等. 基于 MATLAB 的光的干 涉和衍射现象的模拟研究[ J ] . 延边大学学报, 2009,
3(4):319 -322.。
